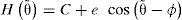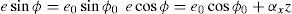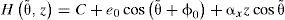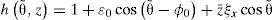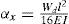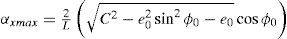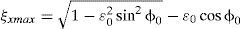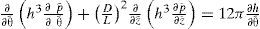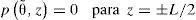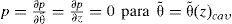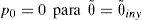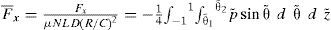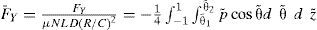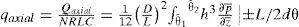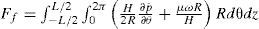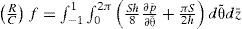Investigación numérica de las condiciones de lubricación en chumaceras hidrodinámicas con el efecto del desalineamiento del eje

Resumen

Las chumaceras hidrodinámicas radiales se usan ampliamente para soportar carga en máquinas rotatorias que giran a alta velocidad. Teóricamente, las chumaceras hidrodinámicas se diseñan para una vida infinita, pero la precisión en el maquinado, el calentamiento o el desalineamiento con el rotor pueden contribuir a problemas de funcionamiento y a un desgaste indeseado. Un problema que no se puede eliminar es el desalineamiento angular del eje provocado por el peso y la flexibilidad del rotor. El desalineamiento cambia el espesor de película del lubricante afectando las condiciones de lubricación hidrodinámica. En este trabajo se presenta una investigación numérica del comportamiento del campo de presión, el flujo axial, el espesor de película y la fricción viscosa, considerando el desalineamiento del eje por el efecto del peso y la flexibilidad del rotor. El campo de presión hidrodinámica se resuelve utilizando la ecuación de la lubricación de Reynolds junto con una expresión modificada del espesor de película que incluye el desalineamiento del eje. También se presenta una expresión para calcular el máximo desalineamiento permitido por una chumacera, en función del punto de equilibrio de estado estable. Los resultados muestran que a medida que el desalineamiento del eje se incrementa el espesor de película se reduce, causando el incremento de la presión máxima y del flujo axial del lubricante, así como pequeños cambios en la fricción viscosa. Con la finalidad de validar los resultados numéricos obtenidos en esta investigación, se compararon con resultados numéricos reportados en la literatura internacional, dando una buena aproximación.

Abstract

The radial hydrodynamic bearings are widely used to support loads in rotating machines that operate at high speed. Theoretically, hydrodynamic bearings are designed for infinite life, but the precision machining, heating or misalignment with the rotor can contribute to performance problems and undesired wear. A problem that cannot be eliminated is the shaft angular misalignment caused by the weight and flexibility of the rotor. Misalignment changes the lubricant film thickness affecting the conditions of hydrodynamic lubrication. In this paper, a numerical investigation of the behavior of the pressure field, axial flow, film thickness and viscous friction considering the misalignment of the shaft by the effect of the weight and flexibility of the rotor, is presented. The hydrodynamic pressure field is solved using the equation of Reynolds lubrication with a modified expression of film thickness including the shaft misalignment. An expression to calculate the maximum misalignment allowed by a bearing based on the equilibrium steady state is also presented. The results show that as the shaft misalignment increases, a reduction in the film thickness is present, causing an increase in both maximum pressure and axial flow of lubricant, and also small changes in viscous drag. In order to validate the numerical results obtained in this investigation they were compared with numerical results reported in international literature, giving a good approximation.

Introducción

Las chumaceras hidrodinámicas se usan principalmente en grandes máquinas rotatorias que giran a altas velocidades. Un buen diseño de la chumacera, suministro y viscosidad del fluido lubricante, permiten que durante la operación de la máquina se forme una cuña de lubricante, la cual separa al eje de la chumacera evitando el contacto entre metal y metal. La capacidad de carga que tienen las chumaceras se debe a la generación del campo de presión en la película de lubricante. Por medio de este campo de presión se puede evaluar si las dimensiones de la chumacera, el claro radial y el lubricante, mantendrán las condiciones adecuadas de lubricación hidrodinámica. Generalmente, la velocidad de giro y el peso del rotor son los datos iniciales a partir de los cuales se determinan la longitud, el diámetro, el claro radial, así como la viscosidad del lubricante. Los parámetros de diseño junto con las tablas y gráficas proporcionadas en la literatura (Raimondi y Boid, 1958) permiten conocer el valor de la presión máxima, el flujo axial, el espesor de película y la fricción viscosa, los cuales cambian con la velocidad de giro del rotor y son importantes para mantener las condiciones de lubricación hidrodinámica.

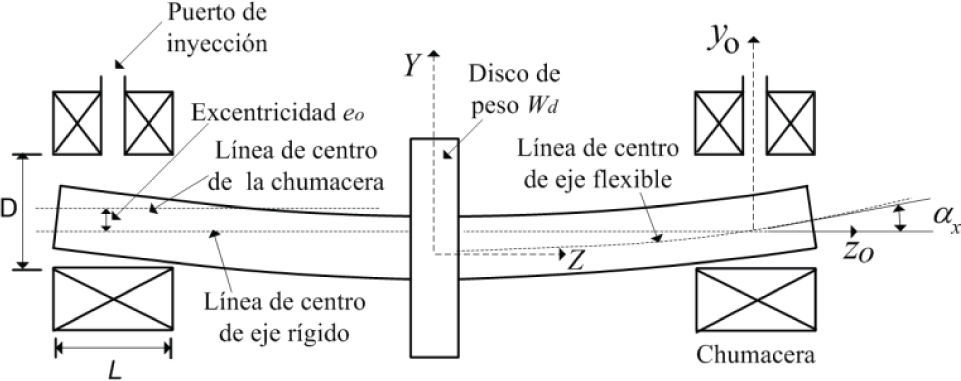
En las tablas y gráficas presentadas por Raimondi y Boid (1958) se considera que la distancia entre las líneas de centro del eje y de la chumacera es constante. Esta distancia se conoce como excentricidad e. En casos reales, las líneas de centro del eje y de la chumacera están sujetas a un cierto grado de desalineamiento angular. El desalineamiento puede ser causado por diversos factores, por ejemplo, inexactitudes por un mal montaje, mal maquinado, el peso del rotor, la flexibilidad del eje, etcétera, aún si el montaje y el maquinado fuesen muy precisos, siempre existirá un cierto grado de desalineamiento debido a la flexibilidad del eje y al peso del rotor. En la figura 1 se considera una configuración simétrica (rotor de Jeffcott) de un sistema rotor-chumaceras, la cual muestra una rotación α_x del eje en un sistema de referencia (y₀, z₀) ubicado en el centro de la chumacera. En este caso, el peso y la flexibilidad del eje provocan que las líneas de centro del eje y de la chumacera no coincidan, haciendo que el espesor de película sea función de la excentricidad del centro del muñón e₀ y del ángulo de rotación α_x (figura 2). Para analizar las condiciones de lubricación en chumaceras hidrodinámicas es necesario calcular el ángulo α_x en cada chumacera, lo cual puede realizarse por medio de la teoría de vigas.

Figura 1.

Rotor soportado por chumaceras hidrodinámicas

Figura 2.

Vista en 3D de una chumacera desalineada

En la literatura internacional se han reportado diversos trabajos teóricos y experimentales sobre el tema del desalineamiento en chumaceras hidrodinámicas. McKee y McKee (1932) realizaron uno de los primeros trabajos experimentales, mostrando que el campo de presión se desarrolla en forma anti-simétrica en la dirección axial. Dubois et al., (1955) estudiaron experimentalmente el cambio en la excentricidad, el flujo axial y las temperaturas locales en chumaceras desalineadas. Galleti y Capriz (1965) hicieron un estudio analítico sobre el par producido en chumaceras hidrodinámicas cortas con desalineamiento. Las investigaciones realizadas por Nicholas (1972) muestran que las chumaceras hidrodinámicas presentan poca resistencia contra el desalineamiento. Nicholas (1972) estableció que la intensidad del par producido por el desalineamiento induce poca influencia sobre la excentricidad y la rapidez del flujo axial, pero que la presión máxima se incrementa significativamente. Mokhtar et al., (1985) hacen una evaluación de las características térmicas en chumaceras desalineadas usando un enfoque adiabático.

Buckholz y Lin (1986) analizaron el efecto del desalineamiento y la cavitación en chumaceras parciales lubricadas con fluidos No-Newtonianos. Qiu y Tieu (1996) desarrollaron un equipo experimental para medir el espesor de película, la presión y la temperatura en chumaceras desalineadas. Guha (2000) investigó las características de estado estable en chumaceras hidrodinámicas desalineadas considerando los efectos de la rugosidad isotrópica. Pierre et al. (2004) hicieron una investigación teórica y experimental de las condiciones de estado estable en chumaceras hidrodinámicas desalineadas, considerando un modelo termo-hidrodinámico. Recientemente, Jun et al., (2005) estudiaron las condiciones de lubricación considerando el desalineamiento en las chumaceras debido a la deformación por el peso del eje a una velocidad de operación fija. Jun et al., (2010) incluyen los efectos termo-hidrodinámicos y una superficie rugosa para el estudio de las condiciones de operación en chumaceras hidrodinámicas con desalineamiento.

En este trabajo se resuelve numéricamente la ecuación de la lubricación de Reynolds para diferentes valores de desalineamiento. Se presenta una expresión del espesor de película h(θ z) que considera el ángulo de desalineamiento α_x causado por el peso W_d y la flexibilidad del rotor. Para una determinada condición de operación se proporciona una expresión del rango de valores posibles para la rotación α_x en función de la e₀ y el ángulo de attitud ϕ₀. El campo de presión resultante se integra para obtener el flujo axial y el coeficiente de fricción viscosa del lubricante. También se obtienen el espesor de película mínimo y la presión máxima del lubricante. Los resultados se presentan en forma de gráficas adimensionales con la finalidad de que se utilicen en el diseño de chumaceras hidrodinámicas, en donde se considere el desalineamiento angular del eje. Para validar los resultados que se obtienen en esta investigación, se hace la comparación de la presión máxima p_max, el flujo axial Q_axial, el espesor de película mínimo h_min y el coeficiente de fricción F_f/W con un caso específico reportado en la literatura por Jun et al., (2005), obteniéndose una buena aproximación.

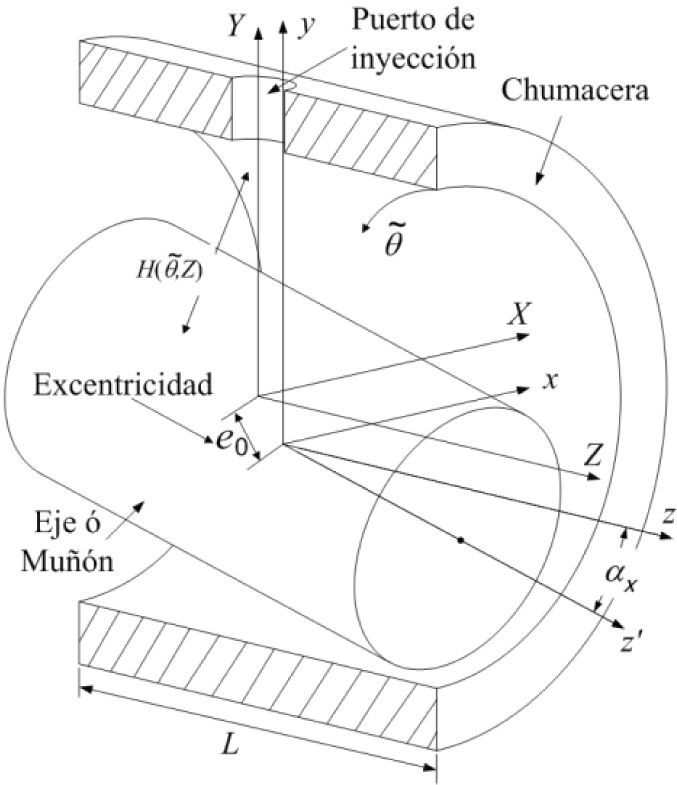
Desarrollo

Espesor de película

En la figura 2 se muestra una chumacera hidrodinámica con el muñón (eje en el interior) en una posición desalineada. Se consideran los sistemas de ejes fijos XYZ y xyz en el centro de la chumacera y en el centro del muñón, respectivamente. La distancia del centro de la chumacera al centro del muñón se conoce como excentricidad e₀ y en el caso alineado es independiente de z. Se puede observar en la figura 2 que el desalineamiento causa una rotación a_x modificando al espesor de película Hθ˜ del caso alineado a Hθ˜,z para el caso desalineado. El espesor de película para el caso alineado está dado por (Childs, 1993; Szeri, 1998):

donde

• C = R − R₁ es el claro radial (figura 3),

  
  

  Figura 3.

  Vista frontal de una chumacera desalineada

• ϕ es el ángulo de attitud y

• θ˜ es la coordenada circular.

Para obtener el espesor de película con desalineamiento que considere el peso y la flexibilidad del eje, es necesario tomar en cuenta el ángulo de rotación α_x del muñón. La relación entre la excentricidad e a una distancia z con la excentricidad del centro del muñón e₀ y el ángulo α_x se obtiene de la figura 3 como se indica a continuación:

Si se sustituyen las ecuaciones (2) en (1) se obtiene la ecuación (3) del espesor de película que considera el desalineamiento angular a_x del muñón.

En forma adimensional:

donde h = H/C, ε₀ = e₀/C, z=L/2z¯,ξx=(R/C)(L/F)α_x, D = R/2 donde e₀ está comprendida entre 0 ≤ e₀ ≤ C o en forma adimensional 0 ≤ ε₀ ≤ 1 y la excentricidad ε a una distancia z = L/2 tendrá como limites ε₀≤ε≤1.

Por medio de la teoría de vigas es posible calcular el ángulo α_x que el eje presenta en cada chumacera. Para una configuración de rotor de Jeffcott como la que se muestra en la figura 1, el ángulo α_x está dado por (Gere y Timoshenko, 1998):

donde

• W_d es el peso del disco,

• l es la logitud del eje entre soportes,

• E es el modulo de Young e

• I es el momento de inercia del eje.

Si se considera que E e I son constantes, entonces el ángulo α_x dependerá del peso W_d del rotor. El claro radial C y la relación L/D son limitantes para el valor máximo que pueda tomar el ángulo α_x, lo que no se considera en la teoría de vigas (ecuación 5). Para calcular el máximo ángulo αx permitido por la geometría de la chumacera se resuelven las ecuaciones (2) haciendo e = C en z = L/2, obteniendo:

o en forma adimensional

Dados W_d, l, E, I, C y la relación L/D, además de e₀ y ϕ₀ de una posición de equilibrio, se procede a calcular el ángulo α_x por medio de la teoría de vigas y el ángulo α_xmax permitido por la geometría de la chumacera. Si α_x < α_xmax entonces el ángulo α_x está dentro del valor permitido por la geometría de la chumacera. Por otra parte, si α_x> α_xmax entonces sólo en la chumacera se considerará que α_x= α_xmax conservándose los valores calculados por la teoría de vigas para el resto del eje. En resumen, el ángulo a_x calculado por la teoría de vigas no puede ser mayor que α_xmax que tiene como limitante la geometría de la chumacera.

Campo de presión

La ecuación adimensional de Reynolds que define el campo de presión de estado estable para chumaceras hidrodinámicas está dada por (Childs, 1993; Szeri, 1998):

donde

• p=μNR/C2p¯,

• μ es la viscosidad y

• N es la velocidad de rotación en rps (revoluciones por segundo).

Para obtener el campo de presión con desalineamiento es necesario resolver la ecuación (8) junto con la ecuación (4) considerando las condiciones de frontera:

y las condiciones de frontera de Swift-Stieber:

La ecuación (9) considera la presión en los extremos de la chumacera tomando como referencia la presión atmosférica. La ecuación (10) considera la cavitación, de tal forma que, tanto la presión como sus gradientes normales a la curva de cavitación no existan en la “frontera de inicio de cavitación”. Esta condición de frontera se implementa numéricamente haciendo cero cualquier presión negativa calculada previamente en cada iteración. Lund y Thomsen (1978) establecen que el perfil de presión calculado de esta manera satisface el requisito del gradiente de presión cero en la frontera de cavitación. Esta condición de frontera ha ganado amplia aceptación en chumaceras hidrodinámicas con cargas estacionarias. El conjunto de condiciones de frontera se completa con la presión en el puerto de inyección p₀ para asegurar la lubricación.

Para mantener el flujo, la presión clásica de inyección P₀ debe ser ligeramente mayor que la presión atmosférica.

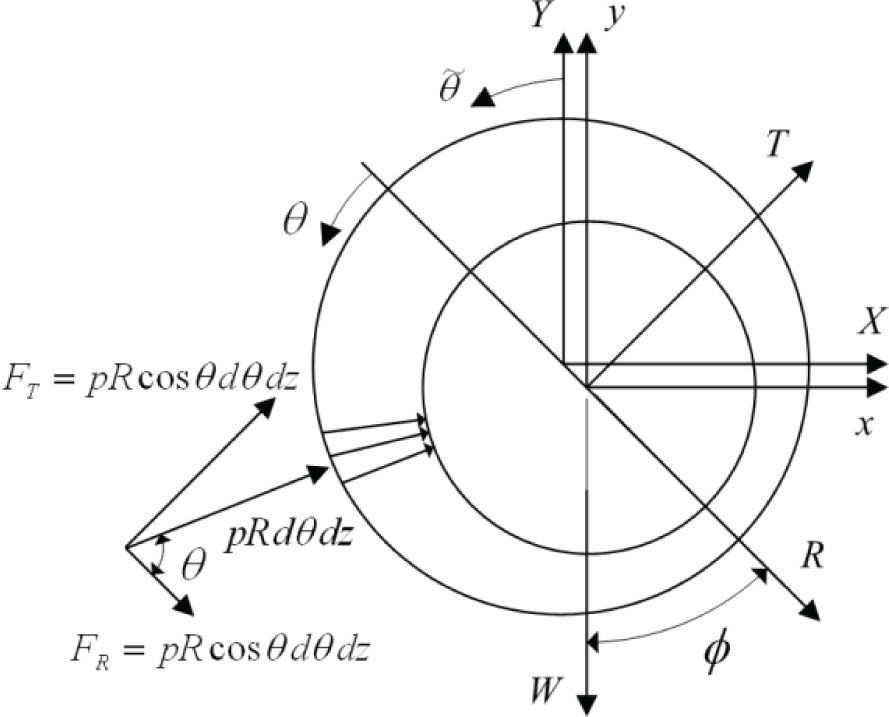
Fuerzas hidrodinámicas

Las fuerzas hidrodinámicas se obtienen integrando el campo de presión sobre el área de la chumacera, como se muestra en la figura 4:

donde θ˜1 es la localización del puerto de inyección y θ˜2 es la localización de la curva de inicio de cavitación. Debido al desalineamiento, el ángulo θ˜2 cambia con respecto a la coordenada z lo que no permite evaluar las fuerzas hidrodinámicas de manera analítica.

Figura 4.

Fuerzas hidrodinámicas desarrolladas por el campo de presión

Flujo axial

El lubricante recircula en el interior de la chumacera y viaja hasta alcanzar la salida en ±L/2. El flujo de salida depende del campo de presión y del espesor de película (ecuación 14).

La cantidad de flujo axial deberá reponerse como flujo de entrada para mantener la lubricación hidrodinámica.

Fricción viscosa

La fuerza de fricción viscosa F_f es la resistencia que se opone a la rotación del muñón debido al esfuerzo cortante del fluido, está dada por (Childs, 1993; Szeri, 1998):

o en forma adimensional:

dondef = F_f/W es el coeficiente de fricción, S=F¯x2+F¯Y2−1/2 es el número de Sommerfeld, el cual es adimensional y está relacionado con la geometría, las propiedades y la carga que soporta la chumacera (S = μNLD(R/C)²/W). El número de Sommerfeld es muy utilizado en el diseño de chumaceras hidrodinámicas, ya que reúne paráme tros geométricos, de operación y la viscosidad del lubricante. A continuación se describen los pasos utilizados en este trabajo para resolver numéricamente la ecuación de Reynolds y obtener las condiciones de lubricación hidrodinámica.

• 1)

  Para valores de ε₀, L/D y ξx (datos de entrada) se propone un valor para el ángulo de attitud ϕ₀.

• 2)

  Se calcula el espesor de película hθ˜,z¯ utilizando la ecuación (4).

• 3)

  La ecuación de Reynolds (8) se resuelve por diferencias finitas considerando las condiciones de frontera (9), (10) y (11). Para acelerar la convergencia se utiliza un coeficiente de sobre-relajación de 1.9.

• (4)

  Se evalúan las fuerzas hidrodinámicas F_X y F_Y. En el caso de estado estable F_X debe ser igual a cero y F_Y igual a la carga W, (W = W_d/2).

• 5)

  Si F_X ≠ 0 se propone un nuevo ángulo ϕ₀ y se repite a partir del paso 2.

• 6)

  Una vez que F_X = 0 finaliza el cálculo del campo de presión.

• 7)

  Una vez conocido el campo de presión, se integran las ecuaciones (14) y (16) para obtener el flujo axial y la fricción viscosa.

Resultados y discusión

Con fines de validación, se hace la comparación de h_min, p_max, Q_axial y F_f/W que se obtienen en este trabajo, y los resultados reportados en la literatura por Jun et al. (2005), donde se considera el desalineamiento del eje. También se hace la comparación con resultados sin desalineamiento (Khonsari y Booser, 2001) con la finalidad de mostrar el cambio que sufren las condiciones de lubricación con el desalineamiento. Jun et al. (2005) presentan resultados numéricos (validados experimentalmente) de las condiciones de lubricación de un sistema rotor-chumaceras de Jeffcott para valores de carga W_d de 200, 400, 600, 800, 1000 y 1200 N a una velocidad de operación fija de 1400 RPM. Los parámetros de la chumacera, del eje, las propiedades del lubricante y las condiciones de operación que utilizaron Jun et al. (2005) son: R = 25 mm, L = 40 mm, C = 0.07 mm, μ = 0.0686 Pa s, l = 1000 mm, d_eje = 40 mm de acero AISI 1045.

Para utilizar el algoritmo presentado en este trabajo es necesario calcular el ángulo ξ_x para cada una de las cargas W_d utilizando la teoría de vigas, verificando que ξ_x < ξ_xmax. Posteriormente, se proponen valores de excentricidad del centro del muñón ξ₀ hasta que el número de Sommerfeld S = μNLD(R/C)²/W coincide con el calculado con los datos proporcionados por Jun et al. (2005). Las figuras 5, 6, 7 y 8 muestran los resultados de la comparación de las condiciones de lubricación.

Figura 5.

Comparación de h_min con y sin desalineamiento del eje

Figura 6.

Comparación de p_max con y sin desalineamiento del eje

Figura 7.

Comparación de Q_axial con y sin desalineamiento

Figura 8.

Comparación de F_f/W con y sin desalineamiento

La figura 5 muestra que entre los resultados de h_min de esta investigación y los reportados por Jun et al. (2005) existe una buena aproximación. La gráfica permite ver que el incremento de W_d causa que h_min disminuya, tanto para el caso alineado como para el caso desalineado. Para el caso alineado h_min = C (1-ε₀) (Khonsari, 2001). Haciendo la comparación de h_min entre el caso alineado y desalineado se tiene que para W_d = 200 N, h_min = 0.0667 mm (caso alineado) y h_min = 0.0594 mm (caso desalineado de este trabajo) existiendo una diferencia de 0.0073 mm. Para W_d = 1200 N, h_min = 0.057 mm (caso alineado) y h_min = 0.0058 mm (caso desalineado), siendo la diferencia de 0.0512 mm. El segundo caso muestra claramente la importancia de considerar el desalineamiento del muñón en el diseño de chumaceras hidrodinámicas. El valor adecuado de h_min dependerá de la rugosidad de los materiales para evitar el contacto entre metal y metal.

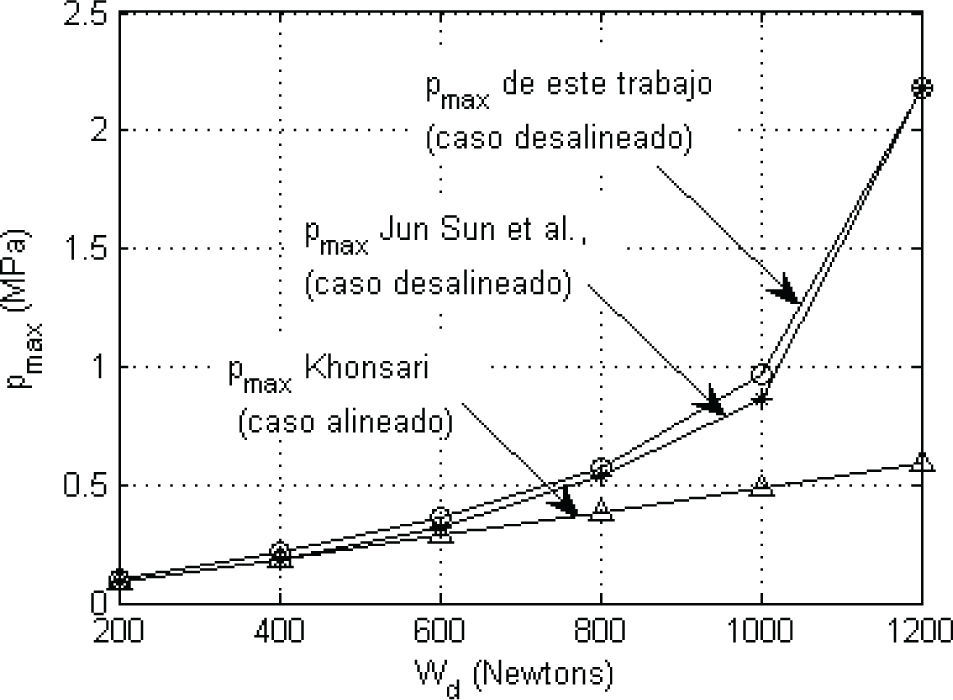
La figura 6 muestra que la comparación entre la p_max de este trabajo y la reportada en la literatura tienen una buena aproximación. Sin considerar el desalineamiento, se tiene para W_d = 200 N una p_max = 0.09236 MPa y para W_d = 1200 N una p_max = 0.59 MPa, (Khonsari y Booser, 2001). La figura 6 muestra, para el caso desalineado (con resultados de este trabajo), una p_max = 0.099 MPa para W_d = 200 N y una p_max = 2.1847 MPa para W_d = 1200 N. Existiendo un incremento en la p_max de 1.072 veces para W_d = 200 N y de 3.7 veces para W_d = 1200 N. El incremento en la presión máxima es una consecuencia de la reducción del espesor de película mínimo.

Es posible ver de las figuras 5 y 6 que el incremento de W_d causa una disminución en h_min y un incremento en p_max, tanto en el caso alineado como en el desalineado, siendo el caso desalineado el que presenta cambios considerables tanto en h_min como en p_max. Por otra parte, el incremento de p_max y la disminución de h_min causan un incremento en Q_axia1 como se observa en la figura 7. Se puede ver que existe una buena aproximación entre los valores de Q_axial con desalineamiento reportados en la literatura y los valores obtenidos en este trabajo. También se puede ver la diferencia entre los resultados de Q_axial con y sin desalineamiento. Por ejemplo, para W_d = 200 N se tiene que Q_axial = 0.4246 × 10⁻⁶ m3/s (caso alineado) y Q_axial = 0.6857 × 10⁻⁶ m3/s (caso desalineado) obteniéndose un incremento de 1.614 en Q_axial. Se puede ver que a medida que la carga W_d se incrementa, también aumenta la diferencia entre la Q_axial del caso alineado y el caso desalineado. La importancia de conocer Q_axial radica en que esta cantidad de lubricante debe reponerse para mantener la lubricación hidrodinámica.

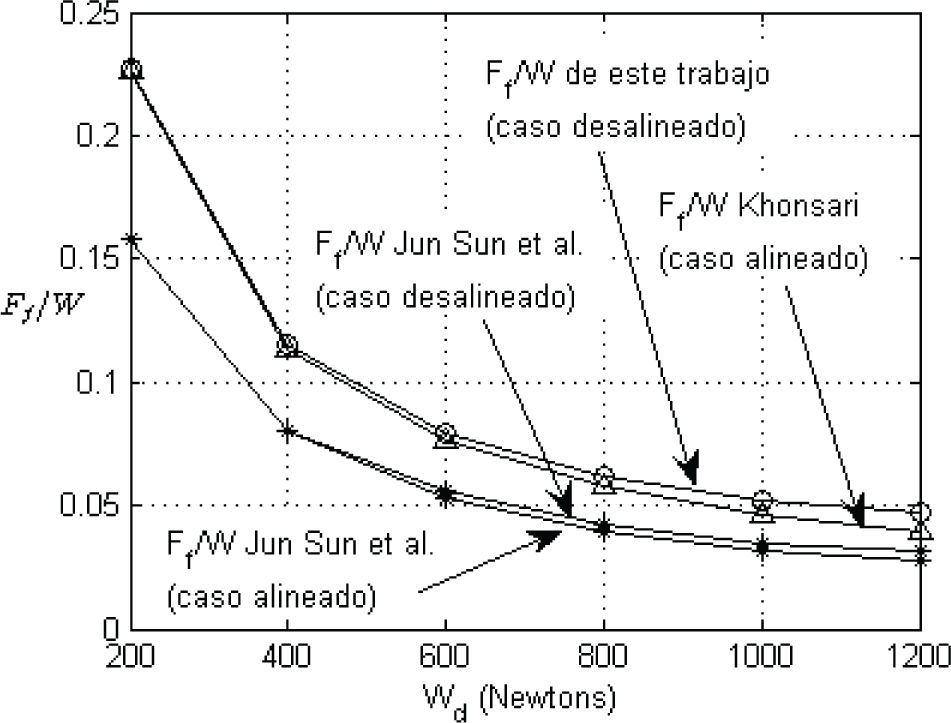
La figura 8 muestra la comparación de F_f/W con desalineamiento obtenida por Jun et al. (2005) y la obtenida eneste trabajo. Se puede ver que aunque los valores llevan la misma tendencia, los resultados de este trabajo son 1.4 veces (aproximadamente) más grandes que los reportados por Jun et al. (2005). También, los resultados sin desalineamiento por Khonsari y Booser (2001) son 1.4 veces (aproximadamente) más grandes que los resultados sin desalineamiento reportados por Jun et al. (2005). La figura 8 muestra que el incremento de carga W_d causa un incremento muy pequeño en F_f/W del caso desalineado con respecto al caso alineado. Por ejemplo, utilizando los valores dados por Jun et al. (2005) para W_d = 1000 N se tiene que F_f/W se incrementa en 1.093 veces. Para la misma carga se tiene un incremento de de F_f/W 1.11 veces entre los valores de Khonsari y Booser (2001) (caso alineado) y los de este trabajo (caso desalineado). Utilizando los resultados de este trabajo se tiene que la fuerza de fricción viscosa F_f = 22.6 N para W_d = 200 N y F_f = 28.5 N para W_d = 1200 N, notando un pequeño incremento en la fuerza de fricción. En resumen, el desalineamiento tiene poco efecto sobre la fuerza de fricción viscosa.

Las figuras 5, 6, 7 y 8 contienen resultados para un caso específico, los cuales aunque son de interés, no son aplicables a un caso de diseño que contenga diferentes parámetros de la chumacera, del eje, propiedades del lubricante y condiciones de operación. Los resultados de este trabajo se presentan en las siguientes figuras de forma adimensional para casos de diseño con relación de L/D = 1 y diferentes valores de ξ_x.

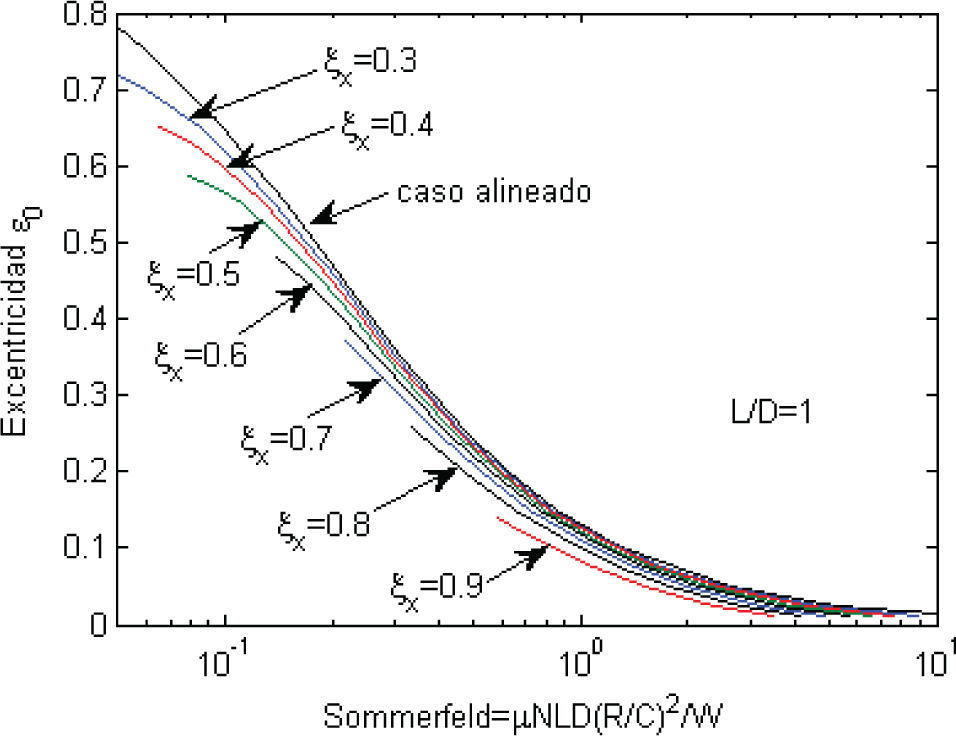
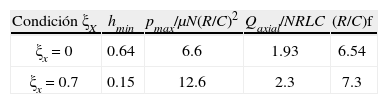
La figura 9 muestra la relación entre el número de Sommerfeld y la excentricidad ε₀ (excentricidad del centro del muñón) para diferentes valores de desalineamiento ξ_x. Esta figura muestra que para un mismo número de Sommerfeld (mismas condiciones de operación) la excentricidad e₉₆ se reduce a medida que el desalineamiento aumenta. Por lo tanto, para determinar las condiciones de lubricación (h_min, p_max, Q_axial y (R/C) f) será necesario determinar primero el punto de equilibro ε₀ del centro del muñón. Por ejemplo, si para determinadas condiciones de operación se tuviese un número de Sommerfeld de 0.3 entonces para el caso alineado ε₀ sería igual a 0.37 y para un caso desalineado con ξ_x = 0.7 el punto de equilibrio ε₀ estaría en 0.30 aproximadamente (figura 9). La tabla 1 muestra las condiciones de operación que se obtienen de las figuras 10, 11, 12 y 13 para ambos casos.

Figura 9.

Excentricidad ε₀ contra número de Sommerfeld

Tabla I.

Comparación de condiciones de operación para Sommerfeld 0.3 y L/D = 1

Condición ξX	hmin	pmax/μN(R/C)^2	Qaxial/NRLC	(R/C)f
ξx = 0	0.64	6.6	1.93	6.54
ξx = 0.7	0.15	12.6	2.3	7.3

Figura 10.

Espesor de película para diferentes valores de ξ_X y L/D = 1

Figura 11.

Presión máxima para diferentes valores de ξ_X y L/D = 1

Figura 12.

Flujo axial en función de ξ_X y L/D = 1

Figura 13.

Fricción viscosa para ξ_X = 0 y ξ_X = 0.9 y para L/D = 1

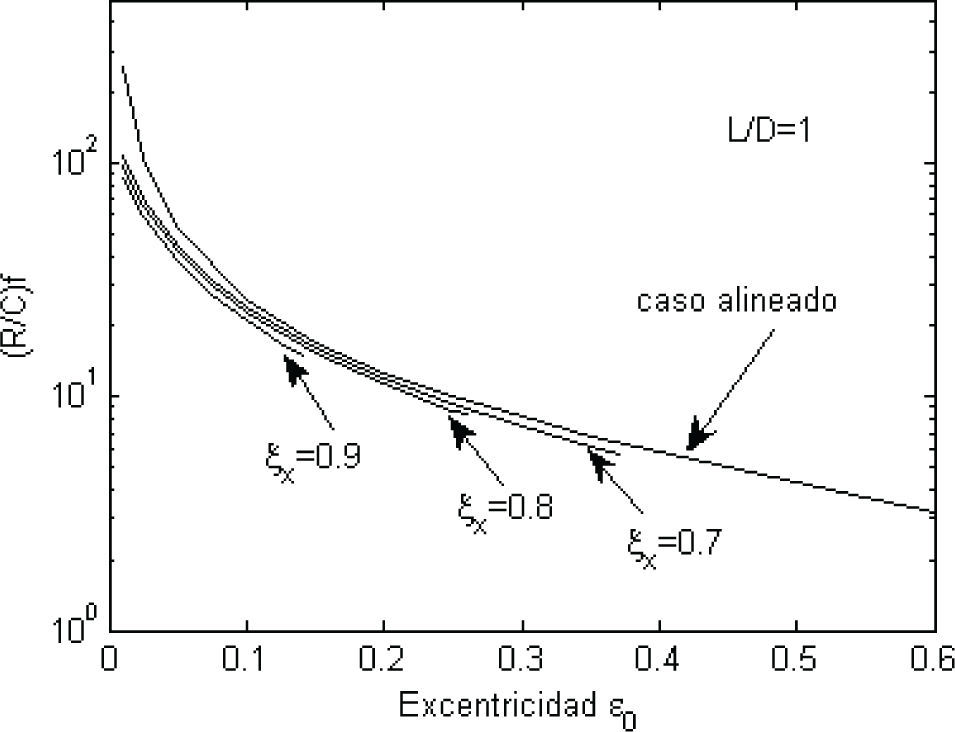
Se puede ver en la figura 10 y la tabla 1 que el espesor de película h₂ disminuye al aumentar el desalineamiento. También se observa en las figuras 11 y 12, y la tabla 1 que la presión máxima y el flujo axial se incrementan al considerar el desalineamiento. Al observar la figura 13 se podría interpretar que el coeficiente de fricción adimensional (R/C) f disminuye al incrementarse el desalineamiento, lo que sería erróneo. La tabla 1 muestra el incremento de (R/C) f al incrementarse ξ_x, esto se debe a que ε₀ cambia de 0.37 del caso alineado a 0.30 para el caso con desalineamiento. Las figuras 10, 11, 12 y 13 requieren la figura 9 para su correcta interpretación y uso. Es importante notar en la figura 9 que el desalineamiento ubica el centro del eje en una nueva posición de equilibrio.

Conclusiones

En este trabajo se presenta la solución numérica de la ecuación de Reynolds que considera el desalineamiento del muñón en la chumacera debido al peso y a la flexibilidad del rotor. Se emplea una expresión modificada del espesor de película que incluye el desalineamiento angular del eje por el efecto del peso del rotor.

El ángulo de desalineamiento a_x se calcula por medio de la teoría de vigas y se presenta una expresión para calcular el máximo ángulo de desalineamiento α_max permitido por la geometría de la chumacera. Los resultados de las condiciones de lubricación con desalineamiento de h_min, p_max, y Q_axial y (R/C) f que se obtienen en este trabajo se comparan con resultados reportados en la literatura, obteniéndose una buena aproximación. También se hace la comparación de los resultados de las condiciones de lubricación con desalineamiento que se obtienen en este trabajo y resultados sin desalineamiento reportados en la literatura, lo que muestra la importancia de considerar el desalineamiento en el diseño de chumaceras hidrodinámicas. Se puede ver que al considerar el desalineamiento, el espesor de película h_mindisminuye y la presión máxima y el flujo axial se incrementan. Por su parte, la fricción viscosa tiene cambios moderados con incrementos del desalineamiento. También se muestra que la excentricidad del centro del muñón ε₀ se ubica en una nueva posición al aumentar el desalineamiento para las mismas condiciones de operación (mismo número de Sommerfeld) lo que debe de tomarse en cuenta para calcular las condiciones de lubricación hidrodinámica.

Los resultados de este trabajo se presentan en forma adimensional para un diseño preliminar de chumaceras hidrodinámicas para L/D = 1 y diferentes valores de desalineamiento angular.

Agradecimientos

Se agradece a la Universidad Tecnológica de la Mixteca por el tiempo asignado para la realización de este trabajo.