La metodología Seis Sigma se utiliza ampliamente en las empresas para el mejoramiento de la calidad, incremento de la productividad y la disminución de costos, repercutiendo en un mejoramiento del negocio. Sin embargo, en la actualidad el desafío consiste en dirigir esas herramientas a las mejoras que tengan un impacto directo sobre la diferenciación de valor, lo cual requiere la alineación de Seis Sigma con las estrategias competitivas de la organización. De ahí la importancia de establecer un sistema de gestión estratégica capaz de medir, analizar, mejorar y controlar el rendimiento corporativo y al mismo tiempo determinar las responsabilidades de liderazgo y el compromiso. El propósito específico de esta investigación es desarrollar un modelo matemático a través de la alineación de objetivos estratégicos (Balanced Scorecard) y herramientas de mejora de la productividad (Seis Sigma) para procesos con múltiples respuestas, que sea lo suficientemente robusto para que pueda servir de base para su aplicación en empresas manufactureras para vincular eficazmente la estrategia de rendimiento y la satisfacción del cliente. Específi- camente se trabajó con un caso real de estudio: Córdoba, Ver.
El modelo postula que si la estrategia, el rendimiento y la satisfacción del cliente están alineados, la organización obtendrá grandes beneficios por la relación intensa que existe entre el rendimiento del proceso y las iniciativas estratégicas. Estos cambios pueden ser medidos por métricas de procesos y de productividad como tiempo de ciclo, las tasas de producción, la eficiencia de producción y porcentaje de los re-procesos, entre otros.
The Six Sigma methodology is widely used in business to improve quality, increase productivity and lower costs, impacting on business improvement. However, today the challenge is to use those tools for improvements that will have a direct impact on the differentiation of value, which requires the alignment of Six Sigma with the competitive strategies of the organization. Hence the importance of a strategic management system to measure, analyze, improve and control corporate performance, while setting out responsibilities of leadership and commitment. The specific purpose of this research is to provide a mathematical model through the alignment of strategic objectives (Balanced Scorecard) and tools for productivity improvement (Six Sigma) for processes with multiple answers, which is sufficiently robust so that it can serve as basis for application in manufacturing and thus effectively link strategy performance and customer satisfaction. Specifically we worked with a case study: Córdoba, Ver. The model proposes that is the strategy, performance and customer satisfaction are aligned, the organization will benefit from the intense relationship between process performance and strategic initiatives. These changes can be measured by productivity and process metrics such as cycle time, production rates, production efficiency and percentage of re-processing, among others.
En los últimos años han surgido diferentes conceptos de iniciativa de mejora, cuyos resultados prometen conducir a un desempeño superior y a una efectiva creación de valor en las organizaciones. Por tal motivo, se ha incrementado el interés por estudiar el proceso de implantación de estrategias eficientes para estos propósitos.
Actualmente la mayoría de las empresas analizan cada una de sus variables de respuesta o indicadores de desempeño, de forma individual e independiente; perdiendo de vista con ello, que estas variables interactúan entre sí y que en la gran mayoría de los casos se encuentran fuertemente correlacionadas, aspecto muy olvidado con mucha frecuencia y, por ende, pocas veces traducido a métricas útiles en la valoración de los resultados de las estrategias implementadas.
Lo anterior pone de manifiesto la urgente necesidad de contar con recursos científicos, que se traduzcan en modelos útiles, los cuales a su vez, permitan obtener medidas de desempeño capaces de reflejar la situación real de las organizaciones desde un punto de vista holístico, con el fin último de optimizar la toma de decisiones estratégicas.
El presente trabajo reporta los resultados de una investigación integrada por el análisis, desarrollo e implementación de un modelo matemático sustentado en los principios y filosofías del cuadro de mando integral (BSC), Seis Sigma y técnicas estadísticas avanzadas, con el propósito de contribuir a llenar el vacío que existe en la actualidad al no disponer de un instrumento con estas características que valore integral y estratégicamente el desempeño de una organización.
Por un lado, el cuadro de mando integral es una herramienta de administración estratégica y sistema de medición del desempeño, diseñado para traducir las estrategias de la organización en planes de acción orientados (Gamal, 2010). Por otro lado, Seis Sigma es una metodología de administración de la calidad que se enfoca en la reducción de la variación existente en los procesos de producción de bienes o servicios, la drástica reducción de los defectos y el mejoramiento de la calidad de productos, procesos y servicios.
La estadística multivariante se encuentra integrada por un conjunto de técnicas avanzadas que relacionan múltiples variables de respuesta mediante modelos matemáticos complejos, los cuales permiten modelar y visualizar, de manera global, las dependencias e interdependencias de un conjunto grande de variables a través de una simplificación coherente y eficiente.
Seis Sigma integral multivariado (SSIM), es el nombre que damos a este nuevo modelo de medición de de- sempeño corporativo. Específicamente, es un sistema que requiere la participación total de la organización en todos sus niveles a través de líderes que inspiran, gerentes que mejoran y empleados que crean e innovan en esfuerzos conjuntos e integrados, los cuales persiguen el propósito de alcanzar el nivel óptimo de rentabilidad y crecimiento. El modelo está basado en principios científicos, prácticas de mejora comprobadas a través de numerosas investigaciones como las mencionadas y técnicas de estadística multivariante, en un marco de principios y valores que guíen los distintos derroteros de la organización.
El objetivo del SSIM es, por un lado, identificar y cuantificar los indicadores relacionados con los procesos clave de la organización e integrarlos en un modelo que valore el desempeño global del proceso corporativo, con el fin de alcanzar el nivel de rentabilidad deseada y, por otro lado, identificar, diseñar e implementar los procesos de mejora correspondientes.
La sinergia generada mediante la fusión de estas tres metodologías, permite que las organizaciones desarrollen la capacidad de:
- •
Mejorar significativamente el rendimiento de la organización.
- •
Proporcionar una visión global del estado de la empresa.
- •
Dimensionar la importancia del liderazgo y el compromiso.
- •
Utilizar una menor cantidad de recursos para la optimización de su proceso clave.
- •
Clarificar la identificación de metas parciales y generales para la mejora de desempeño.
- •
Promover la participación intelectual, activa y comprometida de todos los empleados.
- •
Disponer de un enfoque estratégico que actúe como catalizador en el aprovechamiento de los potenciales subyacentes en todos sus empleados.
El modelo matemático propone calcular un índice global de desempeño corporativo (IGDC), en cual se integra un conjunto de variables dependientes, como una función de un conjunto de variables independientes; es decir:
Las variables independientes incluyen factores relacionados con el enlace entre estrategia, desempeño y clientes. Estas variables pueden incluir:
- •
El vínculo entre las iniciativas estratégicas y la priorización de los proyectos Seis Sigma relacionados con las iniciativas estratégicas.
- •
El vínculo entre los objetivos estratégicos y los objetivos de los proyectos, y posteriormente los niveles funcionales que traducen día a día los planes en acciones.
- •
El vínculo de las medidas del cuadro de mando integral (formulación de estrategias) relacionadas con el proceso, indicadores financieros y satisfacción del cliente.
- •
Las variables dependientes incluyen indicadores de productividad, procesos financieros y los indicadores de satisfacción del cliente.
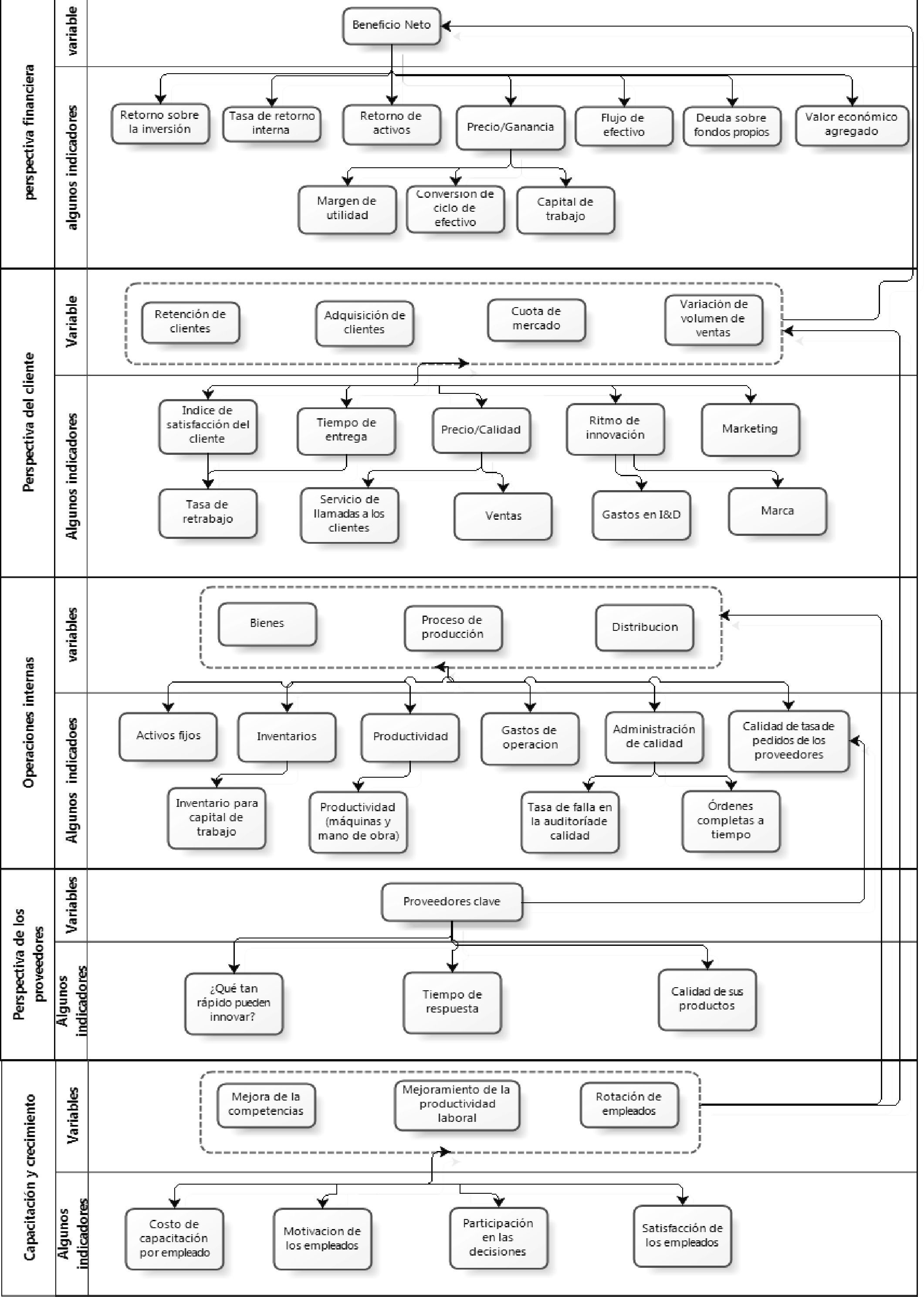
En su libro, The Balanced Scorecard, Kaplan y Norton (1996) muestran cómo un cuadro de control debe implementarse con la finalidad de ir más allá de la supervisión del rendimiento de las medidas financieras y no financieras; con esto se puede determinar, de manera efectiva, la forma en que los indicadores se relacionan unos con otros para mejorar el rendimiento global de una empresa. Es aquí en donde se puede resaltar la importancia de utilizar técnicas multivariantes para identificar, cuantificar y modelar la naturaleza de tales relaciones. En la figura 1 se agrupan los indicadores de desempeño corporativo en 5 bloques: perspectiva financiera, perspectiva del cliente, operacionales internos, perspectiva de los proveedores y de capacitación y desarrollo. La idea principal del diagrama es ofrecer una perspectiva de la correlación efectiva entre cada bloque a través de sus interacciones (flechas).
La alineación de las estrategias de largo, mediano y corto plazo son una gran preocupación de cualquier organización, aspecto que no siempre se logra, sobre todo cuando se presenta una total ausencia de relación entre las actividades que planean, desarrollan e implementan en todos los niveles para mantener una alta y fructífera rentabilidad. La metodología desarrollada y propuesta en este trabajo, aprovecha las ventajas del BSC y de SS para integrar totalmente las estrategias de largo, mediano y corto plazo, con la metodología mostrada en la tabla 1.
Metodología general para la construcción del modelo matemático (IGDC)
| Etapa de BSC | Etapa de SS | Pasos en BSSM |
|---|---|---|
| Planeación | Definir | Establecer dirección de la organizaciónRealizar una definición y descripción de puestos |
| Traducción | Medir | Definir el sistema de mediciónDeterminar la correlación de parámetrosDesarrollar mapa de los grupos de variables |
| Analizar | Identificar áreas como resultado de la correlaciónPresentar indicadores parcialesCalcular el indicador global de desempeño corporativo (IGDC)Construir la escala y rango de medición del IGDC | |
| Ejecución | Mejorar | Calcular la capacidad de proceso para indicadores parcialesCalcular la capacidad de proceso para el IGDCCalcular el nivel de sigmas (z) de la organizaciónIdentificar las áreas que requieran mayor atención |
| Controlar | Construir los gráficos de control para indicadores parcialesConstruir el gráfico de control para el IGDCMonitorear el impacto en el IGDC y la rentabilidad |
De acuerdo al Sistema de Información Empresarial Mexicano (SIEM), en la zona Córdoba-Orizaba del Estado de Veracruz existen 307 empresas de manufactura organizadas en los 5 principales municipios: Orizaba, Córdoba, Amatlán de los Reyes, Ixtaczoquitlán y Fortín de las Flores. La amplia gama de productos manufacturados en todas ellas, hacen por demás interesante y atractivo encontrar soluciones a sus problemas de estrategia empresarial. Así, los primeros pasos del proyecto consistieron en identificar a las empresas en donde se buscó la información pertinente, a través de la determinación de un tamaño adecuado de muestra.
La determinación del tamaño de muestra, por consiguiente, fue uno de los primeros aspectos técnicos del estudio a resolver. El modelo estadístico que proporciona el tamaño de muestra adecuado a un nivel de confianza y porcentaje de error establecido es
donde:
N = total de la población
Zα = 1.96
p = proporción esperada de empresas que acceden a responder el instrumento
q = 1 − p
d = precisión o error máximo admisible
Se utilizó α = 0.05 (confianza de 95%), p = 0.5, q = 0.5 y un error de 0.05. Estos valores de p y q aseguran la máxima variabilidad en la distribución binomial y, en consecuencia, el tamaño de muestra alcanza su nivel más alto, lo cual beneficia al proceso de estimación.
La estructura poblacional bajo estudio condujo a la aplicación de un muestreo aleatorio simple con un tamaño de muestra de 227 empresas, en las cuales se aplicó un instrumento de medición diseñado para cumplir con los propósitos de la investigación. Este instrumento estaba integrado originalmente por 68 ítems, los cuales se redujeron a 59 después de llevar a cabo un análisis detallado de cada uno de ellos.
La confiabilidad del instrumento de medición se determinó mediante el cálculo del Alpha de Cronbach (ecuación 3), estadístico ampliamente utilizado para evaluar la consistencia interna o fiabilidad de instrumentos integrados de múltiples ítems.
donde:k = número de ítems
Σ Si2 = suma de las varianzas de todos los ítems
S2suma = varianza de las puntuaciones totales de cada individuo
A partir de esta expresión se puede deducir fácilmente que los valores de alfa se encuentran en el intervalo [0,1]. Los criterios que se aplican en la evaluación de la confiabilidad de un instrumento son: α < 0.6, inaceptable; 0.6 ≤ α < 0.7, poco aceptable; 0.7 ≤ α < 0.8, respetable; 0.8 ≤ α< 0.9, muy bueno y α ≥ 0.9, se debe considerar una reducción del número de ítems en la escala. Los resultados obtenidos de la fiabilidad del instrumento utilizado en el estudio arrojaron un valor de 0.8496, valor que demuestra que el instrumento es muy confiable.
Para el cálculo de la validez se aplicó el análisis factorial que contribuye directamente aclarando dos puntos fundamentales en la explicación del constructo: su estructura interna y sus relaciones con terceras variables. El análisis factorial se basa en el supuesto de que existe multicolinealidad en la matriz de datos. Esta propiedad se determinó a partir del determinante de la matriz de correlaciones, cuyo valor fue de 0.0000435, con lo cual se dedujo que existe multicolinealidad en la matriz de datos. Se aplicó asimismo, la prueba de esfericidad de Bartlett (que supone ausencia de correlación entre las varia- bles; la prueba de Barlett supone una distribución normal, por lo que se aplicó el gráfico de Chi-cuadrado multivariante, observándose una línea recta, concluyendo que los datos siguen una distribución normal) para complementar el procedimiento del determinante de la matriz de correlaciones; el resultado indica que la hipótesis nula no puede ser aceptada (P = 0.02 < 0.05), lo cual lleva a la misma conclusión antes mencionada.
Por último, se realizó la clasificación de cargas factoriales con la finalidad de integrar los grupos adyacentes correspondientes que tienen el mismo tipo de carga factorial, lo cual demuestra plenamente la validez del instrumento.
Con la información recopilada a través del muestreo realizado, se llevó a cabo un análisis cluster para filtrar e iniciar la agrupación de los indicadores de desempeño en conglomerados de variables relacionadas, las cuales explican el comportamiento de las distintas áreas funcionales de la organización. La figura 2 muestra el dendograma resultante generado mediante el uso del paquete estadístico MINITAB 16.
Ahora queda claro que es necesario integrar a las variables en cinco conglomerados. Cada grupo de variables al interior de cada conglomerado tienen una estrecha relación y, por tanto, una interpretación concreta; a saber: liderazgo, planeación, clientes, crecimiento y productividad y ambiente laboral. Esta clasificación inicial permite mostrar la objetividad de la metodología propuesta.
La siguiente tarea consiste en obtener un modelo matemático que refleje la importancia o peso relativo de las variables dentro de cada conglomerado. Para ello se aplicó el análisis de componentes principales (ACP). La figura 3 muestra el diagrama de sedimentación para el cluster 5, donde se aprecia que con un componente principal se puede explicar la mayor parte de la varianza de ese grupo de variables.
Los modelos obtenidos a través de la aplicación de ACP se pueden escribir como
En donde IPDk = índice parcial de desempeño del clusterk, αki y xki representan las ponderaciones y los indicadores específicos para cada cluster.
La tabla 2 presenta los valores de las ponderaciones y las funciones estratégicas que representa cada IPDK.
Ponderaciones de las funciones estratégicas
| k\i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | Función estratégica | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.555 | 0.521 | 0.155 | 0.521 | 0.105 | 0.337 | Liderazgo | ||||||
| 2 | 0.210 | 0.068 | 0.117 | 0.108 | 0.332 | 0.218 | 0.332 | 0.332 | 0.332 | 0.218 | Planeación | ||
| 3 | 0.378 | 0.378 | 0.378 | 0.378 | 0.195 | 0.378 | 0.235 | Genéricos del cliente | |||||
| IPD | 4 | 0.105 | 0.399 | 0.399 | 0.399 | 0.354 | 0.399 | 0.399 | Crecimiento | ||||
| 5 | 0.271 | 0.271 | 0.271 | 0.52 | 0.252 | 0.221 | 0.252 | 0.271 | 0.271 | 0.271 | 0.271 | Productividad y ambiente laboral |
El indicador global de desempeño corporativo (IGDC) se define como:
En donde wk representa al correspondiente factor de ponderación del indicador parcial de desempeño IPDk. Se explicará a continuación la obtención de dichos factores, considerando la aplicación del proceso de jerarquía analítica (PJA o AHP, analytic hierarchy process).
El proceso de jerarquía analítica presentado por Thomas Saaty (1980), es una herramienta eficaz para hacer frente a la toma de decisiones complejas, el cual ayuda al establecimiento de prioridades para una mejor toma de decisiones, mediante una serie de contrastes por pares para, después, sintetizar de manera ob- jetiva los resultados. La principal ventaja del PJA es que capta tanto los aspectos subjetivos, como los aspectos objetivos de una decisión; además de que permite valorar la consistencia de las evaluaciones del decisor, lo que reduce el sesgo en el proceso de toma de decisiones. A continuación se da una breve explicación de la manera en que se aplicó el PJA para llegar al establecimiento de las prioridades mencionadas líneas arriba.
La figura 4 muestra la estructura jerárquica que corresponde al foco de investigación utilizando el proceso de jerarquía analítica. Este foco representa la importancia de las diferentes áreas de una organización. Las C representan a cada uno de los cinco criterios (indicadores parciales) con que cuenta el modelo (ver ecuación 5), y cada uno de los c que se desprenden de estos, representan a los actores (indicadores individuales) o subcriterios del modelo.
El primer paso consiste en transformar la estructura jerárquica de la figura 4 en una matriz conocida como “matriz por pares” (ver tabla 3); en ella se identifican los factores (indicadores parciales) tanto en las columnas como en los renglones. El PJA contempla que los expertos en el área puedan entregar una puntuación con base a una escala establecida por Saaty (1980). Saaty sustenta sus conclusiones en los resultados de un estudio de base experimental, donde se confirma que una escala de nueve elementos es razonable, y refleja de manera suficiente los distintos grados o niveles en los cuales una persona puede discriminar la intensidad de la relación entre elementos de un conjunto dado. De esta manera, todas las comparaciones y por ende las mediciones, se hacen con base en la misma escala; por ello, la técnica se ajusta al principio de homogenización de la teoría de mediciones.
Matriz de comparación por pares (puntuación final)
| Impacto de las diferentes áreas de la organización en el desempeño empresarial | F1: Liderazgo | F2: Planeación | F3: Genéricos del cliente | F4: Crecimiento | F5: Productividad y ambiente laboral |
|---|---|---|---|---|---|
| F1: Liderazgo | 1 | 2 | 4 | 7 | 4 |
| F2: Planeación | 1/2 | 1 | ¼ | 5 | 5 |
| F3: Genéricos del cliente | ¼ | 4 | 1 | 7 | 7 |
| F4: Crecimiento | 1/7 | 1/5 | 1/7 | 1 | 1 |
| F5: Productividad y ambiente laboral | 1/4 | 1/5 | 1/7 | 1 | 1 |
| SUMA | 2.14 | 7.40 | 5.53 | 21.0 | 18.0 |
Ahora bien, queda por resolver el problema de cómo se obtendrán las opiniones de los expertos; la respuesta se encontró en el método Delphi, el cual es un método de decisión en grupo desarrollado por Dalkey y Hermer (1963) para la Fuerza Aérea de los Estados Unidos. La técnica requiere la repetición de cuestionarios individuales por parte de los participantes en el proceso de toma de decisiones, a fin de evitar un conflicto directo entre los expertos. Se trata de un proceso de respuesta anónima para recibir comentarios por escrito de cada participante/experto de la evaluación sobre un tema en específico; la encuesta suele tardar de 2 a 5 rondas antes de llegar a un consenso de los participantes. Así, las valoraciones finales emanadas de las opiniones de los expertos se muestran directamente en la tabla 3. Estas puntuaciones son la base de cálculos posteriores.
Una vez integradas las puntuaciones en la matriz por pares, se construye una nueva matriz (tabla 4) que dará los niveles asignados a los correspondientes pesos de los factores. Los valores de cada combinación renglón-columna se obtienen mediante el cociente de la puntuación correspondiente de la tabla 3, entre el total de su columna. Finalmente, los pesos de los factores serán el valor promedio de los elementos de cada renglón.
Puntuaciones en la matriz por pares
| Impacto de las diferentes áreas de la organización en el desempeño empresarial | F1: Liderazgo | F2: Planeación | F3: Genéricos del cliente | F4: Crecimiento | F5: Productividad y ambiente laboral | Peso de los factores (valor promedio) |
|---|---|---|---|---|---|---|
| F1: Liderazgo | 0.46666 | 0.27027 | 0.72332 | 0.33333 | 0.22222 | 0.40316 |
| F2: Planeación | 0.23333 | 0.13513 | 0.04520 | 0.23809 | 0.27777 | 0.18590 |
| F3: Genéricos del cliente | 0.11666 | 0.54054 | 0.18083 | 0.33333 | 0.38888 | 0.31205 |
| F4: Crecimiento | 0.06666 | 0.02702 | 0.02531 | 0.04761 | 0.05555 | 0.04443 |
| F5: Productividad y ambiente laboral | 0.11666 | 0.02702 | 0.02531 | 0.04761 | 0.05555 | 0.05443 |
El vector de prioridad VP resultante es:
de donde se desprende que w1 = 0.40316, w2 = 0.18590, w3 = 0.31305, w4 = 0.04443 y w5 = 0.05443.
Finalmente, el modelo matemático que permite obtener el indicador global de desempeño corporativo es
Por lo que se demuestra, que un modelo matemático que integra los principios del cuadro integral de mando, Seis Sigma y métodos estadísticos avanzados, hace posible la obtención de un indicador global de desempeño corporativo (IGDC), el cual constituye la base para identificar y valorar los planes estratégicos de la organización.
Discusión y análisis de resultadosLas métricas de SS están directamente relacionadas con la probabilidad de obtener productos no conformes en un proceso, esta probabilidad a su vez, se transforma en defectos por unidad (DPU), partes por millón (PPM), o defectos por millón de oportunidades (DPMO). Estos términos pueden de igual manera elevarse al nivel corporativo, una vez que se dispone de un índice como el IGDC, específicamente DPU y DPMO se pueden obtener aplicando las siguientes expresiones
La relevancia de las métricas anteriores estriba en que pueden asociarse rápidamente con niveles de calidad sigma, término de fácil manejo y comprensión en relación con la valoración de la calidad de un producto o servicio. Este resultado es de suma importancia, ya que demuestra que los criterios de evaluación del desempeño en todos los niveles de la organización, pueden alinearse perfectamente en el proceso estratégico corpo- rativo, a través de criterios cuantitativos que resultan por demás objetivos y consistentes.
La tabla 5 muestra la equivalencia para valores de DPMO a niveles de sigma. La última columna de la tabla contiene los criterios de evaluación final del desempeño de una empresa de acuerdo con DMPO, rendi- miento y nivel de calidad sigma.
Las ventajas que el modelo ofrece para la valoración a nivel corporativo son:
- •
Provee un nuevo modelo para definir el nivel corporativo de calidad sigma.
- •
Alinea la estructura organizacional con el negocio.
- •
Mantiene la visibilidad de los costos, ganancias y rentabilidad.
- •
Toma en cuenta los indicadores para el liderazgo y la tasa de mejora.
- •
Permite alinear los niveles estratégicos y tácticos con salidas de la organización
- •
Identifica las actividades que afectan directamente el desempeño organizacional y los factores críticos para incorporarlos a un índice de desempeño centrado en el cliente.
- •
Abre la función de calidad más allá, conectando el “qué” puede alcanzar una organización con el “cómo” lo va a cumplir.
- •
Incorpora técnicas estadísticas multivariantes en la evaluación del desempeño corporativo.
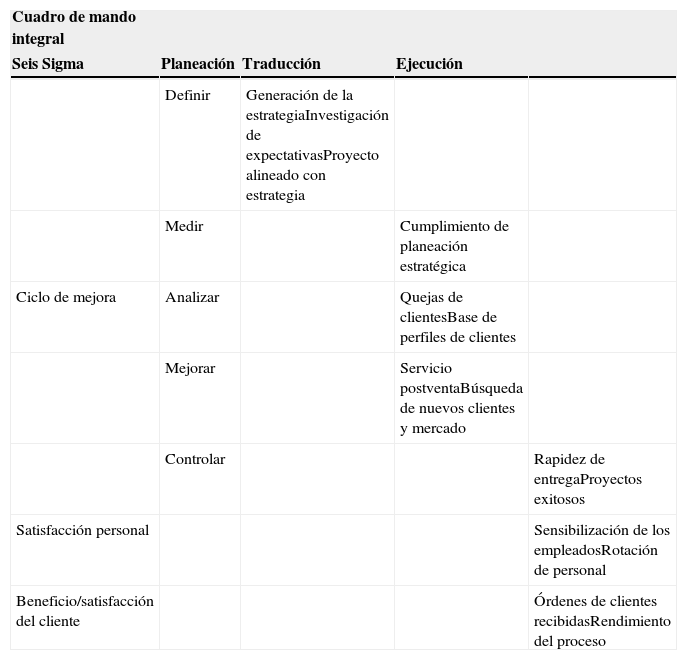
La tabla 6 muestra la clasificación de los indicadores obtenidos en el estudio mediante la alineación de las dos metodologías utilizadas para el desarrollo del modelo.
Indicadores de desempeño alienados con BSC y SS
| Cuadro de mando integral | ||||
|---|---|---|---|---|
| Seis Sigma | Planeación | Traducción | Ejecución | |
| Definir | Generación de la estrategiaInvestigación de expectativasProyecto alineado con estrategia | |||
| Medir | Cumplimiento de planeación estratégica | |||
| Ciclo de mejora | Analizar | Quejas de clientesBase de perfiles de clientes | ||
| Mejorar | Servicio postventaBúsqueda de nuevos clientes y mercado | |||
| Controlar | Rapidez de entregaProyectos exitosos | |||
| Satisfacción personal | Sensibilización de los empleadosRotación de personal | |||
| Beneficio/satisfacción del cliente | Órdenes de clientes recibidasRendimiento del proceso |
Se llevó a cabo una evaluación de las empresas manufactureras de la región Córdoba, Ver., con la finalidad de conocer el nivel de calidad de cada una de ellas, medido en número de sigmas. Tomando las ecuaciones formadas de la tabla 2 se sustituyeron los datos de las 227 empresas muestreadas. La tabla 7 muestra las primeras 5 empresas, ordenadas por su nivel de calidad (sigmas), la columna 2 contiene el valor obtenido de la sustitución de la combinación lineal dada por la primera componente principal (IPD1), la columna 3 muestra el resultado para el IPD2 y así sucesivamente, hasta la columna 6 que muestra el resultado del el IPD5.
Resumen de la evaluación de cada empresa muestreada
| EMPRESA | IPD1 | IPD2 | IPD3 | IPD4 | IPD5 | IGDC | DPU | Núm. EJEC. CEO | DMPO | SIGMA |
|---|---|---|---|---|---|---|---|---|---|---|
| Empresa 9 | 96.163 | 73.848 | 60.312 | 100.623 | 159.914 | 84.4924127 | 0.16850845 | 30 | 5616.94821 | 4.03533772 |
| Empresa 45 | 100.27 | 74.27 | 55.764 | 95.79 | 158.628 | 84.521852 | 0.16816008 | 29 | 5798.6235 | 4.02416806 |
| Empresa 93 | 96.426 | 75.999 | 55.763 | 100.977 | 160.782 | 83.6420436 | 0.17862388 | 30 | 5954.12928 | 4.01485134 |
| Empresa 24 | 100.37 | 75.001 | 55.958 | 94.863 | 150.355 | 84.2664429 | 0.17118647 | 28 | 6113.80242 | 4.0055068 |
| Empresa 105 | 99.975 | 78.669 | 55.644 | 102.015 | 164.362 | 85.7728166 | 0.15346805 | 25 | 6138.7221 | 4.00406798 |
Con la ecuación (7), se calcula la columna 7, correspondiente al valor del índice global de desempeño corporativo por empresa. La ecuación (8) sirve para calcular los DPU en función del número de ejecutivos que le reportan al CEO; en seguida se tiene la equivalencia a DMPO, para finalmente expresar su nivel de desempeño en términos de número de sigmas con que opera cada organización.
De la tabla 7 se puede concluir que la empresa que tiene un mejor desempeño es la 9, con un valor de sigma de 4.03. Sin embargo aún tiene área de oportunidad para mejorar su desempeño global. Dentro de las últimas empresas están aquellas que obtuvieron valores por debajo de 3 sigmas, lo cual es alarmante.
Se obtuvo que 87.22% de las empresas de manufactura tiene un nivel de calidad aceptable (3 sigma o más), sin embargo el resto de ellas están por debajo de 3 sigmas; es justo en estas empresas donde debe implementarse un sistema de control estadístico de procesos, con la finalidad de encontrar las causas que originan las variaciones estadísticas en sus procesos.
ConclusionesEl avance tan rápido que se experimenta, hoy en día, en cuanto a la generación de nuevos conocimientos en la ciencia y la tecnología, genera importantes retos en relación con el desarrollo y aplicación de modelos creativos e innovadores en todas las organizaciones para resolver los diferentes problemas que les aquejan. El aprovechamiento de las ventajas de las tecnologías probadas y su fusión de manera innovadora, con toda seguridad resultan en nuevas formas de abordar y en- frentar eficientemente tales retos.
La evaluación, en tal contexto, resulta ser de suma importancia, ya que sin ella, no se puede determinar con toda precisión en qué condiciones se encuentra una organización, y mucho menos saber qué estrategias tiene disponibles para lograr un futuro más competitivo. Esto, como lo aseguran Kaplan y Norton (1996) aclara y traduce la visión y la estrategia, misma que debe medirse por indicadores cuantitativos, óptimos y objetivos.
El modelo matemático lineal obtenido de la alineación del BSC con SS permite una medición eficaz del desempeño corporativo en empresas manufactureras, pues ese modelo considera las relaciones existentes entre los indicadores de desempeño de una organización; es más sencillo de monitorear y se puede lograr su optimización a través de técnicas de control estadístico multivariante de la calidad.
La aplicación del modelo a las empresas que formaron parte de la investigación, dio como resultado que 87.22% tienen un nivel de calidad aceptable (3 sigma o más), quedando catalogadas como empresas con desempeño bueno o alto; las restantes (12.78%), se califican como empresas con desempeño bajo. Como se estableció en el presente trabajo, una calificación obtenida mediante la aplicación del modelo, identifica las estrategias que deben aplicarse para llevar a la empresa a mejores niveles de desempeño corporativo; sin embargo, este aspecto será motivo de un trabajo futuro.
El proyecto de investigación ha abierto la posibilidad de nuevos retos que atender, entre los inmediatos se pueden mencionar los siguientes entre muchos otros que seguramente surgen de los trabajos realizados:
- •
La aplicación del modelo a empresas manufactureras distintas a las que se refiere el estudio.
- •
El análisis estadístico-matemático del comportamiento de los IPDK.
- •
Valoración de resultados de la aplicación del proceso de jerarquía analítica y la metodología de investigación-acción (mejor conocida como Action Research).
- •
Construcción de intervalos de confianza para el IGDC, que ayuden al pronóstico del comportamiento de este.
Los autores agradecen el apoyo del Parque de Innovación y Desarrollo del Estado de Veracruz (PIDEV) ubicado dentro de las instalaciones del Instituto Tec- nológico y de Estudios Superiores de Monterrey, Campus Central de Veracruz; por su valioso apoyo en la aplicación del método Delphi a los expertos de empresas manufactureras de la región; asimismo, a los evaluadores (árbitros) por sus valiosas y atinadas correc- ciones, observaciones y sugerencias en relación con el desarrollo del presente trabajo.
Este artículo se cita:
Citación Estilo Chicago
Díaz-Castellanos, Elizabeth Eugenia, Carlos Díaz -Ramos, Luis Alberto Barroso-Moreno, Beatriz Pico-González. Desarrollo de un modelo matemático para procesos multivariables mediante Balanced Six Sigma. Ingeniería Investigación y Tecnología, XVI, 03 (2015): 419-430.
Citación Estilo ISO 690
Díaz-Castellanos E.E., Díaz-Ramos C., Barroso-Moreno L.A., Pico-González B. Desarrollo de un modelo matemático para procesos multivariables mediante Balanced Six Sigma. Ingeniería Investigación y Tecnología, volumen XVI (número 3), julio-septiembre de 2015: 419-430.
Elizabeth Eugenia Díaz-Castellanos. Estudiante del doctorado en planeación estratégica y dirección de tecnología en la Universidad Popular Autónoma del Estado de Puebla; se graduó con mención honorífica de la maestría en ingeniería industrial por el Instituto Tecnológico de Orizaba. Es ingeniera química con especialidad en alimentos. Ha trabajado como profesora en el departamento de ingeniería y negocios en el Instituto Tecnológico y de Estudios Superiores de Monterrey, Campus Central de Veracruz, ha sido docente en la carrera de ingeniería industrial en el Instituto Tecnológico de Orizaba y facilitadora en línea en el Instituto Consorcio Clavijero. Ha sido merecedora de premios nacionales como: Premio a la Mejor tesis de Posgrado a nivel nacional, otorgado por la Dirección General de Educación Tecnológica (DGEST) así como primero a los mejores estudiantes de ingeniería a nivel nacional otorgado por la Asociación Nacional de Facultades y Escuelas de Ingeniería (ANFEI).
Carlos Díaz-Ramos. Doctor en ciencias en ingeniería industrial (graduado con mención honorífica) por el Instituto Tecnológico de Orizaba. Es maestro en ciencias en investigación de operaciones por el Instituto Tecnológico y de Estudios Superiores de Monterrey, Campus Monterrey e ingeniero industrial en electricidad por el Instituto Tecnológico de Morelia. Cuenta con reconocimientos internacionales dentro de los que figuran: primer lugar en el sexto concurso nacional de tesis de posgrado, Who¿s Who in the World, Top 100 Engineers en el área de Ingeniería Industrial, premio al mérito académico otorgado por ANFEI. Ha sido Presidente de la Academia de Ingeniería Industrial en el Instituto Tecnológico de Orizaba. Director de tesis a nivel licenciatura, maestría y doctorado.
Luis Alberto Barroso-Moreno. Profesor asistente del Tecnológico de Monterrey Campus Central de Veracruz con doctorado en el área de ingeniería en sistemas por la Texas Tech University. Sus áreas de investigación se enfocan en: sistemas productivos, administración de la tecnología e ingeniería económica. Ha sido director del Departamento de Ingeniería en el Instituto Tecnológico y de Estudios Superiores de Monterrey y consultor de empresas en la región Córdoba-Orizaba.
Beatriz Pico-González. Doctora en planeación estratégica y dirección de tecnología por la Universidad Popular Autónoma del Estado de Puebla. Certificada en Lead auditor Training in Quality Management Systems. Miembro del Instituto Mexicano de Normalización y Certificación del comité técnico Núm. 9 como revisora de normas internacionales ISO 9000. Certificada bajo la Norma Técnica de Competencia Laboral para el Diseño e Impartición de Cursos de Capacitación. Actualmente funge como coordinadora del programa de doctorado y maestría en planeación estratégica y dirección de Tecnología en la Universidad Popular Autónoma del Estado de Puebla, forma parte del grupo de profesores que participan como instructores y o asesores del Cluster Lean Advancement Initiative México con sede en la UPAEP.