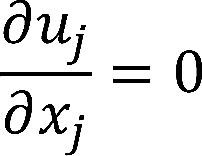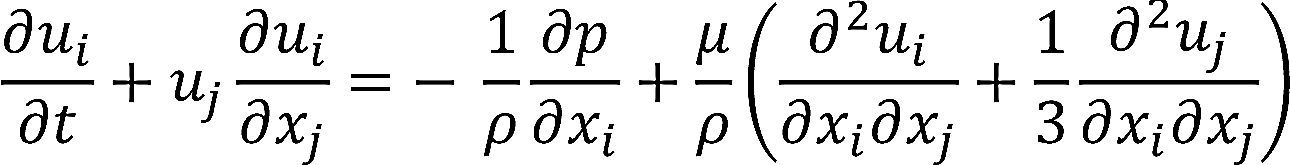Dinámica de fluidos computacional aplicada al estudio del flujo sanguíneo en el cayado aórtico humano y sus principales ramas

Resumen

El presente trabajo consiste en el uso de la dinámica de fluidos computacional para simular el flujo sanguíneo en el cayado aórtico humano y sus principales ramificaciones. Los datos utilizados para la simulación se tomaron de un individuo masculino de 30 años de edad que no presentó patologías en el sistema estudiado, la geometría del dominio se obtuvo a partir de una Tomografía Axial Computarizada y las condiciones de borde de flujo y presión se tomaron de los resultados de Ultrasonido Doppler y Esfigmanometría, respectivamente. Los parámetros impuestos como condiciones de borde variaron en el tiempo según un patrón sinusoidal entre los valores extremos registrados y una frecuencia igual a la del pulso cardiaco. La simulación numérica revela que las regiones sometidas a mayores solicitaciones mecánicas se encuentran en las raíces de las ramificaciones del cayado aórtico.

Abstract

In the present study the computational fluid dynamics approach was used to simulate the blood flow in the human aortic arch and its main branches. The data used in the simulation were obtained from a 30 years-old healthy male without any cardiovascular disease. The geometry of the domain was obtained from a Axial Computed Tomography and the flow and pressure boundary conditions were measured with Doppler Ultrasound and Sphygmomanometry, respectively. The imposed boundary conditions varied over time with a sinusoidal pattern ranging between the extreme registered values and a frequency identical to the heart rate. The numerical simulation reveals that regions subjected to higher mechanical solicitations are located in the roots of the branches of the aortic arch.

Introducción

La simulación del flujo sanguíneo es un problema de gran complejidad que debe considerar su carácter transitorio y pulsátil, además de involucrar geometrías irregulares, la elasticidad de los grandes vasos y el comportamiento no newtoniano de la sangre en pequeños vasos (menores a 100 μm de diámetro).

Modelos unidimensionales con distintos niveles de complejidad han logrado reproducir con gran exactitud la distribución temporal de presión y flujo a lo largo del sistema circulatorio. Trabajos como el de Olufsen et al. (2000) han reportado errores relativos por debajo de 3% al comparar el resultado de modelos unidimensionales contra estimaciones de flujo calculadas a partir de imágenes de resonancia magnética, lo que valida la aplicación de estos modelos para simular flujos hemodinámicos tanto en condiciones normales como patológicas (Fu et al., 2010; Hsiao et al., 2012; Kousera, 2013).

La evolución de las técnicas de dinámica de fluido computacional (CFD) ha permitido en las dos últimas décadas desarrollar simulaciones numéricas tridimensionales para porciones muy pequeñas del sistema cir- culatorio, principalmente para estudiar los patrones de flujo en prótesis y stents (Otha et al., 2003; Murphy y Boyle, 2007; Fu et al., 2010; Bresch et al., 2010; Hsiao et al., 2012), y estudiar variables hemodinámicas relacionadas a la formación de aneurismas y la aterogénesis (Shahcheraghi et al., 2002; Chen y Lu, 2006; Shimogonya et al., 2009).

El comportamiento no-newtoniano de la sangre se ha incorporado en la simulación de flujos en pequeños vasos, utilizando los modelos de viscosidad de Carreu-Yasuda, Casson y las disintas modificaciones de la Ley de Potencia (Prektold et al., 1991; Gijsen et al., 1999; Chen y Lu, 2006; Jozwik y Obidowski, 2010).

La viscosidad sanguínea se determina principalmente por el hematocrito (proporción volumétrica de los eritrocitos, que normalmente se encuentra en el rango de 0.45 a 0.55). Se ha descrito empíricamente que esencialmente dos condiciones generan un comportamiento no-newtoniano de la sangre en condiciones fisiológicas, a saber:

• a)

  bajas tasas de cizallamiento, en las cuales la viscosidad tiende a aumentar y

• b)

  diámetro del vaso inferior a 100 μm, en los cuales la viscosidad tiende a disminuir.

Este último efecto es el de mayor importancia fisiológica y se denomina efecto Fahreus-Lindqvist. Este se atribuye al incremento relativo del espesor de capa libre de células respecto al radio del vaso y al alineamiento axial de los eritrocitos (Nichols et al., 1990).

En vasos de mediano y gran calibre el diámetro eritrocitario, así como la capa limite libre de células adyacente al endotelio es despreciable, en comparación con el diámetro del vaso. De igual manera, en estos vasos las tasas de cizallamiento, presiones y velocidades son significativamente superiores a los de la microcirculación. Esto hace que en condiciones fisiológicas la relación entre el esfuerzo cortante y la tasa de cizallamiento de la sangre sea lineal (viscosidad constante) en los grandes vasos, esto es, se comporta como un fluido newtoniano, por tanto, puede simularse su flujo adecuadamente despreciando su estructura corpuscular y aplicando la teoría del continuo (Nichols et al., 1990). Esta observación se ha validado ampliamente, reportándose errores por debajo de 2% contra mediciones in-vitro e in-vivo para vasos de diámetro superior a 1 mm y concentración normal de hematocrito (Taylor, 1959; Milnor, 1989).

Respecto a las geometrías utilizadas, algunos autores recurren a simplificaciones con volúmenes regulares cuyas dimensiones coinciden con las medidas promedio de diámetro y longitud de los vasos (Chen y Lu, 2004; Nguyen et al., 2008). Para el estudio en vasos grandes se ha logrado utilizar la información adquirida de una tomografía axial computarizada (TAC) para el modelado geométrico del dominio de simulación, por lo general, en pacientes sanos (Shahcheraghi et al., 2002; Fu et al., 2010; Reymond et al., 2012).

Este trabajo consiste en la simulación numérica de un flujo pulsátil en el arco aórtico y sus tres ramificaciones, en donde se utilizó la geometría obtenida mediante TAC de un hombre adulto sin deformaciones patológicas. Las condiciones de borde utilizadas para el problema se basaron en mediciones tomadas directamente del sujeto en cuestión, lo cual abre las posibilidades de su uso en la práctica clínica personalizada.

Metodología

Objeto de estudio

La simulación computacional se realizó con base en la información anatómica y hemodinámica obtenida de un individuo masculino de 30 años de edad, 182 cm de estatura, 72 kg de peso corporal, superficie corporal de 1.90 m² de acuerdo al normograma de Dubois-Dubois e índice de masa corporal de 21.74 kg/m².

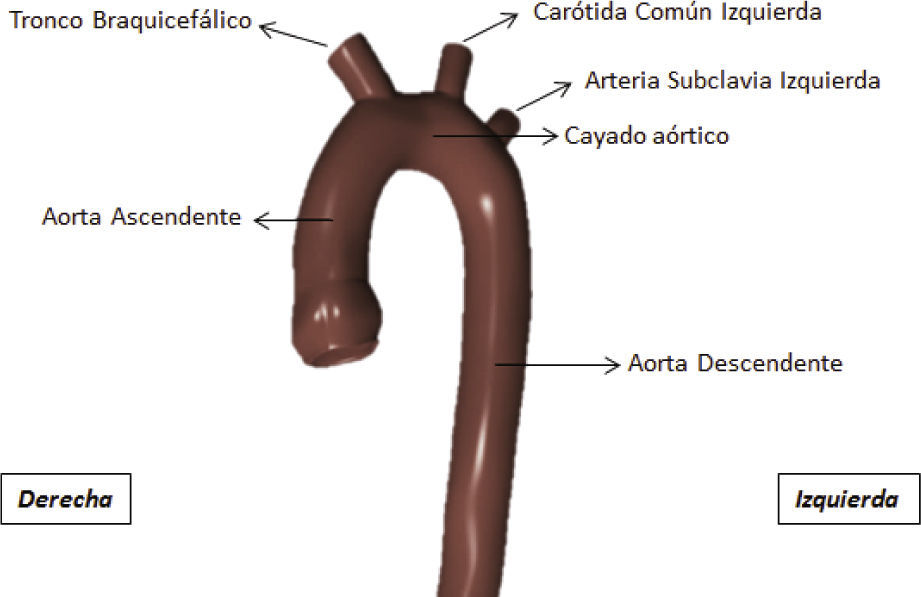
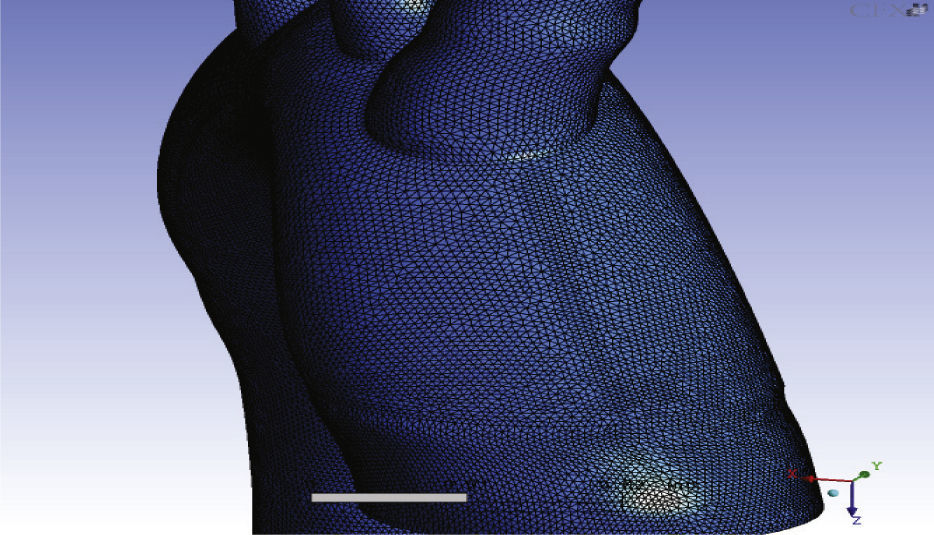
Geometría

El dominio espacial tridimensional de la simulación está comprendido en términos generales por la aorta torácica y el tramo proximal de sus tres ramas, enfocándose la atención en el cayado aórtico en donde se originan las 3 ramas (figura 1).

Figura 1.

Vista frontal de la aorta torácica en donde se señalan sus tramos y ramas.

La TAC se obtuvo con un tomógrafo marca Toshiba® modelo Aquillion de 64 canales (alta resolución) del Servicio de Radiodiagnóstico del Hospital Universitario de Caracas.

Se realizó una venoclisis en la fosa cubital anterior del miembro superior izquierdo a la persona estudiada, a través de la cual se le administró 150 mL de contraste yodado iónico (Iotalamato Meglumina, Conray®). También se sometió a hiperhidratación con solución isotónica (NaCl 0.9% a razón de 1L/hora) por una hora antes y después de la realización de la tomografía, a fin de evitar la nefrotoxicidad del contraste yodado.

Se emplearon los protocolos estandarizados que implican la obtención de un barrido desde el nivel de la segunda vértebra cervical hasta el diafragma en primera instancia sin contraste endovenoso. Posterior a la inyección se realizaron barridos tomográficos con intervalos preestablecidos a fin de obtener imágenes en donde el contraste se encontrara distribuido en el compartimiento venoso, y posteriormente en el arterial. El establecimiento de dichos intervalos es empírico, por lo que en ocasiones se obtuvieron imágenes en fase arterial con presencia residual de contraste en las venas (Seeram, 2001). Se obtuvieron cortes transversales, separados entre sí en el eje axial (caudo-cefálico) por 4 mm. El procedimiento no presentó complicaciones inmediatas, mediatas, ni tardías.

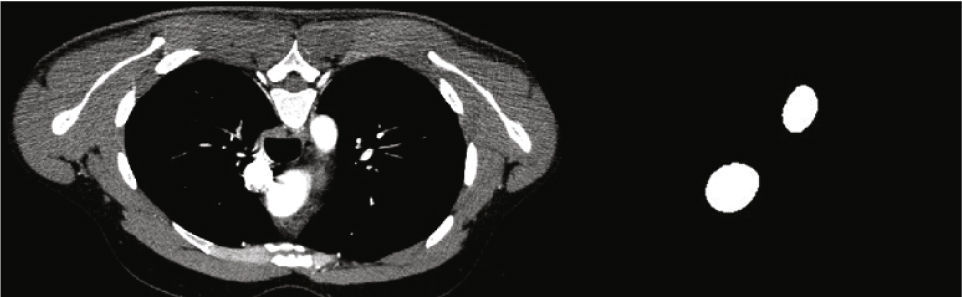
Una vez identificados los contornos de los vasos de interés manipulando el contraste de las imágenes tomográficas (empleando modificaciones de la ventana de unidades Hounsfield, figura 2), se definieron los ejes axiales de los mismos, asimismo se realizaron cortes transversales a dichos ejes cada 4 mm y se calculó el área y las coordenadas de los centroides de dichos cortes referidos a un sistema cartesiano global.

Figura 2.

Identificación de los contornos de la aorta ascendente y descendente a partir del TAC.

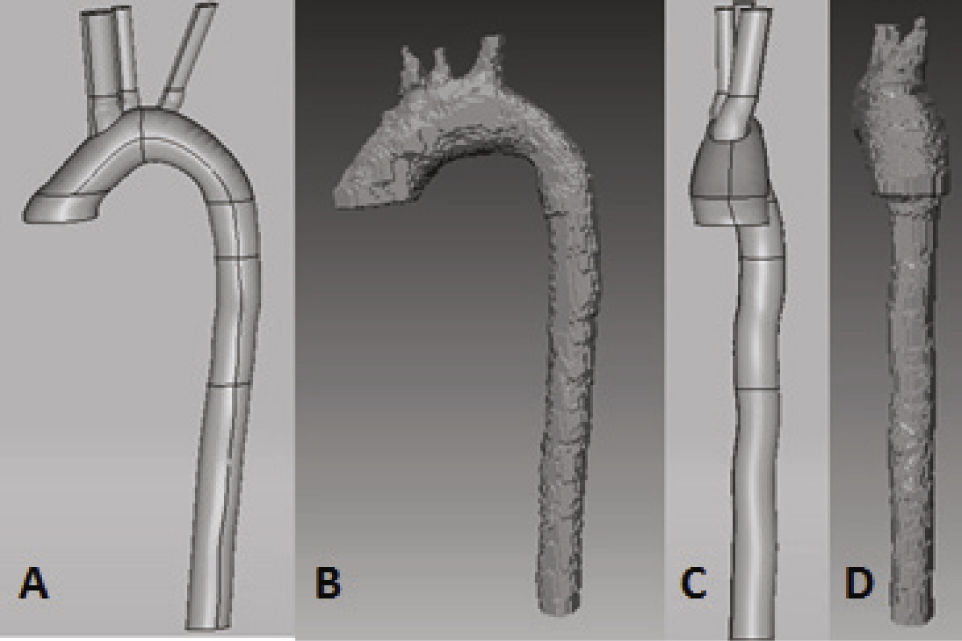
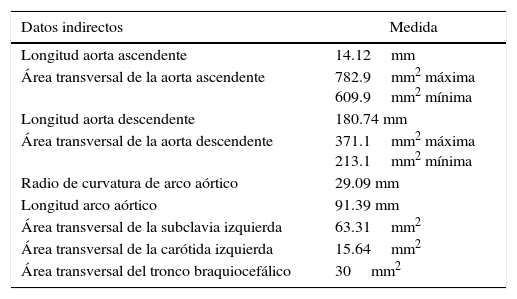
A partir del área y las coordenadas de los centroides, se reconstruyó la geometría sustituyendo los cortes irregulares por circunferencias con la misma área y centroide, a partir de la unión de estas circunferencias se generó un sólido que asegura las mismas áreas de flujo que la reconstrucción tomográfica, pero con superficies más suaves y regulares, lo que facilita el proceso de simulación numérica del flujo sanguíneo (figura 3). Adicionalmente se extendieron los ramales aórticos en trayectoria recta una longitud igual a cinco veces el diámetro del tronco braquicefálico con la misma orientación del último tramo de arteria registrado, esto último para minimizar los efectos de las simplificaciones en las condiciones de borde sobre la solución en el dominio de interés, particularmente la emergencia de las ramas de cayado aórtico por ser asiento preferencial de patologías vasculares. Las características más relevantes de la geometría estudiada se resumen en la tabla 1.

Figura 3.

Comparación de la TAC (B y D) con la reconstrucción geométrica (A y C).

Tabla 1.

Características geométricas del dominio

Datos indirectos	Medida
Longitud aorta ascendente	14.12 mm
Área transversal de la aorta ascendente	782.9 mm^2 máxima 609.9 mm^2 mínima
Longitud aorta descendente	180.74 mm
Área transversal de la aorta descendente	371.1 mm^2 máxima 213.1 mm^2 mínima
Radio de curvatura de arco aórtico	29.09 mm
Longitud arco aórtico	91.39 mm
Área transversal de la subclavia izquierda	63.31 mm^2
Área transversal de la carótida izquierda	15.64 mm^2
Área transversal del tronco braquiocefálico	30 mm^2

Modelo matemático

Para la resolución de los patrones de flujo en el dominio se consideró la sangre como un fluido incompresible, homogéneo y newtoniano, lo que ha demostrado ser una buena aproximación en el estudio del flujo en grandes vasos (Taylor, 1959; Milnor, 1989; Nichols et al., 1990). Para el flujo en grandes arterias como las consideradas en este trabajo (el cayado de la aorta y sus ramas), la consideración de la sangre como un líquido newtoniano es una buena aproximación, es decir, la variación de la viscosidad para una velocidad de corte de 10^-2s^-1 se manifiesta dentro del error experimental, cuando el hematocrito es de 44% y no existe campo del esfuerzo (Chmiel y Walitza, 1980). Se consideró flujo estrictamente laminar en el dominio, por lo que no se incorporó ningún modelo de turbulencia al sistema de ecuaciones. Esto último concuerda con mediciones empíricas hechas in-vivo sobres caninos, equinos y humanos, donde se reportan regímenes de flujo laminar en grandes vasos (Seed y Wood, 1971; Schultz, 1972; Caro et al., 2012). Desde el punto de vista de la mecánica de fluidos se justifica el uso del modelo de flujo laminar, ya que el rango de número de Reynolds reportado en el tramo arterial a estudiar se encuentra entre 400-1100, por debajo del límite universalmente aceptado para la transición a la turbulencia (Nichols et al., 1990).

Tomando en cuenta las consideraciones de la tabla 1, el modelo numérico a resolver en el dominio incluye la ecuación de continuidad (1) y la ecuación de Navier-Stokes (2) en su forma tridimensional cartesiana para flujo incompresible

En donde la densidad se fijó con un valor de r = 1050 kg/m³ y una viscosidad de m = 3.5 mPa s, de acuerdo con los parámetros de normalidad para un individuo con hematocrito = 44% y sin hemoglobinopatías tal como el que se estudió. El término gravitatorio en la ecuación de Navier-Stokes se omitió, ya que su magnitud es despreciable en comparación con los términos advectivo y difusivo.

Condiciones de contorno

Todas las condiciones de contorno impuestas se basaron en mediciones realizadas directamente sobre el objeto de estudio. Se realizaron mediciones de velocidad utilizando ecosonografía Doppler, empleando un equipo Sonoscape modelo ssi-5000 del Servicio de Cardiología del Hospital Universitario de Caracas, operado por el equipo técnico capacitado que lleva a cabo los estudios rutinariamente en dicha unidad. Las presiones impuestas se midieron por el método esfigmanométrico en la arterial braquial, lo cual representa una aproximación razonable con base en reportes invasivos (Kousera et al., 2013; Milnor, 1989), con un error absoluto (instrumental y humano) alrededor de 4% respecto a mediciones invasivas (Bakris et al., 2004). Además, si el contorno de curva presión-tiempo se modifica en la arteria braquial respecto a la subclavia, en términos de magnitudes (y bajo condiciones no patológicas) el error de la aproximación propuesta es del orden de 3% para la presión sistólica (donde es superior en la arterial braquial respecto a la subclavia) y de 1.5% para la diastólica (que es inferior en la arterial braquial) (Nichols et al., 2011). Desde el punto de vista técnico, ambas mediciones se realizaron siguiendo las pautas de la American Heart Association (Bakris et al., 2004).

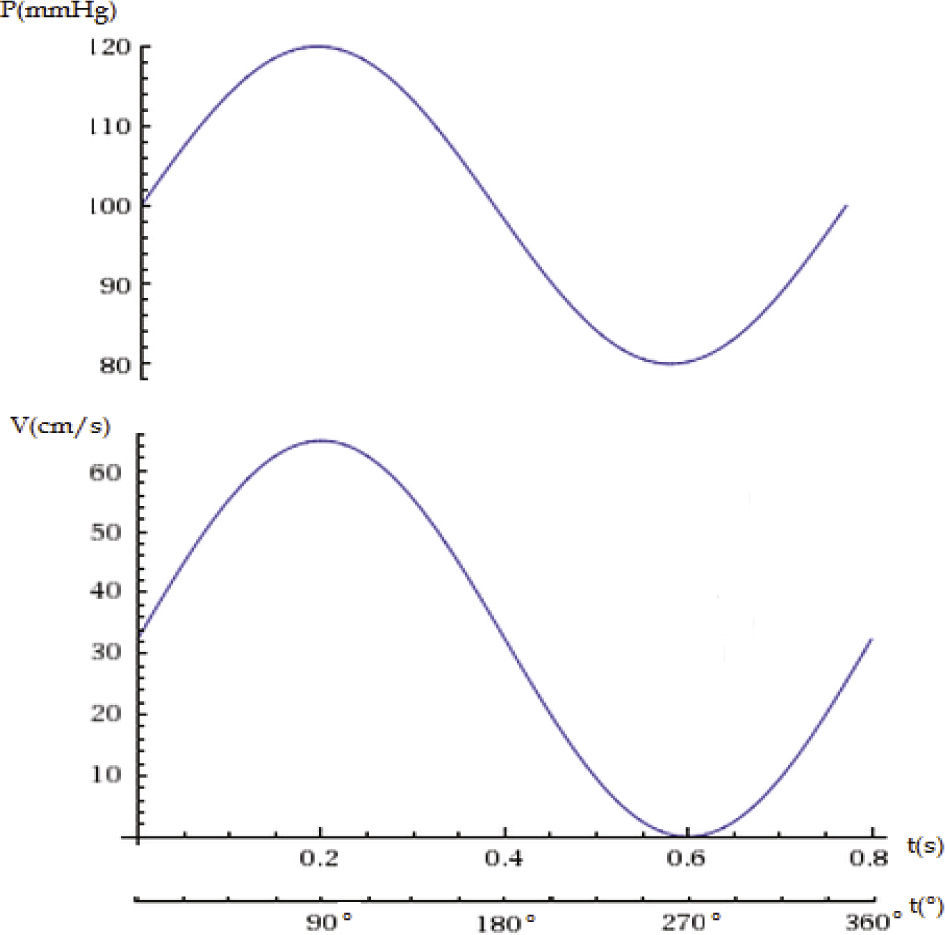
Las paredes de los vasos se consideraron complemente rígidos y en todas ellas se aplicó la condición de no deslizamiento del fluido. En la entrada de la aorta ascendente se impuso un perfil de velocidad uniforme con la magnitud de la velocidad promedio y ortogonal a la superficie. La magnitud de la velocidad de entrada varió con el tiempo, utilizando una función sinusoidal con un período igual al del ciclo cardíaco y una amplitud igual a la diferencia máxima de velocidades registrada por la ecosonografía (figura 4). En la salida de la aorta descendente se impuso un flujo igual a 85% del flujo en la aorta ascendente, este porcentaje se consideró constante en el tiempo (Milnor, 1989).

Figura 4.

Variación temporal de la velocidad impuesta en la entrada de la aorta ascendente y de la presión impuesta en cada descarga de las ramas principales.

En las descargas de las tres ramas se impuso una condición tipo “opening” (abierta) para poder representar el flujo retrógrado esperado durante cada ciclo cardíaco, debido a la desaceleración del flujo, propia de su comportamiento pulsante. En cada una de las tres secciones se impuso una distribución uniforme de presión cuya magnitud se varió en el tiempo según una función sinusoidal en fase con el pulso de velocidad, las magnitudes de la presión máxima y mínima se igualaron a las mediciones de presión sistólica y diastólica realizadas en el objeto de estudio (figura 4). Se utilizó una función sinusoidal, ya que su desviación media en el rango 80-120 mmHg es del orden de 10% cuando se compara con la curva “real” medida en forma invasiva y en el rango 120-80 mmHg la desviación media con la curva “real” es del orden de 20% (Nichols et al., 2011). Indudablemente dicha aproximación es una limitación del presente estudio y en futuros desarrollos se planea incorporar una función presión-tiempo más aproximada a la realidad fisiológica.

Condiciones iniciales

Con el objeto de reducir el tiempo de convergencia de la simulación transitoria se desarrolló en primer lugar una simulación estacionaria, el campo de velocidad y presión obtenido se utilizó como condición inicial de la simulación transitoria. Las condiciones de contorno impuestas para simulación estacionaria se resumen en la tabla 2.

Tabla 2.

Condiciones de contorno para la simulación pulsátil y estacionaria

Borde	Parámetro	Valor (Caso estacionario)	Valor (Caso pulsátil)	Método de medición
Inicio de la aorta ascendente (entrada única)	Velocidad	V = 35.4cm/s	Vmax = 64.9cm/s Vmin = 0	Ultrasonido Doppler
Sección distal de las 3 ramas del cayado aórtico (salidas)	Presión manométrica	P = 100mmHg	Pmax = 120mmHg Pmin = 82 mmHg	Esfigmomanometría
Sección distal de la aorta torácica (salida)	Proporción del caudal	85% del caudal de entrada al dominio	85% del caudal de entrada al dominio (acoplado en términos absolutos a la fluctuación de la velocidad en la entrada)	Velocidad medida por ultrasonido Doppler y el diámetro del vaso medido por imagen tomográfica

Aun cuando en un flujo de características pulsantes la condición inicial no interviene en la solución periódica transitoria (el comportamiento de los campos se repite periódicamente luego de un tiempo suficiente después del inicio del flujo, lo que corresponde al funcionamiento normal del corazón), se define tal condición inicial para comenzar con campos de velocidad y presión tendientes a la solución periódica transitoria, disminuyendo así el número de ciclos necesarios para alcanzar tal condición. En este trabajo la condición de flujo periódico transitorio se alcanzó luego de dos ciclos cardiacos, sin embargo los resultados presentados corresponden al cuarto ciclo cardiaco a fin de evitar la influencia de la condición inicial en la solución.

Resolución numérica

El software Ansys CFX 10 se utilizó para la resolución de las ecuaciones del modelo numérico (1 y 2) mediante el método de volúmenes finitos. Los términos transitorios se discretizaron utilizando un esquema de Euler “hacia atrás” (backward) de segundo orden, mientras que un esquema de alta resolución se utilizó para discretizar los términos advectivos. Los términos difusivos y el gradiente de presión se discretizaron bajo un esquema estándar de funciones de forma para Elementos Finitos, utilizándose interpolaciones trilineales para la estimación de los gradientes de las funciones de forma. Se lograron resultados independientes de la malla de discretización con 487.007 elementos tetraédricos desestructurados. En las figuras 5 y 6 se observan detalles de la malla de cálculo.

Figura 5.

Detalle de la malla de cálculo. Vista lateral derecha (desde la perspectiva de un plano sagital ubicado a la derecha del dominio).

Figura 6.

Detalle de la malla de cálculo. Vista superior (céfalo-caudal) desde la perspectiva de plano transversal superior al dominio. De izquierda a derecha se observan el tronco braquicefálico, la carótida izquierda y la subclavia izquierda.

Resultados y análisis

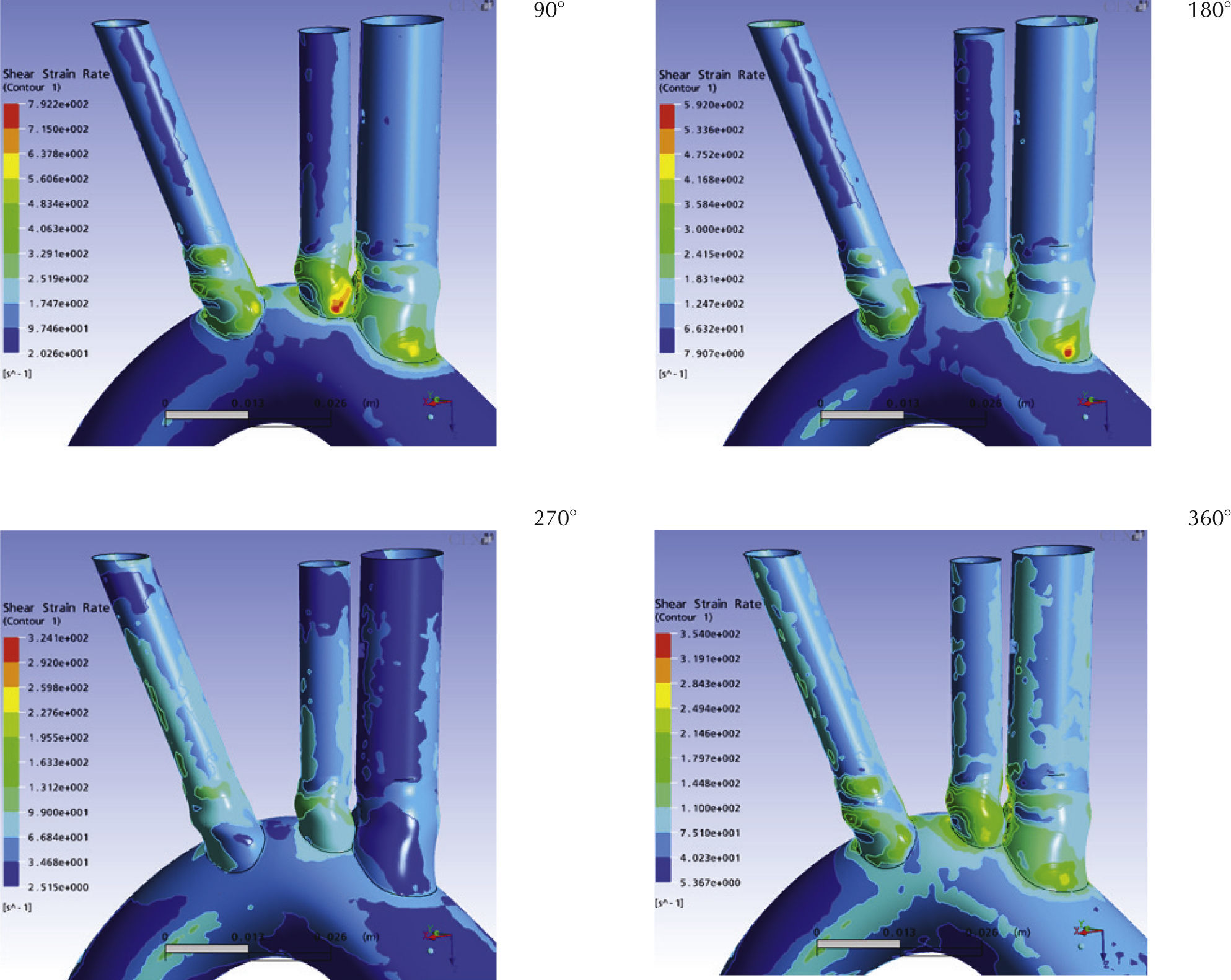
Es importante destacar en esta sección que debido a la irregularidad y asimetría del dominio estudiado la presentación gráfica de resultados requiere la utilización de varios planos de visualización. A continuación se presenta la distribución de las variables velocidad, presión y esfuerzo cortante para cuatro instantes del ciclo simulado, estos son a un cuarto (90°), medio (180°), tres cuartos (270°) y el final del ciclo (360°). Se presta especial interés a la distribución de las variables en el inicio de las ramificaciones del arco aórtico. La frecuencia cardiaca fue de 75 latidos/minuto, por lo que dichos instantes corresponden a 0.2s (90^o); 0.4s (180^o); 0.6s (270^o) y 0.8s (360^o, final del ciclo).

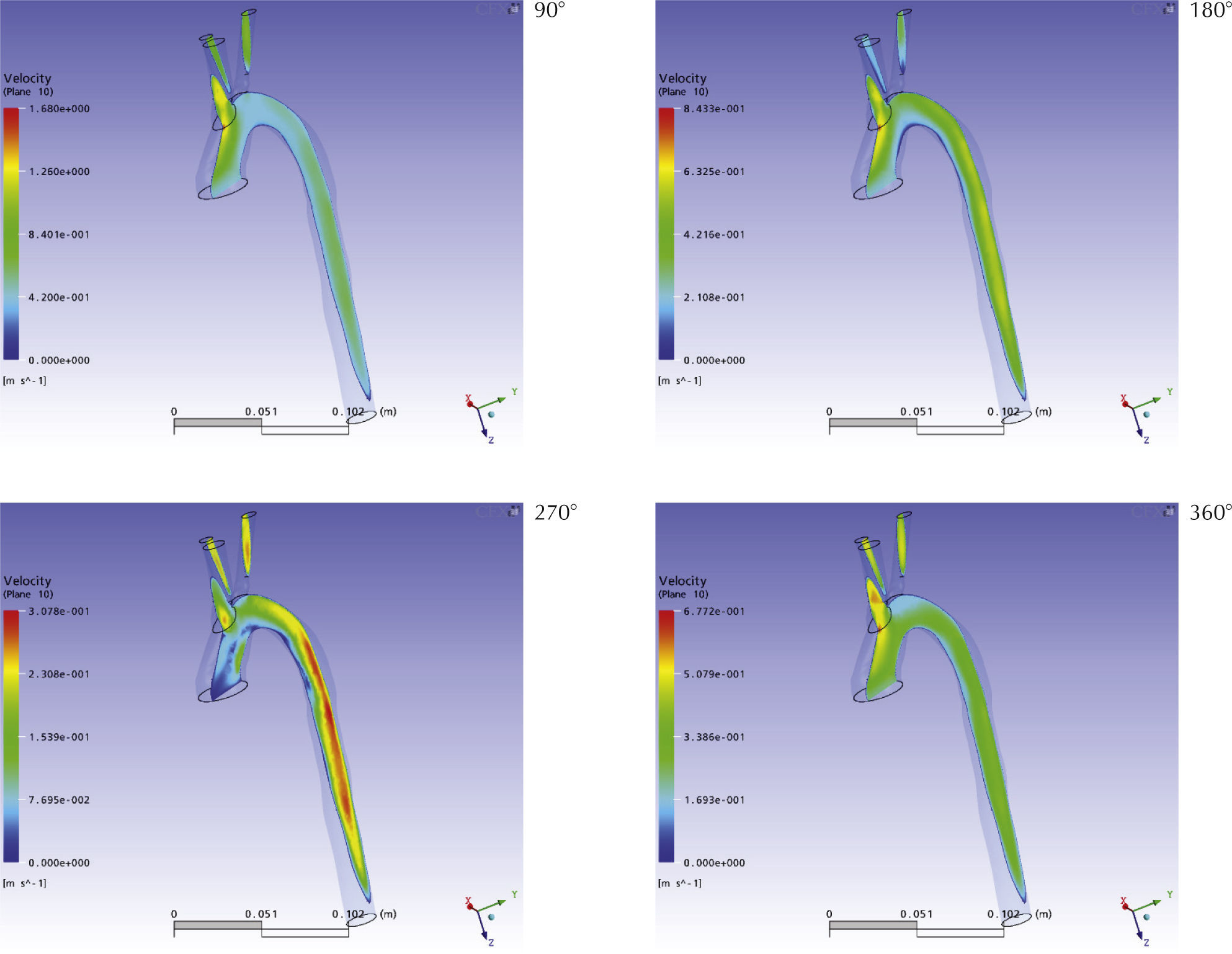
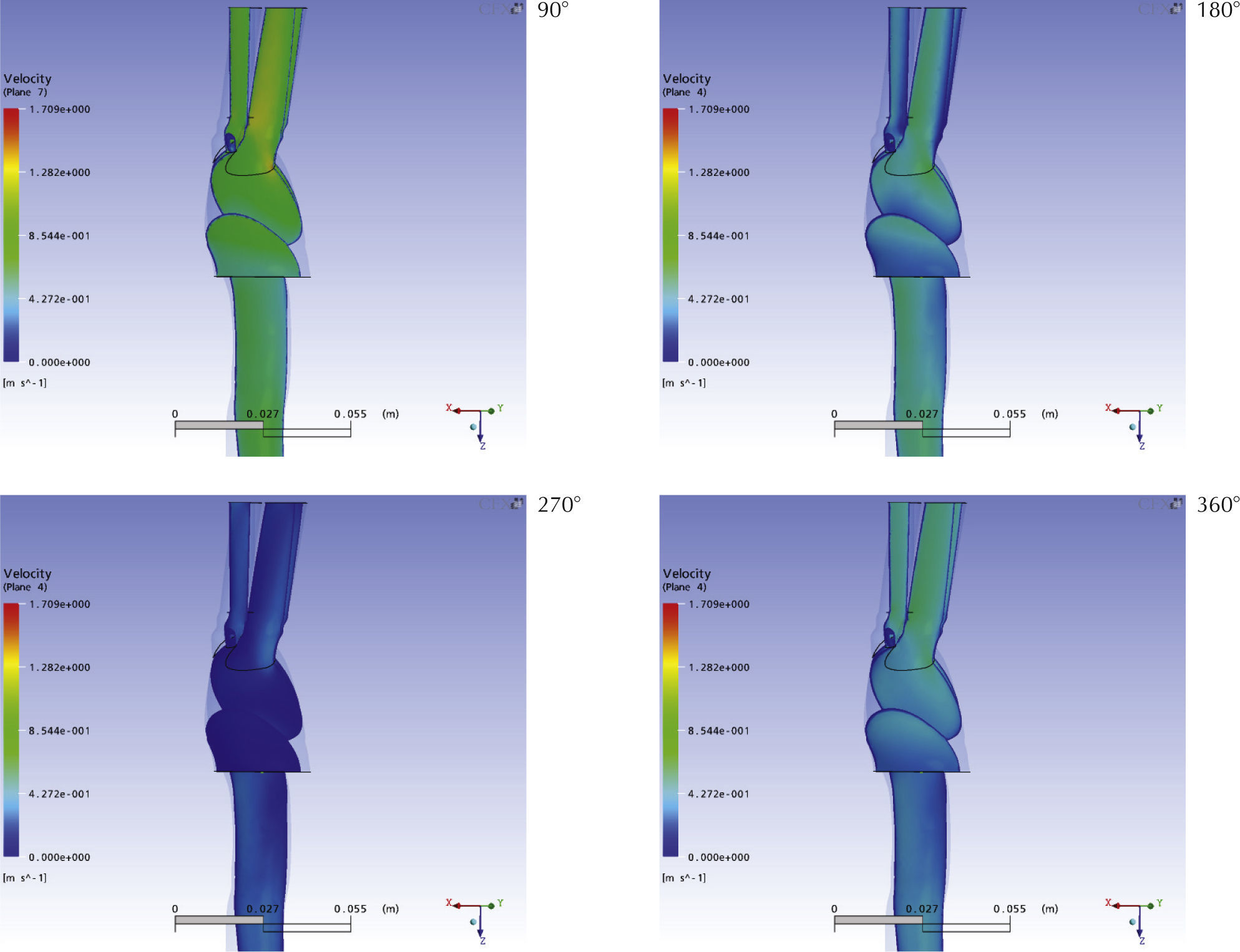
Velocidad

La figura 7 muestra la distribución de magnitud de velocidad en un plano coronal secante al dominio, mientras que la figura 8 muestra la misma variable sobre planos sagitales superpuestos. Ambas figuras son complementarias y en ellas puede apreciarse que a 25% del ciclo (90°) ya existe un perfil de velocidades claramente establecido en la aorta, con mayores velocidades en la mitad proximal del cayado y la aorta descendente, respecto a la segunda mitad del cayado. A su vez, la distribución no es axisimétrica, ya que existen mayores velocidades (del orden de 0.8m/s) hacia la curvatura externa (extrados) del cayado. En cuanto a las ramas, las mayores velocidades axiales se alcanzan en el tronco braquiocefálico. Hacia la mitad del ciclo (180°) el perfil de velocidad parece estar completamente desarrollado, pero ya se evidencia disminución de las velocidades axiales en aproximadamente 0.6m/s. De esta manera el pico de velocidades se alcanza previo a los 180°, momento en el que por otra parte se logran las mayores presiones impuestas como condiciones de frontera.

Figura 7.

Distribución de la magnitud de la velocidad.

Figura 8.

Distribución de la magnitud de la velocidad en planos sagitales superpuestos.

A los 270° las velocidades dentro del dominio son en promedio las menores durante todo el ciclo cardíaco, en donde los máximos valores del orden son de 0.3m/s en el axis en la aorta descendente. En relación con el cayado aórtico, la distribución de velocidades no muestra un perfil evidente con velocidades de 0.06m/s en su primera mitad, e incluso velocidades cercanas a cero en la raíz.

La región crítica del tronco braquiocefálico presenta en este punto velocidades aun superiores a las del cayado (0.3m/s). También es de importancia que en este momento las máximas velocidades en el cayado están situadas en la curvatura mayor de su segunda mitad, con un patrón que se hace continuo con el perfil pseudoparabólico en la aorta descendente.

Al final del ciclo (360°) hay un incremento en las velocidades de la aorta, con cifras de alrededor de 0.4m/s y un perfil poco desarrollado y considerablemente aplanado. Esto tiene relación con el breve período de reaceleración, congruente con el patrón trifásico fisiológico en los grandes vasos.

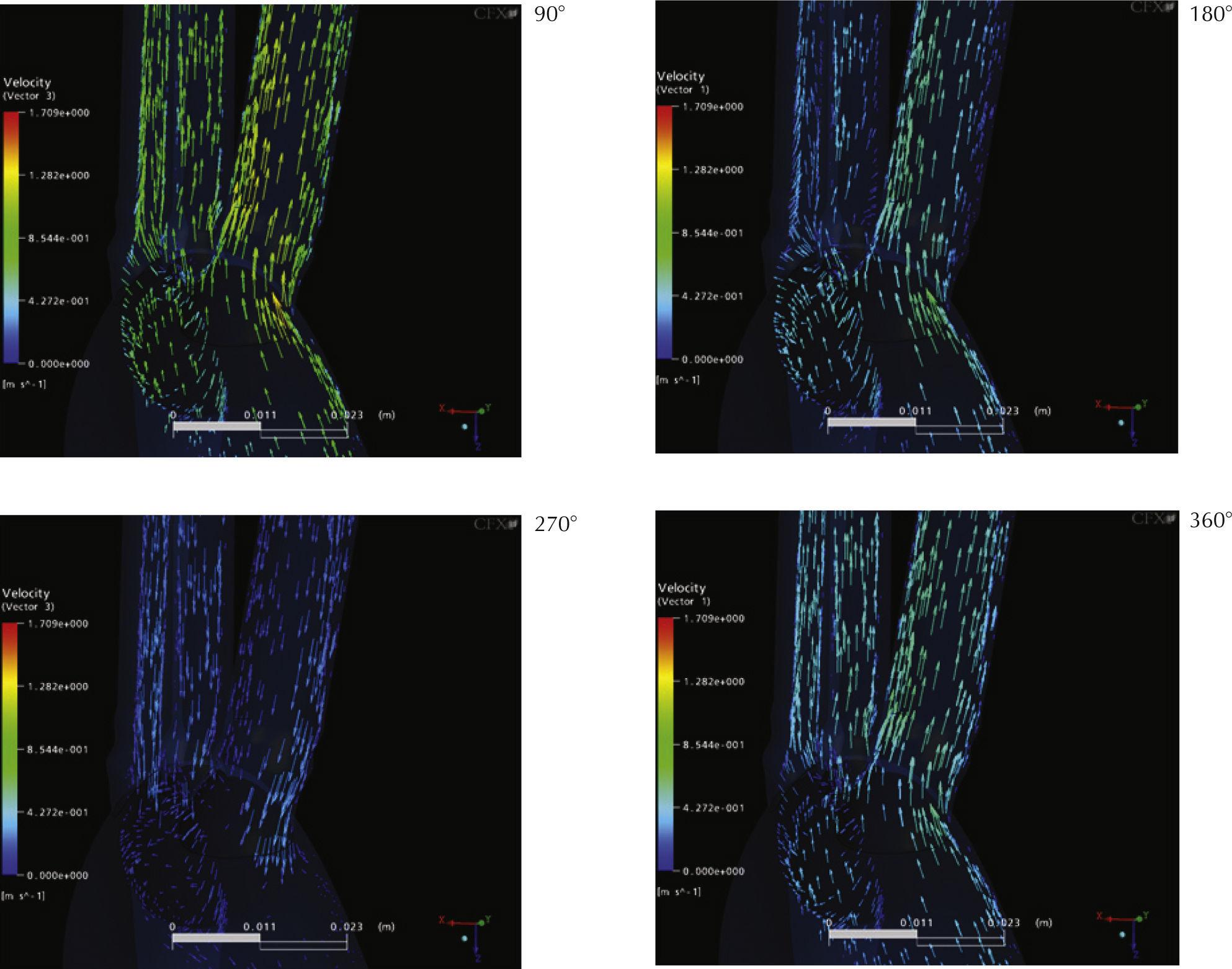
La figura 9 presenta el detalle de los vectores de velocidad en la aorta ascendente, tronco braquiocefálico y carótida izquierda. En esta figura puede apreciarse el fenómeno de flujo retrogrado ocurriendo al- rededor de 75% (270^o) del ciclo, dicho fenómeno responde a la desaceleración del flujo de entrada y la imposición de presiones positivas en los extremos de las ramificaciones. Para el final del ciclo el flujo restituye su dirección anterógrada (“aguas abajo”) tal como en el patrón fisiológico clásicamente descrito (Milnor, 1989).

Figura 9.

Vectores de velocidad en el cayado aórtico, tronco braquiocefálico y carótida izquierda.

La magnitud de las velocidades obtenidas, así como la ocurrencia del fenómeno de flujo retrógrado y su magnitud presentan una considerable congruencia con mediciones experimentales reportadas previamente por Kousera et al. (2013); Milnor (1989) y Nichols et al. (1990). Sin embargo se encontró que los resultados obtenidos, específicamente la ocurrencia de las velocidades extremas y el flujo retrógrado, presentaron un des- fase temporal de acuerdo con lo registrado en la literatura. La razón se discutirá más adelante.

El pico de velocidad reportado en la literatura ocurre aproximadamente a los 70° del ciclo, mientras que en la simulación numérica se obtuvo a los 90°. La ocurrencia del flujo retrógrado se encuentra comúnmente registrada aproximadamente a mitad del ciclo (180°) mientras que en la simulación propuesta ocurre a los 270°.

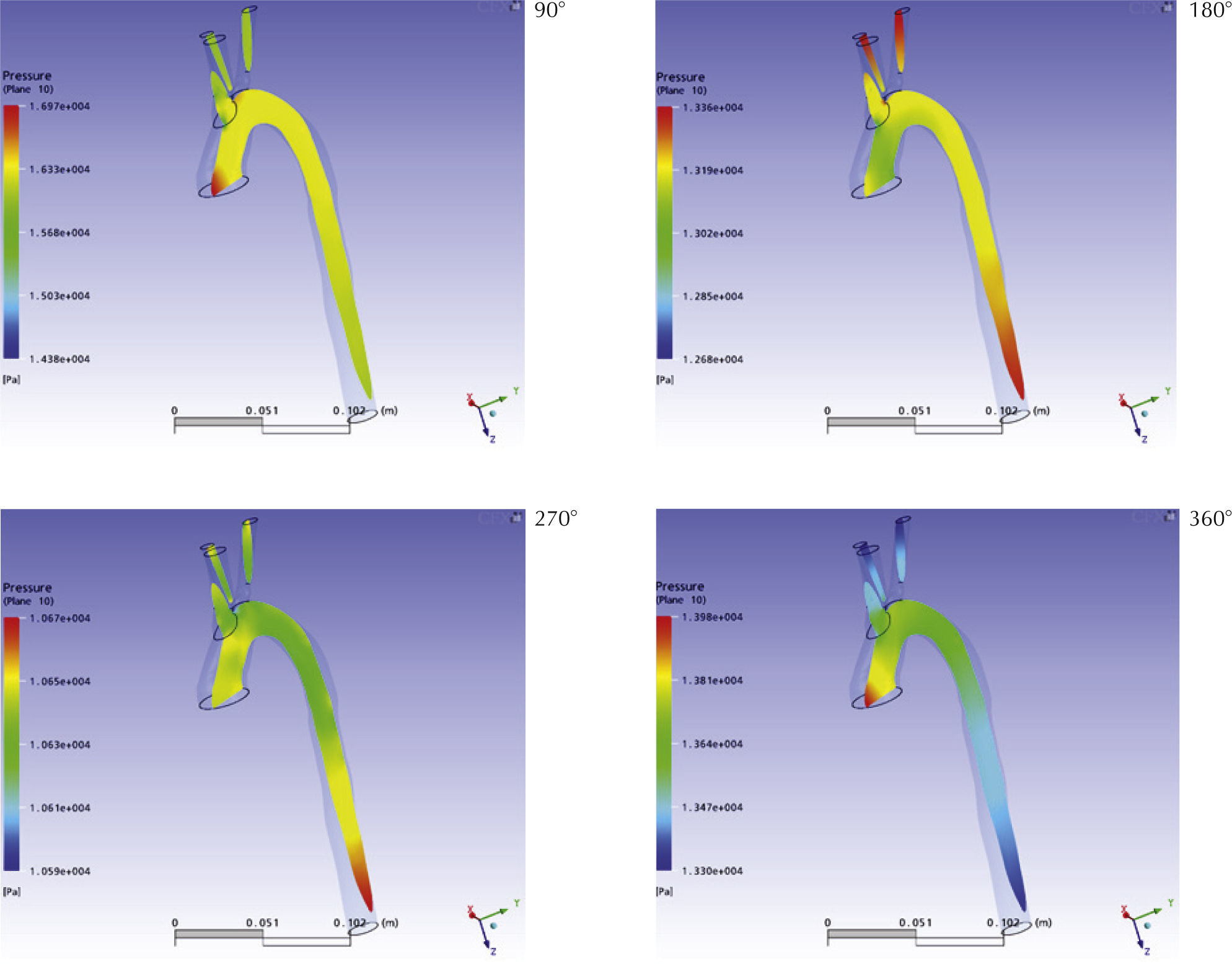
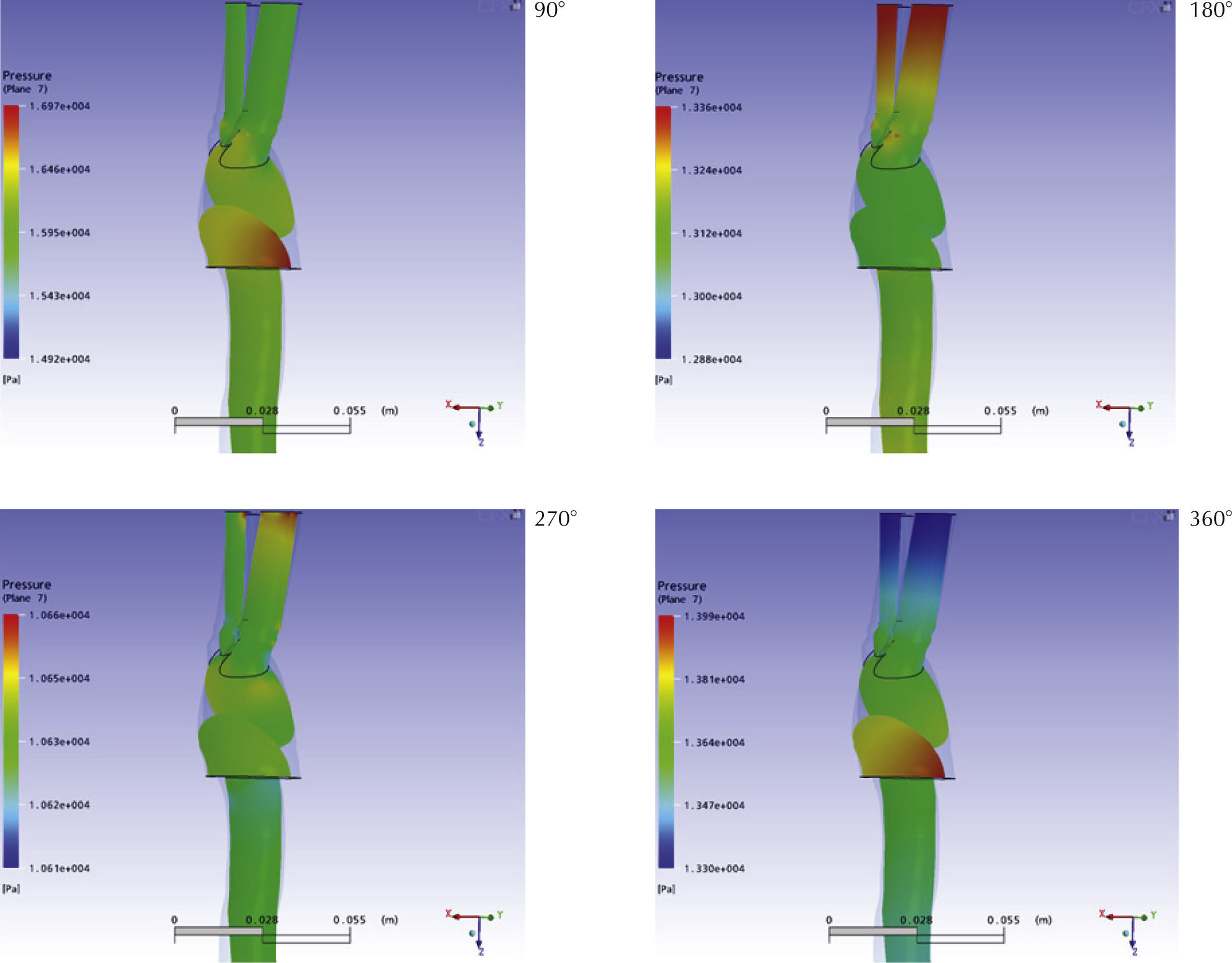
Presión

Las figuras 10 y 11 muestran la distribución de presión estática sobre un plano secante y planos sagitales superpuestos, respectivamente. En ellos se aprecia que la presión en la raíz de la aorta ascendente alcanza su máximo aproximadamente a los 90° con una magnitud de 16 kPa manométricos, dicha presión disminuye hasta alcanzar un mínimo de 10 kPa a los 270° del ciclo para luego incrementarse hasta 13 kPa al final del mismo, observaciones que concuerdan con los patrones descritos en la literatura clásica (Nichols et al., 1990). En cambio, la presión en los extremos de las ramas alcanzan su máximo a los 180° según las condiciones de contorno impuestas, lo que ocasiona que, hacia la mitad del ciclo las presiones en las ramificaciones sean mayores que en cayado, lo que explica la ocurrencia del flujo retrógrado identificado en la sección anterior. La presión en la aorta descendente presentó una distribución temporal similar a la que se encontró en la aorta ascendente, pero con magnitudes aproximadamente 6% inferiores.

Figura 10.

Distribución de presión en un plano coronal aproximadamente congruente con el eje del dominio.

Figura 11.

Distribución de presión. Planos sagitales.

Los resultados obtenidos concuerdan con las observaciones aun válidas de Womersley y McDonald (Nichols et al., 1990) sobre la tendencia de la presión sis- tólica a incrementarse en la dirección del flujo mientras que la diastólica tiende a disminuir.

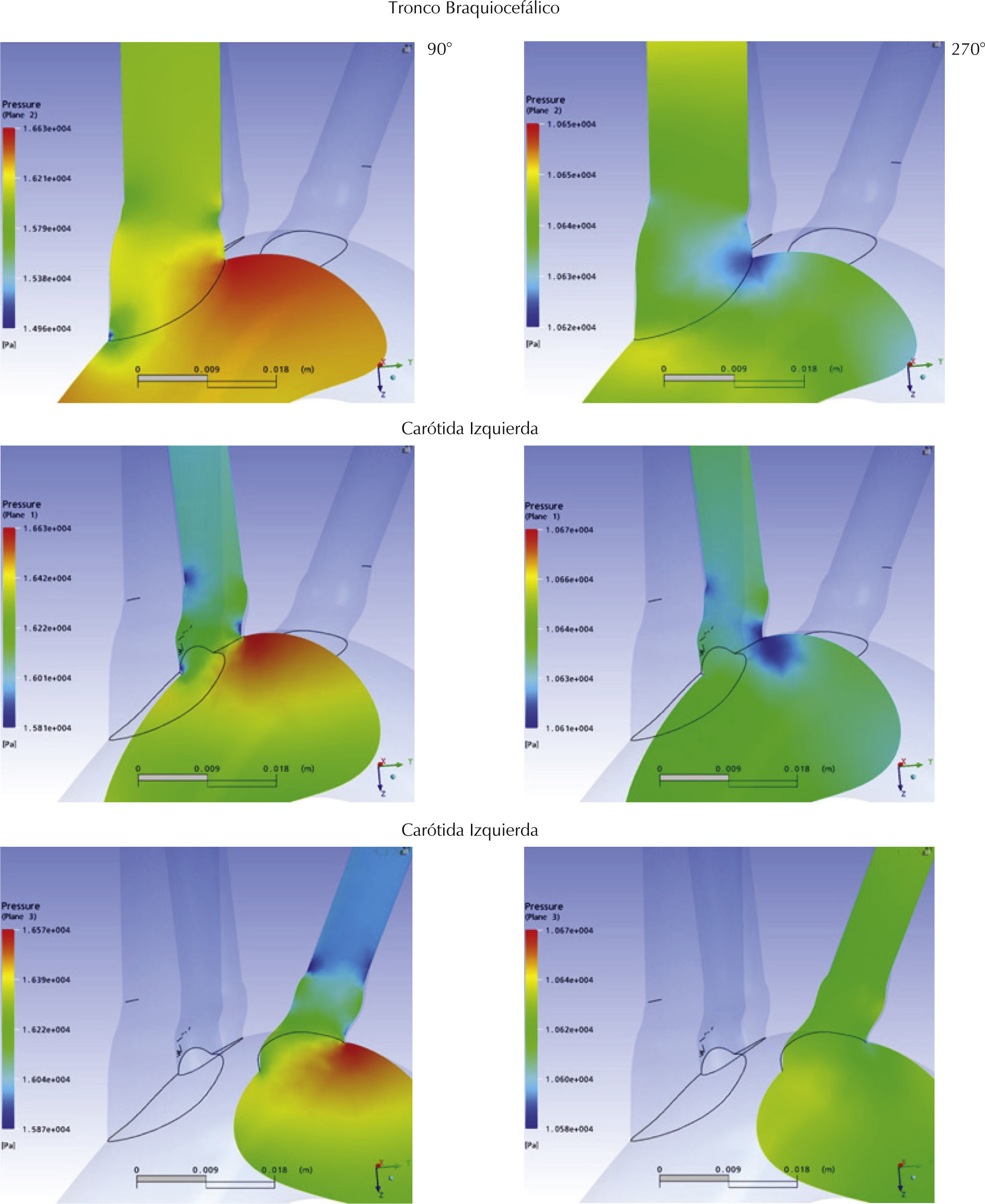
En la figura 12 se muestra el detalle de la distribución de presión en las raíces de las ramificaciones a los 90° y 270°, donde se registraron los máximos y mínimos valores de presión sobre sus paredes. Los planos sobre los que se muestran las distribuciones de presión coinciden con el eje axial del respectivo ramal rotado 45°, respecto al plano sagital axial

Figura 12.

Detalle de la distribución de presiones a los 90^o y 270^o del ciclo cardiaco en la raíz de las tres ramas del cayado aórtico.

Puede observarse en general que las presiones máximas se alcanzan en las raíces de las ramas a los 90° del ciclo, momento en que se registraron las máximas velocidades en la simulación. Los valores mínimos de presión se registraron en los mismos puntos a los 270°, momento en el que el flujo retrógrado alcanza su máximo. De todos los ramales, el tronco braquiocefálico presentó la mayor fluctuación de presión en su raíz, oscilando entre los 16.6 kPa y 10.6 kPa.

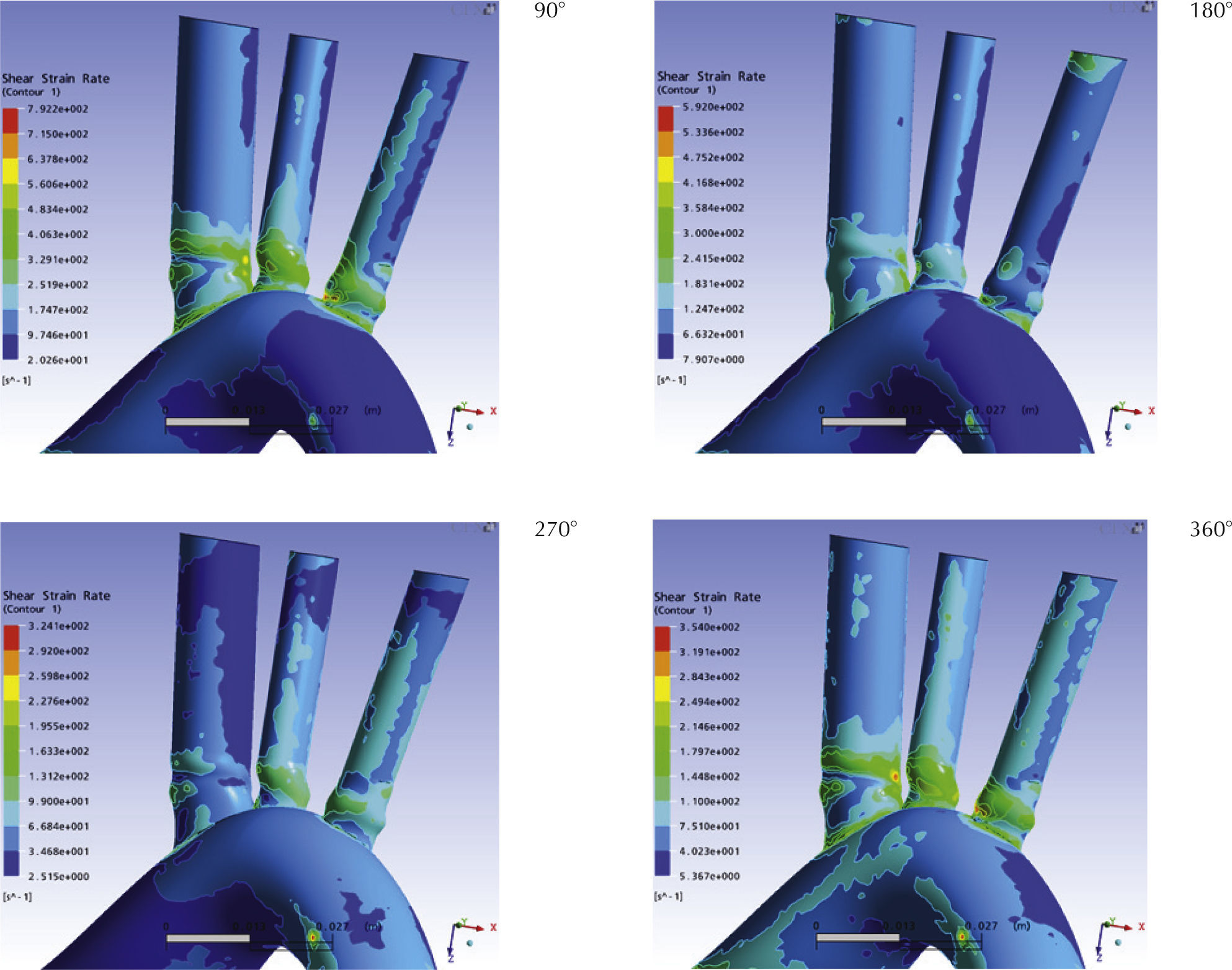
Esfuerzo cortante

Dado que la sangre se simuló como un fluido Newtoniano incompresible, el esfuerzo cortante (shear stress, σ) y la tasa de cizallamiento (shear strain rate, γ) se relacionan linealmente a través de la viscosidad (μ), la cual por definición es constante en los fluidos Newtonianos. Es así como la distribución espacial del esfuerzo cortante es idéntica a la de la tasa de cizallamiento (figura 13), con una magnitud dada por la relación lineal.

Estudios fisiológicos sugieren que el esfuerzo cortante sobre las paredes vasculares es una variable de gran importancia en la fisiopatología cardiovascular, no solo por su impacto mecánico, sino porque las células endoteliales tienen la capacidad de sensar este parámetro físico, a través de moléculas de superficie tal como los receptores de quimiocinas CXCR1 y CXCR2 (Zeng et al., 2011). De esta manera, en los análisis sucesivos se hará particular hincapié en la magnitud de esta variable y su fluctuación en las adyacencias de la pared de los vasos. Debido a que no existen técnicas para la medición directa de esta variable en un organismo vivo el uso de simulaciones numéricas ofrece una alternativa relevante para el estudio de la influencia de esta variable sobre distintas patologías, esencialmente la aterogénesis.

Las figuras 13 y 14 presentan el detalle de los esfuerzos cortantes sobre las paredes de las arterias específicamente en el cayado aórtico y sus principales ramificaciones. En general, se observó que la magnitud del esfuerzo cortante alcanzó sus valores máximos en las raíces de las ramificaciones, asiento preferencial de aterosclerosis. Las máximas magnitudes se registraron a un cuarto de ciclo (90°), estas magnitudes descienden hasta alcanzados los tres cuartos de ciclo (270°) para luego reiniciar su ascenso, constituyéndose un patrón trifásico similar al de la velocidad. Es importante destacar que los puntos donde se alcanzaron los máximos esfuerzos cortantes presentaron también la máxima fluctuación de dicha variable, encontrándose variaciones de hasta 470% en magnitud. Dichos puntos se encontraron en las raíces de las ramas aórticas, coinci- diendo con los puntos de máxima fluctuación de presión, y quizás no casualmente con los puntos más propensos a aterogénesis.

Figura 13.

Tasa de cizallamiento sobre las paredes vasculares, vista anterior.

Figura 14.

Tasa de cizallamiento en las paredes vasculares, vista posterior.

Se observa en los resultados obtenidos que la región sometida a mayores solicitaciones mecánicas (presión y esfuerzo cortante), y mayores fluctuaciones, se encuentra en las raíces de las ramificaciones. De las tres ramificaciones se encontró que el tronco braquiocefálico presenta las mayores solicitaciones mecánicas. Es importante resaltar que estas regiones son las más proclives a aterogénesis en el árbol vascular, lo que apoya a la hipótesis de la influencia de los patrones de flujo, los esfuerzos mecánicos y su fluctuación sobre la generación de ciertas patologías cardiovasculares.

Conclusiones

El avance de las tecnologías para el diagnóstico médico permite obtener datos realistas de la geometría y patrones de flujo en el sistema circulatorio humano con procedimientos no invasivos. El uso de esta data para la realización de simulaciones numéricas de flujo y contribuye a la exactitud de los resultados obtenidos, otorgándole mayor confiabilidad a la información y a los análisis que se derivan de dichas simulaciones.

La simulación que se realizó en este trabajo se basó en mediciones realizadas rutinariamente sobre un paciente. El comportamiento general del flujo en el cayado aórtico y sus ramas obtenido por simulación permitió reproducir el patrón trifásico de flujo y el fenómeno de flujo retrógrado ampliamente estudiado en trabajos previos. Los valores de velocidad y presión máxima obtenidos, así como su ubicación son acordes con lo publicado en la literatura médica clásica.

Se encontró, en el dominio estudiado, que las raíces de las ramas aórticas son las regiones sometidas a mayores solicitaciones mecánicas, así como a su mayor fluctuación, estas condiciones pueden deteriorar los tejidos de las paredes de los vasos y constituir una de las causas de formación de ciertas patologías, esto potenciado por su influencia biológica proinflamatoria sobre el endotelio y la pared de los vasos.

Las distintas etapas del flujo pulsátil presentaron desfases respecto a los tiempos de ocurrencia reales, esto se debe a que los pulsos de presión sanguíneos no responden exactamente a función sinusoidal, por lo que esta es una de las principales mejoras que deben ser incorporadas en estudios posteriores. Adicionalmente, se requieren medidas experimentales de los patrones de velocidad, por ejemplo, usar ultrasonido de alta resolución y compararlas con las logradas con la simulación numérica para realizar los ajustes que sean pertinentes al modelo matemático planteado en este trabajo.

Este artículo se cita:

Citación estilo Chicago

Bracamonte-Baran, William, Johane Bracamonte-Baran, Miguel Baritto-Loreto, Antonio D’Alessandro-Martínez. Dinámica de fluidos computacional aplicada al estudio del flujo sanguíneo en el cayado aórtico humano y sus principales ramas. Ingeniería Investigación y Tecnología, XVII, 01 (2016): 45-60.

Citación estilo ISO 690

Bracamonte-Baran W., Bracamonte-Baran J., Baritto-Loreto M., D’Alessandro-Martínez A. Dinámica de fluidos computacional aplicada al estudio del flujo sanguíneo en el cayado aórtico humano y sus principales ramas. Ingeniería Investigación y Tecnología, volumen XVII (número 1), enero-marzo 2016: 45-60.

Agradecimientos

Los autores desean agradecer a los Profesores Miguel Martín y Wuilian Torres del Centro de Computación Gráfica de la Facultad de Ciencias de la Universidad Central de Venezuela por su valiosa colaboración en el proceso de modelado geométrico a partir de la Tomografía Axial Computarizada. De igual manera a los Servicios de Imagenología y Cardiología del Hospital Universitario de Caracas, quienes colaboraron para la obtención de la información tomográfica y ultrasonográfica.