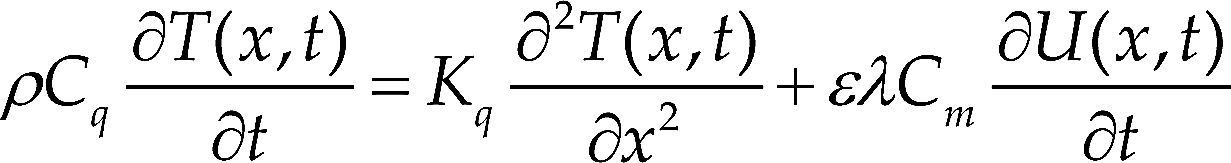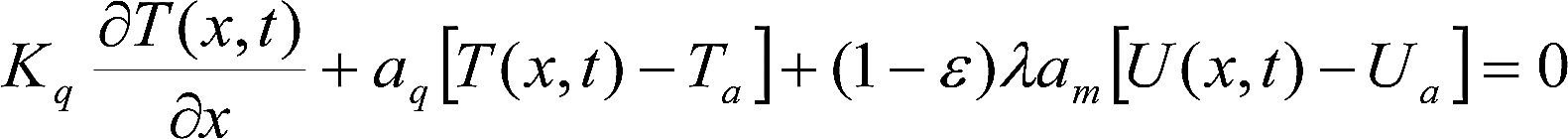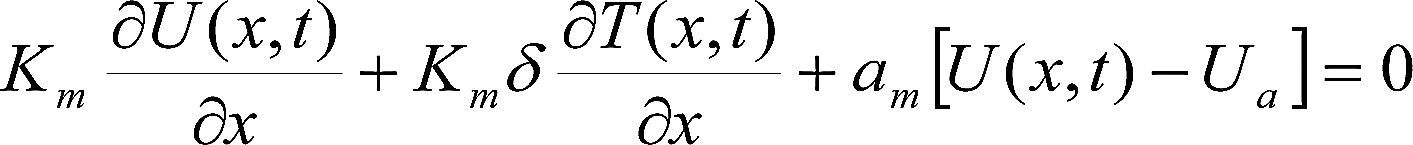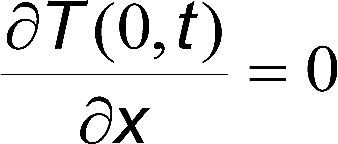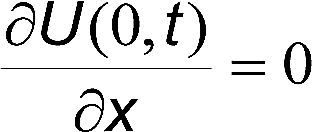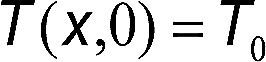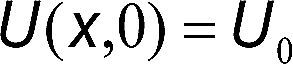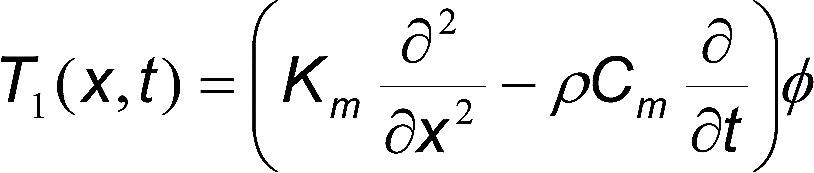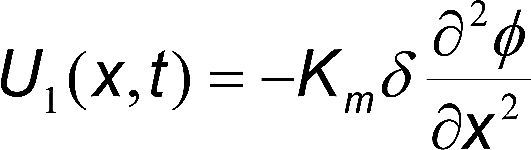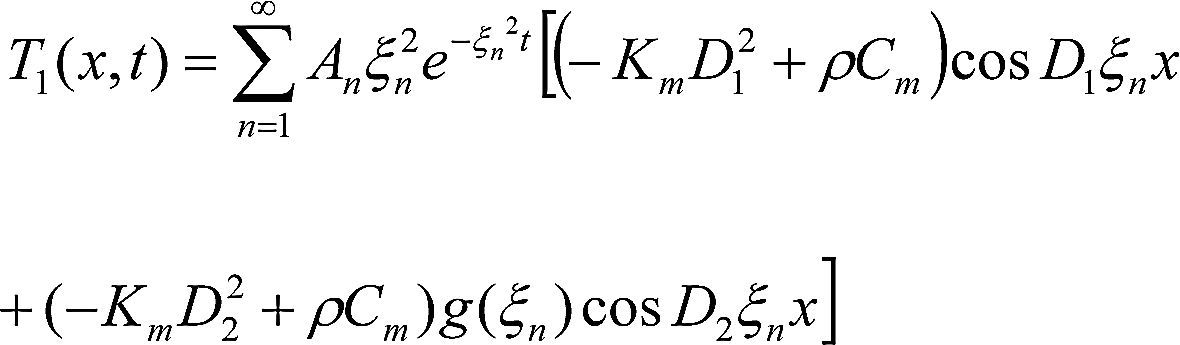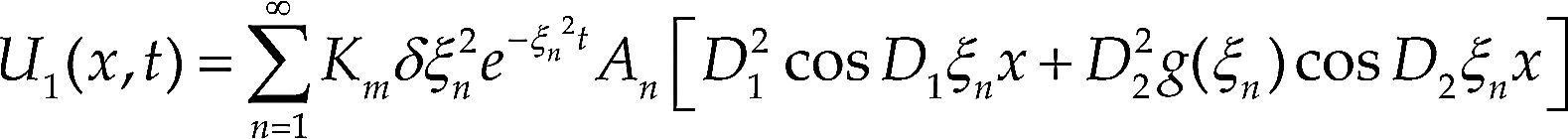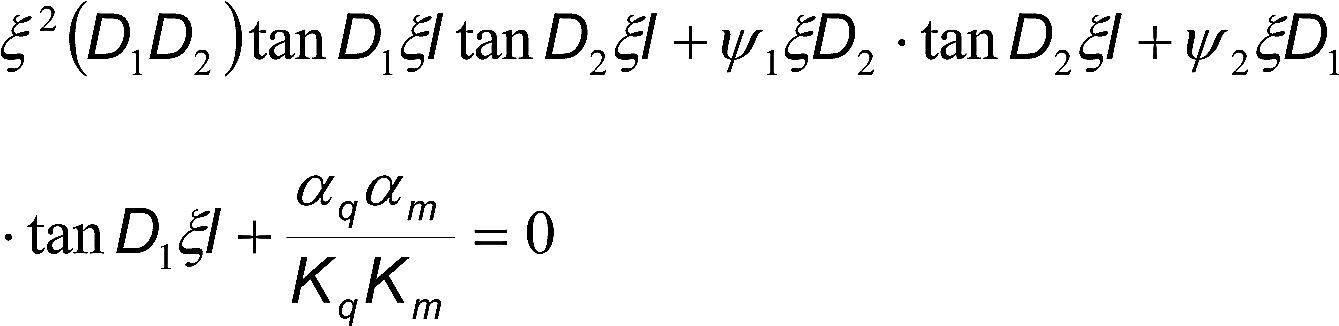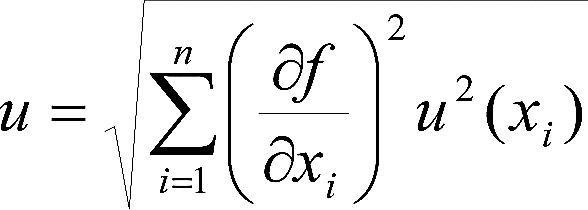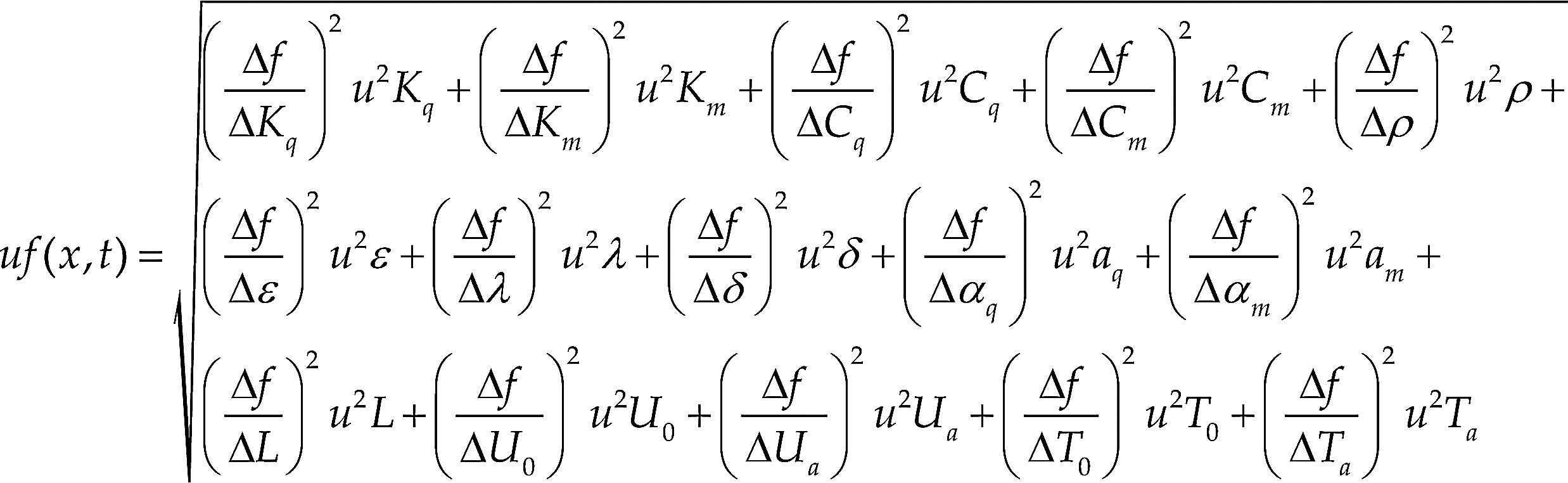Evaluación de los factores de influencia en el modelo de Luikov durante el secado de ladrillo

Resumen

El estudio de la transferencia de calor y de humedad en el secado de materiales sólidos porosos es importante, debido al amplio interés en reducir el agua presente en los materiales, ya que el exceso de humedad tiene efectos adversos en los materiales. En la actualidad, la investigación del secado se realiza de manera experimental, ya que no se cuenta con un modelo universal de secado que aplique satisfactoriamente a todos los materiales sólidos. Los modelos desarrollados se aplican a grupos restringidos de materiales. Uno de los modelos más aceptados para describir la transferencia de humedad en materiales capilares porosos es el modelo de Luikov, el cual se deriva de la termodinámica de procesos irreversibles. Además de la extensa aplicación de este modelo, hace falta identificar las propiedades termofísicas que tienen mayor influencia en los perfiles de secado, ya que existen pocas comparaciones contra datos experimentales. En este trabajo se utilizó la solución del modelo de Luikov obtenida por Liu et al. (1991) para alcanzar los perfiles de humedad en el proceso de secado de muestras de ladrillo a diferentes temperaturas, en donde se realizó una evaluación de los factores de influencia que afectan al perfil obtenido. Se encontró en el análisis, que la difusión es uno de los principales mecanismos que controla la transferencia de humedad. También el modelo se validó experimentalmente en muestras de ladrillo secados a temperaturas de 60 y 80 °C; asimismo los resultados teóricos y experimentales concuerdan satisfactoriamente en la región final del secado, lo cual es útil en la determinación del contenido de humedad.

Abstract

The heat and moisture transfer in the drying of porous solid materials is important, since excessive moisture has adverse effects on these materials; then, it exist a wide interest on the reduction of moisture in them. Nowadays, the research of the drying process is carried out both theoretical, as experimentally, because does not exist a universal model which satisfactorily describe the drying process of all kind of solid materials. The developed models apply to restricted groups of materials. To describe the moisture transfer in capillary porous materials, one of the more accepted theoretical models is the Luikov model, which is derived from the principles of thermodynamics of irreversible processes. This model has been applied to many materials; however, to describe the moisture transfer in capillary porous materials, it is needed a comprehensive analysis to identify the thermophysical properties which have major influence in the drying profiles. Also, it is needed to validate the model for those materials in which the model is applied. In this work, the solution of Luikov model (as obtained by Liu et al., 1991) was used to obtain moisture profiles during the drying of brick at different temperatures. Also, an evaluation of the influence factors which affects to the obtained moisture profiles was carried out. It was found that one of the most important mechanisms which control the drying process is the diffusion of moisture. Also, the experimental validation using brick was performed at temperatures of 60 and 80 °C; the theoretical and experimental results agree in the falling rate period, which is useful in the moisture content determination.

Introducción

El secado de materiales sólidos porosos se ha estudiado ampliamente de manera teórica y experimental; sin embargo, al no existir una teoría general que describa satisfactoriamente este proceso para todos los materiales sólidos (Wang et al., 2007; Mujumdar, 2006) se continúa con el uso de los modelos propuestos.

Algunos de los modelos que se han desarrollado para describir la transferencia de calor y de humedad en el secado, incluyen el modelo de Philips y DeVries (1957), el modelo de Luikov (1975), el modelo de Kowalsky y Strumillo (1997), el modelo de Warren (1983), entre otros.

El modelo de Luikov se desarrolló sobre la base de principios de termodinámica de procesos irreversibles y de las relaciones lineales de difusión de calor y humedad; además, se puede solucionar analíticamente para geometrías conocidas (Fulford, 1969; Shahary, 2012). Este modelo se ha empleado satisfactoriamente para varios tipos de materiales (Hernández y Quinto, 2005; Fulford, 1969; Kerestecioglu et al., 1998; Shahary, 2010).

La solución analítica que se obtiene de este modelo, bajo condiciones específicas, no toma en cuenta la incertidumbre de los factores que afectan a los perfiles de humedad y temperatura, ya que impide saber el nivel de concordancia con los datos experimentales. Adicionalmente, conocer los coeficientes de mayor influencia en los perfiles calculados permite determinar el mecanismo de transferencia de humedad que controla el proceso de secado.

Para evaluar las desviaciones con base en los valores experimentales, es necesario identificar los factores de influencia más importantes. En Liu y Cheng (1991); Alvarez et al. (2001); Efimov et al. (2011); Dantas et al. (2002); Scarpa y Milano (2002) se analiza el efecto que tienen algunos coeficientes en los perfiles de secado; sin embargo estos análisis no toman en cuenta todos los factores presentes, tales como los asociados a las condiciones iniciales y de frontera, entre otros. Martines y Lira (2012) aplicaron el modelo de Luikov para una placa de cerámica; sin embargo, no se realizó la validación experimental correspondiente.

En este trabajo se describe la solución del modelo de Luikov para una muestra de ladrillo, usando la metodología de Liu et al. (1991), donde se evalúan todos los factores de influencia involucrados mediante la ley de propagación de incertidumbre (JCGM100, 2008), lo cual permitió identificar aquellos que tienen mayor contribución.

Por otra parte, se obtuvieron los perfiles experimentales de contenido de humedad y temperatura en muestras de ladrillo, lo que permitió comparar los resultados del modelo con los resultados experimentales en dos valores de temperatura.

Modelo de Luikov

El modelo de Luikov consiste de un sistema acoplado de ecuaciones diferenciales parciales de segundo orden, que describe la transferencia de calor y de humedad en materiales capilares porosos (Luikov, 1975).

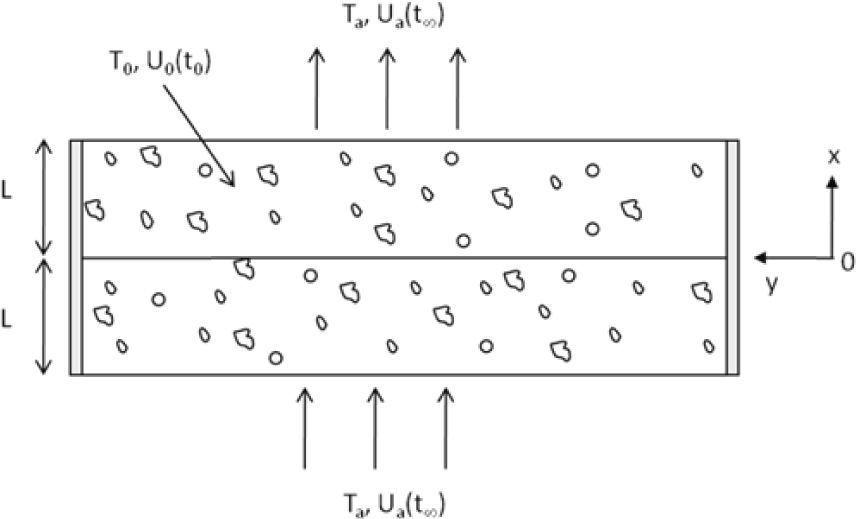
En la figura 1 se muestra el esquema de un ladrillo representado por una placa plana que inicialmente se encuentra a una temperatura T₀ y con un contenido de humedad U₀. Posteriormente, la placa se coloca en un medio de secado convectivo, cuyas condiciones son U_a y T_a.

Figura 1.

Modelo físico para el ladrillo en un medio convectivo.

El modelo de Luikov para una placa plana en una dimensión está dado como

La ecuación (1) describe la transferencia de calor por conducción dentro de un cuerpo e incluye un término para la transferencia de calor debido a cambios de fase del agua dentro del cuerpo; la ecuación (2) describe la transferencia de humedad por difusión e incluye un término que considera la transferencia de humedad debido a gradientes de temperatura.

Si se supone simetría en la placa, entonces el problema se puede solucionar para la mitad, es decir, para 0 ≤ x ≤ L.

Las codiciones de frontera para este problema se derivan mediante balances de masa y energía en la superficie (x = L) y en el centro de la placa (x = 0). En x = ± L.

Donde a_q y a_m son los coeficientes convectivos de transferencia de calor y masa, respectivamente.

La ecuación (3) describe el balance de calor al considerar que el calor se transfiere dentro del cuerpo por conducción y en la superficie por convección; adicionalmente, se incluye un término debido al calor por cambio de fase del agua en los poros. La ecuación (4) describe el balance de humedad debido a la conducción de humedad al interior y por convección en el exterior; además incluye un término que considera el flujo de humedad debido a un gradiente de temperatura.

En x = 0 no hay flujo de calor, ni flujo de humedad, por lo tanto se tiene

Las condiciones iniciales (t = 0) del material son

Método de solución

Para resolver el modelo descrito se hacen las siguientes suposiciones:

• •

  Los coeficientes y propiedades termofísicas tienen valores constantes.

• •

  Dentro de los poros existe agua en forma líquida y vapor.

• •

  La matriz sólida del material no se deforma durante el secado.

• •

  Se ignoran los efectos electromagnéticos y gravitacionales.

• •

  No hay reacciones químicas.

• •

  El cuerpo sólido es isotrópico.

La solución del modelo se obtiene de acuerdo con la metodología descrita por Liu et al. (1991), que comprende los siguientes pasos:

• •

  Transformación del problema no homogéneo en uno homogéneo.

• •

  Aplicación de la función potencial para desacoplar las ecuaciones.

• •

  Obtención de las ecuaciones para los perfiles de humedad y temperatura.

• •

  Cálculo de los valores propios de la ecuación trascendental.

• •

  Obtención de los perfiles de humedad y temperatura.

La función potencial φ (x, t) utilizada para desacoplar el sistema (Liu y Cheng, 1991) está dada como

Donde T_l = T-T_a y U_l = U-U_a

Al usar la función potencial en el sistema homogéneo obtenido de (1) y (2), y aplicar el método de separación de variables (Farlow, 1993) se obtiene la solución general del sistema, el cual se da por las ecuaciones (11) y (12).

Donde

D₁, D₂, K_m, C_m, ρ y δ son constantes; ξ_n son los valores propios que se obtienen de la ecuación transcendental (ecuación 13); los valores A_n y B_n dependen de ξ_n; g(ξ_n) = A_n/B_n.

La ecuación (11) permite obtener los perfiles de temperatura para una placa plana, mientras que la ecuación (12) permite calcular los perfiles de contenido de humedad.

La ecuación trascendental se obtiene al evaluar el modelo en las condiciones iniciales y de frontera, está dada por

La ecuación (13) no es lineal y tiene un número infinito de valores propios, incluso también puede tener valores complejos (Lui y Cheng, 1991; Alvarez et al., 2001; Lobo et al., 1987). La evaluación que se realiza en el presente trabajo solo incluye a los valores propios reales, ya que los valores complejos solo tienen contribución en los primeros instantes del secado; en el periodo de velocidad decreciente los perfiles concuerdan satisfactoriamente Liu y Cheng, 1991; Alvarez et al., 2001).

Los métodos numéricos usados para calcular los valores propios reales (ξ_n) fueron el método de Newton-Raphson y el método de bisección (Hoffman, 1992).

Para el caso de ladrillo, los coeficientes involucrados en el modelo de Luikov se presentan en la tabla 1, cuyos datos están dados en Alvarez et al. (2001).

Tabla 1.

Coeficientes del modelo de Luikov para ladrillo

Propiedad	Kq	Km	Cq	Cm	ρ	¿	λ	δ
Valor	0.44	6.04x10^-8	879	0.0018	1200	0.3	2.5x10^6	0.56
Unidades	W/m·K	Kg/m·s·%	J/kg·K	kg/kg·%	Kg/m^3	adimensional	J/kg	%/K

Evaluación de los factores de influencia en la predicción de los perfiles de humedad y temperatura

La solución obtenida con el modelo de Luikov es exacta; sin embargo, los perfiles de humedad y temperatura loggrados con esta no toman en cuenta la incertidumbre de las propiedades termofísicas, ni la de los parámetros incluidos en las condiciones iniciales y de frontera. Dada la dificultad que se tiene para obtener los valores de incertidumbre de las propiedades involucradas, se realizó un análisis paramétrico haciendo variaciones de los valores en porcentajes específicos de los mismos.

Existen distintos métodos para calcular los coeficientes de sensibilidad que permiten cuantificar su efecto en el perfil de humedad en procesos transitorios (Cacuci, 2003; Goyal y Srinivasan, 2012). La evaluación del efecto de cada parámetro en el perfil total se obtiene al aplicar la ley de propagación de errores, también conocida como la ley de propagación de incertidumbres (JCGM100, 2008), la cual establece que la incertidumbre se puede calcular con la ecuación

Donde

f = contenido de humedad U(x,t) o temperatura T(x,t),

x_i = factores de influencia

∂f / ∂ x_i = coeficientes de sensibilidad

u(x_i) = incertidumbre del factor de influencia x_i

Los valores de los coeficientes de sensibilidad de la ecuación (14) se calculan al derivar directamente la función f (cuando es posible), en otro caso, se estiman al perturbar el valor del coeficiente (x_i) por una cantidad ▵ (manteniendo los otros constantes) y evaluando su efecto en U(x,t) o T(x,t).

En el problema que se presenta aquí, los valores de ▵ corresponden a los porcentajes de variación de los coeficientes. De lo anterior, la ecuación de propagación de incertidumbres para la distribución de temperatura y humedad se puede escribir como en la ecuación (15).

Los factores de influencia en el modelo de Luikov se pueden clasificar como sigue:

• a)

  Coeficientes del modelo son: K_q, K_m, C_q, C_m, ¿, λ, δ, ρ, L.

• b)

  Condiciones iniciales: U₀, T₀.

• c)

  Condiciones de frontera: a_q, a_m, T_a, U_a.

En la tabla 2 se presentan los valores porcentuales de variación de los coeficientes incluidos en el modelo.

Tabla 2.

Porcentaje de variación de las variables de influencia del modelo

Propiedad	Kq	Km	Cq	Cm	ρ	¿	λ	δ	L
± △	5%	10%	5%	10%	10%	10%	10%	10%	0.001 m

Donde f = U(x, t) o T(x,t)

Las condiciones iniciales b) U₀ y T₀ corresponden al contenido de humedad y temperatura que tiene la muestra de ladrillo antes de iniciar el proceso de secado. Las incertidumbres estándar con las que se puede realizar esta medición son 0.5% y 0.06 °C, respectivamente.

Las condiciones a la frontera, cuyos coeficientes están dados en c), corresponden a las condiciones del medio secante; es decir, a las condiciones de contenido de humedad (U_a) y temperatura (T_a) que se alcanzan en el sistema de secado, y al tratarse de un medio convectivo se incluyen los coeficientes convectivos de transferencia de masa (a_m) y de calor (a_q). Los valores de incertidumbre asociados a los coeficientes dados en c) son: u U_a = 0.1%, uT_a = 1.5 °C, ua_m = 10% y ua_q = 10%.

Con el propósito de agilizar el cálculo del efecto de los factores de influencia en los perfiles de contenido de humedad, el análisis se realizó con un valor propio en la función trascendental.

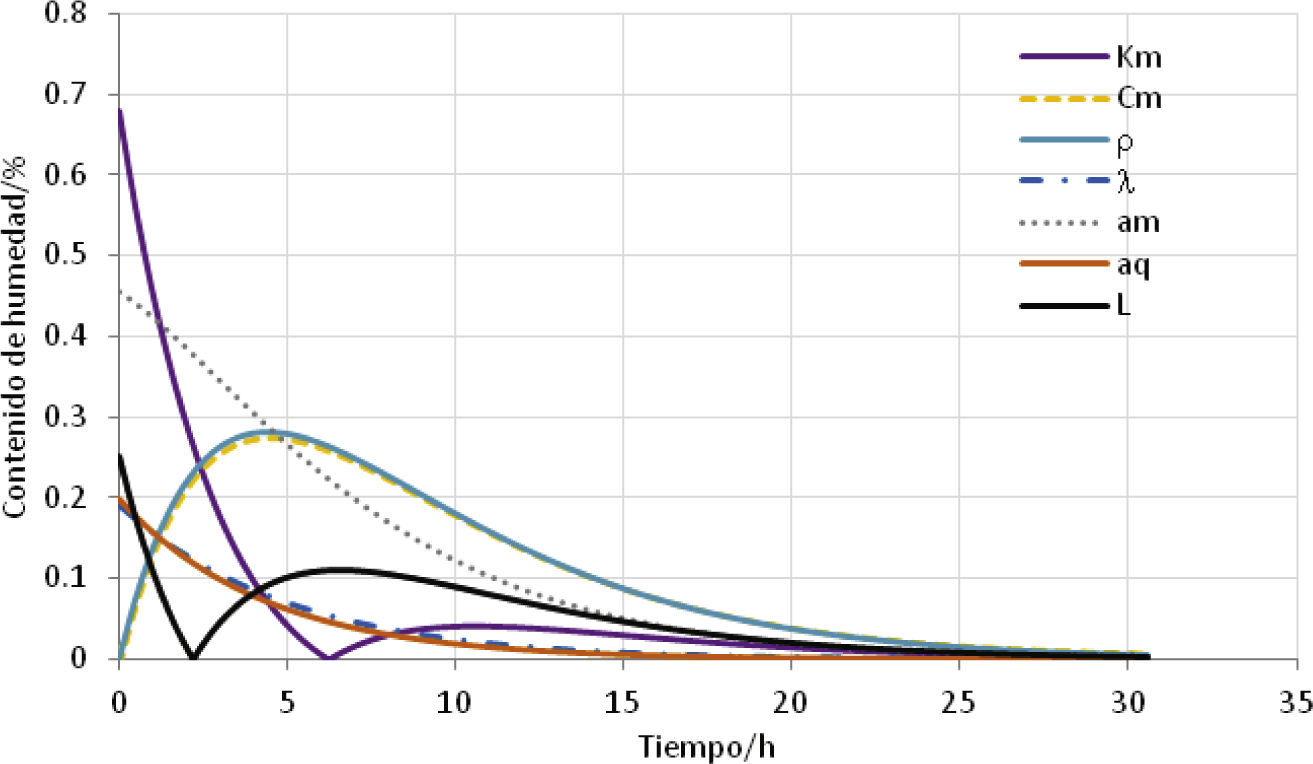
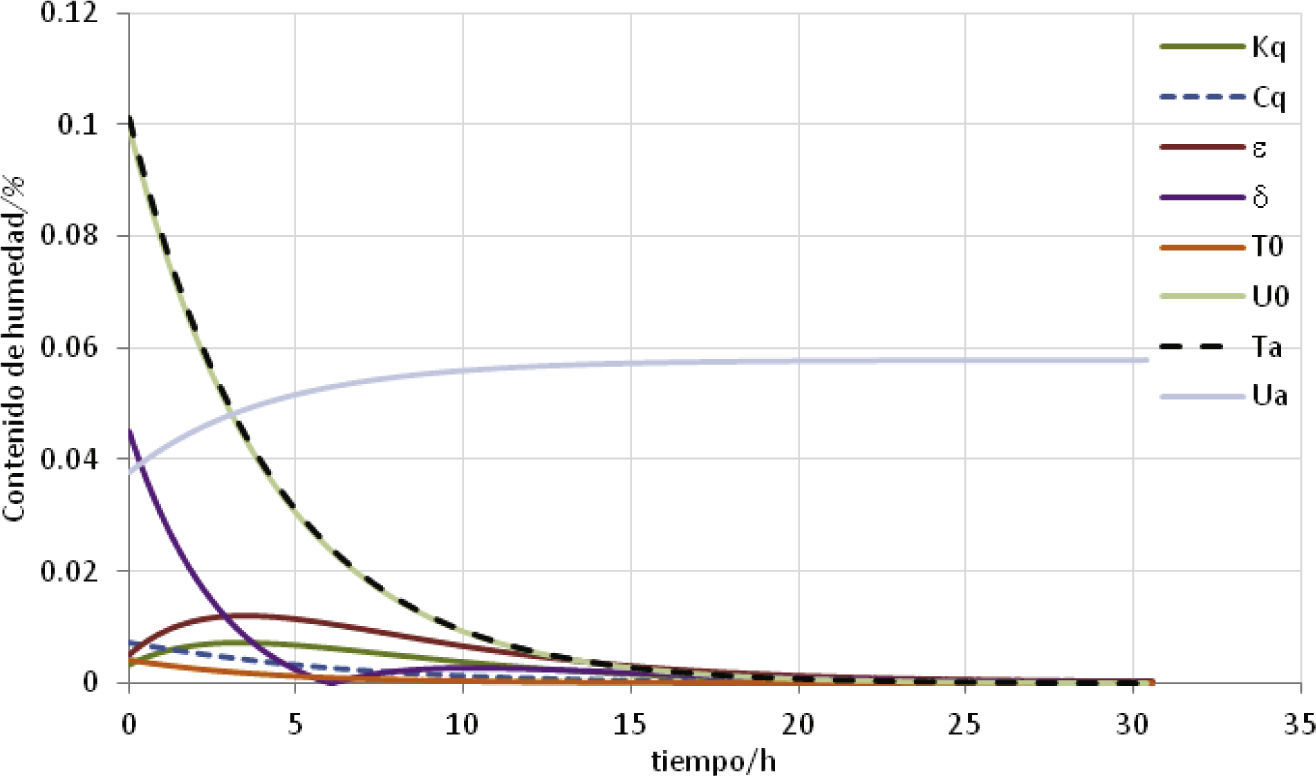
Factores de influencia en la distribución de humedad

Al evaluar la ecuación (15) para cada uno de los coeficientes dados en a), b) y c) se encontraron las contribuciones de cada uno de los coeficientes involucrados. Los resultados obtenidos se muestran en las figuras 2 y 3.

Figura 2.

Factores de mayor influencia en los perfiles de contenido de humedad en el proceso de secado de ladrillo.

Figura 3.

Factores de influencia con menor contribución en los perfiles de contenido de humedad en el proceso de secado.

En la figura 2 se muestran los coeficientes que tienen una contribución mayor de 0.2%, mientras que en la figura 3 aquellos que tienen una contribución menor.

Los factores con mayor contribución fueron:

K_m(a) tiene una contribución máxima de 0.7%; que es el coeficiente de conductividad de humedad (similar a la conductividad térmica), indica la velocidad a la que el material “conduce” la humedad. Se espera que al incrementar el valor de K_m se reduzca el tiempo de secado; en este caso se encontró que al incrementar su valor en 10% el tiempo de secado se reduce en aproximadamente 1.3 h.

a_m (c) es el coeficiente convectivo de transferencia de masa (contenido de humedad). El incremento en 10% del valor del coeficiente redujo el tiempo de secado en 1.3 h. Su contribución máxima es de 0.45% del contenido de humedad.

C_m (a) tiene una contribución de 0.3%; al igual que el calor específico, cuando el valor de C_m crece, el tiempo de secado se incrementa. En este caso un incremento de 10% en el valor de C_m aumentó el tiempo de secado en 3 h.

ρ(a) es la densidad del material, cuya contribución máxima fue de 0.3%. El incremento de 10% en el valor de r aumentó el tiempo de secado en 3 h.

L(a) es el espesor del ladrillo, el cual tiene una contribución máxima de 0.25%. Se encontró que un incremento de 1 mm en el espesor incrementa el tiempo de secado en aproximadamente 2 h.

λ(a) es el calor latente de evaporación e indica que a mayor valor, se requiere mayor cantidad de energía para evaporar el agua líquida presente, lo cual puede prolongar el tiempo de secado. En este caso se encontró que un incremento en 10% de su valor incrementó el tiempo de secado en 0.2 h. Su contribución máxima en la incertidumbre fue de 0. 2% en contenido de humedad.

a_q (c) es el coeficiente convectivo de transferencia de calor, que está acoplado con la transferencia de humedad en las condiciones de frontera; el incremento en 10% del valor de a_q, redujo el tiempo de secado en 0.1 h. La contribución máxima de este coeficiente es de 0.2% de contenido de humedad.

De manera resumida, en la tabla 3 se muestran los valores de los coeficientes con mayor contribución en el perfil de humedad.

Tabla 3.

Coeficientes con mayor contribución en el perfil de humedad de acuerdo con la solución del modelo de Luikov

Propiedad	Km	am	Cm	ρ	L	λ	aq
Contenido de humedad/%	0.70	0.45	0.30	0.30	0.25	0.20	0.20

En la figura 3 se muestra el efecto de los factores de influencia que tienen una contribución menor de 0.2% de contenido de humedad.

Los factores que tienen una contribución entre 0.05 y 0.1% fueron U₀, U_a y T_a, los cuales están relacionados con las condiciones iniciales y de frontera. Según se observa en la figura 3, el contenido de humedad en el medio de secado U_a puede tener un efecto importante en la región final de secado, por lo que para alcanzar la masa seca se requiere tener un horno de secado que genere una atmósfera con mínimo contenido de humedad.

Los coeficientes con contribuciones menores de 0.05% y que se pueden ignorar son: ¿, δ, T₀, K_q y C_q. La contribución de d en el perfil de humedad se reportó en (Liu y Cheng, 1991; Alvarez et al., 2001; Farlow, 1993) con conclusiones similares.

Validación del modelo

Para validar el modelo se usaron muestras de ladrillo tradicional con espesor de 25 mm y un horno de secado comercial que opera por convección forzada, de aproximadamente 40 a 325 °C y tiene una incertidumbre estándar por estabilidad de u_stb = 0.11 °C y una incertidumbre estándar por gradientes de u_grad = 0.86 °C. La medición de temperatura dentro del horno se realizó con termopares (tipo T) colocados en el volumen de trabajo, los cuales se midieron con un multímetro digital, que se comunicó a una computadora para la adquisición de datos.

Las muestras de ladrillo se acondicionaron mediante inmersión en agua por al menos 12 h y luego se expusieron al ambiente para eliminar el agua líquida presente en la superficie, posteriormente se pesaron y se colocaron en el horno para iniciar el secado. Los experimentos de secado se realizaron a 60 y 80 °C.

Las muestras se sacaron del horno por periodos específicos de tiempo hasta que no se observaron cambios en la masa (condición de masa constante). La medición de masa se realizó con una balanza de 3.1 kg con resolución de 0.1 g.

La masa seca del ladrillo requerida para calcular el contenido de humedad (y con ella obtener los perfiles de humedad) se obtuvo al secar la muestra a 130 °C por periodos de 1 h hasta alcanzar masa constante.

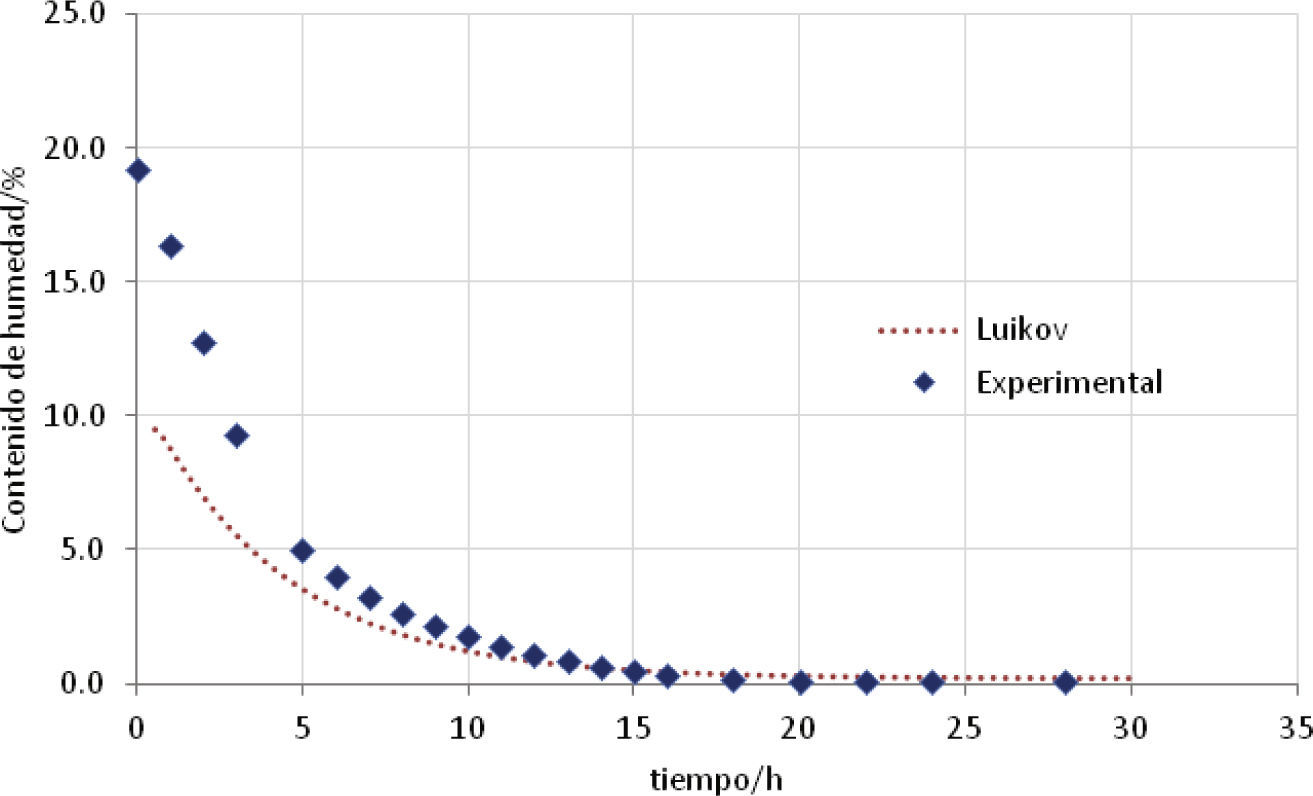
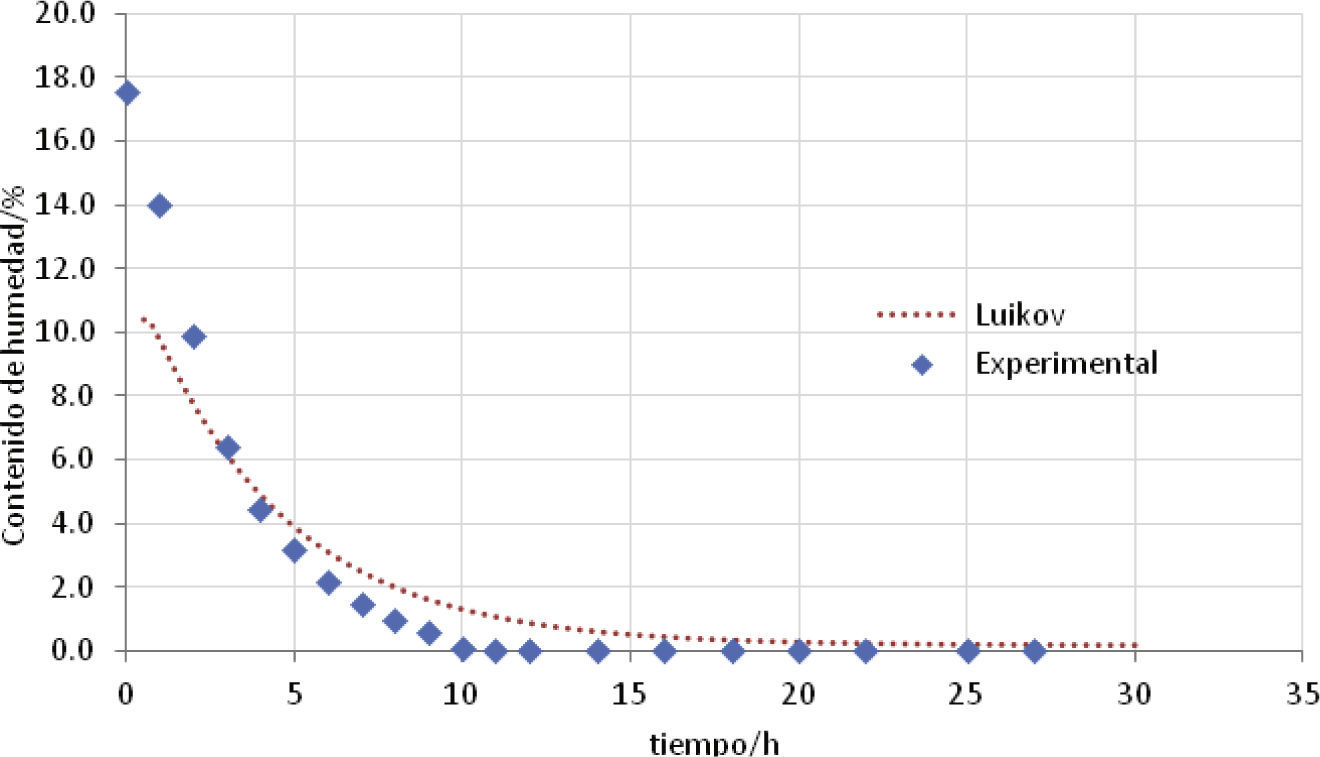
Los perfiles experimentales y los obtenidos con el modelo Luikov a 60 y 80 °C se muestran en las figuras 4 y 5, respectivamente.

Figura 4.

Comparación de los perfiles de humedad teóricos y experimentales de una muestra de ladrillo a una temperatura de 60 °C.

Figura 5.

Secado de una muestra de ladrillo en un horno de secado a una temperatura de 80 °C.

Los perfiles (teóricos y experimentales) de la figura 4 muestran una diferencia en los perfiles en las primeras horas; sin embargo, en la región final del periodo de velocidad decreciente estos concuerdan satisfactoriamente.

Los resultados obtenidos en las figuras 4 y 5 muestran que el secado de ladrillo obtenido experimentalmente es más rápido a 80 °C que a 60 °C, mientras que los valores de contenido de humedad calculados del modelo de Luikov tienen perfiles similares a los diferentes valores de temperatura. La falta de concordancia en las primeras horas, entre los perfiles calculados y experimentales, se debe a que no se consideraron las raíces complejas para obtener el perfil, y que únicamente se usó una raíz en la solución.

La comparación de los perfiles teóricos y experimentales muestra una buena aproximación en las dos primeras horas y se desvían considerablemente en el periodo de 5 h a 10 h; posteriormente los perfiles son muy similares y se ajustan satisfactoriamente en la región final del periodo de velocidad decreciente.

Conclusiones

Se implementó la solución del modelo de Luikov para una muestra de ladrillo tradicional, considerándolo como una placa plana, donde se impusieron condiciones de frontera tipo convectivo para describir el proceso de secado. Esto permitió realizar un análisis paramétrico para identificar los principales factores de influencia que afectan los perfiles de humedad en el proceso de secado.

Los parámetros con mayor contribución en los perfiles de humedad fueron K_m, C_m, ρ, λ, a_m, a_q y L, los cuales tienen una contribución mayor que 0.2% del contenido de humedad, mientras que los coeficientes restantes tienen una contribución menor y, en algunos casos, su contribución se puede ignorar. En la región final de secado las curvas de incertidumbre tienden a reducirse y predomina la incertidumbre del medio de secado. La contribución de los tres primeros coeficientes permite concluir que la difusión de humedad es uno de los principales mecanismos que controla el proceso de secado.

Por último, se realizó la validación experimental del modelo en temperaturas de 60 y 80 °C, lo cual confirmó que el modelo se puede aplicar satisfactoriamente para describir el proceso de secado en la región final del periodo de velocidad decreciente.

Este artículo se cita:

Citación estilo Chicago

Martines-López, Enrique, Leonel Lira-Cortés. Evaluación de los factores de influencia en el modelo de Luikov durante el secado de ladrillo. Ingeniería Investigación y Tecnología, XVII, 01 (2016): 35-44.

Citación estilo ISO 690

Martines-López E., Lira-Cortés L. Evaluación de los factores de influencia en el modelo de Luikov durante el secado de ladrillo. Ingeniería Investigación y Tecnología, volumen XVII (número 1), enero-marzo 2016: 35-44.

Agradecimientos

El presente trabajo se realizó con el apoyo del Centro Nacional de Metrología a través del programa SIDEPRO (DAF.342.659.2008).