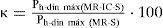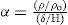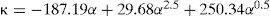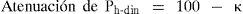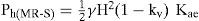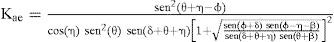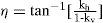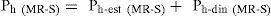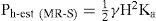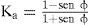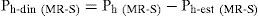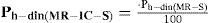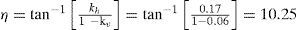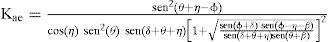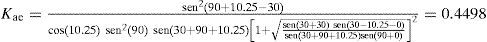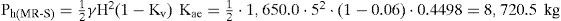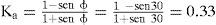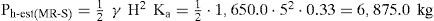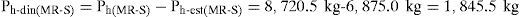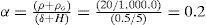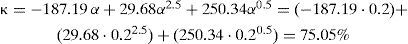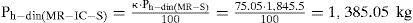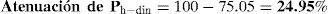Empuje dinámico en estructuras de retención con inclusión compresible

Resumen

Estructuras de retención rígidas se emplean usualmente en obras civiles tales como muros de retención, estribos de puentes y cimentaciones, entre otros. El diseño de estas estructuras se basa en el cálculo de los empujes, estáticos y dinámicos, que ejerce el material retenido sobre la propia estructura. Específicamente, para el caso de acciones dinámicas, el método Mononobe-Okabe (M-O), es el más aceptado internacionalmente para el cálculo de empujes dinámicos sobre muros de retención rígidos. Este trabajo presenta una extensión del método M-O, denominado método modificado M-O (M-M-O), para obtener empujes dinámicos en estructuras de retención rígidas con inclusiones compresibles de poliestireno expandido (EPS) entre la estructura y el material retenido. El uso de inclusiones compresibles consiste en propiciar mecanismos de atenuación de empujes, estáticos y dinámicos, en el respaldo de una estructura de retención rígida.

El método analítico M-M-O parte de resultados experimentales de ensayes en mesa vibradora de modelos (prototipos) de estructuras de retención rígidas de 0.2 m de altura, con rellenos de material granular e inclusiones compresibles de EPS de diferentes densidades (entre 10 y 32 kg/m³) y distintas relaciones espesor/altura (4.7 y 7.8%). Los prototipos se sometieron a movimientos senoidales con aceleraciones de 0.05 y 0.10 g y frecuencias de 1, 2 y 3 Hz.

Abstract

Usually rigid retaining structures are used in civil works such as retaining walls, bridge abutments and foundations, among others. The design of these structures is based on thrust calculation, static and dynamic, exerted by the material retained on the structure. In the case of dynamic actions, internationally the Mononobe-Okabe (M-O) method is the most accepted for the calculation of dynamic thrusts. This paper presents an extension of M-O method, called M-O modified method (M-M-O), to obtain dynamic thrusts on nonyielding rigid retaining walls with a compressible inclusion of expanded polystyrene (EPS), between the structure and the retained material. Compressible inclusions provide thrust attenuation, static and dynamic, on the back of a nonyielding rigid retaining structure. The analytic method M-M-O is based on experimental results from shaking table tests of rigid retaining walls models 0.2 m in height with sand backfill and Expanded Polystyrene compressible inclusions of different densities (between 10 and 32 kg/m³) and variable thickness/height relation (4.7 and 7.8%). Sine wave-type motions with maximum accelerations of 0.05 and 0.10 g and frequencies of 1, 2 and 3 Hz were applied to the models.

Introducción

En zonas de alto riesgo sísmico los empujes dinámicos pueden alcanzar magnitudes que causan daños significativos a las estructuras de retención, llegando en algunos casos a la falla. Como alternativa al diseño de muros capaces de soportar dichos incrementos de presiones, en diversas investigaciones se ha demostrado que es efectivo el uso de inclusiones compresibles (IC) de poliestireno expandido de alta densidad (EPS) en la interfaz muro-relleno, con el fin de atenuar los empujes dinámicos de tierra, es efectivo (Zarnani et al., 2005; Bathurst et al., 2007; Murphy, 1997; Hazarika y Okuzono, 2004).

La función principal de una inclusión compresible es propiciar la reducción de los empujes laterales impuestos por el suelo de relleno, mediante disipación de energía. Fenomenológicamente, en términos de empujes estáticos, la compresión de una inclusión permite que el suelo aledaño a esta se desplace, de manera que la presión de tierra, inicialmente igual al empuje de tierra en reposo, tienda al estado activo provocando una reducción en la presión actuante sobre el respaldo de una estructura de retención (González y Romo, 2012a). Para el caso de los empujes de tierra dinámicos, la compresión de una inclusión favorece el desplazamiento en el suelo de relleno, provocando una gran disipación de energía en el suelo y por ende una atenuación en los empujes dinámicos (González y Romo, 2012b).

A la fecha, los métodos para el análisis dinámico de estructuras de retención convencionales pueden agruparse en métodos seudo-estáticos (Mononobe-Okabe, 1926-1929; Prakash y Nandkumaran, 1979; Morrison y Ebeling, 1995), analíticos (Wood, 1973; Veletsos y Younan, 1994; Theodorakopoulos et al., 2001) y numéricos (Ostadan y White, 1998; Bakhtin, 2002). Sin embargo, el método Mononobe-Okabe es el más aceptado internacionalmente para el cálculo de empujes dinámicos.

En el caso de estructuras de retención con inclusiones compresibles, los métodos de análisis dinámico son escasos, Karpurapu y Bathurst (1992), Athanasopoulos et al. (2007) y Horvath (2008) han presentado algunos de ellos. El método presentado por Horvath (2008), por ejemplo, permite definir el espesor mínimo de una inclusión compresible en función de su rigidez, sin dar la distribución de presiones en el muro y punto de aplicación de la presión máxima. Por consiguiente y en aras de aportar parámetros que permitan vencer estas limitaciones, este trabajo propone una extensión del método M-O, denominado método modificado M-O (M-M-O), para obtener empujes dinámicos en estructuras de retención rígidas con inclusiones compresibles de poliestireno expandido (EPS) y relleno granular. El desarrollo del método se basa en una investigación experimental, la cual se describe en las siguientes secciones.

Etapa experimental

Se llevaron a cabo ensayes en mesa vibradora de modelos (prototipos) de estructuras de retención rígidas de 0.2 m de altura, con rellenos de arena e inclusiones compresibles de EPS. A continuación se describe cada uno de los componentes experimentales, así como el proceso de formación de los rellenos, las características de las señales de excitación y el procesamiento de los registros experimentales.

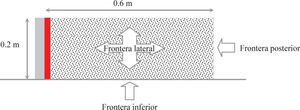
Componentes experimentales

Prototipos de estructura de retención

Se diseñaron y construyeron prototipos de muros de retención de 0.2 m de altura por 0.4 m de longitud, conformadas por placas de aluminio de 0.02 m de espesor (figura 1); la base de los muros se empotró a contendedores de acrílico, con la finalidad de restringir los modos de rotación y traslación de los mismos. Los contenedores de acrílico brindaron el espacio para la formación de depósitos de arena de 0.2 m de altura, 0.4 m de ancho y 0.6 m de longitud.

Figura 1.

Prototipos de estructuras de retención

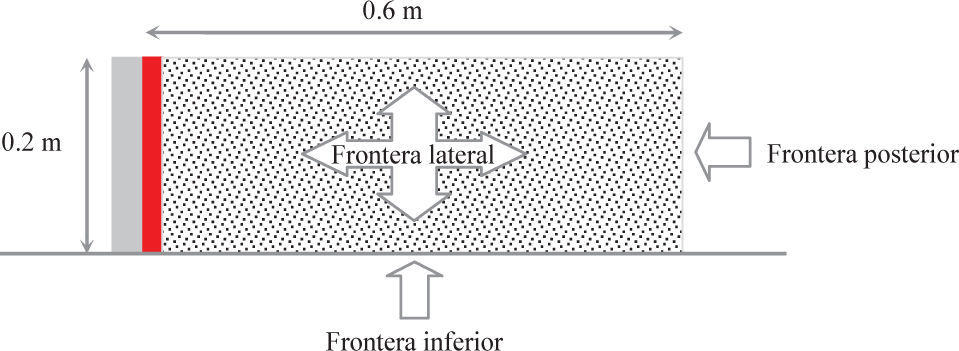
Condiciones de frontera

Las condiciones de frontera de los prototipos se seleccionaron de tal forma que no afectaran las mediciones de los sensores instalados en el respaldo del muro de retención (González, 2012). En el caso de las fronteras laterales (figura 2), las paredes del contenedor se cubrieron con polietileno a fin de aminorar la fricción en dicha frontera (González y Romo, 2008). La frontera posterior (figura 2) corresponde a una condición rígida, provista por una placa de acrílico fija, la cual no ejerce influencia sobre las cargas dinámicas a registrar, debido a la distancia de 0.6 m existente entre el muro de retención de 0.2 m de altura y dicha frontera (Romo et al., 1980); esto, además, se comprobó usando tanto fronteras absorbentes de energía como flexibles (González, 2012). La frontera inferior (figura 2) obedece a una frontera rugosa formada con capas delgadas de arena adheridas a hojas de lija de papel Núm. 80, simulando una condición más cercana a una condición natural suelosuelo; este criterio de frontera con fricción también lo supusieron El-Emam y Bathurst en 2004.

Figura 2.

Fronteras

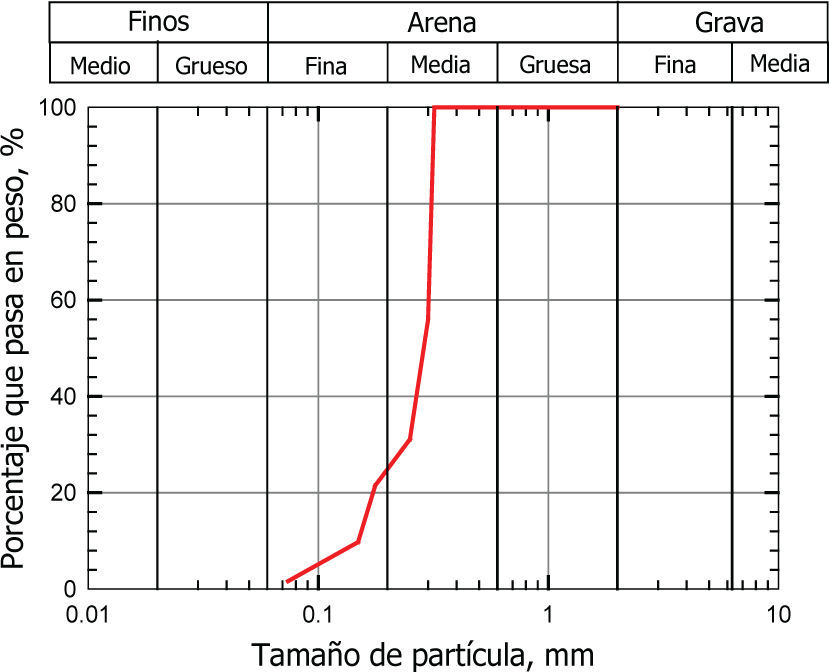
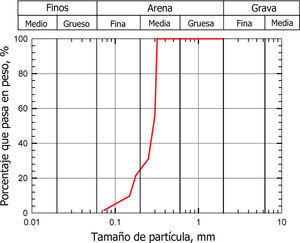
Depósitos de arena

El material empleado como relleno atañe a una arena producto de trituración de roca ígnea (basalto), clasificada como arena mal graduada de fina a media (figura 3), conformada por partículas angulosas y subredondeadas de aspecto vítreo con tonalidades predominantemente cristalinas y en menor cantidad tonos opacos. La arena presenta un ángulo de fricción de 30°, densidad de sólidos de 2.62 y contenido de agua entre 0.2 a 0.7%.

Figura 3.

Distribución granulométrica

Inclusiones compresibles

Se adoptaron inclusiones compresibles conformadas por bloques de poliestireno expandido (EPS) de área 0.2 × 0.4 m², con densidades (ρ) entre 10 y 32 kg/m³ (10.32, 10.89, 23.40, 25.29, 26.11, 26.86 y 32.64 kg/m³). Adicionalmente, se consideraron valores de la relación “espesor de la inclusión/altura del muro” (δ/H) iguales a 4.7 y 7.8%, correspondientes a espesores de 1.0 y 1.5 cm, aproximadamente.

Mesa vibradora

Los ensayes dinámicos se realizaron en la mesa vibradora hidráulica unidireccional del Laboratorio de Mecánica de Suelos del Instituto de Ingeniería de la Universidad Nacional Autónoma de México. Dicha mesa cuenta con capacidad de someter a desplazamientos máximos pico a pico de 0.3 m, modelos y/o prototipos de hasta 800 kg de masa, ubicados sobre una plataforma de trabajo cuadrada de dos metros de lado. Cabe mencionar que la plataforma está formada por tres paquetes de madera Triplay, Kevlar (Aramida) y resina epóxica, con lo que se reduce su peso en 70% con respecto a las plataformas de aluminio tradicionales, para igualdad de resistencia y rigidez.

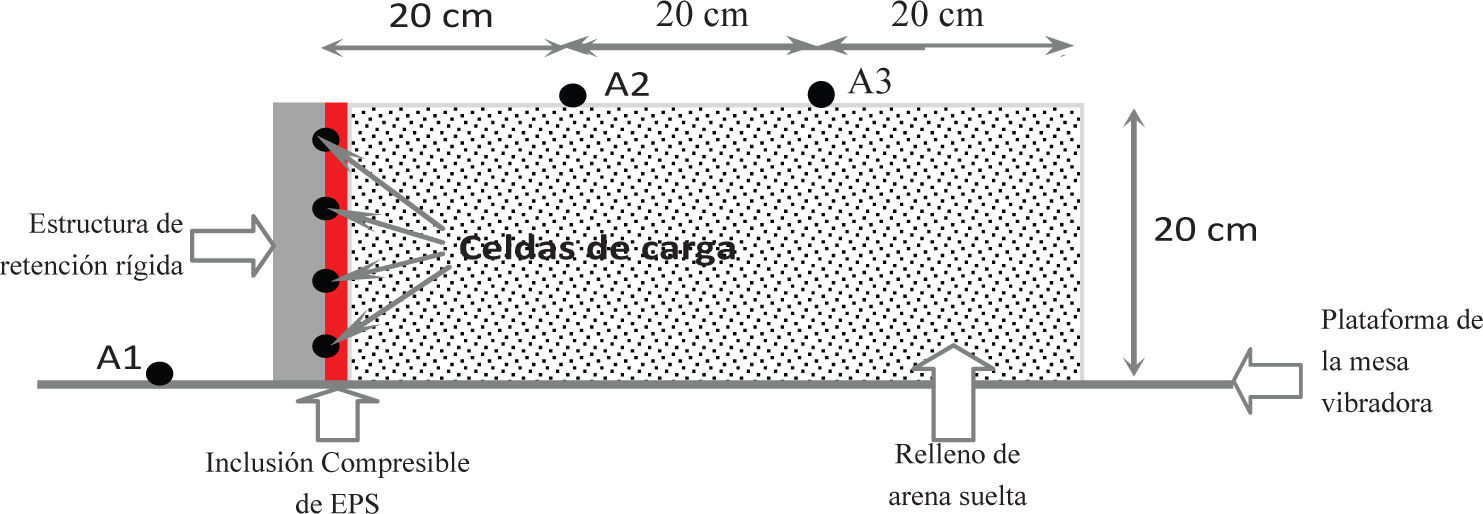
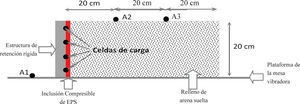
Instrumentación

Con el objetivo de obtener perfiles de carga horizontal en el respaldo de las estructuras de retención de los prototipos, se instalaron arreglos verticales de cuatro celdas de carga ubicados al centro de los muros (figura 4). Adicionalmente, se instalaron tres acelerómetros (A1, A2 y A3, figura 4) con la finalidad de definir las características de vibración del depósito de arena; en este caso, durante los primeros ensayes se observó que los registros de los sensores A2 y A3, ubicados arbitrariamente en los tercios de la longitud del contenedor eran semejantes, por lo cual se omitió finalmente el acelerómetro A3. Previo a los ensayes, todos los sensores fueron debidamente calibrados.

Figura 4.

Instrumentación (esquema fuera de escala)

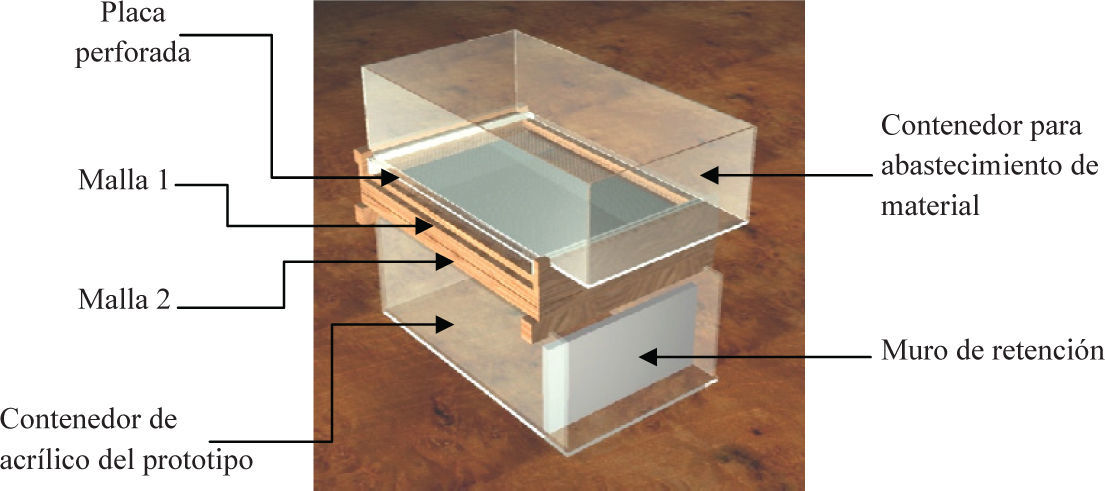
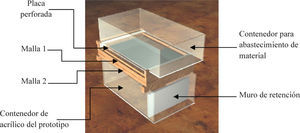
Formación de depósitos de arena

Todos los depósitos de arena se formaron con la técnica de pluviación bajo presión atmosférica propuesta por González y Romo (2011). Dicha técnica consiste en generar una lluvia de arena uniforme en un área determinada, favoreciendo la formación de depósitos homogéneos y reproducibles con dimensiones no convencionales en un laboratorio de mecánica de suelos. El equipo empleado (figura 5) combina el uso de una placa perforada y dos mallas, por lo que se conjugan la característica de dispersión de una placa perforada con la propiedad de homogeneidad en la depositación provista por las mallas. La placa posee un patrón de orificios cuadrado con diámetro y espaciamiento de 4 y 10 mm, respectivamente, mientras que las mallas presentan una abertura de 4.23 mm (1/6″).

Figura 5.

Equipo de pluviación

Señales de excitación

Todos los ensayes se realizaron con movimientos de tipo senoidal, cuyas características corresponden a aceleraciones de 0.05 y 0.10 g, cada una de ellas con frecuencias de 1, 2 y 3 Hz. Estas características son el resultado de considerar la configuración de los prototipos a ensayar, así como las especificaciones de la mesa vibradora a emplear, además de las frecuencias y aceleraciones más incidentes en una base de datos de cuarenta registros acelerográficos correspondientes a sismos fuertes ocurridos en la república mexicana (Sociedad Mexicana de Ingeniería Sísmica, A.C., 1999).

Procesamiento de la información

De acuerdo a los sensores instalados en los prototipos, durante cada ensaye se obtuvieron registros de carga y aceleración. La captura de los datos se realizó cada intervalo de tiempo Δt, establecido previamente en función del periodo y, por ende, de la frecuencia de operación (Δt = T/128, donde T es el periodo en segundos). Cada señal adquirida se procesó a fin de ser analizada posteriormente.

El procesamiento de la información consistió en corregir por línea base cada registro. Después, se obtuvo el espectro de amplitudes de Fourier para continuar con el filtrado pasa baja de la señal, a modo de obtener registros próximos a una señal senoidal, sin alterar apreciablemente los valores máximos experimentales. Finalmente, el registro filtrado fue corregido por línea base (González, 2012).

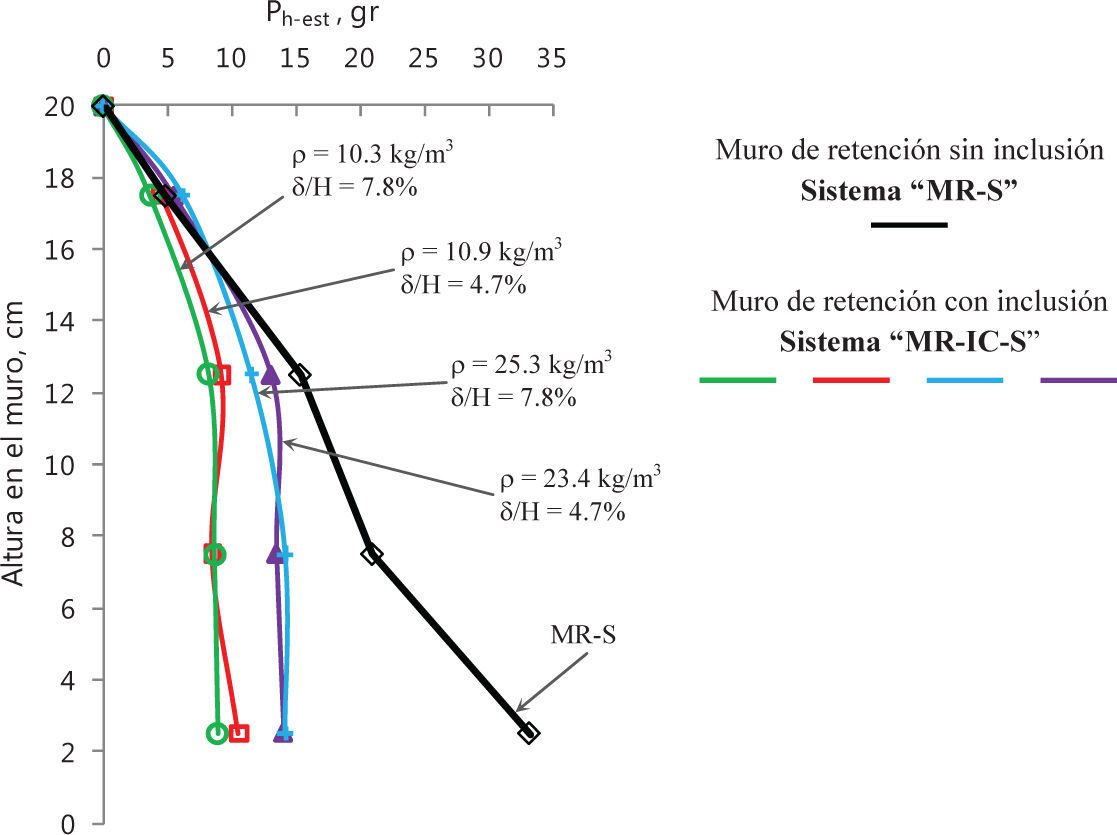
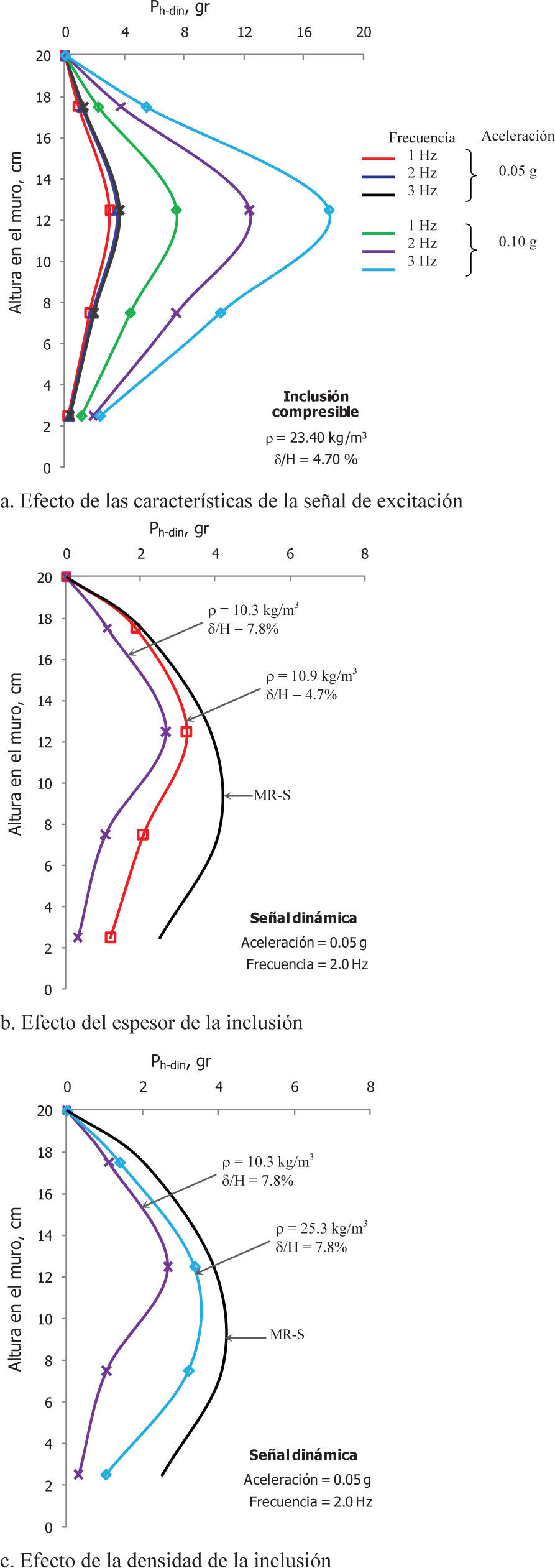
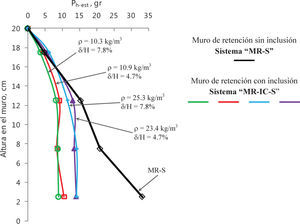
Resultados experimentales

Se llevaron a cabo ensayes en mesa vibradora de los prototipos descritos, aplicando en la base de los mismos las señales tipo senoidal mencionadas. Previo a los ensayes dinámicos, se realizó la adquisición de datos concerniente a la condición estática, permitiendo obtener los perfiles de carga horizontal estática, P_h-est, presentados en la figura 6. En el caso de condición dinámica, la figura 7 presenta resultados representativos de distribuciones de carga horizontal máxima, P_h-din. En términos generales, la presencia de una inclusión compresible en el respaldo de un muro de retención rígido, permite atenuar las cargas horizontales transmitidas al muro por un relleno de material granular hasta en 30%.

Figura 6.

Distribuciones de carga horizontal estática

Figura 7.

Distribuciones de carga horizontal dinámica

La comparación entre la excitación (acelerómetro A1) y las respuestas monitoreadas (acelerómetro A2) indica que la frecuencia fundamental del relleno, debido al confinamiento, es superior a 5 Hz.

Estáticamente, el decremento de los empujes transmitidos al muro es función de las propiedades de la inclusión, ya que a mayor espesor y menor densidad de la misma, el porcentaje de reducción aumenta. En este estudio, la mayor atenuación de carga horizontal estática corresponde al sistema de retención con inclusión compresible de 10.3 kg/m³ de densidad y relación espesor/altura del muro de 7.8% (figura 6).

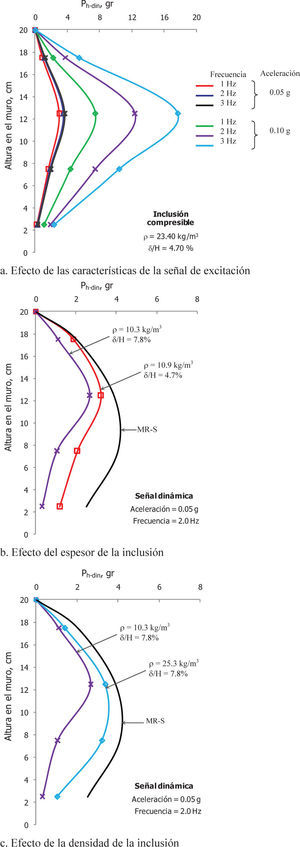
Dinámicamente, las reducciones de carga horizontal dependen tanto de la densidad y el espesor de la inclusión como de las características de la señal de excitación (aceleración y frecuencia). Al aplicar un movimiento tipo senoidal en la base de un muro, la fuerza ejercida por el material de relleno sobre el muro es función de la frecuencia y la aceleración del movimiento, como se muestra en la figura 7a. Nótese que el efecto de la frecuencia de la excitación es depreciable para aceleraciones bajas; sin embargo, para aceleraciones mayores, al aumentar la frecuencia se incrementan los empujes, lo cual es congruente con la respuesta dinámica de cuerpo de alta rigidez del relleno.

En el caso de una misma señal dinámica, el efecto del uso de una inclusión compresible en el respaldo de un muro, así como las propiedades de la misma (espesor y densidad) puede apreciarse en las figuras 7b y 7c. De estas figuras se desprende que la atenuación de las cargas horizontales aumenta a medida que crece el espesor y disminuye la densidad de la IC.

En general, la carga horizontal dinámica máxima cuando existe una IC fue registrada predominantemente por los sensores ubicados a 12.5 cm de la altura del muro, aproximadamente 2/3 de esa altura. En ausencia de IC, la presión máxima ocurrió en cerca de 1/3 de la altura del muro, lo cual discrepa de las hipótesis usuales de que esta actúa a 2/3 de la altura, pero concuerda con resultados obtenidos en ensayes de modelos en mesa vibradora (Sitar y Al-Atik, 2009). Con los resultados de esta investigación, en términos de empujes dinámicos máximos, a continuación se plantean ecuaciones que permiten conocer el porcentaje de atenuación del empuje dinámico en un sistema de retención al emplear una inclusión compresible de cierto espesor y densidad.

Análisis de la información: método M-M-O

Con el objetivo de plantear un método de estimación de empujes dinámicos en sistemas MR-IC-S, método Modificado Mononobe-Okabe (M-M-O), se definieron las relaciones “κ” y “α”. La primera (κ), relaciona la carga horizontal dinámica máxima registrada en los sistemas MR-IC-S, P_{h-din máx (MR-IC-S)}, con la carga correspondiente del sistema MR-S, P_{h-din máx (MR-S)} (ecuación 1); mientras que la segunda relación (α) involucra las propiedades de la inclusión compresible, densidad (ρ) y espesor (δ), normalizadas respecto a la densidad del agua (ρ_o = 1,000.0 kg/m³) y a la altura del muro (H), respectivamente (ecuación 2).

De acuerdo con las expresiones 1 y 2, la relación de cargas κ está en porcentaje y la relación α es adimensional.

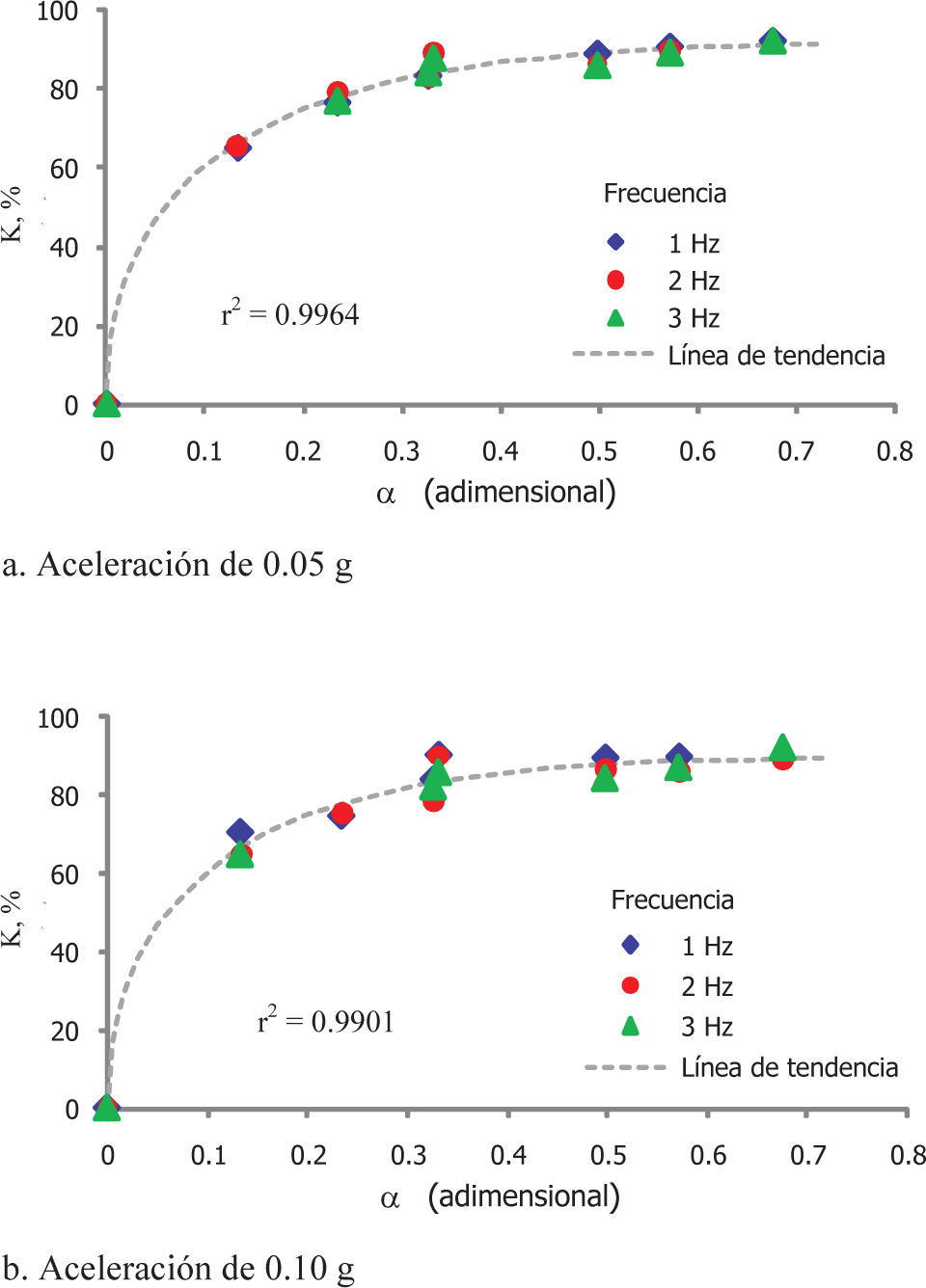
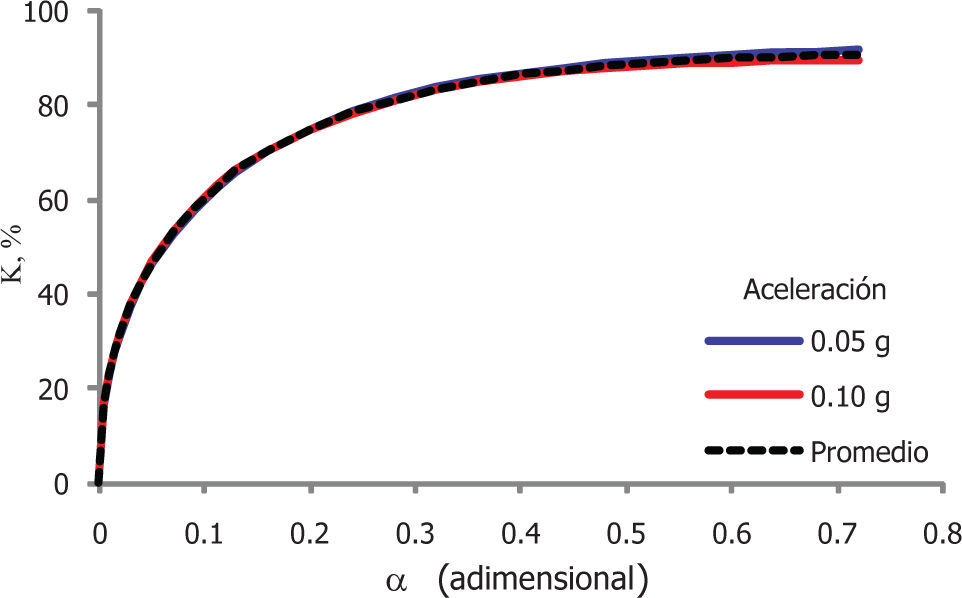
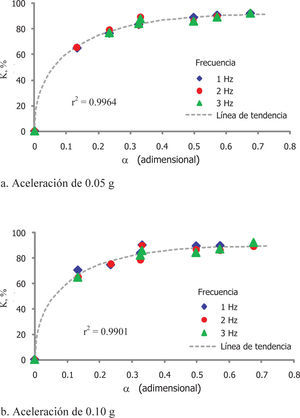
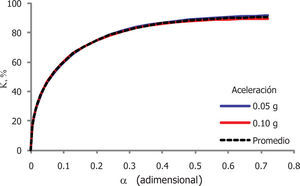
Para cada una de las aceleraciones empleadas (0.05 y 0.10 g), la figura 8 muestra el efecto de las propiedades de las IC (α) en la relación de cargas dinámicas horizontales (κ). En esta figura, se aprecia que la tendencia de κ es prácticamente independiente de la frecuencia de excitación, mientras que la relación de propiedades de la inclusión compresible α exhibe una influencia marcada sobre κ, ya que a medida que aumenta α, el valor de κ es mayor. Agrupando estas tendencias, que se presentan en las figuras 8a y 8b, se obtiene la figura 9, de donde se concluye que la relación κ tampoco depende de la aceleración de excitación y su comportamiento respecto a las propiedades de la inclusión (α), puede describirse con la relación 3, obteniendo un coeficiente de determinación (r²) superior a 0.99.

Figura 8.

Relación α versus k

Figura 9.

Relación teórica κ versus α

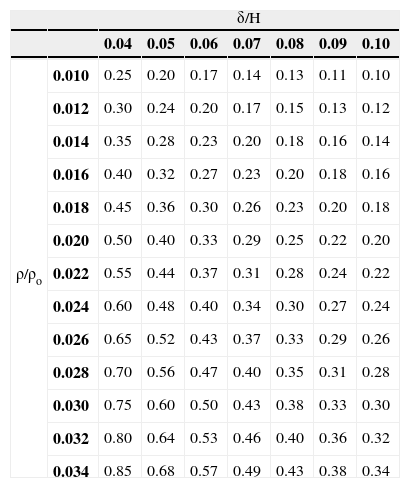
Debido a que los parámetros α y κ resultan de una normalización, se puede argüir que sus valores se mantendrán prácticamente inalterados para prototipos geométricamente diferentes y excitaciones dinámicas con otras características frecuenciales (investigaciones para reforzar o desechar este argumento están en proceso). Para los rangos de densidad y espesor de la IC considerados en esta investigación, la tabla 1 presenta los valores de la relación α correspondientes, observándose que dicha relación decrece a medida que la densidad ρ/ρ° de la inclusión (normalizada con respecto a ρ_o) disminuye y el espesor de la misma (normalizado con respecto a H) aumenta, propiciando un incremento en la atenuación (ecuación 4) de las cargas horizontales, tal como lo indican los resultados experimentales.

Tabla 1.

Valores de la relación α

		δ/H
		0.04	0.05	0.06	0.07	0.08	0.09	0.10
ρ/ρo	0.010	0.25	0.20	0.17	0.14	0.13	0.11	0.10
	0.012	0.30	0.24	0.20	0.17	0.15	0.13	0.12
	0.014	0.35	0.28	0.23	0.20	0.18	0.16	0.14
	0.016	0.40	0.32	0.27	0.23	0.20	0.18	0.16
	0.018	0.45	0.36	0.30	0.26	0.23	0.20	0.18
	0.020	0.50	0.40	0.33	0.29	0.25	0.22	0.20
	0.022	0.55	0.44	0.37	0.31	0.28	0.24	0.22
	0.024	0.60	0.48	0.40	0.34	0.30	0.27	0.24
	0.026	0.65	0.52	0.43	0.37	0.33	0.29	0.26
	0.028	0.70	0.56	0.47	0.40	0.35	0.31	0.28
	0.030	0.75	0.60	0.50	0.43	0.38	0.33	0.30
	0.032	0.80	0.64	0.53	0.46	0.40	0.36	0.32
	0.034	0.85	0.68	0.57	0.49	0.43	0.38	0.34

Cabe destacar que la relación κ, al combinar cargas dinámicas horizontales de sistemas MR-IC-S y MR-S, hace despreciable los efectos de la frecuencia y de la aceleración de la excitación, tal como lo indican las figuras 8 y 9, respectivamente. Sin embargo, tanto la aceleración como la frecuencia de excitación inciden en la magnitud de las cargas horizontales registradas (figura 7a).

Con las relaciones establecidas (κ y α), para conocer el empuje dinámico transmitido a la estructura de retención de un determinado sistema MR-IC-S, es necesario calcular el empuje correspondiente al sistema convencional MR-S. Esto es posible empleando un método tradicional como el método Mononobe-Okabe, descrito someramente a continuación.

Método Mononobe-Okabe (M-O)

El método propuesto por Mononobe y Okabe (1929-1926) obedece a una extensión de la teoría de la cuña deslizante de Coulomb, para condiciones seudo-estáticas. Este método permite obtener presiones dinámicas sobre una estructura de retención con relleno de material granular, considerando propiedades de resistencia del suelo de relleno y de fricción muro-suelo, geometría del muro, aceleración de la gravedad y aceleraciones seudo-estáticas, tal como lo indican las siguientes expresiones.

Donde P_{h (MR-S)} es la presión total activa; Kae es el coeficiente de presión de tierra activa; k_h y k_v son las aceleraciones horizontal y vertical entre la aceleración de la gravedad, respectivamente; γ es el peso volumétrico del suelo; φ es el ángulo de fricción interna del suelo y δ es el ángulo de fricción en el contacto suelomuro; β y θ son los ángulos de inclinación correspondientes de la superficie del relleno y del respaldo del muro (en esta investigación se consideraron horizontal y vertical, respectivamente) y H es la altura del muro.

La presión de tierra activa total (P_{h (MR-S)}) corresponde a la suma de la componente estática (P_{h-est (MR-S)}, ecuación 9) y la dinámica (P_{h-din (MR-S)}), como lo indica la siguiente expresión.

En la ecuación anterior, K_a es el coeficiente de presión de tierra activa en condición estática (ecuación 10).

Note que en este planteamiento se supone que el muro y el suelo de relleno se mueven en fase, lo cual es razonable para el caso de muros empotrados y relleno confinado. Para otras condiciones, el efecto de la inercia del muro se puede incluir. Esta consideración es directamente aplicable a sistemas MR-IC-S.

Finalmente, conjuntando las relaciones κ y α con el método M-O, se propone el Método Modificado Mononobe-Okabe (M-M-O) para obtener empujes dinámicos en sistemas MR-IC-S. La descripción del método se presenta a continuación.

Método Modificado Mononobe-Okabe (M-M-O)

Este método permite obtener las presiones dinámicas sobre una estructura de retención rígida con inclusión compresible de EPS y relleno de material granular. También, brinda el porcentaje de atenuación de empujes respecto a un sistema similar sin inclusión compresible. Al tratarse de una modificación del método planteado por Monobe y Okabe, el método M-M-O considera las siguientes hipótesis:

• –

  Desarrollo de un movimiento que genera una condición activa en el estado de esfuerzos del suelo.

• –

  Al alcanzarse la presión activa mínima, la cuña de suelo detrás del muro estará en un punto incipiente de falla y la resistencia al esfuerzo cortante máxima será movilizada a lo largo de la superficie de falla.

• –

  El suelo de relleno se considera como cuerpo rígido, así que no existe amplificación de la aceleración; por consiguiente, el efecto de un movimiento sísmico puede ser representado mediante fuerzas de inercia.

Para aplicar el método M-M-O, después de tener planteada la geometría y propiedades de los materiales involucrados en el sistema MR-IC-S de interés, es necesario seguir los dos pasos siguientes:

Paso 1: Cálculo del empuje dinámico en el sistema MR-S (P_{h-din (MR-S)}). Para esto se considera el sistema convencional sin inclusión y se aplica la siguiente ecuación.

donde:

P_{h (MR-S)} y P_{h-est (MR-S)} están definidas por las ecuaciones 5 y 9, respectivamente.

Paso 2. Cálculo del empuje dinámico en el sistema MRIC-S (P_{h-din (MR-IC-S)}). En este caso es necesario seguir el procedimiento descrito a continuación.

• •

  Proponer valores de densidad y espesor de la inclusión compresible.

• •

  Obtener la relación “α”, con la ecuación 2.

• •

  Calcular la relación o factor de reducción “κ”, con la ecuación 3.

• •

  Determinar el empuje dinámico del sistema MR-ICS, empleando la ecuación 1 para despejar dicha variable, como se indica en la ecuación 12.

• •

  Finalmente, hallar el porcentaje de atenuación del empuje dinámico, con la ecuación 4.

Método M-M-O: aplicación

Con objeto de ilustrar la aplicación del método M-M-O, se presenta a continuación un ejemplo de aplicación del método M-M-O.

Ejemplo de aplicación

Durante el diseño de un muro de retención de 5 m de altura, que contendrá un depósito de material granular cuyo peso volumétrico es 1,650.0 kg/m³, es necesario conocer el porcentaje de atenuación del empuje dinámico al emplear una inclusión de poliestireno expandido. En este caso se considera una inclusión de 0.50 m de espesor y 20 kg/m³ de densidad.

Paso 1. Cálculo del empuje dinámico en el sistema MR-S (P_{h-din (MR-S)}) – Método M-O

Considerando un sistema de retención convencional (sin inclusión), se empleará el método Mononobe-Okabe para determinar la presión dinámica, ejercida por el material de relleno, sobre la estructura de retención. Para realizar este cálculo se cuenta con la información de la tabla 2.

Tabla 2.

Información general

Coeficiente sísmico horizontal, kh	0.17
Coeficiente sísmico vertical, kv	0.06
Peso volumétrico del relleno, γ	1,650.0 kg/m^3
Ángulo de fricción del relleno, φ	30°
Ángulo de fricción en el contacto suelomuro, δ	30°
Ángulo de inclinación del relleno, β	0°
Ángulo de inclinación del respaldo del muro, θ	90°
Altura del muro, H	5 m

Con la información de la tabla 2, se procede al cálculo del parámetro η (expresión 7), el coeficiente de presión de tierra dinámico K_ae (expresión 6) y el empuje total P_{h (MR-S)} (expresión 5).

Posteriormente, se procede al cálculo de la componente estática del empuje (ecuaciones 9 y 10) y por consiguiente la componente dinámica (ecuación 11).

Paso 2. Cálculo del empuje dinámico en el sistema MRIC-S (P_{h-din (MR-IC-S)}) – Método M-M-O

Una vez calculado el empuje dinámico en el sistema MR-S, P_{h-din (MR-S}), se requiere conocer el empuje que se transmitirá al muro si se emplea una inclusión compresible de poliestireno expandido con densidad de 20 kg/m³ y espesor de 0.50 m, correspondientes a δ/H=10%.

Con la información anterior, se prosigue al cálculo de la relación α (ecuación 2) y posteriormente se halla la relación κ (ecuación 3).

Como κ es la relación entre el empuje del sistema de retención con y sin inclusión, se prosigue con el cálculo del empuje dinámico en el sistema MR-IC-S, utilizando la ecuación 12.

Finalmente, el porcentaje de atenuación del empuje dinámico al emplear una inclusión compresible corresponde a (ecuación 4):

En conclusión, un muro de 5 m de altura que retiene material granular, estará sujeto a un empuje dinámico de 1,845.5 kg. Este empuje se podrá reducir aproximadamente un 25% si se considera una inclusión compresible de EPS, de 0.50 m de espesor y 20 kg/m³ de densidad.

Conclusiones

En muros rígidos de retención empotrados, las presiones laterales ejercidas sobre ellos pueden ser atenuadas, tanto estática como dinámicamente, al considerar una inclusión compresible de poliestireno expandido.

En condiciones estáticas, la atenuación de los empujes de tierra dependerá de las propiedades de la inclusión compresible; mientras que en condiciones dinámicas, la disminución de los empujes estará en función tanto de las propiedades de la inclusión como de las características de las señales de excitación.

En muros rígidos de retención empotrados, con o sin inclusión compresible, las cargas horizontales aumentan a medida que se incrementa la aceleración y/o la frecuencia de la señal de excitación. En el caso de sistemas de retención con inclusión compresible, la atenuación de dichas cargas aumenta a medida que disminuye la densidad o incrementa el espesor de la inclusión compresible.

El método Modificado M-O (método M-M-O) es una extensión analítica del método Mononobe-Okabe (M-O), que permite calcular fácilmente los empujes dinámicos ejercidos en un sistema de retención con inclusión compresible, considerando tanto las características de la señal de excitación como las propiedades de la inclusión.

Agradecimientos

Los autores agradecen a Espumados de Estireno S.A. por proveer los bloques de EPS empleados en este estudio.