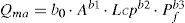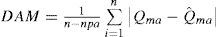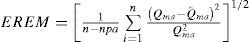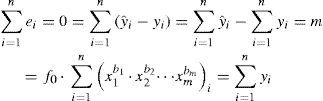Estimación de la creciente media anual en la Región Hidrológica Núm. 10 de México con base en ecuaciones de regresión potencial

Resumen

Las crecientes de diseño son básicas en el dimensionamiento o la revisión hidrológica de todas las obras hidráulicas. En sitios de interés sin información hidrométrica, su estimación se lleva a cabo con métodos regionales, cuyos resultados se deben escalar o dimensionar con base en la creciente media anual (Q_ma). Para estimar la Q_ma en una cuenca sin aforos, los hidrólogos emplean ecuaciones de regresión potencial, desarrolladas para una región homogénea, las cuales relacionan los valores observados de la Q_ma con diversas características fisiográficas de sus cuencas. Debido a la importancia que tiene la estimación de la Q_ma, se justifica la búsqueda de tales regresiones con diversos planteamientos y las mejores técnicas de obtención de sus parámetros de ajuste. En este trabajo se procesaron 22 registros de gasto máximo anual, cuyos lapsos fluctuaron de 21 a 56 años. Se analizaron cuatro ecuaciones de regresión y se aplicaron dos técnicas de ajuste, la de mínimos cuadrados de los residuos en el dominio logarítmico, incluyendo su corrección por sesgo y la otra basada en optimización numérica, empleando el algoritmo de Rosenbrock de múltiples variables no restringidas. Se obtuvieron 28 ecuaciones de regresión, que incluyen cuatro para cada uno de los dos subgrupos de cuencas en que se dividió la región hidrológica. Se realizaron cinco contrastes numéricos en estaciones hidrométricas no utilizadas en la deducción de las ecuaciones de regresión. Por último, se formulan las conclusiones, las cuales destacan la similitud de los resultados y recomiendan aplicar los análisis realizados en otras regiones del país.

Abstract

Design floods are critical in the hydrological sizing or review of all waterworks. In sites of interest without hydrometric information, their estimation is carried out with regional methods, whose results must be scaled or dimensioned based on the average annual flood (Q_aa). In order to estimate the Q_aa in an ungauged watershed, hydrologists use power regression equations developed for a homogeneous region, relating the observed values of the Q_aa with different physiographic characteristics of their watersheds. The importance of estimating the Q_aa justifies the search for such regressions with different approaches and techniques for obtaining the best fit parameters. In this paper, 22 records of annual maximum flows were processed, with periods ranging from 21 to 56 years. Four regression equations were analyzed and two techniques of adjustment were applied: the least-squares of the residuals in the logarithmic domain, including their bias correction, and another based on numerical optimization, using the multivariable unconstrained Rosenbrock algorithm. 28 regression equations were obtained, including four for each of the two watersheds subgroups in which the hydrological region was divided. Five numerical contrasts were applied in the hydrometric stations not used in deriving the regression equations. Finally, the conclusions are formulated, which emphasize the similarity of the results and recommend the application of this analysis for other regions of the country.

Introducción

Las llamadas Avenidas Máximas o Crecientes de Diseño son la estimación hidrológica más común, ya que son la base del dimensionamiento de todas las obras hidráulicas en su etapa de planeación o de diseño; además son imprescindibles cuando se aborda una revisión o se verifica la seguridad de tales obras. El procedimiento más confiable para realizar esta estimación, consiste en ajustar de un modelo probabilístico a los datos del gasto máximo anual y con base en éste, obtener las crecientes asociadas a una cierta probabilidad de excedencia (predicciones), cuyo recíproco es el periodo de retorno. Un problema general de este método, conocido como análisis de frecuencia de crecientes (AFC), es la escasa disponibilidad de registros de crecientes en los sitios de interés.

Para superar tal dificultad se han desarrollado las técnicas regionales del AFC, las cuales consisten en el uso conjunto de toda la información de gastos máximos anuales disponible dentro de una zona o región que puede ser considerada homogénea desde un punto de vista hidrológico. Esto significa que los registros de crecientes tienen cierta similitud estadística, o bien, sus cuencas presentan semejanza en determinadas propiedades físicas. En general, las técnicas regionales del AFC, estandarizan la información de crecientes con su gasto medio anual, antes de utilizarla de manera conjunta y por ello, para estimar crecientes de diseño con tales métodos se deben escalar o dimensionar sus resultados o predicciones adimensionales, es decir, se requiere una estimación de la creciente media anual (Q_ma) en el sitio de interés dentro de la región homogénea.

Las técnicas regionales clásicas que conducen a predicciones adimensionales son, por ejemplo, el método de las estaciones-años y el procedimiento del índice de crecientes, los cuales se pueden consultar en Escalante y Reyes (2002). Recientemente, los momentos L han permitido desarrollar otros enfoques, como el ajuste de modelos probabilísticos regionales adimensionales con base en esos momentos ponderados o estimados (Hosking y Wallis, 1997).

Habiéndose probado en diversos trabajos previos que la Región Hidrológica Núm. 10 (Sinaloa), forma una zona homogénea desde un punto de vista hidrológico (Escalante, 1998; Gutiérrez et al., 2004), el objetivo de este trabajo consistió en desarrollar varias ecuaciones de regresión potencial (ϒ=b0·X1b1·X2b2…Xmbm) para estimar el gasto medio anual (Y) en m³/s, empleando diferentes propiedades físicas de las cuencas (X_i). Se procesaron 22 estaciones hidrométricas y se establecieron 28 ecuaciones de regresión, las cuales se contrastan en 5 estaciones hidrométricas no utilizadas en su deducción.

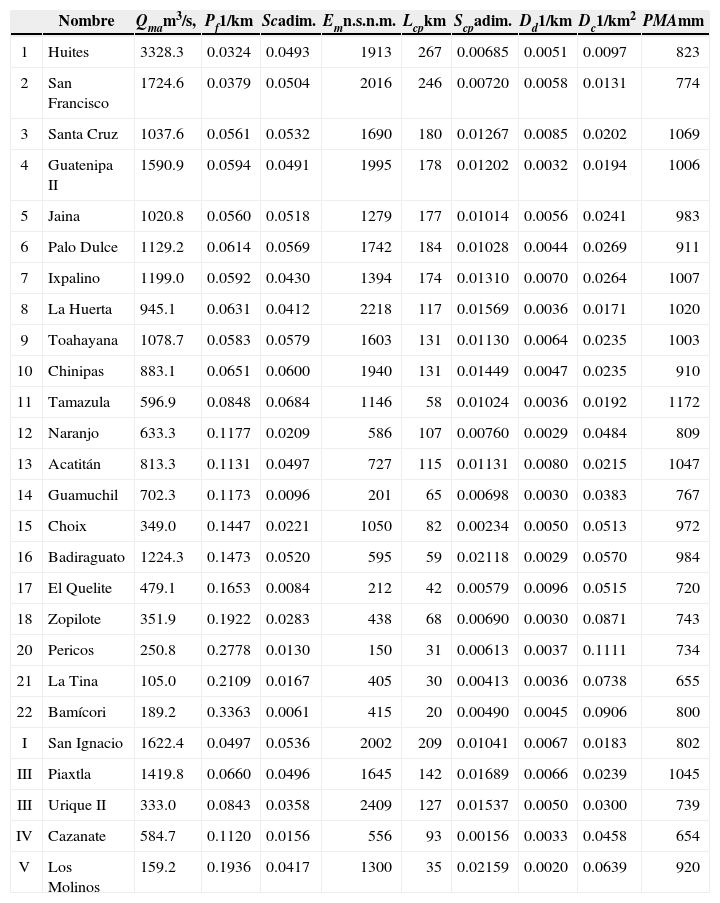
Desarrollo

Información hidrométrica utilizada

Escalante y Reyes (2002) reportan 42 estaciones hidrométricas dentro de la Región Hidrológica Núm. 10 (Sinaloa), que pueden considerarse confiables; de éstas, las que tienen registros de gastos máximos anuales mayores de 20 años y que están disponibles en el sistema BANDAS (IMTA, 2002) son 21. Los datos de la estación San Francisco proceden del Boletín Hidrológico Núm. 36 (SRH, 1975). Las características generales de esas estaciones y de cinco más que serán utilizadas para comparación, cuyos datos del BANDAS se han complementado con los que presentan Escalante y Reyes (2002), se muestran en la tabla 1, expuestas en orden decreciente de magnitud de cuenca. En la tercera columna de la tabla 2 se muestran los datos del gasto medio anual (Q_ma) de cada registro disponible. En la figura 1 se muestra la ubicación, dentro de la Región Hidrológica Núm. 10 (Sinaloa), de las cuencas de las 22 estaciones hidrométricas que serán procesadas y de las 5 que se utilizaron para comparación.

Tabla 1.

Características generales de las 27 estaciones hidrométricas procesadas en la Región Hidrológica Núm. 10 (Sinaloa)

Núm.	Nombre	ClaveBANDAS	LongitudWG	LatitudN	Río o Arroyo	Área decuenca (A, km^2)	Años de registro^*(disponibles^**)
1	Huites	10037	108° 22'	26° 54'	R. Fuerte	26,057	1942–1992 (51)
2	San Francisco	–	108° 07'	26° 54'	R. Fuerte	17,531	1941–1973 (33)
3	Santa Cruz	10040	106° 57'	24° 28'	R. San Lorenzo	8,919	1944–2002 (52)
4	Guatenipa II	10112	107° 13'	25° 21'	R. Humaya	8,252	1969–2001 (32)
5	Jaina	10036	108° 01'	25° 54'	R. Sinaloa	8,179	1942–1998 (56)
6	Palo Dulce	10077	108° 26'	27° 02'	R. Chinipas	6,439	1958–1986 (21)
7	Ixpalino	10065	106° 36'	23° 57'	R. Piaxtla	6,166	1953–1999 (45)
8	La Huerta	10113	106° 42'	25° 22'	R. Humaya	6,149	1970–1999 (28)
9	Toahayana	10110	107° 42'	26° 10'	R. Petatlán	5,281	1958–1987 (27)
10	Chinipas	10064	108° 32'	27° 25'	R. Oteros	5,098	1965–2002 (24)
11	Tamazula	10087	106° 58'	24° 56'	R. Tamzula	2,241	1963–1999 (32)
12	Naranjo	10029	108° 28'	25° 48'	A. Ocoroni	2,064	1939–1984 (45)
13	Acatitán	10070	106° 39'	24° 02'	R. Elota	1,884	1955–2002 (43)
14	Guamuchil	10031	108° 05'	25° 28'	R. Mocorito	1,645	1940–1971 (32)
15	Choix	10066	108° 19'	26° 44'	R. Choix	1,403	1956–2002 (38)
16	Badiraguato	10079	107° 32'	25° 20'	R. Badiraguato	1,018	1974–1999(26)
17	El Quelite	10083	106° 30'	23° 30'	R. Quelite	835	1961–2001 (33)
18	Zopilote	10034	108° 21'	25° 44'	A. Cabrera	666	1939–2001 (56)
19	El Bledal	10027	107° 08'	24° 48'	A. El Bledal	371	1938–1994 (56)
20	Pericos	10086	107° 41'	25° 07'	A. Pericos	270	1961–1992 (30)
21	La Tina	10078	108° 37'	26° 13'	A. Sibajahui	254	1960–1983 (24)
22	Bamícori	10057	108° 29'	26° 22'	A. Barotén	223	1951–1983 (33)
I	San Ignacio	10094	107° 51'	26° 53'	R. San Miguel	10,920	1967–1985 (19)
II	Piaxtla	–	106° 25'	23° 56'	R. Piaxtla	5,307	1958–1973 (16)
III	Urique II	10100	107° 50'	27° 20'	R. Urique	4,000	1968–2002 (29)
IV	Cazanate	10098	108° 46'	26° 36'	A. Alamos	1,813	1968–1985 (19)
V	Los Molinos	–	107° 21'	25° 42'	A. Los Molinos	501	1958–1970 (13)

*

de gasto máximo anual (m³/s)

**

número de años procesados

Tabla 2.

Gasto medio anual y características fisiográficas en las cuencas de las 27 estaciones hidrométricas indicadas de la Región Hidrológica Núm. 10 (Sinaloa)

	Nombre	Qmam^3/s,	Pf1/km	Scadim.	Emn.s.n.m.	Lcpkm	Scpadim.	Dd1/km	Dc1/km^2	PMAmm
1	Huites	3328.3	0.0324	0.0493	1913	267	0.00685	0.0051	0.0097	823
2	San Francisco	1724.6	0.0379	0.0504	2016	246	0.00720	0.0058	0.0131	774
3	Santa Cruz	1037.6	0.0561	0.0532	1690	180	0.01267	0.0085	0.0202	1069
4	Guatenipa II	1590.9	0.0594	0.0491	1995	178	0.01202	0.0032	0.0194	1006
5	Jaina	1020.8	0.0560	0.0518	1279	177	0.01014	0.0056	0.0241	983
6	Palo Dulce	1129.2	0.0614	0.0569	1742	184	0.01028	0.0044	0.0269	911
7	Ixpalino	1199.0	0.0592	0.0430	1394	174	0.01310	0.0070	0.0264	1007
8	La Huerta	945.1	0.0631	0.0412	2218	117	0.01569	0.0036	0.0171	1020
9	Toahayana	1078.7	0.0583	0.0579	1603	131	0.01130	0.0064	0.0235	1003
10	Chinipas	883.1	0.0651	0.0600	1940	131	0.01449	0.0047	0.0235	910
11	Tamazula	596.9	0.0848	0.0684	1146	58	0.01024	0.0036	0.0192	1172
12	Naranjo	633.3	0.1177	0.0209	586	107	0.00760	0.0029	0.0484	809
13	Acatitán	813.3	0.1131	0.0497	727	115	0.01131	0.0080	0.0215	1047
14	Guamuchil	702.3	0.1173	0.0096	201	65	0.00698	0.0030	0.0383	767
15	Choix	349.0	0.1447	0.0221	1050	82	0.00234	0.0050	0.0513	972
16	Badiraguato	1224.3	0.1473	0.0520	595	59	0.02118	0.0029	0.0570	984
17	El Quelite	479.1	0.1653	0.0084	212	42	0.00579	0.0096	0.0515	720
18	Zopilote	351.9	0.1922	0.0283	438	68	0.00690	0.0030	0.0871	743
20	Pericos	250.8	0.2778	0.0130	150	31	0.00613	0.0037	0.1111	734
21	La Tina	105.0	0.2109	0.0167	405	30	0.00413	0.0036	0.0738	655
22	Bamícori	189.2	0.3363	0.0061	415	20	0.00490	0.0045	0.0906	800
I	San Ignacio	1622.4	0.0497	0.0536	2002	209	0.01041	0.0067	0.0183	802
III	Piaxtla	1419.8	0.0660	0.0496	1645	142	0.01689	0.0066	0.0239	1045
III	Urique II	333.0	0.0843	0.0358	2409	127	0.01537	0.0050	0.0300	739
IV	Cazanate	584.7	0.1120	0.0156	556	93	0.00156	0.0033	0.0458	654
V	Los Molinos	159.2	0.1936	0.0417	1300	35	0.02159	0.0020	0.0639	920

Figura 1.

Localización en la Región Hidrológica Núm. 10 (Sinaloa) de las cuencas de las 27 estaciones hidrométricas procesadas

Características fisiográficas utilizadas

Las cuencas son las entidades básicas donde se estudian los procesos hidrológicos que generan el escurrimiento a partir de la lluvia ocurrida en ella. El fin del estudio será, la cuantificación de las respuestas, por lo que las propiedades físicas de las cuencas tienen un papel preponderante. Entre ellas, destaca el área o tamaño de la cuenca, pues ésta dimensiona todos los procesos. Otras propiedades importantes están asociadas a su red de cauces. Éstas y otras propiedades físicas se denominan características fisiográficas porque describen geomorfológicamente a las cuencas.

Las características fisiográficas que se han utilizado en este estudio proceden del Apéndice A de Escalante y Chávez (2002) y corresponden a las siguientes: área o magnitud (A) en km²; parámetro de forma (P^f) definido como el cociente entre la longitud del parteaguas y el área, por ello sus unidades son 1/km; pendiente de la cuenca (Sc), adimensional; elevación media (E_m) en metros sobre el nivel del mar; longitud del cauce o colector principal (L_cp), en km; pendiente promedio del cauce principal (S_cp), adimensional; densidad de drenaje (D_d) o cociente entre la longitud de todos los cauces y el área de cuenca, por lo tanto sus unidades son 1/km; densidad de cauces o corrientes (D_c) o cociente entre el número total de cauces y el tamaño de la cuenca, por lo cual sus unidades son 1/km². En la tabla 2 se tienen las magnitudes de las últimas siete características fisiográficas citadas, correspondientes a cada cuenca de las 27 estaciones hidrométricas que serán procesadas. Por último, en la tabla 2, PMA es la precipitación media anual en cada cuenca, también tomada de Escalante y Chávez (2002).

Ecuaciones de regresión potencial

Los métodos empíricos de estimación son comunes dentro de la ingeniería civil y en especial en hidrología superficial. El método más simple para representar unos datos es el llamado modelo lineal, cuya fórmula es la ecuación de la línea recta. Cuando la variable dependiente (y) está relacionada con varias independientes (x_i), es decir, que existen varios regresores o variables predictivas, se define la regresión lineal múltiple (RLM):

Los coeficientes de ajuste b₀ a b_m de la ecuación 1 se obtienen minimizando la suma de los cuadrados de los residuos, lo cual conduce a una solución matricial que se puede consultar en cualquier texto de métodos numéricos, por ejemplo en Campos (2003). La RLM tiene pocas aplicaciones como modelo empírico y en general, es mucho más frecuente el llamado modelo potencial (McCuen et al., 1990), cuya expresión general es:

Este modelo se vuelve lineal tomando logaritmos en ambos lados de su ecuación, obteniéndose:

La solución de mínimos cuadrados permite obtener los coeficientes de ajuste buscados b_i con i = 1, 2, 3, …, m. Haciendo a₀ = log b₀ de la ecuación 3, entonces el valor de b₀ será igual a 10^a0 o a e^a0 según si se utilizaron logaritmos decimales o naturales. Sin embargo, la solución es óptima únicamente en el dominio logarítmico (McCuen et al., 1990).

Selección de regresores

Siempre que se ajustan ecuaciones de RLM, resulta conveniente evitar el uso de regresares que tienen cierta dependencia lineal con otro o con varios, lo cual conduce a los problemas de multicolinealidad (Montgomery et al., 2002). Para ello, es útil examinar las correlaciones simples (r_xy) entre los regresores candidatos o variables pre- dictivas, para detectar su dependencia. En la tabla 3 se muestra la matriz de coeficientes de correlación cuya expresión es (Campos, 2003):

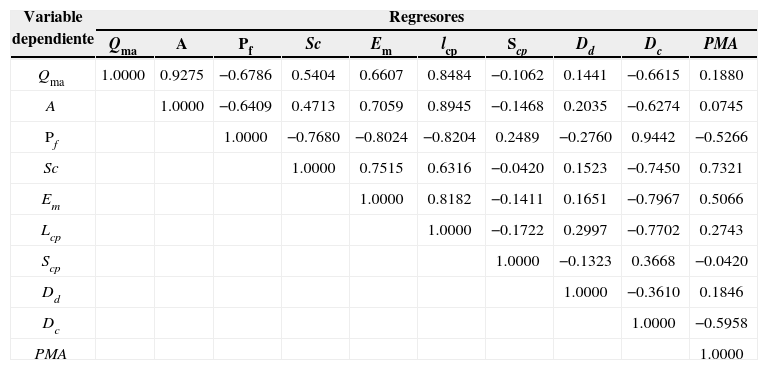
en la cual, n es el número de datos, en este caso 22. En la tabla 3, se ha incluido otro regresor diferente de las ocho características fisiográficas, la precipitación media anual (PMA) en la cuenca de cada estación hidrométri- ca. Los regresores candidatos de la tabla 3, corresponden a los comúnmente empleados en este tipo de búsqueda de ecuaciones de regresión potenciales (Tasker et al., 1996).

Tabla 3.

Matriz de coeficientes de correlación lineal (r_xy) entre el gasto máximo medio anual (Q_ma), las características fisiográficas y la precipitación media anual en las 22 cuencas de la Región Hidrológica Núm. 10 (Sinaloa)

Variable dependiente	Regresores
	Qma	A	Pf	Sc	Em	lcp	Scp	Dd	Dc	PMA
Qma	1.0000	0.9275	−0.6786	0.5404	0.6607	0.8484	−0.1062	0.1441	−0.6615	0.1880
A		1.0000	−0.6409	0.4713	0.7059	0.8945	−0.1468	0.2035	−0.6274	0.0745
Pf			1.0000	−0.7680	−0.8024	−0.8204	0.2489	−0.2760	0.9442	−0.5266
Sc				1.0000	0.7515	0.6316	−0.0420	0.1523	−0.7450	0.7321
Em					1.0000	0.8182	−0.1411	0.1651	−0.7967	0.5066
Lcp						1.0000	−0.1722	0.2997	−0.7702	0.2743
Scp							1.0000	−0.1323	0.3668	−0.0420
Dd								1.0000	−0.3610	0.1846
Dc									1.0000	−0.5958
PMA										1.0000

En la tabla 3 se observa que la correlación más alta se tiene entre P_f y D_c, lo cual es ficticio, ya que en tal caso existe correlación espuria (Benson, 1965), ya que ambos regresores usan como denominador el área de cuenca (A). La siguiente correlación alta ocurre entre el gasto medio anual (Q_ma) y el tamaño de cuenca (A), la cual es muy importante y real. Conviene observar que la longitud del cauce principal (L_cp) presenta correlaciones altas con A y con Q_ma, así como con la elevación media (E_m); con P_f tiene correlación negativa. También se destaca que E_m muestra en general correlaciones destacables con P_f, Sc, A y Q_ma. Por último, el regresor PMA no presentó correlación con los demás.

Con base en las correlaciones obtenidas en el primer renglón de resultados de la tabla 3 y las observaciones generales anteriores se recomienda investigar las cuatro regresiones siguientes:

Ajuste de mínimos cuadrados en toda la región hidrológica

Las cuatro regresiones potenciales planteadas en las ecuaciones 5 a 8, se obtuvieron mediante la solución matricial de una ecuación de RLM en el dominio logarítmico. Los resultados obtenidos con este método de ajuste se muestran en la tabla 4, como ecuaciones Ia a Id.

Tabla 4.

Coeficientes de regresión obtenidos con el método de mínimos cuadrados e índices de desempeño, para las ecuaciones del gasto medio anual en la Región Hidrológica Núm. 10 (Sinaloa)

Subconjunto analizado Número y tipo de ecuación ajustada	Coeficientes de regresión				DAM(m^3/s)	EEM (m^3/s)	EREM–
	b0	b1	b2	b3
Región Hidrológica Núm. 10 (n = 22)
Ia. Qma =b0A^b1	11.6751	0.5258			208.5	309.8	0.3412
Ib. Qma = b0−A^b1−Lcp^b2	11.7598	0.5334	−0.0148		219.4	317.4	0.3496
Ic. Qma=b0·Ab1·Lcpb2·Pfb3	3.5216	1.0450	−0.1343	0.9619	235.2	321.5	0.3205
Id. Qma=b0·Ab1·Lcpb2·Dcb3	11.8767	0.5989	−0.0649	0.0864	234.5	329.9	0.3549
Región Hidrológica Núm. 10 (n = 22)
IIa. Qma. = fo;A^b1	12.1082	0.5258			225.8	313.9	0.3712
IIb. Qma. = foA^b1	12.1992	0.5334	−0.0148		225.7	313.4	0.3709
IIc. Qma=f0·Ab1·Lcpb2·Pfb3	3.6410	1.0450	−0.1343	0.9619	239.4	318.5	0.3391
IId. Qma=f0·Ab1·Lcpb2·Dcb3	12.3119	0.5989	−0.0649	0.0864	241.5	326.2	0.3762
Subgrupo de cuencas grandes (n = 10)
IIa. Qma = bo−A^b1	3.0917	0.6666			289.1	318.6	0.1937
IIIb. Qma = bLcpA^blLcp^bl	2.4784	0.5843	0.1874		321.3	347.3	0.2063
IIIc. Qma=b0·Ab1·Lcpb2·Pfb3	4.5157	0.2610	0.2267	−0.7248	355.6	370.0	0.2116
IIId. Qma=b0·Ab1·Lcpb2·Dcb3	1.5269	−1.1250	2.0292	−1.6371	320.5	344.7	0.1836
Subgrupo de cuencas pequeñas (n = 12)
IVa. Qma = bo−A^b1	5.7136	0.6397			170.9	263.5	0.4302
IVb. Qma = b0;A^blLcp^b2	5.8135	0.6879	−0.0859		189.4	279.5	0.4507
IVc. Qma=b0·Ab1·Lcpb2·Pfb3	1.5556	1.2860	−0.2491	1.1297	209.8	299.3	0.4273
IVd. Qma=b0·Ab1·Lcpb2·Dcb3	4.8676	0.9692	−0.2638	0.3424	225.3	299.2	0.4578

Índices de desempeño de las ecuaciones de regresión

Cuando se tienen varias ecuaciones de RLM, la selección de la más conveniente se puede abordar a través de varios indicadores basados en los residuos (Montgomery et al., 2002; Campos, 2011), es decir, en las diferencias entre la variable observada (y) y la estimada (ŷ) con la ecuación de RLM que se contrasta. Cuando se trabaja con los logaritmos de las variables, tales indicadores, como el coeficiente de determinación o la estadística C_p de Mallows, no son confiables, pues los residuos se evalúan en el dominio logarítmico, como han señalado McCuen et al. (1990).

Por lo anterior, todas las ecuaciones de regresión que se obtengan con los métodos de ajuste que serán aplicados, se evaluarán por medio de los tres índices de desempeño siguientes, calculados en el dominio real (Pandey y Nguyen, 1999):

DAM es la desviación absoluta media con unidades de m³/s, Q_ma y Qˆma son los gastos medios anuales observado y estimado con la ecuación de regresión potencial, n es el número de datos utilizados de cada variable, en este caso 22 (tabla 1) y npa, es el número de parámetro de ajuste, el cual varía de 2 a 4. EEM es el error estándar medio con unidades de m³/s:

Por último, EREM es el error relativo estándar medio, adimensional:

En las columnas 6, 7 y 8 de la tabla 4 se exponen los valores obtenidos para los índices anteriores, relativos a las ecuaciones Ia a Id, obtenidas por mínimos cuadrados de los residuos en el dominio logarítmico.

Corrección por sesgo del ajuste de mínimos cuadrados

Desde la década de los años setenta, se estableció que el ajuste de la ecuación 2 por mínimos cuadrados de los residuos, en efecto los minimiza pero en el dominio logarítmico y por ello se han sugerido varios procedimientos para corregir esta ecuación. McCuen et al. (1990) presentan tres procedimientos para corregir el coeficiente b₀, también llamado ordenada al origen, por la similitud entre la ecuación 1 y la fórmula de la línea recta. Se puede obtener una estimación de b₀ no sesgada haciendo cero los residuos (e_i) en el dominio real, es decir:

el estimador buscado será:

en la obtención de f₀ se está aceptando que el sesgo se puede corregir exclusivamente ajustando b₀, pero ello no implica que los coeficientes b_i poblacionales sean insesgados; de hecho b₀ sólo es insesgado para la muestra utilizada. Los otros dos procedimientos de ajuste de b₀ expuestos por McCuen et al. (1990) se basan en los residuos en el dominio logarítmico. En la tabla 4 se muestran las estimaciones de f₀ obtenidas con la ecuación 13, así como sus índices de desempeño respectivos (ecuaciones II). Se observa que el DAM y el EREM crecen en todas las nuevas ecuaciones de regresión, pero el EEM disminuye en los modelos de dos y tres variables predictivas.

Ajuste de mínimos cuadrados por subgrupos de cuencas

Los estudios previos de homogeneidad regional realizados en la Región Hidrológica Núm. 10 (Sinaloa), por Escalante (1998) y Gutiérrez et al. (2004) han establecido que las cuencas grandes, con áreas mayores a los 5,000 km², pertenecen a la zona montañosa de la región y por ello tienen orografía accidentada, definiendo un subgrupo de cuencas grandes. Este enfoque de subdivisión por tamaños de cuencas es común y ha sido abordado por Tasker et al., (1996) y Pandey y Nguyen (1999).

Con el propósito de comprobar numéricamente la conveniencia de la subdivisión de la región hidrológica en dos subgrupos de cuencas, se aplicó una prueba estadística muy simple que mide la heterogeneidad de un área o zona específica, denominada rango regional normatizado de los coeficientes de variación de las crecientes [RRN(Cv)], definido por Burn (1990) como:

donde R(Cv) y M(Cv) son el rango y la mediana de los valores del Cv de la subregión o zona analizada. Entonces cuando el RRN(Cv) aplicado por subregiones resultaⁱ menor que el de la región total, la subdivisión es conveniente. En la tabla 5 se presentan las 10 y 12 estaciones hidrométricas que integran cada subgrupo y los resultados respectivos de la prueba del RRN(Cv) se muestran con negritas. Se observa que la subdivisión resulta conveniente para el subgrupo de las grandes cuencas, pero no implica gran diferencia en el de las cuencas menores; además los Cv de las crecientes no muestran un agrupamiento o diferenciación acusada entre esos subgrupos. Por lo anterior, es probable que las ecuaciones de regresión obtenidas en cada subgrupo no muestren grandes ventajas estadísticas con respecto a las obtenidas para toda la región hidrológica.

Tabla 5.

Estaciones hidrométricas divididas por subgrupos y prueba de heterogeneidad del rango regional normalizado

Subgrupo de cuencas grandes			Subgrupo de cuencas pequeñas
Núm.	Estación hidrométrica	Cv	Núm.	Estación hidrométrica	Cv
1	Huites	0.995	1	Tamazula	0.655
2	San Francisco	0.841	2	Naranjo	1.053
3	Santa Cruz	1.120	3	Acatitán	1.065
4	Guatenipa II	0.759	4	Guamuchil	0.928
5	Jaina	1.114	5	Choix	0.880
6	Palo Dulce	1.218	6	Badiraguato	1.555
7	Ixpalino	0.905	7	El Quelite	0.869
8	La Huerta	0.593	8	Zopilote	0.806
9	Toahayana	0.645	9	El Bledal	0.915
10	Chinipas	0.666	10	Pericos	0.625
–	Valor mínimo	0.593	11	La Tina	1.471
–	Valormáximo	1.218	12	Bamícori	0.933
–	Valor mediano	0.873	−	Valor mínimo	0.625
–	Valor medio	0.886	−	Valor máximo	1.555
–	Rango regional normalizado	0.716	–	Valor mediano	0.922
	Región Hidrológica Núm. 10 (Sinaloa)		–	Valor medio	0.980
–	Valor mínimo	0.593	–	Rango regional normalizado	1.009
–	Valor máximo	1.555
–	Valor mediano	0.910
–	Valor medio	0.937
–	Rango regional normalizado	1.057

Los resultados concentrados en la tabla 4 para los dos subgrupos procesados (ecuaciones III y IV), ponen de manifiesto, a través de los fuertes cambios que experimentan los coeficientes b_i, no sólo en magnitud sino en signo, que ahora los problemas asociados a la multicolinealidad son más severos, lo cual es lógico, al agrupar a las cuencas por tamaño, ya que los índices de desempeño siempre resultan influenciados por la magnitud de la variable dependiente (y), entonces la DAM y el EEM son menores en el subgrupo de cuencas menores y viceversa en las de mayor área. Lo contrario ocurre con el EREM. En términos generales, no existe evidencia estadística para desechar las ecuaciones de regresión encontradas por subgrupos, pero en realidad tienen menor confiablidad debido al número reducido de datos empleados en su deducción.

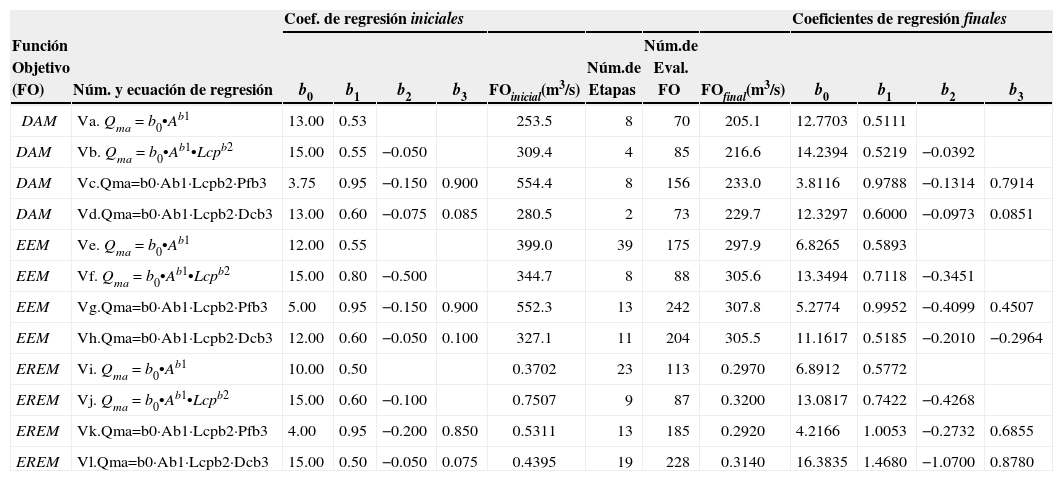
Ajuste a través de optimización numérica

Este procedimiento tiene dos ventajas fundamentales con respecto al ajuste de una ecuación de regresión potencial por mínimos cuadrados de los residuos (ecuación 2), la primera es que trabaja en el dominio real y la segunda es que se puede emplear cualquier función objetivo para buscar su mínimo. Haciendo uso del algoritmo de Rosenbrock de múltiples variables no restringidas (Rosenbrock, 1960; Kuester y Mize, 1973; Campos, 2003), se ajustaron las ecuaciones 5 a 8 empleando como funciones objetivo minimizar las medidas de desempeño definidas con las ecuaciones 9 a 11. Los resultados obtenidos se han concentrado en la tabla 6, observándose que en todos los casos los valores de DAM, el EEM y el EREM alcanzados fueron menores que los de mínimos cuadrados (tabla 4), incluso inferiores a los obtenidos con la corrección por sesgo (ecuación 13).

Tabla 6.

Coeficientes de regresión obtenidos con el método de optimización numérica (algoritmo de Rosenbrock), para las ecuaciones del gasto medio anual en la Región Hidrológica Núm. 10 (Sinaloa)

Función Objetivo (FO)	Núm. y ecuación de regresión	Coef. de regresión iniciales								Coeficientes de regresión finales
		b0	b1	b2	b3	FOinicial(m^3/s)	Núm.de Etapas	Núm.de Eval. FO	FOfinal(m^3/s)	b0	b1	b2	b3
DAM	Va. Qma = b0•A^b1	13.00	0.53			253.5	8	70	205.1	12.7703	0.5111
DAM	Vb. Qma = b0•A^b1•Lcp^b2	15.00	0.55	−0.050		309.4	4	85	216.6	14.2394	0.5219	−0.0392
DAM	Vc.Qma=b0·Ab1·Lcpb2·Pfb3	3.75	0.95	−0.150	0.900	554.4	8	156	233.0	3.8116	0.9788	−0.1314	0.7914
DAM	Vd.Qma=b0·Ab1·Lcpb2·Dcb3	13.00	0.60	−0.075	0.085	280.5	2	73	229.7	12.3297	0.6000	−0.0973	0.0851
EEM	Ve. Qma = b0•A^b1	12.00	0.55			399.0	39	175	297.9	6.8265	0.5893
EEM	Vf. Qma = b0•A^b1•Lcp^b2	15.00	0.80	−0.500		344.7	8	88	305.6	13.3494	0.7118	−0.3451
EEM	Vg.Qma=b0·Ab1·Lcpb2·Pfb3	5.00	0.95	−0.150	0.900	552.3	13	242	307.8	5.2774	0.9952	−0.4099	0.4507
EEM	Vh.Qma=b0·Ab1·Lcpb2·Dcb3	12.00	0.60	−0.050	0.100	327.1	11	204	305.5	11.1617	0.5185	−0.2010	−0.2964
EREM	Vi. Qma = b0•A^b1	10.00	0.50			0.3702	23	113	0.2970	6.8912	0.5772
EREM	Vj. Qma = b0•A^b1•Lcp^b2	15.00	0.60	−0.100		0.7507	9	87	0.3200	13.0817	0.7422	−0.4268
EREM	Vk.Qma=b0·Ab1·Lcpb2·Pfb3	4.00	0.95	−0.200	0.850	0.5311	13	185	0.2920	4.2166	1.0053	−0.2732	0.6855
EREM	Vl.Qma=b0·Ab1·Lcpb2·Dcb3	15.00	0.50	−0.050	0.075	0.4395	19	228	0.3140	16.3835	1.4680	−1.0700	0.8780

Aplicaciones numéricas de contraste

En cada una de las cinco estaciones hidrométricas finales de las tablas 1 y 2, se aplicaron las 28 ecuaciones de regresión potencial que se obtuvieron a través de los análisis y procedimientos descritos. Los resultados se han concentrado en la tabla 7, mostrando 24 estimaciones, pues únicamente se toma un subgrupo de ecuaciones, III ó IV de la tabla 4, de acuerdo con el tamaño de cuenca. Los resultados muestran una gran regularidad en las estimaciones, lo cual está asociado a la veracidad de las características fisiográficas de cada cuenca. Para la selección de la estimación buscada Qˆma, se recomienda dar un “peso” a cada ecuación potencial, es decir, que son más confiables las tipo V (tabla 6), así como las II (tabla 4) y menos las obtenidas por subgrupos (III y IV).

Tabla 7.

Gasto medio anual estimado (Qˆma,m3/s) con las 24 ecuaciones de regresión potencial obtenidas, en las cinco estaciones hidrométricas indicadas de la Región Hidrológica Núm. 10 (Sinaloa)

San Ignacio		Piaxtla		Urique II		Cazanate		Los Molinos
Núm. Ec.	Qˆma	Núm. Ec.	Qˆma	Núm. Ec.	Qˆma	Núm. Ec.	Qˆma	Núm. Ec.	Qˆma
Ia	1551	Ia	1061	Ia	915	Ia	603	Ia	307
Ib	1549	Ib	1060	Ib	913	Ib	602	Ib	307
Ic	1589	Ic	1034	Ic	989	Ic	593	Ic	298
Id	1558	Id	1061	Id	920	Id	606	Id	308
IIa	1608	IIa	1101	IIa	949	IIa	626	IIa	318
IIb	1607	IIb	1100	IIb	947	IIb	624	IIb	319
IIc	1643	IIc	1069	IIc	1022	IIc	613	IIc	309
IId	1615	IId	1100	IId	954	IId	629	IId	319
IIIa	1521	IIIa	940	IIIa	779	IVa	694	IVa	305
IIIb	1543	IIIb	942	IIIb	782	IVb	687	IVb	308
IIIc	1512	IIIc	934	IIIc	709	IVc	657	IVc	298
IIId	1561	IIId	1036	IIId	783	IVd	737	IVd	307
Va	1480	Va	1023	Va	886	Va	591	Va	306
Vb	1479	Vb	1031	Vb	893	Vb	598	Vb	318
Vc	1575	Vc	1023	Vc	956	Vc	575	Vc	286
Vd	1381	Vd	952	Vd	828	Vd	550	Vd	288
Ve	1637	Ve	1070	Ve	906	Ve	568	Ve	266
Vf	1582	Vf	1082	Vf	919	Vf	583	Vf	327
Vg	1595	Vg	1035	Vg	914	Vg	537	Vg	285
Vh	1550	Vh	1064	Vh	879	Vh	548	Vh	310
Vi	1476	Vi	973	Vi	827	Vi	524	Vi	249
Vj	1329	Vj	918	Vj	780	Vj	495	Vj	289
Vk	1436	Vk	938	Vk	861	Vk	514	Vk	268
Vl	1363	Vl	903	Vl	820	Vl	520	Vl	300
Mínimo	1329	–	903	–	709	–	495	–	249
Máximo	1643	–	1101	–	1022	–	737	–	327
Media	1530.8	–	1018.8	–	880.5	–	594.8	–	299.8
Mediana	1550.5	–	1034.5	–	899.5	–	595.5	–	306.5
Qma observ.	1622.4	–	1419.8	–	333.0	–	584.7	–	159.2

En relación con la estimación puntual de cada contraste (tabla 7), se observa una buena aproximación en las estaciones San Ignacio y Cazanate, cuyos registros integrados son los más confiables. El dato disponible de Q_ma = 1419.8 m³/s en la estación Piaxtla se considera bastante elevado, ya que la estación hidrométrica Ixpalino, también sobre el Río Piaxtla, que es 16.2% mayor en área tiene registrado un valor de 1199 m³/s. En tales circunstancias, la estimación de 1035 m³/s obtenida a través de las ecuaciones empíricas se considera bastante acertada.

Lo contrario ocurre en Urique II cuyo valor de Q_ma se considera sumamente bajo, pues la estación Chinipas, con el área de cuenca más parecida tiene 883.1 m³/s. Entonces la estimación empírica de 889.5 m³/s se considera mucho más apegada a la realidad. Finalmente, con respecto a la estimación en la estación hidrométrica Los Molinos, su valor del registro es muy bajo y su estimación empírica es mucho más cercana al valor obtenido por Campos (2008) de 459 m³/s con base en el método racional regional, para el periodo de retorno de 2 años.

Conclusiones

El escalamiento requerido en la aplicación de los resultados de los métodos regionales de estimación de crecientes en cuencas sin aforos, implica la cuantificación, lo más aproximada posible, de su gasto medio anual (Q_ma). Ha sido práctica común, realizar tal cuantificación a través de ecuaciones de regresión que emplean como variables predictivas las características fisiográficas de las cuencas. Dada la importancia de la estimación del Q_ma, se justifica el análisis y búsqueda de tales regresiones con diversos planteamientos y las mejores técnicas de obtención de sus parámetros de ajuste.

En este trabajo se ha expuesto con detalle, cómo establecer las ecuaciones potenciales por analizar y como aplicar el ajuste de mínimos cuadrados en el dominio logarítmico, incluyendo su corrección por sesgo. También se detalló cómo lograr un mejor ajuste de tales ecuaciones, a través de optimización numérica no restringida, empleando el algoritmo de Rosenbrock.

Los resultados concentrados en la tabla 7, para los cinco contrastes realizados en estaciones hidrométricas que no se utilizaron en la deducción de las 28 ecuaciones potenciales, muestran una regularidad bastante acusada, lo cual genera confianza en tales estimaciones. Por lo anterior, se recomienda la aplicación de los planteamientos y técnicas de ajuste utilizadas en este trabajo, en otras regiones del país, para contar con las ecuaciones potenciales que permitan una mejor aproximación del valor buscado del Q_ma.

Agradecimientos

Se agradece a los dos árbitros anónimos sus correcciones sugeridas, las cuales permitieron volver más explícito el trabajo y mejorar su redacción.