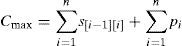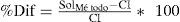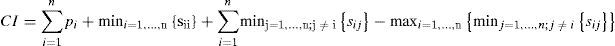En este trabajo se presenta una aplicación de un algoritmo de estrategia evolutiva multi-miembro (μ+λ) – ES para la programación de trabajos en una máquina con tiempos de preparación dependientes de la secuencia con el objetivo de minimizar el makespan (Cmax). La estrategia evolutiva fue evaluada sobre un conjunto de problemas generados en forma aleatoria. Se introduce un procedimiento de mejora de la estrategia evolutiva, generando la población inicial como una vecindad de la solución entregada por otro método, lo que mejora su desempeño. La estrategia evolutiva se comparó con la heurística del mejor vecino y un algoritmo genético, mostrando un mejor desempeño.
A multi-member (μ+λ) – ES evolution strategy algorithm for the single machine scheduling problem with sequence dependent setup times and makespan (Cmax) minimization is presented. The evolution strategy is evaluated on a random generated set of test problems. A procedure to improve the performance of the evolution strategy considering the initial population as a neighborhood of the solution given by another method is introduced. The evolution strategy shows better performance than a greedy constructive heuristic and a genetic algorithm.
La programación de órdenes de producción para la generación de bienes y servicios ayuda a la optimización de recursos productivos limitados satisfaciendo en forma eficiente los requerimientos de los clientes. De esta forma la programación de la producción se ha convertido en una herramienta estratégica para cualquier organización, transformando las necesidades de los clientes en órdenes de producción que se “transforman” en trabajos con fecha de entrega asociada.
Los sistemas de producción por lotes se caracterizan por la obtención de múltiples productos en lotes de producción utilizando la misma instalación, las que se clasifican según la variedad y homogeneidad de los productos a fabricar, y el número de máquinas del sistema (Baker, 1974; Pinedo, 2008). El problema de programación de un taller de una máquina consiste en un sistema de una máquina, que procesa n trabajos de una operación procesados en secuencia, eventualmente, con tiempos de preparación (setup) dependientes de la secuencia.
Se han aplicando varias heurísticas y algoritmos a diferentes problemas de programación de una máquina con setup. Lee y Asllani (2004) comparan la programación matemática entera con algoritmos genéticos para minimizar el número de trabajos atrasados y el makespan. Gupta y Smith (2006) proponen algoritmos GRASP y de búsqueda en una vecindad para minimizar la tardanza, mientras que Liao y Juan (2007) proponen un algoritmo ACO para resolver el mismo problema y comparan con otros algoritmos. Koulamas y Kyparisis (2008) tratan el problema con setups proporcionales al tiempo de proceso optimizando objetivos relacionados con el tiempo de finalización de los trabajos, entre ellos el makespan, aplicando algoritmos de ordenamiento. Lai y Lee (2010) analizan el problema de minimizar el makespan y la tardanza aplicando una función no lineal de deterioro del tiempo de proceso, mientras que Salazar y Sánchez (2011) aplican MMAS (una versión de algoritmo ACO) para minimizar el makespan. Jula y Rafiey (2012) consideran ventanas de tiempo para el inicio del proceso de cada trabajo, cuidando de mantener cierto nivel de trabajo en proceso (objetivo primario) y de minimizar el makespan (objetivo secundario).
Las estrategias evolutivas (ES) fueron introducidas por Rechenberg y Schwefel a mediados de la década del 60 orientadas a la optimización continua de parámetros en problemas de ingeniería (Rechenberg, 1973). En la literatura se encuentran pocas propuestas que adaptan estrategias evolutivas a problemas de secuenciación de trabajos. Filipic y Zupanic (1999) utilizan estrategias evolutivas para programar cortes de energía en un sistema productivo con el objetivo de minimizar el consumo de energía. Hou y Chang (2002) proponen un método de estrategias evolutivas para asignar la producción en un sistema productivo multiplanta. Pierreval et al. (2003) y Salazar y Rojas (2010) tratan problemas de diseño y configuración de sistemas de producción utilizando estrategias evolutivas. Probablemente los trabajos de Ablay (1987), Herdy (1991) y Rudolph (1991) son los primeros trabajos (y tal vez los únicos) en proponer estrategias evolutivas para resolver el problema del vendedor viajero.
Problema de programación de una máquinaEn este trabajo se trata el problema de programar n trabajos en un taller de una máquina con setups dependientes de la secuencia, que consiste en secuenciar los n trabajos de manera que se minimice el makespan (Cmax), es decir, minimiza el tiempo transcurrido entre el inicio del procesamiento del primer trabajo (tiempo de referencia 0) y el tiempo de finalización del procesamiento del último trabajo. El tiempo de proceso de cada trabajo es fijo y existen tiempos de preparación de máquina que dependen del orden en el que se procesan los trabajos en esa máquina. Se consideran los siguientes supuestos:
- •
El tiempo de proceso del trabajo i está dado por pi (i = 1,…, n).
- •
El tiempo de preparación (setup) para procesar el trabajo j después de procesar el trabajo i está dado por sij (i = 1,…,n; j = 1,…, n), donde sii representa la preparación inicial cuando el trabajo i es el primer trabajo procesado en la máquina.
- •
El proceso de un trabajo en la máquina no se puede interrumpir (non preemption).
- •
Todos los trabajos son independientes entre sí y se encuentran disponibles en el instante inicial.
- •
La máquina opera sin fallas en el horizonte de programación.
- •
El objetivo es minimizar Cmax.
Con la notación introducida por Graham et al. (1979), el problema de una máquina caracterizado por los supuestos mencionados se denota por 1|sij|Cmax,, y es un conocido problema NP-Hard (Blazewicz et al., 1996 y Pinedo, 2008), lo que hace impracticable la obtención de la solución óptima para problemas de mediano a gran tamaño (este problema tiene una estructura similar al problema clásico del agente viajero asimétrico ATSP que es una variante del problema del agente viajero en la que las distancias son asimétricas, es decir, la distancia de ida es diferente a la distancia de regreso, esto es dij≠ dji. Los trabajos se asocian a las ciudades y los tiempos de setup sij se asocian a las distancias dij. En este trabajo, se rsuelve el problema 1|sij|Cmax mediante un algoritmo de estrategia evolutiva, comparándolo con la heurística glotona del mejor vecino (MV) y un algoritmo genético estándar. La relevancia de los problemas de programación con tiempos y/o costos de preparación dependientes de la secuencia queda de manifiesto en una amplia gama de configuraciones productivas (Allahverdi et al., 2008).
El makespan (Cmax) se obtiene como la suma de los setups s[i-1][i] que se producen entre el (i–1)-ésimo el i-ésimo trabajos de la secuencia representados por [i–1] e [i], respectivamente, más la suma de los tiempos de proceso de los n trabajos:
El tiempo de setup s[0][1] representa el setup inicial (antes de procesar el primer trabajo de la secuencia). Una heurística simple para resolver la programación para este problema es la heurística glotona del mejor vecino (MV) (figura 1).
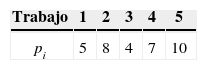
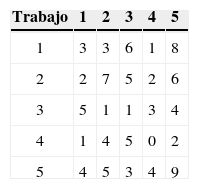
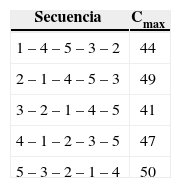
A modo de ilustración, consideremos un problema de 5 trabajos a programar, cuyos parámetros se presentan en las tablas 1 y 2.
Utilizando la heurística MV, se obtienen las 5 secuencias de la tabla 3 y sus respectivos valores de Cmax, donde la mejor secuencia 3 – 2 – 1 – 4 – 5 con Cmax, = 41 es la solución entregada por la heurística. Esta secuencia se obtiene considerando el trabajo 3 como primer trabajo de la secuencia (con setup inicial s33 = 1), luego se selecciona el trabajo 2 ya que es el trabajo no asignado que genera el menor setup (s32 = 1). Después, con el mismo criterio, se seleccionan sucesivamente los trabajos 1 (s21 = 2; en este paso también pudo seleccionarse el trabajo 4 ya que tiene igual setup s24 = 2, pero se aplicó el criterio del primer trabajo con menor setup siguiente), 4 (s14 = 1) y 5 (s45 = 2), lo que produce Cmax = 1 + 1 + 2 + 1 + 2 + 34 = 41 (donde 34 corresponde a la suma de los tiempos de proceso de los 5 trabajos del problema).
La programación de esta solución se muestra en la figura 2; en ésta las barras achuradas corresponden a los tiempos de setup, mientras que la barra sólida corresponde a los tiempos de proceso de los trabajos.
Estrategias evolutivasLas estrategias evolutivas (ES) fueron introducidas originalmente por Rechenberg y Schwefel para resolver problemas de optimización continua (Rechenberg, 1973 y 1994; Schwefel, 1981, 1984 y 1995; Bäck et al. 1991) imitando principios de la evolución natural, asociando el concepto de individuo o miembro a una solución factible del problema, y el de población a un conjunto de individuos (soluciones factibles). Los individuos se evalúan a través de una función de aptitud (fitness) que corresponde a una medida de la calidad del individuo como solución del problema (Michalewicz, 1999). La recombinación de los individuos permite la evolución de una población de generación en generación.
Las estrategias evolutivas multimiembro (μ+λ) – ES y (μ, λ) – ES se diferencian en la forma en que construyen la población de la siguiente generación:
- •
(μ+λ) – ES: se generan λ individuos mediante la recombinación de los individuos de la población de tamaño m, que posteriormente son afectados por una mutación. Luego se seleccionan los m mejores individuos del total m+l individuos para formar la población de la siguiente generación.
- •
(μ, λ) – ES: se generan λ individuos (λ > μ) mediante la recombinación de los individuos de la población de tamaño m (λ > μ), que posteriormente son afectados por una mutación. Luego se seleccionan los m mejores individuos del total de los l nuevos individuos generados para formar la población de la siguiente generación.
La figura 3 muestra una estructura general de una estrategia evolutiva.
Pseudocódigo de un algoritmo de Estrategia Evolutiva (Michalewicz, 1999)
La población inicial se construye en forma aleatoria, es decir, se generan μ individuos al azar para conformar P0 y el proceso de selección de padres durante el proceso evolutivo se realiza de acuerdo con una distribución de probabilidades que determina que un individuo tiene una probabilidad de ser seleccionado proporcional a su función de aptitud (Michalewicz, 1999; Haupt y Haupt, 2004). Esto significa que en el proceso de selección los individuos de mejor valor en su función de aptitud tienen mayor probabilidad de ser seleccionados.
La generación de los l individuos a partir de la población de la generación t – 1 (Pt–1), se realiza de acuerdo con un proceso de recombinación (cruzamiento) de dos individuos seleccionados aleatoriamente de Pt–1, que genera descendencia (hijos); sobre la descendencia opera una mutación. La evaluación de cada uno de los l individuos determina su fitness. La población de la generación t (Pt), se define mediante el proceso de reducción propio de cada estrategia. El proceso evolutivo utiliza un operador de recombinación (cruzamiento) y un operador de mutación, hasta evaluar Ng generaciones. A diferencia de los algoritmos genéticos, en una estrategia evolutiva todos los nuevos miembros generados son descendientes mutados de la generación anterior generados por cruzamiento.
Para el problema de secuenciación de una máquina las estrategias evolutivas pueden utilizar individuos con estructura cromosómica de n elementos similar a la que utiliza un algoritmo genético, la cual representa una lista ordenada de los trabajos a programar. El individuo se evalúa obteniendo el makespan de la asignación de trabajos a la máquina.
Para el problema de programar un conjunto de 5 trabajos, como en el ejemplo de las tablas 1 y 2, la secuencia: 3 – 2 – 1 – 4 – 5 representa un individuo que define una lista ordenada de trabajos que se asignan a la máquina, lo cual produce la programación con Cmax = 41 presentada en la figura 2. El valor del makespan igual a 41 corresponde al valor de este individuo. Como se trata de un problema de minimización, un individuo representa una mejor solución, mientras menor sea este valor (individuo de mejor aptitud).
Se utilizan los operadores genéticos PMX (partially mapped crossover) propuestos por Goldberg y Lingle (1985) como operador de cruzamiento y el operador de intercambio (swap) como operador de mutación. Estos operadores son operadores clásicos y se usan con frecuencia en la literatura en problemas de secuenciación. El operador PMX, selecciona en forma aleatoria dos posiciones copiando la subsecuencia central de dos padres en dos descendientes (hijos). Las posiciones restantes de los hijos se llenan con los trabajos aún no asignados en la misma posición del padre que no aportó la subsecuencia central al hijo, esto es, si el trabajo no se encuentra en la subsecuencia central permanece en la misma posición, en caso contrario se reemplaza por el trabajo que está en la misma posición de la subsecuencia central traspasada al otro hijo. El operador intercambio permuta dos trabajos de un individuo en forma aleatoria.
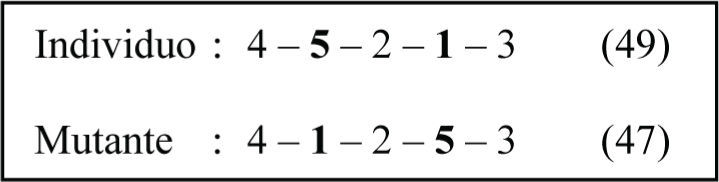
Para el ejemplo de los 5 trabajos, la figura 4 muestra el cruzamiento de dos individuos (padres) de una población con makespan 49 y 50, respectivamente, aplicando el operador de cruzamiento PMX seleccionando en forma aleatoria la subsecuencia que incluye las posiciones 3 a 4, proceso que genera dos hijos, con makespan de 49 y 53, respectivamente. Para el mismo ejemplo, la figura 5 muestra la mutación del hijo 1 intercambiando las posiciones 2 y 4 seleccionadas en forma aleatoria, proceso que genera el mutante con makespan 47.
La variante introducida en este trabajo generando la población inicial de la estrategia evolutiva como una vecindad de la solución entregada por la heurística del mejor vecino, utiliza el operador de mutación inversión propuesto por Holland (1975). Este operador selecciona una subsecuencia en forma aleatoria e invierte el orden de los trabajos. Para el mismo ejemplo, la figura 6 muestra la mutación del hijo 2 del cruzamiento de la figura 4, seleccionando en forma aleatoria la subsecuencia desde la posición 2 a la posición 5 generando el mutante con makespan 55.
Para generar la población inicial se optó por utilizar un operador de mutación diferente al utilizado por la estrategia evolutiva a modo de diferenciarse del proceso de recombinación.
La población inicial se genera como una vecindad de una buena solución obtenida con un método sencillo (en tiempo computacional despreciable), por lo que se espera generar una población inicial de buena calidad (sin incluir la semilla a partir de la cual se genera la vecindad) para que la lógica de la estrategia evolutiva logre mejorar y llegar a mejores soluciones que si parte de una población generada en forma tradicional. No se trata sólo de buscar en una vecindad de una buena solución (esto lo hacen los métodos de búsqueda en vecindad), sino que se trata de observar la evolución de la población (vecindad) inicial.
Estudio experimentalLos métodos evaluados fueron la estrategia evolutiva (μ+λ) – ES con un algoritmo genético (GA), ambos en versiones estándar con operador de cruzamiento PMX y operador de mutación inversión, y con la heurística constructiva glotona del mejor vecino (MV). Posteriormente se introduce una mejora al algoritmo ES, denominada algoritmo pES, basada en la generación de la población inicial generada como una vecindad de la solución entregada por la heurística MV.
La evaluación de los algoritmos se realizó utilizando instancias generadas en forma aleatoria de acuerdo a distribuciones de tiempos de proceso y de setup utilizadas en la literatura. Los tiempos de proceso de los trabajos se generaron con la distribución uniforme discreta entre 1 y 100 (pi ~ UD[1,100]). Los tiempos de preparación dependientes de la secuencia de los trabajos se generaron con la distribución uniforme discreta entre 1 y 50 (sij ~ UD[1,30])
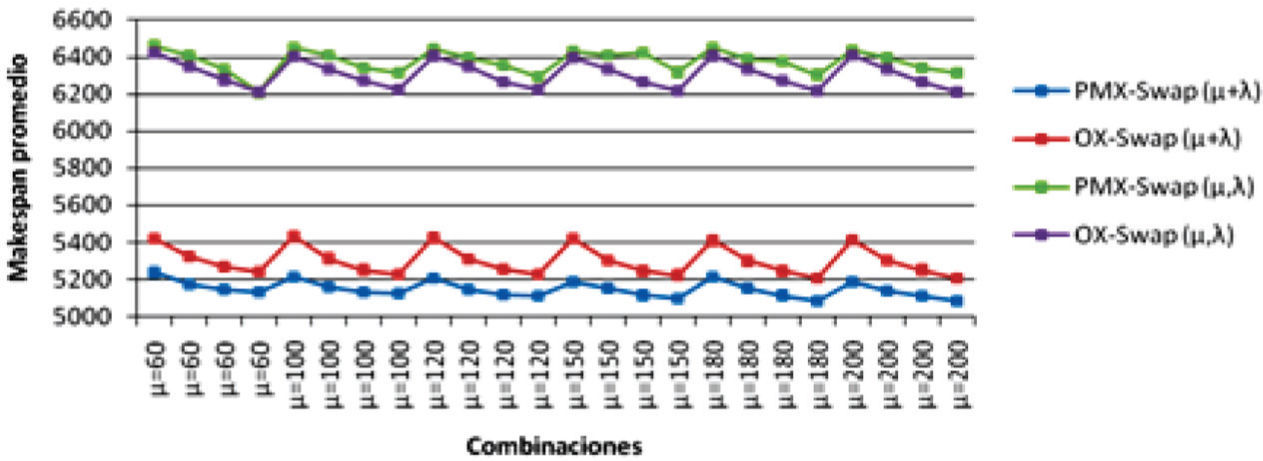
Mediante un análisis experimental preliminar utilizando 5 problemas piloto de 100 trabajos, se determinó que la estrategia (μ+λ) – ES superó a la estrategia (μ, λ) – ES, al igual que la combinación de operadores (PMX, intercambio) superó a la combinación (OX, intercambio) con el operador OX (ordered crossover) propuesto por Davis (1985). Basado en tamaños de población utilizados en algoritmos evolutivos en problemas de secuenciación de trabajos de la literatura, se evaluaron diferentes valores de μ (60, 100, 120, 150, 180 y 200) y l igual a 0.25μ, 0.50μ, 0.75μ y 1.00μ, observando que se obtuvieron los mejores resultados para λ = μ (independiente del valor de μ). El comportamiento graficado en la figura 7 se observó en todos los problemas piloto; las cuatro observaciones en una misma vertical del gráfico corresponden al makespan promedio de 30 réplicas obtenido para cada combinación de operadores – estrategia, para igual combinación de μ y λ. Para μ dado, el orden hacia la derecha de sus cuatro observaciones corresponde a l = 1.00μ, 0.75μ, 0.50μ y 0.25μ, respectivamente. En forma sistemática λ = μ produce en promedio la mejor solución; por otro lado, a través de un análisis de frecuencias se observaron las mejores soluciones para el valor μ = 180.
Para el presente estudio se utilizó μ=180 (con λ = 180). Para el algoritmo genético se optó por valores estándar recomendados en la literatura, utilizando un tamaño de población de 100 y los valores pc = 0.7, pm = 0.01 (Mattfeld y Bierwirth, 2004) Los parámetros restantes son iguales a ES (número de generaciones Ng = 3000 con igual número de réplicas).
Para la comparación de algoritmos se generaron 30 instancias de problemas de 100 trabajos, además se consideró un conjunto de 10 instancias de problemas de 12 trabajos, esto con la finalidad de ver la capacidad de los diferentes algoritmos en encontrar soluciones óptimas en problemas de tamaño reducido. La evaluación de la heurística se realizó por medio de rutinas adaptadas del software SPS_Optimizer (Salazar, 2010), herramienta diseñada para la programación de operaciones.
Para evaluar el desempeño se utilizó el makespan (Cmax) como medida de desempeño, el que se compara con la solución óptima para problemas de tamaño 12 y con una cota inferior (CI) para los problemas de evaluación:
SolMétodo es el valor del makespan obtenido con el respectivo método y CI es la cota inferior:
de la respectiva instancia (en el caso de los problemas de tamaño 12 la comparación se hace con respecto a la solución óptima).
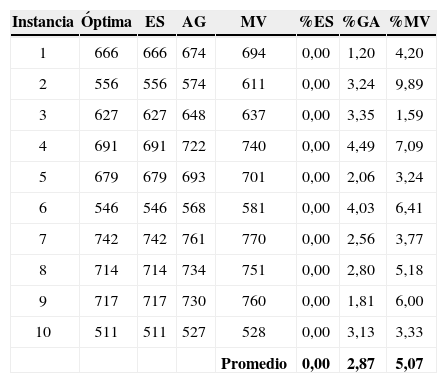
Los resultados del makespan obtenidos por cada algoritmo en cada instancia de los problemas de 12 trabajos se muestran en la tabla 4, columnas Óptima, ES, GA y MV, las columnas %ES, %GA y %MV indican el error porcentual del método en cada instancia.
Valor de Cmax en problemas de tamaño 12
| Instancia | Óptima | ES | AG | MV | %ES | %GA | %MV |
|---|---|---|---|---|---|---|---|
| 1 | 666 | 666 | 674 | 694 | 0,00 | 1,20 | 4,20 |
| 2 | 556 | 556 | 574 | 611 | 0,00 | 3,24 | 9,89 |
| 3 | 627 | 627 | 648 | 637 | 0,00 | 3,35 | 1,59 |
| 4 | 691 | 691 | 722 | 740 | 0,00 | 4,49 | 7,09 |
| 5 | 679 | 679 | 693 | 701 | 0,00 | 2,06 | 3,24 |
| 6 | 546 | 546 | 568 | 581 | 0,00 | 4,03 | 6,41 |
| 7 | 742 | 742 | 761 | 770 | 0,00 | 2,56 | 3,77 |
| 8 | 714 | 714 | 734 | 751 | 0,00 | 2,80 | 5,18 |
| 9 | 717 | 717 | 730 | 760 | 0,00 | 1,81 | 6,00 |
| 10 | 511 | 511 | 527 | 528 | 0,00 | 3,13 | 3,33 |
| Promedio | 0,00 | 2,87 | 5,07 |
Se destaca en los resultados de la tabla 4, que la estrategia evolutiva obtiene en todos los casos la solución óptima, a diferencia del algoritmo genético que a pesar de obtener una solución cercana a la solución óptima no lo logra en ninguna de las instancias, pero superando a la heurística MV.
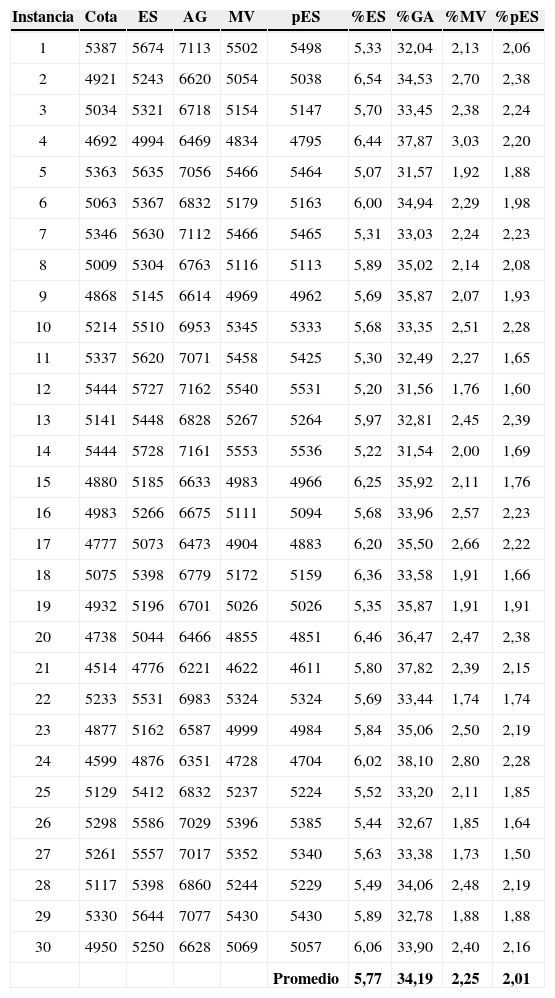
El valor de la cota y los resultados del makespan obtenido por cada algoritmo en las 30 instancias de problemas de 100 trabajos considerados se muestra en la tabla 5 (columnas Cota, ES, GA, MV y ESp), lo mismo que las respectivas diferencias porcentuales respecto a la cota (columnas %ES, %GA, %MV y %pES). En la figura 7 se grafican los resultados comparando los algoritmos ES, GA y MV, en el eje horizontal se tienen las instancias y en el eje vertical el valor de Cmax. En la figura 8 se aprecia que el algoritmo GA presenta el desempeño más bajo (en todos los problemas su gráfica está significativamente arriba de la de todos los otros métodos), mientras que la heurística ES presenta un rendimiento muy similar a MV, pero superado en todas las instancias por ésta. De este resultado sorprende el bajo rendimiento de GA (aunque es una versión estándar) y el buen desempeño de la heurística MV para esta clase de problemas. Esto último obedece a la distribución de los tiempos de setup que hace que mientras mayor sea el tamaño del problema, más aumentan las alternativas para que un procedimiento glotón como la heurística MV genere buenas soluciones.
Resultados de algoritmos problemas tamaño 100
| Instancia | Cota | ES | AG | MV | pES | %ES | %GA | %MV | %pES |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 5387 | 5674 | 7113 | 5502 | 5498 | 5,33 | 32,04 | 2,13 | 2,06 |
| 2 | 4921 | 5243 | 6620 | 5054 | 5038 | 6,54 | 34,53 | 2,70 | 2,38 |
| 3 | 5034 | 5321 | 6718 | 5154 | 5147 | 5,70 | 33,45 | 2,38 | 2,24 |
| 4 | 4692 | 4994 | 6469 | 4834 | 4795 | 6,44 | 37,87 | 3,03 | 2,20 |
| 5 | 5363 | 5635 | 7056 | 5466 | 5464 | 5,07 | 31,57 | 1,92 | 1,88 |
| 6 | 5063 | 5367 | 6832 | 5179 | 5163 | 6,00 | 34,94 | 2,29 | 1,98 |
| 7 | 5346 | 5630 | 7112 | 5466 | 5465 | 5,31 | 33,03 | 2,24 | 2,23 |
| 8 | 5009 | 5304 | 6763 | 5116 | 5113 | 5,89 | 35,02 | 2,14 | 2,08 |
| 9 | 4868 | 5145 | 6614 | 4969 | 4962 | 5,69 | 35,87 | 2,07 | 1,93 |
| 10 | 5214 | 5510 | 6953 | 5345 | 5333 | 5,68 | 33,35 | 2,51 | 2,28 |
| 11 | 5337 | 5620 | 7071 | 5458 | 5425 | 5,30 | 32,49 | 2,27 | 1,65 |
| 12 | 5444 | 5727 | 7162 | 5540 | 5531 | 5,20 | 31,56 | 1,76 | 1,60 |
| 13 | 5141 | 5448 | 6828 | 5267 | 5264 | 5,97 | 32,81 | 2,45 | 2,39 |
| 14 | 5444 | 5728 | 7161 | 5553 | 5536 | 5,22 | 31,54 | 2,00 | 1,69 |
| 15 | 4880 | 5185 | 6633 | 4983 | 4966 | 6,25 | 35,92 | 2,11 | 1,76 |
| 16 | 4983 | 5266 | 6675 | 5111 | 5094 | 5,68 | 33,96 | 2,57 | 2,23 |
| 17 | 4777 | 5073 | 6473 | 4904 | 4883 | 6,20 | 35,50 | 2,66 | 2,22 |
| 18 | 5075 | 5398 | 6779 | 5172 | 5159 | 6,36 | 33,58 | 1,91 | 1,66 |
| 19 | 4932 | 5196 | 6701 | 5026 | 5026 | 5,35 | 35,87 | 1,91 | 1,91 |
| 20 | 4738 | 5044 | 6466 | 4855 | 4851 | 6,46 | 36,47 | 2,47 | 2,38 |
| 21 | 4514 | 4776 | 6221 | 4622 | 4611 | 5,80 | 37,82 | 2,39 | 2,15 |
| 22 | 5233 | 5531 | 6983 | 5324 | 5324 | 5,69 | 33,44 | 1,74 | 1,74 |
| 23 | 4877 | 5162 | 6587 | 4999 | 4984 | 5,84 | 35,06 | 2,50 | 2,19 |
| 24 | 4599 | 4876 | 6351 | 4728 | 4704 | 6,02 | 38,10 | 2,80 | 2,28 |
| 25 | 5129 | 5412 | 6832 | 5237 | 5224 | 5,52 | 33,20 | 2,11 | 1,85 |
| 26 | 5298 | 5586 | 7029 | 5396 | 5385 | 5,44 | 32,67 | 1,85 | 1,64 |
| 27 | 5261 | 5557 | 7017 | 5352 | 5340 | 5,63 | 33,38 | 1,73 | 1,50 |
| 28 | 5117 | 5398 | 6860 | 5244 | 5229 | 5,49 | 34,06 | 2,48 | 2,19 |
| 29 | 5330 | 5644 | 7077 | 5430 | 5430 | 5,89 | 32,78 | 1,88 | 1,88 |
| 30 | 4950 | 5250 | 6628 | 5069 | 5057 | 6,06 | 33,90 | 2,40 | 2,16 |
| Promedio | 5,77 | 34,19 | 2,25 | 2,01 |
Por otra parte, se destaca a la heurística ES (también en una versión estándar) que supera ampliamente a GA, pero con un rendimiento levemente inferior a MV. Este resultado motiva la definición de la estrategia evolutiva pES con población inicial como vecindad de la solución entregada por MV, sin incluir la solución de MV.
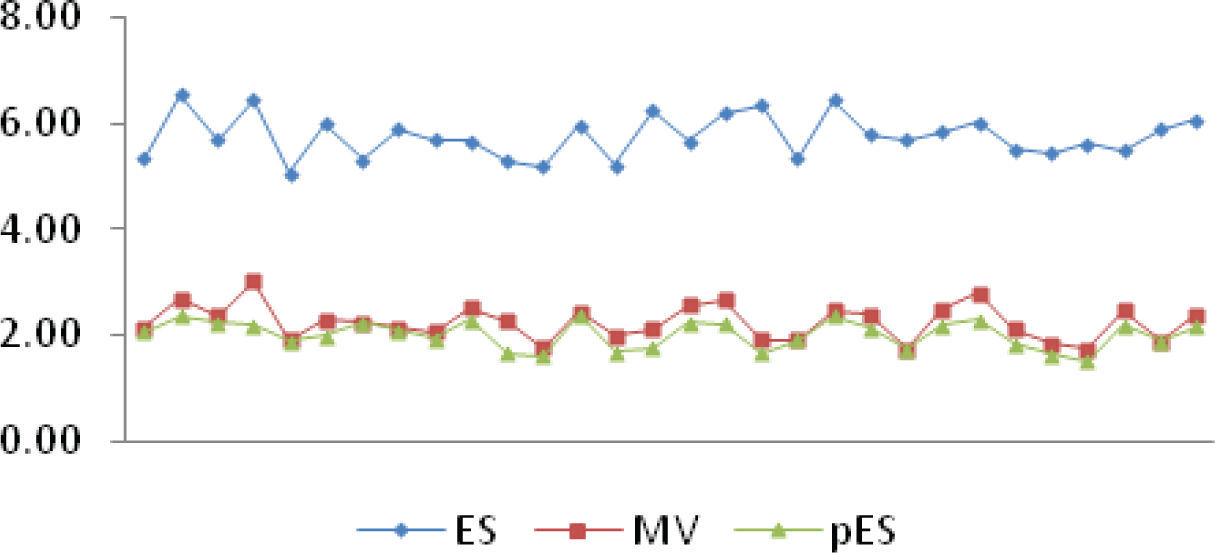
Las diferencias porcentuales de los algoritmos ES, MV y pES se muestran en la figura 9. Se destaca de la figura 9, la significativa mejora de la estrategia evolutiva al generar la población inicial como una vecindad de la solución entregada por la heurística MV, logrando reducir la diferencia con respecto de la cota de 6% a 2%, superando ahora en todas las instancias a la heurística MV. De la tabla 5 se obtienen las diferencias porcentuales promedio de los algoritmos ES, GA, MV y pES con respecto a la cota, lo que se interpreta de la siguiente forma: en promedio las soluciones de estos algoritmos difieren (con poca variabilidad) a lo más en 5.77%, 34.19%, 2.25% y 2.01% de la solución óptima.
La estrategia evolutiva estándar mejora en promedio cerca de 4% la calidad de las soluciones obtenidas al introducir el cambio en la generación de la población inicial. La figura 10 muestra gráficamente la evolución de la calidad de la población, medida como el promedio de Cmax de los individuos de una generación, para una réplica, contrastando este proceso para ES y pES.
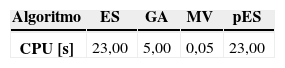
El procesamiento se realizó en un computador Intel Core 2 Duo T7500 de 2.2 GHz de 2 GB de RAM. El orden de magnitud del tiempo CPU por réplica para la ejecución de los algoritmos se presenta en la tabla 6 (para MV se trata del único tiempo CPU, ya que en este caso no hay réplicas).
La mejora de la estrategia evolutiva estándar se logra sin costo significativo en tiempo CPU. La heurística MV obtiene resultados levemente inferiores que pES en un tiempo prácticamente despreciable, obteniendo soluciones que son apenas 0.25% peor que pES, sin embargo la heurística MV no realiza una búsqueda en el proceso de optimización.
El objetivo del estudio se orientó a comparar métodos de solución con relación a su capacidad de encontrar las mejores soluciones posibles; tenemos claro que bajo este prisma los tiempos computacionales difieren significativamente de un algoritmo a otro (tabla 6). Esto se justifica en el siguiente sentido: al resolver un problema específico lo que interesa es obtener la mejor solución posible, sin importar si se obtiene con un algoritmo que requiere un mayor esfuerzo computacional, si es que obtiene una solución significativamente mejor en un tiempo adecuado para la toma de decisiones (en tal caso no es relevante cuánto más tardó).
ConclusionesLa aplicación de estrategias evolutivas en problemas de programación de producción ha sido poco explorada en la literatura. Este trabajo muestra la aplicación de una estrategia evolutiva multi-miembro (μ+λ) – ES para resolver el problema de programación de trabajos en una máquina con tiempos de preparación dependientes de la secuencia.
La estrategia evolutiva estándar se comparó con un algoritmo genético estándar y la heurística del mejor vecino. En los problemas evaluados, la estrategia evolutiva mostró un rendimiento claramente superior al algoritmo genético, pero fue superada en todos los problemas por la heurística del mejor vecino.
La mejora introducida a la estrategia evolutiva generando la población inicial como una vecindad de la solución generada por la heurística del mejor vecino, logró superar en todos los problemas evaluados a esta heurística, representando una mejora significativa en el rendimiento con respecto a la estrategia evolutiva estándar.
El porcentaje medio de diferencia del orden de 2% de las soluciones entregadas por la estrategia evolutiva modificada, con respecto a una cota inferior, hace plantear la hipótesis de que para los problemas evaluados la estrategia evolutiva modificada genera soluciones cerca del óptimo que en promedio difieren de éste a lo más en 2%.
Citación estilo Chicago Salazar-Hornig, Eduardo, Giselle Schrils-Abreu. Ingeniería Investigación y Tecnología, XV, 01 (2014): 1-10.
Citación estilo ISO 690 Salazar-Hornig E., Schrils- Abreu. G. Estrategias evolutivas para la minimización del makespan en una máquina con tiempos de preparación dependientes de la secuencia. Ingeniería Investigación y Tecnología, volumen XV (número 1), enero-marzo 2014: 1-10.
Es ingeniero matemático de la Universidad de Concepción(1984), obtuvo el grado de magíster en investigación de operaciones en laRWTH University of Aachen, Alemania (1992). Su línea de investigación incluyesistemas de producción, planificación y programación de producción y simulación.Es profesor de tiempo completo en el Departamento de IngenieríaIndustrial y Programa de Magíster en Ingeniería Industrial de la Universidadde Concepción, Chile.
Es ingeniero industrial de la Pontificia Universidad CatólicaMadre y Maestra, República Dominicana (2008) y candidata a magíster delPrograma de Magíster en Ingeniería Industrial de la Universidad de Concepción,Chile.