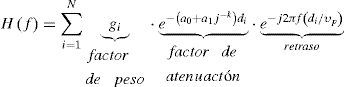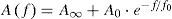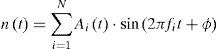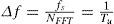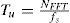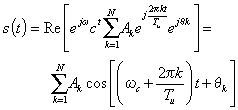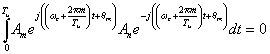En este trabajo se estudia el desempeño de los turbo códigos para el control de errores en transmisiones de datos que se realizan a través de la red eléctrica (Powerline Communications), para el modelado del sistema de esta red de datos se utilizan simulaciones por computadora, basadas en el modelo que se encuentra en la literatura conocido como indoor, y como técnica de modulación se usa la OFDM (Orthogonal Frequency Division Multiplexing). Tomando en cuenta el canal, la modulación y los turbo códigos, se propone una metodología para minimizar la tasa de bit en error (BER), como una función de la relación señal a ruido (SNR) promedio en el receptor.
This paper reports the performance of turbo codes as an error control technique in PLC (Powerline Communications) data transmissions. For this system, computer simulations are used for modeling data networks based on the model classified in technical literature as indoor, and uses OFDM (Orthogonal Frequency Division Multiplexing) as a modulation technique. Taking into account the channel, modulation and turbo codes, we propose a methodology to minimize the bit error rate (BER), as a function of the average received signal noise ratio (SNR).
En el estudio de los sistemas de comunicaciones a través de medios de transmisión de datos con un alto nivel de ruido y poca accesibilidad como los talleres industrials o edificios clasificados como patrimonio de las naciones, se propuso la utilización de la red eléctrica como una opción de un medio de transmisión, lo cual dio como resultado, los sistemas denominados PLC de uso interior, por sus siglas en inglés (Indoor Powerline Communications). En este contexto, la utilización de los códigos turbo como una técnica de control y corrección de errores se presenta como una alternativa viable para resolver el problema de ruido.
En este trabajo se presenta el desarrollo y propuesta de una metodología de diseño de codificación con códigos turbo, adaptada a las comunicaciones PLC que toman en cuenta la interacción entre las partes constitutivas principales de una turbo codificación, es decir: entrelazador, polinomios generadores y matriz de perforado. Con el propósito de optimizar su desempeño para el control de errores.
Adicionalmente, en el estudio se toma en cuenta el uso de una multiplexación ortogonal por división en frecuencia (Orthogonal Frequency División Multiplexing), la cual ha demostrado su robustez en relación con el ruido, al sacar ventaja de su propiedad de ortogonalidad.
La organización del presente trabajo es como sigue, primero se presentan los antecedentes del modelo de comunicaciones PLC, haciendo hincapié en el modelo de ruido asociado y en el tipo de modulación utilizada, enseguida se introducen los parámetros de la codificación turbo, resaltando sus partes constitutivas: entrelazador, polinomios generadores y matriz de perforado. Posteriormente se presenta la metodología propuesta que permite escoger los diferentes parámetros de los turbo códigos, de tal manera que el diseño global genere como resultado una reducción de la probabilidad de error en función de la razón señal a ruido promedio. Los resultados expresados a través de las curvas de probabilidad de error se muestran enseguida, y finalmente se presentan las conclusiones del trabajo.
AntecedentesEl sistema PLCAtenuación y multitrayectoriaZimmermann y Dostert (2002) describen la propagatión de señales en un ambiente de multitrayectoria, el cual detalla cómo con diferentes trayectorias, longitudes e impedancias se generan retrasos en tiempo de la señal de interés.
Al combinar la propagación en multitrayectorias con la atenuación, se puede obtener el modelo de la función de transferencia H (f) dado en (1):
donde el índice i es el número de la trayectoria; a0 y a1 son parámetros de atenuación; k es un exponente de atenuación (cuyos valores experimentales están usualmente en el rango de 0.2 a 1);gi es el factor de peso para la i-ésima trayectoria, físicamente interpretada como los factores de reflexión/transmisión de la trayectoria; di es el largo de la trayectoria i; τi = di/υp es el retraso de la trayectoria i.La ecuación (1) proporciona un modelo paramétrico del fenómeno de la atenuación y de la multitrayectoria, mismo que describe la respuesta en frecuencia de los canales de la red eléctrica, la cual cubre efectos característicos dentro del rango de frecuencias de 500kHz a 20MHz. El número de trayectorias permite controlar la precisión del modelo, cuestión importante para definir los canales de referencia para el sistema PLC (Zimmermann y Dostert, 2002a; Göte et al., 2004).
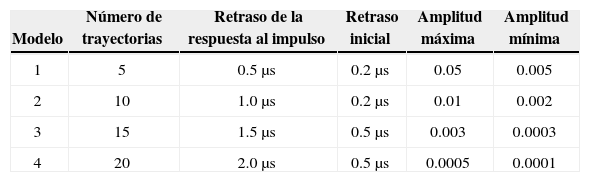
Para el modelo indoor se tienen 4 tipos de canal de referencia, los cuales tienen como principales características las mostradas en la tabla 1.
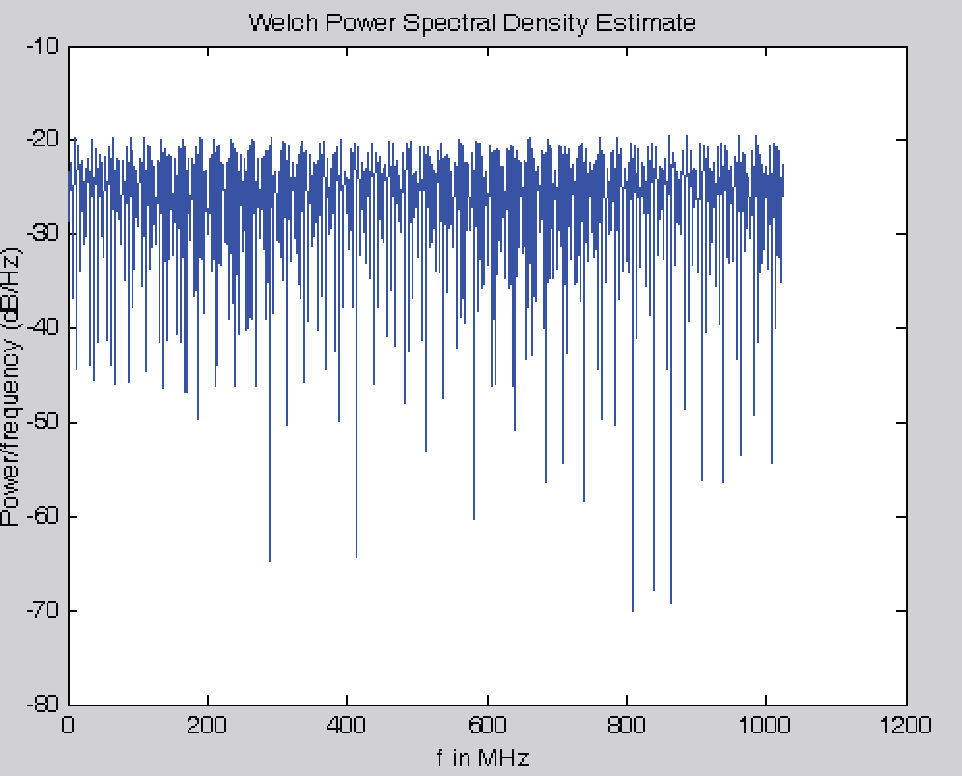
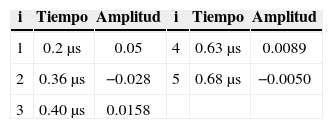
En lo referente a este trabajo nos interesa solo el modelo 1, en la tabla 2 se anotan los tiempos y la amplitud utilizados en las simulaciones, asimismo en la figura 1 se muestra la densidad espectral de potencia de dicho modelo, en donde se ven claramente las grandes atenuaciones en ciertas frecuencias. Para tener más detalles de los modelos indoor el lector puede referirse a (Cañete et al., 2002).
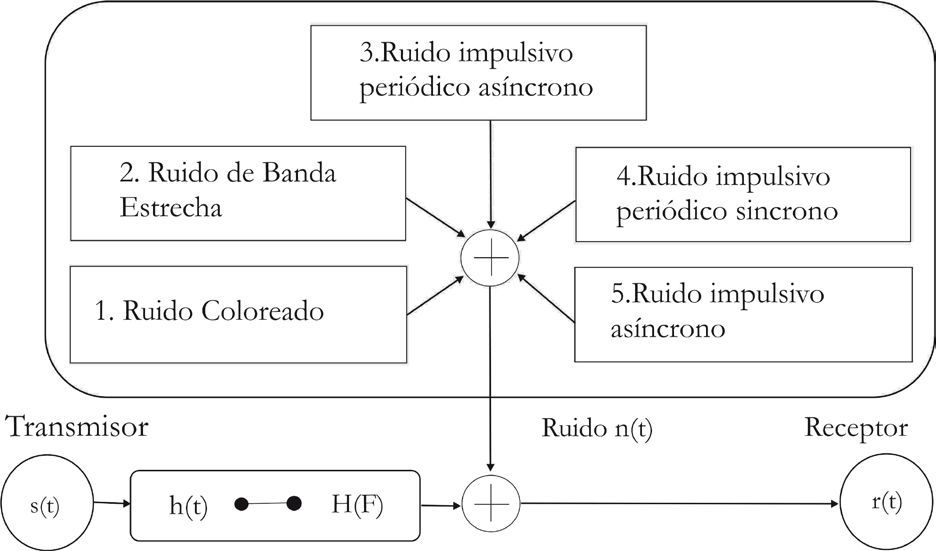
Dado que se trata de un modelo de ruido compuesto por varias perturbaciones, no es posible analizar estos tipos de canales con un modelo de ruido convencional de los sistemas de comunicaciones, como es el modelo de ruido aditivo, blanco, Gaussiano (AWGN). Zimmermann y Dostert (2002b) y Jung (2002) clasifican los diversos tipos de ruido del sistema PLC acorde con la figura 2 y los describen de la siguiente manera:
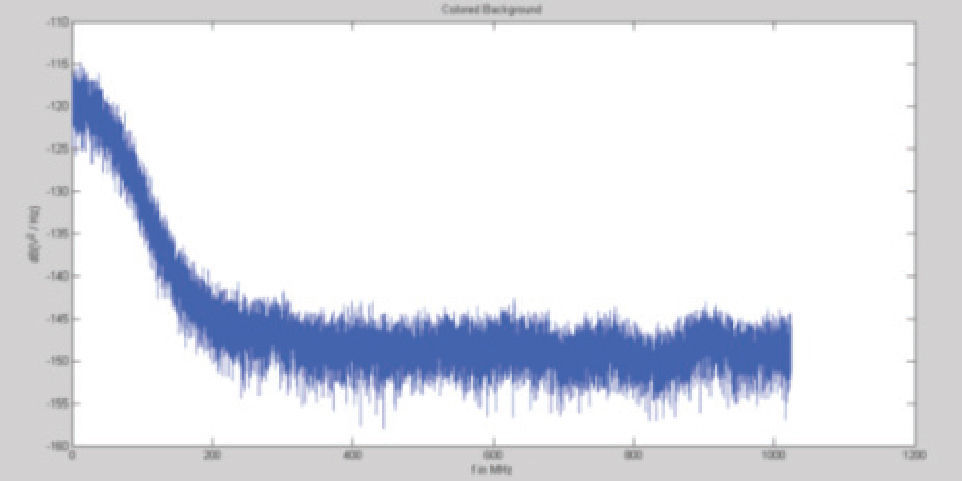
Ruido coloreado: este es ocasionado por la superposición de múltiples fuentes de ruido, es de baja potencia y decrece su densidad espectral de potencia conforme la frecuencia es mayor. La curva de la densidad espectral de potencia se aproxima por una exponencial (Babic et al., 2005). Dicha función está dada por la ecuación 2.
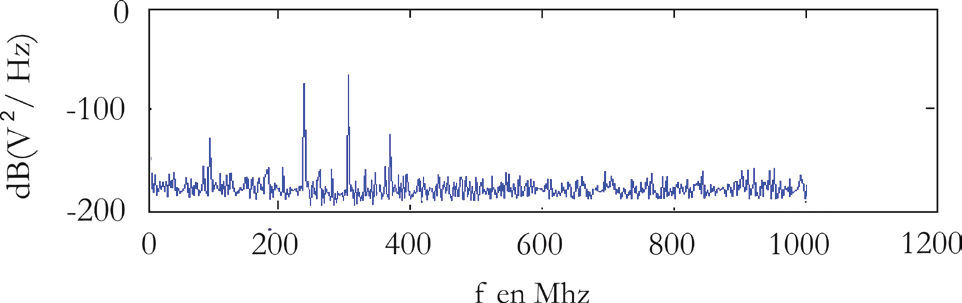
donde A∞ es la densidad espectral de potencia para cuando f → ∞, A0 es la diferencia entre A(0) y A(∞). La cantidad f0 representa la tasa de decaimiento (figura 3).Ruido de banda estrecha: este ruido se compone de señales de radio que se encuentran en el espectro, por esto, la intensidad y la frecuencia dependen del espacio y del tiempo. Este ruido se puede expresar como la suma de funciones sinusoidales con diferentes amplitudes, una representación gráfica está dada en la figura 4.
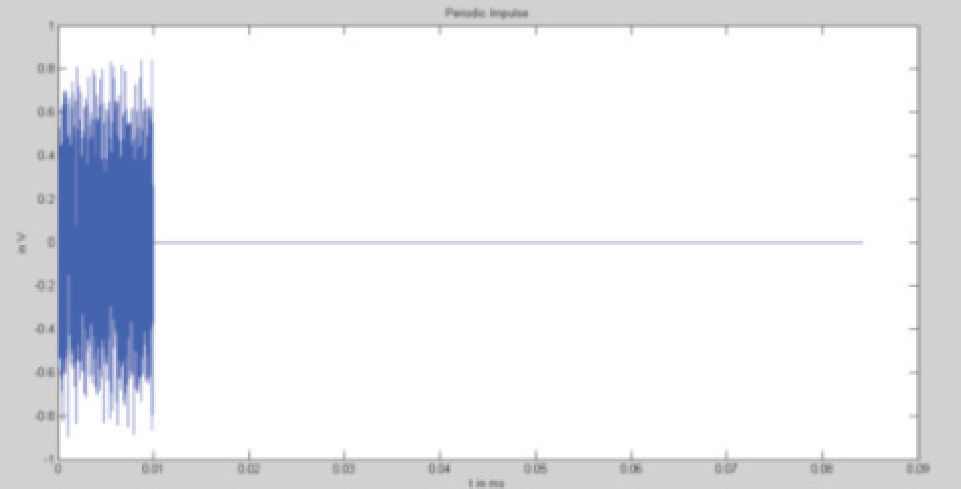
donde las señales tienen diferentes parámetros en frecuencia fi, con amplitud Ai(t) y fase φ.Ruido impulsivo periódico síncrono: en un estudio electromagnético este ruido se encuentra en el rango de frecuencias entre 50Hz y 100Hz, causado por los convertidores de potencia. La figura 5 presenta un ejemplo de este tipo de ruido.
Ruido impulsivo periódico asíncrono: es ocasionado principalmente por fuentes de alimentación conmutadas. El rango de frecuencias en donde actúa está entre 50KHz y 2MHz, sin embargo actúa por cortos tiempos y en bajas potencias, por lo tanto, este puede considerarse como parte del ruido coloreado.
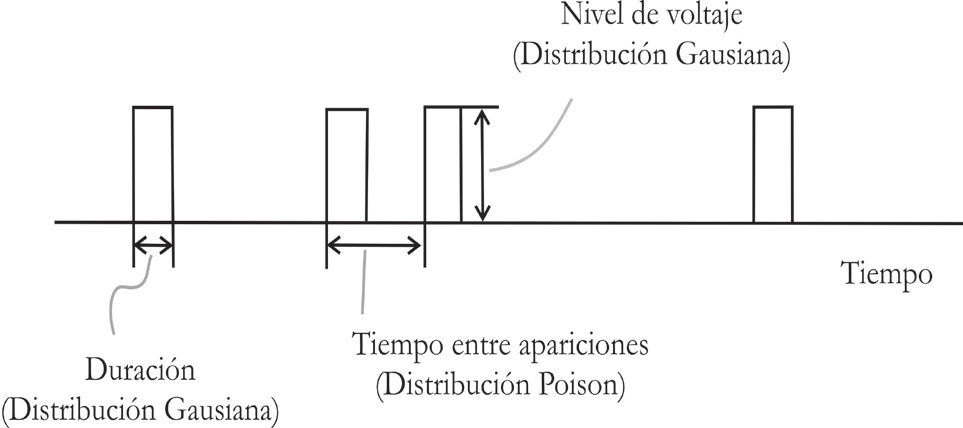
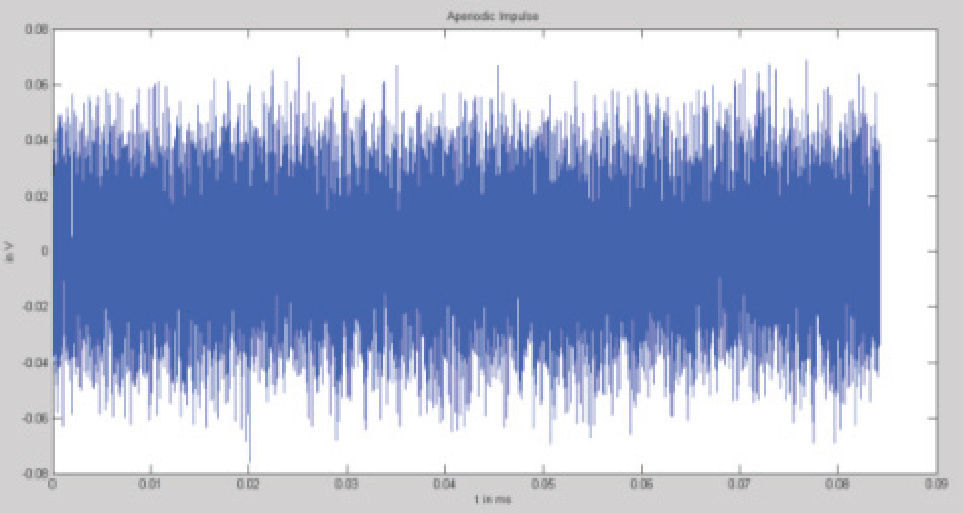
Ruido impulsivo aperiódico: puede considerarse el ruido más perjudicial, debido a todas aquellas operaciones de encendido y apagado de motores, ocasionadas por aparatos electrodomésticos, máquinas electromecánicas, entre otros. Debido a ello, este ruido es aleatorio y a menudo puede ser un ruido de tipo ráfaga.
Este ruido tiene tres parámetros: amplitud, tiempo de impulso y tiempo entre impulsos, estos parámetros no son constantes (figuras 6 y 7).
Para las transmisiones de datos por la red eléctrica este ruido es muy perjudicial, ya que sus caracteristicas de amplitud y densidad espectral de potencia exceden por mucho los parámetros de los otros ruidos.
La multiplexación OFDMDebido a su característica de ortogonalidad posee una fuerte robustez respecto al ruido, por esta razón la multiplexación ortogonal por división en frecuencia OFDM es una técnica usada frecuentemente en comunicaciones inalámbricas. Esta técnica puede operar para grandes tasas de transmisión con suficiente robustez respecto a las características del ruido del canal de comunicaciones. OFDM es una combinación de modulación y multiplexación. Esta multiplexación se aplica a una serie de señales independientes, las cuales se crean a partir de una señal principal.
En contraposición con las comunicaciones típicas, monoportadora o single carrier (SC), donde cada símbolo se transmite en serie (uno a la vez) ocupando todo el ancho de banda disponible, en una modulación multiportadora se envían los símbolos simultáneamente en subportadoras adyacentes, es decir, usando algún tipo de multiplexación por división en frecuencia (FDM). Una representación gráfica se puede apreciar en la figura 8.
A lo largo del desarrollo de las comunicaciones, diversos métodos para multiplexación por división en frecuencia FDM se han utilizado ampliamente para canales selectivos en frecuencia, tal como lo sería un canal con multitrayectoria. El problema recurrente que presentó este tipo de multiplexación es la prevención del traslape entre subportadoras, lo que exige la colocación de una región de espectro de separación entre ellas (bandas de guardia), esta banda de guardia debía ser igual al rango que permitiera la precisión de los filtros en el receptor.
La separación y posterior discriminación entre subportadoras no supone tampoco un aprovechamiento eficiente del ancho de banda. Es entonces que se propone como alternativa OFDM (Babic et al., 2006; Langton, 2004; Litwin y Pugel, 2001).
Como parte teórica fundamental, en lugar de los bancos de osciladores y la inmensa y costosa circuitería de radio frecuencia, RF, la transformada discreta de Fourier (DFT) y su inversa (iDFT), son las herramientas que le han dado viabilidad a OFDM.
En 1971 Weinstein y Ebert introdujeron la iFFT/FFT para OFDM junto con el concepto de intervalo de guardia para evitar la interferencia intersimbólica (ISI) y la interferencia intercanal (ICI).
De la teoría correspondiente se conoce que la FFT (como una implementación de la DFT), también tiene su inversa, la iFFT, que funciona exactamente con el mismo algoritmo. En su operación se toma un número definido de muestras NFFT en el tiempo y da como resultado el mismo número NFFT de muestras en el doinio de la frecuencia.
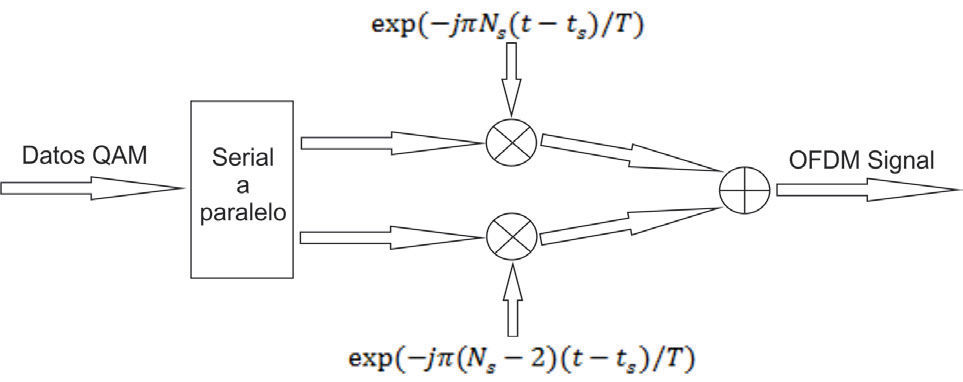
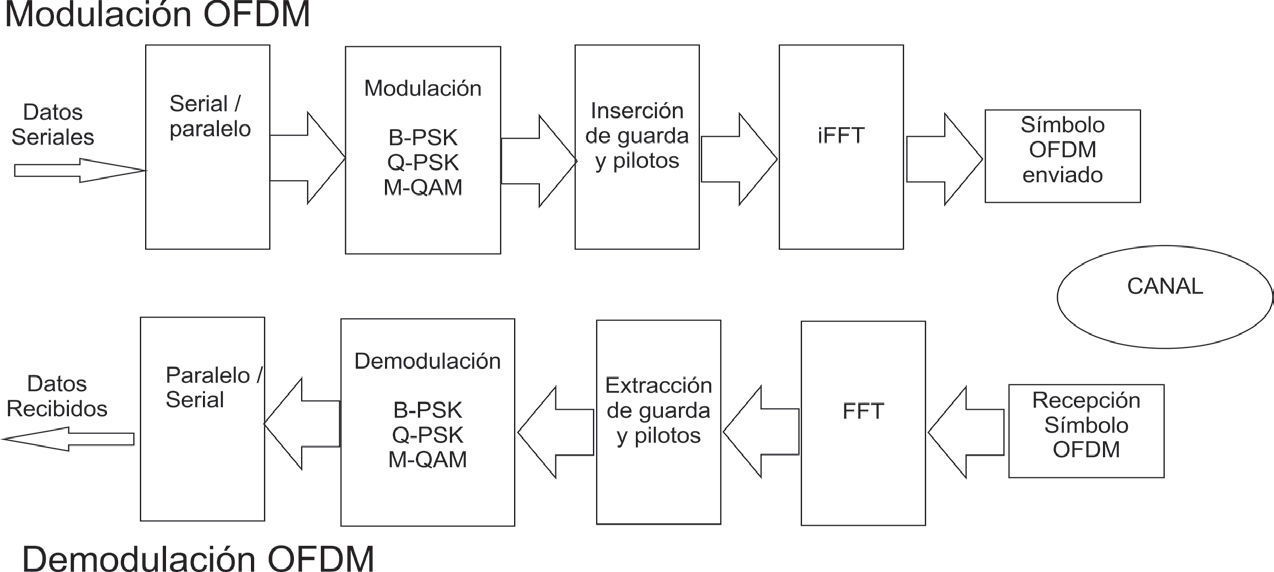
Al requerir OFDM de una señal constituida por la suma de señales, el dominio de la frecuencia corresponde a frecuencias adyacentes, con una separación constante. Esta disposición coincide con la utilizada en la información del contenido espectral que tiene la FFT. Es por eso que para la generación y transmisión de OFDM, se utiliza la transformación inversa iFFT, ya que el paso previo en el esquema de transmisión consiste en hacer un mapeo del contenido de cada subportadora para que luego la transformada inversa convierta esta información en las muestras de una señal en tiempo. En el lado del receptor; por lo tanto, la transformación directa FFT es la que hace la operación de separar los datos entre subportadoras en el demodulador. La figura 11 muestra el esquema general de un sistema OFDM.
De esta manera, de una forma sencilla y muy eficiente con la iFFT se asegura que las subportadoras producidas sean además, ortogonales entre sí.
En OFDM, un número grande de subportadoras ortogonales, superpuestas, de banda estrecha, transmiten información en paralelo, esto es, se comparte entre ellas el ancho de banda total disponible. La separación de las subportadoras es teóricamente mínima de tal manera que la utilización del espectro es bastante eficiente. Una de las caracteristícas y ventajas del uso de OFDM es principalmente el manejo eficaz del receptor respecto a la interferencia debida a la multitrayectoria.
Así, de manera general, OFDM se refiere a la transmisión de una trama digital que requiere una alta tasa de transferencia en subportadoras contiguas y ortogonales mediante NFFT líneas paralelas más lentas, que transportan símbolos independientes que son producto de algún otro tipo de modulación digital, como puede ser: QPSK, 16-QAM, 64-QAM, etcétera, dependiendo del sistema.
Como se indica en (4), la operación con las señales discretas y sus transformadas, implica el trabajo bajo el régimen de un tiempo de muestreo Tu, que es esencialmente el que fija las limitantes básicas de tiempo y, por ende, de alguna de las principales características temporales del sistema.
Es así que el ancho de banda teórico W es igual a fs y el espaciamiento entre subportadoras, o de manera similar, el ancho de banda de subportadora, queda dado por
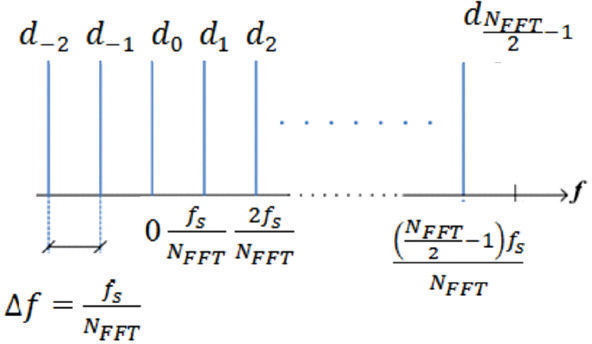
denotando por Tu el tiempo útil del símbolo OFDM. Este valor se puede despejar de (4), reescribiéndola como:En la figura 9 se puede observar la disposición de las subportadoras dentro de un rango de frecuencias. La disposición de las subportadoras, se encuentra en el rango dNFFT2...dNFFT2−1. Considerando fk como la frecuencia correspondiente a la subportadora dk, queda dada por: fk=k.fsNFFT+f0,k∈−NFFT2,NFFT2−1.
Al utilizar N subportadoras ortogonales en un sistema OFDM cualquiera, estas estarán separadas en frecuencia justamente por el valor correspondiente al inverso del tiempo útil del símbolo OFDM (Tu) y durante este periodo se transmitirán N símbolos independientes codificados por alguna de las modulaciones en cuadratura I/Q conocidas como: QPSK, 16-QAM, 64-QAM, etcétera. Entonces la señal modulada puede escribirse mediante la siguiente expresión:
donde las amplitudes Ak y fases θk toman todos los valores posibles de acuerdo con el tamaño de la constelación correspondiente.Si cada fase y amplitud se mantienen estables durante todo el periodo de símbolo, como se especifica en la teoría, entonces se puede demostrar la ortogonalidad que existe entre las subportadoras. Comprobando que para valores diferentes de los índices m y n se cumple que el producto punto de dos cualesquiera señales moduladas está dado por
Para este caso, las partes real e imaginaria corresponden a las partes en fase y en cuadratura de la señal. Tienen que multiplicarse por una forma de onda coseno o una sinusoide para determinar la frecuencia de la señal OFDM. Las figuras 10 y 11 muestran un diagrama a bloques de un modulador OFDM.
El tiempo de guardia o intervalo de guardia (GI), se refiere a aquel periodo que se deja entre símbolos OFDM consecutivos. Esta técnica tiene la finalidad de evitar la interferencia entre símbolos (ISI), e interferencia entre canales (ICI), en canales multitrayectoria. De acuerdo con la teoría, para cumplir con estos objetivos, su duración debe corresponder al menos a la misma duración del tiempo máximo de exceso de retardo (maximum excess delay time) (Tm) que caracteriza al canal.
En una transmisión de datos en un sistema PLC, debido tanto a las características del ruido de banda estrecha, como a las de la respuesta en frecuencia del canal, existen grandes variaciones de la atenuación en ciertas frecuencias o en rangos de ellas y, considerando que la energía de la señal de OFDM se distribuye en un ancho de banda, se tiene la posibilidad de corregir errores, ya que no toda la energía de la señal se afecta con la misma magnitud de la atenuación.
Turbo códigosEn 1993, Berrou y Glavieux publicaron un nuevo concepto de codificación nombrado turbo códigos, el cual alcanza un desempeno cercano al límite de capacidad postulado por Shannon en su segundo teorema, publicado en 1948. El nombre de turbo codificación se debe al principio de las “máquinas de combustión interna tipo turbo”, donde la eficiencia del motor se optimiza reutilizando la energía residual de los gases de escape, es decir, existe un ciclo cerrado. Este concepto extrapolado a la turbo codificación consiste en utilizar un algoritmo iterativo para la decodificación, donde en cada iteración i se mejora la confianza en los símbolos decodificados por medio de una medida de probabilidad. En estadística este concepto se utiliza ampliamente para los algoritmos bayesianos de propagación de creencia (belief propagation) para resolver el problema de la interferencia presente en varios fenómenos físicos (física estadística, visión por computadora, corrección de errores, etcétera). En el trabajo original de Berrou y Glavieux, y de acuerdo con la teoría de Shannon, se consideró una longitud de trama de datos lo suficientemente larga (65536 bits) para reducir la probabilidad de error.
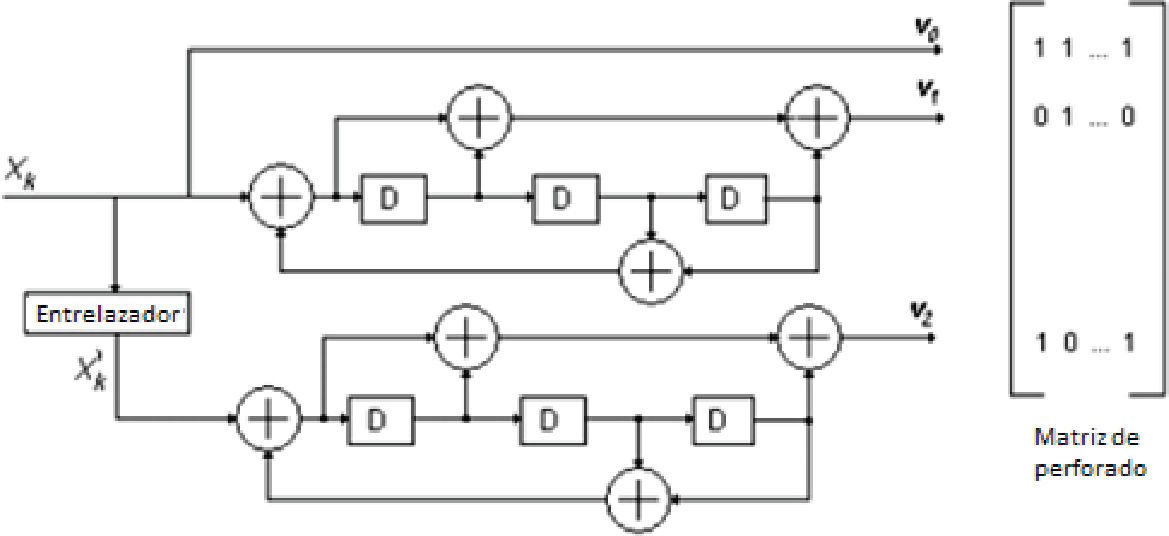
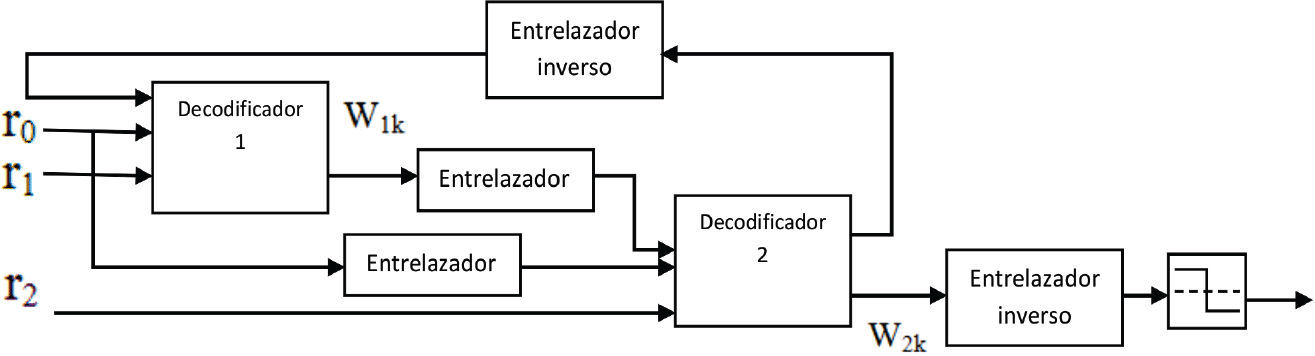
Sin embargo, esto representa un reto, porque en muchas aplicaciones en tiempo real esta longitud es difícil de alcanzar, en consecuencia la pregunta es ¿cómo diseñar un turbo codificador que mantenga sus buenas características de baja probabilidad de bit error, del orden de 10−5, para una razón señal a ruido Eb/N0 también baja, entre 1 y 5dB, pero al mismo tiempo con una longitud de trama de datos de unas cuantas centenas de bits? El esquema general del codificador se muestra en la figura 12, en el cual se puede observar la estructura de dos codificadores convolucionales, así como un entrelazador a la entrada del segundo codificador X′k y adicionalmente una matriz de perforado que permite cambiar la tasa global r del código. Esto es, con la matriz de perforado se anulan o perforan ciertos bits normalmente de las salidas de redundancia: υ1 y υ2, para alcanzar la tasa requerida (Lazcano y García, 2007, 2012). De las tres salidas del codificador, υ0 es la salida sistemática –salida directa de información sin pasar por el codificador, e igual a X′k. Adicionalmente, υ1 y υ2 son las salidas de redundancia respectivas de los codificadores 1 y 2. Por otra parte, en la figura 13 se tiene el diagrama del turbo decodificador, el cual está compuesto por dos decodificadores convolucionales, así como el mismo entrelazador usado en el codificador, y su respectivo desentrelazador. Como se mencionó, el proceso de decodificación es iterativo, el primer decodificador recibe las señales r0 y r1. Su correspondiente salida W1k se envía a través del entrelazador al segundo decodificador, el cual también recibe la señal r0 pasada a través del entrelazador, y la señal r2. La salida del decodificador 2, W2k, se envía a un entrelazador inverso (o desentrelazador) y se trasmite al primer decodificador. Con este lazo se logra el proceso que se describió, llamado “turbo”, mismo que es iterativo. Una vez terminadas las i iteraciones (en la práctica, del orden de una decena), se toma finalmente una decisión dura para determinar el valor de los bits decodificados.
En forma general un turbo codificador está compuesto por al menos un par de codificadores de convolución conectados en paralelo a través de entrelazadores.
Para la decodificación turbo existen básicamente dos tipos de algoritmos equivalentes: los basados en una modificación del algoritmo de Viterbi con entrada y salida suave, llamados SOVA (Soft Output Viterbi Algorithm), y los llamados Max-Log-Maximum a Posteriori (MAP), donde los primeros tienen menor complejidad, son casi óptimos, con entradas suaves y salidas suaves (IEEE Comunications Letters, 1998).
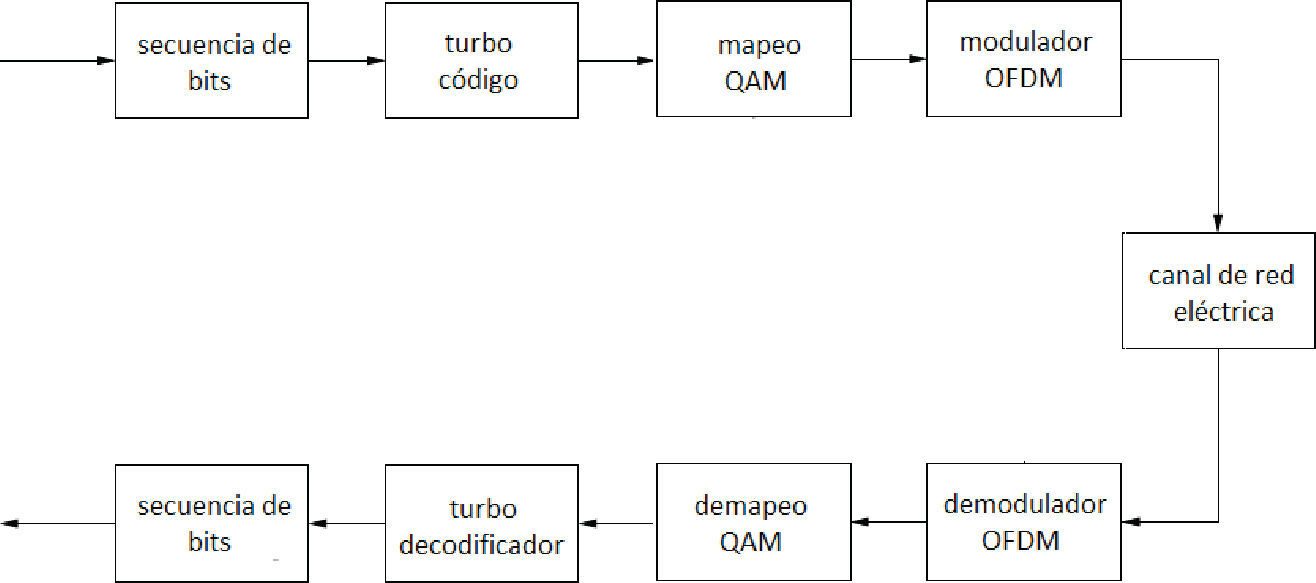
Problema planteado y metodologíaDados los problemas de calidad de la transmisión en los canales PLC del tipo indoor modelo 1, que consisten principalmente en su característica de multitrayectoria, y de los diferentes tipos de ruido descritos: coloredo, de banda estrecha, e impulsivo, por otro lado, considerando la alta capacidad de corrección de los códigos turbo y la fuerte robustez respecto al ruido del canal de la multiplexación OFDM, en este trabajo se ha estudiado el desempeno de esos codificadores en estos canales, haciendo variar sus propiedades de codificación principalmente en función de las propiedades de los entrelazadores, que son partes constitutivas importantes de los turbo códigos; en la tabla 3 se proporcionan los valores de los principales parámetros utilizados en las pruebas simuladas en computadora (Chan y Donaldson, 1989). Efectivamente, en estudios recientes (Rosnes, 2012) se ha mostrado que las propiedades de aleatoriedad y de dispersión logradas con los entrelazadores juegan un papel muy importante en el desempeño global de los turbo códigos, incluyendo el caso práctico de una transmisión con tramas de datos relativamente cortas, es decir, de unas cuantas centenas de bits. En consecuencia, en este trabajo se lleva a cabo un estudio de análisis, clasificación y comparación con estudios previos del desempeño de los turbo códigos en este tipo de canales PLC, dando importancia a los entrelazadores utilizados, considerando también entre ellos los más promisorios, es decir, aquellos denominados HSR (High Spread Random), los cuales se explican con más detalle en esta misma sección. En la figura 14 se puede ver el diagrama general en bloques del sistema de comunicaciones utilizado en las simulaciones en computadora.
Características PLC utilizados en las simulaciones
| Ruido coloreado | A∞ = −147dB (V2/Hz), A0 = −28dB (V2/Hz) = −120dB(V2/Hz), A∞ = −147dB(V2/Hz), una máxima amplitud de 0.03V | |||
|---|---|---|---|---|
| Ruido de banda estrecha | Se generaron en diferentes frecuencias en donde existiera transmisión. En frecuencias hasta 20MHz. | |||
| Ruido impulsivo periódico | Se generó con un ancho de impulso de 10μs, y 1/100 como el tiempo de periodo, con amplitud máxima de 1 Violt | |||
| Ruido impulsivo aperiódico | Tasa | Amplitud | Ancho | Espaciamiento |
| Entre 0.1 y 100 impulsos / seg | Distribución exponencial | |||
| Amplitud máxima d 1.9V | Valor típico 100μs | Valores entre 0.01 s y 1 s | ||
Para tener un punto de referencia común con otras publicaciones (Babic et al., 2006; Wang et al., 2006; Guerrieri et al., 2007) y poder estudiar el desempeño de los codificadores utilizados en todas las simulaciones por computadora realizadas, la tasa de codificación elegida fue de ½, es decir, por cada bit de información se agrega un bit de redundancia, valores comunes en este tipo de codificadores.
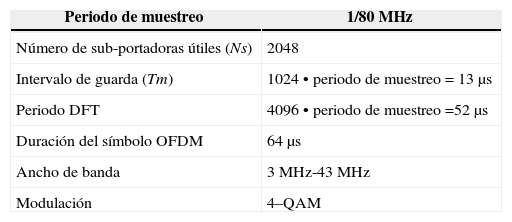
En este contexto de la transmisión de datos a través del canal PLC, las características de la multiplexación OFDM son muy adecuadas para resolver los problemas de ruido y multitrayectoria, como lo muestran múltiples referencias (Babic et al., 2006; Wang et al., 2006; Guerrieri et al., 2007), y los turbo códigos constituyen la mejor opción para disminuir la probabilidad de error (Wang et al., 2006; Guerrieri et al., 2007). Como se detalló, la modulación OFDM realiza una multiplexación ortogonal en frecuencia (figuras 8 y 9) y de acuerdo con los valores de los parámetros de la tabla 4, se tiene que un símbolo OFDM está compuesto por 2048 símbolos QAM, o 4096 bits. Con estos valores, para lograr una mejor adaptación entre el codificador de canal y el modulador es conveniente tener el mismo tamaño de bloque, por ello, en este trabajo se propone que el tamaño máximo del entrelazador del codificador turbo sea también de 2048 bits. Mientras más grande sea el tamaño del entrelazador, mejor será el desempeño del turbo código, porque se logra una mayor descorrelación entre las entradas de los dos codificadores convolucionales conectados en paralelo. En contraparte, la latencia aumenta, lo cual podría ser restrictivo en ciertas aplicaciones en tiempo real. En consecuencia será necesario encontrar un valor intermedio de la longitud de la trama de datos.
En resumen, con el propósito de desarrollar las primeras simulaciones, se ha considerado un turbo código de tasa ½. Y con el objetivo de acoplarse a los parámetros de la multiplexación OFDM, se tienen 4096 bits codificados para una entrada de 2048 bits de información. Esto nos lleva a usar un entrelazador en los turbo códigos de tamaño grande, con un máximo de 2048 bits. Las subportadoras del símbolo OFDM, representan cada una un símbolo 4-QAM y dado que es necesario tener los 2048 datos para el proceso de envío, entonces para efectos prácticos, también puede considerarse la misma duración del tiempo que tarda el turbo codificador en el llenado de su entrelazador (figura 12). De esta manera, los tiempos de latencia no se incrementarán.
De acuerdo con la literatura, por sus propiedades de descorrelación el tipo de entrelazador utilizado es el denominado HSR (Lazcano y García, 2007 y 2012; Crozier, 2000). Su implementación es similar a la del entrelazador S-random (Divsalar y Pollara, 1995), con la variante de que se generan N números reales aleatorios, en vez de N números enteros aleatorios. El entrelazador final se obtiene al ordenar los N números reales aleatorios y su desempeno en términos de la tasa de errores binarios (BER) es superior al obtenido con el entrelazador S-random. En este trabajo, los parámetros del entrelazador HSR que se usaron son matrices de tamaños 256, 1024 y 2048 bits, con condiciones de esparcimiento máximo de 20, 32 y 45, respectivamente.
En lo que concierne a los polinomios generadores del turbo código, por su buen desempeño en términos de probabilidad de bit en error, se usaron los publicados en varios trabajos previos (Lazcano y García, 2007 y 2012), correspondientes al estándar 3GPP (Morelos, 2005): g0(D) = 1 + D2 + D3, g1(D) = 1 + D + D3. Finalmente para la matriz de perforación, con un periodo de perforado de 16, se trabajó principalmente con la de Lazcano y García (2007 y 2012), identificada en esta publicación con el número 1, con el propósito de poder hacer comparaciones. También se trabajó con la matriz de perforación especificada en el sistema, obtenida con la metodología desarrollada en esa misma referencia, con longitudes correspondientes de 256, 1024 y 2048 bits e identificada en esta publicación con el número 2.
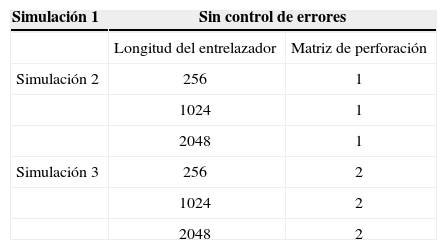
En la tabla 5, se muestran las longitudes de los entrelazadores utilizados en las simulaciones, así como el tipo de matriz de perforación utilizada.
La matriz de perforado puede degradar el desempeño de los turbo códigos, en consecuencia, para realizar el perforado, en este trabajo se utilizó una metodología de diseño que toma en cuenta los entrelazadores utilizados, y los polinomios generadores del turbo código (Lazcano y García, 2007 y 2012). Las principales características de esta metodología son:
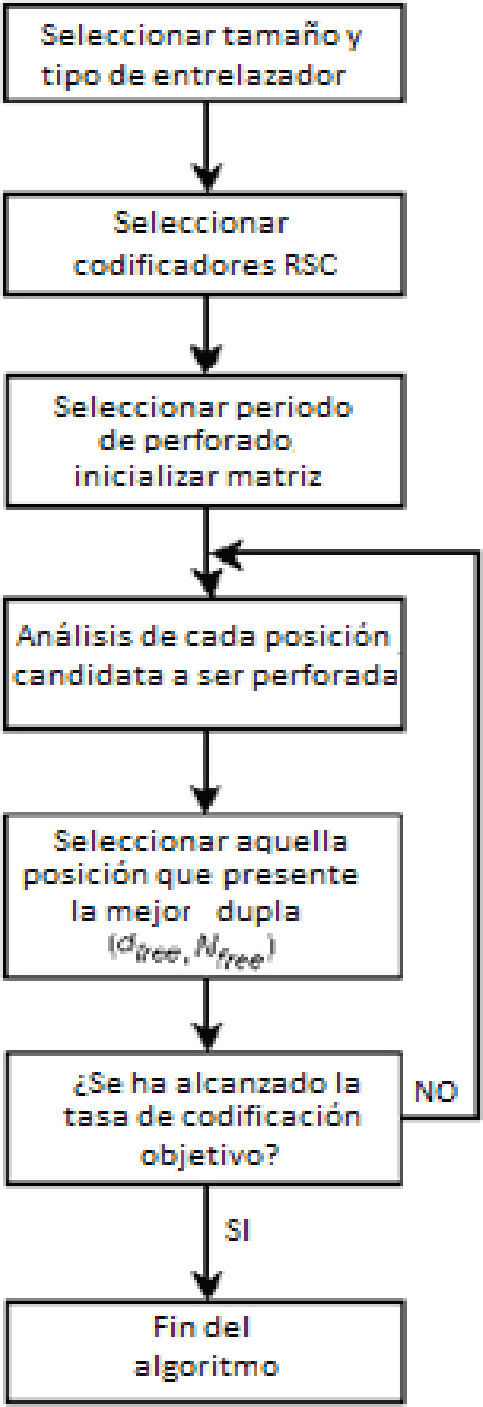
Se hace el análisis de las posiciones “candidatas” a ser perforadas de acuerdo con el siguiente criterio: sea dW el peso mínimo de palabras codificadas generadas por entradas de peso w, y sea NW el número de palabras código de peso dW (Babich et al., 2004). Para w = 2, la dupla (dW, NW) es igual a (dfree′, Nfree), donde dfree es la distancia libre del código convolucional, relacionada con la capacidad de corrección t del código y Nfree es el número de palabras del código de peso dfree. Se consideran posiciones candidatas a ser perforadas solo las correspondientes a los bits de paridad de los codificadores 1 y 2. Los bits sistemáticos del codificador 1 no se perforan (Babich et al., 2004). De acuerdo con una restricción de tasa compatible RCPC (Rate Compatible Punctured Convolutional Code) (Hagenauer, 1988), se analiza cada posición candidata a ser perforada calculando sus duplas (dW, NW). Finalmente se elige como posición a ser perforada, aquella que presente “la mejor” dupla (dW, NW) para no degradar la probabilidad de error, es decir, dW debe ser el valor más alto encontrado (palabras de peso mýnimo grande) y NW el menor valor obtenido posible (poca duplicidad de palabras del mismo peso). Para la obtención de las duplas (dW, NW) se emplea el algoritmo propuesto en Garello et al. (2001). En la figura 15 se muestra el diagrama de flujo de la metodología de diseño de la matriz de perforado descrita.
Diagrama de flujo, metodología de perforado (Lazcano y García, 2007 y 2012)
De acuerdo con los esquemas de control de errores, modulación digital OFDM y modelo de canal PLC utilizados en este trabajo, se realizaron simulaciones en computadora implementando el sistema completo. El primer objetivo fue comparar los resultados con algunas de las publicaciones existentes en la literatura (Babic et al., 2006; Wang, et al., 2006; Guerrieri et al., 2007). El segundo objetivo consistió en corroborar, que al aplicar un sistema de corrección de errores que se adapta lo más posible a las características de la modulación utilizada, se puede obtener una disminución en la probabilidad de error, toda vez que la información se transmite a través del canal de la red eléctrica (PLC) con todos los tipos de ruidos combinados descritos.
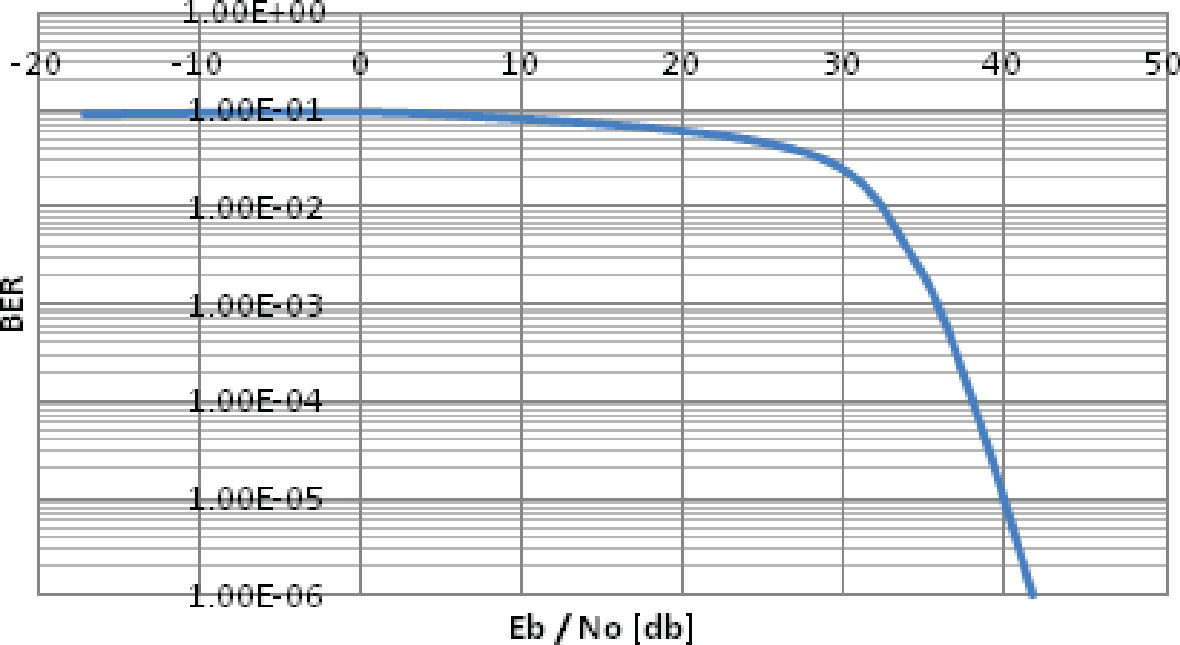
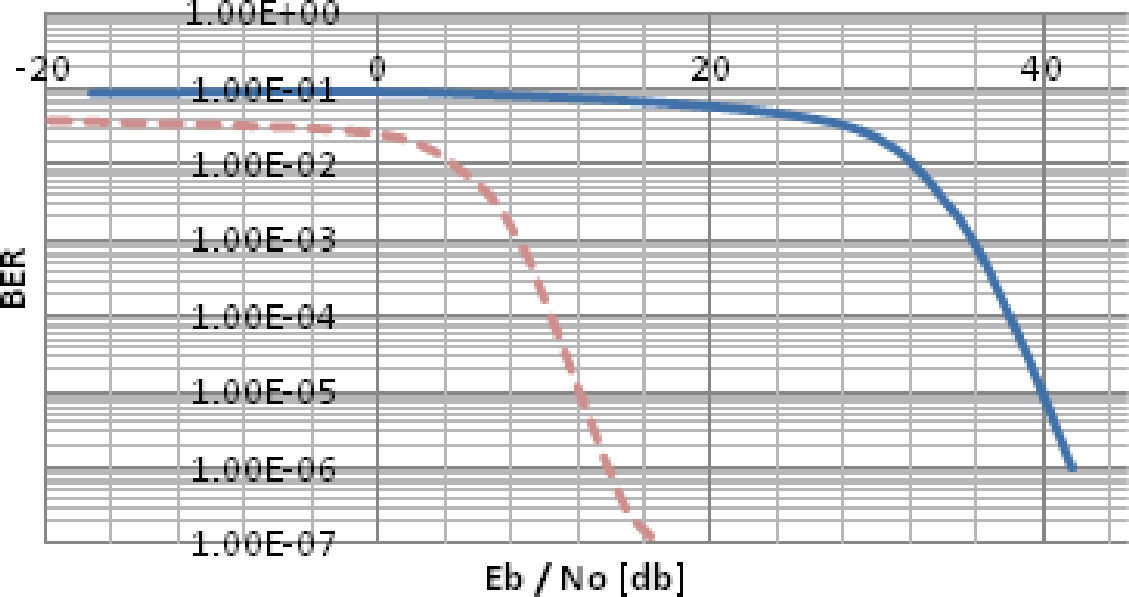
En la figura 16 se muestra la gráfica de la razón señal a ruido Eb/N0 vs la tasa de bits en error BER (Bit Error Rate) del comportamiento del canal, con la modulación OFDM sin el sistema de control de errores y con los parámetros considerados en la tabla 3. Se observa cómo empieza a bajar la curva alrededor de Eb/N0 = 30dB al igual que en las gráficas obtenidas en Babic et al., (2006), también alrededor de Eb/N0=40dB se tiene una tasa de bits en error del orden de 1×10−5.
Otra de las simulaciones realizadas con el sistema de control de errores consistió en la utilización de turbo códigos. En la figura 17 se puede observar la gráfica de probabilidad de error, esta simulación se identifica en la tabla 5 como “simulación 2”, en donde se utilizó la matriz de perforado tipo 1. Se puede hacer notar que es una matriz de perforación óptima para las características definidas en (Lazcano y García, 2007 y 2012), no para las características de ruido de un canal PLC. Sin embargo, como se mencionó, esta simulación es importante para contar con un punto de referencia y, con ello, confirmar que con la obtención de dicha matriz por la metodología de diseño descrita en el párrafo anterior y mediante un estudio más a profundidad para la selección de los parámetros de los códigos turbo adaptados a las condiciones del sistema PLC, seguramente se obtendrán mejores resultados.
El desempeño del sistema de comunicaciones depende principalmente de la modulación y del tipo de codificación de canal. Uno de los objetivos de este trabajo consistió en proponer el diseño de un sistema de transmisión de información donde cada bloque o subsistema constitutivo, se complemente con los demás, es decir, que la modulación digital sea la más adecuada de acuerdo con las características del canal y que el código de corrección de errores se adecue a su vez a las características, principalmente de la modulación. De esa manera se propone una metodología global de diseño de un código turbo incluyendo a la modulación y al modelo del canal PLC (Lazcano y García, 2007 y 2012).
Para las curvas obtenidas en las simulaciones con los turbo códigos, se utilizaron en un primer tiempo los siguientes parámetros: entrelazador HSR de 256, polinomios generadores g0(D) = 1+D2+D3, g1(D)=1+D+D3 (3GPP, 2005) y una matriz de perforado tipo 1 con periodo 16.
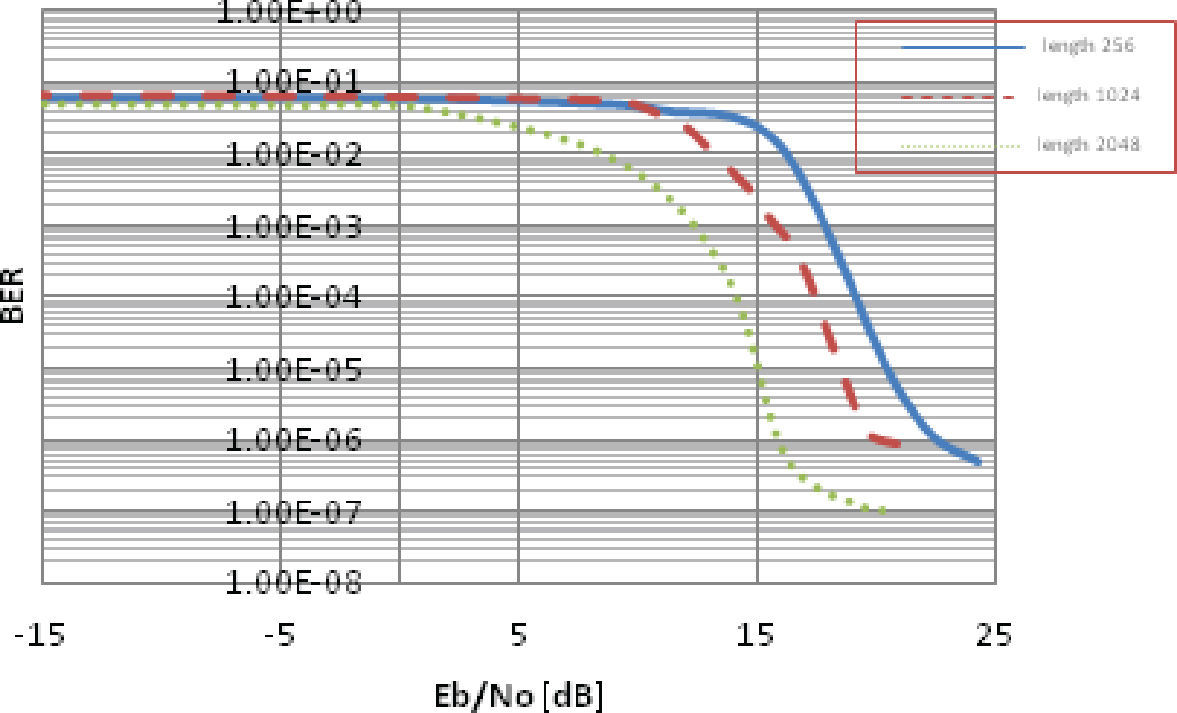
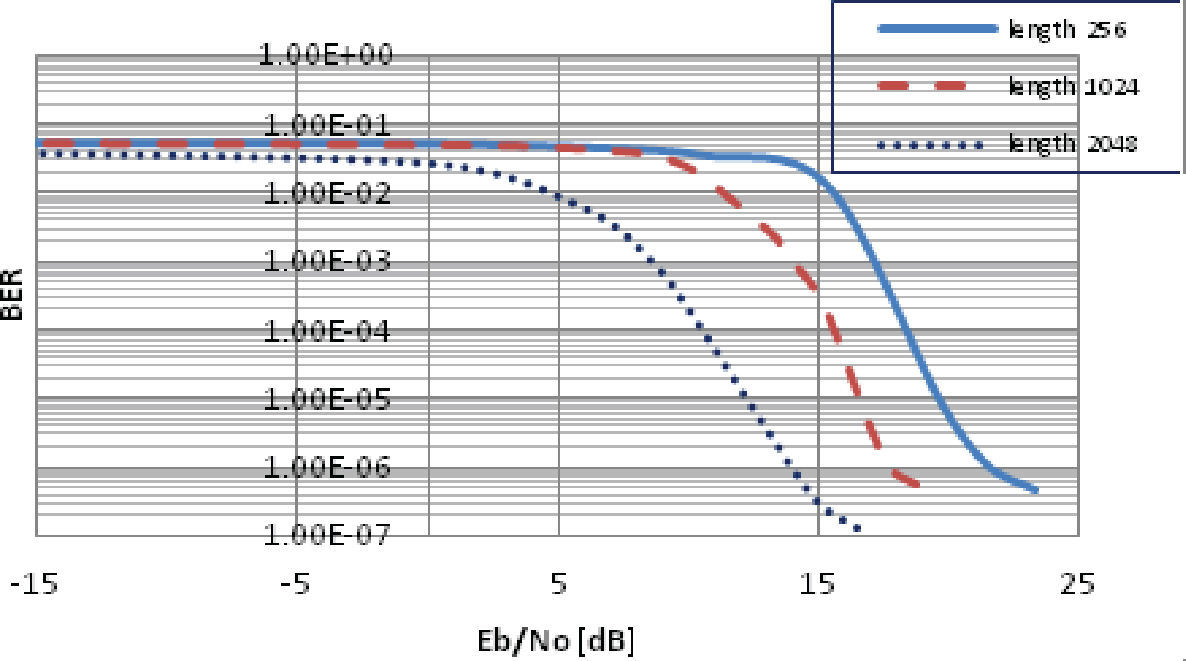
Luego, tomando en cuenta los valores y la forma de operar de la modulación OFDM, se realizó el siguiente cambio: la longitud del entrelazador HSR se aumentó a 1024 y 2048 bits. Como se puede apreciar en las gráficas de la figura 18 con dicha modificación la mejora en el desempeño es significativa, ya que conforme se incrementa el tamaño del entrelazador, aumenta la descorrelación entre su entrada y su salida, aumentando en consecuencia la eficiencia del código, sin embargo, incrementando también la latencia de procesamiento.
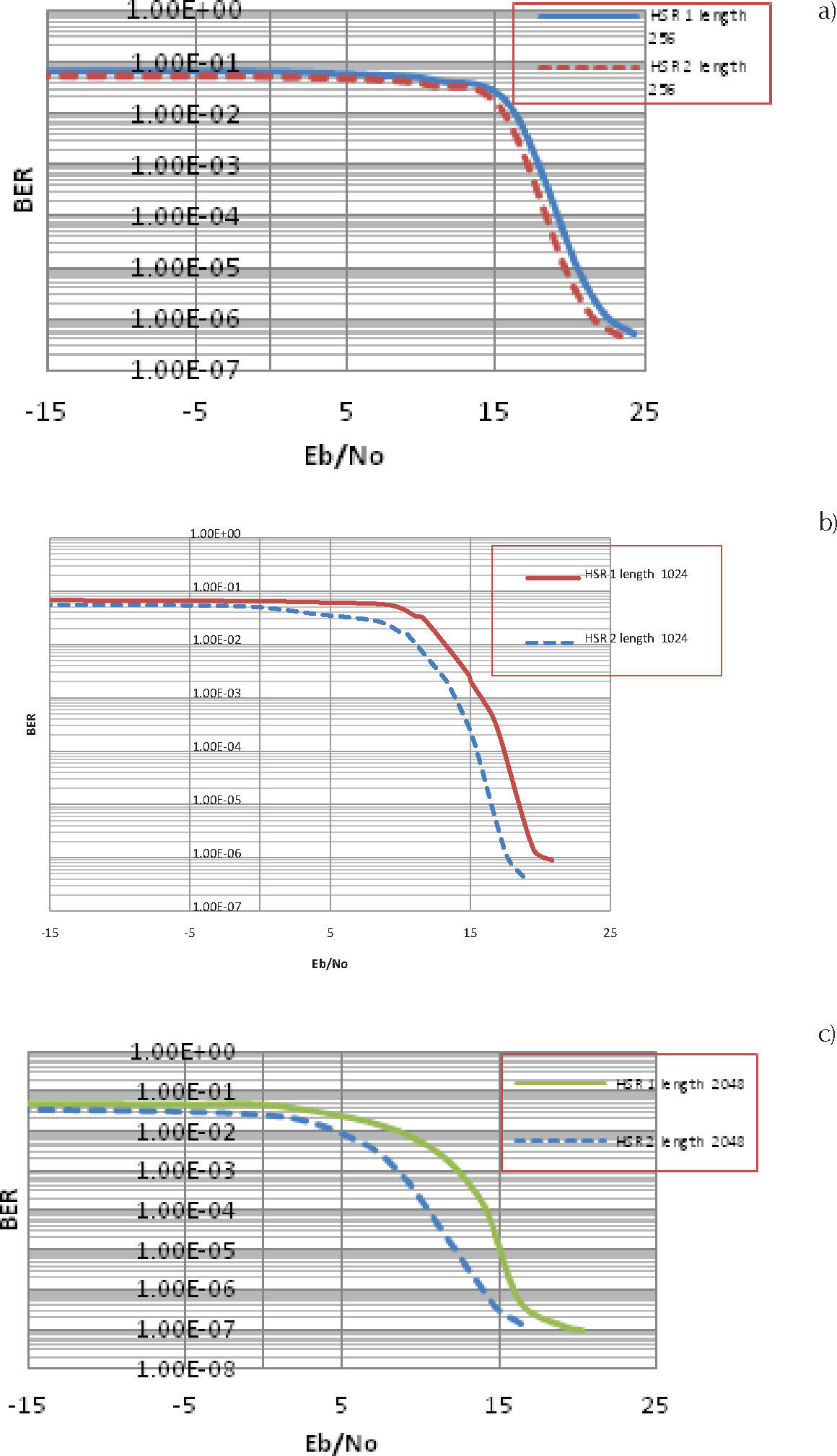
En la figura 19, se tienen las gráficas obtenidas mediante las simulaciones, en las cuales se usó la nueva matriz de perforado tipo 2, la cual fue optimizada para el sistema PLC con modulación OFDM. Esto, permite el uso de entrelazadores de hasta 2048 bits. En estas gráficas se puede constatar que existe una mejoría en el rendimiento, con respecto a las anteriores, en donde no se usaba una matriz de perforado optimizada para nuestros parámetros.
De manera comparativa para una Eb/N0 de 15[db] en la figura 17 con un tamaño de entrelazador de 2048 bits, se tiene un BER de 1E-5 mientras que en la figura 18 se tiene una tasa BER de 3E-7. Este tamaño de entrelazador genera una mayor ganancia en la gráfica y con ello un mejor desempeño en la turbo codificación.
En la figura 19, las gráficas comparan las curvas generadas con diferentes tamaños de entrelazador, a) 256, b) 1024 y c) 2048, respectivamente, y con diferentes matrices de perforado. Las líneas continuas corresponden a la utilización de la matriz de perforado tipo 1, mientras que las líneas punteadas corresponden a las simulaciones con la matriz de perforado tipo 2.
En los tres casos, al utilizar la matriz de perforado tipo 2 la caída de la curva empieza más a la izquierda, lo cual indica una mejora. En c) donde se utiliza el enra trelazador lo más grande posible, 2048, la diferencia es más marcada.
Por último en la figura 20, para una BER de 10−5, la curva generada al utilizar el turbo codificador con un entrelazador HSR y matriz de perforación tipo 2 de longitud 2048 elementos, existe una ganancia de 30dB aproximadamente en la Eb/N0, con respecto a la curva obtenida cuando no se utiliza ningún código de corrección de errores.
ConclusionesDe las primeras simulaciones en computadora realizadas con el sistema que incluye el modelo del canal PLC con sus diferentes ruidos y modulación OFDM, comparando los resultados obtenidos con los correspondientes a las publicaciones encontradas a este respecto (Zimmermann y Dostert, 2002a; Babic et al., 2005 y 2006; Wang, et al., 2006 y Guerrieri et al., 2007), se pudo validar el funcionamiento de nuestro sistema. Tales simulaciones se refieren entonces al comportamiento del canal con una modulación OFDM sin ningún código de corrección de errores.
Se realizaron las simulaciones con los turbo códigos variando los parámetros de longitud de entrelazado, es decir, utilizando el entrelazador HSR con longitudes de 256, 1024 y 2048 elementos.
De acuerdo con los resultados obtenidos, se puede concluir: que los turbo códigos son una excelente opción en cuanto a corrección de errores para un sistema PLC con una modulación OFDM. Además, para estas condiciones de transmisión con los parámetros de la OFDM, se propone usar en el turbo código un entrelazador de hasta 2048 elementos, lo cual hace mucho más eficiente el código, por la mayor descorrelación de los elementos de entrada a los codificadores constitutivos de los códigos turbo (figura 12). Adicionalmente, se puede cambiar la tasa de codificación utilizando una matriz de perforado, cuya metodologia de diseño permite maximizar la distancia libre dfree del código.
Con las simulaciones realizadas se pudo lograr un desempeño mejor al reportado en las referencias de Wang (2006) y Guerrieri (2007). La aportación de este trabajo para lograr este mejor desempeño está en la utilización de una metodología de diseño de los turbo códigos, como un problema de optimización global que maximiza la distancia libre dfree del código, y que optimiza el desempeño global de los mismos a partir de considerar una optimización conjunta de cada una de las principales partes constitutivas: entrelazador-polinomios-matriz de perforado.
Como trabajo futuro se propone el diseño de los entrelazadores utilizando polinomios de permutación cuadráticos o cúbicos, cuyos parámetros de longitud se adapten a las características de la multiplexación OFDM para integrar este diseño a la metodología de optimización del desempeño de los turbo códigos para los sistemas PLC.
Agradecemos a la DGAPA-UNAM por el apoyo para la realización de este trabajo a través del proyecto IN-102410, así como a la CEP-UNAM por la beca de doctorado otorgada.
Carlos Alberto Balbuena-Campuzano. Obtuvo su título como ingeniero en electrónica por la Universidad Autónoma del Estado de México en 2003, igualemente la maestría en ingeniería en telecomunicaciones por la Facultad de Ingeniería de la Universidad Nacional Autónoma de México. Actualmente desarrolla su trabajo doctoral enfocado al tema de turbo codificación en ambientes de red eléctrica, en la Facultad de Ingeniería en la UNAM. Desde 2011 es profesor de tiempo completo en la Universidad Politécnica del Valle de Toluca en el área de Mecatrónica.
Francisco García-Ugalde. Obtuvo su titulo como ingeniero mecánico electricista en la Universidad Nacional Autónoma de México en 1977, en el área de ingeniería de sistemas eléctricos y electrónicos. Su M.C. (Diplôme d'Ingénieur) en sistemas de comunicaciones/electrónica del estado sólido de la Ecole Supérieure d'Electricité de Francia (SUPE-LEC) en 1980. Realizó el doctorado en la Universidad de Rennes I, Francia en 1982, en el área de procesamiento de la información. Desde 1983 es profesor de tiempo completo en la Facultad de Ingeniería de la UNAM. Sus intereses de investigación actuales son: codificación y análisis de imágenes y video digitales, marcado de agua en imágenes digitales, análisis, diseño y desarrollo de herramientas para filtros digitales, teoría y aplicaciones de codificación para el control de errores, turbo codificación, aplicaciones de criptografía, procesamiento paralelo y bases de datos.