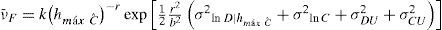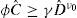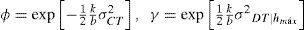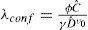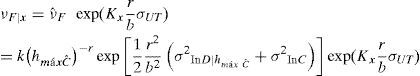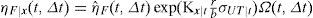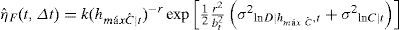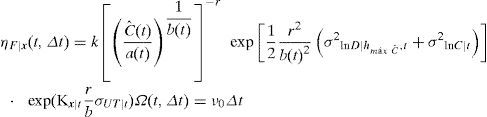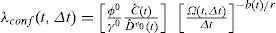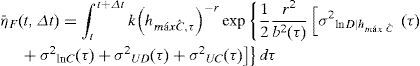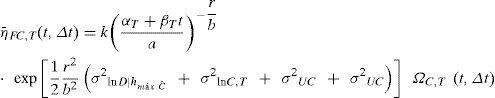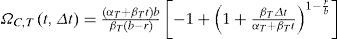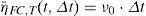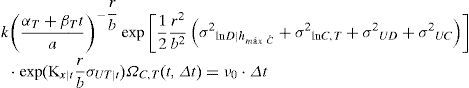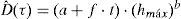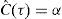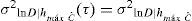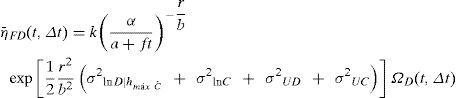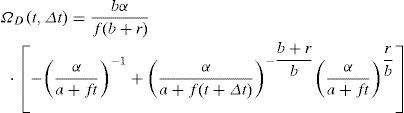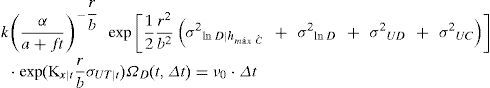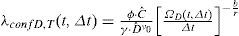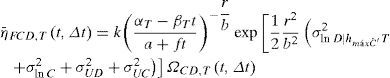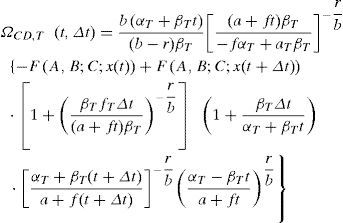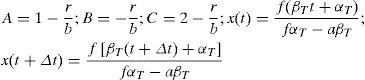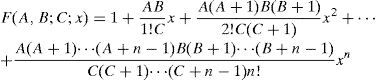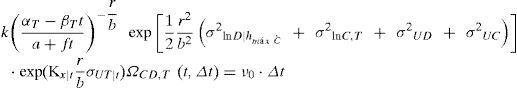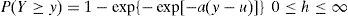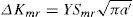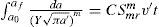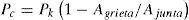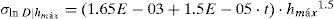Se propone un criterio para evaluar el factor de confianza que obtendrá una estructura después de cierto intervalo de tiempo. El factor de confianza indica lo adecuado que es el nivel de desempeño que presenta una estructura ante solicitaciones externas. Dicho factor considera incertidumbres tanto en la capacidad como en la demanda estructural. La formulación se elabora de acuerdo con el formato de diseño basado en factores de demanda y de capacidad. Se comparan cuatro casos: a) considerando que la capacidad estructural se deteriora con el tiempo, al mismo tiempo que la demanda estructural permanece constante, b) suponiendo que solo la demanda estructural (dada una intensidad) varía en el tiempo, c) considerando que varían en el tiempo simultáneamente la capacidad y la demanda estructural, y d) ignorando el efecto del deterioro estructural. El criterio se aplica a una plataforma marina tipo “jacket”. El deterioro se analiza mediante el crecimiento de grietas ocasionadas por la fatiga en los extremos de algunos elementos estructurales críticos. Se concluye que para evaluar el factor de confianza que tiene la estructura después de cierto tiempo es más significativo considerar la influencia del deterioro en la capacidad que en la demanda estructural; sin embargo, se recomienda considerar en el análisis tanto la degradación de la capacidad estructural como su influencia en la demanda estructural, para una intensidad dada.
An approach to evaluate the confidence factor for structures at the end of an interval of time is proposed. The confidence factor indicates the adequacy of the performance level of a structure subjected to external loads. The factor considers the uncertainties implicit in the structural capacity and in the structural demand. The formulation is made in accordance with the Demand and Capacity Factor Design Format. Four scenarios are compared: a) structural capacity deteriorates over a time interval, while structural demand remains constant, b) only structural demand (for a given intensity) varies in time, c) both structural capacity and structural demand vary simultaneously in time, and d) the effect of structural deterioration is neglected. The approach is applied to an offshore jacket platform. Deterioration is taken into account by analyzing the growth of fatigue cracks in both ends of several critical structural elements. It is concluded that for the evaluation of the confidence factor over an interval of interest, for the case analyzed, it is more significant to consider the variation in time of the structural capacity rather than that of the structural demand; however, it is recommended to consider both (structural capacity and structural demand) in the analysis.
Una estructura sometida a condiciones de carga, esfuerzos y deformaciones durante su vida útil, originadas por sus características de operación y por su exposición a eventos naturales (i.e. sismo, viento, oleaje, etcétera), generalmente sufre, a medida que pasa el tiempo, un deterioro gradual en sus propiedades mecánicas. Esto da lugar a que se debilite su capacidad estructural y, por otro lado, a que se incremente su demanda estructural ante la acción de las solicitaciones a las que está expuesta. Como consecuencia, el valor de su confiabilidad estructural cambia (generalmente disminuye) a medida que pasa el tiempo, por lo que es conveniente contar con herramientas matemáticas que permitan evaluar la confiabilidad para diferentes intervalos de tiempo.
El factor de confianza y su nivel de confianza correspondiente fueron propuestos por Cornell (1996), dentro del formato Demand and Capacity Factor Design (DCFD), para evaluar la confiabilidad de estructuras (Cornell et al., 2002). La formulación original no considera el deterioro que sufren las estructuras con el tiempo.
Posteriormente, se han desarrollado expresiones que toman en cuenta la evolución en el tiempo de la degradación de la capacidad estructural (Torres y Ruiz, 2007; Vamvatsikos y Dolšek, 2011; Tolentino et al., 2012). El factor de confianza, λconf, denota qué tan adecuado es el nivel de desempeño que presenta una estructura ante las solicitaciones externas. Dicho factor considera incertidumbres tanto en la capacidad como en la demanda estructural, por lo que la seguridad con la que realmente se presenta dicho factor de confianza se expresa mediante cierto nivel de confianza, Kx.
En la literatura se han propuesto varios enfoques para evaluar la confiabilidad de las estructuras que sufren deterioro estructural con el tiempo (Mori y Ellingwood, 1993; Montes et al., 2003; Straub, 2009; Pourgharibshahi y Taghikhany, 2012); sin embargo, ninguno de estos estudios evalúa la confiabilidad estructural en el formato DCFD, como se propone en este estudio. En el formato DCFD, de forma análoga a los métodos LRFD (Load and Resistance Factor Design) empleados en varios códigos de diseño, se multiplica la demanda y capacidad estructural por factores de seguridad obtenidos probabilísticamente.
En el presente estudio se desarrollan expresiones matemáticas cerradas, extendiendo la formulación de Torres y Ruiz (2007), con el fin de calcular el factor de confianza λconf(t) y el nivel de confianza, Kx(t), en función del tiempo. Una diferencia entre el presente trabajo y el de Torres y Ruiz (2007) es que estos últimos suponen que la mediana de la capacidad estructural se degrada de manera lineal durante todo el intervalo de tiempo en estudio, mientras que en el presente trabajo se supone que la capacidad decrece linealmente en sub-intervalos de tiempo, de manera que la reducción total de la capacidad puede representarse mediante una función no-lineal en el intervalo total de tiempo.
La ventaja de suponer un comportamiento no lineal de la degradación de la capacidad es la facilidad para generalizar diferentes tipos de problemas con comportamientos más apegados a la realidad, lo cual es complicado cuando se supone que dicha degradación es lineal. Otra aportación del presente trabajo es que se presenta una solución para el caso en que la demanda estructural varía en el tiempo, mientras que la capacidad permanece constante. Se compara, mediante un ejemplo, el factor de confianza para los siguientes casos:
- a)
Cuando la capacidad estructural varía en el tiempo, mientras que la demanda es independiente del tiempo.
- b)
Cuando la demanda estructural (dada una intensidad) varía en el tiempo, al mismo tiempo que la capacidad es independiente del tiempo.
- c)
Cuando varían en el tiempo de manera simultánea, la capacidad y la demanda estructural.
- d)
Cuando no se considera degradación estructural.
El ejemplo de aplicación que se presenta corresponde a una plataforma marina tipo “jacket” instalada en la sonda de Campeche, México. El deterioro estructural se considera a través del crecimiento de grietas causadas por fatiga en algunos nodos críticos de la estructura, originadas por las condiciones de oleaje
Formulación original del factor de confianza λconf (sin considerar deterioro estructural)El valor esperado de la tasa anual de falla, ν¯F, se obtuvo a través del método simplificado planteado por Cornell (1996) y se estableció originalmente para evaluar la confiabilidad sísmica de edificios. Posteriormente, Cornell et al. (2002) lo aplicaron para evaluar la confiabilidad de edificios de acero ante solicitaciones sísmicas. En el presente estudio dicha formulación se adecuó para evaluar la confiabilidad de estructuras sujetas a oleaje (i.e., plataformas marinas). Esto es posible gracias a que los conceptos involucrados en ambos tipos de problemas (i.e., descripción probabilista de la demanda estructural y de la capacidad estructural, curvas de peligro ambiental, representación del deterioro de la capacidad estructural mediante expresiones matemáticas simples, etcétera) son similares. Tomando en cuenta lo anterior, la tasa anual de falla estructural, ν¯F, de una estructura sujeta a oleaje puede calcularse mediante la siguiente expresión (Cornell et al., 2002):
donde hmáx Cˆ=Cˆa1b es la altura máxima de ola, hmáx¸ aso ciada con la mediana de la capacidad, Cˆ;σ2lnD|hmáx Cˆ y σ2ln C son las varianzas de los logaritmos naturales de la demanda, D, dada una altura máxima de ola, hmá¸x, y de la capacidad estructural, C, correspondientes al estado límite de interés; σ2DU y σ2CU representan las varianzas producidas por las incertidumbres epistémicas asociadas a la demanda y a la capacidad, respectivamente; a y b son parámetros que definen la forma de la mediana de la demanda, en función de la altura máxima de ola, hmáx.La ecuación 1 se obtuvo por Cornell et al. (2002) con base en el teorema de probabilidad total, tomando en cuenta todas las posibles intensidades que pueden presentarse en el sitio de interés y la probabilidad condicional de falla de la estructura ante cierto nivel de solicitación, bajo las siguientes suposiciones:
- 1.
La curva de peligro de oleaje, υ(hmáx), se puede representar mediante la expresión υ(hmáx)=k(hmáx)−r, donde k y r son parámetros que se ajustan a la forma de la curva de peligro de oleaje.
- 2.
La mediana de la demanda estructural, Dˆ, se representa como función de la carga de oleaje, hmáx, mediante la expresión Dˆ=a·hmáxb.
- 3.
La demanda estructural para cierta altura máxima de ola, hmáx, tiene una distribución lognormal con desviación estándar del logaritmo natural igual a σlnD hmáx.
- 4.
La capacidad estructural del estado límite presenta una mediana de capacidad, Ĉ, de tipo lognormal, y la desviación estándar del logaritmo natural es igual a σln C.
La ecuación anterior implica que el número anual de fallas, νF, asociadas a un nivel de confianza X está dado por (Cornell et al., 2002):
donde vˆF representa la mediana (50% confianza) de νF. El formato expresado mediante las ecuaciones 5, 6 y 7 se utiliza en los lineamientos establecidos por la SAC (Sociedad compuesta por la Asociación de Ingenieros Estructurales de California, SEAOC, el Consejo de Tecnología Aplicada de EUA, ATC, y las Universidades de California dedicadas a el estudio de la Ingeniería Sísmica, CUREe) a petición del FEMA (Federal Emergency Managment Agency), para la evaluación de estructuras.Formulación del factor y del nivel de confianza en función del tiempoA continuación se extiende la metodología descrita en la sección anterior para el caso en donde las propiedades mecánicas de los elementos estructurales cambien en el tiempo (debido a corrosión, fatiga, deformaciones, etcétera), y como consecuencia, modifiquen el valor de la capacidad o la demanda estructural con el tiempo.
De manera similar a la ecuación 7, el número de fallas asociadas a un nivel de confianza x, al final del intervalo de tiempo [t, t+Δt), se puede expresar como:
donde:La variable ηF|x (t, Δt) representa el número de fallas correspondiente a un nivel de confianza x, dentro del intervalo [t, t+Δt); ηˆF(t,Δt) es la mediana del número esperado de fallas para el intervalo de tiempo [t,t+Δt). Las demás variables significan lo mismo que se describió en la sección anterior excepto que ahora todas se refieren al valor que toma cada variable en el tiempo t. La función Ω(t, Δt) representa un factor de corrección del número esperado de fallas que se expresa mediante funciones matemáticas cerradas, en donde la forma depende del caso que se trate (casos a, b o c, listados en la introducción). Generalmente dicho factor de corrección aumenta el valor del número esperado de fallas por efecto de la degradación de la capacidad estructural (caso a), el aumento de la demanda, dada una altura máxima de ola (caso b), o la combinación de ambos (caso c).Con el fin de llegar a una expresión similar a la ecuación 5, pero en función del tiempo, aquí se establece la condición de que el número de fallas asociadas a un nivel de confianza χ, al final del intervalo de tiempo [t, t+Δt), debe ser igual a cierto valor prefijado ν0 multiplicado por el intervalo de tiempo Δt, es decir:
A partir de esta condición se llega a la siguiente expresión que describe el factor de confianza al final del intervalo de tiempo [t,t+Δt):Las variables φ0 y γ0 pueden resultar función del tiempo dependiendo del caso que se trate (a, b o c). La función Ω(t, Δt) tiene el mismo significado que en la ecuación 8, y su forma también depende del caso que se trate (a, b o c). En las secciones que siguen se deducen las formas de Ω(t, Δt) y de λconf (t, Δt) correspondientes a los casos a, b y c.Factor de confianza correspondiente a los casos a, b y cCaso a. Considerando que la capacidad estructural varía en el tiempo, mientras que la demanda estructural es independiente del tiempoSe parte de que el valor esperado del número de fallas, η¯F(t,Δt), durante un intervalo de tiempo puede expresarse como una extensión de la ecuación 1, como sigue:
donde hmáxCˆ,τ=Cˆ(τ)a(τ)1b(τ) es la altura máxima de ola asociada con la mediana de la capacidad, Ĉ(τ), en el tiempo τ; σ2lnD|hmáx Cˆ(τ) y σ2lnC(τ) son las varianzas de los logaritmos naturales de la demanda estructural dada una altura máxima de ola, hmáx, y de la capacidad estructural, en el instante de tiempo τ; σ2UD (τ); y σ2UC (τ) son las varianzas producidas por las incertidumbres epistémicas relacionadas con la demanda estructural (d) y la capacidad estructural (c) del estado límite de interés, en el instante de tiempo τ, respectivamente.Con el fin de considerar que la capacidad estructural varía en el tiempo, mientras que la demanda es constante, se hacen las siguientes suposiciones:
5. La mediana de la capacidad varía linealmente en un sub-intervalo (T) de tiempo, de la siguiente manera:
donde T es el número de sub-intervalo de tiempo, n es el número de sub-intervalos de tiempo considerados para el análisis. El intervalo total de interés está compuesto por n sub-intervalos.6. La varianza del logaritmo natural de la capacidad estructural, σ2lnC (τ), es constante en cada uno de los sub-intervalos de interés; es decir σ2lnC (τ)=σ2lnC,T.
7. Los parámetros a(τ) y b(τ) son constantes en todo el intervalo de tiempo de interés; es decir a(τ)=a y b(τ)=b.
Tomando en cuenta las suposiciones 1 a 7, la ecuación 12 resulta:
donde:donde ΩC,T (t,Δt) representa un factor de corrección del número esperado de fallas que considera solamente el deterioro de la capacidad estructural y no considera que la demanda estructural varía con el tiempo. Una ecuación similar a la ecuación 14 se obtuvo por Torres y Ruiz (2007), excepto que estos autores consideran que la capacidad estructural disminuye linealmente durante todo el intervalo de tiempo en estudio; mientras que aquí la ecuación 13 se generaliza para que la mediana de la capacidad sea lineal en cada sub-intervalo de tiempo, pero que pueda resultar no-lineal en su conjunto (como se ilustra en el ejemplo que se presenta más adelante).Para obtener la ecuación 2, Cornell et al. (2002) consideraron que ν¯F=ν0; de manera similar, aquí se establece que el número esperado de fallas asociadas a un nivel de confianza x, al término del intervalo de tiempo [t, t+Δt), debe ser igual a un valor prefijado ν0, multiplicado por el intervalo Δt, como sigue:
Sustituyendo la ecuación 14 en la ecuación 16, se tiene:De la ecuación anterior resulta:Esta ecuación permite conocer la variación del factor de confianza al final del sub-intervalo T de tiempo, considerando el deterioro de la capacidad estructural, y suponiendo que la demanda estructural (para cierta intensidad) no varía con el tiempo.Caso b. Considerando que la demanda estructural (para cierta intensidad) varía en el tiempo, mientras que la capacidad estructural es independiente del tiempoEn esta sección se considera exclusivamente la influencia que tiene la demanda estructural (para una intensidad dada) en λconf, manteniendo la capacidad estructural como independiente del tiempo. Para ello se hacen las siguientes suposiciones:
8. La mediana de la demanda estructural como función del tiempo, t, dada una altura máxima de ola, hmáx, está dada por:
Nótese que la ecuación 19 es una función ampliada de la expresión Dˆ(τ)=ayb utilizada por Cornell et al. (2002).9. La mediana de la capacidad Ĉ (τ) es constante durante el intervalo total de tiempo en estudio, por lo que:
10. La varianza del logaritmo natural de la demanda, es constante en el intervalo de tiempo en estudio:
Tomando en cuenta los puntos 1 a 9, excepto el 5, e integrando la ecuación 12, se obtiene:donde:donde ΩD (t,Δt) es un factor de corrección del número esperado de fallas que considera solo la variación de la demanda estructural (para una intensidad dada) en el intervalo de tiempo [t, t+Δt].Suponiendo la misma consideración que se siguió para obtener la ecuación 16, y sustituyendo términos, se tiene:
Realizando algunos arreglos algebraicos, se tiene:La ecuación anterior sirve para evaluar el factor de confianza al final del intervalo [t, t+Δt) cuando únicamente se considera la variación de la demanda estructural (para una intensidad dada) con el tiempo.Caso c. Considerando que varían simultáneamente en el tiempo la capacidad y la demanda (para cierta intensidad)En esta sección se establece la expresión correspondiente al número esperado de fallas al final de cierto intervalo de tiempo [t, t+Δt) en donde se considera de manera simultânea la variación en el tiempo de la capacidad y de la demanda estructural. Para ello se consideran las suposiciones 1 a 10, excepto la 8. A partir de la ecuación 12 se obtiene:
donde:dondedonde ΩCD,T (t,Δt) representa al factor de corrección del número esperado de fallas que considera de manera simultânea la variación de la demanda estructural (para una intensidad dada) y de la capacidad estructural en el intervalo de tiempo [t, t+Δt), Una expresión similar se obtuvo por Tolentino et al. (2012) para el número esperado de fallas al final de un intervalo de tiempo después de la construcción de la estructura; sin embargo, en el presente estudio se generaliza la expresión para sub-intervalos (T) de tiempo, de esta manera es posible que la capacidad pueda presentar un deterioro que tenga forma no-lineal en el tiempo (como se ilustra en el ejemplo que se presenta más adelante). Además, aquí la función hipergeométrica F(A,B;C;x) que interviene en la ecuación 26 se resuelve de manera práctica y sencilla a través de la siguiente serie hipergeométrica (Rainville, 1961):donde A, C y x pueden tomar cualquier número real, B debe ser un número real entero.Finalmente, con las mismas consideraciones que para obtener la ecuación 16, se tiene:
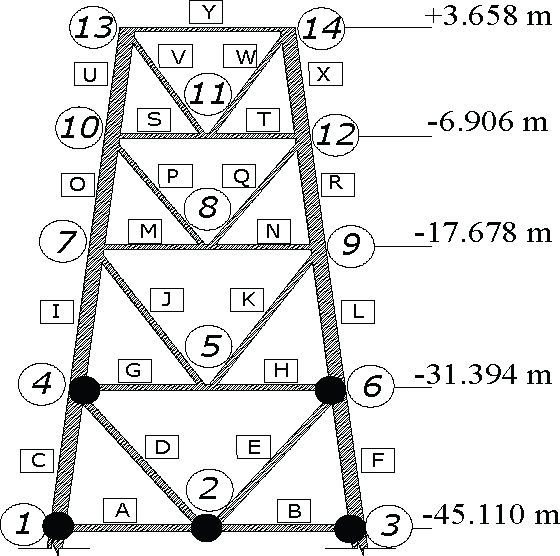
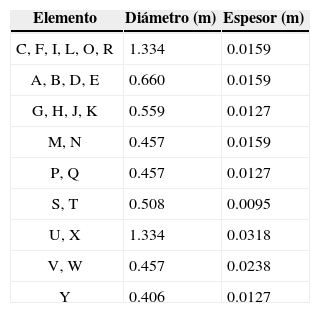
De algunos arreglos algebraicos, se obtiene:donde λconfCD,T (t,Δt) permite evaluar al final de un intervalo de tiempo, el factor de confianza cuando se considera simultáneamente la variación en el tiempo de la capacidad y de la demanda estructural, para cierto nivel de intensidad.Ejemplo ilustrativoDescripción de la plataforma marina y de las cargas ambientalesCon el propósito de presentar los pasos correspondientes al criterio propuesto, se calcula el factor de confianza (ecuaciones 5, 18, 24 y 29) de un modelo estructural 2D simplificado de una plataforma marina de acero tipo “jacket” ubicada en el sitio Akal, sonda de Campeche, México, donde se tiene un tirante de agua de 45.11m. La plataforma tiene una altura de 48m (figura 1). Se modela uno de los marcos interiores de la plataforma con las propiedades geométricas indicadas en la tabla 1. Los elementos son de acero estructural A-36, y se consideran propiedades mecánicas medias.
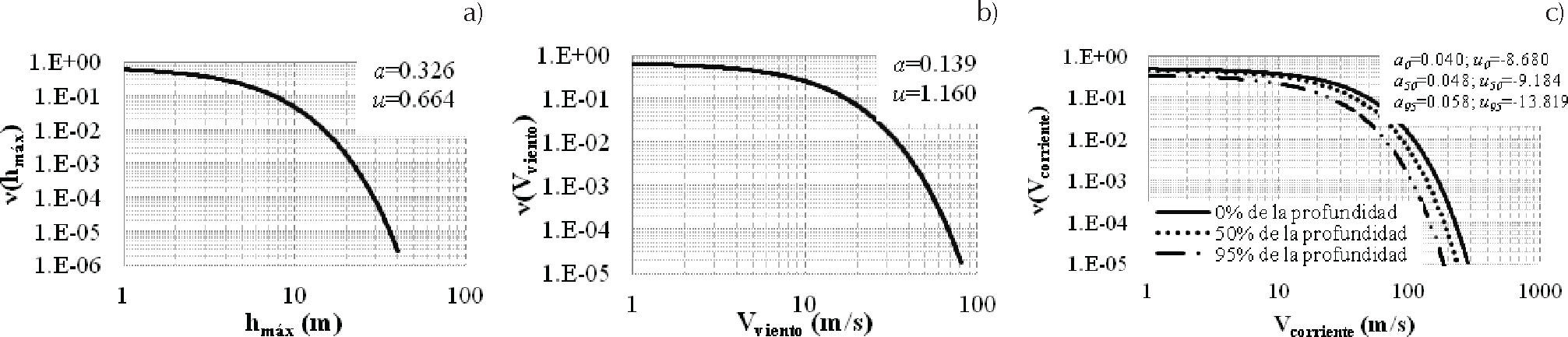
En este estudio se consideraron las condiciones de oleaje, viento y corrientes marinas a partir de la norma NRF-003-PEMEX-2000 para el sitio Akal. En las figuras 2a, b y c se presentan las curvas de peligro ambiental ajustadas mediante una función de probabilidad anual acumulada de valores extremos de Gumbel, que tiene la forma:
donde ϒ representa la altura máxima de ola, velocidad de viento o velocidad de corriente, según sea el caso. Los valores de a y u se muestran en la figuras 2a, b y c.Análisis por fatigaDebido a que la plataforma marina continuamente está sujeta a cargas de oleaje de operación a lo largo de su vida útil, es necesario detectar la presencia de grietas causadas por fatiga en las juntas críticas de la plataforma, y, además, predecir su crecimiento en el tiempo. Los nodos críticos se indican con los números 1, 2, 3, 4 y 6 en la figura 2. Estos se detectaron mediante análisis estáticos no-lineales (”push over”).
El análisis por fatiga se realizó para dos puntos de cada elemento interno que se conecta a un nodo crítico. Estos puntos corresponden a zonas donde se presentan los esfuerzos máximos y mínimos en el sentido transversal del elemento. Se estudiaron dos puntos para los nodos 1 y 3, y cuatro puntos en los nodos 2, 4, y 6 (debido a que en estos nodos se conectan dos elementos).
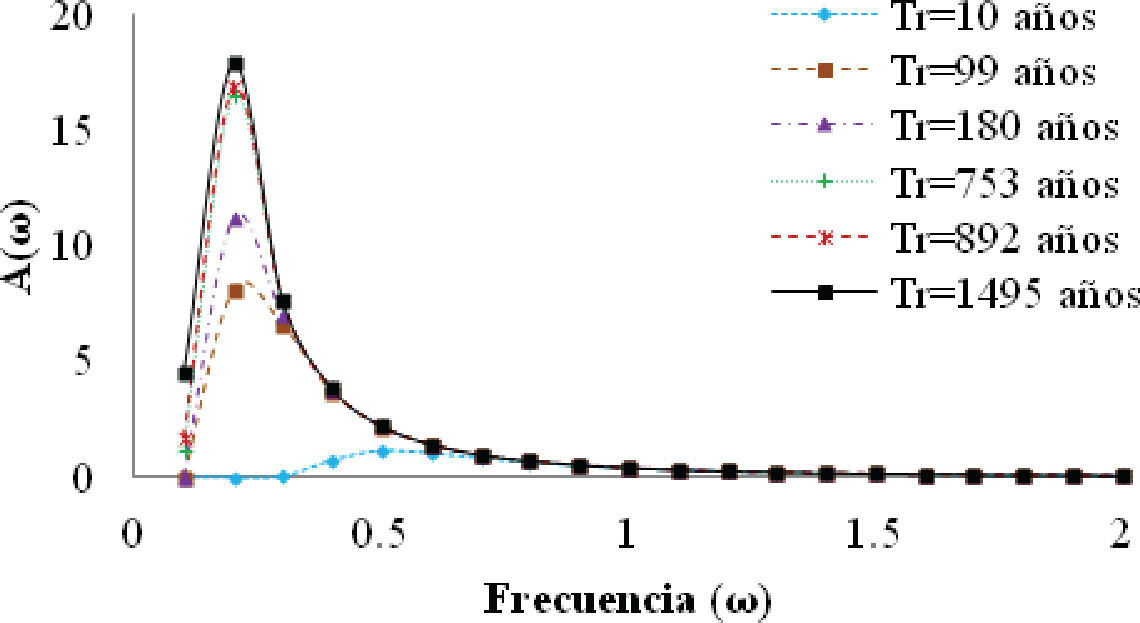
Los esfuerzos mínimos y máximos de los puntos seleccionados se obtuvieron mediante análisis dinámicos “paso a paso” en el tiempo, utilizando un conjunto de oleajes simulados, asociados a diferentes alturas de ola. El contenido de frecuencias de los oleajes se obtuvo a partir de espectros de Pierson-Moskowitz (1964) para la zona. A partir del espectro de Pierson-Moskowitz se obtienen los espectros de amplitudes de ola asociados a diferentes periodos de retorno (Tr), como se muestran en la figura 3.
Para la simulación del oleaje la superficie del mar, h, se representa como un proceso estacionario, homogéneo, Gaussiano, que puede expresarse como una superposición lineal de olas regulares con generación aleatoria en sus ángulos de fase, ϕ, con distribución uniforme entre 0 y 2π.
El crecimiento de grieta promedio de los puntos seleccionados bajo carga aleatoria se obtuvo utilizando la ecuación diferencial modificada (Paris y Erdogan, 1963; Sobczyk y Spencer, 1992):
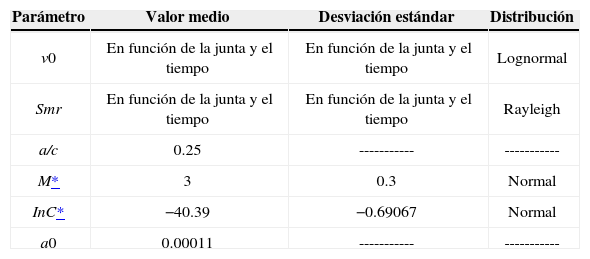
donde C y m son parámetros que dependen de las características del material, ΔKmr es el intervalo de intensidad de esfuerzo medio, ν′ es la tasa de cruces positivos por cero en un cierto tiempo, ϒ es el factor de corrección geométrica (Newman y Raju, 1981), Smr es el intervalo de esfuerzo medio de la respuesta aleatoria de los elementos (Sobczyk y Spencer, 1992), y a′ es el tamaño de la grieta. En esta ecuación se remplaza la carga aleatoria por una carga cíclica equivalente cuya amplitud y frecuencia se expresan en función de las propiedades medias del proceso aleatorio. Sustituyendo la ecuación 32 en la ecuación 31 se obtiene:donde a0 es el tamaño inicial de la grieta y af es el tamaño final de la grieta después de N ciclos de esfuerzos. El proceso de simulación de grietas se realizó mediante la ecuación 33.La descripción probabilista del crecimiento de grietas por fatiga se estimó mediante la técnica de simulación de Monte Carlo. En la tabla 2 se muestran los valores de los parámetros estadísticos que se utilizaron para la simulación de grietas. Los parámetros fueron tomados del trabajo de Silva y Heredia (2004) para plataformas ubicadas en la bahía de Campeche.
Parámetros estadísticos utilizados para la simulación de grietas (Silva y Heredia, 2004).
| Parámetro | Valor medio | Desviación estándar | Distribución |
|---|---|---|---|
| ν0 | En función de la junta y el tiempo | En función de la junta y el tiempo | Lognormal |
| Smr | En función de la junta y el tiempo | En función de la junta y el tiempo | Rayleigh |
| a/c | 0.25 | ----------- | ----------- |
| M* | 3 | 0.3 | Normal |
| InC* | −40.39 | −0.69067 | Normal |
| a0 | 0.00011 | ----------- | ----------- |
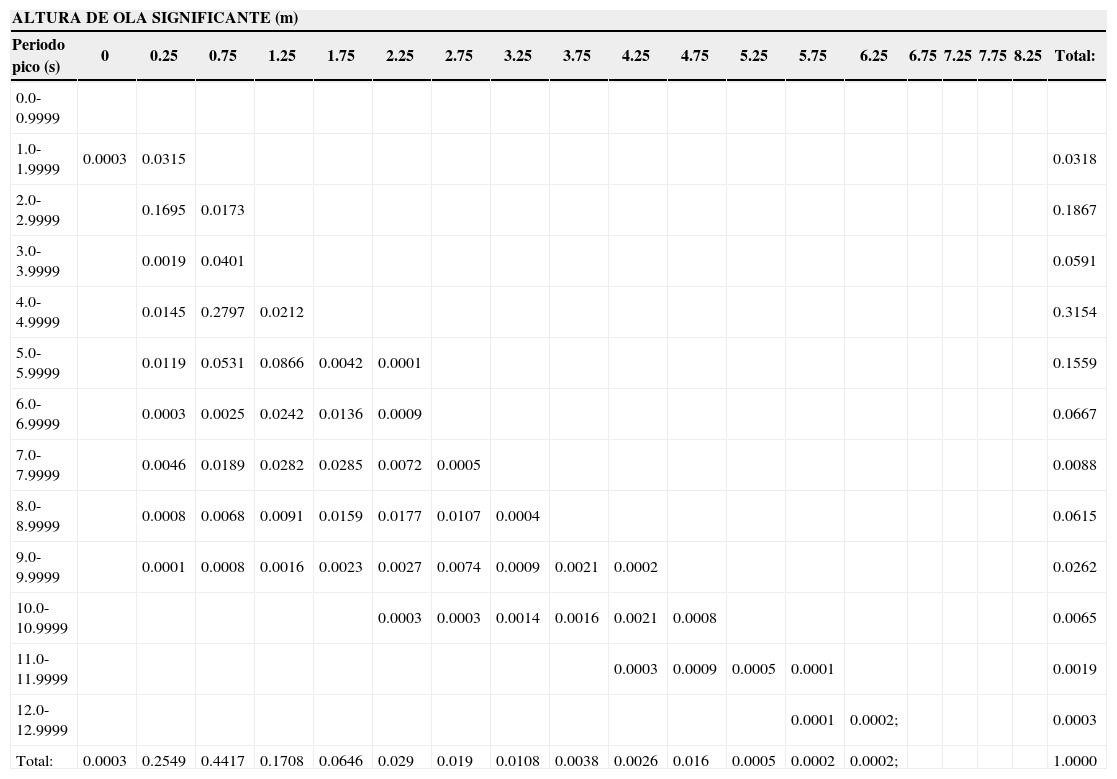
Para el análisis se tomaron en cuenta oleajes tanto de operación como de tormenta. Los tiempos de espera entre tormentas se supusieron con distribución exponencial. Durante el tiempo de espera entre tormentas se consideró que actuaba el oleaje de servicio; asimismo que la altura máxima de ola asociada a una tormenta sigue una distribución de Gumbel (tomando la derivada normalizada de la curva de peligro de oleaje), y que el tamaño de grieta a′, en un cierto tiempo t, presenta una distribución lognormal. En la tabla 3 se muestran las características del oleaje de operación en donde se relaciona la altura de ola, el periodo pico de ola significante y la probabilidad de ocurrencia de cada estado de mar, obtenidos a partir de la norma NRF-003-PEMEX-2000.
Información oceanográfica para el análisis de fatiga. Condiciones de operación
| ALTURA DE OLA SIGNIFICANTE (m) | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Periodo pico (s) | 0 | 0.25 | 0.75 | 1.25 | 1.75 | 2.25 | 2.75 | 3.25 | 3.75 | 4.25 | 4.75 | 5.25 | 5.75 | 6.25 | 6.75 | 7.25 | 7.75 | 8.25 | Total: |
| 0.0-0.9999 | |||||||||||||||||||
| 1.0-1.9999 | 0.0003 | 0.0315 | 0.0318 | ||||||||||||||||
| 2.0-2.9999 | 0.1695 | 0.0173 | 0.1867 | ||||||||||||||||
| 3.0-3.9999 | 0.0019 | 0.0401 | 0.0591 | ||||||||||||||||
| 4.0-4.9999 | 0.0145 | 0.2797 | 0.0212 | 0.3154 | |||||||||||||||
| 5.0-5.9999 | 0.0119 | 0.0531 | 0.0866 | 0.0042 | 0.0001 | 0.1559 | |||||||||||||
| 6.0-6.9999 | 0.0003 | 0.0025 | 0.0242 | 0.0136 | 0.0009 | 0.0667 | |||||||||||||
| 7.0-7.9999 | 0.0046 | 0.0189 | 0.0282 | 0.0285 | 0.0072 | 0.0005 | 0.0088 | ||||||||||||
| 8.0-8.9999 | 0.0008 | 0.0068 | 0.0091 | 0.0159 | 0.0177 | 0.0107 | 0.0004 | 0.0615 | |||||||||||
| 9.0-9.9999 | 0.0001 | 0.0008 | 0.0016 | 0.0023 | 0.0027 | 0.0074 | 0.0009 | 0.0021 | 0.0002 | 0.0262 | |||||||||
| 10.0-10.9999 | 0.0003 | 0.0003 | 0.0014 | 0.0016 | 0.0021 | 0.0008 | 0.0065 | ||||||||||||
| 11.0-11.9999 | 0.0003 | 0.0009 | 0.0005 | 0.0001 | 0.0019 | ||||||||||||||
| 12.0-12.9999 | 0.0001 | 0.0002; | 0.0003 | ||||||||||||||||
| Total: | 0.0003 | 0.2549 | 0.4417 | 0.1708 | 0.0646 | 0.029 | 0.019 | 0.0108 | 0.0038 | 0.0026 | 0.016 | 0.0005 | 0.0002 | 0.0002; | 1.0000 | ||||
Considerando que el deterioro estructural en la plataforma se presenta por la aparición de grietas en las juntas tubulares, Stacey et al. (1996), proponen que la capacidad de la junta intacta, Pk, sea modificada por un factor de reducción lineal, como se indica en la ecuación 34. El valor de Pk se puede obtener de acuerdo con el API (1993).
donde Ajunta es el área de la sección transversal, Agrieta es el área de la grieta, producto de la suma de las áreas de las grietas de los puntos seleccionados en la sección de interés, y Pc es la capacidad remanente de la junta agrietada.Evaluación de la capacidad en el tiempo de la estructuraPara evaluar la capacidad estructural se sometió la estructura a una serie de análisis estáticos no lineales (”push-over”) utilizando 20 perfiles de carga diferentes, obtenidos a partir de los oleajes simulados. Los perfiles que se utilizaron obedecen a las fuerzas actuantes cuando el oleaje simulado produce el máximo cortante basal. Se considera como condición de daño la aparición y crecimiento de grietas, con la consecuente reducción de la capacidad estructural.
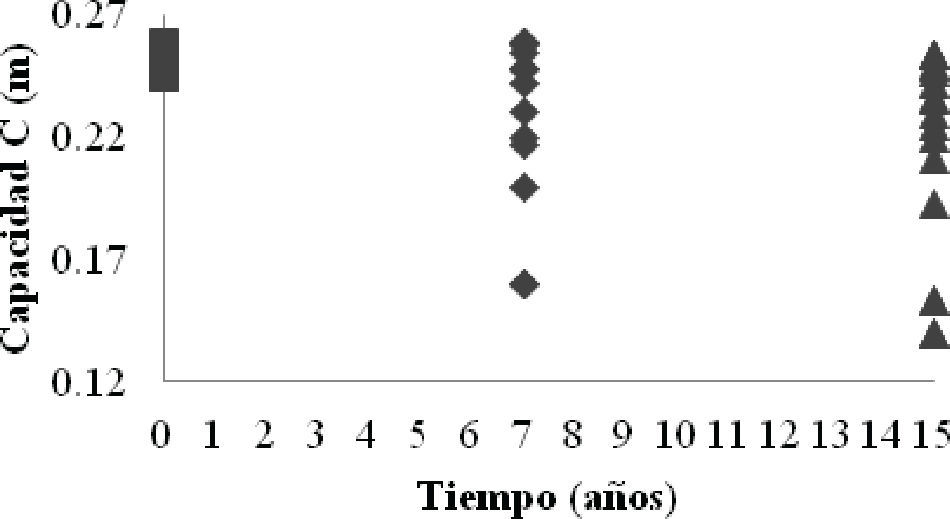
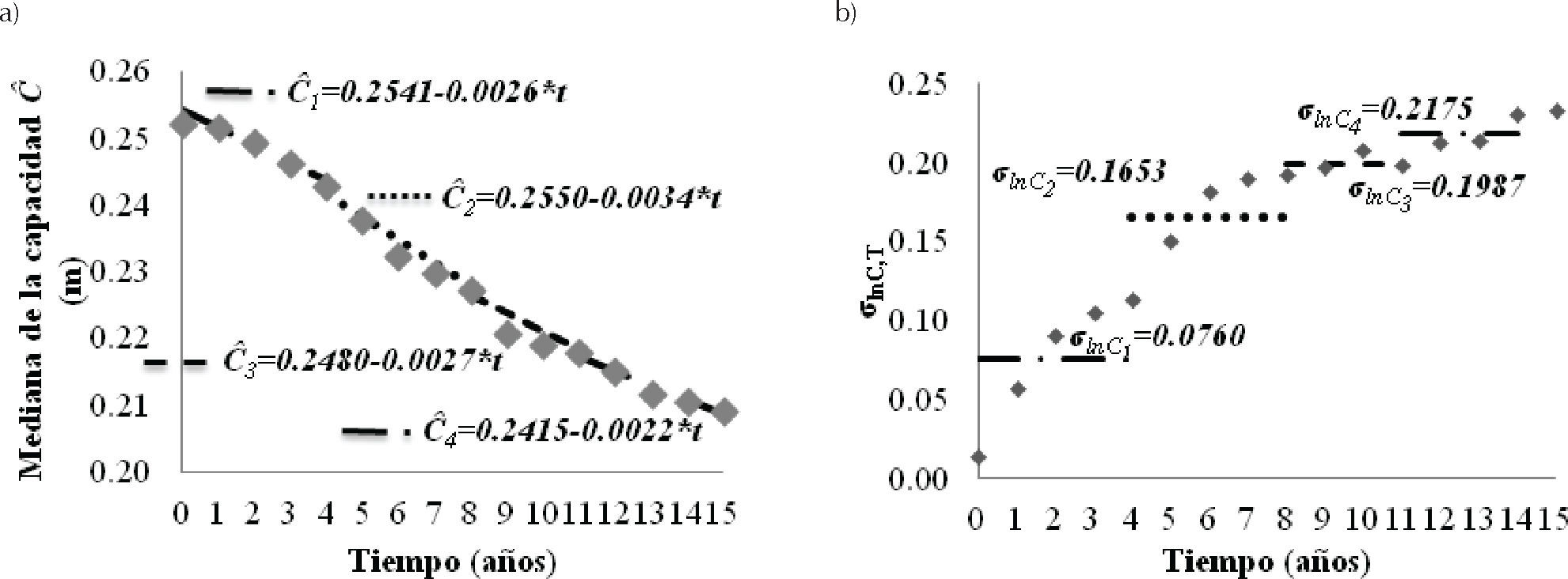
A partir de las 20 curvas de capacidad para cada intervalo de tiempo se obtienen las medianas de la capacidad, ĈT, y las desviaciones estándar del logaritmo natural, σlnC,T. A partir de la figura 4 se puede verificar que la capacidad presenta una distribución de probabilidades de tipo lognormal, tomando como ejemplo los intervalos de tiempo iguales a 0, 7 y 15 años.
En la figura 5a se presentan las medianas de la capacidad, ĈT, en términos del desplazamiento global de la plataforma (correspondiente al nodo 14 de la figura 2), para cuatro sub-intervalos (T) de tiempo. Los ajustes de las medianas de la capacidad se realizan como se expresa en la ecuación 13. En la figura 5b se muestran las desviaciones estándar del logaritmo natural de la capacidad estructural, σlnC,T. En la figura 5b se puede ver que los valores de las desviaciones estándar del logaritmo natural de la capacidad se incrementan a medida que transcurre el tiempo. Esto se debe a que mientras más grande sea el intervalo de tiempo, existe una probabilidad mayor de que la estructura esté sometida a más oleaje de operación y de tormenta, y con ello se acumula más daño estructural en las juntas críticas, por lo que se tiene una mayor variabilidad en la respuesta de la estructura.
Demanda estructural en el tiempo, para cierto nivel de altura máxima de olaCon el fin de evaluar la demanda estructural en el tiempo, se sometió la plataforma marina a una serie de análisis dinámicos “paso a paso” en el tiempo. Se utilizó un conjunto de oleajes simulados, asociados a diferentes alturas máximas de ola y las mismas simulaciones de oleaje que se emplearon para estimar el crecimiento de grietas y, con ello, las mismas reducciones de las capacidades de las juntas críticas que se emplearon para evaluar la capacidad, Ĉ, en el tiempo.
El valor de la mediana de la demanda estructural, dada una altura máxima de ola, se ajustó mediante la ecuación 19: Dˆ(t)=(3.75E−04+5.0E−08·t)·(hmáx)2.0; con la misma forma de ecuación se ajustó la desviación estándar del logaritmo natural de la demanda, dada una altura máxima de ola. Su expresión es como sigue:
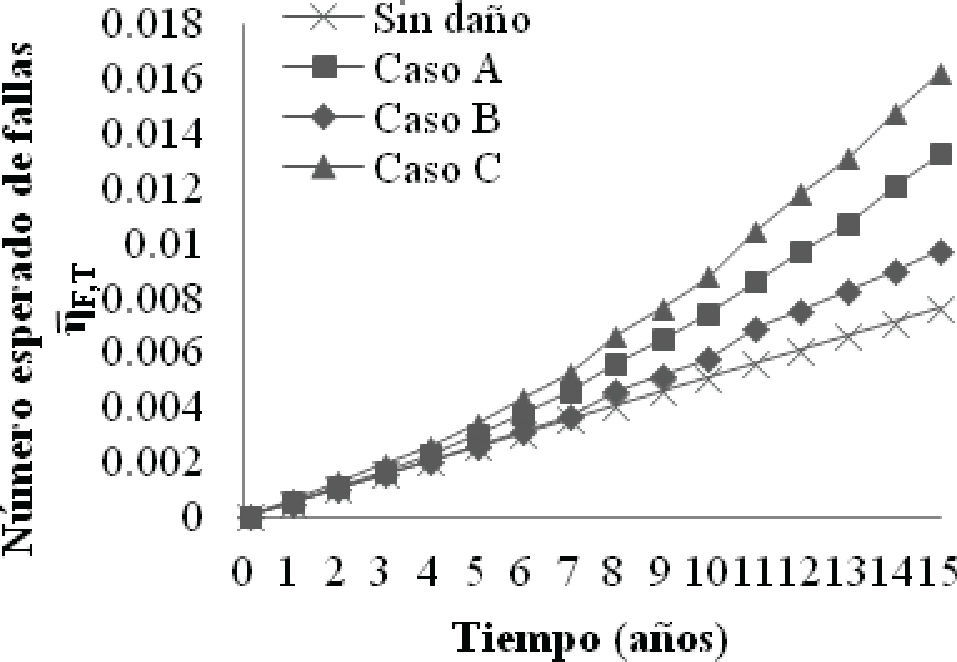
Factor de corrección y número esperado de fallas en el tiempoEn la figura 6 se muestra el número esperado de fallas en el tiempo (ecuaciones 14, 21, 25 y 12) correspondientes a los casos a, b, c y sin daño, respectivamente. Los valores de los parámetros k y r que se ajustan a la forma de la curva de peligro de oleaje mediante la expresión ν(hmáx)=k•(hmáx)−r, son iguales a k=5×103 y r=5. Estos corresponden a la región de la curva de peligro de oleaje donde se presenta la máxima altura de ola hmáx=23m asociada a un periodo de retorno de 1485 años, según la norma NRF-003-PEMEX-2000. Por otro lado, en este estudio se supone que σ2UD=σ2UC=0.15. La figura 6 indica que los valores son mayores para el caso c que para los casos a y b, y que esta diferencia crece a medida que el intervalo de tiempo es mayor.
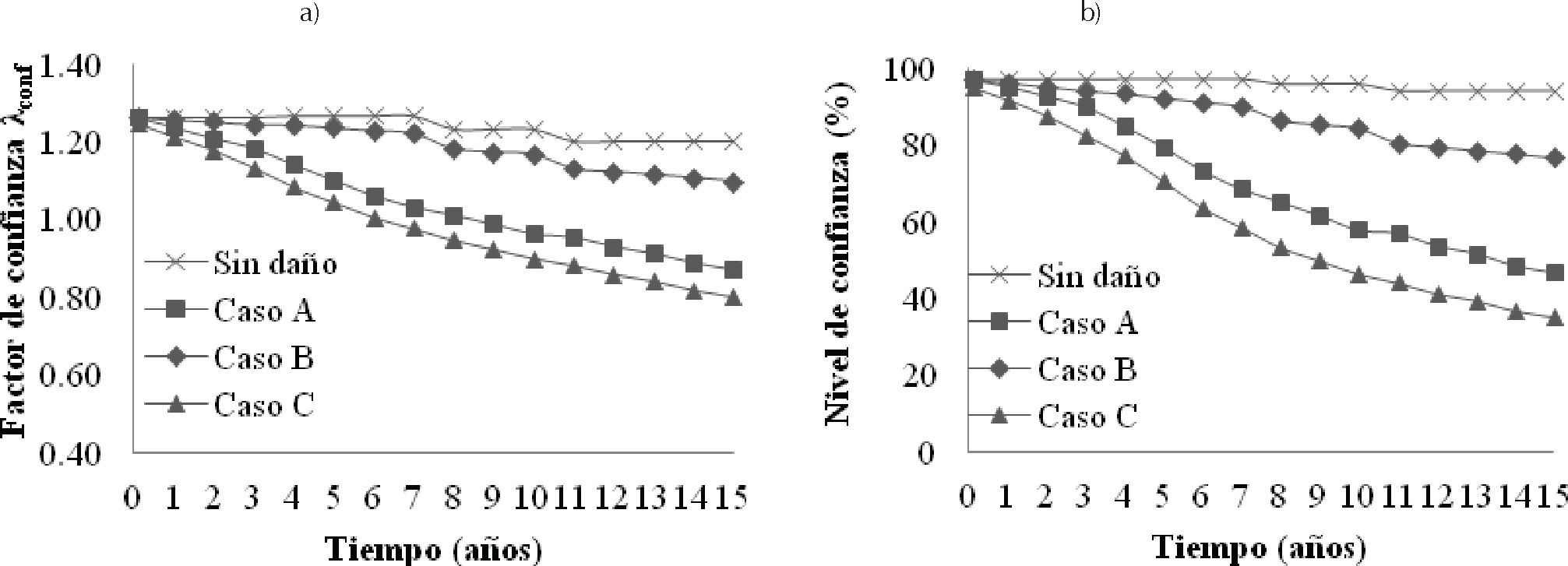
Factor de confianza y su correspondiente nivel de confianza en el tiempoLos factores de confianza al término de diferentes intervalos de tiempo para los casos a, b, c y sin considerar dano (ecuaciones 18, 24, 29 y 5, respectivamente) se muestran en la figura 7a. Los porcentajes de decremento del factor de confianza con respecto al caso en el que no se considera deterioro estructural, al final de un intervalo de 15 años, son del orden de 27%, 9% y 34% para los casos a, b y c, respectivamente. El nivel de confianza, Kx, asociado a los factores de confianza presentados anteriormente se presentan en la figura 7b. Se indica que el nivel de confianza para los casos de estudio disminuye a medida que el intervalo de tiempo aumenta. Para el caso en el que no se considera daño, el valor de Kr se mantiene prácticamente constante con valor de 94%; sin embargo, al término de 15 años el nivel de confianza disminuye de 94% a 77%, 47% y 36%, para los casos a, b y c, respectivamente.
ConclusionesEl criterio que se presenta tiene la ventaja de utilizar expresiones matemáticas cerradas que son útiles para evaluar la confiabilidad de diferentes tipos de estructuras (por ejemplo, edificios, puentes, torres de transmisión, estructuras fuera de la costa, etcétera) después de cierto intervalo de tiempo. El criterio puede adaptarse para considerar solicitaciones asociadas a diferentes tipos de fenómenos naturales (como sismo, viento, oleaje) y/o a diferentes estados límite (como servicio, colapso, etcétera).
Los resultados del ejemplo ilustrativo (plataforma marina con crecimiento de grietas causadas por fatiga) hacen ver que para evaluar el factor de confianza después de cierto intervalo de tiempo, se debe considerar tanto la degradación de la capacidad estructural como su influencia en la demanda estructural (para una intensidad dada).
Los resultados indican que es más significativo considerar la influencia del deterioro en la capacidad estructural que en la demanda estructural. Por ejemplo, el factor de confianza que se calcula después de 15 anos de construida la plataforma cuando se considera la degradación de la capacidad estructural es 27% menor con respecto al caso en que no se considera acumulación de daño estructural; sin embargo, dicho porcentaje es de solo 9% para el caso en que únicamente se considera el deterioro estructural en el tiempo de la demanda estructural. El valor de los porcentajes antes mencionados son relativamente altos en este ejemplo, debido a la simplificación que se hizo del modelo estructural (2D y poco redundante, figura 1) y, a la hipótesis que se hace relativa a que las grietas aparecen de manera simultánea en los nodos 1, 2, 3, 4 y 6. Es de esperar que los valores de los porcentajes antes mencionados sean menores para el caso en que se analice un modelo estructural tridimensional (3D, con un alto nivel de redundancia), y si además, las grietas aparecen de manera aleatoria y no simultáneamente.
El criterio aquí propuesto para evaluar la confiabilidad al final de cierto intervalo de tiempo es útil para tomar decisiones sobre el mantenimiento estructural basado en confiabilidad o en optimación de los costos esperados en el ciclo de vida de una estructura, así como para el diseño de estructuras en las que se establezcan requisitos de confiabilidad al final de cierto intervalo de tiempo.
Se agradece a De León D. y a Silva F.L. los valiosos comentarios al inicio de este estudio. También se agradecen las atinadas observaciones de los revisores anónimos. Este estudio se realizó con apoyo de la DGAPAUNAM dentro del proyecto PAPIIT IN107011. El segundo autor agradece a CONACYT la beca para realizar sus estudios de doctorado.
Sonia E. Ruiz-Gómez. Doctora en ingeniería (estructuras) por la UNAM. Es investigadora del Instituto de Ingeniería y profesora de la Facultad de Ingeniería, UNAM. Ha dirigido 81 tesis, incluyendo de licenciatura, maestría y doctorado. Pertenece al Sistema Nacional de Investigadores y a la Academia Mexicana de Ciencias. Fungió como presidenta de la Sociedad Mexicana de Ingeniería Sísmica. También fue coordinadora de investigación y desarrollo tecnológico, y presidenta de la Comisión de Especialidad de Ingeniería Civil de la Academia de Ingeniería. En 2011, el Colegio de Ingenieros Civiles de México le otorgó el premio “Nabor Carrillo Flores” a la Investigación.
Dante Tolentino-López. Es ingeniero civil por el Instituto Politécnico Nacional y maestro en ingeniería civil con especialidad en estructuras por la Universidad Nacional Autónoma de México (UNAM). Actualmente es candidato al grado de doctor. Realizó su investigación doctoral en el Instituto de Ingeniería, UNAM. Sus áreas de interés son confiabilidad estructural, deterioro estructural y optimización.
Marco A. Torres Pérez-Negrón. Es ingeniero civil por la FES-Acatlán, obtuvo la maestría y el doctorado en ingeniería con especialidad en estructuras por la UNAM. En 2008 recibió el premio a la mejor tesis doctoral del Instituto de Ingeniería con el tema: «Criterios costo/beneficio para la inspección y mantenimiento de plataformas marinas». Cuenta con alrededor de 25 publicaciones en congresos y revistas técnicas sobre temas de confiabilidad y análisis de riesgo estructural. Candidato a Investigador Nacional en el SNI-CONACyT. Actualmente labora en proyectos de evaluación de riesgos ante amenazas naturales en la Coordinación de Ingeniería Sismológica del Instituto de Ingeniería de la UNAM.