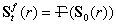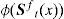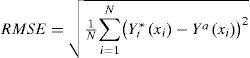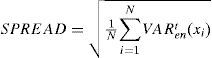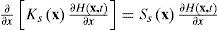Simulación de campos aleatorios espacio-temporales utilizando un filtro de Kalman modificado

Resumen

Un campo aleatorio espacio-temporal es un modelo probabilista utilizado para representar fenómenos que, además de variar espacialmente, cambian con el tiempo. Este tipo de modelo es de gran interés práctico en ingeniería porque permite representar fenómenos transitorios y generar configuraciones o imágenes de la distribución de un atributo o variable condicionado a observaciones temporales. En este artículo se propone una formulación alternativa de una variante del método EnKF (Ensemble Kalman Filter) (Evensen, 2007) basada en conceptos comunes en geoestadística y explica con detalle su desarrollo numérico. La utilidad del método se ilustra resolviendo un problema de flujo de agua transitorio en un medio poroso aleatorio completamente saturado.

Abstract

A spatiotemporal random field is a probabilistic model used to represent phenomena that, besides varying spatially, evolve in time. Such kind of model is of great interest in engineering for representing transient phenomena and generating configurations or images of the distribution of an atribute or variable conditional to temporal observations. In this paper an alternative formulation of a variant of the EnKF method (Ensemble Kalman Filter (Evensen, 2007) based on concepts commonly used in geostatistics is proposed and its numerical implementation is explained in detail. The benefits of the method are illustrated by solving a transient flow problem in a fully saturated random porous media.

Introducción

Un campo aleatorio espacio-temporal es un modelo probabilista utilizado para representar fenómenos que, además de variar espacialmente, cambian con el tiempo. Un modelo de este tipo presenta el reto de incorporar observaciones de un fenómeno temporal. Por lo tanto, las realizaciones del campo aleatorio tienen que ser compatibles con las observaciones en diferentes instantes.

Los campos aleatorios espacio-temporales se han empleado en las ciencias físicas para representar una gran variedad de fenómenos (Christakos, 1996) y muy recientemente en ingeniería geotécnica para modelar procesos transitorios de flujo de agua (Vázquez y Auvinet, 2012) y de hundimiento por consolidación en suelos (Rungbanaphan et al., 2012).

En la literatura científica se encuentran algunos formalismos útiles para simular este tipo de campos (Christakos, 2000). Se dispone de algunas metodologías establecidas para realizar esta tarea, pero tienen orientaciones específicas (Gómez et al., 1997). Una técnica general basada en la teoría del filtro de Kalman (Gelb, 1974) ha sido aceptada recientemente en diversas áreas del conocimiento (Evensen, 1994; 2003; Houtekamer, 1998). El método se denomina EnKF (Ensemble Kalman Filter) y ha sido descrito ampliamente por Evensen (2007).

El formalismo del método se basa en un esquema Bayesiano secuencial e implícito aplicado a modelos dinámicos representados por las ecuaciones estocásticas del problema físico. Una posible variante del método consiste en efectuar una anamorfosis Gaussiana (Rosenblat, 1952) de las densidades de probabilidad de los parámetros y de las variables de estado o respuesta del modelo dinámico. Esta variante, aunque identificada tiempo atrás por los autores, fue implementada por primera vez por Zhou et al. (2011) y Shöniger et al. (2012). En este artículo se propone una formulación alternativa basada en conceptos comunes en geoestadística (Chilès y Delfiner, 1999) y se explica con detalle su implementación numérica.

La utilidad del método se presenta a través de los resultados de un ejemplo ilustrativo en el cual se considera un fenómeno transitorio representado por la ecuación diferencial estocástica que describe el flujo de agua en un medio poroso completamente saturado en régimen transitorio. La segunda sección presenta con detalle el método EnKF modificado mientras que la tercera muestra su utilidad. Por último se presentan las conclusiones.

El método EnKF modificado

Esta sección presenta una descripción conceptual del método, así como los detalles para su desarrollo numérico. Se propone además una formulación alternativa basada en conceptos comunes en geoestadística. Primeramente se describe el método original EnKF.

Descripción del método original EnKF

El método original EnKF es un esquema que resuelve el problema estocástico inverso de un modelo dinámico. Cuando se usa para resolver el problema inverso, utiliza una representación del tipo campo aleatorio para los parámetros del modelo, la cual se integra en el tiempo utilizando las ecuaciones estocásticas para obtener una representación del mismo tipo en la respuesta. El esquema permite además incorporar observaciones de las variables de estado mediante un proceso de condicionamiento en el cual tanto los parámetros como la respuesta dinámica se actualizan en cada tiempo en que se dispone de observaciones (figura 1). De esta manera, es posible generar realizaciones de un campo aleatorio condicionadas por observaciones dinámicas.

Figura 1.

Diagrama conceptual del método EnKF

El esquema es del tipo bayesiano secuencial, en el cual las densidades de probabilidad a posteriori en el tiempo t = t₁ se convierten en las densidades de probabilidad a priori en el tiempo t = t₂. Sin embargo, la solución es implícita porque la función de máxima verosimilitud requerida para la aplicación del teorema de Bayes, no se obtiene explícitamente.

Algunas características básicas del método son las siguientes:

• 1)

  Si las densidades de probabilidad a priori de los parámetros son gaussianas y el modelo dinámico es lineal, entonces las densidades de probabilidad de la respuesta serán gaussianas y bastarán los primeros momentos de las variables para definir las densidades de probabilidad a posteriori con el proceso de condicionamiento.

• 2)

  Si el modelo dinámico no es lineal, las densidades de probabilidad de la respuesta no serán gaussianas aunque las densidades de probabilidad de los parámetros del modelo lo sean y el condicionamiento basado en primeros momentos será subóptimo.

• 3)

  Si alguna de las densidades a priori no es gaussiana, entonces se puede recurrir a una anamorfosis gaussiana y efectuar el condicionamiento con primeros momentos, pero nuevamente este será subóptimo.

La observación del punto 3, aunque fue identificada tiempo atrás por los autores, fue primero implementada por Zhou et al. (2011) y Shöniger et al. (2012). En este artículo se propone una formulación alternativa del formalismo basada en conceptos comunes en geoestadística (Chilès y Delfiner, 1999) y se detalla su desarrollo numérico.

Planteamiento del método EnKF modificado

El método propuesto requiere la simulación de un conjunto de realizaciones para representar la distribución a priori de los parámetros del modelo dinámico. Dicho conjunto y el modelo dinámico se utilizan para pronosticar las respuestas transitorias. Cada realización del campo aleatorio de parámetros y de variables de estado se actualiza secuencialmente, en cada instante en que se dispone de observaciones, por medio de un proceso de condicionamiento basado en una interpolación por cokriging simple (Deutsch y Journel, 1992; Wackernagel, 1995) en espacio y tiempo. Las covarianzas necesarias se obtienen estadísticamente a partir de los conjuntos de realizaciones. El método se realiza en el “espacio gaussiano” aplicando la anamorfosis gaussiana tanto a las densidades de probabilidad de los parámetros como a las de las variables de estado.

Al final de cada condicionamiento se obtiene un conjunto de realizaciones condicionadas por las observaciones de las variables de estado, es decir, para cada realización, tanto parámetros como variables de estado estarán condicionadas por las observaciones temporales. Los conjuntos de realizaciones condicionales obtenidos en cada instante se pueden utilizar para hacer predicciones de los valores esperados locales de los parámetros y variables de estado.

Formulación

Considerando una representación del tipo campo aleatorio para uno de los parámetros del modelo dinámico en el tiempo t = t₀, es decir ¿(x, t₀) con x en el dominio en estudio Ωy Ω en una línea (ℜ¹), área (ℜ²) o volumen (ℜ³). Considerando además una representación del mismo tipo para una de las variables de estado en el tiempo t = t₀, es decir, H(χ, t₀) con χ ∈Ω ⊂ℜ^p (p = 1, 2 o 3). Para cada realización r con r = 1, Nr de los campos aleatorios ¿ (x, t₀) y H(χ, t₀), se defne un vector de parámetros Y = {y_i,..., y_n}^T de dimensión n y un vector de estado H = {h_j,..., h_m}^T de dimensión m.

Sea S₀(r), un vector conjunto llamado vector de estado, tal que

donde T significa transpuesta

Las principales etapas del método se pueden formular como sigue:

a) Pronóstico (superíndice f):

Esta etapa involucra la transición de cada vector de estado S₀(r) del tiempo t = t₀ al tiempo t = t₁ utilizando la función de transferencia Ғ(·) (modelo dinámico) con el propósito de pronosticar el estado del sistema en el tiempo t = t₁, H(χ, t₁) mientras que los parámetros del mismo permanecen constantes, es decir, ¿ (x, t₀).

b) Transformación (φ(·)):

En esta etapa se aplica la anamorfosis gaussiana φ(·) (con media cero y varianza uno) a las funciones de distribución acumulativa locales del campo aleatorio ¿ (x, t₀) y del campo aleatorio H(χ, t₁). Las funciones de distribución acumulativa se obtienen estadísticamente utilizando el conjunto de realizaciones en cada caso. Luego se forma un vector de estado con los valores transformados al tiempo t = t₁ para cada realización, es decir: Ŝ^f_t(r).

c) Condicionamiento o actualización (superíndice u):

En esta etapa se considera que se cuenta con observaciones en las posiciones ¿(x_α, t₁) = y_α,t1 con α = 1,…,N_α y H(χ_β, t₁) = h_β,t1 con β = 1,…,N_β. Ambos tipos de observaciones se encuentran en el tiempo t = t₁. Se forma un vector conjunto Z_obs,t(r) de dimensión N_α + N_β con las observaciones transformadas por anamorfosis gaussiana (que en este caso se reduce a una simple estandarización) para cada realización. También se forma un vector V(r) de dimensión N_α + N_β con los valores transformados que contiene el vector Ŝ^f_t(r) en las posiciones de las observaciones.

El condicionamiento o actualización del vector de estado se realiza entonces:

donde Ŝ^u_t(r) = vector de estado actualizado en el tiempo t = t₁ y K_t = una matriz de orden (n+m) × (N_α + N_β) que contiene las contribuciones asignadas a cada una de las observaciones por la técnica de interpolación.

Esta matriz, en el contexto del método EnKF, se conoce como “Kalman gain”.

La ecuación 4 equivale, por tanto, a realizar una estimación con cokriging simple en un tiempo fjo t = t₁. Los coeficientes de la matriz K_t se obtienen de la solución del sistema de ecuaciones para el caso general de covarianzas no estacionarias (Deutsch y Journel, 1992; Wackernagel, 1995). Estas covarianzas se determinan utilizando las variables transformadas en la etapa anterior.

d) Transformación inversa (φ⁻¹(·)):

Al ser la anamorfosis gaussiana, de hecho una función monótonamente creciente, su inversa existe, luego es posible aplicar el inverso de la anamorfosis gaussiana φ⁻¹(·) a cada función de distribución acumulativa local de los campos aleatorios ¿(x, t₁) y H(χ, t₁) en el tiempo t = t₁. Las funciones de distribución locales se obtienen estadísticamente utilizando el conjunto de realizaciones. Observe que ahora los campos aleatorios son condicionales. Después se forma un vector de estado actualizado para cada realización, que contiene las estimaciones en el tiempo t = t₁, es decir Utu(r).

Algoritmo

La formulación propuesta en la sección anterior se puede aplicar siguiendo el algoritmo que se muestra en la figura 2. Sus principales etapas se describen en esta sección.

• Etapa 1. Para cada una de las realizaciones del campo aleatorio de parámetros en el tiempo t = t₀, es decir ¿(x, t₀), se resuelven las ecuaciones correspondientes del modelo dinámico Ғ(·) y se obtiene el campo aleatorio de variables de estado en el tiempo t = t₁, es decir, H(x, t₁). En esta etapa se puede contar además con observaciones en las posiciones ¿(x_α, t₁) = y_α,t1 con α = 1,…, N_α y H(c_β, t₁) = h_β,t1 con β = 1,…, N_β en el tiempo t = t₁.

• Etapa 2. Se obtienen las funciones de distribución acumulativa locales F_¿(y) y F_H(h) de los campos aleatorios de parámetros y de variables de estado, respectivamente, utilizando los conjuntos de realizaciones correspondientes. Después, se aplica la anamorfosis Gaussiana φ(·) en cada caso y se obtienen las funciones locales correspondientes. También, se obtienen los valores estandarizados de las observaciones. Con los valores transformados se crean, para cada una de las realizaciones r, los vectores conjuntos de estado Ŝ^f_t(r) y de observaciones Z_obs,t(r).

• Etapa 3. Se obtiene el vector de estados actualizado para cada realización Ŝ^u_t(r), utilizando la ecuación 4.

• Etapa 4. Se obtienen las funciones de distribución acumulativa locales de los campos aleatorios condicionales ¿(x, t₁) y H(χ, t₁), estadísticamente usando el conjunto de realizaciones y se aplica el inverso de la anamorfosis Gaussiana a cada una de ellas, es decir, φ^–1(F_¿(y)) y φ^–1 (F_h(h)). Los valores correspondientes definen nuevas realizaciones, pero ahora condicionadas por las observaciones en el tiempo t = t₁. Los valores transformados de los parámetros y variables de estado se pueden agrupar en un vector conjunto U^u_t(r). El condicionamiento se repetirá en cada tiempo en que se disponga de observaciones, pero ahora el campo aleatorio de parámetros a priori será el campo ¿(x, t₁).

Figura 2.

Algoritmo del método EnKF modificado

Análisis del error en la solución

Debido a que en el esquema EnKF las densidades de probabilidad locales se obtienen en forma estadística a partir del conjunto de realizaciones, el desempeño numérico del método dependerá del número de realizaciones del conjunto. Por lo tanto, conviene evaluar cuantitativamente el desempeño del método en función del número de realizaciones del campo aleatorio inicial de parámetros.

El error en la estimación del campo de referencia de log-permeabilidades se puede obtener para cada etapa del proceso de actualización o condicionamiento. Comúnmente se obtiene una medida del error de la estimación con respecto al campo “real” (suponiendo que se conoce) llamada RMSE (root mean square error) dado por:

donde:

N = total de parámetros en la región de interés;

ϒt*(xi) = valor estimado en la posición x_i en el tiempo t;

¿^a(x) = valor “real” del campo en la posición x_i.

También se emplea una medida de la incertidumbre en la estimación a través de la medida llamada SPREAD:

donde VAR^t_en(x) es la varianza de la estimación en el tiempo t del conjunto de realizaciones en la posición x_i.

Estas medidas pueden resultar inestables numéricamente en el caso de la estimación de campos no-gaussianos por lo que normalmente se complementan con otras medidas.

Implementación

La implementación del algoritmo descrito en la sección anterior se ha codificado en FORTRAN para LINUX y se ha ejecutado en el cluster “Tonatiuh” del Instituto de Ingeniería de la UNAM. El algoritmo se puede incorporar en forma eficiente a cualquier modelo dinámico de interés.

Aplicación

La metodología propuesta se aplica a un modelo dinámico unidimensional. Se analiza también la evolución de la incertidumbre en las simulaciones generadas.

Planteamiento

El modelo dinámico considerado es la ecuación diferencial que describe el flujo de agua en un medio poroso completamente saturado en régimen transitorio de una región de flujo unidimensional (Zhang, 2002):

sujeta a las condiciones iniciales y de frontera:

donde, A es la carga hidráulica inicial, B es la carga hidráulica preescrita en los segmentos de frontera ã de Dirichlet y Ω es la región de flujo unidimensional.

Los parámetros de este modelo son la conductividad hidráulica o permeabilidad saturada K_s(x) y el almacenamiento específico S_s(x). La variable de estado o respuesta del modelo es la carga hidráulica H(x, t). Cuando K_s(x) y/o S_s(x) se considera una función aleatoria, la ecuación 8 se convierte en una ecuación diferencial estocástica y H(x, t) en cada tiempo, será también un campo aleatorio. En este artículo se considera que la distribución de valores de K_S en la región de flujo se puede representar convenientemente con una distribución de probabilidad lognormal. Por lo tanto, su logaritmo natural, ¿ = ln(K_s) tendrá una distribución de probabilidad gaussiana (normal). Con esta transformación el campo aleatorio ¿(x) será gaussiano y quedará descrito completamente por su esperanza o valor medio µ_¿(x) = E{¿(x)}, varianza σϒ2(x)=VAR[ϒ(x)] y función de autocovarianza C_¿(X₁, X₂) = E{[¿(x₁) − µ_¿(x₁)] [¿(x₂) − µ_¿(x₂)]}.

Para resolver la ecuación 8 se dispone de varios métodos (Zhang, 2002). En este artículo se utiliza el método de Monte Carlo, es decir, se simulan múltiples realizaciones independientes del campo aleatorio ¿(x) y la ecuación 8 se resuelve para cada una de ellas con los valores deterministas de cada realización transformados como: k_s(x) = exp(µ_¿(x) + y(x)σ_¿(x)). La ecuación 8 se convierte entonces en una ecuación determinista. Los parámetros estadísticos del campo aleatorio H(x, t) en un tiempo específico, así como las covarianzas cruzadas entre la log-conductividad y la carga hidráulica se obtienen en forma estadística a través de los conjuntos de realizaciones.

Para generar una distribución de permeabilidades se simula un campo aleatorio gaussiano ¿(x) = ln(K_s(x)) con media cero, varianza unitaria y función de autocovarianza exponencial con distancia de correlación a = 150 m. Se acepta que ambos parámetros son constantes en todo el dominio y que la función de autocovarainza depende de la separación entre variables aleatorias, es decir, que el campo aleatorio es estacionario en el sentido amplio (Zhang, 2002). K_s(x) tiene unidades de m/día. Se simulan 10 realizaciones de este campo aleatorio y se elige una de ellas. Esta realización se denomina campo de referencia o “estado de la naturaleza”. Los descriptores estadísticos de esta realización se muestran en la figura 3. Se supone además que se dispone de observaciones de este campo en las posiciones indicadas en la misma figura.

Figura 3.

Campo de referencia de la logpermeabilidad. Los valores de este campo que se suponen conocidos se indican con las cruces

Utilizando el campo de referencia y los valores numéricos de las condiciones iniciales y de frontera indicadas en la figura 4 se resuelven las ecuaciones de flujo transitorio mediante elementos finitos (Smith y Griffiths, 2004). De la solución de las ecuaciones se obtiene una historia de 50 cargas hidráulicas a cada t = 0.001 días en cada nodo de la malla. En el ejemplo se supone que únicamente se conocen las observaciones piezométricas a cada t = 0.003 días en las posiciones mostradas en la figura 5. En otras palabras, se cuenta con 17 mediciones en cada una de las 12 posiciones mostradas en la figura 5. En el análisis se considera además que el coeficiente de almacenamiento es determinista e igual a 0.001.

Figura 4.

Condiciones iniciales y de frontera consideradas en el análisis de flujo transitorio

Figura 5.

Distribución de la carga hidráulica transitoria. Los cuadros y los triángulos indican los valores observados

De las 12 historias piezométricas, cada una compuesta por 17 observaciones transitorias, se forman dos grupos. Uno de ellos incluye 8 historias y el otro 12. Las lecturas de los piezómetros del grupo de 8 historias se indican por los cuadros en la figura 5. Las lecturas piezométricas del grupo de 12 historias se indican por los cuadros y los triángulos en la misma figura. El objetivo es generar realizaciones de la permeabilidad y de la carga hidráulica, condicionadas por las observaciones disponibles de la permeabilidad (figura 3) y por la historia de cargas hidráulicas de cada grupo por separado utilizando el método EnKF modificado.

Campo aleatorio inicial de parámetros

El campo aleatorio inicial de parámetros representa una primera aproximación al campo “real”. Sus parámetros descriptivos no siempre se podrán determinar en forma estadística a partir de las observaciones. En ocasiones estos se definirán con un alto contenido subjetivo. El conocimiento a priori incorporado en la representación del campo aleatorio de la log-permeabilidad se muestra en la tabla 1. El valor esperado E{¿(x)} y varianza Var[¿(x)] del campo a priori se estimaron estadísticamente utilizando las observaciones indicadas en la figura 3. Se eligió arbitrariamente un modelo de autocovarianza exponencial y se asignó un valor tentativo de 200 m a la distancia de correlación. Observe que este conocimiento no es del todo subjetivo, también se basa en la evidencia de las observaciones.

Tabla 1.

Parámetros descriptivos del campo aleatorio inicial de log-permeabilidades

E{Y(x)} [ln(m/día)]	Var[Y(x)] [(ln(m/día))^2]	Distancia de correlación	Función de autocovarianza	Número de realizaciones
0.287	1.43	200 m	Exponencial	200, 400, 800

Estabilidad de la solución

La evolución del error en la estimación de las log-permeabilidades se muestra en la figura 6 para 200, 400 y 800 realizaciones del campo aleatorio inicial de parámetros (tabla 1). El número de historias piezométricas utilizadas en el proceso de condicionamiento en todos los casos es 8 historias. Se puede observar que conforme aumenta el número de realizaciones ambas medidas tienden a estabilizarse con el tiempo indicando la convergencia del método hacia una solución consistente. Se debe destacar que, independientemente del número de realizaciones del conjunto inicial, la contribución del primer conjunto de registros piezométricos en la reducción del error es muy significativa. Además, el RMSE presenta ciertas fuctuaciones temporales con una tendencia no necesariamente decreciente. El SPREAD, por el contrario, disminuye sistemáticamente con el tiempo.

Figura 6.

Evolución del error en la estimación del campo de referencia de log-permeabilidades en las diferentes etapas de condicionamiento utilizando 8 historias piezométricas, a) evolución de la medida RMSE en función del número de realizaciones del campo aleatorio inicial, b) evolución de la medida SPREAD en función del número de realizaciones del campo aleatorio inicial

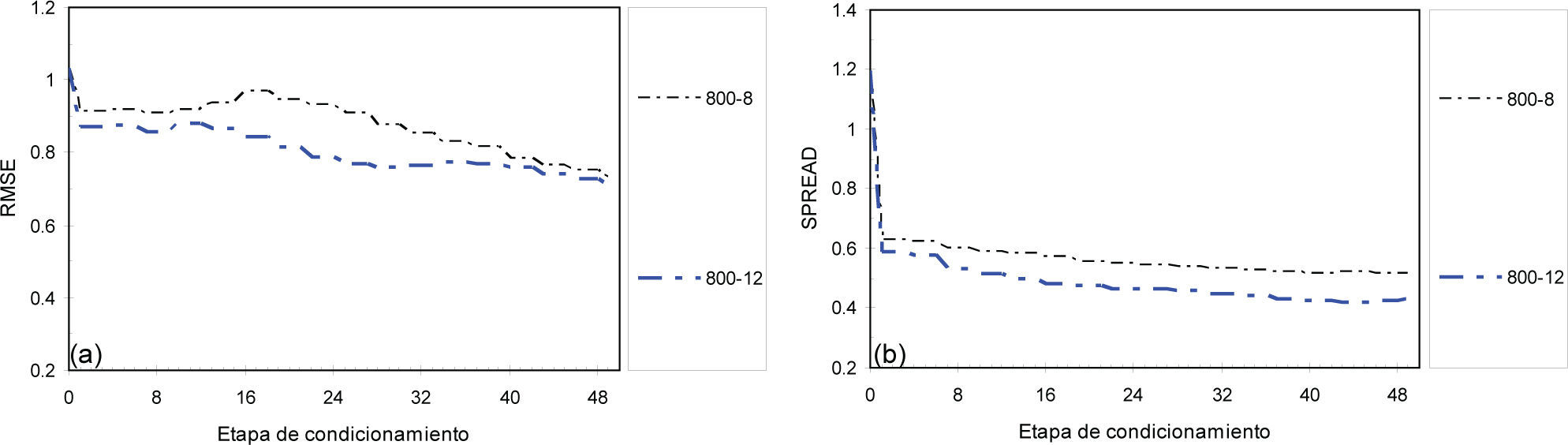
En la figura 7 se presentan los resultados de ambas medidas cuando el condicionamiento se realizó utilizando 8 y 12 historias piezométricas con un conjunto inicial compuesto por 800 realizaciones. Se puede apreciar que el error disminuye con más rapidez en el tiempo, cuando el número de historias piezométricas consideradas en el condicionamiento aumenta. El primer conjunto de observaciones del registro es trascendental en la reducción del error.

Figura 7.

Evolución del error en la estimación del campo de referencia de log-permeabilidades en las diferentes etapas de condicionamiento utilizando 8 y 12 historias piezométricas con 800 realizaciones del campo aleatorio inicial de parámetros, a) evolución de la medida RMSE, b) evolución de la medida SPREAD

Simulación condicional del campo aleatorio de conductividad hidráulica

En esta sección se muestran los resultados del condicionamiento del campo aleatorio de permeabilidades por las 8 historias piezométricas. Los resultados corresponden al valor esperado del campo en diferentes etapas del condicionamiento. En la etapa 1, es decir al tiempo t = 0.001 días se toman en cuenta, además, las 7 observaciones disponibles de la permeabilidad. En las etapas subsecuentes solo se toman en cuenta las observaciones piezométricas.

En la figura 8 se muestra el valor esperado de la permeabilidad para las etapas de condicionamiento 1, 10 y 49 realizadas con 8 historias piezométricas. En las posiciones donde se cuenta con observaciones directas de la permeabilidad, el valor esperado es el valor observado. En las posiciones no observadas, conforme aumenta el número de registros piezométricos transitorios considerados para el condicionamiento, el valor esperado tiende en general al valor del campo de referencia. Sin embargo, como era de esperarse, la estimación “suaviza” el perfil y no refleja totalmente los valores extremos del campo de referencia.

Figura 8.

Valor esperado de la log-permeabilidad en diferentes etapas del proceso de condicionamiento utilizando 8 historias piezométricas. La línea sólida señala el campo de referencia, a) valor esperado en la etapa 1, b) valor esperado en la etapa 10, c) valor esperado en la etapa 49

La desviación estándar de la permeabilidad para las etapas de condicionamiento mostradas en la figura 8 se muestra en la figura 9. Esta se define localmente utilizando el conjunto de realizaciones condicionales. Los resultados presentados en la figura 9a corresponden al condicionamiento del campo utilizando 8 historias piezométricas, mientras que los resultados de la figura 9b corresponden al condicionamiento efectuado con las 12 historias piezométricas. La incertidumbre en ambos casos es nula en las posiciones donde se cuenta con observaciones directas. En las posiciones no observadas, en general, la incertidumbre tiende a disminuir, pero localmente esta puede aumentar. La evolución de la incertidumbre en la estimación de la permeabilidad por lo tanto, no necesariamente es decreciente.

Figura 9.

Distribución de la desviación estándar en diferentes etapas de condicionamiento, a) utilizando 8 historias piezométricas en el condicionamiento, b) utilizando 12 historias piezométricas en el condicionamiento

Simulación condicional del campo aleatorio de carga hidráulica

En la figura 10 se muestra el valor esperado de la carga hidráulica para las etapas de condicionamiento 1, 10 y 49 realizadas con 8 historias piezométricas. Se puede observar que en las posiciones el valor esperado es, en efecto, el valor observado. Esta condición se cumple además en las fronteras donde la carga hidráulica es prescrita. La aproximación al campo de referencia en los distintos tiempos es bastante satisfactoria aun en las posiciones en donde no se cuenta con mediciones. Por lo tanto, el condicionamiento del campo aleatorio produce los resultados esperados en forma satisfactoria.

Figura 10.

Valor esperado de la carga hidráulica en distintas etapas de condicionamiento utilizando 8 historias piezométricas, a) valor esperado en la etapa 1, b) valor esperado en la etapa 10, c) valor esperado en la etapa 49

La desviación estándar de la carga hidráulica para las etapas de condicionamiento mostradas en la figura 10 se muestra en la figura 11a con 8 historias piezométricas y en la figura 11b con 12 historias piezométricas. Esta se define a partir del conjunto de realizaciones condicionales. La incertidumbre en ambos casos es nula en las posiciones donde se cuenta con observaciones y en las fronteras donde se impuso un valor determinista. En las posiciones no observadas, la evolución de la incertidumbre no es clara en ninguno de los dos casos. Sin embargo, es notoriamente inferior cuando el número de historias piezométricas consideradas en el condicionamiento es mayor.

Figura 11.

Distribución de la desviación estándar en diferentes etapas de condicionamiento, a) con 8 historias piezométricas en el condicionamiento, b) con 12 historias piezométricas en el condicionamiento

Conclusiones

En este trabajo se propone un método que permite simular campos aleatorios espacio-temporales. El método permite generar configuraciones o imágenes de la distribución de un atributo condicionadas a observaciones temporales. El método requiere tres elementos: 1) una representación a priori del campo aleatorio para los parámetros de un modelo dinámico, 2) las ecuaciones estocásticas del modelo dinámico y 3) observaciones de las variables de estado en diferentes tiempos.

El campo aleatorio inicial de parámetros se utiliza con las ecuaciones del modelo dinámico para obtener una representación del mismo tipo en las variables de estado. El método permite incorporar observaciones de las variables de estado a través de un proceso de condicionamiento en el cual tanto los parámetros como la respuesta dinámica se actualizan en cada tiempo en que se dispone de observaciones. De esta manera, es posible generar realizaciones de un campo aleatorio condicionadas por observaciones dinámicas.

La utilidad del método se ilustra resolviendo un problema de flujo de agua transitorio unidimensional en un medio poroso aleatorio completamente saturado. Se generaron realizaciones de la permeabilidad y carga hidráulica condicionadas por observaciones de la permeabilidad y además por observaciones transitorias de la carga hidráulica. Ambos tipos de observaciones se generaron sintéticamente utilizando un campo de permeabilidades de referencia.

El desempeño numérico del método se puede ver afectado por el número de realizaciones en la representación del campo aleatorio a priori de parámetros. Por lo tanto, es necesario revisar la convergencia del método después de cada etapa de condicionamiento y verificar que el número de realizaciones utilizado produzca valores estables de ciertas medidas de error. El número de realizaciones del conjunto inicial requerido se debe determinar en cada caso particular.

En el ejemplo presentado en este artículo el campo aleatorio inicial representativo de la variabilidad espacial de los parámetros del modelo dinámico fue del tipo gaussiano.

En diversas situaciones de la práctica un campo aleatorio de este tipo puede no ser representativo de la variabilidad espacial. La utilidad del método en presencia de una dependencia espacial no gaussiana se explorará en trabajos subsecuentes.

Agradecimientos

Este trabajo fue financiado parcialmente con una beca otorgada al primer autor por el Instituto de Ingeniería de la UNAM. Los autores agradecen profundamente los comentarios y sugerencias de dos revisores anónimos, además de las observaciones del Dr. Ernesto Heredia Zavoni. Todas estas contribuciones brindaron mayor claridad al contenido de este artículo.