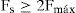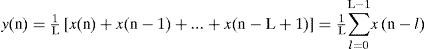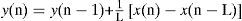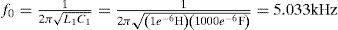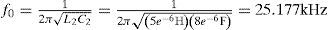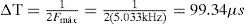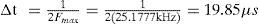En este artículo se desarrolla una nueva extensión del modelo dependiente de la frecuencia (FD-Line) para simular redes eléctricas en paralelo y con múltiples pasos de tiempo. El objetivo principal de dicho modelo es lograr simulaciones más eficientes de transitorios electromagnéticos, producidos principalmente por operaciones de maniobra y fallas, sin sacrificar su precisión. Para lograr esto, el modelo de línea FD-Line se utiliza como enlace entre dos subredes eléctricas funcionando con diferentes tasas de muestreo. Adicionalmente, el des acoplamiento en tiempo del modelo FD-Line permite dividir redes eléctricas y lograr su ejecución en paralelo.
This paper develops a new extension of the frequency-dependent line model (FD-Line) for simulating power networks in parallel with multiple time steps. The main goal of this model is to achieve more efficient simulations of electromagnetic transients, produced mainly by switching operations and faults, without sacrificing its accuracy. To achieve this, the FD-Line model serves as interface between two subnetworks running at different sampling rates. Additionally, the decoupling-in-time of the FD-Line model allows splitting power networks and then, its execution in parallel.
Desde hace varias décadas, los programas tipo EMTP1 (Electromagnetic Transient Program) se han consolidado como la herramienta más usada y aceptada a nivel mundial para simular transitorios electromagnéticos en sistemas eléctricos de potencia (Dommel, 1960). Una característica importante de estos programas es que utilizan un método de integración de paso único (por ejemplo, las reglas de integración trapezoidal y Euler) para resolver las ecuaciones diferenciales de los componentes del sistema en el dominio del tiempo (Semlyen, 1993). Sin embargo, la limitante del método es el excesivo tiempo de cómputo cuando se seleccionan pasos de integración muy pequeños para simular redes eléctricas de gran tamaño. Por lo tanto, para superar esta limitante, varios autores han propuesto la necesidad de nuevos tipos de programas EMTP capaces de llevar a cabo simulaciones con múltiples pasos de tiempo en redes eléctricas (Moreira et al., 2002, 2003 y 2005 y Naredo et al., 2009).
En este artículo se reporta una nueva extensión del modelo de línea de transmisión dependiente de la frecuencia (FD-Line), propuesto por J. Martí en 1982, para ejecutar simulaciones multi-resolución de redes eléctricas en Simulink (Marti et al., 1982; Iracheta, 2010; Iracheta y Ramos, 2010). La función principal de este modelo de línea es utilizarlo como un medio de enlace entre dos subredes, las cuales, son simuladas con diferentes pasos de integración y de forma independiente en programas tipo EMTP. El desacoplamiento natural en tiempo en este modelo permite que ambas subredes puedan ejecutarse en paralelo. Los cambios en la tasa de muestreo de las variables de enlace se manejan, dentro del modelo FD-Line, mediante un algoritmo multi-resolución.
Dicho algoritmo se plantea conforme a la teoría multi-resolución de procesamiento digital de señales con el fin de evitar los errores de aliasing (o “pérdida de información”) e imagen (Proakis, 2007). Ese modelo de línea se conoce como el modelo FD-Line multiresolución y su implementación práctica requiere herramientas de cosimulación disponibles en el ambiente Simulink.
Por último, para validar el modelo propuesto se presenta un caso de estudio de una red eléctrica con dos dinámicas distintas. El proceso de validación consiste en comparar los resultados de simulación multi-resolución de una red eléctrica en Simulink con simulaciones de un paso de integración en el EMTP.
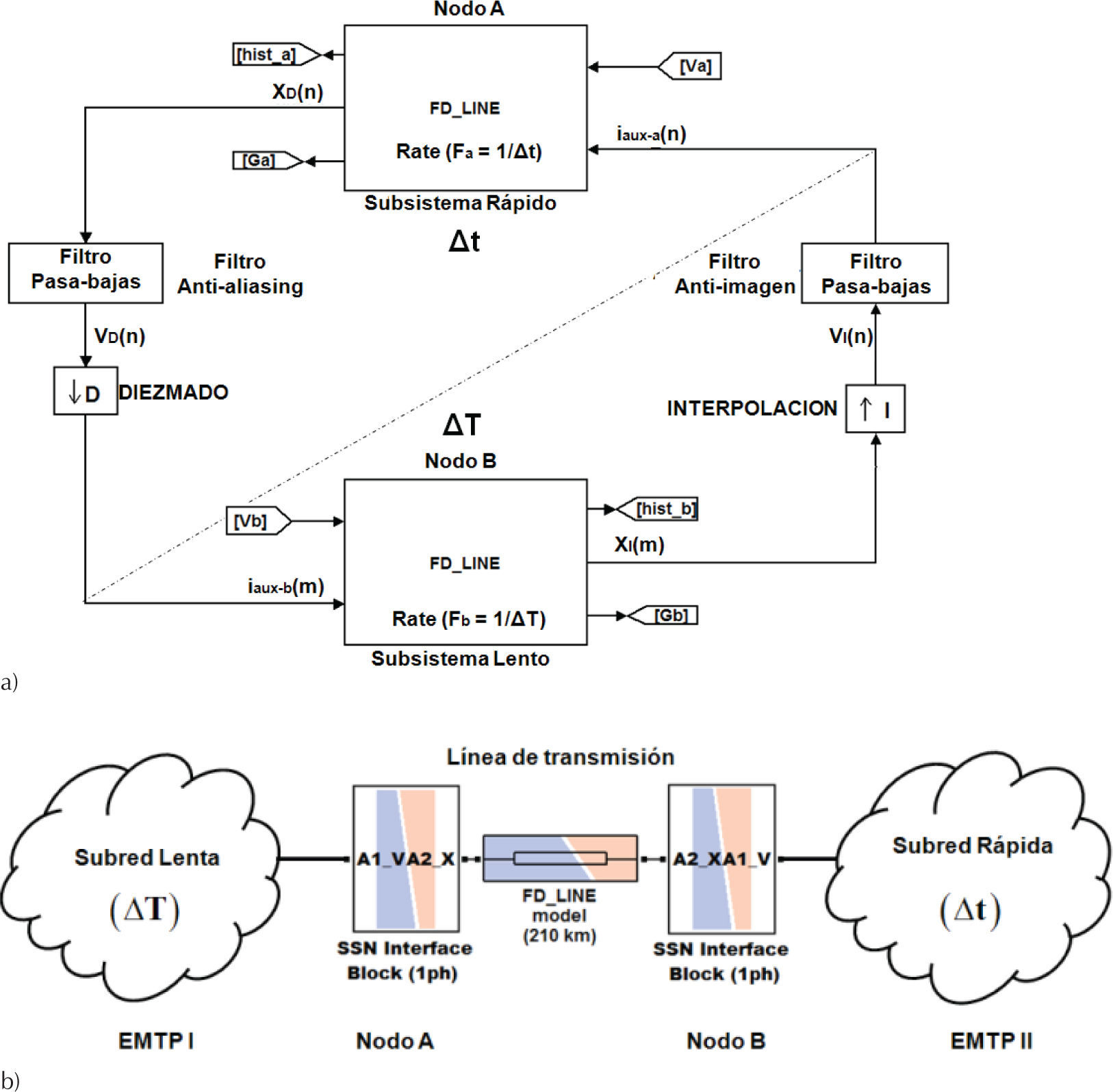
Modelo FD-Line multi-resoluciónLa figura 1 ilustra el modelo de línea de transmisión dependiente de la frecuencia que permite realizar simulaciones multi-resolución de transitorios electromagnéticos en sistemas eléctricos de potencia. La línea de transmisión está formada por dos bloques, cada uno representa un extremo de la línea, A y B. Cada bloque es un circuito equivalente Norton con paso de integración diferente.
Las variables de interface entre los bloques que integran el modelo de línea multi-resolución ocurren únicamente a través de las corrientes auxiliares (im,aux). Esas corrientes están en cantidades modales y deben pasarse a través de procesos de diezmado e interpolación con la finalidad de evaluar correctamente la contribución correcta entre bloques con diferente tasa de muestreo.
La aplicación práctica del modelo FD-Line multiresolución se ilustra en la figura 1b. Básicamente, este modelo de línea se utiliza como un medio natural para dividir una red eléctrica en dos subredes resultantes. Estas subredes se simulan de forma independiente y con diferentes pasos de integración (Δt y ΔT) en programas tipo EMTP.
Para la selección de los pasos integración en el modelo FD-Line multi-resolución se requiere conocer el ancho de banda máximo (Fmáx) alcanzado por la dinámica interna de cada subred. Luego, con base en el teorema de Nyquist (Proakis, 2007), se calculan los pasos de tiempo como sigue:
donde Fs es la frecuencia de muestreo y está dada por
Un requerimiento muy importante para la operación correcta del modelo FD-Line multi-resolución es que los pasos de integración Δt y ΔT deben ser, cuando menos, 2 y 3 veces más pequeños que el tiempo de viaje de la línea de transmisión para aplicaciones de procesamiento en serie y paralelo, respectivamente. Además, por conveniencia el paso de integración del subsistema lento debe ser un múltiplo entero del subsistema rápido. El cambio en la tasa de muestreo de las variables de enlace se maneja con los procesos de diezmado e interpolación que se describen a continuación.
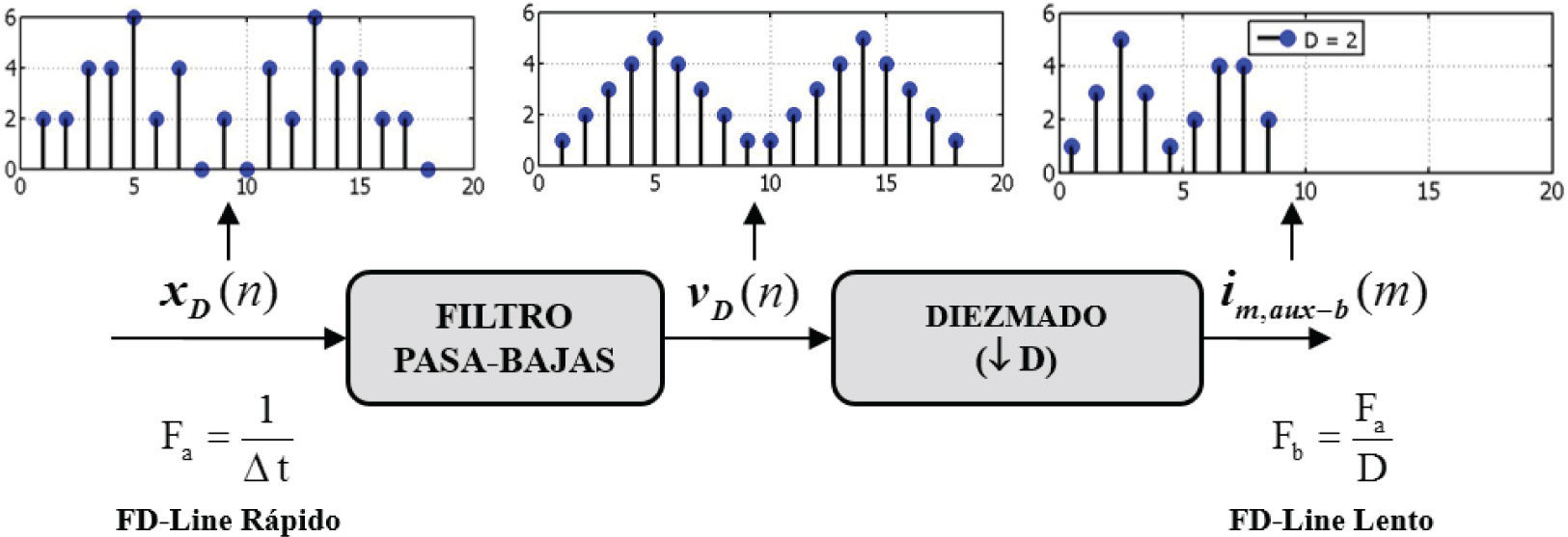
Proceso de diezmadoEn la figura 2 se ilustra el proceso de diezmado utilizado en el modelo FD-Line multi-resolución para reducir la tasa de muestreo por un factor entero D. La secuencia xD(n) que sale del subsistema rápido, con una tasa de muestreo Fa = 1/Δt, se pasa a través de un filtro pasa-bajas para obtener la secuencia vD(n). El filtro pasa-bajas elimina las altas frecuencias en la secuencia de entrada con el fin de prevenir el fenómeno de aliasing (Proakis, 2007). Luego, la secuencia vD(n) es diezmada por un factor entero D y se obtiene la secuencia im,aux- b(m) que alimenta al subsistema lento.
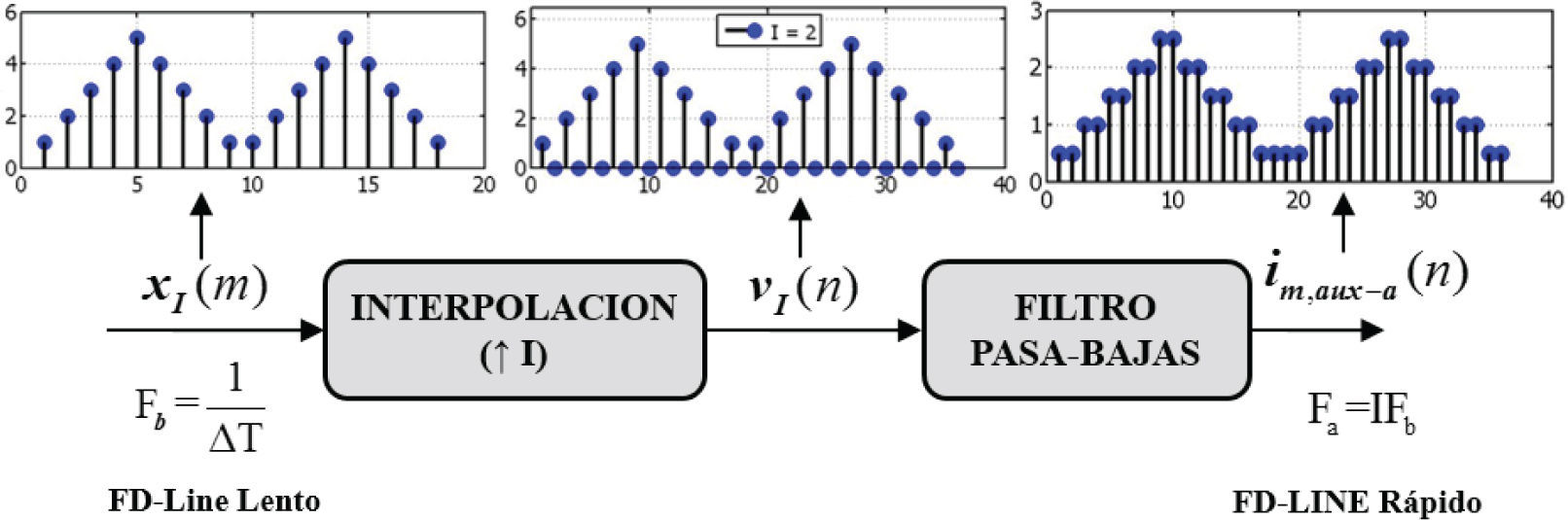
Proceso de interpolaciónEn la figura 3 se ilustra el proceso de interpolación usado en el modelo FD-Line multi-resolución para incrementar la tasa de muestreo por un factor entero I. Aquí, la secuencia xI(m) procesada en el subsistema lento opera con una tasa de muestreo I veces más baja que el subsistema rápido. Por lo tanto, para igualar la tasa de muestreo del subsistema rápido, la secuencia XI(m) debe sobremuestrearse con un bloque interpolador que inserta I – 1 muestras con valores de ceros entre las muestras consecutivas de la entrada. Del sobremuestreo se obtiene la secuencia vI(n). Luego, para obtener la secuencia de salida iaux-a(n), la secuencia vI(n) se pasa a través de un filtro pasa-bajas. El proceso de filtrado tiene la función de eliminar las réplicas en alta frecuencia de VI(n) que causa el bloque interpolador. Con esto se previenen los posibles errores de imagen del modelo FD-Line multi-resolución en el dominio del tiempo (Proakis, 2007).
La descripción general del modelo FD-Line multiresolución muestra por qué se eliminan las altas frecuencias con los filtros pasa-bajas. Asimismo, se utiliza un solo canal para intercambiar las muestras entre los subsistemas rápido y lento.
Filtros pasa-bajas usados en el modelo FD-Line multi-resoluciónSe proponen los filtros de media móvil (MA) y de múltiple paso para llevar a cabo los procesos de interpolación y diezmado en el modelo FD-Line multi-resolución. Dichos filtros se prefieren en muchas aplicaciones prácticas porque su uso y comprensión son muy sencillos. La ecuación en diferencias que describe al filtro MA más simple está dada por:
donde L es la longitud del filtro o el número de puntos de su respuesta al impulso, x(n) es la secuencia de entrada y y(n) es la secuencia de salida. La característica principal que tiene el filtro pasa-bajas, descrito en la ecuación (2), es ofrecer una solución óptima para atenuar las discontinuidades.
Cuando la señal de salida y(n) se vuelve a pasar como señal de entrada x(n) dos o más veces sobre el mismo filtro (2) se tiene como resultado un filtro MA de múltiple paso. Estos tipos de filtros tienen como principal ventaja la característica de que al incrementarse el número de pasos se obtiene una mejor realización en frecuencia. Sin embargo, con el mayor número de pasos también se incrementa su carga computacional.
La implementación práctica de los filtros MA simples y de múltiple paso se puede hacer más eficiente con la siguiente ecuación recursiva:
Esta ecuación solo requiere dos sumas. Sin embargo, es necesario contar con una memoria de L+l ubicaciones para mantener L muestras [x(n−2), x(n−2),..., x(n−L−l)].
Protocolos de comunicación usados en el modelo FD-Line multi-resoluciónEn esta sección se describen los protocolos de comunicación serie y paralelo que pueden utilizarse en el modelo FD-Line multi-resolución para calcular y enlazar las variables interface (im,aux). Adicionalmente, se explica el tratamiento de las variables de interface de acuerdo con los fundamentos de sistemas multi-resolución (Proakis, 2007):
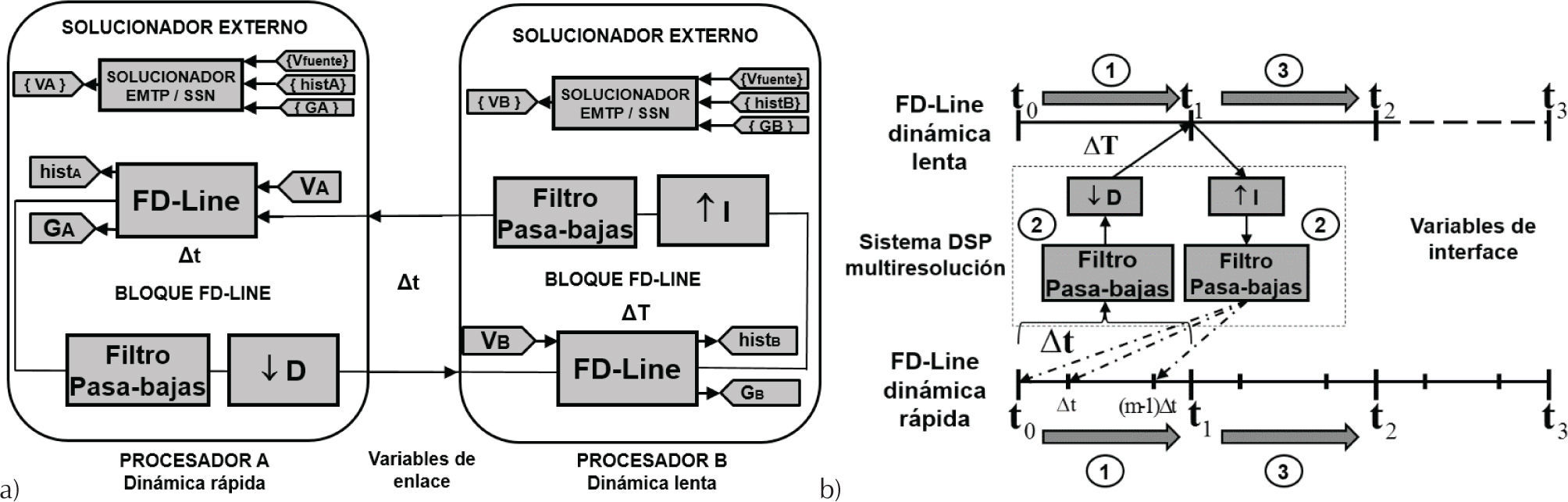
Protocolo serieEn la figura 4a se muestra el protocolo de comunicación serie del modelo FD-Line para su implementación en un procesador. En dicha figura se observa que los dos bloques principales que conforman el modelo FD-Line multi-resolución son interdependientes uno del otro. Esto significa que cuando un bloque se está ejecutando el otro se mantiene en reposo.
La figura 4b muestra el diagrama de flujo con la solución algorítmica del modelo FD-Line multi-resolución. Se puede observar en esta figura que las dinámicas lenta y rápida de los extremos finales de la línea se calculan por separado. Adicionalmente, dentro de estos bloques, las corrientes de historia se actualizan a partir de los voltajes nodales en cada paso de tiempo. En la figura 4b también se puede observar que los bloques lento y rápido procesan el mismo número de operaciones cuando se considera un solo paso de integración. Sin embargo, el paso de integración grande es un múltiplo entero del paso de integración pequeño, por lo tanto, el número de operaciones en el bloque FD-Line rápido se incrementa por el factor D o I para igualar el tiempo de simulación del bloque FD-Line lento. Adicio-nalmente, se utiliza un algoritmo DSP multi-resolución en el modelo de línea para tratar el cambio en la tasa de muestreo de las variables de interface.
La figura 4c muestra la secuencia en tiempo del protocolo serie y los puntos donde se intercambian las variables de enlace. Los pasos de esta secuencia se explican a continuación:
| Paso 1: | El bloque FD-Line lento se ejecuta de t0 a t1. |
| Paso 2: | El bloque FD-Line rápido se ejecuta de t0 a t1. |
| Paso 3: | Las muestras de las corrientes auxiliares (im,aux) actualizadas en el paso 1 pasan por un proceso de interpolación. Las muestras que salen del proceso se transfieren al bloque FD-Line rápido en cada paso de tiempo (Δt). Sin embargo, el paso de tiempo (ΔT) es el punto de referencia para sincronizar las variables de interface en ambos bloques FD-Line. |
| Paso 4: | Las muestras de las corrientes auxiliares (im,aux) actualizadas en el paso 2 se pasan por un proceso de diezmado. Las muestras que salen de este proceso se transfieren al bloque FD-Line lento primero en t1 y luego, en cada múltiplo de ΔT. |
| Paso 5: | El bloque FD-Line de dinámica lenta se ejecuta de t1 a t2 después de la resincronización. Este paso se repite hasta el final de la simulación. |
| Paso 6: | El bloque FD-Line de dinámica rápida se ejecuta de t1 a t2 después de la resincronización. Este paso se repite hasta el final de la simulación. |
La figura 5a muestra el protocolo de comunicación paralelo del modelo FD-Line multi-resolución para su implementación en un ordenador de dos procesadores. La característica principal de este protocolo es que ambos bloques de línea se ejecutan simultáneamente en todo el tiempo de simulación. La actualización y transferencia de variables de enlace en el modelo de línea ocurre en cada paso de integración Δt, mientras tanto, su sincronización ocurre en cada múltiplo entero del paso de integración ΔT. En la figura 5a se observa también un mismo número de operaciones por paso de integración en cada procesador.
La secuencia en tiempo del protocolo de comunicación paralelo se muestra en la figura 5b. Los pasos de esta secuencia se explican a continuación:
| Paso 1: | La actualización de las variables de enlace, en ambos bloques del modelo de línea, es el punto de partida para el comienzo de la simulación en t0. Esta actualización permite la ejecución del modelo de línea de t0 a t1. |
| Paso 2: | La sincronización de las variables de enlace en el modelo FD-Line multi-resolución ocurre por primera vez en t1. Luego, este proceso se repite en cada múltiplo entero del paso de integración ΔT. |
| Paso 3: | Los dos bloques que forman parte del modelo de línea se ejecutan simultáneamente e independientemente de t1 a t2. Luego, se repiten los pasos 2 y 3 hasta el final de la simulación. |
La solución algorítmica del modelo FD-Line multi-resolución fue realizada en Simulink por medio de una función S. Las ventajas que se obtienen de la realización son: 1) el uso del ambiente visual y gráfico de Simulink, 2) la interacción del modelo con una gran variedad de solucionadores de paso fijo y 3) se facilita la realización de simulaciones multi-resolución. Adicionalmente, como complemento a este modelo de línea, se requiere contar con un solucionador de red capaz de simular redes eléctricas con varios pasos de integración. Por ejemplo, en Simulink se puede usar alguno de los solucionadores ya existentes en la librería PSB (Power System Blockset) (SimPowerSystems User’s Guide, 2009). Sin embargo, su diseño no permite simular redes eléctricas con varios pasos de integración. Por lo tanto, se proponen las cosimulaciones como última alternativa para simular redes eléctricas con varios pasos de integración. Los programas y/o herramientas que se utilizan en las cosimulaciones son: los bloques Matlab/Simu-link, la librería PSB/Simulink y el programa comercial PSIM (SimPowerSystems User’s Guide, 2009; Simulink. User’s Guide, 2009 and PSIM Demo version 8.0, 2009).
En la figura 6a se ilustra un ejemplo de cosimulación la red eléctrica mostrada en la figura 7. La subred de dinámica lenta siempre se simula con bloques Matlab/ Simulink, mientras que la red de dinámica rápida se simula con los bloques de la librería PSB/Simulink. El uso práctico de este ejemplo de cosimulación está limitado a pequeñas subredes con dinámica lenta. La razón principal de esto es que el modelado de grandes subredes con bloques Matlab se vuelve muy complicado.
La figura 6b ilustra un ejemplo de cosimulación para la misma red eléctrica con los programa PSIM y PSB/Simulink (PSIM Demo version 8.0, 2009). En dicha figura se observa que la subred de dinámica lenta (subred A) se simula con el programa PSIM y de forma opuesta, la subred de dinámica rápida se simula con PSB/Simulink (subred B). Esta observación siempre es aplicable para cualquier tipo de topología de red dado que el solucionador de red PSB/Simulink requiere, para su ejecución en serie y/o paralelo, un paso de integración más pequeño. La ventaja que tiene esta implemen-tación con respecto a la mostrada en la figura 6a es la disponibilidad del programa PSIM para simular cualquier tipo de topología de red en el subsistema de dinámica lenta.
Para terminar, la figura 6c muestra un ejemplo de cosimulación de una red eléctrica con los programas PSIM y Simulink. En esta ejecución solo se utiliza el solucionador de red del PSIM para simular de manera independiente y en diferentes archivos cada una de las subredes eléctricas. La ventaja que ofrece esta realización con respecto a las anteriores, figuras 6a y 6b, es su versatilidad para simular cualquier tipo de topología de red. Sin embargo, cuando se utiliza una versión no profesional del programa PSIM, se tiene la limitante de que solo se puede usar un número limitado de elementos para construir el circuito que compone cada subred.
Resultados de simulaciones multi-resoluciónLa figura 7a muestra el diseño de una red monofásica que se utiliza como caso de prueba para llevar a cabo simulaciones multi-resolución de transitorios magnéticos en Simulink. Esta red eléctrica se energiza en t = 0 s. En este tiempo, el interruptor al final de la línea se encuentra abierto. En t = 2ms el interruptor se cierra y luego, en t = 3ms el interruptor se abre otra vez y se mantiene abierto. Los datos de la línea de transmisión para este sistema se proporcionan en la figura 7b.
La línea de transmisión sirve como medio natural para dividir la red eléctrica en dos subredes resultantes con diferente dinámica. Cada una de estas subredes se clasifica de acuerdo con su frecuencia de resonancia, como de dinámica lenta o rápida. Aquí conviene aclarar que la frecuencia de resonancia es siempre menor que el máximo ancho de banda (Fmáx) alcanzado por la dinámica de la subred. Sin embargo, dicho parámetro es un buen indicativo para diferenciar las distintas dinámicas de la red. Por ejemplo, los circuitos de alimentación y carga tienen las frecuencias de resonancias
respectivamente. Por lo tanto, se asigna la subred de dinámica lenta al circuito de alimentación y la subred de dinámica rápida al circuito de carga. Adicionalmente, con base en el criterio de Nyquist establecido en las expresiones la y 1b, se tiene que los pasos de integración máximos para simular las subredes de dinámica lenta y rápida son
respectivamente. Sin embargo, para tener una buena resolución de la respuesta transitoria se requiere que los pasos de tiempo ΔT y Δt sean considerablemente menores a los establecidos por las expresiones 6 y 7. Para probar el modelo FD-Line multi-resolución se proponen los siguientes casos de simulación:
- a)
Simulación multi-resolución, Δt = 1 μs y ΔT = 20 μs con una relación ΔT/Δt de m = 20 mediante el uso de filtros pasa-bajas MA de 1, 2 y 3 pasos.
- b)
Simulación multi-resolución, Δt = 1 μs y ΔT = 20 μs con una relación ΔT/Δt de m = 20. Se eliminan los filtros pasa-bajas.
En ambos incisos se cumple con la condición de que los pasos de integración, para simular cada subred, son menores que los máximos permitidos.
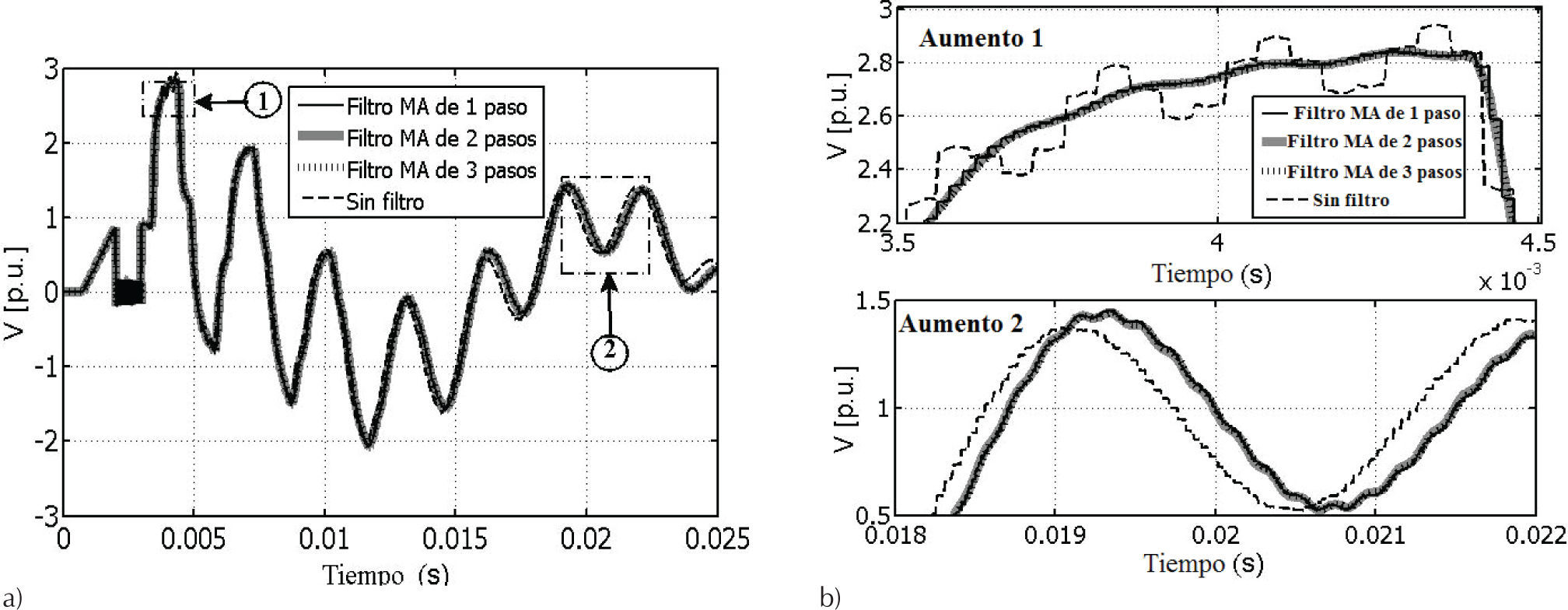
En la figura 8 se ilustra la comparación de la respuesta transitoria de voltaje en el nodo B, la cual corresponde a la subred de dinámica rápida, para las diferentes simulaciones multi-resolución descritas en los incisos a y b. Se muestra en esa figura que las respuestas transitorias de voltaje, obtenidas con los filtros MA de 1, 2 y 3 pasos dentro del modelo FD-Line multi-resolución, están siempre en fase durante todo el tiempo de simulación. Adicionalmente, cuando se utilizan distintos tipos de filtros pasa-bajas se observan pequeñas diferencias en la magnitud de las respuestas transitorias de voltaje. Sin embargo, cuando se suprimen los filtros pasa-bajas en el modelo FD-Line multi-resolución se producen grandes errores debidos al fenómeno de aliasing en el dominio del tiempo.
Validación del modelo FD-Line multi-resoluciónEl proceso de validación consiste en comparar las simulaciones multi-resolución con las siguientes simulaciones clásicas del programa EMTP:
- c)
Simulación de un paso de integración, Δt = 1 μs;
- d)
Simulación de un paso de integración, ΔT= 20 μs.
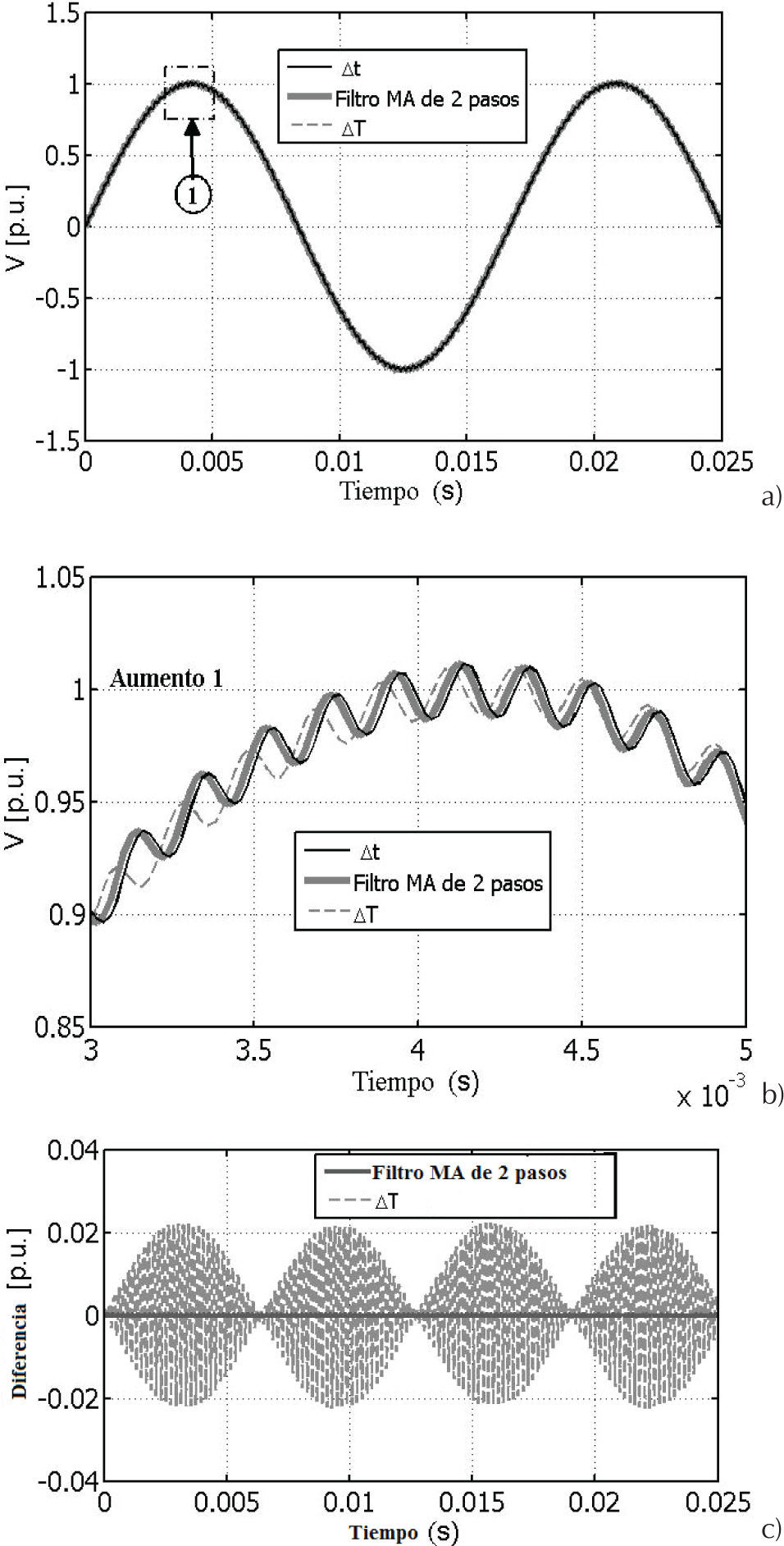
La figura 9 muestra la comparación de las respuestas transitorias de voltaje obtenidas en el nodo A para el ejemplo de red eléctrica descrito en la figura 7. Las respuestas transitorias se obtuvieron con simulaciones clásicas del programa EMTP, como se describió en c) y d), así como la simulación multi-resolución descrita en el caso a) para un filtro MA de dos pasos. La simulación realizada con el paso de tiempo Δt se considera la referencia. Se puede observar en las figuras 9a y 9b que el voltaje de la respuesta transitoria en el nodo A que fue obtenido en la simulación multi-resolución es el más cercano al que se obtiene con el paso de integración Δt. Por el contrario, los resultados de simulación con el paso de integración ΔT producen los resultados más pobres. Las diferencias entre estas respuestas transitorias se muestran en la figura 9c.
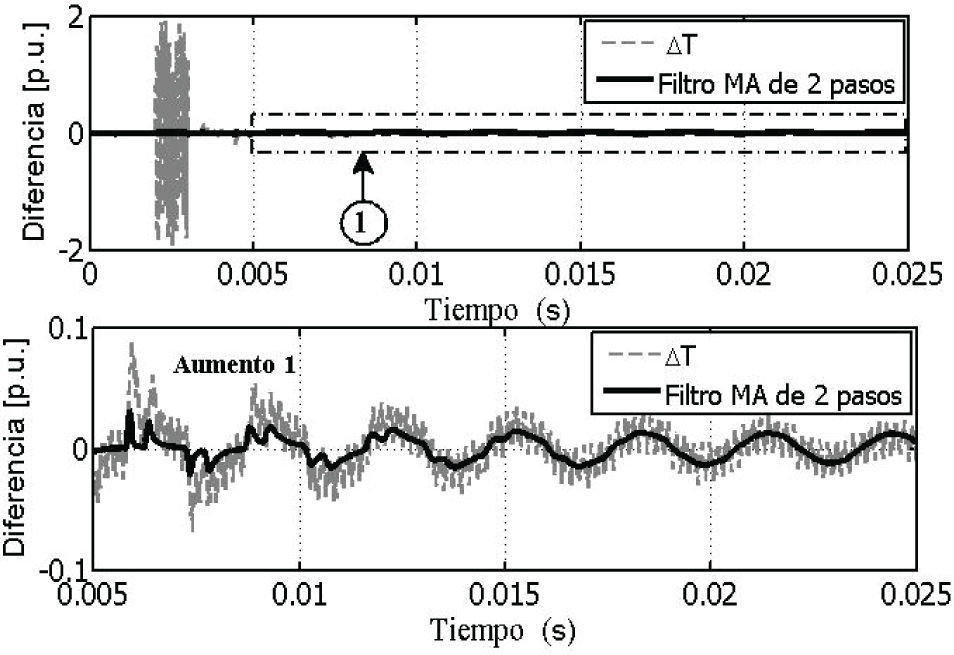
La figura 10 presenta las comparaciones entre diferentes respuestas de voltaje transitorio en el nodo B para el ejemplo de la red eléctrica de la figura 7. Las respuestas transitorias fueron obtenidas con simulaciones clásicas del programa EMTP, como se describió en c) y d), así como con la simulación multi-resolución descrita en a) para un filtro MA de dos pasos. Como en la figura anterior, la simulación multi-resolución produce los resultados más cercanos a la referencia, mientras que la simulación llevada a cabo con el paso de integración ΔT produce los resultados más pobres. La figura 11 muestra las diferencias entre las respuestas transitorias de voltaje de la figura 10.
Diferencias en las formas de onda en el nodo B mostrado en la figura 9
Uno de los requerimientos para representar de forma precisa la dinámica lenta de la subred A consiste en tener pasos de tiempo Δt y ΔT menores a 99.34 μs. Sin embargo, con un paso de tiempo ΔT mayor a 19.85 μs la dinámica rápida no se puede representar de manera precisa en el nodo B.
Por otro lado, las simulaciones multi-resolución proporcionan resultados con precisión intermedia. Los tiempos de retardo generados por los filtros pasa-bajas se compensan, dentro del modelo FD-Line multi-resolución, con los retardos de la línea. Así, la respuesta transitoria obtenida en las simulaciones multi-resolución resulta siempre en fase con las simulaciones clásicas del EMTP.
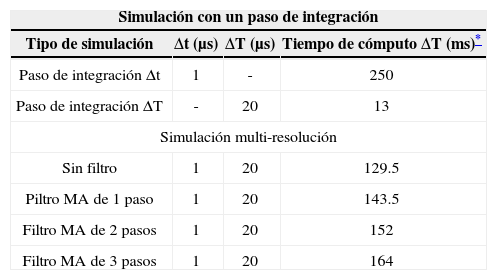
La tabla 1 muestra los tiempos computacionales promedio para simular un tiempo de 20 μs para cada caso de simulación propuesto en esta sección y la anterior. Los tiempos se obtuvieron con una simulación fuera de línea en una PC convencional a través de un protocolo serie.
Tiempos computacionales
| Simulación con un paso de integración | |||
|---|---|---|---|
| Tipo de simulación | Δt (μs) | ΔT (μs) | Tiempo de cómputo ΔT (ms)* |
| Paso de integración Δt | 1 | - | 250 |
| Paso de integración ΔT | - | 20 | 13 |
| Simulación multi-resolución | |||
| Sin filtro | 1 | 20 | 129.5 |
| Piltro MA de 1 paso | 1 | 20 | 143.5 |
| Filtro MA de 2 pasos | 1 | 20 | 152 |
| Filtro MA de 3 pasos | 1 | 20 | 164 |
Los resultados proporcionados en la tabla 1 muestran que las simulaciones realizadas con el paso de integración Δt son altamente demandantes de tiempo computacional. Por el contrario, la simulación llevada a cabo con el paso de tiempo ΔT es la más rápida. Además, las simulaciones multi-resolución requieren menos tiempo computacional que las simulaciones realizadas con el paso de tiempo Δt.
Por otro lado, cuando se comparan las simulaciones multi-resolución, se obtienen tiempos computacionales promedio muy similares. Las pequeñas diferencias observadas se deben a las memorias determinadas para los filtros MA de 1, 2 y 3 pasos. Adicionalmente, la carga computacional es mínima cuando se suprimen los filtros pasa-bajas dentro del modelo de línea multi-resolución. Finalmente, es importante mencionar que con las simulaciones multi-resolución se pueden lograr ahorros computacionales de hasta 50%.
ConclusionesSe presentó una descripción completa del modelo FD-Line multi-resolución para simular transitorios electromagnéticos en redes eléctricas con múltiples pasos de tiempo. En la solución algorítmica del modelo de línea se utilizaron los conceptos de la teoría algorítmica de procesamiento digital de señales (DSP) para proporcionar un acondicionamiento adecuado a las variables de interface. Es importante mencionar que se propusieron e utilizaron los filtros MA de múltiples pasos en el modelo FD-Line multi-resolución, a fin de prevenir los efectos indeseados causados por la conversión en la tasa de muestreo. También, los retardos en tiempo generados por los filtros MA de múltiples pasos se compensaron fácilmente por medio de los retardos en tiempo propios de las líneas de transmisión.
Se demostró que la ausencia de solucionadores de red multi-resolución, en los programas clásicos tipo EMTP, puede superarse mediante el uso de varias técnicas de cosimulación dentro del ambiente Simulink. Las herramientas del programa para llevar a cabo estas cosimulaciones son los bloques Matlab, PSIM y la librería de sistemas de potencia (PSB) en Simulink (Sim-PowerSystems User’s Guide, 2009; Simulink. User’s Guide, 2009 and PSIM Demo version 8.0, 2009).
Se validó el modelo FD-Line multi-resolución mediante comparaciones con simulaciones del programa EMTP. Los resultados numéricos muestran que las simulaciones multi-resolución siempre tienen una precisión intermedia con respecto a las simulaciones de un solo paso de integración Δt y ΔT. Sin embargo, las respuestas transitorias de voltaje y corriente son muy similares a las obtenidas en el EMTP con el paso de integración Δt. Las pequeñas diferencias observadas se deben a errores propios del método de integración numérica usado para resolver las ecuaciones diferenciales del modelo de línea. En contraste, los resultados de simulación más imprecisos se obtuvieron con la simulación de un paso de integración ΔT. Las grandes diferencias observadas se debieron principalmente a que la selección del paso de integración no fue la adecuada para cumplir con el criterio de Nyquist. En cuanto a la eficiencia del método, se puede decir que con el modelo FD-Line multi-resolución se reducen considerablemente los tiempos computacionales de simulación.
El producto final de esta investigación es una versión para uso académico del modelo FD-Line multi-resolución en el ambiente Simulink. La implementación práctica del modelo de línea contribuye enormemente al desarrollo de nuevas tecnologías o tendencias de simulación en los futuros programas comerciales tipo EMTP.
Reynaldo Iracheta-Cortez. Egresó de la carrera de Ingeniero Mecánico Electricista en 2003, recibió el grado de Maestro en Ciencias de la Ingeniería Eléctrica con Orientación en Sistemas Eléctricos de Potencia en 2007, ambos grados por la Facultad de Ingeniería Mecánica de la Universidad Autónoma de Nuevo León. Actualmente es alumno del programa de doctorado en el CINVESTAV, Unidad Guadalajara. Sus principales intereses son la simulación de transitorios electromagnéticos en sistemas eléctricos de potencia y energías renovables.
Citación estilo Chicago Iracheta-Cortez, Reynaldo. Simulaciones de redes eléctricas con múltiples pasos de integración a través del modelo FD-Line. Ingeniería Investigación y Tecnología, XVI, 01 (2015): 13-24. Citación estilo ISO 690 Iracheta-Cortez R. Simulaciones de redes eléctricas con múltiples pasos de integración a través del modelo FD-Line. Ingeniería Investigación y Tecnología, volumen XVI (número 1), enero-marzo 2015: 13-24.