Stochastic Analysis of a Non Uniform Surface of Bridges

Abstract

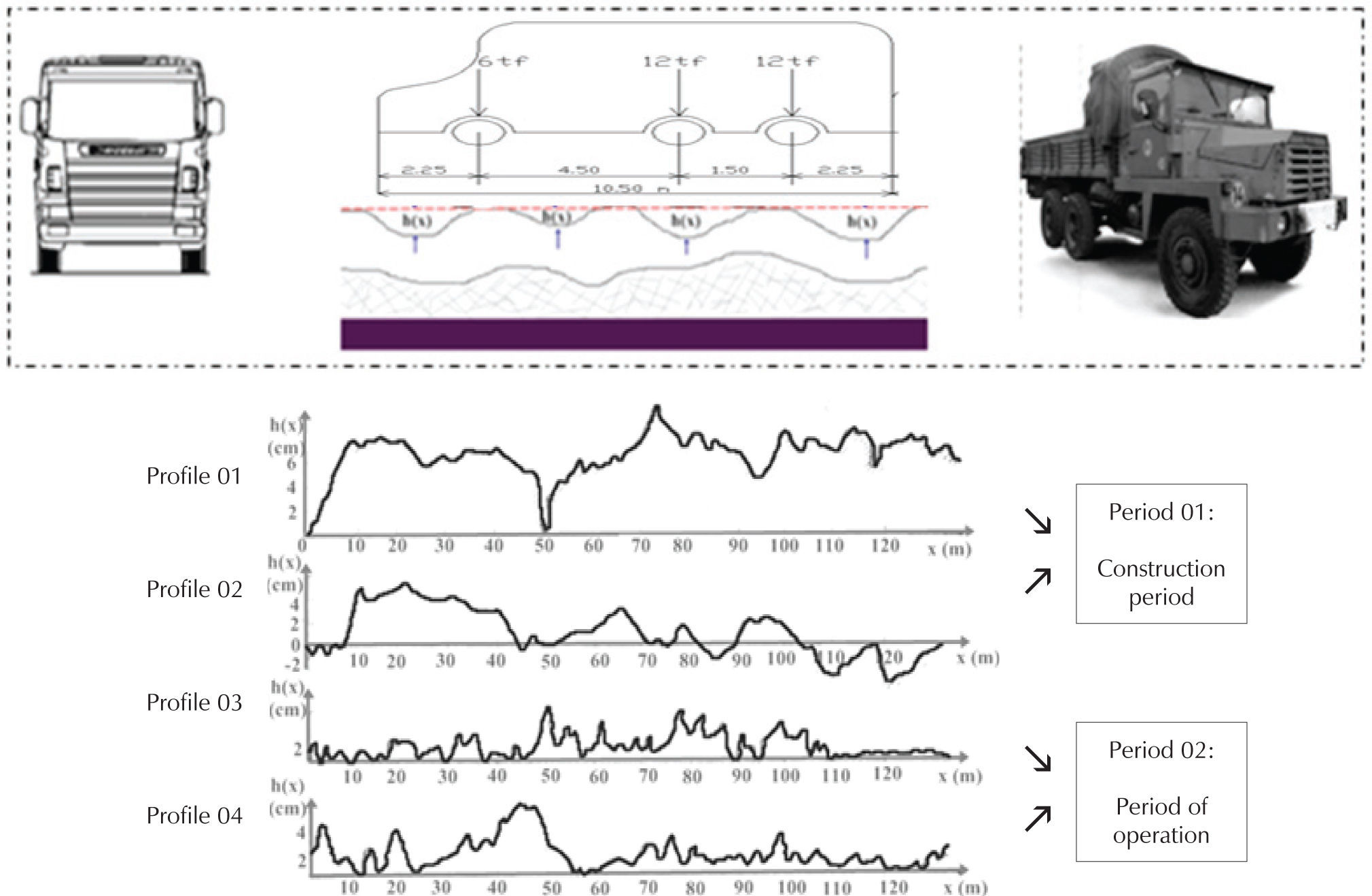
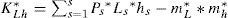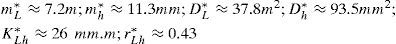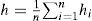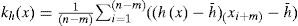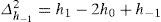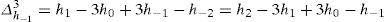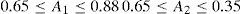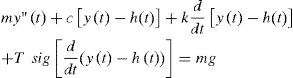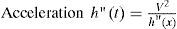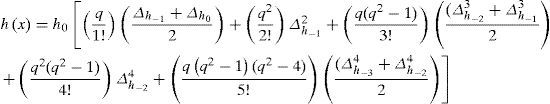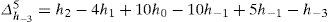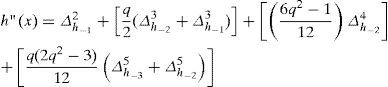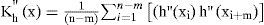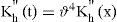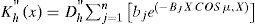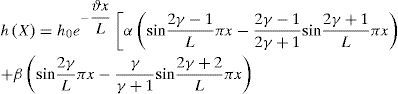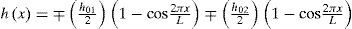The study of the problem of effects of surface roughness in bridges has been a topic of interest for over a century. For the treatment of this problem, multiple longitudinal profiles of pavements during different periods of life of bridges could be addressed. First, the construction period, the profile is linked to anomalies due to design errors and embodiments, other anomalies are due to vibrations parasitic. For the 2^nd period, we study two profiles, one that reflects the state of the slab or platform of the bridge just after it was in service and for the 2^nd profile after a certain time, which can range up to 15 years. In this context, we propose a stochastic analysis to fully understand the behavior of a structure in service while including a set of parameters often not considered in the normative evaluation procedures.

Resumen

El estudio del problema de los efectos de la rugosidad de la superficie en el puente ha sido un tema de interés por más de un siglo. Para el tratamiento de este problema, varios perfiles longitudinales de los pavimentos en distintos períodos de la vida de los puentes podrían abordarse. En primer lugar, en el periodo de construcción, el perfil está vinculado a anomalías debidas a errores de diseño y realizaciones, otras anomalías se deben a las vibraciones parásitas. Para el periodo segundo, se estudian dos perfiles, uno que refleja el estado de la losa o plataforma del puente justo después de que iniciara su servicio y para el segundo perfil después de cierto tiempo, que puede ir hasta 15 años. En este contexto, se propone un análisis estocástico para entender completamente el comportamiento de una estructura en servicio, mientras que incluye un conjunto de parámetros que a menudo no se consideran en los procedimientos normativos de la evaluación.

Introduction

The study of the problem of effects of surface roughness in bridges has been a topic of interest for over a century. For the treatment of this problem, multiple longitudinal profiles of pavements during different periods of the life of bridges could be addressed.

First, the construction period, the profile is linked to anomalies due to design errors and embodiments, other anomalies are due to parasitic vibrations.

For the 2^nd period, we can study two profiles, one that reflects the state of the slab or platform of the bridge just after it started service and for the 2^nd profile after a certain time, which can range up to 15 years, i.e. after the start of the material fatigue in the wearing course (asphalt concrete).

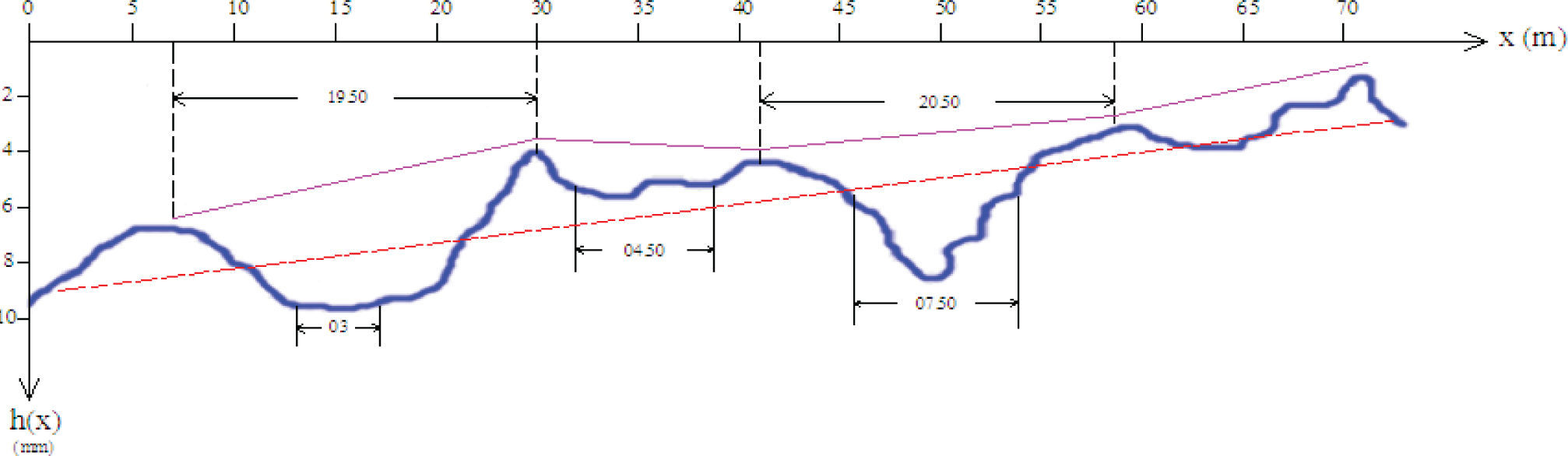
Generally the non-uniformity of the surface layer is characterized by the heights of the roughness of the road h(x) and its propagation length X that can appear on a few profiles in which the anomalies of the calculation, design and implementation are in majority (Figure 1).

Figure 1.

The different longitudinal profiles of the road (work in the Laboratory of the University Faculty LENINAVADE bridges and tunnels)

According to the results obtained, one notices that all the anomalies are due to several categories of problems, such as:

• •

  Problem of design, realization and calculation.

• •

  Problem of heat or heat gradient.

• •

  Problem of the dynamic overloads which are not taken into account in calculate of roadway or apron of the work (parasitic dynamic effects) (Cantieni, 1992).

All the factors quotes above are random elements and their evolutions in time and space is random functions, and by consequence we have to make recourse to the stochastic process.

Our study was based on the following data, for the determination of the profiles.

• •

  Determination of the singular points in the profile longitudinally and the various profiles across the road in general and on the level of the work in particular.

  

• •

  The probable depth of each point of the profile studied h_i.

• •

  The probable length of distribution of the profiles of no regularity of the roadway Li*.

Thus each one of the profiles studied is characterized by two random parameters (h_i, L_i,). For the study of these two parameters, one must determine and analyze the mathematical stochastic values, such as:

Expected value:

where P_s, P_hi, are the probabilities of realization of the event

Dispersion:

Moment of correlation between two random variables:

Correlation coefficient (h_i, L_i,):

According to the studies carried out by several European and American engineering and design departments, we can fix the values for the various stochastic parameters (Cantieni, 1992)

According to the studies and the results obtained, one can determine the heights of non regularities of the roadway or the bridge deck for the various points, by the following expression:

• h = height in mm

• L = length in mm

• k = 1, according to the CPC 61 (Al-Khaleefi and Abdel, 1999), from where:

From this expression, one can take the quadratic variance heights of the various points of the various profiles to be studied like the following:

0.50 mm < σ_h < 1.26 mm

Note: if, one considers the part of apron of an infinitely rigid structure, either in B.A or in B.H.P, one can take:

Therefore: h′ = 4.0+ε* L with 2 ≤ ε ≤ 3

To simplify and generalize the coefficient ε or (K) in all our cases, we take its arithmetic mean.

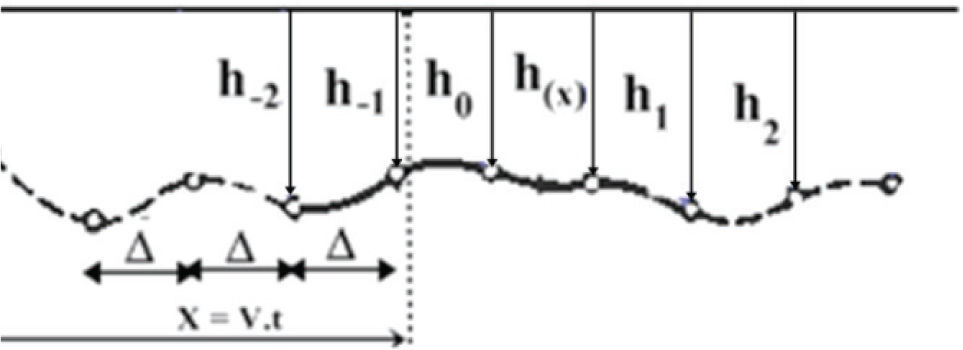
Evaluation of surface by function of correlation

The profile of part of the surface of an apron can be analyzed by the method of the random functions (Kim and Kawatani, 2001), the micro profile of the roadway after its study and its analysis and regarded as a random function h(x), by considering that this function is stationary (periodical), and the ordinates of the irregularities of the profile will be studied and evaluated by the normal law, the main randomness of the micro profile that usually has to be studied are regarded as mathematical expectation h, dispersion heights of the irregularities is D_h, and the function of correlation k_h(x) is determined by the following expression:

with m=0,1…….L≤n,n=LΔX,X=L*mn

where

L = length of realization

X = correlation interval equal to L*mn

Determination of the correlation function

Using steps of ΔX such as: ΔX = 0.05 ÷ 0.1 m.

In determining the ordinates of the surface irregularities of movement of intermediate points by the interpolation method linear or STERLING polynomial interpolation (Guilpin, 1997), taking into account rotation angles in the curve to the right and left of seen or studied, in this case we use the STERLING polynomial interpolation of 3rd degree:

with q=X−X0Δ

Where, Δ presents the distance between two consecutive profiles (Al-Khaleefi and Abdel, 1999).

Note: we can use the correlation function of any profile of the bridge deck (Hwang and Nowak, 1991), to determine a linear relationship, which allows us to determine ordinates of these points of profile such as:

According to the graphs of figure 4 of the function ρh(x), the two curves I and II of two different parts out of the asphaltic concrete, the difference between the two curves is in the presentation or the formulation of the non regularity of the roadway by the method of the stationary random function, and choice of the curve or line of the expectation in more use of function of approximation ρh(x), which contains two exponential with empirical coefficients which depend on the manner of realization of the profiles, and which are ∝ ₁ and α ₂ and one coefficient μ, which reflects or which takes into account the period of repetition of the density or the frequency of circulation.

where Leffective=2πμ≈3.2m÷16m that is 3.2m≤Leffective≤16m

from where the dispersion height of the none regularities of the roadway is:

Figure 4.

The function of approximation ρh(X)

The influence of the travelling overloads on the geometry of the profile depends on the diameter of the wheel of the overload and the pressure in the kennels of the travelling overloads such as Mr. C80 and MC120.

The deformation of the roadway under the effect of the travelling overloads also depends on the ray of the wheels and to release it kennels for the overload on kennels such as Mr. C80 and MC120.

The non regularity of the profiles of the roadway under the various factors also depends on the function of Kh*(x) correlation (ISO 8608, 1995).

The Equation of the movement of the mass M with the characteristics of rigidity and the pressure of the overload is given by the following relations:

We put u(t)=[y(t)−h (t)]w2=Cm2∝=kmT0=Tm from where, we obtain:

Note: for the various movements of the overloads: X = V * t

To obtain more exact results, one uses the polynomial of STERLING of n order, by increasing the number of the nodes, and one takes the step of unevenness of the deformation of the profiles of the equal roadway as 1.00 m.

To determine the central difference, we have:

From where the expectation converges to zero, but the function itself h“(x) is regulated in order, as equal to:

All this gives a possibility with a great base of calculation by slang and its stationnarity, more than it has even way that h(x).

The evaluation of the function of correlation of second order Kh“(x), in particular for a discrete calculation (discrete variables) (Kawatani et al., 1993) with help of a numerical calculation, can be determined by the following expression:

with x=L*mn

The function of correlation by the method of acceleration:Kh“(t) for the uniform movements of the travelling overloads is to determine immediately has through function of correlation of second order Kh“(x) and the speed of circulation of the travelling overloads.

For the approximation of the functions of correlation Kh“(x), one can use in exponential form one function cosine.

b_j, μ_j, B_j: are respectively the coefficient of the travelling weights of the overloads, and the frequency and damping coefficients of the various decompositions of the traffic (Hoogvelt and Ruijs, 1997)

In general the deformation of the profiles of a roadway in B.B is

h₀, y, β, L are constants γ = 0, 1, 3,……

To simplify calculations, we can take

h′ (0) = 0

h′ (0) = h″ (0) = 0 from where, we obtain

where h₀, h₀₁, h₀₂, are the unevennesses of the various nodes of the profiles and L= length of profile deformed.

Conclusions

According to analysis results, we noticed that the main causes of the deformation of the surface layer are due to:

• •

  The long duration of application of charges and surcharges dynamic mobile surcharges, which are not in the standards for the calculation of structures (CPC 61).

• •

  The high density of traffic during peak hours and non-compliance with safety distances between vehicles in the same lane or in different lanes of movement (the consequences are very important braking forces which result in very high horizontal dynamic stresses and in distortions).

• •

  Failure to comply with traffic speeds.

We noted that the irregularities in the bridge surface can have significant effects on the dynamic responses of a bridge and vehicles on it. We also noted that the “moving mass” simulation may not lead to reasonable estimates of the effects of bridge surface roughness upon bridge dynamics.

Finally, we observed that the distribution of Dynamic Amplification Factor can be described well by the double log-normal probability function.