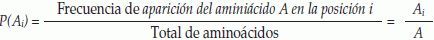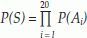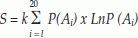Una de las proteínas del merozoito de Plasmodium falciparum, la EBA-140, también conocida como BAEBL o PfEBP-2, comparte características estructurales y homología con EBA-175 y EBA-181. Estudios de la localización sub-celular sugieren que está localizada en los micronemas.
Por medio de la construcción de un espacio de probabilidad, donde se cuantificó la posibilidad de aparición por posición para los 20 aminoácidos en péptidos con tamaño de 20 residuos para 6 secuencias de alta unión de la proteína EBA-140, se calculó la probabilidad, sumatoria de probabilidad y Entropía para las 61 secuencias de 20 residuos de la proteína EBA-140, para posteriormente caracterizar matemáticamente los péptidos de alta unión y los que no lo son. Adicionalmente se realizaron las mismas medidas para péptidos teóricos análogos, donde se cambiaron por Glicinas aminoácidos comprobados experimentalmente como críticos, y se efectuaron los cálculos.
Los valores de probabilidad, Sumatoria de Probabilidad y Entropía para las secuencias comprobadas experimentalmente de alta unión varían entre los rangos asociados al macroestado unión, mientras que todos estos mismos valores para los péptidos comprobados de baja unión se encuentran fuera de los rangos asociados al macroestado de unión. Los valores de probabilidad, sumatoria de probabilidad y Entropía diferencian los péptidos de alta unión de los de baja unión, acertando en el 100% de los casos estudiados, según estudios experimentales.
El fenómeno de unión de la proteína estudiada presenta un orden subyacente, que es caracterizable a partir de las leyes de la probabilidad y de la Entropía de forma objetiva y reproducible.
One of the Plasmodium falciparum merozoite proteins, EBA-140, also known as BAEBL or PfEBP-2, shares structural features and homology with EBA-175 and EBA-181. Studies on the sub-cellular localization suggest a micronem localization.
A probability space was built where the possibility of appearance by position for each of the 20 amino acids in EBA-140 protein 20-mer peptides based on 6 high-binding previously described sequences was quantified. Then, the probability, the addition of probability and the Entropy for 61 EBA-140 protein 20-mer sequences were calculated to mathematically characterize the high-binding peptides and the non-high-binding peptides. Additionally, the same measures for theoretical peptide analogs were made, in which calculations were made after those amino acids tested experimentally as critical were substituted by Glycine.
The probability values, probability summation and Entropy for the experimentally verified high-binding sequences, vary between the ranges associated to the binding macrostate, while every value for the nonhigh- binding peptides are outside of the binding macrostate range. The probability values, probability summation and Entropy differentiate the high-binding peptides from the low-binding, making a right guess in 100% of the cases studied according to experimental studies.
The binding phenomenon of the studied protein has an underlying order, which is objectively and reproductively characterizable starting from probability laws and Entropy.
La probabilidad es una medida matemática adimensional que cuantifica la posibilidad de la ocurrencia de un evento en el futuro(1-4). Las teorías que desean resolver el problema de determinar el estado dinámico de sistemas como el gaseoso, los cuales están compuestos por un número de moléculas de orden del número de Avogadro, 1023, son la termodinámica y la mecánica estadística. Con el fin de caracterizar el estado de sistemas como el gaseoso los conceptos de macroestado y de microestado se han enunciado, el macroestado determina una distribución general del sistema, mientras que el microestado está relacionado con las configuraciones particulares que puede tener una de estas distribuciones; por ejemplo si deseamos determinar la temperatura de un gas (macroestado) en una habitación, encontramos que un mismo valor de temperatura se corresponde con múltiples configuraciones de las velocidades (microestados)(5, 6).
El primer concepto de Entropía fue enunciado por Carnot, en el contexto de la termodinámica como una teoría que busca determinar las relaciones entre las propiedades de la materia sin tener en cuenta su estructura interna, encontrando que la proporción entre el calor dado a una máquina ideal y el valor de la temperatura del contenedor que cede dicha temperatura, y la proporción entre el calor cedido por la máquina a otro contenedor con otra temperatura son iguales; a esta igualdad la denominó Entropía y fue definida inicialmente como una variable de estado. Posteriormente Boltzmann, en el contexto de la teoría cinética de los gases, redefine la Entropía como una medida proporcional al logaritmo del número de microestados, es decir de las diferentes configuraciones particulares que posee un sistema en estado de equilibrio para que éste siga siendo el mismo desde un punto de vista macroscópico. La Entropía para los sistemas en equilibrio aumenta proporcionalmente al número de microestados que este posea. Posteriormente, en la mecánica estadística, la cual es una teoría que abarca a la termodinámica, la Entropía fue redefinida y generalizada para los sistemas fuera del equilibrio partiendo de la cuantificación de las probabilidades de las distribuciones microscópicas, y es una medida proporcional a la suma de los productos de la probabilidad de cada microestado por su logaritmo, siendo la constante de proporcionalidad la constante de Boltzmann. Esta fórmula para la Entropía abarca la fórmula definida anteriormente por Boltzmann, pues al aplicar esta fórmula para cualquier sistema equiprobable, es decir, para aquellos en los que todas las probabilidades son las mismas, el cálculo se reduce a multiplicar el logaritmo del número de microestados posibles por la constante de Boltzmann.
En este caso la Entropía se maximiza cuando el sistema es equiprobable(6, 7).
En el contexto de la teoría de la información Shannon encontró la misma expresión asociada a la Entropía de la mecánica estadística cuando buscaba la forma de cuantificar la cantidad de información que contiene cualquier mensaje, y esta medida es interpretada como una medida objetiva de la cantidad de información que posee un sistema(8).
La malaria se presenta principalmente en zonas tropicales, tomando allí la forma de epidemia. El ciclo eritrocítico de la malaria es caracterizado por la invasión periódica de merozoitos del Plasmodium a los eritrocitos. Dicha invasión es mediada por interacciones específicas receptor-ligando(9, 10) involucradas en los procesos de reconocimiento, unión, orientación e interiorización del merozoito dentro del eritrocito. Esta enfermedad es una de las principales causas de morbimortalidad en el mundo entero(11).
Se ha sugerido que el proceso de invasión del merozoito requiere de numerosas interacciones entre las proteínas del complejo apical y los receptores del eritrocito. Los compartimentos que conforman este complejo incluyen los micronemas y roptrias que descargan la proteína, facilitando la unión, entrada y residencia dentro del eritrocito(12-16). Un ligando del Plasmodium falciparum denominado antígeno de unión eritrocitaria 140 (EBA-140), también conocido como BAEBL o PfEBP-2, comparte características estructurales y homología con las proteinas EBA-175 y EBA-181(17, 18). Estudios de la localización subcelular sugieren que está localizada en los micronemas, la misma localización que el EBA-175 y el EBA-181; estas proteínas se unen a las sialo-glicoproteínas sobre la superficie de las células rojas de sangre (RBC).
En un trabajo previo(19), 61 péptidos del EBA-140 de la cadena 3D7(20) fueron sintetizados en 20 residuos no sobrelapados para determinar la especificidad de unión de ellos, encontrando que 6 péptidos tienen unión selectiva y específica a los eritrocitos.
El propósito de la presente investigación es caracterizar matemáticamente la especificidad de unión de péptidos de 20 residuos de la EBA-140 al receptor del glóbulo rojo a partir de la teoría de la probabilidad, y la ley de la Entropía.
DEFINICIONESMacroestado unión: Corresponde al conjunto de secuencias que presentan alta unión.
Macroestado no unión: Corresponde al conjunto de secuencias que no presentan alta unión.
Microestado: Cualquier secuencia específica de veinte aminoácidos.
Probabilidad Laplaciana: La probabilidad de un aminoácido A en una posición específica i se define como el cociente entre la frecuencia de aparición de este aminoácido en dicha posición y el total de aminoácidos(1, 4).
Sumatoria de probabilidad: La sumatoria de la probabilidad de un péptido específico (S), se define como la sumatoria de las probabilidades asociadas a los aminoácidos que la componen por posición específica i.
Probabilidad de una Secuencia: La probabilidad de un péptido específico (S), se define como la multiplicación de las probabilidades asociadas a los aminoácidos que la componen por posición específica i(1, 4).
Entropía: En un sistema cuyos microestados no son equiprobables la Entropía de un péptido está dada por:
Donde k es igual a la constante de Boltzmann, 1.38x10-23 (J/k), S el valor de la Entropía(5, 6) y P(Ai) es el valor de la probabilidad del aminoácido A en la posición i.
MATERIAL Y MÉTODOEsta metodología está basada en un trabajo previo en donde se aplicó la teoría de la probabilidad y la Entropía con el objetivo de caracterizar los péptidos de alta unión de la proteína de superficie de merozoito 1 (MSP-1)(21).
Partiendo de las 61 secuencias no sobrelapadas con un tamaño de 20 residuos cada una pertenecientes a la proteína EBA-140 y de las cuales 6 son comprobadas experimentalmente de alta unión(19), se calculó la frecuencia de aparición de cada uno de los 20 aminoácidos esenciales en cada una de las 20 posiciones para los péptidos comprobados experimentalmente de alta unión, posteriormente se evaluó la probabilidad de cada uno de los 20 aminoácidos esenciales en cada posición para todas las secuencias estudiadas, a través del cálculo de la probabilidad Laplaciana (Ecuación 1).
Partiendo del espacio de probabilidad construido, el cual cuantifica la posibilidad de aparición de cada uno de los 20 aminoácidos esenciales en cada una de las 20 posiciones, se realizaron los cálculos de sumatoria de probabilidad (Ecuación 2), probabilidad (Ecuación 3) y Entropía (Ecuación 4), para cada una de las 61 secuencias de la proteína EBA- 140.
Se escogió la proteína completa con el fin de caracterizar matemáticamente los dos macroestados en su totalidad (ver definiciones) y construir un espacio de probabilidad no equiprobable que cuantifique las secuencias de alta unión.
Finalmente, se realizaron cálculos con análogos teóricos de los péptidos de unión para desde esta mirada comparar el péptido de unión normal con el análogo, donde se reemplazan aminoácidos críticos por Glicina, para con estas mutaciones teóricas ver desde estas leyes si aumentan, se mantienen igual o disminuyen los valores evaluados respecto al valor del péptido sin cambios, y qué implicaciones tiene esto, es decir, evaluar los cambios al reemplazar en el péptido un aminoácido crítico, luego dos, luego tres, etc.
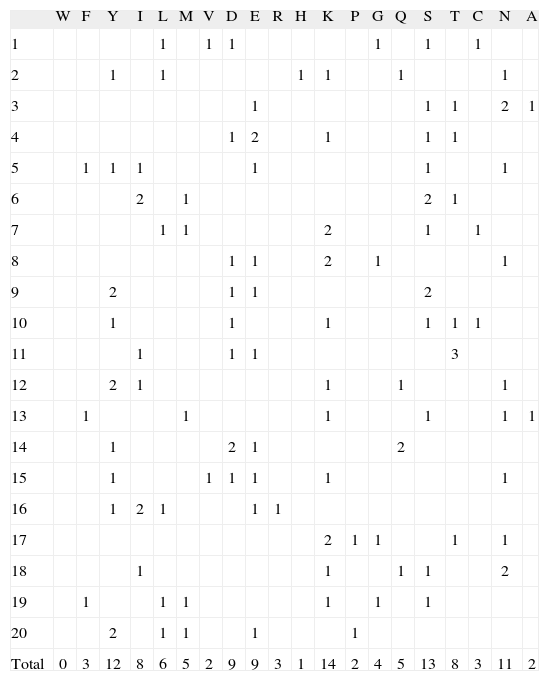
RESULTADOSPara las secuencias asociadas al macroestado unión se encontró que las frecuencias de aparición para los veinte aminoácidos en todas las posiciones variaron entre 0 y 14. Estos valores corresponden a los aminoácidos Triptófano (W) y Lisina (K), respectivamente. La posición con mayor número de repeticiones de un mismo aminoácido fue la número 11, siendo este aminoácido la Treonina (T) (Tabla I).
Frecuencias de aparición de los 20 aminoácidos por posición del macroestado unión*
| W | F | Y | I | L | M | V | D | E | R | H | K | P | G | Q | S | T | C | N | A | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||
| 2 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||
| 3 | 1 | 1 | 1 | 2 | 1 | |||||||||||||||
| 4 | 1 | 2 | 1 | 1 | 1 | |||||||||||||||
| 5 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||
| 6 | 2 | 1 | 2 | 1 | ||||||||||||||||
| 7 | 1 | 1 | 2 | 1 | 1 | |||||||||||||||
| 8 | 1 | 1 | 2 | 1 | 1 | |||||||||||||||
| 9 | 2 | 1 | 1 | 2 | ||||||||||||||||
| 10 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||
| 11 | 1 | 1 | 1 | 3 | ||||||||||||||||
| 12 | 2 | 1 | 1 | 1 | 1 | |||||||||||||||
| 13 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||
| 14 | 1 | 2 | 1 | 2 | ||||||||||||||||
| 15 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||
| 16 | 1 | 2 | 1 | 1 | 1 | |||||||||||||||
| 17 | 2 | 1 | 1 | 1 | 1 | |||||||||||||||
| 18 | 1 | 1 | 1 | 1 | 2 | |||||||||||||||
| 19 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||
| 20 | 2 | 1 | 1 | 1 | 1 | |||||||||||||||
| Total | 0 | 3 | 12 | 8 | 6 | 5 | 2 | 9 | 9 | 3 | 1 | 14 | 2 | 4 | 5 | 13 | 8 | 3 | 11 | 2 |
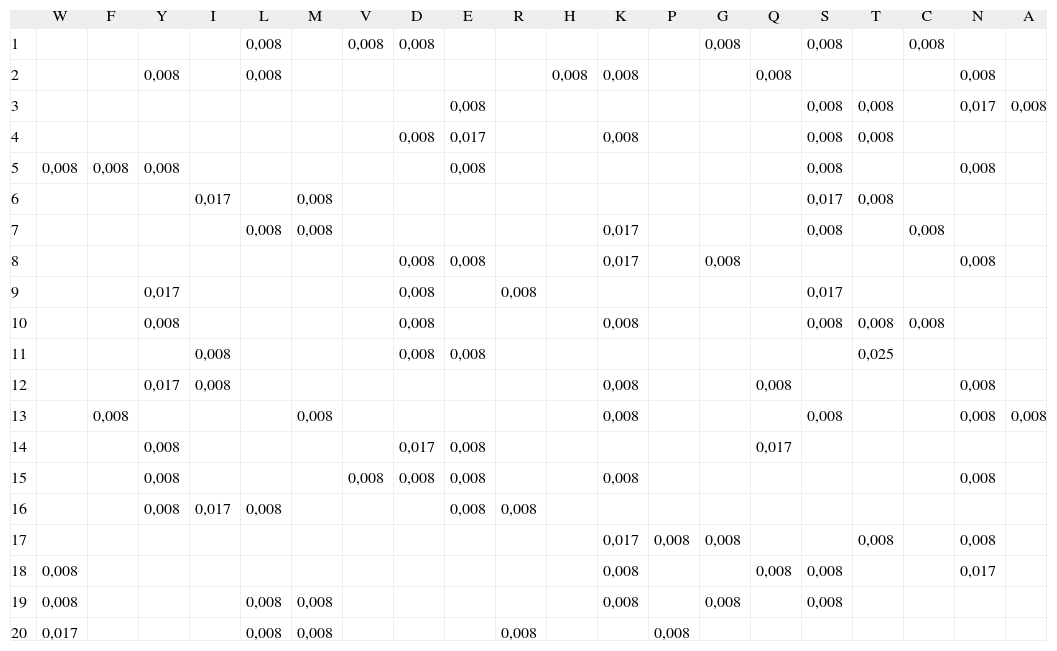
Para las secuencias asociadas al macroestado unión los valores de la probabilidad Laplaciana por posición para los veinte aminoácidos varió en un rango de 0 a 0,025, siendo el valor máximo el de la Treonina en la posición 11, encontrando 297 posiciones con un valor igual a cero de las 400 totales (Tabla II).
Cálculos de la probabilidad laplaciana para los 20 aminoácidos por posición del macroestado unión*
| W | F | Y | I | L | M | V | D | E | R | H | K | P | G | Q | S | T | C | N | A | |
| 1 | 0,008 | 0,008 | 0,008 | 0,008 | 0,008 | 0,008 | ||||||||||||||
| 2 | 0,008 | 0,008 | 0,008 | 0,008 | 0,008 | 0,008 | ||||||||||||||
| 3 | 0,008 | 0,008 | 0,008 | 0,017 | 0,008 | |||||||||||||||
| 4 | 0,008 | 0,017 | 0,008 | 0,008 | 0,008 | |||||||||||||||
| 5 | 0,008 | 0,008 | 0,008 | 0,008 | 0,008 | 0,008 | ||||||||||||||
| 6 | 0,017 | 0,008 | 0,017 | 0,008 | ||||||||||||||||
| 7 | 0,008 | 0,008 | 0,017 | 0,008 | 0,008 | |||||||||||||||
| 8 | 0,008 | 0,008 | 0,017 | 0,008 | 0,008 | |||||||||||||||
| 9 | 0,017 | 0,008 | 0,008 | 0,017 | ||||||||||||||||
| 10 | 0,008 | 0,008 | 0,008 | 0,008 | 0,008 | 0,008 | ||||||||||||||
| 11 | 0,008 | 0,008 | 0,008 | 0,025 | ||||||||||||||||
| 12 | 0,017 | 0,008 | 0,008 | 0,008 | 0,008 | |||||||||||||||
| 13 | 0,008 | 0,008 | 0,008 | 0,008 | 0,008 | 0,008 | ||||||||||||||
| 14 | 0,008 | 0,017 | 0,008 | 0,017 | ||||||||||||||||
| 15 | 0,008 | 0,008 | 0,008 | 0,008 | 0,008 | 0,008 | ||||||||||||||
| 16 | 0,008 | 0,017 | 0,008 | 0,008 | 0,008 | |||||||||||||||
| 17 | 0,017 | 0,008 | 0,008 | 0,008 | 0,008 | |||||||||||||||
| 18 | 0,008 | 0,008 | 0,008 | 0,008 | 0,017 | |||||||||||||||
| 19 | 0,008 | 0,008 | 0,008 | 0,008 | 0,008 | 0,008 | ||||||||||||||
| 20 | 0,017 | 0,008 | 0,008 | 0,008 | 0,008 |
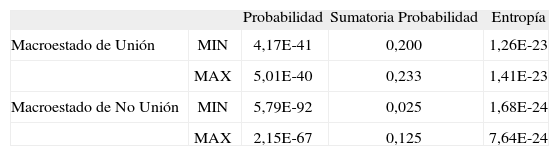
Para las 61 secuencias cuantificadas los valores de Probabilidad variaron entre 4,17E-41 y 5,01E-40, los de Sumatoria de Probabilidad entre 0,200 y 0,233 y los de Entropía entre 1,26E-23 y 1,41E-23 para todas las secuencias específicas asociadas al macroestado unión, y para las secuencias específicas asociadas al macroestado no unión los valores de Probabilidad variaron entre 5,79E-92 y 2,15E-67, Sumatoria de Probabilidad entre 0,025 y 0,125 y Entropía entre 1,68E-24 y 7,64E-24 (Tabla III).
Valores máximos y mínimos de sumatoria de probabilidad, probabilidad y Entropía para los macroestados de unión y no unión para cada péptido estudiado
| Probabilidad | Sumatoria Probabilidad | Entropía | ||
| Macroestado de Unión | MIN | 4,17E-41 | 0,200 | 1,26E-23 |
| MAX | 5,01E-40 | 0,233 | 1,41E-23 | |
| Macroestado de No Unión | MIN | 5,79E-92 | 0,025 | 1,68E-24 |
| MAX | 2,15E-67 | 0,125 | 7,64E-24 |
Se encontró que los valores de Probabilidad, Sumatoria de Probabilidad y Entropía para las secuencias específicas comprobadas experimentalmente de alta unión varían entre los rangos asociados al macroestado unión, mientras que por lo menos uno de los valores (de la sumatoria de probabilidad, de probabilidad o de Entropía) para los péptidos que no son de alta unión se encuentran fuera de los rangos asociados al macroestado de unión.
Para las 7 secuencias teóricas en el péptido 26135 los valores de Probabilidad variaron entre 1.252E-40 y 5.008E-40, los de Sumatoria de Probabilidad entre 0.217 y 0,233 y los de Entropía entre 1.330E-23 y 1.408E-23. Tres presentaron valores iguales al péptido original, con uno, dos y tres cambios de aminoácidos críticos por Glicinas, respectivamente. Uno presentó valores mayores, con un solo cambio, mientras que tres presentaron valores menores, con dos con uno y uno con cuatro cambios, respectivamente. Todos presentaron valores incluidos en el macroestado de unión (datos no mostrados).
Para las 5 secuencias teóricas en el péptido 26144 los valores de Probabilidad variaron entre 1.043E-41 y 4.173E-41 los de Sumatoria de Probabilidad entre 0.183 y 0.200 y los de Entropía entre 1.179E-23 y 1.258E-23. Dos presentaron valores iguales al péptido original, con uno y tres cambios de aminoácidos críticos por Glicinas, respectivamente. Uno presentó valores mayores, con un solo cambio, mientras que dos presentaron valores menores, con uno y dos cambios respectivamente. Tres de los péptidos se asociaron al macroestado de Unión, dos con un cambio y uno con dos, mientras que dos se asociaron al macroestado de No Unión, con uno y dos cambios, respectivamente (datos no mostrados).
Para las 9 secuencias teóricas en el péptido 26147 los valores de Probabilidad variaron entre 8.347E-41 y 4.173E-41, los de Sumatoria de Probabilidad entre 0.208 y 0.200 y los de Entropía entre 1.297E-23y 1.258E-23. Seis presentaron valores iguales al péptido original, cuatro con un cambio de aminoácidos críticos por Glicinas, uno con dos y otro con tres. Tres presentaron valores mayores, con uno, cuatro y cinco cambios respectivamente, mientras que seis presentaron valores menores, cuatro con un cambio, uno con dos y uno con tres. Todos presentaron valores incluidos en el macroestado de unión (datos no mostrados).
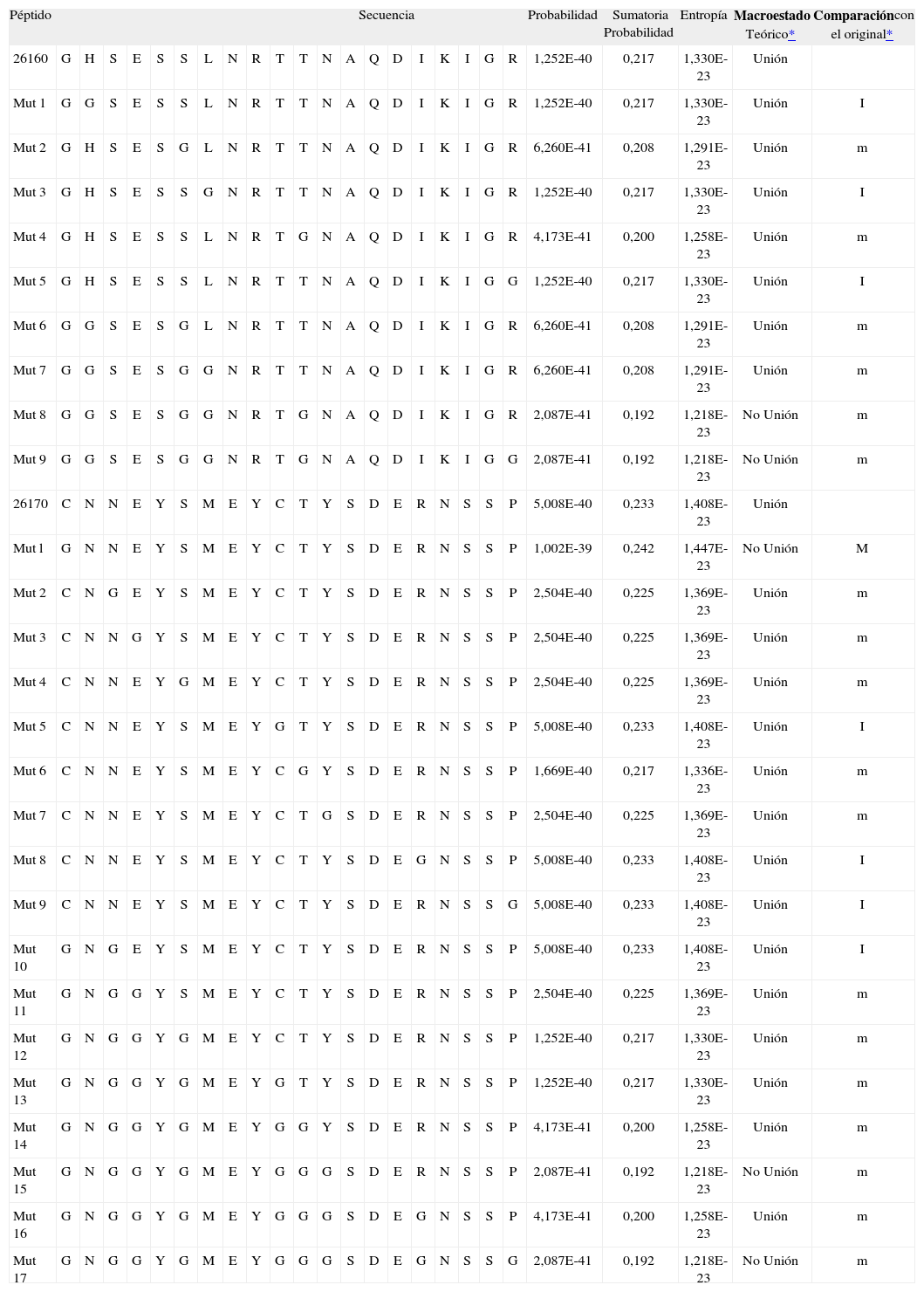
Para las 9 secuencias teóricas en el péptido 26160 los valores de Probabilidad variaron entre 2.087E-41y 1.252E-40, los de Sumatoria de Probabilidad entre 0.192 y 0.217 y los de Entropía entre 1.218E-y 1.330E-23. Tres presentaron valores iguales al péptido original, con un solo cambio de aminoácidos críticos por Glicinas. Los seis restantes presentaron valores menores, dos con un cambio, y el resto con dos, tres, cuatro y cinco cambios, respectivamente. Siete de los péptidos se asociaron al macroestado de Unión, cinco con un cambio, uno con dos y uno con tres, mientras que dos se asociaron al macroestado de No Unión, con cuatro y cinco cambios, respectivamente (Tabla IV).
Mutaciones teóricas de los péptidos de Unión 26160 y 26170
| Péptido | Secuencia | Probabilidad | Sumatoria Probabilidad | Entropía | Macroestado Teórico* | Comparacióncon el original* | |||||||||||||||||||
| 26160 | G | H | S | E | S | S | L | N | R | T | T | N | A | Q | D | I | K | I | G | R | 1,252E-40 | 0,217 | 1,330E-23 | Unión | |
| Mut 1 | G | G | S | E | S | S | L | N | R | T | T | N | A | Q | D | I | K | I | G | R | 1,252E-40 | 0,217 | 1,330E-23 | Unión | I |
| Mut 2 | G | H | S | E | S | G | L | N | R | T | T | N | A | Q | D | I | K | I | G | R | 6,260E-41 | 0,208 | 1,291E-23 | Unión | m |
| Mut 3 | G | H | S | E | S | S | G | N | R | T | T | N | A | Q | D | I | K | I | G | R | 1,252E-40 | 0,217 | 1,330E-23 | Unión | I |
| Mut 4 | G | H | S | E | S | S | L | N | R | T | G | N | A | Q | D | I | K | I | G | R | 4,173E-41 | 0,200 | 1,258E-23 | Unión | m |
| Mut 5 | G | H | S | E | S | S | L | N | R | T | T | N | A | Q | D | I | K | I | G | G | 1,252E-40 | 0,217 | 1,330E-23 | Unión | I |
| Mut 6 | G | G | S | E | S | G | L | N | R | T | T | N | A | Q | D | I | K | I | G | R | 6,260E-41 | 0,208 | 1,291E-23 | Unión | m |
| Mut 7 | G | G | S | E | S | G | G | N | R | T | T | N | A | Q | D | I | K | I | G | R | 6,260E-41 | 0,208 | 1,291E-23 | Unión | m |
| Mut 8 | G | G | S | E | S | G | G | N | R | T | G | N | A | Q | D | I | K | I | G | R | 2,087E-41 | 0,192 | 1,218E-23 | No Unión | m |
| Mut 9 | G | G | S | E | S | G | G | N | R | T | G | N | A | Q | D | I | K | I | G | G | 2,087E-41 | 0,192 | 1,218E-23 | No Unión | m |
| 26170 | C | N | N | E | Y | S | M | E | Y | C | T | Y | S | D | E | R | N | S | S | P | 5,008E-40 | 0,233 | 1,408E-23 | Unión | |
| Mut l | G | N | N | E | Y | S | M | E | Y | C | T | Y | S | D | E | R | N | S | S | P | 1,002E-39 | 0,242 | 1,447E-23 | No Unión | M |
| Mut 2 | C | N | G | E | Y | S | M | E | Y | C | T | Y | S | D | E | R | N | S | S | P | 2,504E-40 | 0,225 | 1,369E-23 | Unión | m |
| Mut 3 | C | N | N | G | Y | S | M | E | Y | C | T | Y | S | D | E | R | N | S | S | P | 2,504E-40 | 0,225 | 1,369E-23 | Unión | m |
| Mut 4 | C | N | N | E | Y | G | M | E | Y | C | T | Y | S | D | E | R | N | S | S | P | 2,504E-40 | 0,225 | 1,369E-23 | Unión | m |
| Mut 5 | C | N | N | E | Y | S | M | E | Y | G | T | Y | S | D | E | R | N | S | S | P | 5,008E-40 | 0,233 | 1,408E-23 | Unión | I |
| Mut 6 | C | N | N | E | Y | S | M | E | Y | C | G | Y | S | D | E | R | N | S | S | P | 1,669E-40 | 0,217 | 1,336E-23 | Unión | m |
| Mut 7 | C | N | N | E | Y | S | M | E | Y | C | T | G | S | D | E | R | N | S | S | P | 2,504E-40 | 0,225 | 1,369E-23 | Unión | m |
| Mut 8 | C | N | N | E | Y | S | M | E | Y | C | T | Y | S | D | E | G | N | S | S | P | 5,008E-40 | 0,233 | 1,408E-23 | Unión | I |
| Mut 9 | C | N | N | E | Y | S | M | E | Y | C | T | Y | S | D | E | R | N | S | S | G | 5,008E-40 | 0,233 | 1,408E-23 | Unión | I |
| Mut 10 | G | N | G | E | Y | S | M | E | Y | C | T | Y | S | D | E | R | N | S | S | P | 5,008E-40 | 0,233 | 1,408E-23 | Unión | I |
| Mut 11 | G | N | G | G | Y | S | M | E | Y | C | T | Y | S | D | E | R | N | S | S | P | 2,504E-40 | 0,225 | 1,369E-23 | Unión | m |
| Mut 12 | G | N | G | G | Y | G | M | E | Y | C | T | Y | S | D | E | R | N | S | S | P | 1,252E-40 | 0,217 | 1,330E-23 | Unión | m |
| Mut 13 | G | N | G | G | Y | G | M | E | Y | G | T | Y | S | D | E | R | N | S | S | P | 1,252E-40 | 0,217 | 1,330E-23 | Unión | m |
| Mut 14 | G | N | G | G | Y | G | M | E | Y | G | G | Y | S | D | E | R | N | S | S | P | 4,173E-41 | 0,200 | 1,258E-23 | Unión | m |
| Mut 15 | G | N | G | G | Y | G | M | E | Y | G | G | G | S | D | E | R | N | S | S | P | 2,087E-41 | 0,192 | 1,218E-23 | No Unión | m |
| Mut 16 | G | N | G | G | Y | G | M | E | Y | G | G | G | S | D | E | G | N | S | S | P | 4,173E-41 | 0,200 | 1,258E-23 | Unión | m |
| Mut 17 | G | N | G | G | Y | G | M | E | Y | G | G | G | S | D | E | G | N | S | S | G | 2,087E-41 | 0,192 | 1,218E-23 | No Unión | m |
Abreviaciones: Unión: valores correspondientes al macroestado de unión de acuerdo con la metodología desarrollada; No Unión: valores correspondientes al macroestado de no unión de acuerdo con la metodología desarrollada; M: valores mayores de probabilidad, sumatoria de probabilidad y Entropía; m: valores menores de probabilidad, sumatoria de probabilidad y Entropía; I: valores iguales de probabilidad, sumatoria de probabilidad y Entropía.
Para las 17 secuencias teóricas en el péptido 26170, los valores de Probabilidad variaron entre 2.087E-41 y 1.002E-39, los de Sumatoria de Probabilidad entre 0.192 y 0.242 y los de Entropía entre 1.218E-23 y 1.447E-23. Cuatro presentaron valores iguales al péptido original, tres con un cambio y uno con dos cambios de aminoácidos críticos por Glicinas. Uno presentó valores mayores, con un sólo cambio, mientras que los doce restantes presentaron valores menores, cinco con un cambio, y el resto con tres, cuatro, cinco seis, siete, ocho y nueve cambios, respectivamente. Catorce de los péptidos se asociaron al macroestado de Unión, ocho con un cambio, y uno con dos, tres, cuatro, cinco, seis y ocho cambios, respectivamente, mientras que tres se asociaron al macroestado de No Unión, con uno, siete y nueve cambios, respectivamente (Tabla IV).
Las medidas evaluadas en los péptidos análogos evidencian variaciones inesperadas, que revelan cambios drásticos y constituyen un primer punto de partida para comprender el fenómeno desde una perspectiva física y teórica.
DISCUSIÓNEste es el primer trabajo en el que se realiza una caracterización matemática de la especificidad de unión para péptidos no sobrelapados de 20 residuos de la proteína del merozoito de P. falciparum EBA-140. La aplicación de las leyes de la probabilidad y de la Entropía revela un orden matemático en el fenómeno de unión a los receptores del eritrocito. La definición de un espacio de probabilidad que cuantifica la aparición de cualquier aminoácido en cualquier posición posible, muestra que la aplicación de las leyes adecuadas en el contexto de una generalización permite evidenciar el orden de fenómenos aparentemente complejos. En este caso, la distribución no equiprobable por aminoácido y por posición, que es posteriormente aplicada a través de los cálculos de probabilidad sumatoria de probabilidad y Entropía para cada secuencia específica (microestados), permite diferenciar matemáticamente todos los péptidos de alta unión de aquellos que no lo son según resultados experimentales.
El cambio progresivo de aminoácidos críticos por Glicinas, y la evaluación de los cambios de probabilidad, sumatoria de probabilidad y Entropía en estos casos, sugiere que en el fenómeno de unión hay un orden matemático de fondo, pues al comparar las investigaciones experimentales de los análogos, con las mutaciones teóricas, se presentan cambios drásticos en ambos casos. Es decir, al reemplazar un aminoácido crítico se presentan cambios drásticos en la unión observada experimentalmente(19). De forma interesante, los cambios de las mutaciones teóricas realizadas con un solo aminoácido crítico o con tres producen cambios drásticos en los valores de las ecuaciones que necesitan de una explicación más profunda, donde se necesitarán más datos experimentales, mayor cantidad de cálculos al mismo tiempo y, si es posible, desarrollar una teoría que logre hacer predicciones sobre este fenómeno tan complejo. En el péptido 26177 no se evaluaron mutaciones teóricas pues no presenta aminoácidos críticos.
J. Rodríguez ha realizado varios trabajos aplicando teorías físicas y matemáticas para la comprensión de los fenómenos inmunológicos. Así, calculó la dimensión fractal del repertorio inmune T y de clones de células Th contra un alergeno específico, el Poa P9, de un paciente alérgico (en presencia y ausencia de interferón alfa), evidenciando el comportamiento fractal de estos repertorios y el patrón Th, constituyendo una metodología de medición objetiva y reproducible en inmunoterapias y encontrando correlaciones clínicas y matemáticas respecto a la salud y a la enfermedad(22). Con la teoría de conjuntos(23) y la teoría de la probabilidad y la Entropía(21) caracterizó el fenómeno de alta unión de la proteína de membrana MSP-1 al receptor de glóbulo rojo, encontrando órdenes matemáticos que diferencian los péptidos que presentan alta unión, de los péptidos que no, de forma objetiva y reproducible. En este trabajo se sigue esta misma línea, con el fin de constituir, en conjunto con los trabajos mencionados, una recopilación de información descriptiva desde una perspectiva físico-matemática del problema de unión de péptidos de malaria a su receptor en glóbulo rojo, lo cual constituye un primer paso para el posible desarrollo futuro de una teoría.
Dicho camino fue desarrollado en el fenómeno de unión de péptidos al HLA clase II, donde inicialmente, desde la perspectiva de la teoría de conjuntos, se encontró un comportamiento caracterizable a partir de reglas halladas experimentalmente en péptidos nonaméricos específicos, logrando diferenciar péptidos de unión y no unión mediante operaciones matemáticas(24). Dicho trabajo sirvió como base para el desarrollo de una teoría de unión de péptidos nonaméricos al HLA clase II basada en las leyes de probabilidad, combinatoria y de Entropía(25), aplicada a 161 péptidos naturales, sintéticos y teóricos, la cual diferencia los péptidos de unión de los de no unión con un 100% de efectividad. En esta investigación se desarrolla una caracterización matemática y física acausal, que, del mismo modo que las caracterización desarrollada para el HLA clase II, puede servir como base para el desarrollo de una teoría basada en leyes y principios de la física para poder desarrollar predicciones. Sin embargo, una de las grandes dificultades para poder desarrollar una teoría predictiva con los péptidos de malaria y llevar este trabajo a un estadio superior, consiste en la arbitrariedad del número de aminoácidos del péptido, comparado con los nueve aminoácidos en la hendidura de unión del HLA clase II.
Los métodos usados para predecir péptidos en la actualidad buscan combinar la información experimental disponible con el uso de algoritmos en el contexto de metodologías computacionales que permiten cuantificar la capacidad de unión, éstos métodos necesitan muestras previas para su construcción, por lo que se convierten en metodologías que dependen del análisis usado y de la muestra de estudio y prueba(26, 27). A diferencia de esos trabajos, en éste se parte de la construcción de un espacio de probabilidad y la posterior cuantificación de cada secuencia a partir de éste, lo cual permite su posible aplicación a diferentes proteínas(21) con la diferencia de que en este trabajo se evalúan cambios de análogos desde las leyes aplicadas al realizar las mutaciones teóricas. La ventana de 20 aminoácidos es abierta arbitrariamente, pero a pesar de la longitud arbitraria este trabajo evidencia órdenes físicos y matemáticos subyacentes desde las leyes utilizadas. En este trabajo no existen causas o motivos que permitan distinguir si un péptido es o no de alta unión, sino un orden matemático de la totalidad del péptido por medio de una cuantificación matemática de todos los aminoácidos para todas las posiciones en el contexto de un espacio de probabilidad, pues así como en las teorías fundamentales actuales de la física(28) no hay causas para la descripción y comprensión de los fenómenos sino órdenes físicos y matemáticos acausales. Debido a que este trabajo es una caracterización física y matemática no requiere de análisis estadísticos ni del uso de grandes cantidades de datos experimentales.
CONCLUSIONESLa distribución de los aminoácidos en las 20 posiciones para las secuencias asociadas al macroestado unión presenta una distribución no equiprobable que permite asociar un microestado particular con los valores de la probabilidad, de la suma de probabilidad y de la Entropía del macroestado al que pertenece, comprobando los resultados experimentales.
Se desarrolló una caracterización física y matemática de las secuencias de alta unión de la proteína EBA-140 a los receptores del eritrocito basada en la probabilidad y la Entropía, encontrando un orden físico y matemático subyacente al fenómeno estudiado que es evidenciado en las leyes, los cálculos aplicados, y las distribuciones de probabilidad, diferenciando claramente los péptidos de alta unión de los otros péptidos de la proteína.
Se encontró que los valores de Probabilidad, Sumatoria de Probabilidad, y los de Entropía para las secuencias específicas comprobadas experimentalmente de alta unión varían entre los rangos asociados al macroestado unión, mientras que todos estos valores para las secuencias comprobadas de no unión se encuentran fuera de los rangos asociados al macroestado de unión.
DECLARACIÓN DE CONFLICTO DE INTERÉSLos autores declaran no tener conflictos de interés.
A la Facultad de Medicina de la Universidad Militar Nueva Granada por apoyar nuestras investigaciones.