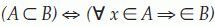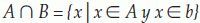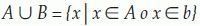MSP-1 es una proteína de membrana de superficie del merozoíto de Plasmodium falciparum que interactúa con el receptor de membrana del eritrocito, y por lo tanto es una proteína implicada en el reconocimiento del merozoito al glóbulo rojo.
La teoría de conjuntos y datos experimentales fueron utilizados para realizar una caracterización matemática de 79 secuencias de la proteína MSP-1, mediante la definición de 5 reglas asociadas a la alta unión al receptor del glóbulo rojo.
Todos los péptidos de alta unión y de baja unión fueron caracterizados acertadamente según estudios experimentales.
Estudiando más proteínas implicadas en la invasión, ésta metodología podría ser útil para diferenciar péptidos de alta unión en la proteína MSP-1 y en otras proteínas de una forma objetiva y reproducible; el fenómeno de unión puede ser descrito a partir de características matemáticas.
MSP-1 is a surface membrane protein of Plasmodium falciparum merozoites that interacts with the erythrocyte membrane receptor and therefore it is a protein involved in its recognition by the red globule.
The set theory and experimental data have been used to make a mathematical characterization of 79 different MSP-1 protein sequences, by means of the definition of five rules associated with high binding to the red globule receptor.
All the high binding and low binding peptides were correctly characterized according to experimental determinations.
Studying more proteins involved in the invasion, this methodology could be useful to detect peptides with high binding in the MSP-1 protein and in other proteins in a more objective and reproducible way. Thus, the binding phenomenon can be described starting from mathematical characteristics.
La teoría de conjuntos permite diferenciar elementos particulares a partir de reglas generales al realizar operaciones como la unión, la intersección, la diferencia y la diferencia simétrica(1). La teoría de conjuntos es una teoría matemática que se fundamenta en nociones como pertenencia, y cumple una serie de axiomas que definen las relaciones matemáticas entre elementos. Un conjunto es la reunión en un todo de objetos bien definidos y diferenciables entre sí, que se llaman elementos del mismo. Los elementos denotan relaciones de pertenencia a los conjuntos, de tal modo que si 'a' es un elemento del conjunto A, existe la relación de pertenencia a ∈ A, de lo contrario, si 'a' no es un elemento de A se denota a ∉ A. De esta misma forma, entre los conjuntos se establecen relaciones que definen las operaciones posibles entre éstos.
Ahora bien, la malaria es una de las principales causas de morbimortalidad en el mundo entero(2). Por sus características, la enfermedad se presenta principalmente en zonas tropicales, tomando allí la forma de epidemia, como ocurre en Colombia.
La reorientación e invaginación del merozoito durante la invasión al glóbulo rojo(3), pueden ser aclaradas por interacciones receptor-ligando de alta y baja afinidad. Estas interacciones de membrana receptor-ligando son cruciales para la invasión de los glóbulos rojos por los merozoitos del Plasmodium. Es probable que la disección de estas interacciones conduzca al desarrollo de nuevas estrategias inmunoprofilácticas(4). Varias proteínas del merozoito del Plasmodium falciparum han mostrado interactuar con el glóbulo rojo, y estas incluyen: La proteína-1 de superficie del merozoito (MSP-1), el antígeno de unión del eritrocito (EBA-175kDa), la proteína de unión de la glicoforina (GBP-130), y la proteína-2 de superficie del merozoito (MSP-2), entre otras(5–7).
MSP-1 es una proteína polimórfica de superficie de membrana(7), que contiene secuencias variables, semiconservadas y constantes. Durante su maduración, la proteína es sometida a una serie de rupturas proteolíticas. La primera, independiente de calcio, rompe la proteína en cuatro fragmentos: un fragmento terminal N de 83 kDa, dos fragmentos centrales de 30 y 38 kDa, y un fragmento terminal C de 42 kDa(8,9). Los cuatro fragmentos proteolíticos se autoensamblan en una asociación compleja no covalente en la membrana del merozoito, la cual está involucrada directamente en el proceso invasivo(10). Después de tal ruptura, e inmediatamente antes de la invasión, el fragmento de 42 kDa es sometido a una proteolisis dependiente de calcio por una serin proteasa presente en la membrana del merozoito(9), resultando en un fragmento terminal N de 33 kDa y un fragmento terminal C de 19 kDa. Este último permanece unido a la membrana del merozoito y es el único fragmento de proteína llevado por el parásito dentro del glóbulo rojo(3).
La MSP-1 completa(11), sus fragmentos de proteína recombinantes(12) y los péptidos sintéticos basados en la MSP-1(13) inducen inmunidad protectora parcial o completa en simios. Los péptidos también inducen inmunidad parcial en humanos infectados experimentalmente(14); anticuerpos monoclonales y policlonales dirigidos contra la MSP-1 inhiben la invasión del glóbulo rojo por merozoitos in vitro(15). Los péptidos sintéticos contra la malaria, SPf66, contienen una secuencia conservada del fragmento de 83 kDa(14).
En un trabajo previo, donde se estudiaron los aminoácidos de las secuencias de la MSP-1 involucrados en la unión e invasión a las células rojas de sangre en humanos(4); se escogieron 79 péptidos no sobrelapados con un tamaño de 20 aminoácidos, que fueron sintetizados químicamente usando la técnica de síntesis de fase sólida para múltiples péptidos(16,17), encontrando que 9 de ellos presentan alta unión al receptor del glóbulo rojo.
Los estudios de la unión de péptidos a las moléculas de HLA de clase I y II han encontrado una alta aparición de aminoácidos específicos en posiciones específicas, los denominados motivos de unión(18) que han sido el fundamento para el desarrollo de métodos predictivos basados en secuencias(19), en este trabajo se realiza una analogía de dichos motivos cuantificando aminoácidos específicos a través de reglas que definen conjuntos. Desde la perspectiva de la teoría de conjuntos en un trabajo previo, Rodríguez desarrolló un trabajo de péptidos de unión al HLA de clase II, encontrando un comportamiento caracterizable a partir de reglas halladas experimentalmente en péptidos nonaméricos específicos, logrando diferenciar péptidos de unión y no unión mediante operaciones matemáticas(20).
El propósito de la presente investigación es construir una metodología capaz de caracterizar matemáticamente la unión de péptidos del MSP-1 al receptor del glóbulo rojo, partiendo de resultados experimentales(4) y de un análisis matemático por medio de la teoría de conjuntos.
DefinicionesConjunto: selección de elementos que cumplen una regla P(x), definida previamente. El conjunto A se define como:
Subconjunto: Si A es subconjunto de B, A está contenido en B:
Intersección:La intersección de los conjuntos A y B, se define como:
Unión:La unión de los conjuntos A y B, se define como:
MATERIAL Y MÉTODOSe estudiaron 79 secuencias de péptidos no sobrelapados de la proteína MSP-1 de Plasmodium falciparum, a partir de la distribución de los aminoácidos que las conforman y de las características químicas de éstos. Posteriormente se establecieron cinco reglas que definen la pertenencia o no de un péptido a cuatro conjuntos diferentes.
La determinación de estas reglas se hizo partiendo de observaciones experimentales de los péptidos, con las propiedades químicas involucradas en la unión de los aminoácidos. Las reglas 1 y 5 cuantifican la aparición de aminoácidos cargados positivos y negativos en el péptido, la regla 2 realiza una analogía con los motivos de unión(18,19), cuantificando aminoácidos específicos en posiciones específicas, finalmente las reglas 3 y 4 cuantifican la forma en que se repiten aminoácidos específicos, para con ellas encontrar diferencias concretas de los péptidos que se unen y los que no para sintetizarlas y así poder diferenciar los péptidos de alta unión de la MSP-1
Las reglas para la determinación de los conjuntos son:
- •
Regla 1. Valores de 2, 3, 4, 6 ó 7 en la suma de la frecuencia de aparición de los aminoácidos D, E, H y R en la secuencia.
- •
Regla 2. Presencia de los aminoácidos K, N, G, A, V, L, F, M, P, R, E, T ó I en las posiciones 1, 11 y 15 o en las posiciones 2, 3, 6, 7, 8, 10, 11, 16, 19, y 20.
- •
Regla 3. Presencia de la cadena KK, TT, SS, NN-ENE, ó KXK en el péptido. Donde NN-ENE quiere decir que además de la cadena NN hay una cadena ENE separada en la secuencia y KXK se define por la presencia de dos lisinas (K) separadas por Y ó E.
- •
Regla 4. Presencia de la cadena LL, EE, MM, VV, ó VNV en el péptido.
- •
Regla 5. Valores de 4, 5, 6, 7 ó 9 en la suma de la frecuencia de aparición de los aminoácidos K, D, E, H y R en la secuencia.
A partir de las reglas anteriores se definieron los siguientes conjuntos:
- •
I = {χ | χ cumplen la primera regla}
- •
II = {χ | χ cumplen la segunda regla}
- •
III = {χ | χ cumplen la tercera regla y no cumplen la cuarta regla}
- •
IV = {χ | χ cumplen la quinta regla}
Donde χ ∈ S. Y S es el conjunto de todas las posibles cadenas peptídicas de 20 aminoácidos de MSP-1.
Posteriormente, estas reglas fueron evaluadas en los 79 péptidos no sobrelapados de la proteína MSP-1, con un tamaño de 20 aminoácidos cada uno, tomados de un estudio experimental ((4), ver Anexo 1). Finalmente se realizan las intersecciones de los cuatro conjuntos, definida ésta como el conjunto (Unión): Unión = {((I ∩ II) ∩ III) ∩ IV)}. Por tratarse de una metodología matemática no requiere de análisis estadísticos ni el uso de una gran cantidad de datos experimentales.
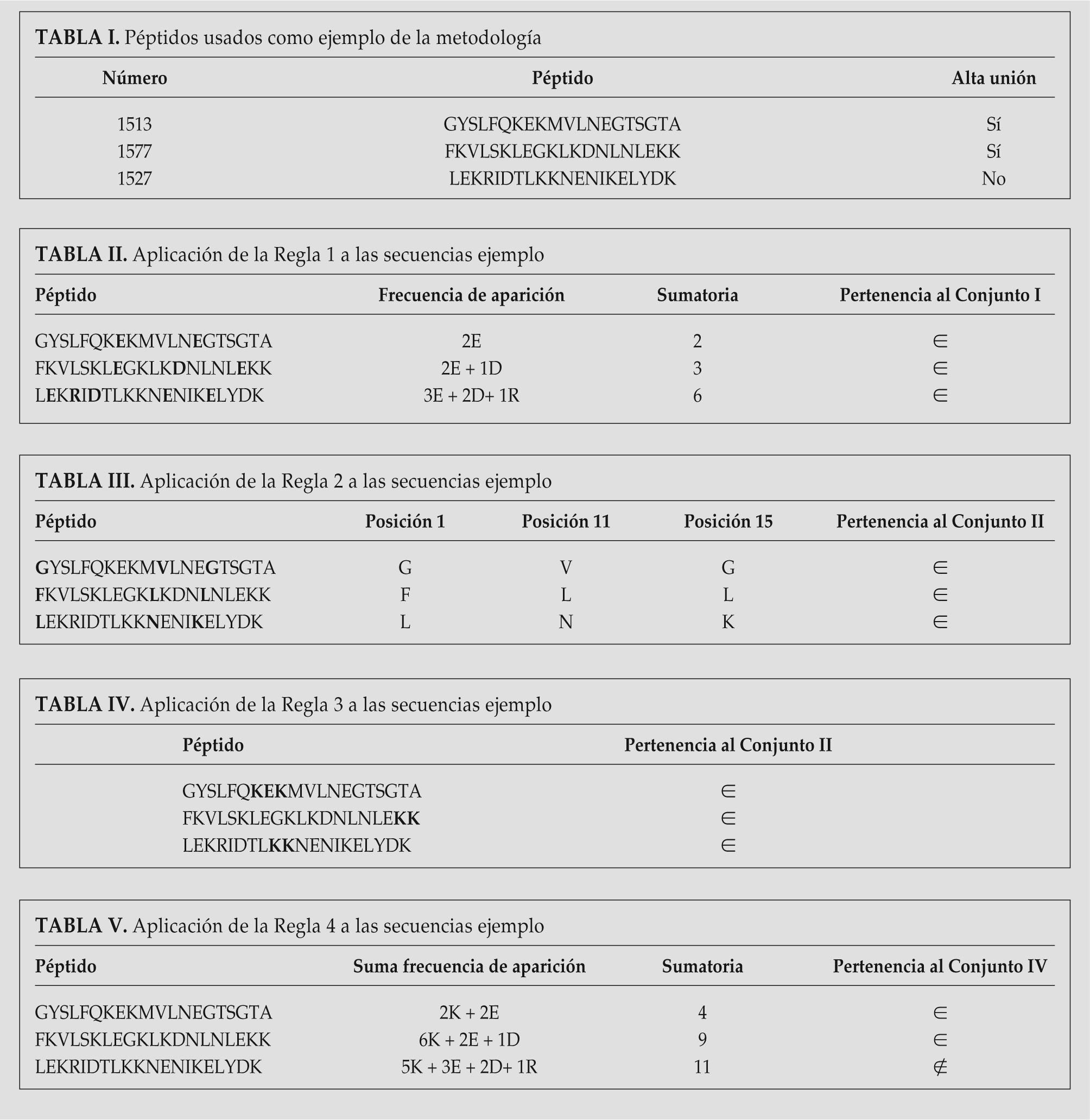
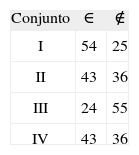
RESULTADOSDe los 79 péptidos evaluados, 54 pertenecen al conjunto I, 43 pertenecen al conjunto II, 24 pertenecen al conjunto III, y 43 pertenecen al conjunto IV (Tabla I).
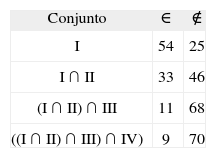
De los 79 péptidos, 33 pertenecen al conjunto I ∩ II, 11 pertenecen al conjunto (I ∩ II) ∩ III, y 9 pertenecen al conjunto ((I ∩ II) ∩ III) ∩ IV), (Tabla II), estos 9 péptidos corresponden a los péptidos de alta unión comprobados experimentalmente: 1513, 1522, 1577, 1582, 1585, 1589, 1590, 1591, 1598, siendo este conjunto el que define los péptidos de alta unión.
DISCUSIÓNEste es el primer trabajo en el que, a partir de la teoría de conjuntos, de observaciones experimentales y de reglas diferenciadoras, se caracteriza el fenómeno de alta unión de la proteína de membrana MSP-1 al receptor de glóbulo rojo, encontrando órdenes matemáticos que diferencian los péptidos que presentan alta unión, de los péptidos que no, de forma objetiva y reproducible.
Por medio de observaciones experimentales, se establecieron 5 reglas que definen la pertenencia a 4 conjuntos de péptidos. Estas reglas se basan en patrones matemáticos que representan las propiedades de las cadenas aminoacídicas componentes de los péptidos, evidenciando desde de la teoría de conjuntos órdenes matemáticos acausales asociados a los péptidos de alta unión, que permiten diferenciarlos de los péptidos de baja unión. Las operaciones entre los conjuntos establecidos por las cuatro reglas describen un orden físico y matemático acausal que determina los péptidos de alta unión al glóbulo rojo.
Este trabajo permite, mediante reglas específicas que se sintetizan con la teoría de conjuntos, encontrar un orden en la unión de los péptidos de alta unión al receptor del glóbulo rojo en el proceso de invasión a éste, a diferencia del trabajo de unión al HLA clase II basado también en la teoría de conjuntos(20) donde se diferencian péptidos de unión a la molécula presentadora en el proceso antigénico para la respuesta inmune.
Algunos trabajos de predicción de unión de péptidos usan algoritmos evolucionarios junto con redes neuronales artificiales partiendo de grandes bases de datos para predecir qué péptidos se unirán, basados en resultados experimentales(21–25). Otro tipo de desarrollo para predecir unión de péptidos es un SVM (Support Vector Machine), que no utiliza una gran cantidad de datos, sin embargo sus predicciones no obtienen altos porcentajes de correlación experimental(24). Este es un trabajo teórico práctico que desarrolla una metodología que evidencia órdenes matemáticos objetivos y reproducibles, determinados por medio de la teoría de conjuntos, cuyas correlaciones se corroboran experimentalmente. No se necesitan análisis estadísticos, pues los péptidos son caracterizados a través de reglas simples, establecidas desde la teoría de conjuntos.
Limitaciones del estudioLa metodología presentada para la determinación de péptidos de alta unión ha sido corroborada hasta ahora únicamente para caracterizar la unión al glóbulo rojo en esta proteína específica. Para su generalización sería útil estudiar reglas similares a éstas, para moléculas importantes en la unión ligando-receptor de malaria y de otras enfermedades como tuberculosis, VIH y cáncer, entre otras.
AGRADECIMIENTOSAl Grupo Insight por obligarme a publicar éste trabajo, que estaba hecho hace muchos años.
Al doctor Manuel Elkin Patarroyo por apoyar mi internado especial y mi rural especial en los años 1996 y 1997 en el Instituto de Inmunología, los cuales dediqué a profundizar en la esencia teórica acausal del Universo de la física moderna (Mecánica estadística, Mecánica cuántica y Teoría del Caos). DEDICACIÓN: A mis hijos. A Alejandro Cáceres, "científico de cafetería", quien fue mi Maestro de Física Cuántica y quien me dio formación para entender los fenómenos acausalmente y confiar en este resultado acausal en esta rama del conocimiento tan causalista y determinista, como la interacción ligando-receptor de la Biología Molecular.
CONFLICTO DE INTERÉSEl autor declara no tener conflicto de interés.