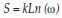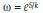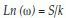El propósito de esta investigación es aplicar la teoría de predicción de unión de péptidos a la región central del HLA clase II, a los péptidos nonámeros de MSA-2, y la proteína AMA-1 del Plasmodium falciparum, y a los 492 péptidos nonámeros sobrelapados de tres proteínas teóricas, de 500 aminoácidos cada una.
Se aplicó una teoría predictiva de unión al HLA clase II basada en la proporción S/k para la predicción del fenómeno de unión de péptidos de las proteínas MSA-2 y AMA-1 a la totalidad de secuencias de 20 aminoácidos de dichas proteínas. Se calcularon los valores de probabilidad, combinatoria y entropía de 300 secuencias nonámeras sobrelapadas de la proteína MSA- 2 y 372 de AMA-1. Finalmente se construyeron tres proteínas teóricas de 500 aminoácidos cada una a partir de una simulación computacional y se aplicó la teoría para cuantificar la unión de todos los péptidos nonámeros sobrelapados de las mismas.
Se predijo que 35 secuencias de MSA-2 y 60 de AMA-1 están asociadas al macroestado de unión mientras que 265 de MSA-2 y 317 de AMA-1 están asociadas al macroestado de no unión. Se predijo que 102, 104 y 101 secuencias de las tres proteínas construidas están asociadas al macroestado de unión, mientras que las restantes 390, 388 y 391 se asocian al macroestado de no unión respectivamente.
La predicción teórica desarrollada puede facilitar la escogencia de péptidos implicados en el desarrollo de vacunas, evidenciando que existe un orden físico y matemático subyacente a la presentación antigénica.
The aim of this research is apply the predictive nonameric binding methodology to HLA class II central region, to nonameric peptides of MSA-2 and AMA-1 proteins from Plasmodium falciparum, and to 492 nonameric overlapped peptides for three theoretical proteins with size of 500 residues.
A predictive binding theory to HLA class II based on S/k proportion was applied in order to predict binding peptides of MSA-2 and AMA-1 proteins to all sequences with 20 residues size from these proteins. The probability, combinatory and entropy values were calculated for 300 nonameric overlapped sequences of MSA-2 and 372 of AMA-1. Finally three theoretical proteins of 500 residues each one were made, starting from a computational simulation and the theory was applied, quantifying binding for all nonameric overlapped peptides for these proteins.
35 sequences for MSA-2 and 60 for AMA-1 associated to binding macrostate while 265 for MSA-2 and 317 for AMA-1 associated to non binding macrostate were predicted. 102, 104 and 101 sequences associated to binding macrostate for the theoretical proteins while the others 390, 388, and 391 associated to non binding macrostate respectively were predicted.
The theoretical prediction developed can facilitate the selection of peptides implied in vaccine development, showing that mathematical and physical order lies to antigenic presentation.
Actualmente, la malaria representa la enfermedad parasitaria de mayor importancia mundial al generar cerca de 500 millones de casos/año en todo el mundo y cerca de 3 millones de muertes sólo en África(1,2). Dado que las estrategias clásicas de control han fallado, se han desarrollado múltiples trabajos dirigidos al conocimiento del proceso de invasión al humano, para el desarrollo de vacunas. Los procesos implícitos a dicha invasión están mediados por interacciones receptor ligando específicas.
La segunda de las proteinas principales de la superficie del merozoito del Plasmodium falciparum es conocida como MSA-2, y es una glicoproteína de 35±56kDa(3,4), que se expresa doce horas antes de la invasión del merozoito, y presenta su máxima concentración 42 horas después(5,6). Hace parte del grupo de antígenos reconocidos por anticuerpos que aglutinan merozoitos(7,8) y se ha encontrado que anticuerpos de MSA-2 inhiben invasión de una forma dosis-dependiente in vitro(9-11). Por otro lado, Plasmodium falciparum AMA-1 es una proteína de 83kDa caracterizada por una alta conservación en la transmembrana menor de la molécula. Dentro de su estructura, tiene un ectodominio putativo, el cual contiene 16 cisteinas, así como tres subdominios de 19, 13 y 13kDa, respectivamente(12). En el proceso de ruptura del esquizonte, esta proteína se asocia con el complejo apical y se desplaza a la superficie del merozoito(13). La función biológica de la AMA-1 es desconocida, sin embargo, podría tratarse de una proteína de unión eritrocitaria.
El HLA, o antígeno leucocitario humano es un complejo proteínico que tiene como función la presentación de antígenos a las células T para la activación de la respuesta inmune. Los antígenos asociados al HLA clase I son reconocidos por las células T CD8+, mientras que los asociados al HLA clase II son reconocidos por las células T cooperadoras CD4+(14). El HLA clase II está compuesto por dos cadenas polimórficas y su región central está formado por los dominios α1 y β1 de las dos cadenas, conformando una hendidura que constituye la región de unión a los antígenos(15). Al estar abierta en sus extremos(16-19), a ella se unen péptidos con tamaños muy variables, que oscilan entre 13 y 16 aminoácidos(20-23). Sin embargo estudios experimentales del fenómeno de unión han sugerido que sólo una región central compuesta por nueve aminoácidos es fundamental en este proceso de unión(24). Adicionalmente se ha encontrado una alta frecuencia de aparición de grupos de aminoácidos en posiciones específicas, posiciones de anclaje, denominados motivos de unión(25), determinados a partir de grupos seleccionados, tales como librerías M13 de péptidos presentados.
Dado que el HLA clase II es esencial en el reconocimiento de organismos ajenos, resulta de gran utilidad para el desarrollo de vacunas determinar si existen péptidos de las proteínas de MSA-2 y AMA-1 que puedan ser reconocidos por dicha molécula. Recientemente, Rodríguez(26) desarrolló una teoría para la predicción de péptidos a la región central del HLA clase II, con base en las teorías de probabilidad, combinatoria y entropía. En dicho trabajo, las secuencias peptídicas fueron estudiadas realizando una analogía con los macroestados de la mecánica estadística, los cuales pueden caracterizarse por múltiples particularidades, como las múltiples posibles formas de organización de las moléculas de un gas(27), que cumplen con ciertas condiciones generales que les permiten ser incluidas dentro de un mismo macroestado. Esta teoría se basó en un experimento mental físico y experimental en el cual se conceptualizó la región central de unión como un fenómeno probabilístico, en el cual estaban implicados un número finito de aminoácidos que podían tomar cada lugar, encontrando que ciertos lugares tenían una mayor probabilidad de presentar ciertos grupos de aminoácidos respecto a otros, en el caso de unirse al HLA clase II. De este modo se realizó la suposición de lo que ocurriría en el caso de encontrar un péptido con todos los aminoácidos iguales, así como un péptido que presentara todos sus aminoácidos diferentes, encontrando que los péptidos de unión se caracterizan por ciertas repeticiones y diferencias que podían cuantificarse al agrupar los aminoácidos de acuerdo a grupos y características especificas, con base en las leyes de probabilidad y combinatoria. Al tratarse de un fenómeno probabilístico, la autoorganización general del sistema podía ser evaluado con las leyes de la entropía, encontrando diferencias cuantitativas en la relación S/k en el fenómeno de unión respecto al de no unión. De este modo, se caracterizaron matemáticamente 161 péptidos, con una eficacia del 100% partiendo de péptidos teóricos, sintéticos, naturales y promiscuos, tanto de unión como de no unión. En un trabajo previo, en proceso de evaluación se aplicó esta misma metodología a dos proteínas el HER2/neu y la API m1, y se comprobaron los resultados con los hallazgos experimentales de estas proteínas y se comparó el desempeño con los resultados de los métodos de predicción de péptidos disponibles en línea de mayor cobertura alélica, obteniendo los mayores valores para la sensibilidad, valor predictivo positivo y exactitud.
Las leyes de probabilidad permiten la cuantificación de la posibilidad de la ocurrencia de un evento(28-31). Al estudiar la organización de aminoácidos para la construcción de un péptido como un fenómeno probabilístico, es posible realizar cuantificaciones que dan cuenta de la combinación de los aminoácidos en las secuencias. Por otro lado, la entropía es un concepto que ha recibido varias interpretaciones(27,32-34). Boltzmann enunció la fórmula de la entropía equiprobable, la cual se enuncia en términos del número de microestados de un sistema en equilibrio(32,33). Siguiendo la teoría desarrollada por Rodríguez(26), haciendo una analogía con los microestados de la mecánica estadística, cada conjunto de aminoácidos que conforma las secuencias de los péptidos, pueden analizarse mediante la ecuación de Boltzmann, para cuantificar el fenómeno de unión de los péptidos de las proteínas antigénicas.
En la presente investigación se aplicará la teoría de predicción de unión de péptidos a la región central del HLA clase II, a los péptidos nonámeros de MSA-2, y la proteína AMA-1, y a los 492 péptidos nonámeros sobrelapados de tres proteínas teóricas, de 500 aminoácidos cada una.
DEFINICIONESMacroestado: conjunto de secuencias que presentan alta unión o no unión al HLA clase II, por lo tanto existen dos clases de macroestados, asociados a cada una de estas condiciones específicas.
Microestado: Toda secuencia específica de nueve aminoácidos.
Tipo de secuencia: Microestados que presenten el mismo valor en su combinatoria y su evaluación con los criterios definidos.
Probabilidad Laplaciana: La probabilidad de un tipo de secuencia A es definida como la cantidad de microestados Na asociados a este tipo de secuencia dividida entre el total de posibles microestados N(29). Ver ecuación 1.
Ley combinatoria para determinar la cantidad de microestados ω: De acuerdo con la metodología desarrollada por Rodríguez(26), cada posición del péptido tiene asociada un número de posibles aminoácidos. Para calcular el número de posibles microestados asociados a un tipo de secuencia se multiplican los valores asociados a cada posición, que dependen del número de posibles aminoácidos asociados a cada lugar, los cuales a su vez están determinados por el grupo al que pertenezcan y sus repeticiones en el tipo de secuencia(30,31). Para las cuantificaciones específicas ver tablas de criterios evaluadores y tablas de grupos de aminoácidos de la teoría realizada.
Entropía: En un sistema con microestados equiprobables la entropía se define de acuerdo con la ecuación 2:
Donde k es igual a la constante de Boltzmann, 1.38x10-23 (J/k), ω los posibles microestados y S el valor de la entropía(27).
MATERIAL Y METODOInicialmente se determinaron los péptidos nonámeros sobrelapados constituyentes de las 25 secuencias no sobrelapadas de 20 aminoácidos de la proteína MSA-2, y de las 31 secuencias de 20 aminoácidos sobrelapados cada diez aminoácidos de la proteína AMA-1, así como los péptidos nonámeros sobrelapados de tres proteínas teóricas compuestas por 500 residuos. Posteriormente se aplicó la metodología desarrollada por Rodríguez(26) para la determinación de su macroestado de unión o no unión. Para ejemplificar la aplicación de la metodología a continuación se presenta un ejemplo para el péptido nonámero predicho de unión por la teoría desarrollada FLPTGAFKA que pertenece al péptido 20-mero de alta unión 4325 de la proteína AMA-1.
Paso 1: La primera posición F tiene un valor de 7 pues pertenece al grupo 1 (Tabla I); en la posición dos a L se le otorga un valor de 6 pues pertenece al grupo 1 y el valor decrece por la aparición previa de un aminoácido del mismo grupo y diferente; en la posición tres a P se le otorga un valor de 4 pues pertenece al grupo 3; a la siguiente posición, a T se le otorga un valor de 9 pues pertenece al grupo 2; la siguiente posición G toma un valor de 3, pues pertenece al grupo 3 y el valor decrece por la aparición previa de un aminoácido del mismo grupo y diferente a G; la siguiente posición A toma un valor de 6, pues pertenece al grupo de motivos para dicha posición; en la siguiente posición la F toma un valor de 1, pues el aminoácido ya había aparecido, la K toma un valor de 5, dado que está dentro del grupo de aminoácidos cargados; finalmente, en la última posición la A toma un valor de 1 dado que dicho aminoácido ya había aparecido.
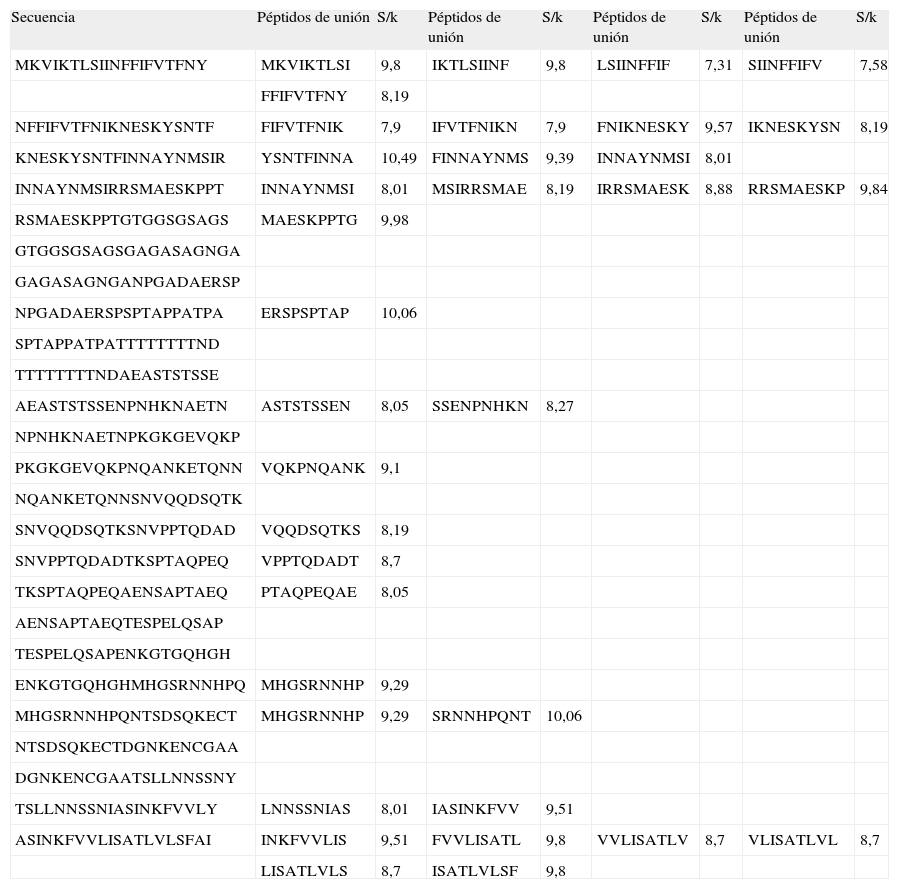
Péptidos de unión de la proteina MSA-2, junto con sus valores de la proporción S/k para los pasos finales
| Secuencia | Péptidos de unión | S/k | Péptidos de unión | S/k | Péptidos de unión | S/k | Péptidos de unión | S/k |
| MKVIKTLSIINFFIFVTFNY | MKVIKTLSI | 9,8 | IKTLSIINF | 9,8 | LSIINFFIF | 7,31 | SIINFFIFV | 7,58 |
| FFIFVTFNY | 8,19 | |||||||
| NFFIFVTFNIKNESKYSNTF | FIFVTFNIK | 7,9 | IFVTFNIKN | 7,9 | FNIKNESKY | 9,57 | IKNESKYSN | 8,19 |
| KNESKYSNTFINNAYNMSIR | YSNTFINNA | 10,49 | FINNAYNMS | 9,39 | INNAYNMSI | 8,01 | ||
| INNAYNMSIRRSMAESKPPT | INNAYNMSI | 8,01 | MSIRRSMAE | 8,19 | IRRSMAESK | 8,88 | RRSMAESKP | 9,84 |
| RSMAESKPPTGTGGSGSAGS | MAESKPPTG | 9,98 | ||||||
| GTGGSGSAGSGAGASAGNGA | ||||||||
| GAGASAGNGANPGADAERSP | ||||||||
| NPGADAERSPSPTAPPATPA | ERSPSPTAP | 10,06 | ||||||
| SPTAPPATPATTTTTTTTND | ||||||||
| TTTTTTTTNDAEASTSTSSE | ||||||||
| AEASTSTSSENPNHKNAETN | ASTSTSSEN | 8,05 | SSENPNHKN | 8,27 | ||||
| NPNHKNAETNPKGKGEVQKP | ||||||||
| PKGKGEVQKPNQANKETQNN | VQKPNQANK | 9,1 | ||||||
| NQANKETQNNSNVQQDSQTK | ||||||||
| SNVQQDSQTKSNVPPTQDAD | VQQDSQTKS | 8,19 | ||||||
| SNVPPTQDADTKSPTAQPEQ | VPPTQDADT | 8,7 | ||||||
| TKSPTAQPEQAENSAPTAEQ | PTAQPEQAE | 8,05 | ||||||
| AENSAPTAEQTESPELQSAP | ||||||||
| TESPELQSAPENKGTGQHGH | ||||||||
| ENKGTGQHGHMHGSRNNHPQ | MHGSRNNHP | 9,29 | ||||||
| MHGSRNNHPQNTSDSQKECT | MHGSRNNHP | 9,29 | SRNNHPQNT | 10,06 | ||||
| NTSDSQKECTDGNKENCGAA | ||||||||
| DGNKENCGAATSLLNNSSNY | ||||||||
| TSLLNNSSNIASINKFVVLY | LNNSSNIAS | 8,01 | IASINKFVV | 9,51 | ||||
| ASINKFVVLISATLVLSFAI | INKFVVLIS | 9,51 | FVVLISATL | 9,8 | VVLISATLV | 8,7 | VLISATLVL | 8,7 |
| LISATLVLS | 8,7 | ISATLVLSF | 9,8 |
Para el paso dos se verifica que este péptido no cumple ninguno de los criterios establecidos, por lo tanto el número de microestados asociados es 136080, la entropía de 1,63E-22, y la relación S/k de 11,82, por lo cual se realizan los pasos siguientes:
Paso 3: La primera posición F tiene un valor de 5 pues es Hidrofóbico de alta unión (Tabla II); en la posición dos a L se le otorga un valor de 5 pues pertenece al grupo 4, en la posición tres a P se le otorga un valor de 4 pues pertenece al grupo 4 y el valor decrece por la aparición previa de un aminoácido del mismo grupo; en la siguiente posición, a T se le otorga un valor de 6 pues pertenece al grupo de Puentes de hidrógeno; la siguiente posición G toma un valor de 3 pues pertenece al grupo 4 y el valor decrece por la aparición previa de un aminoácido del mismo grupo; la siguiente posición A)toma un valor de 2, pues pertenece al grupo 4 y el valor decrece por la aparición previa de un aminoácido del mismo grupo; en la siguiente posición la F toma un valor de 1, pues el aminoácido ya había aparecido; la K toma un valor de 3, dado que está dentro del grupo de cargados positivos; finalmente la última posición la A toma un valor de 1 dado que dicho aminoácido ya había aparecido.
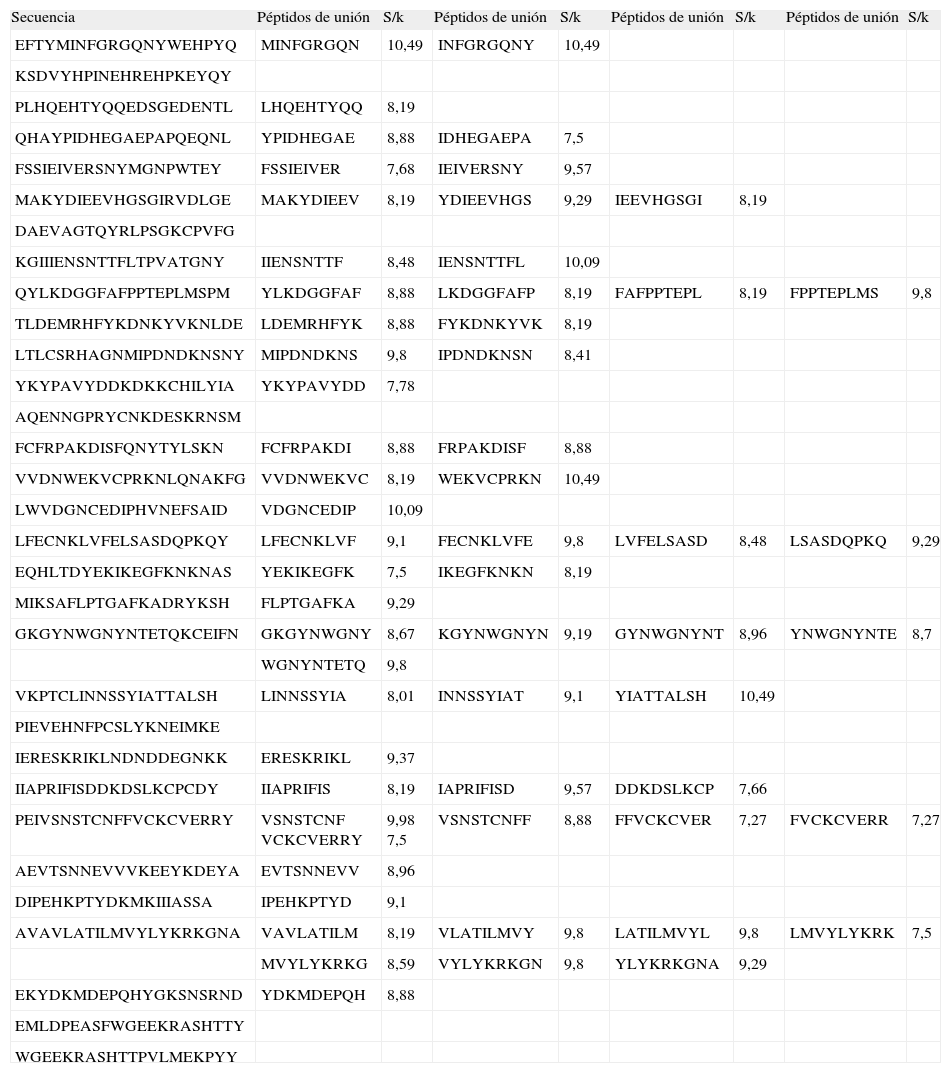
Péptidos de unión de la proteina AMA-1, junto con sus valores de la proporción S/k para los pasos finales
| Secuencia | Péptidos de unión | S/k | Péptidos de unión | S/k | Péptidos de unión | S/k | Péptidos de unión | S/k |
| EFTYMINFGRGQNYWEHPYQ | MINFGRGQN | 10,49 | INFGRGQNY | 10,49 | ||||
| KSDVYHPINEHREHPKEYQY | ||||||||
| PLHQEHTYQQEDSGEDENTL | LHQEHTYQQ | 8,19 | ||||||
| QHAYPIDHEGAEPAPQEQNL | YPIDHEGAE | 8,88 | IDHEGAEPA | 7,5 | ||||
| FSSIEIVERSNYMGNPWTEY | FSSIEIVER | 7,68 | IEIVERSNY | 9,57 | ||||
| MAKYDIEEVHGSGIRVDLGE | MAKYDIEEV | 8,19 | YDIEEVHGS | 9,29 | IEEVHGSGI | 8,19 | ||
| DAEVAGTQYRLPSGKCPVFG | ||||||||
| KGIIIENSNTTFLTPVATGNY | IIENSNTTF | 8,48 | IENSNTTFL | 10,09 | ||||
| QYLKDGGFAFPPTEPLMSPM | YLKDGGFAF | 8,88 | LKDGGFAFP | 8,19 | FAFPPTEPL | 8,19 | FPPTEPLMS | 9,8 |
| TLDEMRHFYKDNKYVKNLDE | LDEMRHFYK | 8,88 | FYKDNKYVK | 8,19 | ||||
| LTLCSRHAGNMIPDNDKNSNY | MIPDNDKNS | 9,8 | IPDNDKNSN | 8,41 | ||||
| YKYPAVYDDKDKKCHILYIA | YKYPAVYDD | 7,78 | ||||||
| AQENNGPRYCNKDESKRNSM | ||||||||
| FCFRPAKDISFQNYTYLSKN | FCFRPAKDI | 8,88 | FRPAKDISF | 8,88 | ||||
| VVDNWEKVCPRKNLQNAKFG | VVDNWEKVC | 8,19 | WEKVCPRKN | 10,49 | ||||
| LWVDGNCEDIPHVNEFSAID | VDGNCEDIP | 10,09 | ||||||
| LFECNKLVFELSASDQPKQY | LFECNKLVF | 9,1 | FECNKLVFE | 9,8 | LVFELSASD | 8,48 | LSASDQPKQ | 9,29 |
| EQHLTDYEKIKEGFKNKNAS | YEKIKEGFK | 7,5 | IKEGFKNKN | 8,19 | ||||
| MIKSAFLPTGAFKADRYKSH | FLPTGAFKA | 9,29 | ||||||
| GKGYNWGNYNTETQKCEIFN | GKGYNWGNY | 8,67 | KGYNWGNYN | 9,19 | GYNWGNYNT | 8,96 | YNWGNYNTE | 8,7 |
| WGNYNTETQ | 9,8 | |||||||
| VKPTCLINNSSYIATTALSH | LINNSSYIA | 8,01 | INNSSYIAT | 9,1 | YIATTALSH | 10,49 | ||
| PIEVEHNFPCSLYKNEIMKE | ||||||||
| IERESKRIKLNDNDDEGNKK | ERESKRIKL | 9,37 | ||||||
| IIAPRIFISDDKDSLKCPCDY | IIAPRIFIS | 8,19 | IAPRIFISD | 9,57 | DDKDSLKCP | 7,66 | ||
| PEIVSNSTCNFFVCKCVERRY | VSNSTCNF VCKCVERRY | 9,98 7,5 | VSNSTCNFF | 8,88 | FFVCKCVER | 7,27 | FVCKCVERR | 7,27 |
| AEVTSNNEVVVKEEYKDEYA | EVTSNNEVV | 8,96 | ||||||
| DIPEHKPTYDKMKIIIASSA | IPEHKPTYD | 9,1 | ||||||
| AVAVLATILMVYLYKRKGNA | VAVLATILM | 8,19 | VLATILMVY | 9,8 | LATILMVYL | 9,8 | LMVYLYKRK | 7,5 |
| MVYLYKRKG | 8,59 | VYLYKRKGN | 9,8 | YLYKRKGNA | 9,29 | |||
| EKYDKMDEPQHYGKSNSRND | YDKMDEPQH | 8,88 | ||||||
| EMLDPEASFWGEEKRASHTTY | ||||||||
| WGEEKRASHTTPVLMEKPYY |
Para el paso cuatro se verifica que este péptido no cumple ninguno de los criterios establecidos por lo tanto el número de microestados asociados es 10800, la entropía de 1,28E-22, y la relación S/k de 9,28, por lo tanto dicho péptido pertenece al macroestado Unión.
Predicciones físicas y matemáticasLa predicción teórica desarrollada por Rodríguez(26) se calcula con base en el rango de microestados y de entropía asociado a la unión, determinando el número de microestados equivalentes y la configuración específica que deben tener los péptidos de unión al HLA clase II, mediante el despeje de ω en la ecuación de Boltzmann (Ecuación 2), que es el número de microestados asociados a cada tipo de secuencia. De este modo, se realiza la deducción física y matemática de las secuencias de aminoácidos que se unen, Ecuación 3.
Después, con base en la Ecuación 2, se despeja el valor de S/k, Ecuación 4.
La proporción S/k permite predecir cuales son los valores de los péptidos asociados al macroestado de unión y cuales son los asociados al macroestado de no unión. De este modo se evalúan las proporciones S/k entre 8,55 y 12,8 para los primeros pasos y entre 6,98 y 10,5 para los últimos pasos como relacionadas con el macroestado de unión al HLA clase II de acuerdo con la teoría desarrollada previamente(26).
RESULTADOSDe los 300 péptidos nonámeros analizados para MSA-2, 35 corresponden al macroestado de unión, 11.6% respecto a la totalidad, mientras que 265 corresponden al macroestado de no unión (Tabla I). De los 377 péptidos analizados de AMA-1, 60 corresponden al macroestado de unión, 15.91% respecto a la totalidad, mientras que 317 corresponden al macroestado de no unión (Tabla II). Las proporciones S/k de los péptidos asociados al macroestado de unión oscilaron entre 7,31 y 10,49 para MSA-2, y entre 7,27 y 10,49 para AMA-1 (Tablas I y II).
De los 492 péptidos analizados en cada una de las proteínas teóricas, se encontró que 102, 104 y 101 corresponden respectivamente al macroestado de unión de cada una, mientras que las restantes 390, 391 y 388 corresponden al macroestado de no unión (ver Anexos 1, 2 y 3). El porcentaje de unión respecto a la totalidad de péptidos corresponde al 20.73% para la secuencia teórica 1, al 21.13% para la 2 y al 20.52% para la 3.
Secuencia teórica número 1 y péptidos nonámeros de unión de acuerdo con la predicción. Los números a la derecha de la numeración del péptido indican el lugar del péptido dentro de la secuencia.
| LKKGRHLNYKHFHHYDRFRYRWCFSSGIKGSEKQSWVYPTDLNSEDWLSESDHGYKVFHTMNEALAEWSFSGQVDIEMRMLKNLPKQKRGEGKWVENREVCLYEWTIKGRYLQHWCVTLRVHHEEQGKWMLPNVYQGIEQIETMKLPWEDPMMNSYLLALIMKMITPRTCALCPGMRWMFSRHLVQCSGLRIGVKQYCICTDCWGRSSTAWELGGSQECHSYYVIYMQGLENSFNDREMDAALTKTWVHLKFSKYRWNDHWNLHMQVEAQFGNYEWECNWDGVMMCDTCNWDWHHKHTQPRCNPTSNMVWDRYLWPDCQYPNHAAAQCDIHYCSFHRTRLFMSTAQEFRNWEHSDSSFTFNMDIKRTISDCMGPAWPFCPLIICYPRFLQSDKGWKKDPWSQFHNPQDMRFKGYQT NKTVEGFMYFMYRNNEVDQYKPAFVFEWTEICFMLVKIAWWCWVLEYCGFHIPYVVWPNTKCCSFQDVCHLVCAGHWSESTMKE | |||
| 1-1. LKKGRHLNY | 27-146. LPWEDPMMN | 53-255. YRWNDHWNL | 79-423. FMYFMYRNN |
| 2-7. LNYKHFHHY | 28-148. WEDPMMNSY | 54-257. WNDHWNLHM | 80-424. MYFMYRNNE |
| 3-13. HHYDRFRYR | 29-152. MMNSYLLAL | 55-271. FGNYEWECN | 81-425. YFMYRNNEV |
| 4-15. YDRFRYRWC | 30-153. MNSYLLALI | 56-274. YEWECNWDG | 82-426. FMYRNNEVD |
| 5-16. DRFRYRWCF | 31-156. YLLALIMKM | 57-276. WECNWDGVM | 83-428. YRNNEVDQY |
| 6-22. WCFSSGIKG | 32-158. LALIMKMIT | 58-280. WDGVMMCDT | 84-436. YKPAFVFEW |
| 7-24. FSSGIKGSE | 33-160. LIMKMITPR | 59-283. VMMCDTCNW | 85-440. FVFEWTEIC |
| 8-25. SSGIKGSEK | 34-161. IMKMITPRT | 60-308. MVWDRYLWP | 86-441. VFEWTEICF |
| 9-28. IKGSEKQSW | 35-162. MKMITPRTC | 61-309. VWDRYLWPD | 87-442. FEWTEICFM |
| 10-42. LNSEDWLSE | 36-165. ITPRTCALC | 62-310. WDRYLWPDC | 88-447. ICFMLVKIA |
| 11-47. WLSESDHGY | 37-167. PRTCALCPG | 63-313. YLWPDCQYP | 89-449. FMLVKIAWW |
| 12-48. LSESDHGYK | 38-172. LCPGMRWMF | 64-320. YPNHAAAQC | 90-450. MLVKIAWWC |
| 13-61. MNEALAEWS | 39-176. MRWMFSRHL | 65-335. FHRTRLFMS | 91-451. LVKIAWWCW |
| 14-68. WSFSGQVDI | 40-192. IGVKQYCIC | 66-340. LFMSTAQEF | 92-452. VKIAWWCWV |
| 15-74. VDIEMRMLK | 41-197. YCICTDCWG | 67-348. FRNWEHSDS | 93-454. IAWWCWVLE |
| 16-76. IEMRMLKNL | 42-204. WGRSSTAWE | 68-351. WEHSDSSFT | 94-456. WWCWVLEYC |
| 17-81. LKNLPKQKR | 43-211. WELGGSQEC | 69-358. FTFNMDIKR | 95-457. WCWVLEYCG |
| 18-84. LPKQKRGEG | 44-213. LGGSQECHS | 70-362. MDIKRTISD | 96-463. YCGFHIPYV |
| 19-88. KRGEGKWVE | 45-222. YYVIYMQGL | 71-364. IKRTISDCM | 97-466. FHIPYVVWP |
| 20-94. WVENREVCL | 46-223. YVIYMQGLE | 72-372. MGPAWPFCP | 98-468. IPYVVWPNT |
| 21-95. VENREVCLY | 47-234. FNDREMDAA | 73-376. WPFCPLIIC | 99-470. YVVWPNTKC |
| 22-103. YEWTIKGRY | 48-236. DREMDAALT | 74-378. FCPLIICYP | 100-471. VVWPNTKCC |
| 23-134. VYQGIEQIE | 49-239. MDAALTKTW | 75-381. LIICYPRFL | 101-481. FQDVCHLVC |
| 24-138. IEQIETMKL | 50-243. LTKTWVHLK | 76-395. WKKDPWSQF | 102-484. VCHLVCAGH |
| 25-141. IETMKLPWE | 51-247. WVHLKFSKY | 77-411. FKGYQTNKT | |
| 26-144. MKLPWEDPM | 52-248. VHLKFSKYR | 78-420. VEGFMYFMY | |
Secuencia teórica número 2 y péptidos nonámeros de unión de acuerdo con la predicción. Los números a la derecha de la numeración del péptido indican el lugar del péptido dentro de la secuencia.
| QECPVTSRDHMLCAIVDPYDMSMSPRGRRDWFPVKWIYEIQFQMWWETNTFMVISDSAWRPPQNTAARWVECMEGRYISQIAWESECIFAQHGHPQPYKGFCCYNVHCDSVSKRHLSNRQDACLPAKDWFPISVMQYNFITWWWNFDYNMITSWHKNWAGHCSMPRRADWDTRRRWHKNCKEDIKQVWKKANGVWCSTKVGPMMGECDLGTSMCWNKNDEETLRGMRVHNWCRNCMNARVRANHGWEYMMLCNITCYRYGQVGDQENRNVDEDARLLIKWDWVMYNTSHADYEFSRNMTTYMIVTEWMLCIDCIEMGMHKYDLKWNGCKTLHMPLWNRNDCLYIVTFGPQREIKWVSATYMGNGSHYDFSGSWHVPGYRVHYTFSMIIYINSYHMNCVEFPNDSWWRHAEQSDVLNERDRHHLELFMCNYPQLESAMDVDYTFLTRRMDCCWWHMGIPHLYCEPCAPFVMKNEMWHAHRQFFRIMMFHFGYDATNLDRWV | |||
| 1-15. IVDPYDMSM | 27-111. VSKRHLSNR | 53-277. LIKWDWVMY | 79-389. YINSYHMNC |
| 2-16. VDPYDMSMS | 28-124. LPAKDWFPI | 54-278. IKWDWVMYN | 80-395. MNCVEFPND |
| 3-19. YDMSMSPRG | 29-140. ITWWWNFDY | 55-280. WDWVMYNTS | 81-398. VEFPNDSWW |
| 4-21. MSMSPRGRR | 30-142. WWWNFDYNM | 56-294. FSRNMTTYM | 82-405. WWRHAEQSD |
| 5-23. MSPRGRRDW | 31-143. WWNFDYNMI | 57-298. MTTYMIVTE | 83-406. WRHAEQSDV |
| 6-25. PRGRRDWFP | 32-154. WHKNWAGHC | 58-301. YMIVTEWML | 84-423. LELFMCNYP |
| 7-28. RRDWFPVKW | 33-164. MPRRADWDT | 59-302. MIVTEWMLC | 85-433. LESAMDVDY |
| 8-31. WFPVKWIYE | 34-172. TRRRWHKNC | 60-303. IVTEWMLCI | 86-437. MDVDYTFLT |
| 9-32. FPVKWIYEI | 35-176. WHKNCKEDI | 61-307. WMLCIDCIE | 87-443. FLTRRMDCC |
| 10-34. VKWIYEIQF | 36-187. VWKKANGVW | 62-309. LCIDCIEMG | 88-444. LTRRMDCCW |
| 11-36. WIYEIQFQM | 37-188. WKKANGVWC | 63-310. CIDCIEMGM | 89-445. TRRMDCCWW |
| 12-37. IYEIQFQMW | 38-200. VGPMMGECD | 64-311. IDCIEMGMH | 90-446. RRMDCCWWH |
| 13-38. YEIQFQMWW | 39-203. MMGECDLGT | 65-314. IEMGMHKYD | 91-447. RMDCCWWHM |
| 14-40. IQFQMWWET | 40-204. MGECDLGTS | 66-318. MHKYDLKWN | 92-448. MDCCWWHMG |
| 15-44. MWWETNTFM | 41-215. WNKNDEETL | 67-323. LKWNGCKTL | 93-452. WWHMGIPHL |
| 16-45. WWETNTFMV | 42-226. MRVHNWCRN | 68-331. LHMPLWNRN | 94-453. WHMGIPHLY |
| 17-51. FMVISDSAW | 43-228. VHNWCRNCM | 69-335. LWNRNDCLY | 95-457. IPHLYCEPC |
| 18-54. ISDSAWRPP | 44-231. WCRNCMNAR | 70-367. YDFSGSWHV | 96-460. LYCEPCAPF |
| 19-59. WRPPQNTAA | 45-232. CRNCMNARV | 71-369. FSGSWHVPG | 97-461. YCEPCAPFV |
| 20-77. YISQIAWES | 46-236. MNARVRANH | 72-375. VPGYRVHYT | 98-468. FVMKNEMWH |
| 21-81. IAWESECIF | 47-248. YMMLCNITC | 73-378. YRVHYTFSM | 99-469. VMKNEMWHA |
| 22-88. IFAQHGHPQ | 48-249. MMLCNITCY | 74-382. YTFSMIIYI | 100-474. MWHAHRQFF |
| 23-89. FAQHGHPQP | 49-251. LCNITCYRY | 75-384. FSMIIYINS | 101-475. WHAHRQFFR |
| 24-98. YKGFCCYNV | 50-259. YGQVGDQEN | 76-386. MIIYINSYH | 102-478. HRQFFRIMM |
| 25-104. YNVHCDSVS | 51-262. VGDQENRNV | 77-387. IIYINSYHM | 103-484. IMMFHFGYD |
| 26-106. VHCDSVSKR | 52-276. LLIKWDWVM | 78-388. IYINSYHMN | 104-485. MMFHFGYDA |
Secuencia teórica número 3 y péptidos nonámeros de unión de acuerdo con la predicción. Los números a la derecha de la numeración del péptido indican el lugar del péptido dentro de la secuencia.
| AVYSFSVWNNVNSEYCLCNEIIHVNMMKWCMVALTNNHLMSKYPESNIEEGAECDIVFPCTSGSSTYVRHFTICHPKIKSMFKIMQMQNDAMHVNSYDPNMIMIGSYEPGPGNTHVYWGCEQNKHWCSDLYAMKCQHNGTETWGNGPFFWGHDSCIHQLKESIAMLKHMNAQSYMRRIVPRKKKKWSHEYALLARDESYPNDYNNEWFGFSDIAYKKKWFPKREAYYGWCGVHQHHLTHLDGILATPDWRRVGSLLQNKRWMGGNKYYKRITVQPASQDSQTSLWRWWNEMAVAVVTVQMDNADPCTRHSGGQYDLNFVKQSTYKSDFHHPIPFGAHGDRHYAAYWMIHKGQYWGKWSRWCQAKVMFWYYDTDPHDPWFRRTCDDMKYFVGAEHNQCWDYSEIQDERRIAMNVVIQGGFVNRKRHNERCMYLCIHSGHMIYNRPHVLFPGWMRWMGNNCMVVFGWYAIPLSTFSVCQVFMDVFFQIRQAYTTCCANIYFE | |||
| 1-2. VYSFSVWNN | 27-97. YDPNMIMIG | 53-273. VQPASQDSQ | 79-414. VIQGGFVNR |
| 2-3. YSFSVWNNV | 28-101. MIMIGSYEP | 54-284. LWRWWNEMA | 80-432. LCIHSGHMI |
| 3-5. FSVWNNVNS | 29-102. IMIGSYEPG | 55-285. WRWWNEMAV | 81-434. IHSGHMIYN |
| 4-6. SVWNNVNSE | 30-103. MIGSYEPGP | 56-287. WWNEMAVAV | 82-446. VLFPGWMRW |
| 5-7. VWNNVNSEY | 31-107. YEPGPGNTH | 57-288. WNEMAVAVV | 83-447. LFPGWMRWM |
| 6-8. WNNVNSEYC | 32-118. WGCEQNKHW | 58-290. EMAVAVVTV | 84-448. FPGWMRWMG |
| 7-11. VNSEYCLCN | 33-138. NGTETWGNG | 59-291. MAVAVVTVQ | 85-450. GWMRWMGNN |
| 8-15. YCLCNEIIH | 34-156. IHQLKESIA | 60-293. VAVVTVQMD | 86-451. WMRWMGNNC |
| 9-17. LCNEIIHVN | 35-159. LKESIAMLK | 61-295. VVTVQMDNA | 87-452. MRWMGNNCM |
| 10-21. IIHVNMMKW | 36-163. IAMLKHMNA | 62-318. FVKQSTYKS | 88-454. WMGNNCMVV |
| 11-22. IHVNMMKWC | 37-175. MRRIVPRKK | 63-324. YKSDFHHPI | 89-455. MGNNCMVVF |
| 12-24. VNMMKWCMV | 38-186. WSHEYALLA | 64-328. FHHPIPFGA | 90-460. MVVFGWYAI |
| 13-26. MMKWCMVAL | 39-192. LLARDESYP | 65-334. FGAHGDRHY | 91-461. VVFGWYAIP |
| 14-32. VALTNNHLM | 40-199. YPNDYNNEW | 66-345. YWMIHKGQY | 92-468. IPLSTFSVC |
| 15-34. LTNNHLMSK | 41-203. YNNEWFGFS | 67-346. WMIHKGQYW | 93-470. LSTFSVCQV |
| 16-43. YPESNIEEG | 42-207. WFGFSDIAY | 68-348. IHKGQYWGK | 94-473. FSVCQVFMD |
| 17-48. IEEGAECDI | 43-213. IAYKKKWFP | 69-353. YWGKWSRWC | 95-475. VCQVFMDVF |
| 18-58. FPCTSGSST | 44-219. WFPKREAYY | 70-354. WGKWSRWCQ | 96-478. VFMDVFFQI |
| 19-67. YVRHFTICH | 45-220. FPKREAYYG | 71-366. MFWYYDTDP | 97-479. FMDVFFQIR |
| 20-73. ICHPKIKSM | 46-226. YYGWCGVHQ | 72-370. YDTDPHDPW | 98-480. MDVFFQIRQ |
| 21-78. IKSMFKIMQ | 47-229. WCGVHQHHL | 73-378. WFRRTCDDM | 99-482. VFFQIRQAY |
| 22-81. MFKIMQMQN | 48-232. VHQHHLTHL | 74-379. FRRTCDDMK | 100-486. IRQAYTTCC |
| 23-82. FKIMQMQND | 49-237. LTHLDGILA | 75-380. RRTCDDMKY | 101-490. YTTCCANIY |
| 24-84. IMQMQNDAM | 50-240. LDGILATPD | 76-407. RRIAMNVVI | |
| 25-85. MQMQNDAMH | 51-249. WRRVGSLLQ | 77-411. MNVVIQGGF | |
| 26-94. VNSYDPNMI | 52-261. WMGGNKYYK | 78-413. VVIQGGFVN | |
Este es el primer trabajo donde se realiza una predicción de péptidos nonámeros de MSA-2 y AMA-1 que pueden unirse al HLA clase II con base en una teoría basada en las leyes de probabilidad, combinatoria y entropía, determinando que existen 35 péptidos incluidos dentro del macroestado de unión para MSA-2, y 60 para AMA-1 como posibles antígenos útiles para el desarrollo de vacunas. Adicionalmente se predijeron péptidos de unión en tres proteínas teóricas, encontrando 102, 104 y 101 péptidos de unión respectivamente, evidenciando física y matemáticamente que el fenómeno de unión es caracterizado por una alta especificidad útil en su predicción. Las proteínas teóricas fueron construidas sin ningún parámetro de ordenamiento, pues el algoritmo equiprobable cumple con las condiciones de ser un generador de números pseudo aleatorios, sin embargo se encontró un orden constante de la proporción de péptidos predichos respecto a la totalidad posible cercano al 20%, evidenciando un orden subyacente a este fenómeno aparentemente aleatorio.
Trabajos anteriores en predicción de unión de péptidos han utilizado Redes neuronales artificiales, ANN por sus siglas en ingles, programación lineal, vectores de máquina, entre otros, con el objetivo de cuantificar la unión de péptidos al HLA(35-38). Uno de los trabajos más recientes desarrollados, disponible en internet y de amplia cobertura alélica es el NetMHCIIPAN(39), basado en redes neuronales; su entrenamiento integra datos de todos los alelos, región central de péptidos, composición y tamaño de los residuos de flanqueamiento de los terminales N y C, tamaño del péptido recurso, así como la afinidad normalizada de unión. Este método supone que la integración de todos estos datos en una red neuronal permite la predicción del fenómeno de unión al HLA clase II, sin embargo sus parámetros dependen de la muestra de entrenamiento, por lo que los resultados están condicionados a la misma y a la muestra usada para probarlo, haciendo limitada su generalización. A diferencia de estos planteamientos, este trabajo se basa en una metodología de carácter general que parte de una inducción física con 7 péptidos nonámeros, donde se desarrolla una metodología que no requiere entrenamientos y además no depende de la muestra de estudio para desarrollarse, pues está basada en un experimento mental en el contexto de leyes físicas y matemáticas permitiendo cuantificar la totalidad de posibilidades existentes de péptidos(26).
El oncogen HER-2/neu es reconocido por producir una respuesta efectiva como antígeno tumoral, especialmente en cáncer de mama y de ovario, por lo cual se considera un buen candidato para desarrollar vacunas(40), mientras que el API m1 constituye un tratamiento adecuado para los pacientes que sufren de graves reacciones a picaduras de abeja(41). Siete secuencias del HER-2/neu estudiadas experimentalmente (HER62, HER605, HER648, HER765, HER822, HER883, HER1124), así como la totalidad de péptidos nonámeros del API m1 fueron evaluados con la teoría utilizada en el presente trabajo, comprobando los resultados con los hallazgos experimentales de estas proteínas y se comparó el desempeño con los resultados de los métodos de predicción de péptidos disponibles en línea de mayor cobertura alélica, obteniendo los mayores valores para la sensibilidad, valor predictivo positivo y exactitud.
La teoría planteada deja a un lado los costosos procesos experimentales de ensayo y error, por predicciones fisicas y matemáticas logrando una simplificación en la escogencia de los péptidos. En este caso, en lugar de realizar un análisis de la totalidad de las secuencias de las proteínas, los esfuerzos del trabajo de laboratorio se dirigirían al 11.67% de los péptidos en el caso de la proteína de MSA-2 y al 15.92% en la proteína AMA-1, pues son las que presentan las características matemáticas necesarias para unirse la HLA II según la teoría aquí planteada.
Como en las teorías fundamentales actuales de la física(34,42,43) no hay causas sino órdenes físicos y matemáticos acausales para la descripción y comprensión del fenómeno estudiado. Por ser una teoría no requiere de análisis estadísticos ni del uso de grandes cantidades de datos experimentales. Desde esta perspectiva física acausal han sido desarrolladas investigaciones en diversos campos de la medicina con resultados de aplicación experimental y clínica. Por ejemplo, la teoría de conjuntos ha sido utilizada para el desarrollo de una caracterización del fenómeno de unión de la proteína MSP-1 al receptor de glóbulo rojo(44), así como a la unión de péptidos nonaméricos al HLA clase II(45). Del mismo modo, con base en las teorías de probabilidad y entropía se caracterizó la unión entre el receptor del eritrocito y los péptidos de la proteina MSP-1(46). Siguiendo este camino, la teoría desarrollada(26) logra simplificar este fenómeno tan complejo, mediante una generalización que obvia la especificidad alélica, caracterizando el fenómeno de unión a partir de representaciones numéricas de tipos de secuencias y no de aminoácidos específicos. Al transformar la información experimental en información numérica en el contexto de leyes de la física este trabajo evidencia un orden físico y matemático subyacente al fenómeno de unión entre el péptido y el HLA clase II, desde una perspectiva acausal que permite realizar predicciones útiles para el desarrollo de vacunas.
DECLARACIÓN DE CONFLICTO DE INTERÉSLos autores declaran no tener conflictos de interés.
DEDICACIÓNA nuestros hijos.
A la Universidad Militar Nueva Granada, en especial al Doctor Estrada y al Doctor Forero, por apoyar al Grupo de Investigación Insight.