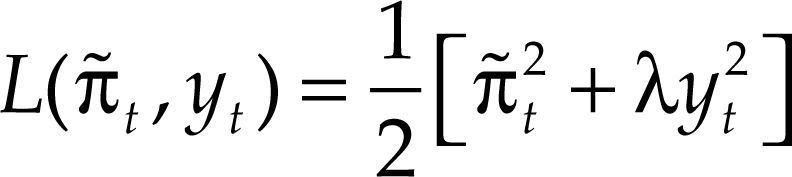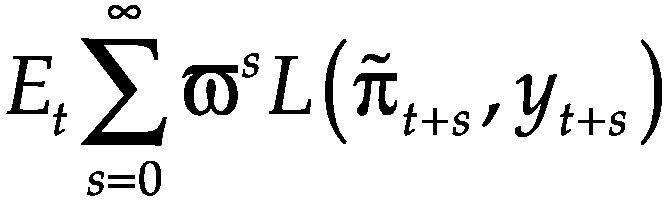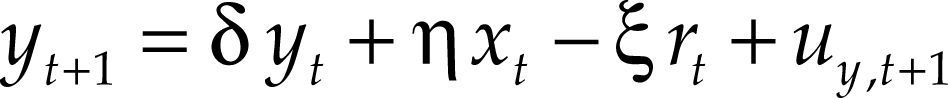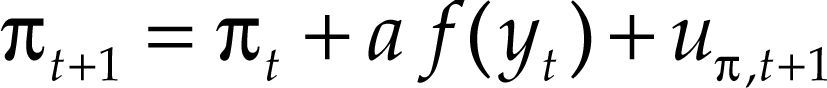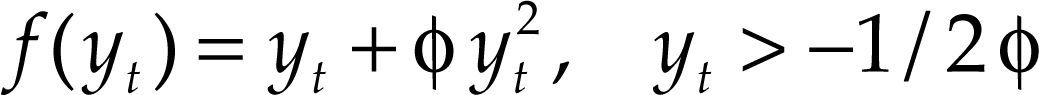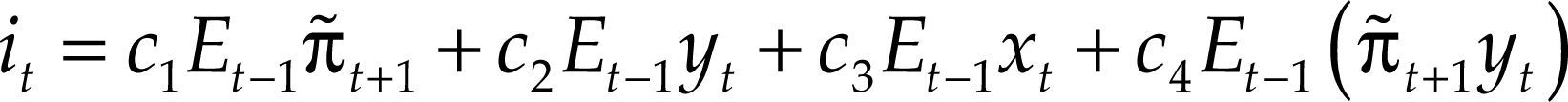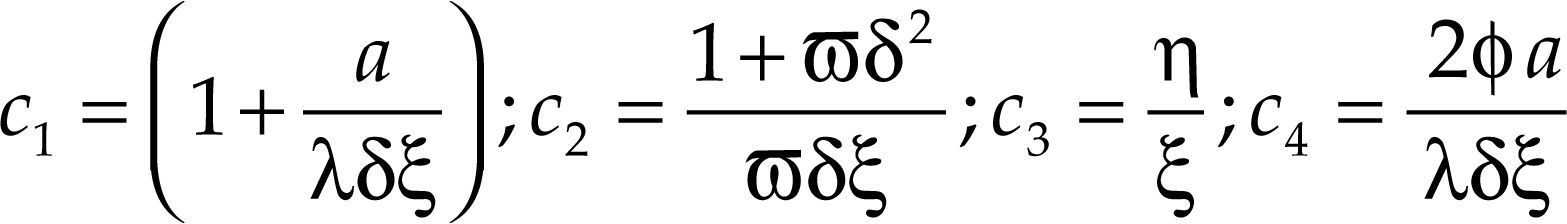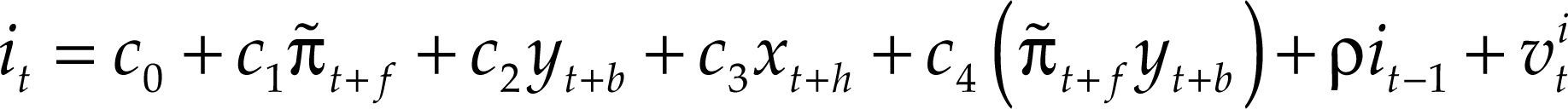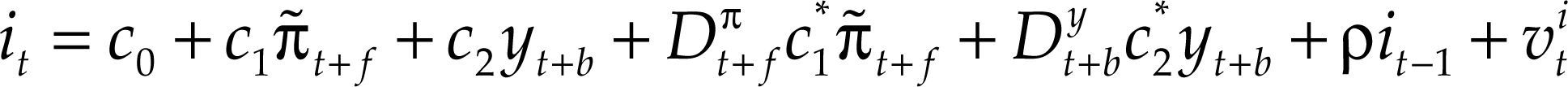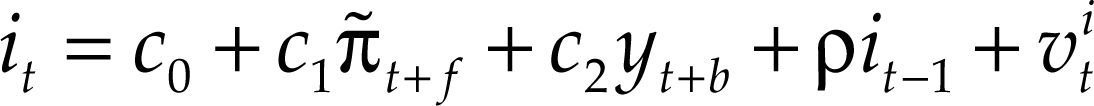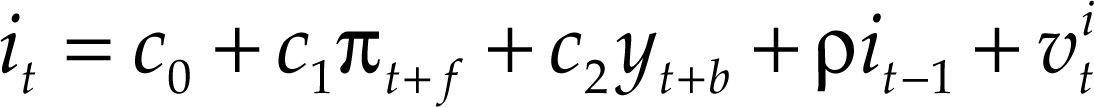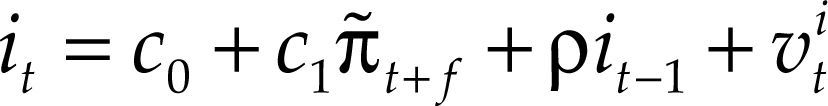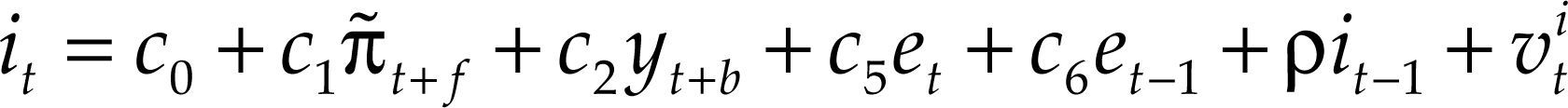Los bancos centrales pueden adoptar un comportamiento asimétrico cuando establecen los tipos de interés a corto plazo. Esta posibilidad existe si la autoridad monetaria asume una función de preferencias asimétrica o si la estructura económica presenta una curva de Phillips no lineal. En tal caso, el banco central responde con desigual intensidad ante las desviaciones positivas de la inflación respecto de su objetivo, que ante desviaciones negativas. Lo mismo cabría esperar de las respuestas ante las desviaciones de la producción respecto de la producción potencial. Mediante el MGM realizamos la contrastación de diferentes reglas óptimas de política monetaria. Y con el propósito de probar la robustez de los resultados, investigamos la presencia de asimetrías a través de variables ficticias para las desviaciones de la inflación y la brecha del producto. En ambos enfoques, el principal resultado es la ausencia de comportamientos asimétricos en la conducción de la política monetaria por parte de la Fed.
La innovación financiera en productos y medios de pago imprime sobre los agregados monetarios una dosis de inestabilidad que dificulta su control por parte del banco central (BC). Ante esta situación, el instrumento que utiliza un BC con objetivo de estabilidad de precios es el tipo de interés nominal a corto plazo. Utilizando las operaciones de mercado abierto, el BC orienta el proceso de transmisión monetaria a través del efecto del tipo de interés sobre los componentes más dinámicos de la demanda agregada. El tipo de interés nominal será modificado siguiendo el principio de Taylor (1993), según el cual, el tipo de interés real deberá aumentar cuando la inflación supere su objetivo y en situaciones de output gap o brecha del producto positiva.
Por otra parte, la autoridad monetaria deberá resolver el problema de optimización consistente en la minimización de su función de pérdidas, sujeta a la estructura de la economía. En la primera, el BC pondera las desviaciones de la inflación y de la producción respecto de sus objetivos. La estructura de la economía está representada por una curva de Phillips o una función de oferta agregada que relacionan paro o producción e inflación, y una curva IS que muestra la relación entre la producción y el tipo de interés en el equilibrio del mercado de bienes y servicios.
La regla de política monetaria que adopta el BC será la función de reacción óptima del problema de optimización al que se enfrenta la autoridad monetaria. El BC aumentará (reducirá) el tipo de interés nominal a corto plazo cuando la tasa de inflación y el crecimiento de la producción real superen (se sitúen por debajo de) los objetivos establecidos.
Entendemos que existe simetría en el comportamiento del BC cuando éste modifica el tipo de interés con igual intensidad cuando la inflación se sitúa por encima o por debajo del objetivo; es decir, el BC aumenta el tipo de interés cuando la desviación de la inflación es positiva y lo reduce en la misma proporción cuando la desviación de la inflación es negativa. Y lo mismo reacciona respecto a la brecha del producto. Por el contrario, existe asimetría en el comportamiento cuando la reacción del BC es de intensidad diferente cuando las desviaciones son positivas frente a la reacción que experimenta ante desviaciones negativas.
Cuando la función que representa las preferencias del BC (función de preferencias o función de pérdidas) es cuadrática y la función de oferta agregada es lineal, como en Svensson (1997), la función de reacción del BC es una función lineal o simétrica, como en Taylor (1993) o en Clarida, Galí y Gertler (1998; 2000).
Un enfoque separado de la tradicional función de pérdidas cuadrática, que se describe en la siguiente sección, surge en la primera década del siglo XXI en torno a la potencial asimetría en el comportamiento del BC.
El presente trabajo tiene por objetivo rechazar la hipótesis de asimetría en las decisiones de política monetaria adoptadas por la Reserva Federal (Fed) durante el periodo 1966-2012, que dividiremos en dos submuestras, utilizando como línea divisoria el momento de la llegada de Paul Volcker a la presidencia de la Fed. Para realizar este análisis, estimaremos la función de reacción de la autoridad monetaria estadounidense, utilizando el método generalizado de los momentos (MGM) con datos trimestrales. A su vez, la posible presencia de asimetrías será abordada a través de la inclusión de variables ficticias para la inflación y la brecha del producto.
Incluimos en el periodo analizado la importante crisis financiera y económica que alcanzó su punto más álgido en el 2008 con la quiebra del banco de inversión Lehman Brothers. Al recortar los tipos de interés hasta cerca de cero en diciembre de 2008, la Fed puso en marcha una política monetaria no convencional (quantitative easing) que incluyó medidas como la provisión de cantidades extraordinarias de liquidez a las instituciones financieras en condiciones favorables, el abastecimiento de liquidez a diferentes segmentos de los mercados de crédito y la adquisición de títulos financieros de deuda pública y privada a largo plazo.
Cuando abordamos la linealidad de la regla de política monetaria de la Fed, incluiremos en el análisis tres variables exógenas de especial relevancia en la economía estadounidense: la oferta monetaria, la deuda pública (que alcanzó niveles muy elevados en los últimos años) y el tipo de cambio real.
Tras esta introducción, en la sección dos exponemos el estado de la literatura sobre reglas asimétricas; en la sección tercera se explica el modelo a utilizar en el análisis empírico; las secciones cuatro y cinco presentan los datos empleados y los resultados del trabajo empírico. Finalmente, ofrecemos algunas conclusiones.
EL ESTADO DE LA LITERATURA SOBRE REGLAS ASIMETRICASUna cuestión central en materia de reglas asimétricas de política monetaria es conocer el origen de las asimetrías. La literatura disponible establece dos posibles causas que explicarían un comportamiento asimétrico por parte del BC en la gestión de la política monetaria: una relacionada con las preferencias de política y otra con la pendiente del trade-off entre inflación y la brecha del producto. Se ha de notar que es suficiente una sola de ellas para configurar una función de reacción no lineal del BC.
Respecto a la primera causa, una función de preferencias asimétrica supone que los policy makers o hacedores de política económica muestran una diferente aversión ante las desviaciones positivas de la inflación que ante las negativas o ante una brecha positiva o negativa y, en consecuencia, modifican el tipo de interés con diferente intensidad en función del signo de la desviación.
Para representar dichas preferencias asimétricas por parte del BC, Dolado, María-Dolores y Ruge-Murcia (2002), Ruge-Murcia (2001), Surico (2003; 2007a; 2007b), Nobay y Peel (2003), Caglayan, Jehan y Mouratidis (2012), entre otros, adoptan una función de pérdidas lineal-exponencial, como en Varian (1975), Zellner (1986) y Nobay y Peel (1998).1 A diferencia de los autores anteriores, Cukierman (2000; 2004), Gerlach (2000), Bec, Salem y Collard (2002) y Cukierman y Muscatelli (2007) no parten de una función de pérdidas tipo linex, sino de una función cuadrática definida por tramos, en la que las pérdidas del BC dependen del momento del ciclo económico.
Por lo que se refiere al trade-off entre inflación y paro, que describe la curva de Phillips, o entre la desviación de la inflación y la brecha del producto, que determina la forma de la curva de oferta agregada (OA), puede ser no lineal y adoptar, por el contrario, una forma convexa o cóncava. Así, ante una curva de oferta agregada convexa, incrementos sucesivos de la brecha se corresponden con cambios crecientes de la desviación de la inflación respecto de su objetivo. La literatura recoge varios orígenes de un trade-off no lineal en el corto plazo entre inflación y producción. En primer lugar, la rigidez a la baja de los salarios monetarios es la justificación keynesiana de una curva de Phillips (o OA) convexa. Las rigideces salariales dan lugar a un trade off inflación-producto a corto plazo con una mayor pendiente cuando el producto se sitúa por encima que cuando está por debajo de su nivel natural.
Ante una disminución de la demanda y una caída en los precios, los keynesianos rechazan la capacidad del mercado laboral para ajustarse a la nueva situación a través del mecanismo de los salarios monetarios. Si el equilibrio en el mercado del factor trabajo no se alcanza a través de salarios flexibles, se conseguirá vía cantidades, apareciendo una disparidad entre oferta y demanda de empleo. Por lo tanto, la rigidez a la baja de los salarios producirá una situación de desempleo involuntario, y una mayor caída en la producción que la que se produciría en una situación de salarios flexibles. En consecuencia, la curva de oferta agregada es más plana para aquellos niveles de producción compatibles con el tramo horizontal (rigidez a la baja de los salarios nominales) de la oferta de empleo, y aumenta su pendiente para salarios nominales superiores a la banda de rigidez. El tramo más plano de la oferta agregada se corresponde con un tramo más plano de la curva de Phillips. Así, una política expansiva de demanda, fiscal o monetaria, sobre el tramo más plano de la oferta agregada provoca un menor aumento de los precios y un mayor aumento de la producción (un mayor incremento del empleo). Sobre el tramo más plano de la curva de Phillips, un menor incremento de la inflación es suficiente para reducir el desempleo en mayor proporción.
En segundo lugar, la llamada hipótesis de capacidad restringida justifica la convexidad de la curva de Phillips y de la oferta agregada (Laxton, Meredith y Rose, 1995). Ante un aumento continuo en el nivel agregado de gasto en la economía, las firmas pueden tener problemas para ampliar su capacidad de producción en el corto plazo debido a la presencia de costos de ajuste de capital. Estos costos están asociados a restricciones tecnológicas (costos en que incurre una empresa cuando decide modernizar o ampliar su stock de capital) o financieras (racionamiento del crédito). Ambas impiden a las empresas desarrollar proyectos de inversión, limitando así la posibilidad de ampliar su stock de capital. De esta manera, las restricciones a la ampliación de la capacidad disponible harán que los precios se incrementen de manera exponencial en la medida que la economía no pueda elevar su nivel de producción al mismo ritmo que una demanda en expansión. Por lo tanto, en el corto plazo, la curva de Phillips y la curva OA son convexas, con una asíntota vertical cuando la economía alcanza el límite de la capacidad.
Entre los trabajos que derivan una función de reacción óptima del BC cuando la estructura de la economía está caracterizada por una curva de Phillips convexa, debemos considerar los de Schaling (1998; 2004), Nobay y Peel (2000), Dolado, María-Dolores y Naveira (2005), Iglesias, Pateiro Rodríguez y Salcines (2013).
Schaling (1998) parte de una función de preferencias del BC cuadrática y una curva de Phillips convexa. En la función de pérdidas sólo incluye el objetivo de inflación. Se trata, por tanto, de un BC que aplica una política monetaria de strict inflation targeting o esquema de metas de inflación estricto. El resultado es una función de reacción, o regla de política monetaria, asimétrica, que implica unos tipos de interés nominales más altos que los derivados de una regla lineal. Schaling (2004) amplía el análisis incluyendo el objetivo de la brecha del producto y también concluye que la regla de política monetaria óptima es asimétrica. Es decir, el tipo de interés es una función no lineal de las desviaciones de la inflación y de la brecha.
Dolado, María-Dolores y Naveira (2005) profundizan en el análisis anterior. Parten de una función de preferencias del BC cuadrática respecto a las desviaciones de la inflación y el producto, como Svensson (1997), y una curva de Phillips convexa. Con un enfoque similar, Iglesias, Pateiro Rodríguez y Salcines (2013) no descubren la presencia de comportamiento asimétrico del Banco Central Europeo (BCE) en el periodo 1999-2008.
Por lo que respecta a la literatura empírica sobre el comportamiento simétrico o asimétrico de la Reserva Federal, diversos autores han estudiado periodos muestrales distintos a los analizados en este trabajo, obteniendo conclusiones contradictorias. Dolado, María-Dolores y Ruge-Murcia (2002) encuentran que para el periodo 1983-2000 la autoridad monetaria ponderó en mayor medida las desviaciones positivas de la inflación respecto al nivel objetivo que las desviaciones negativas. Por su parte, Bec, Salem y Collard (2002), utilizando datos mensuales para el periodo 1982-1998, concluyen también la existencia de un comportamiento asimétrico por parte de la autoridad monetaria estadounidense. Surico (2003) afirma que es posible detectar asimetrías en el comportamiento de la Fed en el periodo que abarca desde julio de 1997 hasta octubre de 2002. Sin embargo, Surico (2007b) obtiene que la gestión de la Fed responde a una regla de política no lineal sólo durante el periodo anterior al nombramiento de Paul Volcker (1979) como presidente de dicho organismo y la no linealidad que predomina es la de la brecha del producto. Gerlach (2000) llega a la misma conclusión. Hacedores
Con una metodología distinta a la vista en los anteriores autores, utilizando regresiones con transición suave (STR, por sus siglas en inglés), Cukierman y Muscatelli (2007) concluyen que hay evidencia a favor de la no linealidad de la regla de política monetaria puesta en práctica por los policy makers de Estados Unidos (EE.UU.) durante los periodos 1960-1970, 1970-1979 y 1987-2005. En el primer periodo, la Fed presentó un comportamiento asimétrico respecto al objetivo de inflación, y en los dos últimos respecto a la estabilidad del producto. Florio (2006), utilizando también esta metodología, estudia el comportamiento asimétrico de la Fed respecto al objetivo de estabilidad en los tipos de interés. Concluye que durante el periodo de Volcker al frente de la Fed (1979-1987), la importancia del objetivo de estabilidad de precios motiva un comportamiento asimétrico respecto a la variación de los tipos de interés, adoptando un proceso más gradual en el descenso que en el incremento de los mismos, mientras que la asimetría es la contraria en la segunda etapa analizada (1987-2004), en consonancia con la importancia que durante la era Greenspan se otorgó a evitar la recesión económica y facilitar el funcionamiento de los mercados financieros. En el extremo contrario, Dolado, María-Dolores y Ruge-Murcia (2002) concluyen un comportamiento simétrico o lineal por parte de la autoridad monetaria estadounidense durante el periodo 1960-1979, y Dolado, María-Dolores y Naveira (2005), al estudiar el periodo 1984-2001, obtienen para EE.UU. una regla de política monetaria lineal. Kim, Osborn y Sensier (2005) concluyen que no es posible encontrar evidencia empírica acerca de que la Fed hubiese aplicado una regla de política monetaria asimétrica en el periodo que abarca desde el tercer trimestre de 1979 hasta el cuarto del 2000.
La posible presencia de asimetrías es abordada por algunos trabajos (Moura y de Carvalho, 2010 y Flores et al., 2000) mediante la incorporación de variables ficticias definidas en función de los valores que tomen las desviaciones de la inflación respecto a su nivel objetivo y de la brecha del producto.
Paralelamente al tipo de asimetrías estudiado en este trabajo, existe una extensa literatura que trata de descubrir la presencia de asimetrías de naturaleza distinta. Así, por ejemplo, Karras (2013), en un interesante trabajo, investiga si las variaciones de la base monetaria en Estados Unidos producen efectos asimétricos de signo y tamaño sobre el producto, concluyendo la existencia de tales asimetrías, tanto cuando se incluye el periodo de política monetaria no convencional (quantitative easing) como en otros casos. En esta misma línea se sitúan los trabajos de Cover (1992), Sensier, Osborn y Ocal (2002), Florio (2004), Ravn y Sola (2004) y Lo y Piger (2005), entre otros.
EL MODELO TEORICOSiguiendo a Dolado, María-Dolores y Naveira (2005), la autoridad monetaria trata de minimizar una función de pérdidas cuadrática en las desviaciones de la inflación y de la brecha del producto, sujeta a una estructura de la economía. En cada periodo, la autoridad monetaria fija el tipo de interés nominal (i) de manera que la inflación sea igual a su objetivo, es decir ππ¯=π−π*, y que la brecha del producto (y) se mantenga próxima a cero. Asumiendo la función de pérdidas cuadrática:
el objetivo del BC será minimizar en cada periodo t el valor presente esperado de las pérdidas de cada periodo:
sujeto a las restricciones que describen la estructura de la economía:
con
Et es el operador esperanza condicional, ω¯ es el factor de descuento, ω¯ y δ∈[0,1) y uy,t+1 y uπ,t+1 son shocks de producción e inflación respectivamente, que siguen una distribución normal de media cero. La ecuación [3] representa la relación IS donde la brecha depende de sus valores pasados, del tipo de interés real rt = it –EtPt+1 y de una variable exógena (xt) que puede contener determinantes del tipo de interés en economías abiertas. La ecuación [4] representa una curva de Phillips, donde la relación entre inflación y brecha del producto puede adoptar una forma no lineal, como muestra la ecuación [5].
Como puede observarse, si ϕ = 0, estamos ante una curva de Phillips lineal (Pt+1 = Pt + ayt + uP,t+1). Para cualquier otro valor de ϕ, la relación de Phillips adopta una forma no lineal. Cuando ϕ > 0 (ϕ < 0), la función será convexa (cóncava). Dolado, María-Dolores y Naveira (2005) utilizan la convención, frecuente en la literatura (también utilizada por Svensson, 1997), según la cual las variaciones del tipo de interés afectan al producto con un periodo de retardo y éste a la inflación con otro periodo de retardo. El proceso de transmisión, que utilizamos para la obtención de la ecuación de Euler, se puede expresar así: Δit ⇒ Δyt+1 ⇒ Δπt+2.
El tipo de interés que el BC elegirá en cada momento es el que expresa la ecuación de Euler,2 resultante de diferenciar totalmente la ecuación [2] respecto a it, sujeto a las restricciones [3], [4] y [5]. La regla de tipo de interés expresada en la ecuación [6] es una regla tayloriana óptima.
donde:
La función de reacción óptima de tipos de interés [6] presentaría una forma lineal si no fuera por el último término de la derecha (interacción entre previsiones de inflación y la brecha del producto o término rectangular), del que pueden derivarse comportamientos asimétricos del BC cuando establece los tipos de interés. En efecto, si la inflación esperada está por encima de su objetivo en t+1, el tipo de interés real estará por debajo de su nivel de equilibrio en el periodo t, lo que originará una mayor brecha en t+1, y, en consecuencia, mayor inflación en t+2. En este contexto, en el caso lineal, el policy maker variará el tipo de interés en la cuantía c1Et−1π˜t+1. Sin embargo, si la curva de Phillips es convexa, F > 0, las presiones inflacionistas futuras provocadas por una mayor brecha serán más elevadas que en el caso lineal. El policy maker, anticipando presiones inflacionis- tas de mayor intensidad, reflejadas en el término c4Et -1 (π˜t+1yt), provocará una mayor variación en el tipo de interés. En este caso, c4 > 0.
Por el contrario, si la curva de Phillips es cóncava, F < 0, las presiones infla- cionistas futuras serán más reducidas que en el caso lineal y el incremento en el tipo de interés será más reducido, c4 < 0.
De la misma manera, si el producto se sitúa por encima del nivel potencial en el momento t, la brecha del producto del momento t+1 también será positiva, como muestra la ecuación [3], llevando a mayores presiones inflacionistas en el momento t+2 que en el caso lineal debido a la convexidad de la curva de Phillips. El policy maker reaccionará con mayor intensidad sobre el tipo de interés de acuerdo con el término c4Et -1 (π˜t+1yt) con c4 > 0.
Para propósitos de comprobación empírica, reemplazamos las expectativas por los valores realizados y reescribimos la ecuación [6] como:
donde:
El modelo será backward looking o forward looking, en función del signo de los subíndices temporales f, b y h. Introducimos el término Rit–1, que refleja el fenómeno conocido como interest-rate smoothing o pretensión de los bancos centrales de realizar ajustes lentos en los tipos de interés (Goodfriend, 1991; Woodford, 2003), según el cual la autoridad monetaria ajusta el tipo de interés de forma gradual como respuesta a la inflación y a la brecha del producto, evitando así los denominados first round effects.
LOS DATOSHemos analizado la gestión de la política monetaria realizada por la Reserva Federal durante el periodo 1966:Q1-2012:Q4, con datos trimestrales. Dividimos el periodo muestral en dos etapas: la primera desde 1966:Q1 a 1979:Q2, y la segunda desde 1983:Q1 a 2012:Q4.3
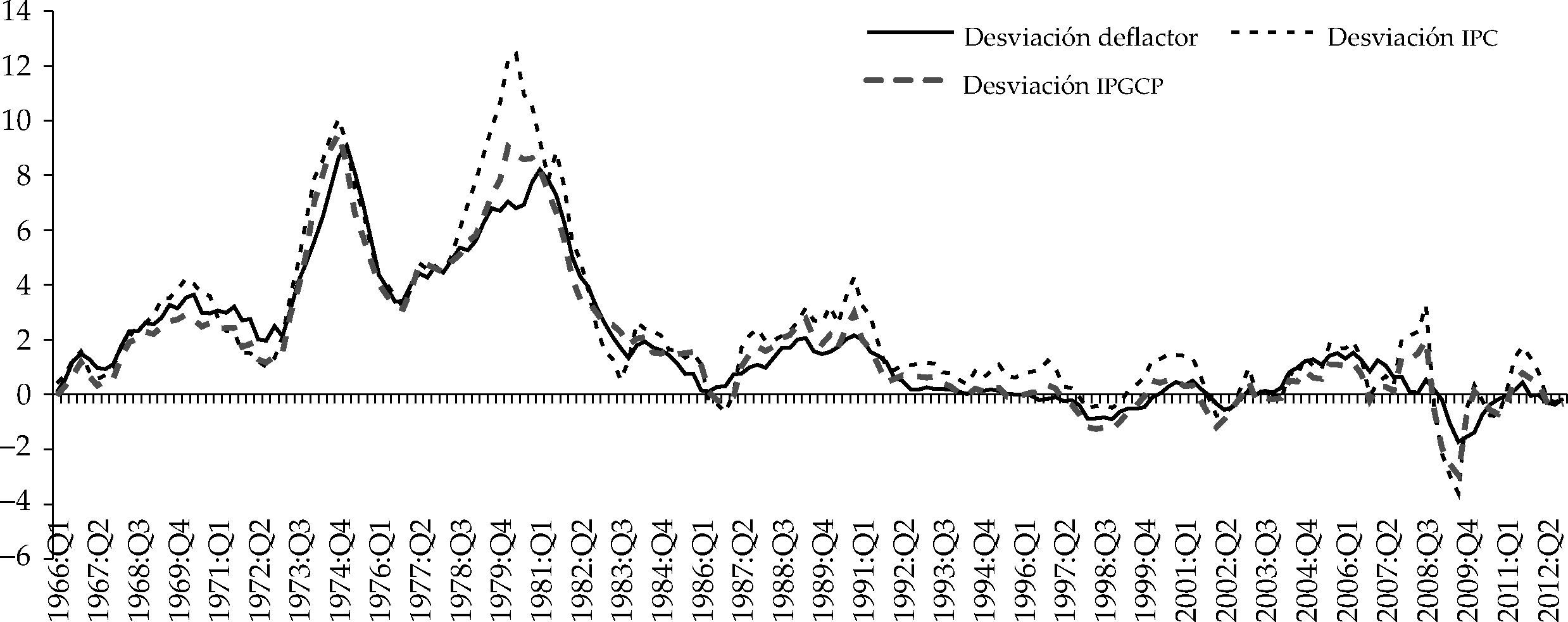
Como medida de la inflación, utilizamos, alternativamente, el deflactor del producto interno bruto (PIB), la tasa de variación interanual del Índice de Precios al Consumo (IPC), la tasa de variación interanual del IPC sin incluir la energía y los alimentos no procesados, o inflación subyacente, la tasa de variación interanual del Índice de Precios Implícito en el Gasto en Consumo Personal (IPGCP),4 así como la inflación subyacente calculada a partir del IPGCP. Tanto el IPC como el IPGCP tienen periodicidad mensual y tomaremos como dato trimestral la media aritmética de los tres datos mensuales del trimestre.
Respecto al objetivo de inflación, históricamente, los bancos centrales no han hecho público el nivel marcado como socialmente óptimo a medio/largo plazo. Sin embargo, a partir de la crisis económica de los años 1970 esta práctica fue puesta en entredicho, y, desde entonces, muchos bancos centrales han adoptado de manera pública una tasa de inflación objetivo en el entorno de 2%,5 de acuerdo con la abundante literatura que apoya unas bajas tasas de inflación y los beneficios de hacer público este objetivo, sobre todo la reducción de la incertidumbre y los efectos sobre la formación correcta de las expectativas de inflación a largo plazo.
En el caso de la Fed, fue en enero de 2012 cuando su Comité de Política Monetaria (el Federal Open Market Committee, FOMC) publicó su objetivo de inflación, que fija en 2%, medido como la tasa de cambio anual del IPGCP. Sin embargo, los Economic Reports of the President del Council of Economic Advisers de años anteriores recogen ya este objetivo de 2 por ciento.
Por ello, tomaremos como objetivo de inflación el 2% para el segundo periodo muestral analizado (1983:Q1-2012:Q4). En el periodo 1966:Q1-1979:Q2, de tasas de inflación elevadas, al obtener las desviaciones respecto a un hipotético objetivo de 2%, éstas son muy importantes (gráfica 1). Para solucionar el sesgo derivado de la utilización de una tasa de inflación objetivo errónea podríamos optar, como Kim, Osborn y Sensier (2005), por utilizar la tasa de inflación objetivo implícita hallada por Clarida, Galí y Gertler (2000) para el periodo muestral 1960:Q1-1979:Q2, que sitúan en 4.24%, pero hemos decidido utilizar para el primer subperiodo muestral, como medida alternativa del objetivo de inflación, la tendencia mostrada al aplicar a los valores de inflación observados el filtro de Hodrick-Prescott (HP), con un coeficiente de 1.600, al tratarse de datos trimestrales.
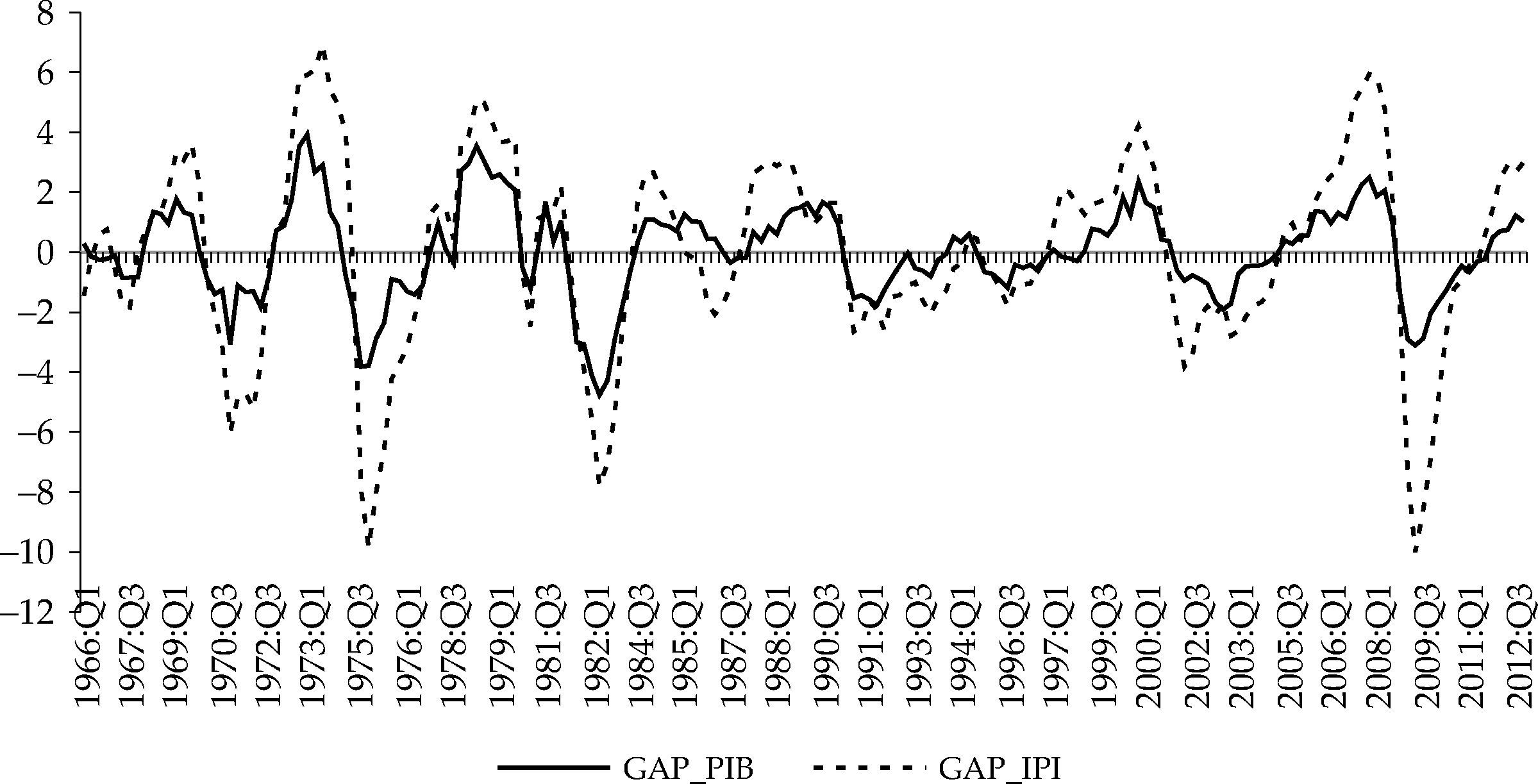
Para el cálculo de las desviaciones del nivel de producción respecto a su valor tendencial o brecha del producto, yt, medimos la producción, alternativamente, a partir de los volúmenes encadenados del PIB a precios de mercado ajustado estacionalmente, con año de referencia 2005, y a partir del Índice de Producción Industrial (IPI) ajustado estacionalmente con base 2007 = 100.6 En lo referente al IPI, al presentar periodicidad mensual, utilizamos como dato trimestral la media aritmética de las tres observaciones de cada trimestre.
Clarida, Galí y Gertler (2000) aproximan la brecha a través de la desviación del logaritmo del PIB respecto a una tendencia cuadrática, y Clarida, Galí y Gertler (1998) utilizan la desviación del logaritmo de la producción industrial respecto a una tendencia cuadrática. Esta medida consiste en tomar los residuos de una regresión de mínimos cuadrados ordinarios (MCO) del logaritmo del PIB o del IPI sobre una constante, una tendencia lineal y una tendencia cuadrática (Favero, 2001).
Siguiendo a Dolado, María-Dolores y Ruge-Murcia (2002), Dolado, María-Dolores y Naveira (2005), Surico (2007a; 2007b), entre otros autores, hemos utilizado el filtro de Hodrick-Prescott para hallar el valor tendencial del nivel de producción. Así, en el primer caso, medimos la brecha del producto como la diferencia entre el logaritmo neperiano del PIB y el filtro HP del mismo, con un parámetro de alisamiento de 1.600. De igual forma, definimos la brecha cuando utilizamos el IPI, en el segundo caso.
La gráfica 2 compara las dos medidas alternativas de la brecha del producto utilizadas en este trabajo.
El tipo de interés a corto plazo utilizado es el Federal Funds Rate.
La información referida a las variables hasta aquí comentadas está disponible en la base de datos del Federal Reserve Bank of St. Louis, disponible en: <http://research.stlouisfed.org/fred2/>.
Por lo que se refiere al valor de f y b hemos optado, como Clarida, Galí y Gertler (1998) o Dolado, María-Dolores y Naveira (2005), por f = 4 y b = 0, es decir, hemos elegido una especificación forward looking o hacia futuro respecto a las desviaciones de la inflación. Cuando los datos son trimestrales, como en este caso, es habitual tomar un f = 4, dado que los bancos centrales tienden a utilizar el horizonte de un año a la hora de fijar previsiones de inflación.
En cuanto al término que recoge el interest rate smoothing, hemos utilizado como regresor el tipo de interés retardado un periodo.7
LA CONTRASTACION EMPIRICAEn primer lugar, trataremos de detectar la potencial presencia de asimetría en el comportamiento de la Fed en los dos subperiodos estudiados a través del modelo teórico descrito en la sección tres. La presencia de una política monetaria asimétrica puede ser también investigada mediante la inclusión de variables ficticias, tanto en relación con la desviación de la inflación como de la brecha del producto, como se describe en la parte final del siguiente epígrafe. El trabajo empírico aborda ambos análisis, lo que nos permite contrastar la robustez de los resultados. Por último, nos centramos en la estimación de las funciones lineales de política monetaria.
¿Es asimétrico el comportamiento de la Fed?Para detectar la presencia de asimetrías, estimamos la ecuación [7] utilizando el método generalizado de los momentos, MGM,8 desarrollado por Hansen (1982), como generalización del método de los momentos (MM). El MGM resulta una alternativa econométrica adecuada para la estimación de los parámetros profundos en problemas de optimización temporal en presencia de agentes con expectativas racionales. Para construir los estimadores MGM de los parámetros de la ecuación, utilizamos el conjunto de condiciones de ortogonalidad dado por E(vti | Zt = 0, que descansan en la elección de un grupo de instrumentos (Zt) a partir de las variables que forman parte del conjunto de información del BC, tales como las variables retardadas que contribuyen a elaborar las previsiones de inflación o del producto o cualquier otra variable contemporánea que esté incorrelacionada con el shock de política monetaria (vi). La condición para asegurar que el vector de parámetros estimados a través del MGM, con variables instrumentales, sea fuertemente consistente, asintóticamente normal y eficiente, es la estacionariedad de las variables instrumentales, así como de las variables que conforman la regla tayloriana a estimar. Las pruebas de raíz unitaria Phillips-Perron y Dickey Fuller Aumentada confirman la estacionariedad de las series utilizadas. La correspondiente al endeudamiento público como porcentaje del PIB, es estacionaria en primeras diferencias.
Como variables instrumentales hemos incluido los tres primeros retardos de la desviación de la inflación, la brecha del producto y la variable exógena,9 cuando sea oportuno, es decir, el comportamiento observado a lo largo del año inmediatamente anterior.
Teniendo en cuenta que el conjunto de instrumentos y, por tanto, el número de condiciones de ortogonalidad excede el de parámetros a estimar, será nece- sario contrastar la validez de las restricciones de sobreidentificación. Hansen (1982) sugiere una prueba que permite realizar este contraste y que puede considerarse una extensión de la prueba de especificación propuesta por Sargan (1958). La prueba de Hansen puede implementarse utilizando el estadístico J,10 que se distribuye asintóticamente como una distribución de probabilidad X2 con I-R grados de libertad, donde I es el número de instrumentos y R el número de regresores. Si se cumple que J < XI−R2, entonces no se rechaza la hipótesis nula y las restricciones de sobreidentificación no implican que exista evidencia en contra del modelo económico propuesto y, por tanto, éste se encuentra correctamente especificado.
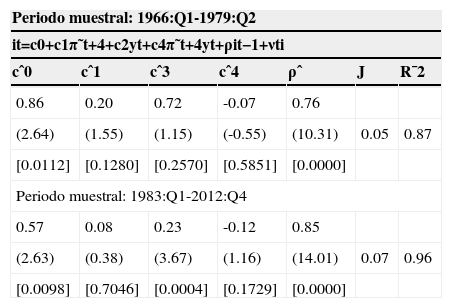
Los resultados obtenidos muestran un coeficiente c4 negativo y estadísticamente no significativo, tanto para el primer periodo como para el segundo, tal y como aparece recogido en el cuadro 1. Estos resultados nos permiten afirmar que la Fed no muestra un comportamiento asimétrico durante las etapas analizadas.
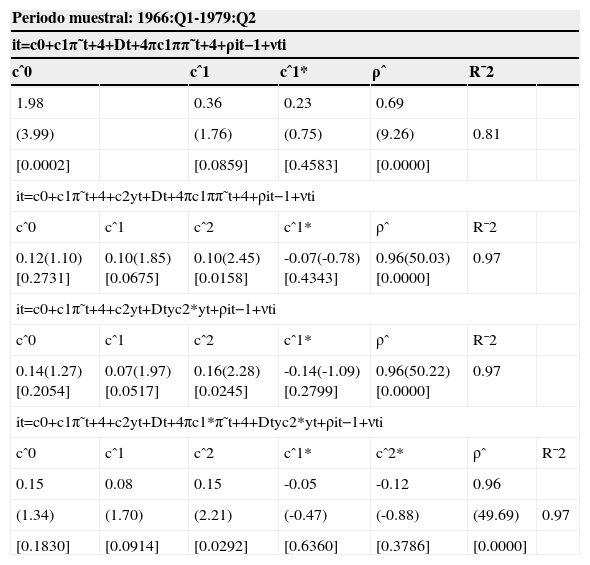
Fed, función de reacción asimétrica
| Periodo muestral: 1966:Q1-1979:Q2 | ||||||
|---|---|---|---|---|---|---|
| it=c0+c1π˜t+4+c2yt+c4π˜t+4yt+ρit−1+νti | ||||||
| cˆ0 | cˆ1 | cˆ3 | cˆ4 | ρˆ | J | R¯2 |
| 0.86 | 0.20 | 0.72 | -0.07 | 0.76 | ||
| (2.64) | (1.55) | (1.15) | (-0.55) | (10.31) | 0.05 | 0.87 |
| [0.0112] | [0.1280] | [0.2570] | [0.5851] | [0.0000] | ||
| Periodo muestral: 1983:Q1-2012:Q4 | ||||||
| 0.57 | 0.08 | 0.23 | -0.12 | 0.85 | ||
| (2.63) | (0.38) | (3.67) | (1.16) | (14.01) | 0.07 | 0.96 |
| [0.0098] | [0.7046] | [0.0004] | [0.1729] | [0.0000] | ||
Notas: Desviación de la inflación = tasa de variación anual del deflactor del PIB – 2%.
Brecha de producto = logaritmo neperiano del PIB – filtro de HP del logaritmo neperiano del PIB.
Entre paréntesis el estadístico t de Student y entre corchetes el nivel de significación mínimo para que se rechace la hipótesis de nulidad de los coeficientes de los regresores.
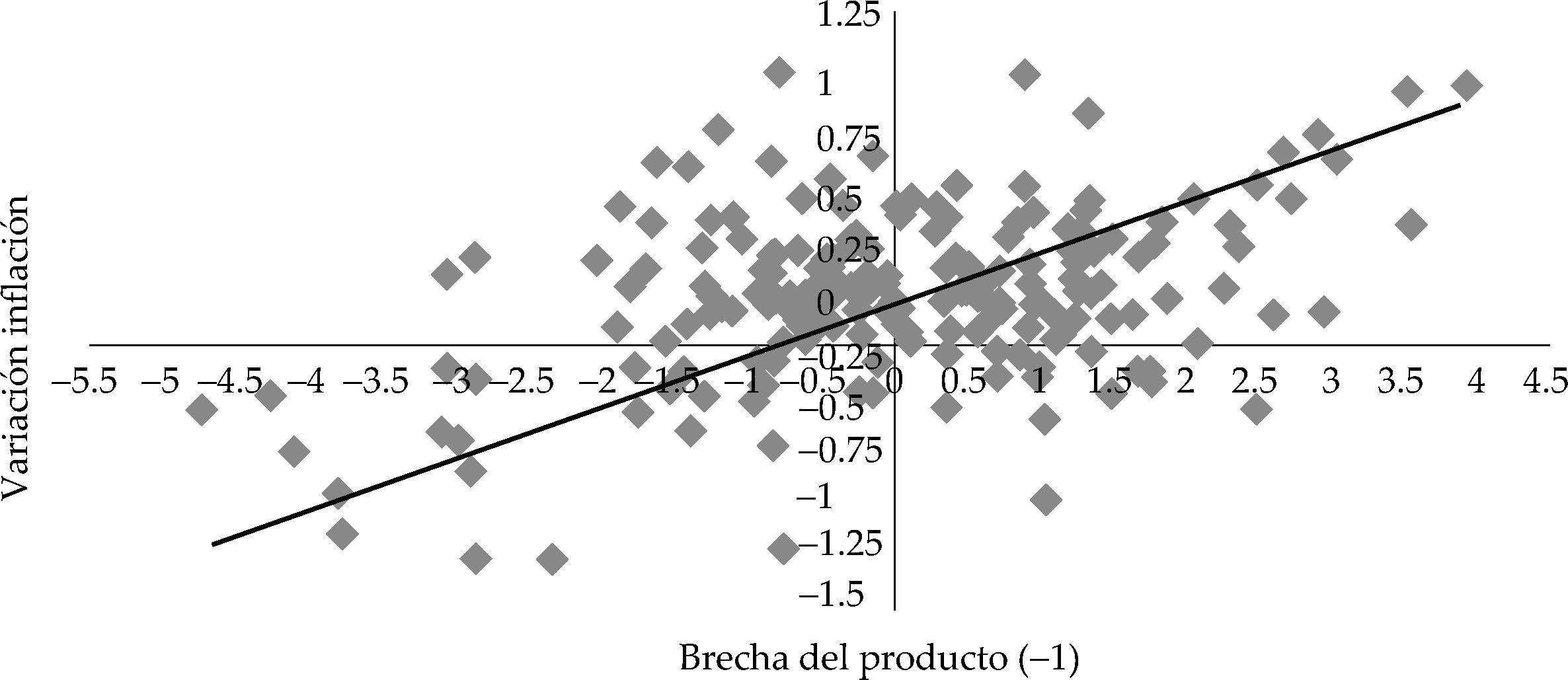
Esta afirmación es compatible con la existencia de una función de Phillips lineal en la economía estadounidense, donde la autoridad monetaria no parece adoptar unas preferencias asimétricas respecto a la inflación o la brecha del producto. La gráfica 3 recoge la relación de Phillips para el periodo 1966-2012 y, como vemos, es razonable pensar en una relación lineal.
Con el propósito de descubrir la robustez del resultado relativo a la ausencia de asimetrías en la gestión de la política monetaria por parte de la Reserva Federal en el periodo analizado, hemos explorado la posibilidad de un comportamiento asimétrico al incluir en la función de reacción [8] las variables ficticias DP y Dy, multiplicando a las variables explicativas:
donde:
Por lo tanto:
El cuadro 2 recopila los resultados obtenidos al estimar por MCO la ecuación [8]. Como vemos, en ningún caso se puede rechazar la hipótesis nula de un comportamiento lineal o simétrico por parte de la Fed, tanto en su objetivo de inflación como de producto.11 Por lo tanto, estos resultados refuerzan los obtenidos a través del MGM descrito más arriba, en el sentido de que podemos concluir la ausencia de un comportamiento asimétrico por parte de la Reserva Federal.
Fed, función de reacción asimétrica
| Periodo muestral: 1966:Q1-1979:Q2 | ||||||
|---|---|---|---|---|---|---|
| it=c0+c1π˜t+4+Dt+4πc1ππ˜t+4+ρit−1+νti | ||||||
| cˆ0 | cˆ1 | cˆ1* | ρˆ | R¯2 | ||
| 1.98 | 0.36 | 0.23 | 0.69 | |||
| (3.99) | (1.76) | (0.75) | (9.26) | 0.81 | ||
| [0.0002] | [0.0859] | [0.4583] | [0.0000] | |||
| it=c0+c1π˜t+4+c2yt+Dt+4πc1ππ˜t+4+ρit−1+νti | ||||||
| cˆ0 | cˆ1 | cˆ2 | cˆ1* | ρˆ | R¯2 | |
| 0.12(1.10)[0.2731] | 0.10(1.85)[0.0675] | 0.10(2.45)[0.0158] | -0.07(-0.78)[0.4343] | 0.96(50.03)[0.0000] | 0.97 | |
| it=c0+c1π˜t+4+c2yt+Dtyc2*yt+ρit−1+νti | ||||||
| cˆ0 | cˆ1 | cˆ2 | cˆ1* | ρˆ | R¯2 | |
| 0.14(1.27)[0.2054] | 0.07(1.97)[0.0517] | 0.16(2.28)[0.0245] | -0.14(-1.09)[0.2799] | 0.96(50.22)[0.0000] | 0.97 | |
| it=c0+c1π˜t+4+c2yt+Dt+4πc1*π˜t+4+Dtyc2*yt+ρit−1+νti | ||||||
| cˆ0 | cˆ1 | cˆ2 | cˆ1* | cˆ2* | ρˆ | R¯2 |
| 0.15 | 0.08 | 0.15 | -0.05 | -0.12 | 0.96 | |
| (1.34) | (1.70) | (2.21) | (-0.47) | (-0.88) | (49.69) | 0.97 |
| [0.1830] | [0.0914] | [0.0292] | [0.6360] | [0.3786] | [0.0000] | |
Notas: Desviación de la inflación = tasa de inflación calculada a partir del IPGCP – 2%.
Brecha de producto = logaritmo neperiano del PIB – filtro de HP del logaritmo neperiano del PIB.
Entre paréntesis el estadístico t de Student y entre corchetes el nivel de significación mínimo para que se rechace la hipótesis de nulidad de los coeficientes de los regresores.
Si, como hemos visto, la Fed no adopta un comportamiento asimétrico, resulta conveniente interpretar el tipo de interés a corto plazo a través de funciones de reacción óptimas lineales. Para ello, estimamos, para ambos periodos, la regla de política monetaria lineal que obtenemos al eliminar el término rectangular o de interacción de la ecuación [7]:
Y alternativamente:según utilicemos como regresor la desviación de la inflación respecto a su objetivo (ecuación [9]) o el nivel de inflación (ecuación [10]). La regla tayloriana representada por la ecuación [9] coincide con la regla lineal propuesta por Dolado, María-Dolores y Naveira (2005), y la ecuación [10] es la regla de tipos de interés óptima propuesta por Clarida, Galí y Gertler (1998; 2000). Al igual que en el caso anterior, la estimación se realiza mediante el MGM.
Al estimar las funciones de reacción lineales, representadas por las ecuaciones [9] y [10], para el subperiodo 1966:Q1-1979:Q2, los resultados arrojan coeficientes estimados con signos contrarios a los esperados y variables explicativas no significativas, es decir, parecen mostrar que la Fed, durante el periodo 1966-1979, a la hora de diseñar su política monetaria, toma en consideración la brecha del producto sólo en cuanto a indicador adelantado de la inflación.
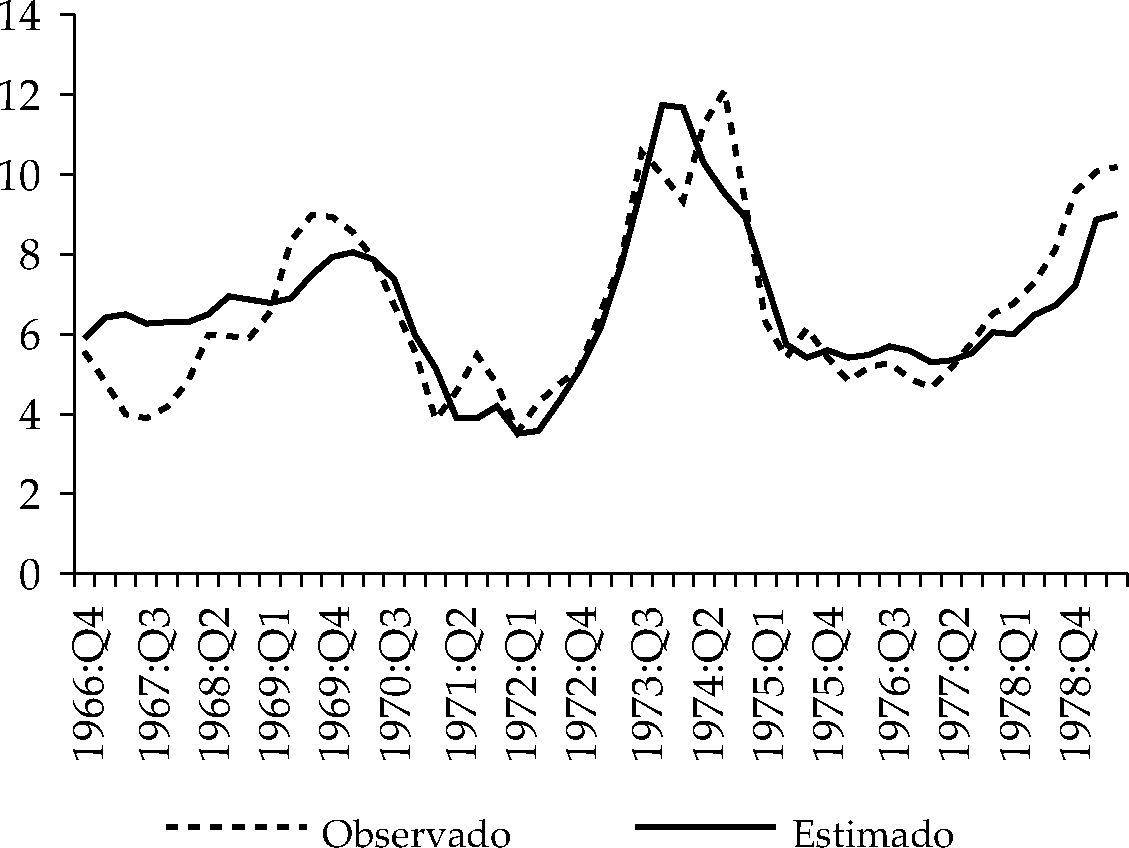
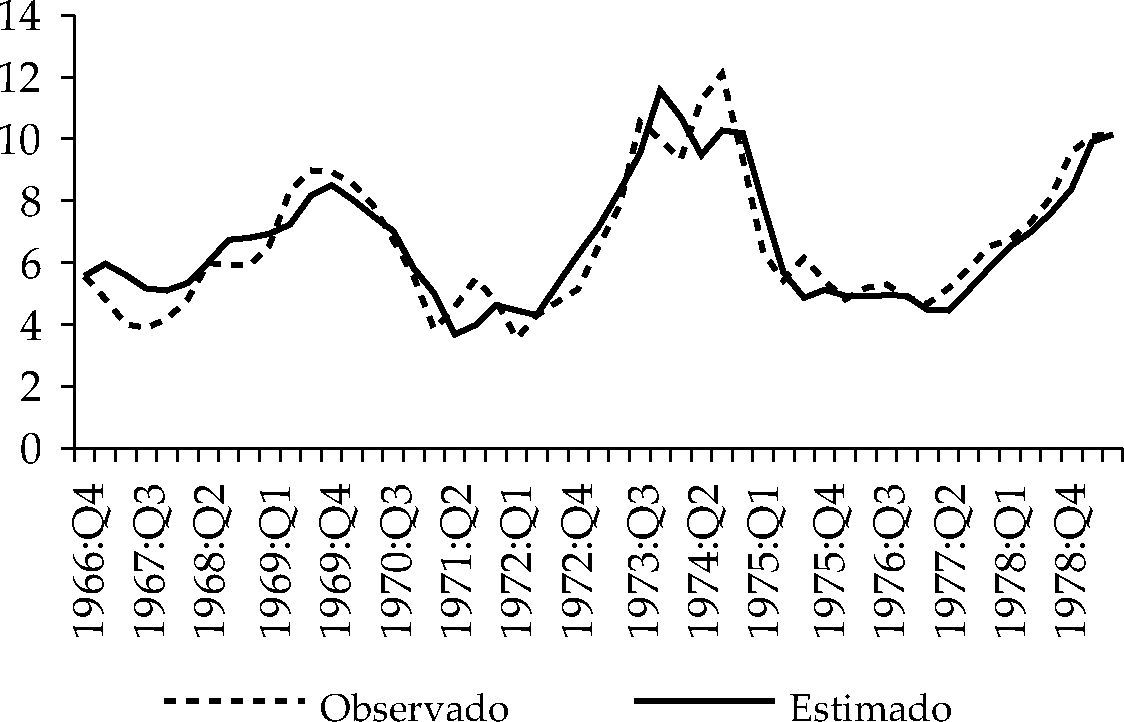
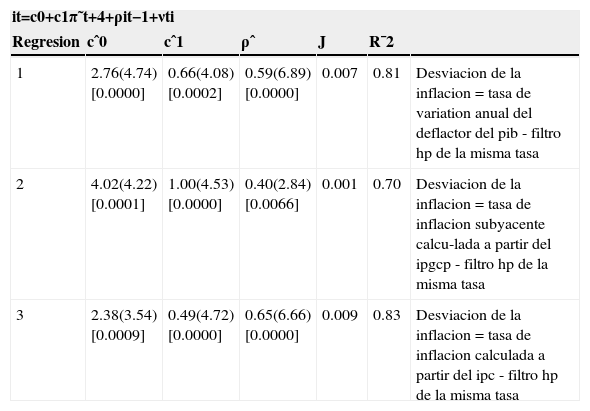
El cuadro 3 muestra los resultados obtenidos al estimar la función de reacción [11], que no contempla la brecha como variable explicativa. Todos los regresores tienen el signo correcto y son estadísticamente significativos:
Función de reacción lineal, 1966:Q1-1979:Q2
| it=c0+c1π˜t+4+ρit−1+νti | ||||||
|---|---|---|---|---|---|---|
| Regresion | cˆ0 | cˆ1 | ρˆ | J | R¯2 | |
| 1 | 2.76(4.74)[0.0000] | 0.66(4.08)[0.0002] | 0.59(6.89)[0.0000] | 0.007 | 0.81 | Desviacion de la inflacion = tasa de variation anual del deflactor del pib - filtro hp de la misma tasa |
| 2 | 4.02(4.22)[0.0001] | 1.00(4.53)[0.0000] | 0.40(2.84)[0.0066] | 0.001 | 0.70 | Desviacion de la inflacion = tasa de inflacion subyacente calcu-lada a partir del ipgcp - filtro hp de la misma tasa |
| 3 | 2.38(3.54)[0.0009] | 0.49(4.72)[0.0000] | 0.65(6.66)[0.0000] | 0.009 | 0.83 | Desviacion de la inflacion = tasa de inflacion calculada a partir del ipc - filtro hp de la misma tasa |
Nota: entre paréntesis el estadístico t de Student y entre corchetes el nivel de significación mínimo para que se rechace la hipótesis de nulidad de los coeficientes de los regresores. Vemos que las variables explicativas son estadísticamente significativas en las tres especificaciones. Asimismo, no rechazamos la hipótesis nula de validez de las variables instrumentales utilizadas en ningún caso, dado que P (x12 ≤ 3.84 = 0.95 y J = 0.007(51) = 0.357 < 3.84, J = 0.001(51) = 0.051 < 3.84 y J = 0.009(51) = 0.459 < 3.84.
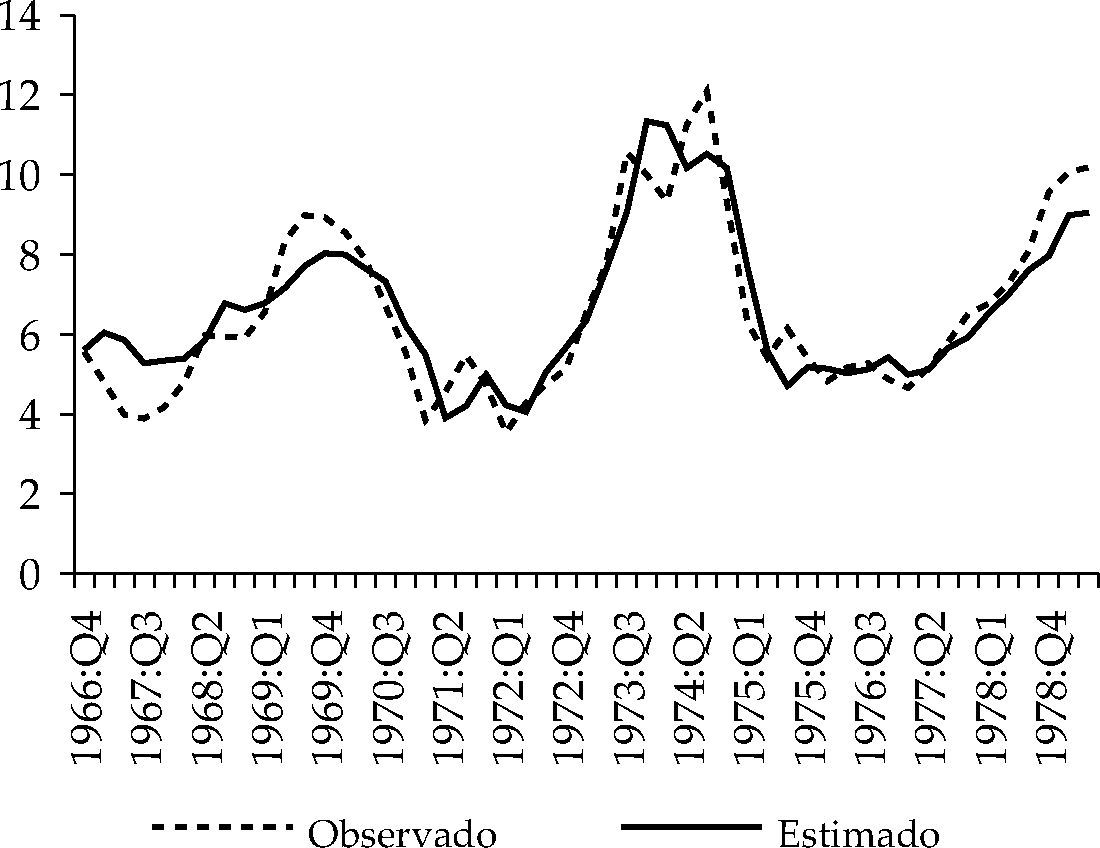
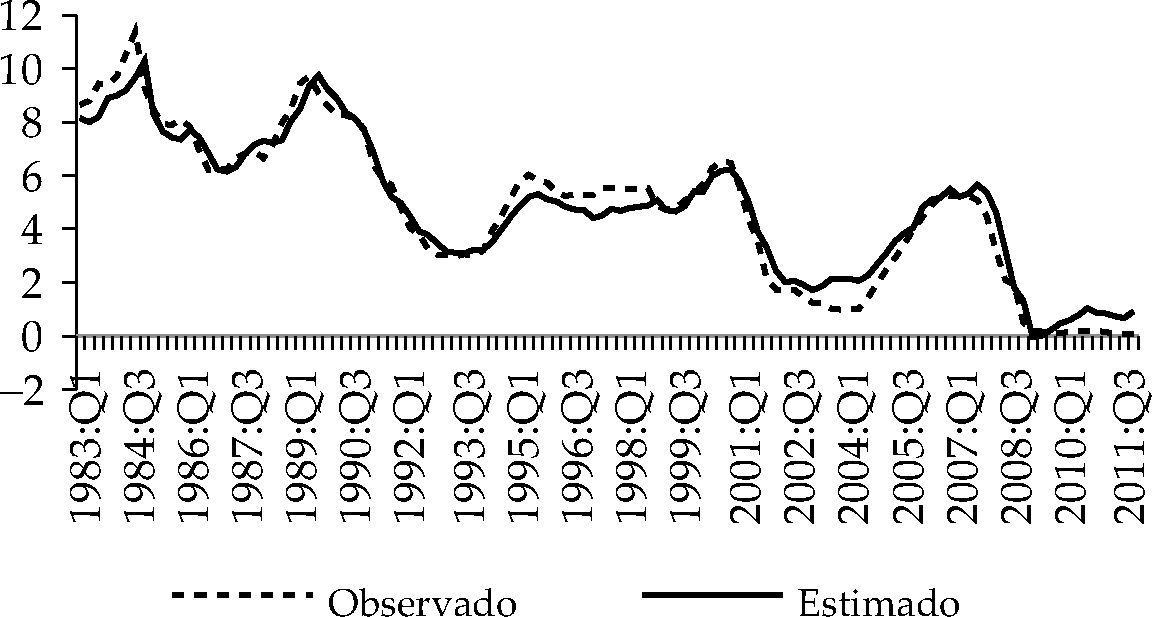
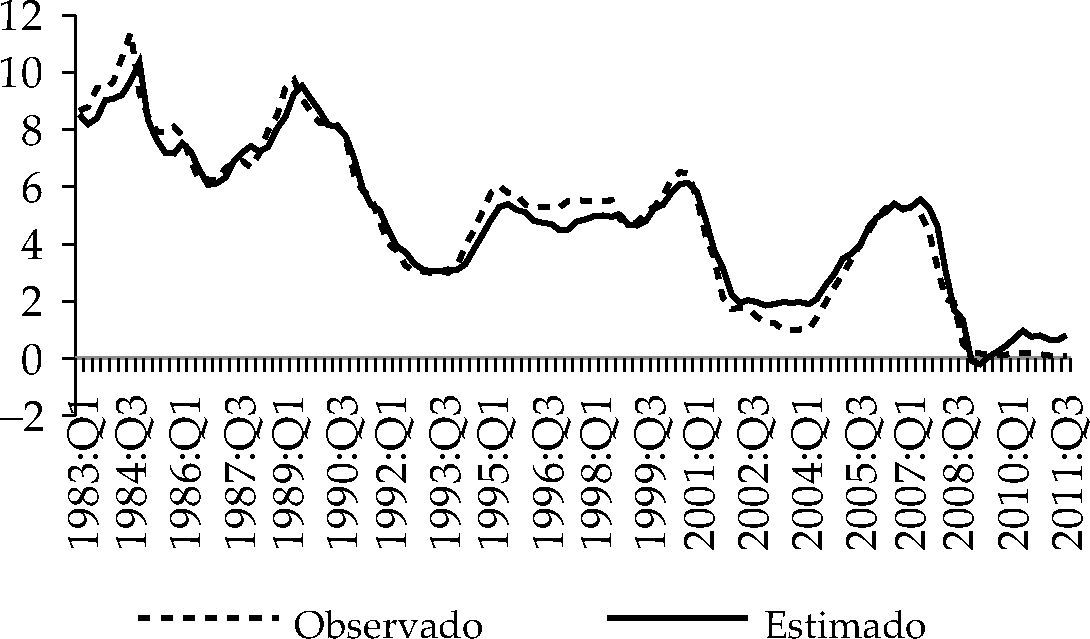
Las gráficas 4,5 y 6 muestran cómo las reglas de tipos de interés 1, 2 y 3 del cuadro 3 capturan el comportamiento mostrado por el tipo de interés durante el periodo analizado. En 1966-1968 observamos que la política monetaria aplicada por la Fed fue sensiblemente más expansiva que la aconsejada por cualquiera de la reglas taylorianas estimadas. Con la inflación en el entorno de 3.5%, el gobierno demócrata de Lyndon B. Johnson pudo haber presionado a la autoridad monetaria para generar estímulos rápidos en la economía. Asimismo, se presentan también divergencias en el periodo 1973:Q3-1974:Q1. En este caso, el tipo de interés observado es inferior al estimado por la aplicación de la regla, mostrando una relajación de la política monetaria. Una situación contraria se observa en el periodo 1974:Q2-197:5Q1.
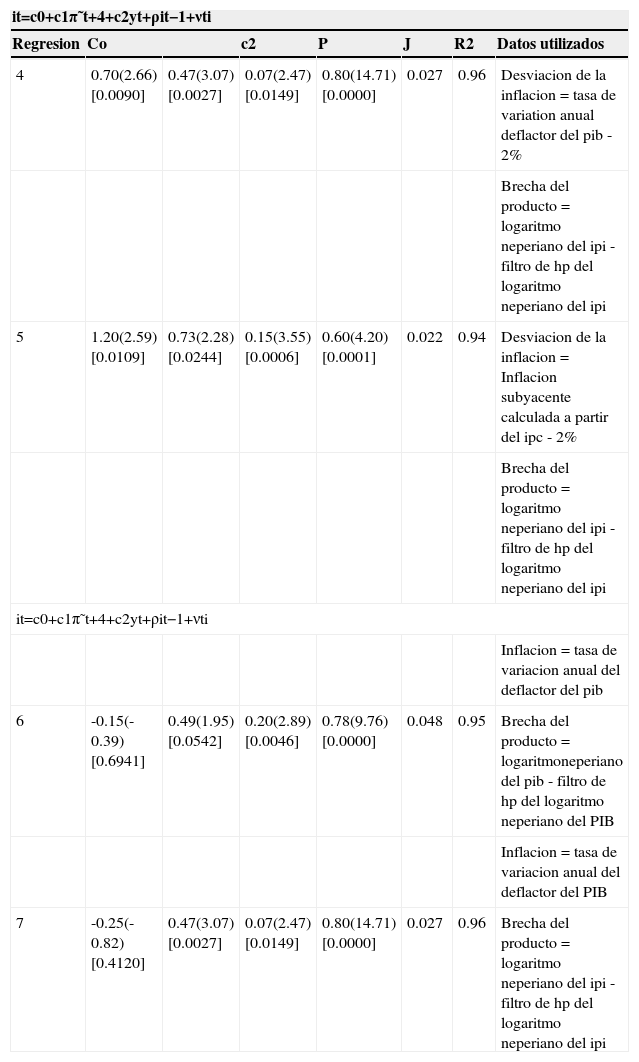
El cuadro 4 muestra los resultados obtenidos para el segundo subperiodo gráficas 8,9.
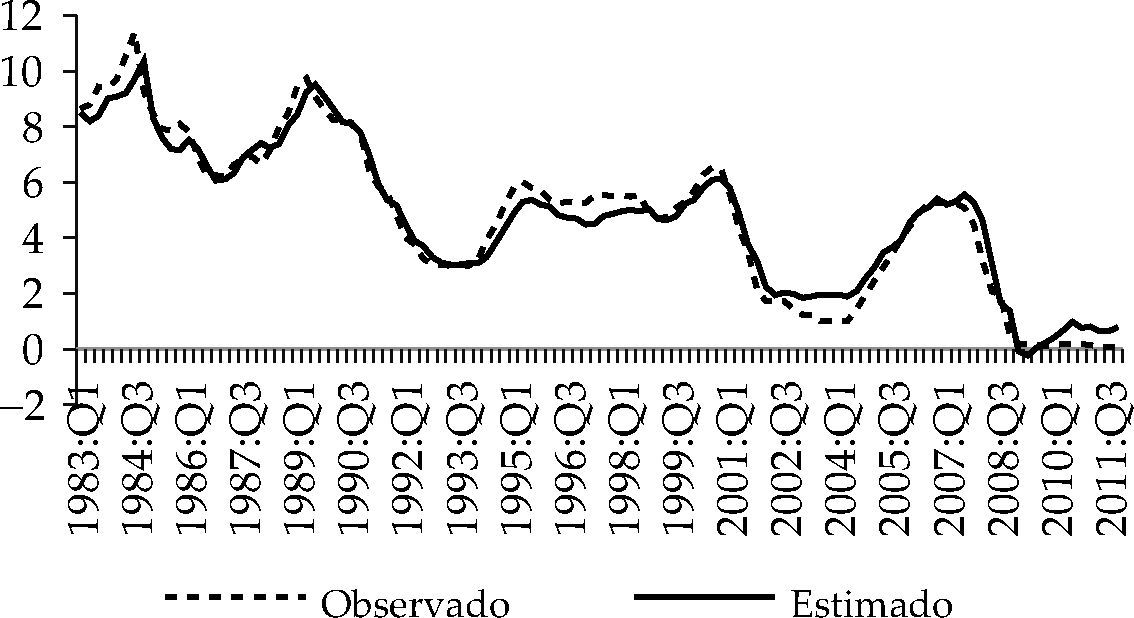
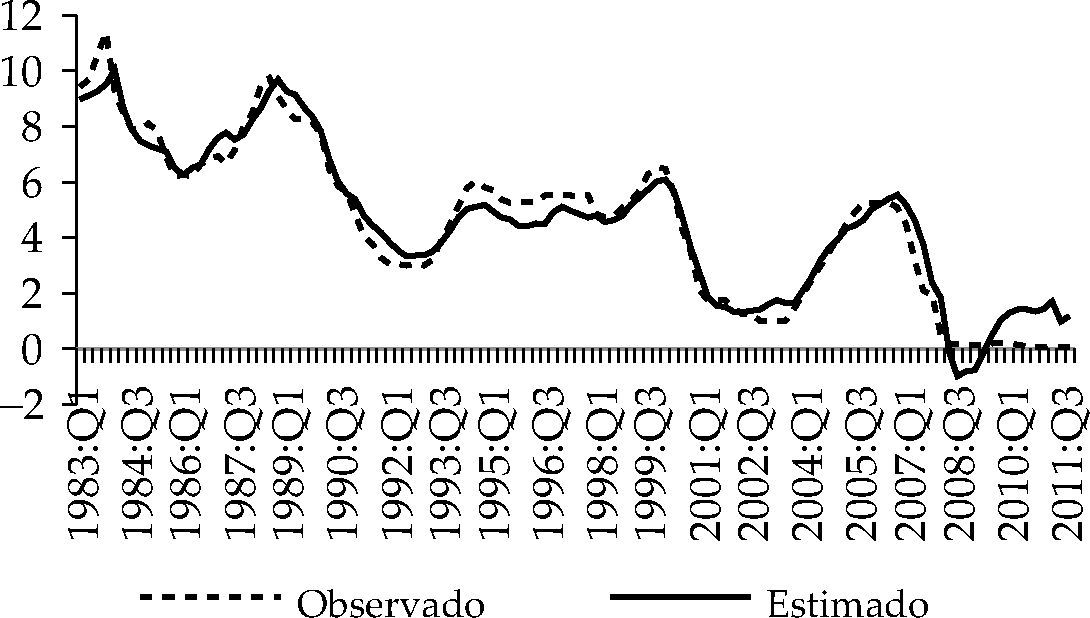
Función de reacción lineal, 1983:Q1-2012:Q4
| it=c0+c1π˜t+4+c2yt+ρit−1+νti | |||||||
|---|---|---|---|---|---|---|---|
| Regresion | Co | c2 | P | J | R2 | Datos utilizados | |
| 4 | 0.70(2.66)[0.0090] | 0.47(3.07)[0.0027] | 0.07(2.47)[0.0149] | 0.80(14.71)[0.0000] | 0.027 | 0.96 | Desviacion de la inflacion = tasa de variation anual deflactor del pib - 2% |
| Brecha del producto = logaritmo neperiano del ipi - filtro de hp del logaritmo neperiano del ipi | |||||||
| 5 | 1.20(2.59)[0.0109] | 0.73(2.28)[0.0244] | 0.15(3.55)[0.0006] | 0.60(4.20)[0.0001] | 0.022 | 0.94 | Desviacion de la inflacion = Inflacion subyacente calculada a partir del ipc - 2% |
| Brecha del producto = logaritmo neperiano del ipi - filtro de hp del logaritmo neperiano del ipi | |||||||
| it=c0+c1π˜t+4+c2yt+ρit−1+νti | |||||||
| Inflacion = tasa de variacion anual del deflactor del pib | |||||||
| 6 | -0.15(-0.39)[0.6941] | 0.49(1.95)[0.0542] | 0.20(2.89)[0.0046] | 0.78(9.76)[0.0000] | 0.048 | 0.95 | Brecha del producto = logaritmoneperiano del pib - filtro de hp del logaritmo neperiano del PIB |
| Inflacion = tasa de variacion anual del deflactor del PIB | |||||||
| 7 | -0.25(-0.82)[0.4120] | 0.47(3.07)[0.0027] | 0.07(2.47)[0.0149] | 0.80(14.71)[0.0000] | 0.027 | 0.96 | Brecha del producto = logaritmo neperiano del ipi - filtro de hp del logaritmo neperiano del ipi |
Nota: en todos los casos, se rechaza la hipótesis de nulidad de los coeficientes para niveles de significación inferiores al 5%. No rechazamos la hipótesis nula de validez de las variables instrumentales utilizadas, dado que P (x32 ≤ 7.81 = 0.95 y J = 0.027(116) = 3.132 < 7.81, J = 0.048(116) = 5.568 < 7.81 y J = 0.027(116) = 3.1327 < 7.81.
Las gráficas 7 al 10 muestran cómo las reglas 4, 5, 6 y 7 del cuadro 4 aproximan de forma adecuada los tipos de interés estimados a los observados durante el periodo 1983:Q1-2012:Q4. Advertimos lo apuntado por Taylor (1993) respecto a la relajación de la política monetaria adoptada por la Fed como respuesta al crash bursátil de 1987. Asimismo, las gráficas reflejan también que en el periodo 1994-1998 la Fed aplicó una política monetaria más restrictiva que la prevista por las reglas de tipos de interés estimadas, mientras que en el periodo 2001-2005 fue más expansiva de lo previsto. Durante el mandato de Alan Greenspan al frente de la Reserva Federal (1987-2006) distinguimos una primera etapa en la que presta una especial atención al objetivo de estabilidad de precios, siguiendo la estela de su predecesor, Paul Volcker, y una segunda etapa en la que aplicó una política monetaria sensiblemente más expansiva de lo que las reglas taylorianas estimadas en este trabajo aconsejan. Este resultado está apoyado por las tesis de diversos autores según los cuales Greenspan aplicó una política monetaria demasiado laxa. Taylor (2007; 2009) sostienen que la Fed mantuvo, entre 2002 y 2006, una política monetaria demasiado expansiva, alimentando la burbuja residencial que vivió EE.UU. en la primera década del siglo XXI.
Lo mismo podemos decir respecto a la gestión de la política monetaria de la Fed dirigida por Ben Bernanke durante la actual crisis económica: el tipo de interés observado es sensiblemente menor al previsto por cualquiera de las funciones de reacción que hemos estimado para el periodo 1983-2012.
Otras variables exógenas en la determinación del tipo de interés de la FedLos bancos centrales pueden tener en cuenta otras variables en la determinación de los tipos de interés. En nuestro trabajo analizamos el papel de la deuda pública, del crecimiento de la oferta monetaria y del tipo de cambio real.
A la vista de la evolución mostrada por el endeudamiento público estadounidense como porcentaje del PIB, incluimos esta variable como exógena al estimar la función de reacción de la Fed del segundo periodo, 1983:Q1-2012:Q4. No analizamos el periodo 1966:Q1-1979:Q2 porque presenta reducidos y decrecientes niveles de deuda pública con relación al PIB.
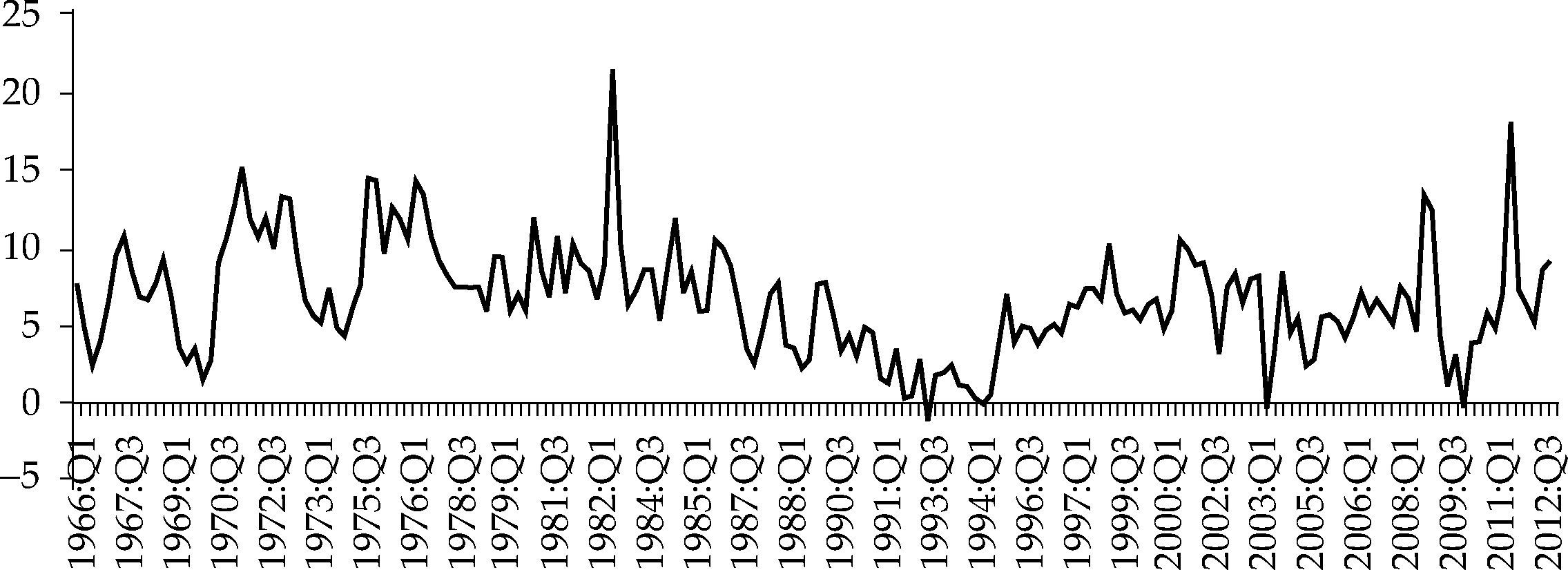
Por lo que se refiere a la evolución de la oferta monetaria, medida por la tasa de variación del agregado monetario M2 retardada un periodo (véase la gráfica 11), se incluye como variable exógena en ambos periodos. Clarida, Galí y Gertler (1998) incluyen la variable oferta monetaria al estudiar el periodo 1979:10-1994:12 y Dolado, María-Dolores y Naveira (2005) en el periodo 1984:1-2001:9.
En cuanto al tipo de cambio, Ball (1999), Svensson (2000), Batini, Harrison y Millard (2001), Edwards (2006), Wollmershäuser (2006) y García, Restrepo y Roger (2011), entre otros, han defendido que en una economía abierta el tipo de cambio juega un papel importante en el mecanismo de transmisión de la política monetaria, por lo tanto esta variable debe estar incluida de forma explícita en la regla de política monetaria, dando lugar así a resultados macroeconómicos más estables. Para el estudio del papel que juega el tipo de cambio en el diseño de la política monetaria por parte de la Fed, utilizaremos la siguiente especificación de la regla de tipos de interés, comúnmente empleada en la literatura empírica.
donde et es la variación en el tipo de cambio real, medida como la tasa de variación interanual en el Real Trade Weighted U.S. Dollar Index: Major Currencies.
Las monedas contra las que está calculado el tipo de cambio del dólar incluyen las de la Eurozona, Canadá, Japón, Reino Unido, Suiza, Australia y Suecia.
La extraordinariamente expansiva política monetaria de la Fed a partir de 2008 podría haber provocado en el corto plazo un notable incremento del tipo de cambio real, toda vez que la expansión monetaria induce una sobrerreacción del tipo de cambio nominal, dados los precios exteriores. Sin embargo, esta sobrerreacción del tipo de cambio real es neutralizada por el aumento paulatino de los precios internos, de tal manera que, a largo plazo, el tipo de cambio real tiende al valor inicial de equilibrio.
Los cuadros 5 al 8 recopilan los resultados obtenidos.
Función de reacción lineal con endeudamiento público como variable exógena, 1983:Q1-2012:Q4
| it=c0+c1π˜t+4+c2yt+c3xt+ρit−1+νti | ||||||
|---|---|---|---|---|---|---|
| cˆ0 | cˆ1 | cˆ3 | cˆ4 | ρˆ | J | R¯2 |
| 5.60(1.79)[0.0766] | 0.92(2.78)[0.0064] | 0.23(2.79)[0.0062] | -0.06(-1.63)[0.1062] | 0.48(2.32)[0.0219] | 0.039 | 0.87 |
Notas: Desviación de la inflación = tasa de variación anual del deflactor del PIB – 2%.
Brecha del producto = logaritmo neperiano del PIB menos el filtro de HP del logaritmo neperiano del PIB. Variable exógena=deuda pública como porcentaje del PIB.
Entre paréntesis el estadístico t de Student y entre corchetes el p-valor. Se rechaza la hipótesis de nulidad de los coeficientes de todas las variables explicativas a un nivel de significación inferior a 10%, excepto en el caso de la deuda pública, que es de 10.62 por ciento.
Dado que P (x52 ≤ 11.1 = 0.95 y J = 0.039(116) = 4.524 < 11.1, no rechazamos la hipótesis nula de validez de las variables instrumentales utilizadas.
Función de reacción lineal con oferta monetaria como variable exógena, 1966:Q1-1979:Q2
| it=c0+c1π˜t+4+c2yt+c3xt−1+ρit−1+νti | ||||||
|---|---|---|---|---|---|---|
| cˆ0 | cˆ1 | cˆ3 | cˆ4 | ρˆ | J | R¯2 |
| 0.75(0.56)[0.5785] | 0.21(2.08)[0.0430] | 0.10(2.39)[0.0209] | -0.003(-0.04)[0.9700] | 0.66(3.86)[0.0004] | 0.059 | 0.84 |
Notas: Inflación = inflación subyacente (tasa anual) medida a partir del IPC.
Brecha del producto = logaritmo neperiano del IPI – filtro de HP del logaritmo neperiano del IPI. Variable exógena = tasa de variación del agregado monetario M2.
Entre paréntesis el estadístico t de Student y entre corchetes el p-valor. En el caso de la variable exógena, no rechazamos la hipótesis nula de que dicha variable no es significativa para explicar el comportamiento de los tipos de interés. Dado que P (x52 ≤ 11.1 = 0.95 y J = 0.059(50) = 2.95 < 11.1, no rechazamos la hipótesis nula de validez de las variables instrumentales utilizadas.
Función de reacción lineal con oferta monetaria como variable exógena, 1983:Q1-2012:Q4
| it=c0+c1π˜t+4+c2yt+c3xt−1+ρit−1+νti | ||||||
|---|---|---|---|---|---|---|
| cˆ0 | cˆ1 | cˆ3 | cˆ4 | ρˆ | J | R¯2 |
| 0.60(2.33)[0.0216] | 0.39(1.74)[0.0839] | 0.19(2.53)[0.0129] | -0.03(-0.94)[0.3516] | 0.81(12.86)[0.0000] | 0.040 | 0.95 |
Notas: Desviación de la inflación=inflación calculada a partir del IPC – 2%.
Brecha del producto = logaritmo neperiano del PIB menos el filtro de HP del logaritmo neperiano del PIB. Variable exógena = tasa de variación del agregado monetario M2.
Entre paréntesis el estadístico t de Student y entre corchetes el p-valor. No se rechaza la hipótesis de nulidad del coeficiente de la variable exógena. Dado que P (x52 ≤ 11.1 = 0.95 y J = 0.040(116) = 4.64 < 11.1, no rechazamos la hipótesis nula de validez de las variables instrumentales utilizadas.
Función de reacción lineal con tipo de cambio como variable exógena, 1983:Q1-2012:Q4
| it=c0+c1π˜t+4+c2yt+c5et+c6et−1+ρit−1+νti | |||||||
|---|---|---|---|---|---|---|---|
| cˆ0 | cˆ1 | cˆ2 | cˆ5 | cˆ6 | ρˆ | J | R¯2 |
| 0.42(1.26)[0.2098] | 0.49(2.54)[0.0125] | 0.22(1.95)[0.0532] | -0.12(-1.90)[0.0608] | 0.10(2.00)[0.0478] | 0.85(11.90)[0.0000] | 0.014 | 0.92 |
Notas: Desviación de la inflación = inflación calculada a partir del IPGCP – 2%.
Brecha del producto = logaritmo neperiano del PIB menos el filtro de HP del logaritmo neperiano del PIB. Variable exógena = tasa de variación del tipo de cambio real.
Entre paréntesis el estadístico t de Student y entre corchetes el p-valor. No se rechaza la hipótesis de nulidad del coeficiente de la variable exógena. Dado que P (x42 ≤ 9.49 = 0.95 y J = 0.014(112) = 1.568 < 9.49, no rechazamos la hipótesis nula de validez de las variables instrumentales utilizadas.
En resumen, de acuerdo con el trabajo empírico realizado, la Fed parece mostrar un comportamiento simétrico respecto a las desviaciones positivas y negativas de la inflación y de la producción en los dos periodos analizados.
Durante la primera etapa analizada, la Fed no parece tener en cuenta la brecha del producto a la hora de diseñar su política monetaria, es decir, la Fed sigue una política monetaria strict inflation targeting durante la etapa anterior a 1979. En el segundo periodo analizado, las desviaciones del producto respecto a su nivel tendencial, aunque estadísticamente significativas, presentan una escasa importancia a la hora de explicar el comportamiento de la Reserva Federal. Clarida, Galí y Gertler (2000), utilizando datos trimestrales para el periodo 1979:Q3-1996:Q4, concluyen que la Fed, durante esta etapa, sólo presta atención a la brecha en cuanto a variable que le permite estimar la inflación futura. Y a esta misma conclusión llegan Clarida, Galí y Gertler (1998) utilizando datos mensuales entre 1979 y 1994.
El coeficiente referido al tipo de interés retardado es relativamente alto, sugiriendo una importante inercia en la gestión de la política monetaria por parte de la Fed, tanto en el primer periodo considerado como en el segundo. Es este un resultado frecuente en la literatura empírica: Clarida, Galí y Gertler (1998; 2000), Orphanides y Wieland (1998), Gerlach (2000), Surico (2007b), García (2007), García y Pateiro (2009), García Iglesias Pateiro Rodríguez y Salcines (2013), entre otros, obtienen un peso importante de los valores pasados del tipo de interés al explicar el valor actual del mismo. El comportamiento alisado de los tipos de interés afecta positivamente a la estabilidad del sistema financiero y a la formación de expectativas.
El endeudamiento público, aunque presenta unos niveles considerablemente altos y crecientes durante el segundo periodo, 1983:Q1-2012:Q4, resulta estadísticamente no significativo cuando la incluimos en la estimación de la función de reacción.
El coeficiente de la variación de la oferta monetaria tiene el signo correcto en ambos periodos, pero resulta no significativo. Diferentes estudios, desde 1966 hasta la actualidad, concluyen que o bien no se puede rechazar la hipótesis de nulidad del coeficiente correspondiente o éste presenta unos valores estimados muy reducidos. Clarida, Galí y Gertler (1998) descubren que la evolución de M2 es significativa en el periodo 1979:10-1994:12, y también entre 1982:10 y 1994:12, si bien con un coeficiente más reducido. Pero los propios autores aclaran que con datos trimestrales el crecimiento de la oferta monetaria apenas tiene impacto en la función de reacción de la Fed para el periodo completo y es no significativo para el periodo 1982:10-1994:12.12
Los coeficientes relativos al tipo de cambio son reducidos, bastante por debajo de los valores c5 = –0.45 y c6 = 0.45 propuestos por Svensson (2000) o c5 = –0.37 y c6 = 0.17 defendidos por Ball (1999). Resultado coherente al tratarse de una economía grande. Dado que c5 + c6 ≈ 0, el efecto sólo dura un trimestre.
CONCLUSIONESEl análisis empírico realizado nos permite concluir que la Fed ha mostrado un comportamiento simétrico respecto a las desviaciones positivas y negativas de la inflación y de la producción en los dos periodos analizados (1966:Q1-1979:Q2 y 1983:Q1-2012:Q4).
En efecto, en las distintas estimaciones realizadas de la regla de política monetaria óptima (ecuación [7]), el coeficiente relativo al término rectangular o de interacción se muestra como no significativo.
De la misma manera, los resultados obtenidos, cuando utilizamos variables ficticias (ecuación [8]), nos permiten rechazar la hipótesis de asimetría.
Estos resultados evidencian que la Fed no presenta en la etapa analizada una función de preferencias asimétrica ni existen indicios de que la economía estadounidense presente una curva de Phillips convexa. La función de pérdidas cuadráticas que parece mostrar la Fed durante el segundo periodo estudiado, pone de manifiesto que la política monetaria extraordinariamente laxa, aplicada durante la actual crisis económica, no responde a preferencias asimétricas por parte de la autoridad monetaria estadounidense, sino a una cierta relajación en la aplicación de una regla monetaria lineal.
El coeficiente relativo a la brecha del producto es no significativo en las distintas estimaciones realizadas para la primera etapa, y muy reducido en las estimaciones del segundo periodo. La Fed parece aproximarse a un strict inflation targeting. Los resultados presentan un fuerte alisamiento del tipo de interés, como se deduce de los elevados valores del coeficiente R y su nivel de significación, obtenidos en las diferentes estimaciones realizadas, es decir, se evidencia una importante inercia en la gestión de la política monetaria por parte de la Fed.
Por otra parte, ni el endeudamiento público, que alcanzó niveles elevados en el periodo 1983-2012, ni el crecimiento de la oferta monetaria parecen ser variables determinantes en el diseño de la política monetaria por parte de la Reserva Federal. En el trabajo econométrico, dirigido al análisis de estas variables exógenas en la instrumentación de la política monetaria por parte de la Fed, se obtienen coeficientes muy reducidos y poco significativos.
Por lo que se refiere al tipo de cambio real, la estimación de la ecuación [12] evidencia que esta variable es significativa, aunque los valores obtenidos para el coeficiente correspondiente son muy reducidos, en ningún caso alcanzan los valores propuestos por la literatura especializada. De todas formas, al resultar estadísticamente significativa, podemos decir que la Fed incluye esta variable en su función de reacción, esto es, adelanta el ajuste en la política monetaria al momento en que el tipo de cambio real varía, sin esperar al efecto de éste sobre la inflación y el producto.
Por último, la amplitud del periodo de análisis llevado a cabo en este trabajo encuentra evidencia para apoyar las tesis de aquellos autores que han defendido que la política monetaria aplicada por Greenspan, durante el periodo 2002-2006, fue demasiado expansiva, al igual que la gestión de la política monetaria durante la actual crisis financiera y económica.
Departamento de Análisis Económico y ADE de la Facultad de Economía y Empresa de la Universidade da Coruña, Campus de Elviña (España), <esther.barros@udc.es> y <cpateiroudc@gmail.com> respectivamente. </cpateiroudc@gmail.com> </esther.barros@udc.es>
Departamento de Economía de la Universidad de Extremadura (España), <jmgarcia@unex.es> . Los autores agradecen los valiosos comentarios de los revisores anónimos de la revista. </jmgarcia@unex.es>
Varian (1975) y Zellner (1986) introducen esta forma funcional en el contexto del análisis macroeconómico bayesiano, y Nobay y Peel (1998) la utilizan en el estudio de la política monetaria óptima.
Para un desarrollo completo, véase García Iglesias, Pateiro Rodríguez y Salcines (2013).
Eliminamos el periodo intermedio en el que la Fed, bajo la presidencia de Paul Volcker, cambió su procedimiento operativo, centrándose en el objetivo de reservas propias, de la misma forma que Dolado, María-Dolores y Ruge-Murcia (2002), Surico (2007b) y Cukierman y Muscatelli (2007), entre otros.
Las diferencias entre el IPC y el IPGCP pueden resumirse en: a) efecto fórmula, b) efecto ponderación, y c) efecto escala. Hemos utilizado el IPC porque es el comúnmente empleado en la literatura empírica sobre reglas monetarias, y el IPGCP porque es el utilizado por la Fed para definir, en el 2012, su objetivo de inflación.
La autoridad monetaria de la eurozona fija como objetivo mantener la tasa de inflación “por debajo, cerca del 2%” (BCE, 2003). Galí et al. (2004) interpretan el “cerca del 2%” como una manera opaca de transmitir que el objetivo de estabilidad de precios se establece en el rango 1-2%. Otros bancos centrales recurren también a rangos para definir la inflación objetivo. Suecia, Australia, Nueva Zelanda o Canadá fijan este rango en el 1-3 por ciento.
El IPI es el indicador más directamente relacionado con la actividad productiva global, pero presenta una importante volatilidad.
Clarida, Galí y Gertler (1998), utilizando datos mensuales para el periodo 1979-1994, incluyen dos regresores: el tipo de interés retardado un periodo y el tipo de interés retardado dos periodos; lo mismo que Dolado, María-Dolores y Naveira (2005) para el periodo 1984:1-2001:9. También Clarida, Galí y Gertler (2000), con datos trimestrales para el periodo 1960:Q1-1996:Q4, utilizan dos retardos. Surico (2007b) utiliza un retardo de un trimestre analizando el periodo muestral 1960:Q1-2003:Q2.
Hemos utilizado el programa EViews. Como matriz de ponderación empleamos la matriz de covarianzas consistente con heterocedasticidad y autocorrelación (HAC). En la estimación de esta matriz hemos utilizado el kernel Bartlett, y respecto a la selección del bandwidth hemos optado por el método Newey-West fijo.
EViews siempre incluye una constante en la lista de instrumentos.
El estadístico J que registra EViews está dividido entre el número de observaciones, por lo que para el contraste multiplicamos el valor de J registrado por EViews por el número de observaciones.
En cuanto al objetivo de output, no lo hemos incluido en el primer periodo muestral, porque, como veremos de nuevo más adelante, se muestra como no significativo.
La diferencia puede estar explicada por el hecho de que cuando utilizan datos trimestrales emplean el PIB para el cálculo del output y cuando utilizan datos mensuales el IPI. El cálculo de la brecha del producto a partir del PIB puede dar una mejor aproximación a la verdadera brecha que cuando se aproxima por el IPI. Y el hecho de que la brecha esté peor medida al utilizar datos mensuales puede justificar que la variable crecimiento de la oferta monetaria sea significativa en un caso y no en el otro.