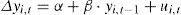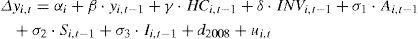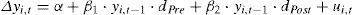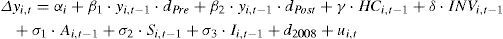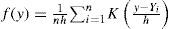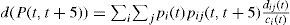Disparidades regionales en la ue-15: un enfoque de convergencia

Resumen

Este trabajo trata de contribuir a la literatura existente sobre disparidades regionales en Europa a partir del análisis, durante el periodo 1995–2008, de distintos conceptos de convergencia. Para ello, y tras una sucinta revisión de la literatura empírica existente, se utilizan dos metodologías alternativas aunque complementarias: el enfoque clásico de convergencia y el enfoque de la dinámica distributional. Los resultados obtenidos apuntan a la existencia de un proceso de convergencia regional en el pib per cápita en Europa, así como a la presencia de una cierta, aunque no muy elevada, movilidad dentro de la distribución.

Introducción

Las disparidades regionales y su evolución han sido temas ampliamente estudiados en el ámbito económico, especialmente en las últimas décadas. Sin ánimo de extendernos en exceso en esta cuestión, ya de sobra debatida, podemos aludir al principio de eficiencia y a la búsqueda de una mejor asignación de recursos para justificar esta extensa literatura referida a la necesidad de reducir las disparidades, sobre todo allí donde éstas son política o socialmente inadmisibles. La afirmación anterior cobra aún más significado, si cabe, cuando nos referimos, como sucede en el presente trabajo con la Unión Europea (en adelante ue), a entramados económicos embarcados en un proceso de unificación.

Estrechamente unido al tema de las disparidades regionales y su evolución temporal se encuentra el término convergencia. Como es sobradamente conocido, un proceso de convergencia tiene lugar cuando las regiones menos desarrolladas crecen a mayor ritmo que las regiones más desarrolladas y, como consecuencia de ello, las desigualdades entre ellas tienden a reducirse en el transcurso del tiempo. A este respecto, la literatura sobre crecimiento económico pone especial énfasis en la existencia o no de convergencia entre países o regiones. Dentro de esta rama de conocimiento conviene destacar dos grandes corrientes de pensamiento: la escuela neoclásica y la escuela de crecimiento endógeno.

En relación con la primera, y de acuerdo con el trabajo seminal de Solow (1956), el crecimiento económico lleva aparejado un proceso de convergencia debido a la presencia de rendimientos marginales decrecientes del capital; dicho de otra forma, se da un proceso de convergencia entre el centro (regiones más ricas) y la periferia (regiones más pobres) de modo que todas las regiones acaban desplazándose hacia un mismo estado estacionario en el largo plazo. En otro trabajo seminal, Solow (1957) descompone el crecimiento económico en varios componentes asociados a la acumulación de capital y trabajo, así como el conocido como residuo de Solow, asociado al progreso tecnológico.

Por lo que se refiere a la segunda escuela de pensamiento, en los años ochenta surgen, como respuesta a la manifiesta debilidad de los modelos de crecimiento neoclásicos, los modelos de crecimiento endógeno, entre los que cabe citar los trabajos de Romer (1986, 1990), Lucas (1988), Rebelo (1991) y Barro (1991). Los modelos de crecimiento endógeno explican la innovación tecnológica formalizando un mecanismo endógeno a través del cual se produce el cambio tecnológico. Como resultado, estos modelos arrojan serias dudas sobre la existencia de un proceso de convergencia. La explicación es, hasta cierto punto, bastante simple: en los modelos de crecimiento endógeno la función de producción presenta rendimientos constantes o crecientes a escala.

En este escenario, y debido al amplio debate en torno a la existencia o no de un proceso de convergencia ligado a un proceso de crecimiento económico, este trabajo, de naturaleza eminentemente empírica, se propone analizar hasta qué punto la evidencia apoya los postulados de ambas escuelas de pensamiento.¹Para ello, hay cuatro aspectos que es necesario precisar: la variable de análisis, la muestra de datos utilizada, el periodo de estudio y la metodología empleada.

Respecto al primero de ellos, y a pesar de que la desigualdad entre regiones se puede medir a partir de distintas variables económicas, en este trabajo se recurre a la más utilizada en la literatura, el ingreso per cápita: más concretamente, empleamos el producto interior bruto per cápita (pib per cápita) en paridad de poder adquisitivo (ppa).² Concerniente al ámbito de estudio, el análisis se realiza a nivel europeo debido a la importancia, más que conocida, que posee la evolución de las disparidades regionales en el viejo continente; esta cuestión ya se puso de manifiesto en el preámbulo del Tratado de Roma (1957) y continua vigente en la actualidad. En cuanto al periodo de estudio, y aunque se dispone de datos más recientes, el análisis se realiza para el periodo 1995–2008. Esta decisión obedece a que la crisis económica ha ocasionado una serie de cambios estructurales, de tal forma que considerar dos o tres años más tras su estallido en 2008 supondría, por un lado, un horizonte demasiado corto para medir su impacto y, por otro, alteraría artificialmente los resultados obtenidos en este trabajo. En lo referente a cuestiones de índole metodológica, se utilizan dos enfoques complementarios con la intención de poder ofrecer diferentes aproximaciones al estudio de la convergencia: el enfoque clásico y el enfoque de la dinámica distribucional.

En definitiva, en este trabajo, y usando metodologías alternativas, se examina la evolución de las disparidades en el pib per cápita entre las regiones (nuts2) de la Unión Europea de 15 países miembros (ue-15) —lo que supone una muestra de 215 regiones— para el periodo 1995–2008. Los datos utilizados en este estudio se han extraído de Eurostat. La modesta contribución de este trabajo a la literatura existente es triple: en primer lugar, y debido al intenso debate existente sobre las técnicas asociadas al análisis de la convergencia, la presente investigación se centra no sólo en el enfoque tradicional de convergencia (sigma y beta), sino que también emplea el enfoque de la dinámica distribucional; concretamente, este trabajo se sirve de una herramienta de visualización relativamente reciente (los llamados stacked conditional density y highest conditional density plots), así como de un índice de movilidad, también relativamente novedoso, basado en el enfoque de cadenas de Markov. En segundo lugar, y precisamente por su enfoque metodológico, este trabajo ofrece diversos resultados sobre convergencia que, a nuestro parecer, resultan interesantes al tiempo que complementarios (por ejemplo, los relativos a la forma externa de la distribución, a la movilidad intra-distribucional y a la polarización). En tercer lugar, este trabajo adopta una perspectiva regional en lugar de nacional, permitiendo así manejar una amplia y homogénea muestra de datos y, por consiguiente, obtener resultados más fiables.

Con las precisiones anteriores, el presente artículo se estructura de la siguiente manera. En la sección dos se revisa brevemente la literatura empírica sobre disparidades regionales en Europa. Como parte fundamental del trabajo, en la siguiente sección se realiza un análisis de convergencia a partir de los enfoques clásico y de dinámica distribucional. Finalmente, en la sección cuarta se indican las principales conclusiones del trabajo.

Revisión de la literatura

En los últimos tiempos la literatura empírica sobre disparidades regionales en el pib per cápita (o productividad) para el caso de la ue ha sido prolífica. Mientras una gran mayoría de trabajos apuntan hacia la existencia de algún grado de convergencia, otros muestran una tendencia hacia el estancamiento o, incluso, un proceso de divergencia. Todo parece indicar que esta falta de consenso viene motivada, en última instancia, por las diferencias en los enfoques de convergencia empleados, en la escala geográfica o en el periodo de análisis considerado. De estas tres consideraciones, la primera, relativa al enfoque de convergencia utilizado, ha sido tenida en cuenta en esta sección como criterio para la revisión de la literatura. Más concretamente, y aunque el estudio de convergencia se ha realizado atendiendo a diferentes criterios, a continuación hacemos alusión a algunos de los trabajos, a nuestro juicio más destacados, dentro del enfoque clásico de convergencia y de dinámica distribucional, así como a trabajos que combinan ambos enfoques.³

Antes de pasar propiamente a la revisión de la literatura, parece conveniente indicar que los dos enfoques presentan una serie de fortalezas. El enfoque clásico de convergencia permite responder claramente a la pregunta de si las economías más pobres están convergiendo con las más ricas, tal y como predicen los modelos de crecimiento neoclásicos convencionales. Sin embargo, el enfoque clásico, al prestar atención únicamente a los primeros momentos de la distribución, plantea dos inconvenientes que limitan su contribución, pero que son debidamente resueltos por el enfoque de la dinámica distribucional: 1) no proporciona información sobre la forma externa de la distribución y sus cambios a lo largo del tiempo y, 2) no tiene en cuenta los cambios en la posición relativa de las regiones durante el periodo de estudio (dinámica intra-distribucional). Por estas razones consideramos que la combinación de estos dos enfoques es la mejor decisión para obtener una mejor visión de los mecanismos de convergencia; esta cuestión se aborda en la siguiente sección del trabajo.

En cuanto a la revisión literaria, y comenzando con el enfoque clásico de convergencia, conviene indicar que se trata de la metodología mayoritariamente utilizada en el análisis de las disparidades económicas entre regiones europeas. Para ello se emplean dos medidas alternativas de convergencia, que son la convergencia sigma y beta (términos acuñados por Barro, 1991; Barro y Sala-i-Martin, 1992), y esta última en sus dos versiones: convergencia beta absoluta y beta condicionada. Así, cabe citar el estudio de Dewhurst y Mutis-Gaitan (1995), quienes concluyen que, durante el periodo 1981–1991, las regiones europeas experimentaron un proceso de convergencia, si bien el mismo se produjo a diferentes velocidades entre regiones. Paci (1997), a partir de una muestra de 109 regiones de la ue-12 para los años ochenta, apunta hacia la existencia de un proceso de convergencia en la productividad agregada y sectorial, aunque sin indicios de convergencia en términos de pib per cápita. Otro trabajo a destacar es el de Cuadrado-Roura, Mancha-Navarro y Garrido-Yserte (2000), que obtiene como principal conclusión la existencia de un proceso de convergencia en términos de productividad entre las regiones europeas durante los años ochenta; el principal detonante de la convergencia fue un proceso de catching-up de las regiones menos desarrolladas, que experimentaron mayores tasas de crecimiento relativas. Unido a lo anterior, Cuadrado-Roura, Mancha-Navarro y Garrido-Yserte (2000) muestran que las regiones europeas se caracterizan por un comportamiento heterogéneo en términos de productividad, empleo y producción.

Por otro lado, un número considerable de estudios han utilizado el enfoque de la dinámica distribucional, tanto en sus versiones discreta como continua, para estudiar la convergencia entre regiones europeas. Esta metodología, como su nombre indica, se centra en el estudio de la distribución y su evolución temporal, mostrando de esta forma tanto cambios en su forma externa como en la dinámica intra-distribucional. Dentro de este enfoque, la versión discreta más conocida es el llamado enfoque de cadenas de Markov, el cual se basa en el cómputo de matrices de transición. Utilizando esta técnica, Fingleton (1997), en un estudio para el periodo 1975–1993, pone de relieve la existencia de una elevada movilidad en los niveles de producción per cápita regionales que, dada su dirección, trajo consigo la aparición de un proceso de convergencia en Europa. Con la misma metodología, Magrini (1999) centra su análisis en la importancia del concepto de región empleado y cómo éste determina los resultados. Sus conclusiones ponen de manifiesto que en el periodo 1979–1990 hubo una tendencia hacia la divergencia entre lo que se denominan Regiones Funcionales Urbanas (que no son más que áreas metropolitanas) y un proceso de lenta convergencia entre regiones administrativas (nuts2). En ambos casos, sin embargo, se puede identificar un pequeño grupo de regiones líderes en el proceso de crecimiento. Otro trabajo destacable es el de Le Gallo (2004), quien, a partir de una versión espacial del enfoque discreto, demuestra que la convergencia regional fue muy fuerte durante el periodo 1980-1995.

Si pasamos al enfoque continuo de dinámica distribucional, hay que señalar que la mayoría de trabajos ha recurrido a la estimación de kernels estocásticos y, más recientemente, a técnicas novedosas como el llamado highest conditional density region approach. Bajo este último enfoque, Pittau y Zelli (2006) muestran que desde 1977 hasta 1996 tuvo lugar, por un lado, un proceso de convergencia regional muy lento y, por otro, una tendencia a la creación de un pequeño polo o grupo de regiones muy ricas. Los resultados obtenidos por Meliciani (2006) van en parecida línea, al obtener evidencia de un lento proceso de convergencia en el ingreso per cápita entre regiones pertenecientes a diferentes países, junto con la ausencia de convergencia entre regiones pertenecientes a un mismo país. Por su parte, Fischer y Stumpner (2008), cuya contribución más destacada es la utilización de un procedimiento de filtrado espacial, llegan a similares conclusiones que Pittau y Zelli (2006). Finalmente, Maza y Villaverde (2011) apuntan a un proceso de convergencia regional entre 1995 y 2006, siendo éste más rápido entre las regiones metropolitanas que entre las administrativas.

Asimismo, cabe destacar que ambas versiones del enfoque de dinámica distribucional (discreta y continua) suelen combinarse con objeto de obtener resultados más detallados. Entre estos trabajos cabe citar el estudio deLópez-Bazo et al. (1999), donde, para el periodo 1980–1992, no se detecta ningún signo aparente de convergencia en el pib per cápita entre las regiones de la ue-12. Este trabajo, que también incluye referencias de tipo espacial, concluye que es la persistencia de clusters espaciales a niveles de ingreso per cápita muy bajos, lo que provoca la falta de convergencia. Por su parte, Maza, Hierro y Villaverde (2010) abordan el estudio de la dinámica intra-distribucional en el ingreso per cápita para los periodos 1980–1993 y 1993–2005, concluyendo que la movilidad en el primero de los periodos, además de resultar más alta que en el segundo, favoreció un proceso de convergencia entre regiones europeas. En un trabajo más reciente, Maza, Hierro y Villaverde (2012) analizan el papel desempeñado por la situación geográfica a la hora de explicar la distribución regional del ingreso per cápita en Europa para el periodo 1980–2005. Sus resultados revelan que aquellas regiones pobres rodeadas de regiones ricas tienen mayores posibilidades de escapar de la trampa de la pobreza que otras regiones pobres.

Finalmente, en la literatura sobre convergencia tiene también cabida el uso conjunto de técnicas clásicas y de dinámica distribucional (discretas y continuas), en sintonía con una mejor compresión de la evolución de las disparidades regiones. Así, por ejemplo, Cuadrado-Roura (2001) señala, utilizando un análisis clásico de convergencia y matrices de transición, que entre los años 1977 y 1994 tuvieron lugar cambios significativos en la posición relativa de las regiones, así como un lento proceso de convergencia regional. Ahondando en esta cuestión, Cuadrado-Roura, Mancha-Navarro y Garrido-Yserte (2002) demuestran que la movilidad regional resulta ser un factor decisivo para explicar el proceso de convergencia en la ue entre 1977 y 1998, aunque el ritmo de reducción de las disparidades regionales en términos de pib per cápita y productividad ha ido decreciendo. Por otra parte, varios trabajos han adoptado un enfoque continuo de la dinámica interna como complemento al análisis tradicional de convergencia. En esta línea de análisis Maza y Villaverde (2004) concluyen, a partir de técnicas no-paramétricas y espaciales aplicadas a una muestra de regiones de la ue-12, que las disparidades regionales fueron amplias y persistentes durante el periodo 1980–1996, que el grado de movilidad regional fue bastante bajo, y que existían signos claros de polarización y dependencia espacial. Chapman y Meliciani (2011), por otro lado, encuentran signos de convergencia entre regiones europeas durante el periodo 1998–2005 que parecen obedecer al comportamiento de las regiones de reciente adhesión. Asimismo, ponen de relieve la existencia de una fuerte correlación espacial dentro de la distribución a partir de un análisis de convergencia beta con efectos espaciales.

Disparidades regionales en Europa: un enfoque de convergencia

Tras revisar de forma muy sucinta la literatura existente sobre convergencia regional en Europa, el objetivo de esta sección es doble. En primer lugar, se realiza un análisis de convergencia desde una perspectiva clásica (véanse los trabajo seminales de Barro, 1991 y Barro y Sala-i-Martin, 1992). En segundo lugar, y con la finalidad de abordar las limitaciones del análisis anterior, se adopta un enfoque de dinámica distribucional.

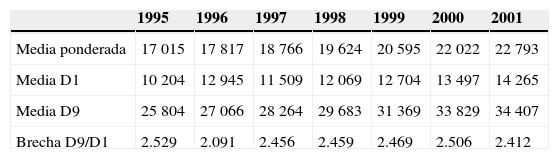
En cualquier caso, antes de abordar estas cuestiones parece pertinente presentar una visión general de las disparidades regionales en la ue. Para ello, en el cuadro 1 se muestran una serie de estadísticos descriptivos que dan idea de la intensidad y evolución de estas disparidades durante el periodo 1995–2008.

Cuadro 1.

Disparidades regionales en pib per cápita, 1995–2008

	1995	1996	1997	1998	1999	2000	2001
Media ponderada	17 015	17 817	18 766	19 624	20 595	22 022	22 793
Media D1	10 204	12 945	11 509	12 069	12 704	13 497	14 265
Media D9	25 804	27 066	28 264	29 683	31 369	33 829	34 407
Brecha D9/D1	2.529	2.091	2.456	2.459	2.469	2.506	2.412

	2002	2003	2004	2005	2006	2007	2008
Media ponderada	23 484	23 673	24 598	25 442	26 655	27 936	27 822
Media D1	14 668	14 853	14 280	15 311	16 233	16 981	16 934
Media D9	35 664	35 907	37 010	39 513	40 462	42 871	42 715
Brecha D9/D1	2.431	2.417	2.592	2.581	2.493	2.525	2.522

Nota: datos en euros constantes de 1999. D1 y D9 denotan el primer y último decil respectivamente.

Fuente: Eurostat y elaboración propia.

Una primera impresión del alcance de las disparidades regionales se puede obtener comparando la media europea con la media del primer y último decil. Como se puede observar, el último decil (el 10% de las regiones con mayor pib per cápita) está situado 1.5 veces por encima de la media global, tanto en 1995 como en 2008, mientras que el primer decil (el 10% de las regiones más pobres) se sitúa 1.7 veces por debajo de la media total en 1995 y 1.6 veces en el 2008. En cuanto al ratio entre deciles, el 10% de las regiones más ricas obtienen 2.5 veces más ingreso per cápita que el 10% de las regiones más pobres, tanto en el año inicial como en el final. Queda probada, por lo tanto, la existencia de considerables diferencias regionales, por lo que resulta conveniente estudiar más en detalle su evolución y la presencia o no de un proceso de convergencia regional.

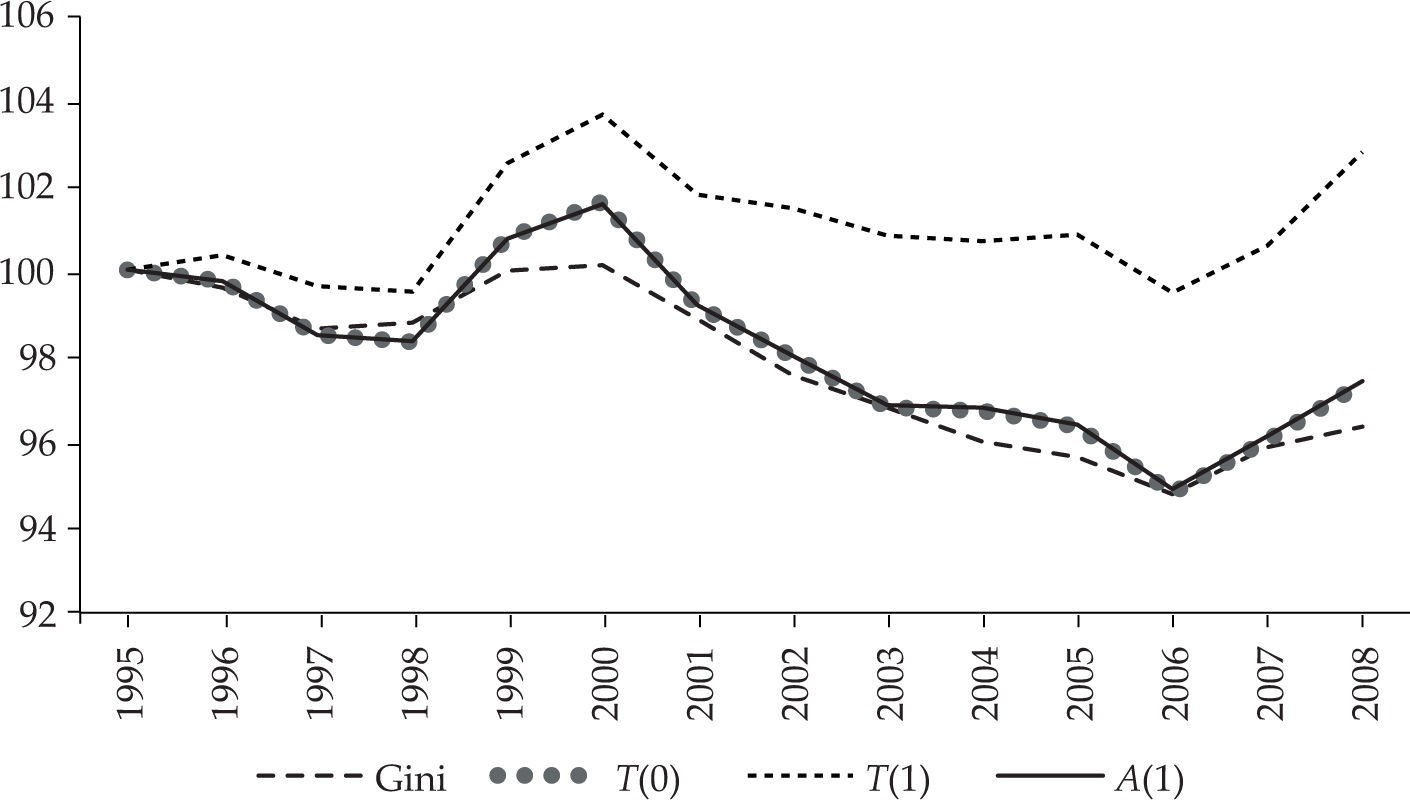
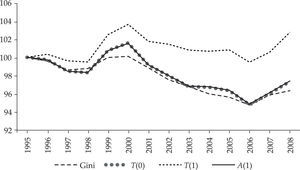
Convergencia clásica

En este apartado se analiza la existencia de convergencia regional en su versión clásica (sigma y beta). De forma sintética, existe un proceso de convergencia sigma cuando la dispersión (en el pib per cápita en este caso) entre regiones se reduce en el tiempo. Dado que no hay unanimidad acerca de qué indicador es el más apropiado para medir la convergencia sigma, para testar la robustez de nuestros resultados se han considerado varios indicadores de desigualdad, en particular el índice de Gini (G), dos versiones del índice Theil [T(0)y T(1)] y una versión del índice de Atkinson [A(1)].⁴ Los resultados, tomando el año inicial como base 100, se muestran en la gráfica 1.

Gráfica 1.

Convergencia sigma (1995 = 100)

Fuente: Eurostat y elaboración propia.

Como puede apreciarse, todos los indicadores de desigualdad muestran una evolución muy similar a lo largo del periodo de análisis: en los tres primeros años su valor desciende ligeramente; a continuación, y hasta el 2000, presentan una tendencia creciente; y, por último, a partir de este año su valor vuelve a caer con un pequeño rebote, especialmente apreciable en el indicador T(1), en los dos últimos años. En definitiva, todos los indicadores presentan un comportamiento similar y, con la única excepción del indicador T(1), apuntan hacia una leve reducción de las disparidades en el ingreso per cápita en Europa. Por consiguiente, en el caso de existir convergencia sigma, su intensidad no ha sido muy elevada.

Otro método complementario de análisis de las disparidades regionales en el pib per cápita es la convergencia beta. Dicha convergencia existe cuando se da una relación inversa entre la tasa de crecimiento de la variable analizada (pib per cápita) y su valor en el año inicial. Existen dos tipos de convergencia beta: absoluta y condicionada. En el caso de la convergencia beta absoluta se asume que todas las regiones de la muestra convergen hacia el mismo estado estacionario. Por el contrario, en el caso de la convergencia beta condicionada se supone que las regiones no convergen necesariamente hacia el mismo estado estacionario, al depender éste de factores propios de carácter económico, institucional, etcétera.

Bajo la hipótesis de convergencia beta absoluta se estima la siguiente ecuación de regresión (Barro y Sala-i-Martin, 1992):

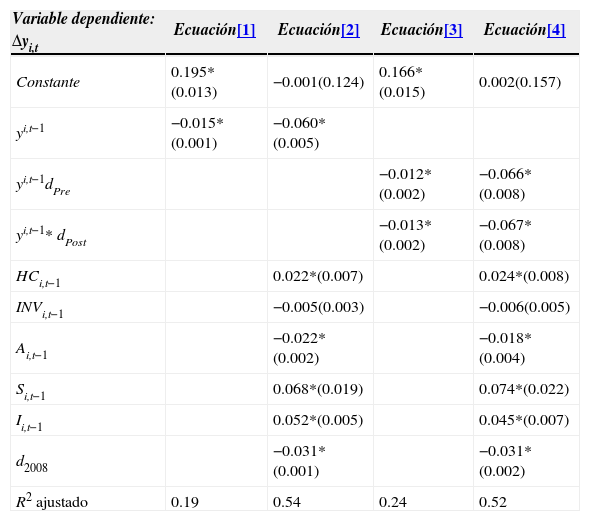
donde Δy_i,t denota la tasa de crecimiento del pib per cápita (calculada como diferencia de logaritmos) e y_i,t−1 el pib per cápita (en logaritmos) en el año anterior. Existirá convergencia beta absoluta cuando el parámetro β estimado en la ecuación de regresión tome un valor negativo y estadísticamente significativo. La estimación de la ecuación [1] se ha realizado utilizando mínimos cuadrados generalizados (mcg) —la prueba de Breusch-Pagan indicaba la presencia de problemas de heterocedasticidad en la muestra—, mostrándose los resultados en el cuadro 2. Como se puede ver, el coeficiente β toma un valor de —0.015 y es estadísticamente significativo a 99%, de tal forma que nuestros resultados respaldan la existencia de un débil proceso de convergencia beta absoluta.

Cuadro 2.

Convergencia beta

Variable dependiente: Δyi,t	Ecuación[1]	Ecuación[2]	Ecuación[3]	Ecuación[4]
Constante	0.195*(0.013)	−0.001(0.124)	0.166*(0.015)	0.002(0.157)
y^i,t−1	−0.015*(0.001)	−0.060*(0.005)
y^i,t−1dPre			−0.012*(0.002)	−0.066*(0.008)
y^i,t−1* dPost			−0.013*(0.002)	−0.067*(0.008)
HCi,t−1		0.022*(0.007)		0.024*(0.008)
INVi,t−1		−0.005(0.003)		−0.006(0.005)
Ai,t−1		−0.022*(0.002)		−0.018*(0.004)
Si,t−1		0.068*(0.019)		0.074*(0.022)
Ii,t−1		0.052*(0.005)		0.045*(0.007)
d2008		−0.031*(0.001)		−0.031*(0.002)
R^2 ajustado	0.19	0.54	0.24	0.52

Notas: errores estándar entre paréntesis. (*) Significativo a 99%. Se han incluido efectos fijos.

Fuente: Eurostat y elaboración propia.

Una vez analizada la convergencia beta absoluta, se pasa a estudiar la convergencia beta condicionada, para lo cual se incluyen una serie de variables (expresadas en logaritmos a excepción de la variable dummy) en la ecuación de regresión con el objeto de capturar la situación particular de cada una de las regiones. Concretamente se consideran:

• 1.

  El nivel de capital humano (HC), ya que parece evidente que la dotación de capital humano guarda una relación directa con el crecimiento económico de un país. Como variable proxy del capital humano⁵ se utiliza el porcentaje de empleo en tecnología y en sectores intensivos en conocimiento.

• 2.

  El nivel de inversión sobre el pib (INV) porque, tal y como sucede con el nivel de capital humano, la inversión se considera un factor impulsor del crecimiento económico.

• 3.

  La distribución sectorial, para lo cual se incluyen la participación del empleo en sectores tales como agricultura y pesca (A), servicios (S) e industria excluyendo la construcción (I).

• 4.

  Una variable dummy temporal para 2008, ante la necesidad de controlar por los primeros efectos de la crisis económica.

Con todo lo anterior, se estima la siguiente ecuación de regresión:

Llegados a este punto, es preciso puntualizar dos aspectos sobre la ecuación [2]. Tal y como se puede observar, se ha considerado, apoyándose en los resultados obtenidos en la prueba de Hausman, un modelo de efectos fijos para minimizar el riesgo de variables omitidas; de esta forma, se consigue aislar los efectos específicos de cada región no incluidos en el modelo y que pueden influir de manera directa en el crecimiento del ingreso. Además, a fin de abordar potenciales problemas de endogeneidad, queremos señalar que inicialmente se estimó la ecuación [2] por el método de los momentos generalizado (gmm) propuesto por Arellano y Bond (1991). Finalmente, sin embargo, se descartó esta técnica de estimación ya que tanto el test de correlación serial de segundo orden en los residuos como la prueba de Sargan arrojaron resultados bastante pobres. Por este motivo, la estimación se realiza por mcg.⁶

Los resultados de la estimación se muestran en la tercera columna del cuadro 2. Como factor más destacable hay que señalar que el coeficiente β aumenta (en términos absolutos) a 0.06, mostrando que el proceso de convergencia es más intenso cuando las regiones convergen a diferentes estados estacionarios, siendo éste un resultado muy común en la literatura. En cuanto a la relevancia de las variables de control, el coeficiente asociado al capital humano es positivo y estadísticamente significativo; esto es, el hecho de tener una alta cualificación laboral fomenta el crecimiento económico. Sin embargo, la inversión no resulta estadísticamente significativa a la hora de explicar el crecimiento del pib per cápita; este resultado, aunque contra intuitivo, no es tan inusual en la literatura (véase, por ejemplo, Hammond y Thompson, 2008; Crihfield y Panggabean, 1995). Respecto al peso de los sectores en el pib, los resultados apuntan a que, mientras los sectores industria y servicios contribuyen al crecimiento, el sector agricultura podría dificultarlo. Atendiendo a los efectos fijos (resultados disponibles bajo petición), la mayoría de ellos resultan ser estadísticamente significativos, lo que pone de manifiesto que las regiones muestran comportamientos diferenciados que no se recogen en la especificación del modelo, todos ellos consecuencia de factores sociales, políticos e institucionales.

Para finalizar, creemos que conviene dedicar unas líneas al estudio del posible efecto que ha tenido el euro en el proceso de convergencia regional en Europa. Para ello, se contrasta la estabilidad de los parámetros beta durante el periodo anterior y posterior a la implementación del euro. En particular, y siguiendo a Maza, Villaverde y Hierro (2014), se divide el periodo en: 1) Era pre-euro; 2) Era post-euro. Seguidamente, se construyen dos variables dummy (una para cada subperiodo), que denotamos por d_Pre y d_Post, y se multiplican por la variable original y_i,t−1. Si la diferencia entre los parámetros asociados a estas nuevas variables (β₁ y β₂) resulta ser estadísticamente significativa, la hipótesis sobre una diferente velocidad de convergencia antes y después de la introducción del euro quedaría probada. De acuerdo con estas premisas, las ecuaciones a estimar son las siguientes, la primera de ellas correspondiente a la convergencia beta absoluta y la segunda a la condicionada:

Los resultados obtenidos se muestran en las dos últimas columnas del cuadro 2. Centrando nuestros comentarios en las variables de interacción, se observa que todos los parámetros asociados son negativos y estadísticamente significativos; esto sugiere que el proceso de convergencia existe tanto en la época pre-euro como en la post-euro. Con relación a sus diferencias, se puede ver que los parámetros β₁ y β₂ son casi idénticos tanto en la ecuación [3] como en la [4], aceptándose la hipótesis de igualdad según la prueba de Wald. En consecuencia, no parece existir evidencia que apoye un efecto significativo del euro en la convergencia regional. Por esta razón, y con la pretensión de no ser repetitivos, esta cuestión no será abordada en el resto del trabajo.

Enfoque sobre la dinámica distribucional

Como se ha indicado con anterioridad, el enfoque clásico presenta varios inconvenientes, los cuales pretenden ser abordados en esta sección utilizando el así conocido enfoque de la dinámica distribucional.

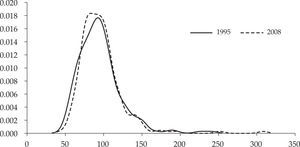
Forma externa

En primer lugar, se examina la forma externa de la distribución mediante funciones de densidad univariantes. Una función de densidad es una curva suavizada que representa la distribución de probabilidad de una variable aleatoria continua. La función de densidad se estima de forma no paramétrica utilizando el método Kernel. En términos formales, la estimación de la función de densidad de una serie Y en un punto y viene dada por la expresión:

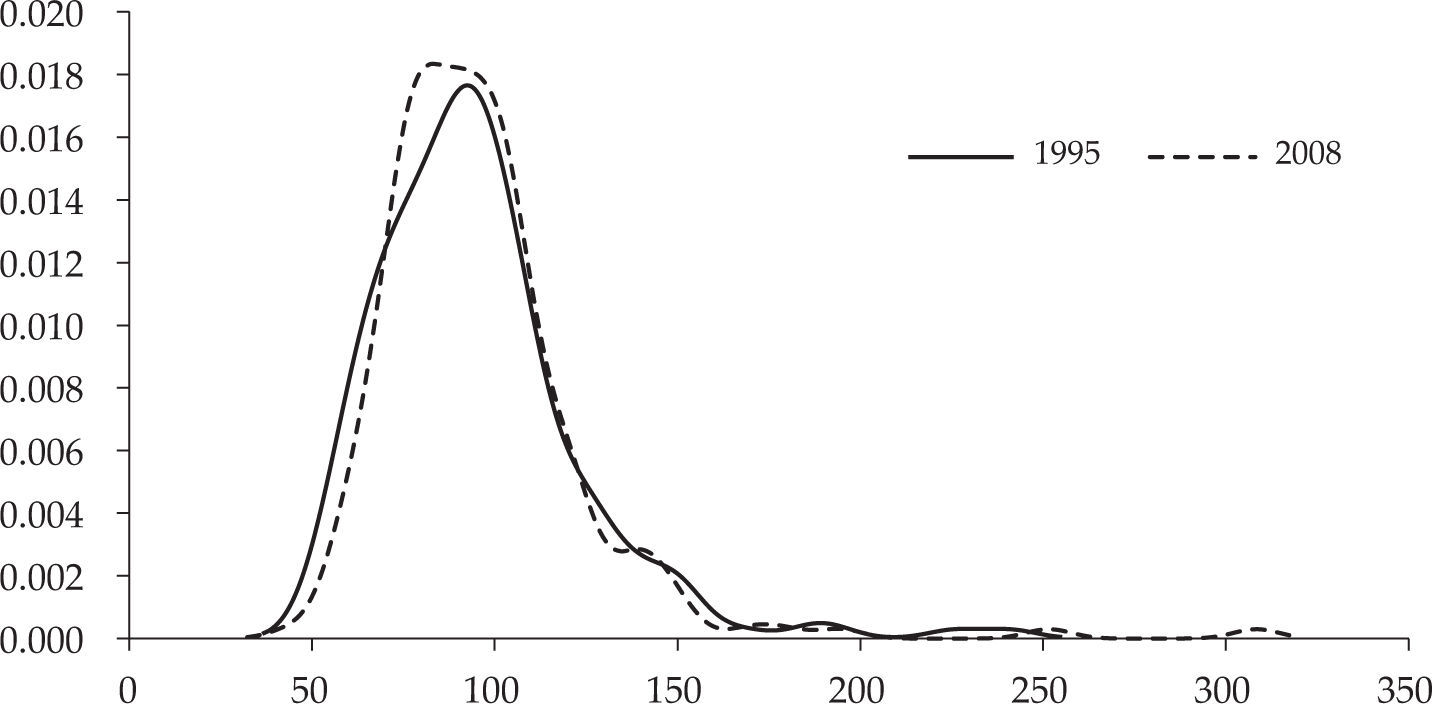
donde n es el número de observaciones, K la función kernel, h el parámetro de suavizado, Y_i los valores de la variable independiente y, finalmente, y representa el valor de la variable independiente para el que se desea obtener la estimación. En nuestro caso concreto, para estimar la ecuación [5] se emplea un kernel Gaussiano con amplitud de banda óptima siguiendo la regla de Silverman (Silverman, 1986).

Con todo lo anterior, la gráfica 2 muestra la forma externa de la distribución del ingreso per cápita para los años inicial y final del periodo muestral. Los valores están expresados en términos relativos considerando la media regional europea como base 100 para, de esta forma, eliminar los cambios absolutos que se han producido en el transcurso del tiempo. Los resultados obtenidos revelan una concentración ligeramente mayor en la masa de probabilidad en torno a la media en 2008, así como una débil reducción de los valores extremos respecto al año inicial. Este resultado concuerda con la evidencia proporcionada en la sección previa, esto es, la existencia de un débil proceso de convergencia regional.

Gráfica 2.

Funciones de densidad (ue-15 = 100)

Fuente: Eurostat y elaboración propia.

Dinámica intra-distribucional

El análisis de la forma externa de la distribución, aunque relevante, no proporciona información alguna sobre los cambios ocurridos dentro de la distribución. Esta limitación puede ser resuelta mediante el estudio de la dinámica intra-distribucional. Dentro de este marco existen dos enfoques alternativos: el continuo y el discreto. El enfoque continuo tiene la ventaja de que sus resultados no dependen de ninguna discretización, mientras que la ventaja del enfoque discreto es que, mediante el cálculo de un índice, permite cuantificar la movilidad intra-distribucional. Dado que estos dos enfoques son claramente complementarios, en este trabajo hemos decidido aplicar ambos. Más concretamente, y por tratarse de una práctica habitual en muchos estudios de dinámica intra-distribucional, se ha optado por evaluar los cambios ocurridos entre los años t y t + 5, es decir, hemos considerado un periodo de transición de cinco años.

Comenzando con el enfoque continuo, en este trabajo se utiliza el conocido como highest conditional density region approach, ya que proporciona mejores propiedades estadísticas y herramientas de visualización que el enfoque estándar de kernel estocásticos (Hyndman, Bashtannyk y Grunwald, 1996). Esta técnica consiste en la estimación de una función de densidad condicionada para una variable, en este caso el ingreso per cápita en el año t + 5(ϒ_t+5), dado el ingreso per cápita en el año t(ϒ_t).

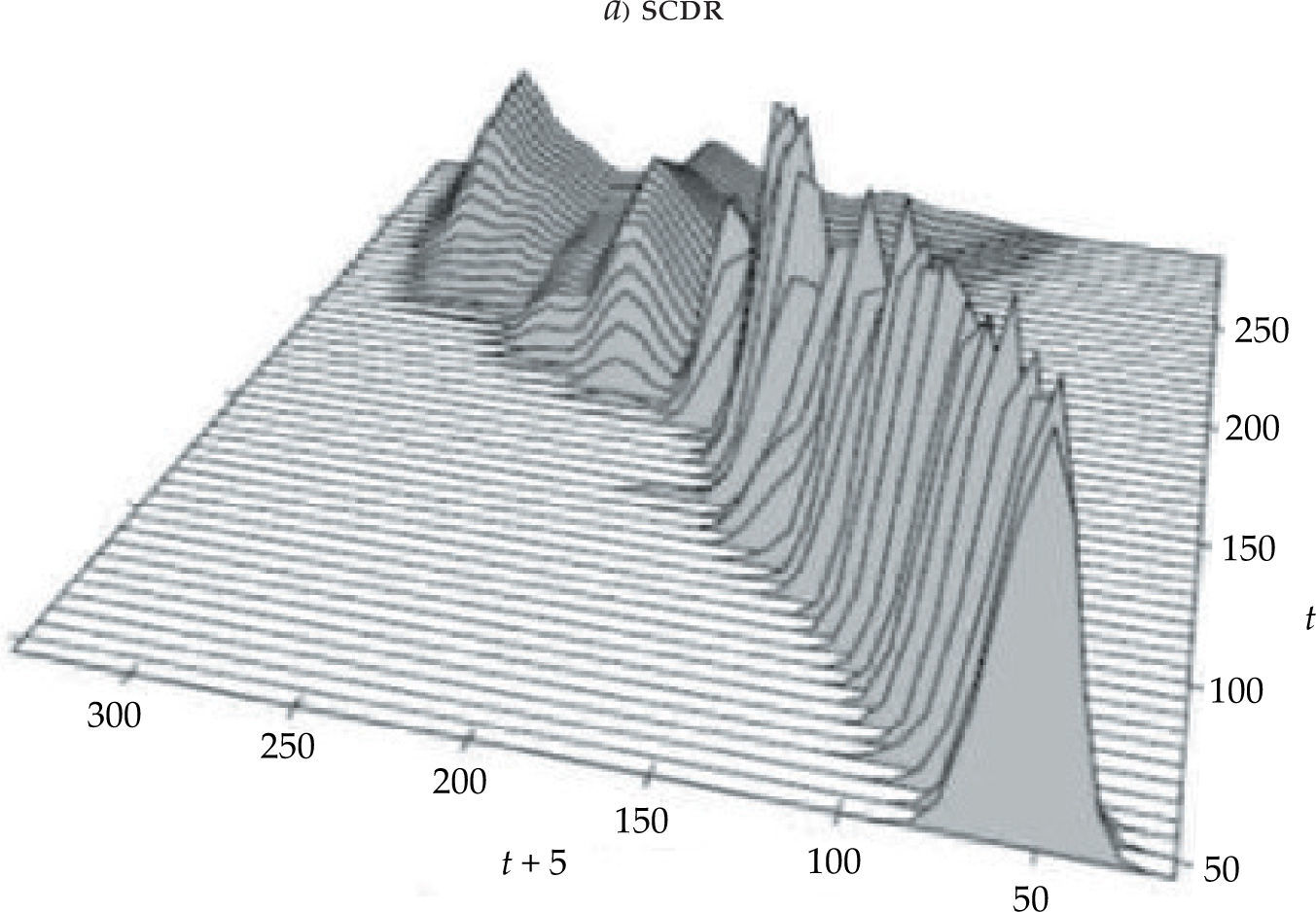
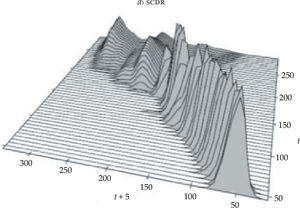
Dejando a un lado los aspectos técnicos (véase, a modo de ejemplo, Maza, Hierro y Villaverde, 2010), se estiman y representan los llamados stacked conditional density region (scdr) y highest conditional density region (hcdr) plots. Para ello, se emplea un kernel gaussiano y una amplitud de banda óptima siguiendo las reglas fijadas por Bashtannyk y Hyndman (2001). Los resultados del scdrplot se muestran en la gráfica 3a. Como se puede apreciar, esta gráfica recoge un número preestablecido de densidades condicionadas (en este caso 50). Así, este método permite observar los cambios en la forma de la distribución del ingreso per cápita entre t y t + 5 para distintos valores del ingreso per cápita en el año t. Los resultados obtenidos parecen indicar que las regiones europeas han mantenido, en general, sus niveles relativos de ingreso per cápita, aunque al tiempo resulta patente que se han producido algunos movimientos significativos en la cola superior de la distribución.

Gráfica 3.

Movilidad intra-distribucional: scdryhcdrplots

Fuente: Eurostat y elaboración propia.

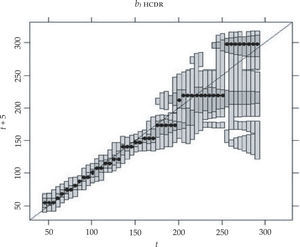
Otra forma de representar los cambios sucedidos en la distribución del ingreso per cápita, más informativa, es el hcdrplot (gráfica 3b). La llamada highest density region se define como “la región más pequeña del espacio muestral que contiene una probabilidad dada” (Hyndman, Bashtannyk y Grunwald, 1996: 327). De esta forma, cada banda vertical representa la densidad condicionada para un nivel de ingreso per cápita en el año t. En particular, esta gráfica revela las llamadas highest density regions para probabilidades de 50% (áreas más oscuras) y 99% (área más clara). Asimismo, el hcdrplot recoge, mediante el símbolo •, la moda (valor del ingreso per cápita en t + 5, donde la función de densidad toma su valor máximo) para cada densidad condicionada y valor de ingreso per cápita en el año t. Los resultados con esta herramienta demuestran que, aunque la movilidad en la cola izquierda de la distribución es ciertamente muy baja, las regiones más pobres (las situadas en la primera banda) han mejorado significativamente sus niveles de ingreso (tanto la moda como el área que representa probabilidades de 50% se sitúan por encima de la diagonal). Sin embargo, para el resto de regiones por debajo de la media en el año t las modas se sitúan bajo la diagonal, al tiempo que la masa de probabilidad de 50% toca dicha diagonal, lo que indica que la movilidad es muy reducida. Por otro lado, la situación de las regiones con un ingreso per cápita superior a 150% de la media ha empeorado en términos globales (las modas y la mayoría de las highest density regions correspondientes a 50% se sitúan por debajo de la diagonal); especial mención merecen las regiones más ricas, mostrando claros síntomas de polarización. Un resultado similar se muestra en el trabajo de Maza (2004), aunque con un número más reducido de regiones pertenecientes a la ue-12, así como en Fischer y Stumpner (2008) para el caso de las regiones de la ue-27.

Pasando a la versión discreta, en este trabajo se utiliza el enfoque de cadenas de Markov porque, como ya se ha indicado, permite medir la movilidad intra-distribucional. Para definir de una manera sencilla el concepto de matriz de transición, supongamos que las regiones pueden ser agrupadas en una serie de estados exhaustivos y mutuamente excluyentes de acuerdo a su ingreso per cápita en los instantes t₀ y t₁, siendo p(t₀) y p(t₁) las distribuciones inicial y final del ingreso respectivamente. El nexo de unión entre ambas distribuciones viene dado por p(t₁) = p(t₀)⋅P(t₀,t₁), donde el operador P(t₀,t₁) representa la matriz de probabilidades de transición, con elementos genéricos p_ij(t₀,t₁). La ecuación anterior describe la evolución temporal de p(t₀), esto es, los cambios en la distribución del ingreso entre t₀ y t₁. Así, la interpretación de una matriz de transición resulta bastante intuitiva: cada una de sus celdas p_ij(t₀,t₁) proporciona la probabilidad de desplazarse desde un estado con ingreso per cápita i hacia otro j entre t₀ y t₁.

Para aplicar este enfoque, y a diferencia del enfoque continuo, es necesario dar una definición de los estados. Siguiendo el mismo criterio utilizado por una gran mayoría de trabajos que aplican esta técnica en el contexto de la ue, en este trabajo las regiones europeas se agrupan en los siguientes cinco estados de ingreso per cápita en t: [0, 75), [75, 90), [90, 110), [110, 125), [125, +∞). Esta agrupación nos permite diferenciar, así, entre regiones con niveles de ingreso per cápita bajos, medio-bajos, medios, medio-altos y altos, respectivamente.

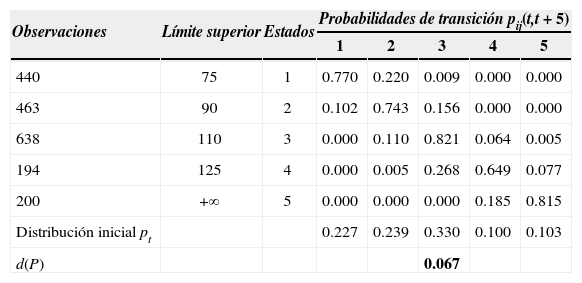
Una vez definidos los estados, otra decisión importante afecta a la longitud del periodo de transición. En este caso, como se explicó anteriormente y para mantener la concordancia con el análisis anterior, se ha optado por estimar una matriz de transición de cinco años. En consecuencia, los elementos de la matriz de transición p_ij(t,t + 5) representan la probabilidad de moverse desde un estado i a otro j entre t y t + 5. Como es habitual, las probabilidades de transición se han estimado por máxima verosimilitud. Los resultados se muestran en el cuadro 3.⁷ Los altos valores obtenidos para la diagonal principal de la matriz de transición sugieren que, en general, existe una alta persistencia en la posición relativa de regiones dentro de la distribución. Merece la pena subrayar que la persistencia es particularmente elevada para el caso de regiones con niveles de ingreso per cápita intermedios.

Cuadro 3.

Movilidad intra-distribucional: matriz de transición de cinco años e índice de movilidad

Observaciones	Límite superior	Estados	Probabilidades de transición pij(t,t + 5)
			1	2	3	4	5
440	75	1	0.770	0.220	0.009	0.000	0.000
463	90	2	0.102	0.743	0.156	0.000	0.000
638	110	3	0.000	0.110	0.821	0.064	0.005
194	125	4	0.000	0.005	0.268	0.649	0.077
200	+∞	5	0.000	0.000	0.000	0.185	0.815
Distribución inicial pt			0.227	0.239	0.330	0.100	0.103
d(P)					0.067

Nota: la primera columna recoge el número de pares región/año que empiezan en el respectivo estado en t. Debido a cuestiones de redondeo, las filas de la matriz de transición en la distribución inicial no siempre suman exactamente la unidad.

Fuente: Eurostat y elaboración propia.

Otro resultado destacado es que la mayoría de las transiciones se dirigen hacia estados contiguos, lo que nos lleva a sospechar que la movilidad intra-distribucional no es muy elevada. No obstante, y para abordar adecuadamente esta cuestión, se ha estimado el indicador de movilidad propuesto por Maza, Hierro y Villaverde (2010). Este indicador viene dado por la siguiente expresión:

donde p_i(t) es la proporción de regiones en el estado de ingreso i en t (esto es, el tamaño de cada estado de ingreso), p_ij(t,t + 5) denota las probabilidades de transición, dij(t)=y¯j(t)−y¯i(t), esto es, la diferencia absoluta entre el ingreso per cápita medio de los estados considerados; y, por último, c_i(t) es un elemento introducido en la ecuación para normalizar el indicador de movilidad y que se define como el máximo valor encontrado en la fila i de la matriz D(t) [matriz de distancias con elementos genéricos d_ij(t)]. De este modo, tres son los elementos incluidos para cuantificar la movilidad: tamaño (p_i), transiciones (p_ij) y distancia (d_ij) La interpretación de este índice es inmediata: cuanto más se aproxime su valor a 1, mayor será el grado de movilidad. Teniendo presente, no obstante, que la obtención de un valor del índice próximo a la unidad es prácticamente imposible desde el punto de vista económico (conllevaría movimientos generalizados a polos opuestos), se han llevado a cabo varias simulaciones con el objetivo de diferenciar entre grados de movilidad que consideramos altos, medios y bajos (véase el cuadro 4). De acuerdo con lo anterior, el valor del índice de movilidad, de 0.067 (véase el cuadro 3), confirma nuestra sospecha inicial de que la movilidad intra-distribucional no es demasiado alta; según nuestras simulaciones se puede calificar como media, con un valor que se sitúa, de hecho, en el límite entre movilidad media y baja. Este resultado contrasta, en cierta medida, con el bajo grado de movilidad obtenido por Maza, Hierro y Villaverde (2010) para el periodo 1980–2005.

Cuadro 4.

Caracterización del grado de movilidad

Grado de movilidad	Condición	Límites
Alto	Más de 40% de las regiones se mueve hacia un estado contiguo	d(P) ≥ 0.119
Medio	Entre 20 y 40 por ciento de las regiones se mueve hacia un estado contiguo	0.060 ≤ d(P) < 0.119
Bajo	Menos de 20% de las regiones se mueve hacia un estado contiguo	d(P) < 0.060

Fuente: Eurostat y elaboración propia.

Conclusiones

En este trabajo se ha analizado la evolución de las disparidades regionales en torno al pib per cápita en Europa durante el periodo 1995–2008. Para ello, y tras contextualizar el objetivo de este estudio dentro de la literatura existente, se han empleado dos enfoques de convergencia: la convergencia clásica y el enfoque de la dinámica distribucional. Las principales conclusiones que se extraen de los resultados obtenidos son las que se recogen enseguida.

Respecto al enfoque clásico de convergencia, se aprecia la existencia de un débil proceso de convergencia sigma. Asimismo, la evidencia empírica apoya la presencia de un proceso de convergencia beta absoluta, aunque de nuevo de forma poco intensa. A continuación se han incluido una serie de variables en la ecuación de convergencia para relajar la hipótesis clásica de que todas las regiones convergen hacia el mismo estado estacionario. Los resultados confirman que ha existido un proceso de convergencia beta condicionada, obteniéndose una velocidad de convergencia considerablemente más alta. Los resultados también revelan el papel desempeñado por el capital humano y la participación de los sectores industria y servicios en el pib como motores del crecimiento económico, así como la existencia de factores regionales específicos que sesgan, al alza o a la baja dependiendo del caso, el crecimiento de las regiones europeas. Finalmente, el presente trabajo revela que el impacto del euro sobre el proceso de convergencia no ha sido significativo.

Dados los inconvenientes que plantea el enfoque clásico de convergencia, se ha adoptado un enfoque de dinámica distribucional que aporta conclusiones adicionales. En lo que respecta a la forma externa de la distribución, se aprecia que tanto en el año inicial (1995) como en el final (2008) la masa de probabilidad se concentra en torno a la media europea. No obstante, se observa un ligero proceso de convergencia debido a que en el 2008 esta concentración se acentúa; además, las colas de la distribución se acortan en el 2008 respecto a 1995.

El análisis de la dinámica intra-distribucional se ha abordado tanto desde una perspectiva continua como discreta. Desde una perspectiva continua, se ha recurrido a una técnica relativamente novedosa, the highest conditional density region approach. Sus resultados revelan la existencia de un cierto grado de movilidad en la distribución durante el periodo de análisis, al tiempo que existen signos de polarización entre las regiones más ricas —mientras que algunas de estas regiones han mejorado su posición relativa, la mayoría de ellas ha visto empeorada su situación. Desde una perspectiva discreta, la estimación del indicador de movilidad propuesto por Maza, Hierro y Villaverde (2010) pone de relieve que la intensidad de la movilidad intra-distribucional se puede catalogar como de grado medio, siendo la mayoría de las transiciones hacia estados contiguos.

En suma, los enfoques adoptados a la largo del presente trabajo apuntan hacia la existencia de un débil proceso de convergencia en el ingreso per cápita entre las regiones europeas, así como de un grado de movilidad intra-distribucional no excesivamente elevado. Por otra parte, en un escenario económico como el actual (crecimiento económico lento en el mejor de los casos), en el que la evidencia empírica pone de relieve que las regiones más pobres son precisamente las más vulnerables, una conclusión adicional que surge de este trabajo es que nos encontramos en un momento decisivo para intensificar los esfuerzos hacia las políticas de cohesión. De lo contrario, el proceso de convergencia podría incluso revertirse, lo que, como se ha indicado en la introducción del trabajo, va en contra de los pilares sobre los que se basó la creación de la ue.