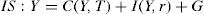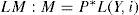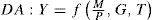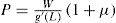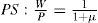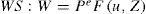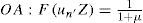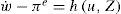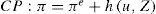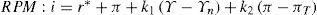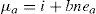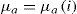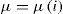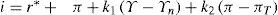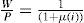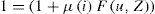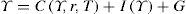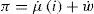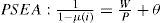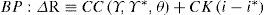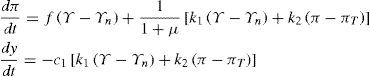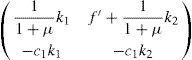El presente trabajo reinterpreta el modelo canónico del Nuevo Consenso Macroeconómico (ncm) a la luz de la teoría clásico-keynesiana del valor y la distribución formalizada en tiempos relativamente recientes por Sraffa (1966 [1960]). El objetivo consiste en mostrar que la política monetaria puede influir en la distribución del ingreso, y alcanzar, contrariamente a lo sostenido por los autores del ncm, efectos persistentes en los niveles de producto y empleo.
§1. Actualmente, dentro del pensamiento neoclásico (o marginalista) podemos distinguir entre dos grupos de autores: los ‘nuevos clásicos’ y los ‘nuevos keynesianos’. Ambos grupos parecen coincidir en que las dotaciones factoriales, la tecnología disponible y las preferencias de los consumidores son los determinantes últimos de los precios, cantidades y distribución del ingreso que observamos día a día en el mercado.1 Manifestación del acuerdo en el pensamiento de ambos grupos de economistas es lo que actualmente se conoce como el ‘Nuevo Consenso Macroeconómico’ (de aquí en más, ncm). A partir de un modelo básico que pretende ser una representación fiel de los esquemas de ‘Metas de Inflación’ implementados en distintos países durante los últimos 20 años, el ncm intenta explicar por qué las políticas fiscales y monetarias son supuestamente incapaces de aumentar persistentemente los niveles de empleo y producto de la economía. A pesar de que el mensaje central de esta tradición se inscribe dentro del pensamiento marginalista prekeynesiano de, e.g., Pigou (1927) o Wicksell (1934[1901]), y luego retomado por la síntesis neoclásica, en algunas presentaciones del modelo (cf. e.g. Blanchard, 2003; Carlin y Soskice, 2005; 2006) se suelen perder de vista sus elementos específicamente marginalistas. Por ejemplo, si bien el modelo predice que la economía tiende en el largo plazo hacia niveles de producto y empleo ‘naturales’, en la determinación del nivel de ingreso y de la distribución del ingreso la existencia de monopolios y sindicatos tiene un papel central. Más aún, la posición hacia dónde la economía tiende es una posición de desempleo involuntario persistente, la cual es incompatible con los resultados generales de la teoría marginalista. Sin embargo, estos resultados pierden gran parte de su fuerza, y por ende plausibilidad, cuando se los enmarca dentro de la explicación que los mismos autores del ncm dan de los determinantes últimos de la distribución del ingreso en general, y de la tasa de beneficios en particular. Es decir, como el resultado de la escasez relativa de los factores de la producción, i.e. el trabajo, la tierra y el capital.
En este contexto, nuestra contribución se inserta dentro del vasto debate que ha surgido en los años 1990 en torno a la posibilidad de establecer una correspondencia entre el modelo del ncm y la observación (cf. e.g. Colander, 1995; Dutt, 1997; Palley, 1997; Lavoie, 2000, 2007; Romer, 2000; Woodford, 2003; Serrano y Tabares, 2004; Docherty, 2009; Stockhammer, 2011). Argumentamos que dicha posibilidad requiere dejar de lado los pilares marginalistas sobre los que se basa la explicación de los factores que, en última instancia, regulan el comportamiento de la tasa de beneficios dentro del modelo del ncm. Para ello, reformulamos dicho modelo sobre la base de la teoría clásica del valor y la distribución rigurosamente formulada en tiempos relativamente recientes por Sraffa (1966 [1960]), y examinamos las consecuencias sobre los niveles de empleo y producto de suponer, en línea con dicha teoría, que la tasa de beneficios es susceptible de ser determinada por la autoridad monetaria. Mostraremos que una vez que se acepta que el Banco Central puede ejercer una influencia persistente sobre la tasa de interés, y a través del accionar de la competencia en la tasa de beneficios, las políticas monetaria y fiscal sí pueden tener efectos permanentes sobre el empleo y producto agregados.
El modelo del ncm en la formulación de Blanchard§2. En esta sección presentamos brevemente los elementos centrales que definen el modelo del ncm. Dada la relevancia de Olivier Blanchard dentro del conjunto de autores que forman el nuevo consenso, nos basaremos en su presentación del modelo (cf. Blanchard, 2003: capítulos 6 a 9).2 El modelo se caracteriza por cuatro ecuaciones básicas, que podemos dividir en dos grandes bloques: uno que describe el comportamiento de la demanda de la economía y otro el de la oferta. El primer bloque se conforma por las ecuaciones IS y LM:
donde Y es el nivel de ingreso, C el de consumo, G el de gasto público, r es la tasa de interés real, M la oferta de dinero, L la demanda real de dinero, P el nivel de precios e i la tasa de interés nominal. Si denominamos Xj a la derivada parcial de la variable X respecto a la variable j, tenemos que 0<CY<1, CT<0, IY>0, Ir<0, LY>0 y Li<0. De este primer bloque de ecuaciones se deriva la curva de demanda agregada (DA) que, como es conocido, tiene pendiente negativa en el plano P-Y.§3. El segundo bloque de ecuaciones caracteriza el comportamiento de la oferta a partir del proceso de determinación de precios y salarios, y también se conforma por dos ecuaciones, la PS y la WS. Es necesario, para nuestros objetivos, describir en cierto detalle la lógica que subyace detrás de estas curvas, ya que los supuestos sobre los que las mismas se edifican serán objeto de crítica (sección tercera) y modificación (secciones cuarta y quinta). Es importante, entonces, mencionar que los autores del ncm postulan la existencia de empresas forma-doras de precios y sindicatos. La regla de fijación de precios por parte de las empresas consiste en adicionar un margen fijo (μ) sobre los costos salariales. Así, el precio P del producto —una canasta representativa del producto bruto Y de la economía— viene determinado por la siguiente ecuación:
donde W es el salario nominal y g'(L) es el producto marginal del trabajo.3 Blanchard no sólo asume que el producto marginal es constante, i.e. Y = g(L) = aL, sino que por simplicidad también supone que a = 1. Sobre esta base derivamos la ecuación PS:Esta relación muestra que el salario real (W/P) queda unívocamente determinado por el nivel exógenamente dado del margen. El modelo sugiere, entonces, que la distribución es un fenómeno ‘real’: en este caso depende del ‘poder de mercado’ de las firmas (volveremos sobre este punto en la tercera sección). La segunda ecuación de este bloque, la WS, describe el comportamiento de los trabajadores en el proceso de determinación del salario:4
Blanchard plausiblemente asume que los trabajadores están organizados en sindicatos, y fijan su salario nominal sobre la base de un nivel esperado de precios (Pe), que puede o no coincidir con el nivel efectivo, y una función F(.) que resume su poder de negociación, el cual depende negativamente del nivel de desempleo (u), i.e. Fu<0, y de ciertos parámetros “institucionales” (ibíd., 2003: 121) (e.g. la existencia de seguros de desempleo) capturados por la variable Z, con FZ >0.
Sobre un periodo de tiempo lo suficientemente largo como para que los precios esperados sean correctos (Pe = P) —el “mediano plazo” en términos de Blanchard—, de las ecuaciones [4] y [5] es posible derivar dos tipos de condiciones: en primer lugar, los niveles de empleo y de salario real que garantizan la consistencia distributiva entre firmas y sindicatos. En segundo lugar, se obtiene el nivel de producto que tenderá a prevalecer en el largo plazo a partir de la curva de oferta agregada (OA):
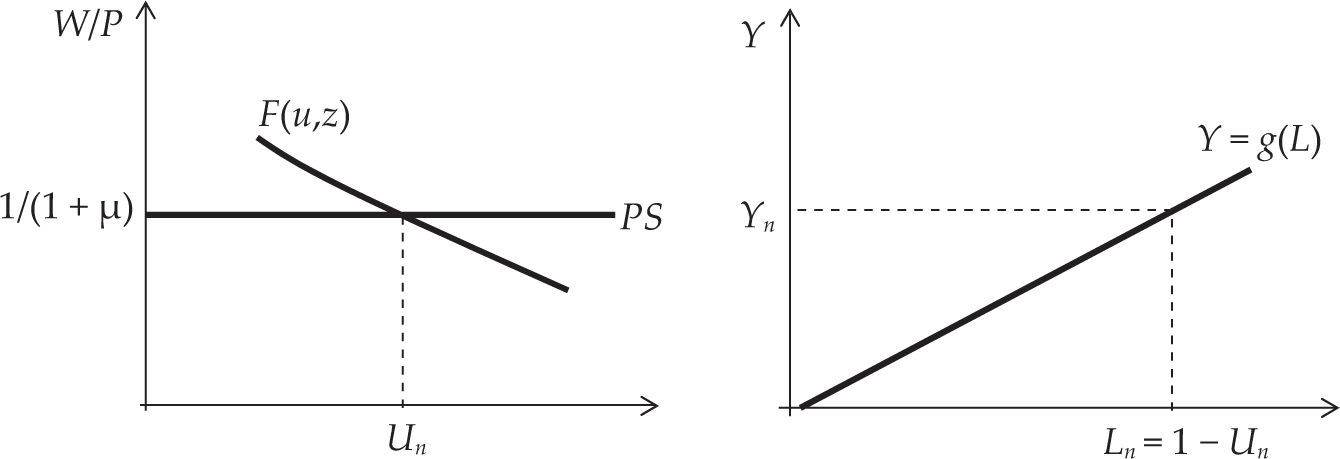
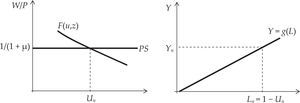
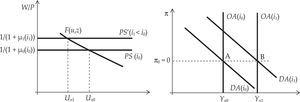
La lógica detrás de esta ecuación es la siguiente: dado el nivel de margen, el salario real queda determinado por la relación [4], y éste determina, a partir de la función F(.) en [5], el nivel de “desempleo natural” (Blanchard, 2003: 128) (un) que convalida esa distribución.5 A este nivel de desempleo corresponden un nivel de empleo (Ln) y otro de producto [Yn = g(Ln)], que Blanchard denomina “producto natural” (ibíd.: 129). En términos gráficos:
El siguiente resultado merece ser destacado: se desprende de la condición [6] y —se aprecia en la gráfica 1— que en el equilibrio de mediano plazo el nivel de empleo compatible con la coincidencia entre las aspiraciones de los trabajadores y la política de precios de las firmas viene determinado independientemente de las condiciones de demanda agregada, ergo del accionar de las políticas monetaria y fiscal. La implicación es la imposibilidad de este tipo de políticas de influir persistentemente en el nivel de producto, y sólo ejercer esa influencia en el corto plazo, cuando los precios esperados difieren de los precios efectivos. Estos resultados son esencialmente equivalentes tanto a los obtenidos por la tradición prekeynesiana como a aquellos obtenidos por la ‘síntesis neoclásica’.
§4. El modelo canónico del ncm (cf. Carlin y Soskice, 2005; 2006) presenta dos diferencias fundamentales respecto a la formulación de Blanchard. La primera es que el modelo debe reexpresarse en tasas de variación. De este modo, de la ecuación de precios [4] se obtiene que π=w˙+μ˙, donde π es la tasa de inflación y w˙ y μ˙ representan, respectivamente, la tasa de variación de los salarios nominales y del margen. A su vez, los autores del nuevo consenso asumen que durante el proceso inflacionario la distribución del ingreso en términos reales no se modifica: las firmas indexan la totalidad del incremento salarial logrado por los sindicatos, por lo que el conflicto distributivo se resuelve enteramente a favor de las primeras, es decir, el nivel del margen permanece inalterado. Bajo este supuesto,6 la ecuación [4] toma la siguiente forma (cf. por ejemplo Carlin y Soskice, 2006: 71):
A su vez, la ecuación [5] resulta:
La variable πe es la tasa de inflación esperada (por ejemplo, la del periodo anterior, π−1; cf. Carlin y Soskice, 2006: 74), y la función h(.) conserva las propiedades de F(.) (hu < 0 y hz > 0) Si combinamos [4'] con [5'] obtenemos una curva de Phillips ‘ampliada por expectativas’ (CP):
El modelo queda de este modo reespecificado en tasas. Su representación gráfica requiere simplemente reemplazar π por P para graficar la oferta y la demanda agregadas. En equilibrio el ingreso coincide con el ingreso natural, pero los precios ya no están fijos, si no que crecen al mismo ritmo que el salario nominal (para una productividad del trabajo constante).
§5. La segunda modificación al modelo original consiste en reemplazar la curva LM por una regla de política monetaria (RPM). De hecho, es ésta la diferencia central entre el modelo de Blanchard (en tasas) y las formalizaciones más recientes, como aquélla de Carlin y Soskice (2005; 2006). En efecto, estas últimas generalmente postulan la existencia de una Rpm en la cual la tasa de interés depende positivamente, entre otras cosas, del nivel de actividad Y y de la tasa de inflación π. Formalmente:
donde kj con j =1,2, son parámetro positivos, r* es la tasa real objetivo del banco central —de acuerdo a las formulaciones del ncm, la tasa ‘natural’— y πT es el target o meta de inflación de la política monetaria. De este modo, cuando el nivel de ingreso es mayor (menor) al nivel natural (o, alternativamente, cuando la inflación es mayor al nivel deseado por la autoridad monetaria), se presume que el banco central reacciona elevando (disminuyendo) la tasa de interés nominal [lo suficiente como para incrementar (disminuir) también la tasa real], lo cual contrae (expande) la economía. El resultado de esta hipótesis de comportamiento por parte del banco central7 es que la curva que se deriva de la RPM luce como una tradicional curva LM esto es, con pendiente positiva en el plano r-Y. Volveremos sobre este punto en la cuarta sección.§6. En síntesis, el esquema desarrollado por Blanchard captura la esencia del pensamiento macroeconómico neoclásico moderno, principalmente la existencia de: 1) fuerzas ‘reales’ que determinan la distribución del ingreso y 2) tasas ‘naturales’ de producto y empleo que impiden a las políticas monetaria y fiscal ser efectivas en el largo plazo. Sin embargo, también es cierto que este modelo posee ciertas características difíciles de incorporar dentro de dicho pensamiento. Más concretamente: a) existe un nivel de producto compatible con un nivel de desempleo involuntario persistente, y no sólo transitorio como asume la teoría neoclásica, y b) la inflación no emerge solamente como el resultado del exceso de demanda en el mercado de bienes, sino también del conflicto distributivo entre trabajadores y capitalistas. No osbtante, la idea subyacente de que existen unos niveles de producto y empleo, por un lado, y de salario real, por el otro, ‘naturales’ y determinados por fuerzas ‘reales’, otorga a los elementos a) y b) un papel secundario: en primer lugar, como veremos en mayor detalle en la próxima sección, la idea parece subyacer de que, bajo condiciones de competencia, i.e. si no existieran sindicatos y si las firmas no tuvieran poder de mercado, habría una tendencia al pleno empleo de los recursos, con la distribución del ingreso determinada por la escasez relativa de los factores productivos. En segundo lugar, la determinación ‘real’ de la distribución implica que no es clara la razón que empuja a los trabajadores a realizar reclamos continuos sobre el nivel de salario nominal: conseguido su objetivo, dado el margen, el aumento del salario nominal termina, indefectiblemente, trasladándose en una proporción uno a uno al nivel de precios, i.e. deja la distribución del ingreso inalterada (cf. ecuación [4']). En la próxima sección y en la subsiguiente intentaremos argumentar que los elementos a) y b) adquieren mayor relevancia si al modelo del ncm se lo enmarca dentro de la teoría clásica de la distribución del ingreso y los precios relativos. En otras palabras, asumiremos, en acuerdo con la teoría clásica, que el margen no está dado independientemente de las fuerzas monetarias que rigen el comportamiento de la economía. Como veremos, esta modificación, menor en términos formales respecto al modelo del ncm, alterará radicalmente tanto las conclusiones del modelo respecto a los determinantes del producto natural y el nivel de empleo como a los posibles efectos del conflicto distributivo sobre el nivel de precios.
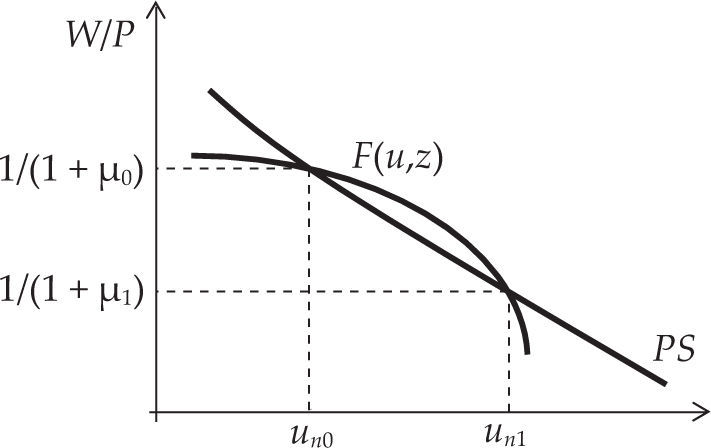
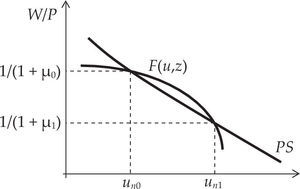
Sobre la relación entre el margen, la tasa de beneficios y la tasa de interés en el esquema de Blanchard§7. Las conclusiones sobre la supuesta inefectividad en el “mediano plazo” de las políticas fiscal y monetaria sobre los niveles de producto y empleo (y de sus correspondientes efectos permanentes en el nivel de precios) dependen, dada la curva WS, de la forma funcional que toma la curva PS. Dicha forma depende, a su vez, crucialmente de dos tipos de supuestos: en primer lugar, de que la productividad marginal del trabajo es constante en el nivel de actividad. En segundo lugar, de que el margen es constante e independiente del nivel de empleo. En efecto si, e.g., admitiéramos la posibilidad de que, ante la presencia de desempleo —y por ende de capacidad ociosa— la productividad del trabajo pudiera incrementarse con el nivel de actividad (g'(L)>0), la curva PS (ecuación [4]) tendría pendiente negativa. Si asumimos una curva F(u,z) estrictamente cóncava al origen en el plano W/P-u, existiría la posibilidad de más de un único nivel de desocupación compatible con un nivel de precios constante, i.e. la existencia de equilibrios múltiples en el plano W/P-u (véase la gráfica 2). Al mismo resultado llegaríamos si μ fuera decreciente en el nivel de actividad. En este contexto, la política económica podría, mediante su accionar, mover la economía de un equilibrio a otro, un elemento que no es mencionado por Blanchard (aunque sí es reconocido por Carlin y Soskice, 2006).
Ahora bien, independientemente del supuesto debatible sobre la constancia de la productividad y del margen ante modificaciones en el nivel de empleo, es central notar que, si bien esta última variable juega un papel decisivo en el esquema desarrollado en la sección dos, i.e., es la única variable que determina el nivel de salario real en equilibrio, sus determinantes son vagamente explicados por Blanchard. La idea subyacente es que el margen es el resultado de la ausencia de libre competencia en los distintos mercados. “Si los mercados fueran perfectamente competitivos”, sostiene de este modo el autor, “el precio sería simplemente igual al costo y μ sería igual a cero” (Blanchard, 2003: 124). Parece, entonces, emerger en Blanchard la idea de que, dadas las técnicas de producción, la tasa normal de beneficios en libre competencia debería ser igual a cero, lo cual es simplemente inaceptable. Si se rechaza esta proposición, y se asume más plausiblemente que la tasa de margen μ está formada por dos componentes, i.e. por una tasa de beneficios considerada ‘normal’ y por un componente que debería compensar, usando las palabas de Kaldor (1959: 287), los factores de “riesgo y problemas” específicos de cada actividad productiva —los cuales pueden, en un primer grado de aproximación, incorporar también el ‘grado de monopolio’ existente en las distintas actividades, referido por los autores del ncm—, es claro que los factores capaces de influenciar la primera quedan largamente indeterminados en el modelo.8
§8. Si pasamos ahora a examinar los posibles determinantes de la tasa normal de beneficios, encontramos esencialmente dos explicaciones dentro de la teoría económica: por un lado, la explicación que brinda la teoría neoclásica o marginalista, de acuerdo a la cual sobre un periodo de tiempo suficientemente largo, i.e. ‘el mediano plazo’ dentro del esquema del ncm, la tasa efectiva de beneficios tendería a gravitar en torno a su valor ‘natural’ (e.g. Wicksell, 1934), determinado por fuerzas ‘reales’, i.e. por la oferta y la demanda de capital. Precisamente, esta es la explicación a la cual Blanchard (2003) parece adscribir en la cuarta parte de su libro (capítulos 10 a 13) (cf. también Carlin y Soskice, 2006: capítulo 13), en donde se analizan los determinantes del crecimiento económico. En efecto, Blanchard recurre allí al modelo de Solow (1956) para explicar las tendencias de muy largo plazo de la economía; y como es bien sabido, en dicho modelo, en cada momento del proceso de acumulación —momentos, notemos, los cuales resultan cada uno de ellos equivalentes al equilibrio de mediano plazo de Blanchard— el salario real y la tasa de beneficios son determinados por la escasez relativa de los factores de la producción, i.e. trabajo y capital.
No es el propósito de este artículo analizar en detalle los serios inconvenientes que encuentra la explicación de la distribución ofrecida por la escuela marginalista. Nos limitaremos aquí a mencionar brevemente algunos de ellos (cf. Garegnani, 1990; Petri, 2004, para un análisis detallado). En primer lugar, notemos que la determinación de una posición en la que el capital invertido en todas las industrias rinda una tasa uniforme —es decir, una posición que reúna las características del mediano plazo de Blanchard—9 requiere que la composición del stock de capital en equilibrio sea determinada de forma endógena. Pero, dado que —como es distintivo en la teoría neoclásica— el capital es parte de los datos de la teoría, esto implica que aquél sea tratado como una magnitud homogénea, capaz de cambiar de forma física sin modificar su cantidad. Como es bien sabido, la única forma general de tratar al capital como una magnitud homogénea es medirlo en términos de valor, lo cual es simplemente inaceptable: dicho valor claramente depende de la distribución del ingreso, i.e. de la tasa de interés, precisamente una de las variables que la teoría pretende determinar.
A este problema, que podemos identificar como un problema relativo a la oferta de capital, debemos agregar uno adicional, en este caso relativo a la posibilidad de determinar una función de demanda de capital con pendiente negativa respecto a la tasa de interés, central para justificar la unicidad y estabilidad del equilibrio neoclásico. En efecto, como ha sido demostrado en los años 1960 durante las ‘Controversias del capital’ (cf. Harcourt, 1972; Kurz, 1985), una vez que se reconoce que el valor del capital depende de los precios relativos bien puede ocurrir que el valor de los medios de producción demandados por parte de las firmas aumente con incrementos en la tasa de interés. Análogamente, la cantidad demandada de trabajo puede variar positivamente con el salario real. En otras palabras, no hay bases para excluir la posibilidad de que las curvas de exceso de demanda de los distintos factores tengan una pendiente positiva respecto a su precio de alquiler, i.e. el equilibrio es inestable. La implicación es que no es posible concluir que existe una tendencia al equilibrio determinado por la teoría marginalista y, por ende, al uso eficiente de los recursos productivos. Finalmente, notemos que incluso haciendo abstracción de los problemas recién mencionados, la explicación marginalista de la distribución tiene como corolario la tendencia al pleno empleo de los recursos sobre un periodo de tiempo suficientemente largo. Pero este resultado es contradictorio con los resultados del modelo presentado por Blanchard, ya que este autor intenta mostrar que el desempleo involuntario es una posición persistente de la economía, es decir, incluso en el largo plazo.
En resumen, la crítica a la teoría neoclásica del capital nos obliga a abandonar la explicación del valor y la distribución como una explicación basada en la escasez relativa de los ‘factores de la producción’ en general, y la de la tasa de beneficios como el resultado de la escasez del capital en particular. A su vez, la imposibilidad de esta teoría de concebir situaciones persistentes de desempleo involuntario es un reflejo de su inadecuación para servir de base a los objetivos del modelo de Blanchard, dentro del cual la existencia de este tipo de desempleo es un resultado central. Es así que dicha explicación debe ser abandonada.
§9. Pasamos ahora a examinar la segunda explicación del valor y la distribución que encontramos en la historia del análisis económico: aquélla de los autores clásicos (y Marx), y formalizada en tiempos relativamente recientes por Sraffa (1966 [1960]). Sraffa demuestra que sobre la base de la técnica dominante de producción y una de las variables distributivas, i.e. la tasa de salario real o la tasa de beneficios, es posible determinar aquellos precios relativos que permiten satisfacer la uniformidad en la tasa de retorno sobre el capital invertido, y que, como tales, puedan actuar como un centro de gravitación de los precios efectivamente observados sobre un periodo suficiente de tiempo. Sobre la base de estos mismos datos, la variable distributiva restante emerge como un residuo. Ahora bien, la elección de la variable distributiva exógenamente considerada al momento de estudiar el sistema de precios no viene determinada por una ley general: el sistema clásico es lo suficientemente flexible como para permitir, dependiendo de las características específicas de la economía bajo estudio, que tanto la tasa de salario real como la tasa de beneficios puedan ser consideradas dadas. De este modo, en los clásicos y en Marx es la tasa de salario real, determinada al nivel de subsistencia (subsistencia que también incluye elementos sociales y culturales), la variable distributiva exógena al momento de la determinación de los precios relativos de las distintas mercancías.10 Por otra parte, en un contexto en el cual los trabajadores participan del excedente, parece perfectamente posible que sea la tasa de beneficios la variable distributiva que viene determinada exógenamente; y de hecho es el propio Sraffa (1966 [1960]: 55–6) quien sugiere esta alternativa para el caso de las economías capitalistas modernas, ya que la tasa de beneficios es susceptible de ser manipulada, e.g., por el banco central mediante la fijación de la tasa de interés monetaria.11 La explicación ‘monetaria’ de la distribución del ingreso ha sido desarrollada por varios autores contemporáneos (cf. e.g. Panico, 1988; Pivetti, 1991; 2007), explicación que puede resumirse de la siguiente forma: si asumimos que en cada industria pueden identificarse elementos específicos de “riesgo y problemas” lo suficientemente estables —e independientes de la tasa de interés establecida por parte de la autoridad monetaria— que justifican la existencia de “un beneficio normal de empresa” en dicho sector (Pivetti, 1991: 25), la tasa real de beneficios del sector genérico a (μa) vendrá determinada por:
donde i es la tasa de interés que fija la autoridad monetaria y bnea representa los beneficios normales obtenidos en el sector por encima de la tasa de interés monetaria, en compensación por los distintos “riesgos y problemas” específicos derivados de invertir una cierta cantidad de capital en dicha actividad.§10. De la ecuación [7] se desprende claramente que en este esquema, dado el nivel de bne en cada sector, es la tasa de interés la que regula el comportamiento de la tasa de beneficios, la cual se mueve en la misma dirección que aquélla. En otras palabras, de acuerdo a la ecuación [7]:
con μ'a(i)>0. Si, por ejemplo, el banco central decide disminuir la tasa de interés de i a i', al nivel inicial de §a se tendrá que μa > i′ +bnea, i.e. las inversiones en capital productivo podrán realizar beneficios mayores a las inversiones en el sector financiero. En esta situación la competencia no tardará en hacer sentir sus efectos: tenderán a crearse nuevas empresas, lo cual causará un aumento en la oferta de la mercancía genérica a y una caída en su respectivo precio monetario (Pa). Es decir, la tasa de beneficios realizable en el sector productivo tenderá a caer hasta que, neta de riesgos, oscile nuevamente alrededor de la rentabilidad del sector financiero. Lo contrario ocurrirá si el banco central decide aumentar la tasa de interés. Notemos que, dada la tasa monetaria de salarios, una variación en la tasa de interés —y las consecuentes variaciones en el mismo sentido tanto en los precios monetarios como en la tasa de beneficios— tenderán a provocar una variación contraria del salario real.12 En síntesis, la tasa de interés monetaria, junto al salario monetario y la técnica dominante, emergen como los determinantes de los precios normales o de largo plazo de las distintas mercancías.Notemos que esta dirección de causalidad entre la tasa de interés y la tasa de beneficios es precisamente la inversa de la que se deriva del esquema del ncm desarrollado por Blanchard. En efecto, recordemos, allí el valor de μ está plenamente determinado por factores ‘reales’: la intersección entre la oferta y la demanda de capital explica el valor normal mínimo de la tasa de beneficios, mientras el grado de concentración en las distintas industrias determina las desviaciones persistentes (i.e. aquéllas que prevalecerán incluso en el largo plazo) respecto a dicho valor. De este modo, un cambio en esos factores reales obliga a la autoridad monetaria a acomodar pasivamente la tasa de interés en pos de evitar desviaciones sistemáticas del producto y empleo efectivos con relación a sus valores naturales; desviaciones que no hacen más que modificar el nivel de precios o, eventualmente, acelerar (o desacelerar) la tasa de inflación de la economía. Por el contrario, el esquema clásico de la distribución considerado en el párrafo anterior no contempla la existencia de una posición ‘natural’ hacia donde la economía tiende a gravitar que sea independiente del comportamiento de la autoridad monetaria, y a la cual ésta debe pasivamente acomodarse.
Las consecuencias de esta diferencia respecto al esquema del ncm serán examinadas en la próxima sección. Por el momento parece suficiente notar que el esquema presentado en §9 captura de forma más transparente una característica central del modelo del ncm formalizado por Blanchard, pero que choca necesariamente con los elementos neoclásicos que, según hemos visto en §8, el autor se ve eventualmente obligado a considerar en su necesidad de dar mayor determinación a los factores que regulan el comportamiento de la tasa de beneficios: el esquema clásico aquí presentado es perfectamente compatible con la existencia de desempleo, ya que no contempla ningún mecanismo general (como lo es la sustitución factorial dentro de la teoría neoclásica) que tienda a empujar a la economía hacia el pleno empleo de los recursos.
Margen endógeno, distribución del ingreso y niveles de producto, empleo y precios§11. En esta sección procedemos a examinar qué ocurre con los niveles de producto y empleo, con la distribución del ingreso y con el nivel de precios una vez que asumimos, de acuerdo con los lineamientos de la teoría clásica contemporánea de la distribución expuestos en §9 y §10, que el margen no depende de fuerzas reales como asumen los autores del ncm, sino que puede ser manipulado por la autoridad monetaria. En otras palabras, que en línea con la ecuación [8] el margen promedio de beneficios que obtiene el sector productivo en la elaboración del bien compuesto que forma el producto Y tiende a variar en la misma dirección que la tasa de interés fijada por el banco central:
donde, recordemos, μ'(i)>0. Sobre la base de la ecuación [8'] es posible invertir los papeles que poseen el producto y la tasa de interés naturales dentro del modelo del ncm. Examinemos la cuestión un poco más de cerca sobre la base de un modelo análogo al modelo de Blanchard, pero que incorpora la ecuación [8'], y en donde, en línea con las nuevas formulaciones del modelo del ncm, la tasa de interés viene determinada por la autoridad monetaria con base en una ecuación como la [2']:En equilibrio, Y = Yn y πT = π con lo cual i = r* + πT es decir, la tasa nominal en equilibrio debe ser igual a la tasa real objetivo del banco central más la tasa de inflación. Para hacer compatible el análisis con el modelo de Blanchard, que es un modelo en niveles, asumimos que la tasa de inflación objetivo es igual a cero, i.e. πT = 0, por lo que en equilibrio i = r*.
Respecto al papel de la ecuación [8'], éste se manifiesta en la regla de formación de precios. Esto es, P=(1 + μ(i))W. La curva PS toma, entonces, la siguiente forma:
Esto implica que el nuevo nivel de producto de mediano plazo está dado por:
El modelo queda entonces caracterizado por tres ecuaciones: la curva IS (ecuación [1]) y la regla de política monetaria [2'], de las cuales se deriva la curva DA[3], y la ecuación [6”], que caracteriza el equilibrio en el mercado de trabajo y permite derivar la curva OA. Notemos que, respecto al modelo del ncm, la modificación más importante es la introducción de μ(i) en la ecuación [6”].
§12. Antes de analizar con mayor profundidad las implicancias de reemplazar la ecuación [6] por la [6”], es conveniente hacer un breve paréntesis y examinar un punto importante relativo a la pendiente de la curva DA en el plano P-Y, pendiente sobre la que reposa a su vez la estabilidad del equilibrio entre las curvas OA-DA. ¿Es aceptable mantener una relación inversa entre la demanda agregada y el nivel de precios en nuestro modelo? En el modelo original de Blanchard dicha relación se basa, esencialmente, en la idea de que la demanda de inversión es una función decreciente de la tasa de interés. Esta relación aparece directamente en la curva IS, e indirectamente en la curva LM por medio del llamado ‘efecto Keynes’: para una cantidad dada de dinero, una caída en el nivel de precios aumenta la oferta real de dinero, lo cual disminuye la tasa de interés, aumentando la inversión y con ella la demanda agregada. Ahora bien, por las razones discutidas en §8 no existe razón alguna de carácter general para sostener sobre la base de la teoría neoclásica —que como hemos visto sustenta el modelo de Blanchard— que para un nivel de producción dado la inversión tenderá a aumentar cuando la tasa de interés disminuye.13 Así, si la inversión es insensible a la tasa de interés la curva IS es una recta vertical: variaciones en el nivel de precios, si bien desplazan a la curva LM, dejan inalterado el nivel de actividad, i.e. la DA es también una curva vertical en el plano precios-nivel de actividad.
Una segunda vía para justificar la pendiente negativa de la curva DA es recurrir al efecto saldos reales, también conocido como ‘efecto Pigou’. De acuerdo a este mecanismo, una caída en el nivel de precios incrementa las tenencias reales de dinero de los agentes por encima de sus niveles deseados, lo cual incrementa su demanda de consumo, ergo el producto. El accionar de este mecanismo puede ser criticado sobre la base de dos tipos de observaciones: en primer lugar, a nivel empírico la magnitud del efecto Pigou no parece ser lo suficientemente importante como para constituir una base general de la explicación de la relación negativa entre demanda agregada y nivel de precios (cf. e.g. Davis y Palumbo, 2001). En segundo lugar, el accionar de este efecto bien puede ser contrarrestado por mecanismos que operan en sentido contrario, como el ‘efecto Fisher’ (o deflación de deudas), el cual puede causar la quiebra de firmas y desalentar la inversión, o el ‘efecto expectativas’ de Tobin, el cual induce a los consumidores a posponer compras en vista de que los precios futuros podrían resultar más bajos que los precios corrientes.14 Si estos efectos prevalecen sobre el efecto Pigou, la curva DA tiene pendiente positiva, es decir, el equilibrio es inestable: una situación de insuficiencia (exceso) de demanda reduce (incrementa) los precios provocando una ulterior caída (aumento) de la demanda agregada y no su aumento, como la teoría presupone.15,15
En nuestra formulación, por el contrario, la justificación de la relación negativa entre tasa de interés y nivel de actividad pone al centro de la escena el hecho de que la dinámica de la tasa de interés afecta la distribución del ingreso: nuestro modelo asume que la caída en la tasa de interés objetivo por parte del banco central induce un movimiento en la misma dirección de la tasa de beneficios y ello provoca la tendencia del salario real a subir. Si bien es cierto que el efecto de un cambio en la distribución del ingreso sobre el nivel de actividad es “contingente” y “variable” (Pivetti, 1991: 296–7), parece plausible asumir en un primer nivel de abstracción que la propensión marginal al consumo de los trabajadores es mayor a la de los capitalistas, con la implicancia de que un aumento del salario real tenderá a incrementar el consumo agregado. De este modo, en nuestro modelo la tasa de interés afecta el nivel de actividad por medio de sus efectos en el nivel de consumo derivados de un cambio en la distribución del ingreso. Formalmente, la curva IS viene modificada de la siguiente forma:
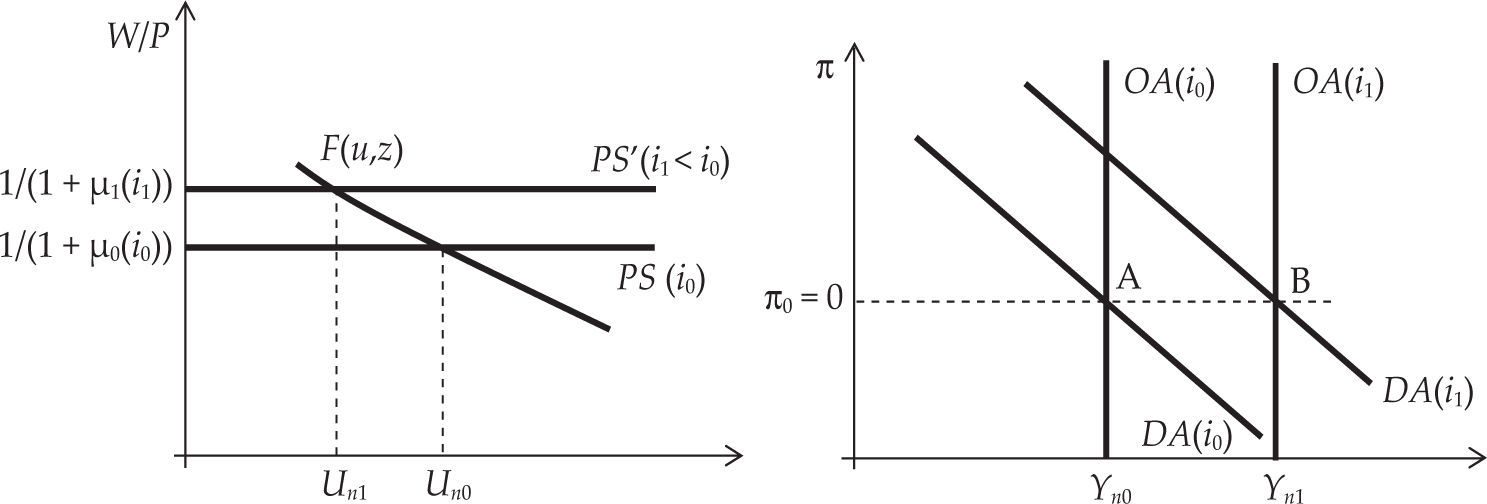
con Cr < 0. Esta modificación en la curva IS no altera los resultados respecto al modelo original de Blanchard: dado que una caída en la tasa de interés real incrementa la demanda agregada, continúa siendo válido que la IS tiene pendiente negativa en el plano r-Y. La negatividad de la DA en el plano P-Y se desprende del comportamiento de la autoridad monetaria de acuerdo a la RPM[2']: si el nivel de precios disminuye, el banco central reacciona disminuyendo la tasa nominal de interés lo suficiente a fin de hacer caer la tasa real, lo cual incrementa la DA a través de su efecto en el consumo y el producto. Notemos, finalmente, que si bien el efecto de la tasa de interés sobre el nivel de consumo tiende a asegurar la tendencia al equilibrio, el hecho de que el margen bruto de beneficios dependa de la tasa de interés introduce un potencial elemento de inestabilidad: de acuerdo a la RPM[2'], cuando π > πT el banco central reacciona aumentando la tasa de interés, lo cual, dada la ecuación [4”], tiende a incrementar el nivel de precios, y no a disminuirlos como supone la teoría marginalista.17 Pero este incremento induce al banco central a subir la tasa aún más, y así sucesivamente. En el apéndice a este trabajo, sin embargo, discutimos las condiciones que aseguran la estabilidad dinámica del modelo.§13. Pasemos ahora sí a examinar las implicancias de introducir la ecuación [6”]. Supongamos que el banco central decide disminuir de forma permanente la tasa de interés real objetivo r*. Dicha modificación desplaza la curva RPM[2'] hacia la derecha y, dada la pendiente negativa de la IS, aumenta el nivel de actividad. Este resultado, al menos para el ‘corto plazo’, coincide con lo predicho por el ncm. La diferencia fundamental se expresa en las curvas PS-WS. Porque a diferencia de lo que ocurre en el modelo de Blanchard, donde los niveles de empleo y producto de mediano plazo permanecen inalterados ante un cambio en la tasa de interés (ecuación [6]), ahora la caída en la tasa de interés hace disminuir el margen a través de la ecuación [8'], desplazando hacia arriba la curva PS (ecuación [4”]) y disminuyendo el nivel de desempleo; así, los niveles de empleo y producción de equilibrio aumentan permanentemente(ecuación [6”]).18 En otras palabras, como se ve en la gráfica 3, la modificación de la tasa de interés por parte de la autoridad monetaria no sólo desplaza la curva de demanda agregada hacia la derecha, sino que también desplaza en la misma dirección la curva OA.19 El resultado es un aumento permanente en el nivel de actividad.
En resumen, una vez que se reconoce que el margen de beneficios es regulado por la tasa monetaria de interés, su fijación por parte del Banco Central adquiere un papel preponderante en la determinación del producto ‘natural’, i.e. aquel nivel de producto donde se cruzan las curvas WS y la PS (asumiendo, como hace Blanchard, que estas curvas se cruzan una única vez). Pero el concepto de producto natural pierde en este contexto el significado que tenía dentro del ncm, ya que mediante su accionar el banco central es capaz de afectar permanentemente la distribución del ingreso y con ella los niveles de desempleo y producto. En este sentido, el siguiente punto merece ser destacado: dado que en nuestro esquema la tasa de interés depende del valor que el banco central cree que posee la tasa real incorporada en su regla de política monetaria [2'], esa regla auto-impuesta por la autoridad monetaria termina transformándose en una profecía auto-cumplida (Aspromourgous, 2007), manifestación de que la tasa de interés posee un carácter puramente convencional, y cuya determinación no es susceptible de ninguna ley de carácter general y mecánica (Pivetti, 1991). En otras palabras, si de acuerdo a la regla de política monetaria el nivel observado de la tasa de interés resulta ser demasiado bajo respecto a lo que la autoridad monetaria considera como su valor natural r*, es decir, el nivel de producto observado es demasiado alto, el banco central tenderá a corregir esa discrepancia mediante una política monetaria restrictiva. Ello tendrá el efecto de convalidar las expectativas del banco central, ya que el incremento de la tasa monetaria —a través de su efecto en la distribución del ingreso y el consumo— tendrá el efecto de reducir los niveles de producción y de empleo.
§14. Finalizamos esta sección con algunas breves observaciones generales sobre la dinámica de los precios. Si consideramos la ecuación [4”] en tasas de variación, se obtiene:
donde, nuevamente (cf. ecuación [4']), π y w˙ representan las tasas de variación en el tiempo de los precios y de los salarios nominales respectivamente, y μ˙i=μ′i1+μididt es la tasa de variación en el tiempo del margen bruto de beneficios, que ahora depende de la variación de la tasa de interés nominal. Consideremos el caso en que los trabajadores logran imponer un incremento en el nivel de salario nominal. Para un nivel de precios dado, ello tenderá a causar la caída en la tasa de beneficios e incrementar el nivel de salario real. Sin embargo, esta redistribución del ingreso en favor de la clase trabajadora tendrá un carácter puramente temporario. Dado el nivel de la tasa de interés, dicho incremento en el salario real resulta incompatible con el sistema de precios de largo plazo que emerge de la condición [7] (o su análoga [8]). La competencia entre los capitalistas de los sectores financiero y productivo no tardará en hacer sentir sus efectos: los precios monetarios mostrarán una tendencia al alza a fin de mantener inalterada la tasa de beneficios y, por ende, también el salario real. En línea con la ecuación [4'”], el aumento en los salarios nominales se traduce exactamente en un aumento en el nivel de precios. Si bien esta conclusión es equivalente al resultado obtenido dentro del modelo del ncm (ecuación [4']), la diferencia fundamental es que en un contexto ‘clásico’ la autoridad monetaria puede ejercer un papel activo dentro de la puja distributiva: dado que la tasa de retorno tiende a moverse pan passu con la tasa de interés fijada por el banco central, éste puede, si así lo considera, disminuir la tasa de interés monetaria y los precios, convalidando de esta forma el aumento en los salarios nominales, i.e. garantizando que el aumento en los salarios nominales tienda a traducirse en un incremento efectivo del salario real (cf. Garegnani, 1979: 81). En términos de la ecuación [4'”], ante un incremento inicial en los salarios monetarios, mediante una apropiada caída en la tasa monetaria, la tasa de variación de los precios puede permanecer inalterada. Pero la autoridad monetaria podría alternativamente tener el objetivo de dejar inalterada la tasa real de beneficios μ en todo momento (es decir, no sólo luego del incremento en el nivel de precios), si bien a costa de aceptar una tasa de inflación creciente. Para ello, ante un incremento en la tasa nominal de salarios, puede incrementar la tasa de interés nominal.20 De acuerdo a la ecuación [4'”], tanto el nivel de salarios nominales como la tasa bruta de beneficios se incrementan, lo cual causa un mayor nivel de inflación que en el caso en que la tasa de interés permanece constante.21La apertura económica§15. En esta sección reexaminamos los resultados obtenidos hasta el momento cuando se considera la interacción entre la economía interna y el resto del mundo. ¿Puede en esas circunstancias el banco central, a través del manejo de la tasa de interés, continuar influyendo en la distribución del ingreso como lo hacía en una economía cerrada? Argumentaremos quela explicación monetaria de la distribución continúa teniendo validez en un contexto de apertura económica. Sin embargo, deberemos también considerar que el banco central ahora enfrenta nuevas restricciones que pueden limitar aún más su capacidad de acción. En particular, a los límites que imponen al accionar de la política monetaria los potenciales conflictos distributivos entre capitalistas y trabajadores en una economía cerrada (véase §14), ahora es también necesario considerar esencialmente los efectos sobre la cuenta corriente y la cuenta capital, y más en general sobre el resultado del balance de pagos. Para afrontar estos problemas será conveniente distinguir entre una economía ‘periférica’ y una economía ‘hegemónica’, es decir, una economía cuya moneda es utilizada internacionalmente como unidad de cuenta, medio de pago y reserva de valor.
§16. La apertura económica nos obliga a considerar la influencia de los bienes provenientes del exterior en la mercancía compuesta que forma el producto bruto, y así en el salario real. Una manera posible de hacerlo es introducir in-sumos importados. Bajo esta modificación, la ecuación de precios [4”] toma la siguiente forma: P=(1+μ(i))(W+bEP*), donde b representa la cantidad del insumo importado por unidad de producto, P* el precio internacional de los insumos y E el tipo de cambio nominal. Si normalizamos las unidades de medida de forma tal que b=1 y dividimos por P, obtenemos la curva PS para el caso de una economía abierta (PSEA):
donde θ≡EP*P es el tipo de cambio real.22 Notemos, entonces, que la variable θ introduce un nuevo grado de libertad a la relación PS. La implicancia más inmediata es que en una economía abierta se rompe la relación negativa que se establece en una economía cerrada —y para un nivel de productividad dado— entre la tasa de beneficios y el salario real. La consistencia distributiva entre capitalistas y trabajadores ahora es compatible con el incremento del salario real y de la tasa de beneficios, si a su vez se produce una apreciación real (i.e. θ cae). Alternativamente, para una tasa de interés dada (y, dado el nivel de margen bne —ecuación [7]—, dada la tasa de beneficios), existe una relación inversa entre el tipo de cambio real y el salario real; o, finalmente, dado el salario real, existe una relación negativa entre la tasa de interés y el tipo de cambio real. En síntesis, la ecuación [9] muestra que los movimientos en la tasa de interés generalmente influirán en el valor del tipo de cambio real. Si a su vez recordamos que la tasa de interés no tiende a gravitar en torno a un valor ‘natural’, sino que se encuentra gobernada esencialmente por factores históricos, políticos e institucionales dentro de los cuales la política monetaria posee un papel preponderante, se desprende que esos mismos factores influyen necesariamente en la determinación del tipo de cambio real. En otras palabras, al igual que la tasa de interés, el tipo de cambio real también posee una naturaleza “convencional” (Vernengo, 2001).§17. Lo anterior no significa, sin embargo, que la regulación del tipo de cambio a partir del manejo de la tasa de interés no enfrente ningún tipo de obstáculos cuando la economía se encuentra expuesta a la competencia internacional. Vimos en §14 que un incremento en los salarios nominales, si el banco central decide dejar inalterada la tasa de interés, tenderá a traducirse en un incipiente proceso inflacionario. A partir de la ecuación [9] es posible observar que el incremento en el nivel de precios provocará en este caso un efecto adicional: dados i y el tipo de cambio nominal (E), tenderá a observase una apreciación real con la consiguiente pérdida de competitividad de la economía interna. Ello afectará negativamente el nivel de exportaciones netas, causando un deterioro de la cuenta corriente. Para examinar más de cerca las ulteriores consecuencias de este proceso es conveniente introducir la condición que determina el balance de pagos (BP), ausente en el caso de una economía cerrada.
donde ΔR representa la variación de reservas, CC el resultado de la cuenta corriente, CK el de la cuenta de capital, Y* es el ingreso del resto mundo e i* la tasa de interés internacional. Seguimos la práctica usual y asumimos: CCY* > 0, CCθ > 0 y CKi-i* > 0. De este modo, la apreciación real reduce el saldo de cuenta corriente, lo cual, dada la tasa de interés y el tipo de cambio nominal, lleva a una pérdida de reservas. Es cierto que el banco central puede compensar este efecto al inducir la entrada de capitales mediante un incremento en la tasa de interés interna respecto al nivel i*. Aquí cobra, sin embargo, particular relevancia distinguir entre una economía hegemónica y una periférica. Porque para el caso de la segunda parece plausible asumir que, tarde o temprano, la acumulación de deuda tenderá a reducir considerablemente las posibilidades de financiamiento externo si comienzan a ponerse en duda las posibilidades de pago, en particular si la tasa de interés necesaria para atraer capitales es mayor a la tasa de crecimiento del producto. De este modo, es plausible asumir que, para el caso de una economía cuya deuda con el resto del mundo es emitida en moneda extranjera, la oferta de financiamiento externo deviene una suerte de curva vertical a partir de un determinado nivel de déficit corriente. Es decir: CC(Y, Y*, θ) ≥ ΔDMAX, donde ΔDMAX representa el máximo nivel en el cambio del stock de deuda que el resto del mundo se encuentra dispuesto a financiar a la economía nacional. Por el contrario, el resultado de la cuenta corriente no parece imponer una restricción significativa a aquella economía que posee el liderazgo financiero internacional. Como es reconocido por autores de diversas corrientes de pensamiento, la economía hegemónica puede mantener déficit de cuenta corriente por periodos considerables, precisamente por detentar el ‘privilegio’ de emitir la moneda internacionalmente aceptada como reserva de valor y medio de pago (cf. e.g. Vernengo, 2001: 267; McKinnon, 2005: 5).23La asimetría entre una economía periférica y otra hegemónica puede apreciarse también desde un segundo punto de vista. Consideremos una política monetaria expansiva: mientras la posible salida de capitales que tenderá a realizarse no parece representar un problema significativo para una economía hegemónica, la disminución de la tasa de interés por debajo de su valor internacional no parece ser una política sostenible de manera persistente para un país periférico, ya que la pérdida de reservas obligará al banco central a subir la tasa nuevamente, a enfrentar una devaluación, o a una combinación de ambas, con consecuencias negativas para el salario real, el producto y el empleo. La implicación más importante que se deriva de lo anterior es que en un contexto de apertura económica es el banco central de la economía hegemónica (e.g. la Reserva Federal de los Estados Unidos) quien, a partir de la manipulación de i*, posee la verdadera capacidad de influir en la distribución del ingreso, mientras que la distribución en una economía periférica, como afirma Pivetti (1991: 34) “se verá largamente afectada por la política monetaria de largo plazo seguida por las grandes economías”.24
De todos modos, las restricciones que enfrenta una economía periférica dificultan pero no impiden a las políticas fiscal y monetaria influenciar en la distribución y en el nivel de empleo de mediano plazo, especialmente si la economía logra alcanzar una situación de superávit de cuenta corriente. Supongamos que las autoridades de una economía periférica en equilibrio de cuenta corriente deciden implementar una política fiscal contractiva. Los niveles de actividad y empleo disminuyen, se debilita la posición de los sindicatos y el salario nominal disminuye. De acuerdo a la ecuación PSEA, el nivel de precios tiende a caer, pero necesariamente en menor proporción que la caída en el nivel de salarios nominales porque E e i permanecen en principio inalterados. El resultado es, por un lado, una depreciación real y, por el otro, una caída del salario real, ergo en el nivel de actividad.25 Ambos efectos tienden a volver superavitario el saldo de la cuenta corriente. Si el banco central permite que el ingreso de divisas cause la posterior apreciación del tipo de cambio nominal, parecería plausible esperar que tanto la recuperación de los salarios reales como la apreciación real causen la tendencia al reequilibrio externo. Sin embargo, la autoridad monetaria puede impedir este proceso acumulando reservas y esterilizando sus efectos monetarios.26 La implicación es la tendencia de la economía a exhibir niveles persistentes, y no sólo transitorios, de actividad y de salario real más bajos, y un tipo de cambio real más alto que en la situación inicial. A su vez, es significativo notar que son los propios autores del ncm quienes aceptan que en caso de superávit corriente no parece haber fuerzas relevantes, de naturaleza exclusivamente económica, que tiendan a eliminarlo. Carlin y Soskice (2006: 366-8), por ejemplo, sostienen que el superávit genera un “efecto riqueza” positivo en la economía nacional, lo que tiende a estimular el consumo y las importaciones. “Estas fuerzas por sí solas”, sin embargo admiten, “son poco probables de ser lo suficientemente poderosas para asegurar el equilibrio de largo plazo [en el balance de pagos]” (p. 367, traducción nuestra). “Si los efectos riqueza son débiles”, continúan, “un país puede generar un superávit corriente por un periodo largo de tiempo. Ello sugiere que existe una asimetría entre países con déficit y superávit” (ibíd., p. 368). Y concluyen que la tendencia al reequilibrio externo puede, entonces, provenir de “presiones políticas” (ibíd.) ejercidas por los países hegemónicos; un argumento plausible, pero que, notemos, pone el acento en factores extrae-conómicos que dependen del contexto histórico considerado, y que, por ende, chocan con la explicación mecánica de la distribución y el empleo, determinados por factores ‘reales’, ofrecida por estos autores.
§18. Puede ser útil concluir esta sección haciendo algunas consideraciones sobre los efectos de la apertura económica sobre el margen neto de beneficios promedio del sector productivo, bne = μ - i, a la luz de los obstáculos que puede enfrentar la economía periférica para determinar la tasa de interés. Reexpresemos la ecuación [9] como 1=(i + bne)((W/P) + θ) y notemos que esos obstáculos bien pueden implicar que, ante una situación de crecimiento económico e incrementos salariales, sean los capitalistas del sector productivo quienes, en pos de no perder su cuota de participación en el mercado mundial, se vean obligados a aceptar una reducción en el nivel de bne (y así en la tasa de beneficios bruta). Simétricamente, consideremos una economía poco dinámica, donde la apertura económica permite a las empresas extranjeras, de mayor productividad, desplazar a una porción de la producción local, ejerciendo, de este modo, efectos nocivos sobre los niveles de producto y empleo nacionales, y debilitando, así, el poder de negociación de los sindicatos. Si asumimos que la autoridad monetaria de la economía en cuestión se ve impedida a reducir la tasa de interés para evitar los efectos negativos de la caída del empleo sobre el salario real, sobre la base de la curva de precios PSEA es esperable que el resultado de la competencia internacional sea el incremento del margen de beneficios detentado por el capital productivo y una depreciación real que acentúe la caída del salario real.
Consideraciones finales§19. En el presente trabajo hemos introducido algunas consideraciones propias de un esquema clásico-keynesiano del valor, la distribución, el producto y el empleo dentro del modelo del ncm y hemos visto que, utilizando el mismo instrumental analítico del ncm, la posibilidad, convalidada por la experiencia práctica, de que la autoridad monetaria sea capaz de manipular persistentemente el valor de la tasa de interés monetaria (cf. e.g. Romer, 2000) implica poner de cabeza los resultados del ncm: con su accionar, la política monetaria es también capaz de influir de manera persistente en las trayectorias de la distribución del ingreso, el empleo y el producto. Finalmente, hemos mostrado que los resultados obtenidos se mantienen cuando se consideran los efectos de la apertura económica: esencialmente, sólo una economía periférica con déficit en su cuenta corriente encontrará serios obstáculos de regular la distribución a través de su política monetaria. En el resto de los casos parece haber suficientes grados de libertad para que la autoridad monetaria influya en el nivel de salario real y el empleo que la economía tiende a realizar, reforzando nuestra conclusión sobre el carácter ‘convencional’ de la tasa de interés en las economías modernas, ergo de la distribución del ingreso y del nivel de actividad. De este modo, nuestro modelo parece capaz de captar fenómenos que para los autores del ncm se presentan necesariamente como “enigmas” (cf. e.g. Barth III y Ramey, 2002: 200), explicables sólo a través de supuestos ad hoc que resultan contradictorios con la teoría general del valor y la distribución marginalista a la que adscriben esos mismos autores.
El apéndice desarrolla las condiciones que aseguran la estabilidad dinámica del modelo base (sección cuarta).2727 Las condiciones presentadas abajo se basan en Setterfield (2005). La diferencia principal es que nuestro análisis incorpora el efecto de la tasa de interés en el margen de beneficios. Si π=πT y Y=Yn, entonces i-1 = r* + π–1. Valiéndonos de: dr/dt = (i - i–1) – (π – π–1), en un periodo arbitrariamente corto de tiempo y usando la regla [2'] se obtiene la expresión que figura en el texto.
Finalmente, a causa de su efecto en el consumo ante cambios en la distribución (cf. §12), la demanda agregada es una función negativa de la tasa de interés, por lo cual: Y = c0 + C1(π - i), donde hemos reunido los factores adicionales bajo el intercepto c0. Diferenciando respecto al tiempo obtenemos: C) dydt=−c1drdt Insertando A) en B) y en C), obtenemos un sistema dinámico en la tasa de inflación y el producto:
La linealización del sistema [D] evaluada en el punto de equilibrio, resulta en una matriz Jacobiana dada por:
Las condiciones suficientes de estabilidad son Det > 0 y Tr < 0. El determinante es siempre positivo dados los parámetros del modelo,2929 Partiendo de: Det=−11+μk1c1k2+c1k1f′+11+μk2. Para que el determinante sea positivo, debe cumplirse: 11+μk2<f′+11+μk2, condición que se satisface siempre, pues f'>0. Para entender por qué es esperable que ello sea así, notemos, como vimos en la sección cuarta (§10), que cuando el banco central incrementa la tasa de interés, los precios suben, lo que lleva a éste a aumentar la tasa de interés nuevamente, lo cual incrementa los precios, etcétera. Es decir, es en el factor k1 donde se encuentra el germen de la inestabilidad (i.e. de no existir interdependencia entre el margen y la tasa de interés, la matriz del sistema se reduce a: 0f′−c1k1−c1k2, con lo cual la traza es siempre negativa y el determinante es siempre positivo, i.e. el modelo es estable, cf. e.g. Woodford, 2003). Es esperable, entonces, que el banco central, al menos sobre un periodo de tiempo considerable, se dé cuenta de que es su propio accionar el causante de la inestabilidad y corrija su comportamiento disminuyendo k1.
Universidad de Buenos Aires y Consejo Nacional de Investigaciones Científicas y Técnicas (conicet), Argentina, y Universidad de Massachussets, Amherst, Estados Unidos, respectivamente. Los autores agradecen los valiosos comentarios de dos dictaminadores anónimos de la revista. Los errores y omisiones son entera responsabilidad de los autores.
La diferencia entre ambos grupos radica, esencialmente, en la velocidad de ajuste de los valores de mercado hacia aquéllos determinados por la teoría: para los nuevos clásicos el ajuste es instantáneo mientras que para los nuevos keynesianos opera sobre un periodo de tiempo considerable.
En los párrafos §4 y §5 señalaremos las modificaciones necesarias para transformar al modelo de Blanchard en un modelo canónico del ncm. Como veremos, el modelo de Blanchard es un caso particular de este modelo canónico en el cual el nivel de inflación de equilibrio es cero.
La ecuación de precios es el resultado de un proceso de maximización de beneficios de la firma representativa bajo condiciones de competencia imperfecta (cf. Carlin y Soskice, 2006: 48–50).
La ecuación [5] puede derivarse del comportamiento de los sindicatos a partir de, por ejemplo, la teoría de los ‘salarios de eficiencia’ (Carlin y Soskice, 2006: capítulo 15, apéndice). En nuestro análisis trabajamos directamente con la ecuación [5] pues escapa de nuestro objetivo estudiar la solidez de este tipo de ‘micro-fundamentos’ (para una crítica a la teoría de los salarios de eficiencia, cf. Curie y Steedman, 1993).
Dado que F(.) es estrictamente monótona en u, el nivel de desempleo es único.
Cf. Serrano (2010) para un análisis de los límites de este supuesto. Nosotros levantaremos este supuesto cuando examinemos los determinantes de la inflación (cuarta sección, §14).
Este comportamiento del banco central también puede ser ‘micro-fundamentado’ de una manera sencilla. Se asume que el gobierno minimiza una ‘función de pérdida’ que depende de las desviaciones del producto y de la inflación de sus niveles naturales (cf. Carlin y Soskice, 2005: apéndice)
La explicación de la tasa de beneficios sobre la base de un margen sobre el nivel de costos enfrenta otras dificultades que por razones de espacio no podemos discutir aquí. Cf. Stirati (2001: 428–9).
En efecto, sería contradictorio describir al mediano plazo como una posición en la que el nivel general de precios esperado coincide con el nivel efectivo, pero que al mismo tiempo la tasa de retorno sobre el capital invertido no fuera uniforme en las distintas ramas productivas. De ocurrir una discrepancia en la tasa de retorno (neta de riesgo), la composición de la producción se modificará en los periodos siguientes, provocando cambios en los precios relativos de las distintas mercancías y, por ende, en el nivel general de precios.
Para un análisis de los determinantes del salario real en los autores clásicos y en Marx, cf. Stirati (1994).
La idea de una tasa de interés determinada por fuerzas extraeconómicas, y susceptible de ser manipulada por la autoridad monetaria también emerge en la Teoría General de Keynes (2001 [1936]: 175).
Notemos que, dado el nivel del salario monetario, un cambio permanente en la tasa de interés monetaria provocará también cambios en los precios relativos de las distintas mercancías debido a que el peso de la tasa de interés en los costos varía en los distintos sectores. De este modo, ante e.g. un aumento en la tasa de interés, el salario real tenderá a disminuir en distinta proporción de acuerdo a la mercancía considerada (cf. Pivetti, 1991: 22).
En Blanchard (2003: capítulo 5) es posible encontrar una explicación de la negatividad de la demanda de inversión respecto a la tasa de interés que no depende de los mecanismos de sustitución factorial: en cada momento del tiempo el emprendedor se enfrenta a la posibilidad de invertir en diferentes proyectos de inversión, los cuales pueden ser ordenados de acuerdo a sus respectivas tasas de retorno esperadas, las cuales pueden a su vez derivarse de los ingresos esperados futuros del proyecto. La función de inversión agregada se deriva de calcular, para cada nivel de la tasa de interés, la suma de todos los proyectos de inversión que resulta beneficioso implementar. Cuanto más baja es la tasa de interés, más proyectos poseen una tasa interna de retorno superior a la tasa de interés de mercado, por lo cual el nivel de inversión agregada resulta ser una función decreciente de la tasa de interés. Este argumento, sin embargo, es seriamente defectuoso pues supone que el rendimiento futuro de los proyectos de inversión es independiente de la tasa de interés de mercado. El argumento pasa por alto el hecho de que la tasa de interés es un costo de producción, con lo cual una caída en la tasa implicará también una caída en el rendimiento futuro de los proyectos de inversión (cf. Petri, 2004: 262-8, para un análisis detallado de los problemas de esta justificación de la función de inversión).
No resulta entonces extraño que Patinkin (1987: 100), conocido por sus contribuciones sobre el accionar del efecto Pigou, concluya que es extremadamente dudoso que el efecto Pigou “sea lo suficientemente fuerte como para contrarrestar el efecto negativo en las expectativas generado por una caída en el nivel de precios, incluyendo aquéllas generadas por una ola de quiebras que bien podrían ser causadas por una severa caída [en el nivel de precios]” (traducción nuestra).
A estos inconvenientes se suma un problema adicional: si la oferta monetaria se comporta de manera pasiva, entonces la cantidad de dinero se acomoda ante los cambios en la demanda, dejando inalterada la tasa de interés real y la demanda agregada. Si la economía se aparta del equilibrio, los cambios en el nivel de precios no afectan el nivel de actividad y, por lo tanto, no pueden restablecer el equilibrio. El ncm soluciona este problema introduciendo una regla de política monetaria como la especificada por medio de la ecuación [2”], ya que ésta tiende a contener o impulsar la demanda agregada, operando como mecanismo estabilizador. Esto ha llevado a algunos autores a argumentar que una oferta monetaria endógena no implica inestabilidad (Woodford, 2003: capítulo 1). Para un análisis crítico de la posición de Woodford, cf. Docherty (2009).
Cf. Serrano y Tabares Ribeiro (2004) para un análisis detallado de los problemas dentro del ncm de derivar una relación negativa entre el nivel de demanda agregada y el nivel de precios.
Este efecto de la tasa de interés sobre el nivel de precios se conoce dentro de la literatura marginalista como la ‘paradoja de Gibson’; en realidad esta relación no posee nada de paradojal cuando se reconoce que la tasa de interés es un costo de producción.
Es también posible que un cambio en la tasa de interés objetivo desplace la curva WS, ya que el accionar de la política monetaria es uno de los posibles factores institucionales Z que afectan la curva F(.). Por simplicidad omitimos examinar esta posibilidad en este trabajo.
A una conclusión muy similar llegan autores del ncm como Barth III y Ramey (2002: 200) en su intento de dar una explicación al aparente enigma —dado el marco del ncm en el que estos autores se mueven— del efecto de la política monetaria en el nivel de actividad. Un shock en la política monetaria, sostienen, “puede ser visto como un desplazamiento tanto de la oferta como de la demanda agregadas en la misma dirección, causando un gran incremento en el nivel de producto y un menor efecto en los precios” (traducción nuestra).
Como afirma Pivetii (2007), “manipulando la tasa de interés nominal es siempre posible en principio —aunque al costo de sostener una inflación creciente— dejar inalterada la distribución luego de un incremento en el nivel de salarios” (traducción nuestra).
El alza en la tasa de interés también tiene el efecto indirecto de contraer el nivel de actividad, lo cual reduce a su vez el nivel de empleo. De este modo, la presión sobre los salarios ejercida por los trabajadores disminuye, ergo aquélla sobre los salarios. En el texto principal hacemos abstracción de este efecto, para concentrarnos en el efecto directo sobre el nivel de precios debido al aumento de la tasa de interés.
Las otras ecuaciones relevantes son esencialmente las mismas que las utilizarlas en la sección cuarta: la curva IS (ecuación [1']), que debe ser modificada para incluir el nivel de exportaciones netas, XN=XN(Y*, Y), donde Y* es el nivel de ingreso del resto del mundo, y NXY*>0, XNY<0 y XNθ > 0, y la curva RPM (ecuación [2']). Veremos en el parágrafo §17 que, además de estas condiciones, debe tenerse en cuenta la restricción que puede imponer a las economías periféricas el saldo del balance de pagos.
En palabras de McKinnon (2005: 5): “En el siglo XXI, el dólar es la moneda definitiva […] Cuando se encuentran amenazados por eventos domésticos, los extranjeros no cuentan con un activo monetario más importante en el cual refugiarse […] Consecuentemente, solo los Estados Unidos tienen la posibilidad de tomar fuertes deudas con el resto del mundo en su propia moneda” (traducción nuestra).
Si bien los determinantes de la distribución en nuestro modelo difieren radicalmente de los que explican la distribución para los autores del ncm, nuestra conclusión sobre la jerarquía entre países periféricos y hegemónicos (o economías “grandes”), y el hecho de que son las condiciones que rigen en las últimas las que primordialmente determinan la tasa de interés —y la distribución— en las primeras, son similares. Carlin y Soskice (2010: 3) e.g. sostienen: “[E]n las economías cerradas la tasa de interés real […] o la tasa natural o la tasa Wicskelliana de interés lleva al equilibrio la demanda agregada y la oferta agregada […] Pero en una economía pequeña, la tasa de interés real de mediano plazo está fijada por la tasa de interés internacional” (traducción nuestra). Pero a este punto es legítimo preguntarse, ¿qué determina la tasa de interés internacional dentro del esquema de ncm? Si bien los autores no ofrecen una explicación detallada, sí aceptan que las condiciones que rigen al interior de una economía hegemónica (o “grande”) influyen en la tasa de interés internacional: ‘Por virtud de su tamaño” explican, “una caída en la tasa de interés en la Eurozona causará una caída de la tasa internacional, i*” (Carlin y Soskice, 2006: 333, traducción nuestra).
Asumimos que el efecto contractivo de la caída del salario real más que compensa el efecto expansivo derivado de la depreciación real (cf. Krugman y Taylor, 1978).
Si bien una parte importante de la literatura ha tendido a cuestionar la posibilidad de la esterilización, en general se ha concentrado en situaciones de déficit corrientes. Para situaciones de superávit, bajo condiciones suficientemente generales puede demostrarse que la esterilización es sostenible (cf. e.g. Bonfiger y Wollmehauser, 2003; Frenkel, 2007).
Las condiciones presentadas abajo se basan en Setterfield (2005). La diferencia principal es que nuestro análisis incorpora el efecto de la tasa de interés en el margen de beneficios.
Si π=πT y Y=Yn, entonces i-1 = r* + π–1. Valiéndonos de: dr/dt = (i - i–1) – (π – π–1), en un periodo arbitrariamente corto de tiempo y usando la regla [2'] se obtiene la expresión que figura en el texto.
Partiendo de: Det=−11+μk1c1k2+c1k1f′+11+μk2. Para que el determinante sea positivo, debe cumplirse: 11+μk2<f′+11+μk2, condición que se satisface siempre, pues f'>0.
Para entender por qué es esperable que ello sea así, notemos, como vimos en la sección cuarta (§10), que cuando el banco central incrementa la tasa de interés, los precios suben, lo que lleva a éste a aumentar la tasa de interés nuevamente, lo cual incrementa los precios, etcétera. Es decir, es en el factor k1 donde se encuentra el germen de la inestabilidad (i.e. de no existir interdependencia entre el margen y la tasa de interés, la matriz del sistema se reduce a: 0f′−c1k1−c1k2, con lo cual la traza es siempre negativa y el determinante es siempre positivo, i.e. el modelo es estable, cf. e.g. Woodford, 2003). Es esperable, entonces, que el banco central, al menos sobre un periodo de tiempo considerable, se dé cuenta de que es su propio accionar el causante de la inestabilidad y corrija su comportamiento disminuyendo k1.