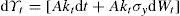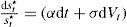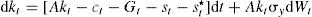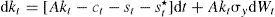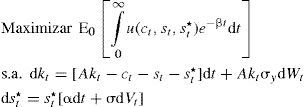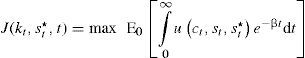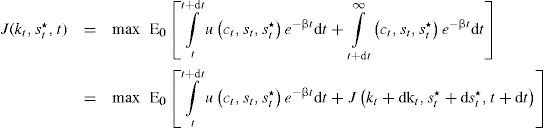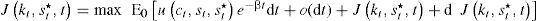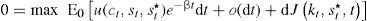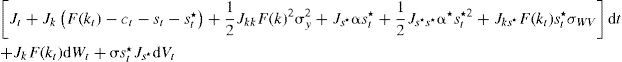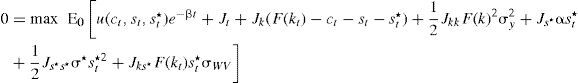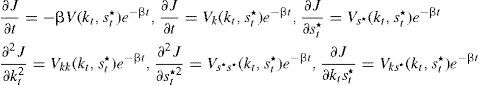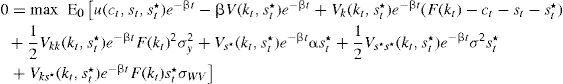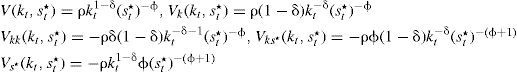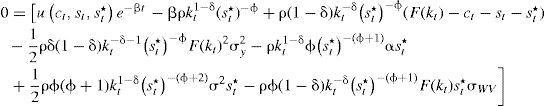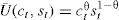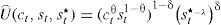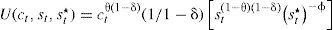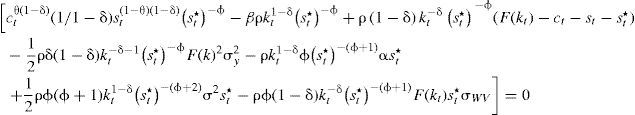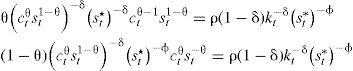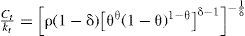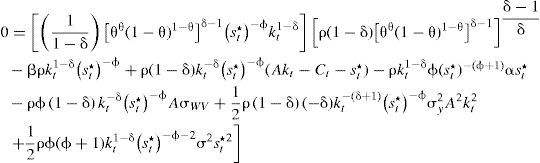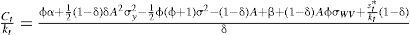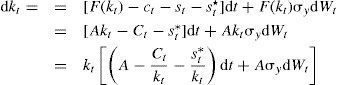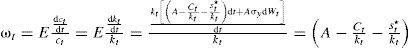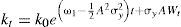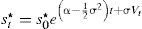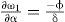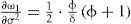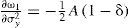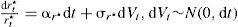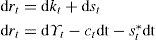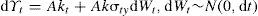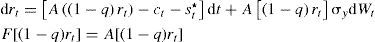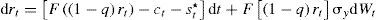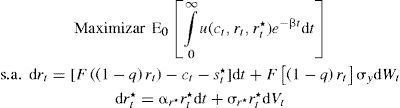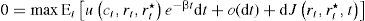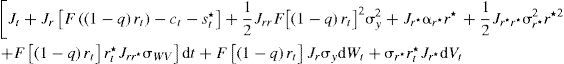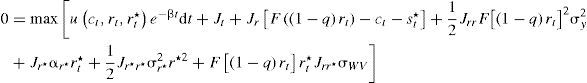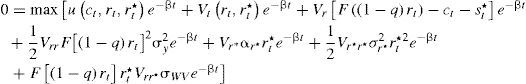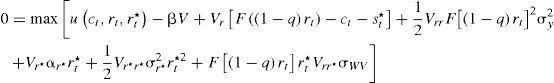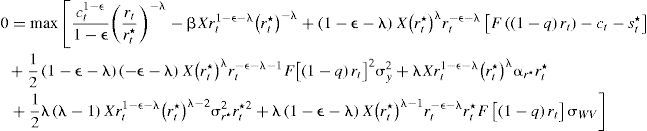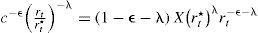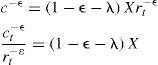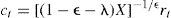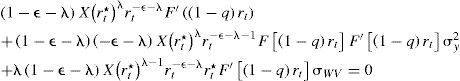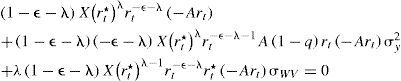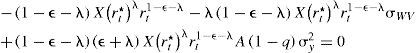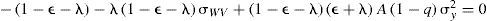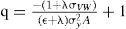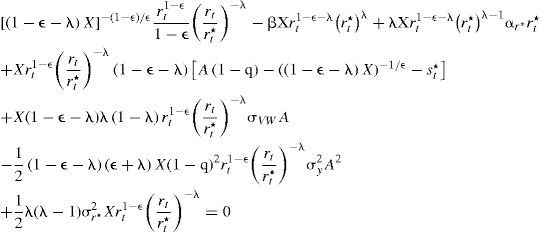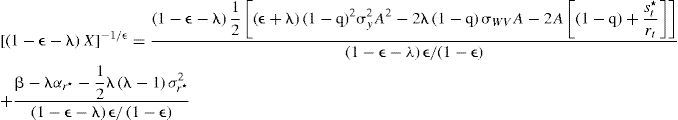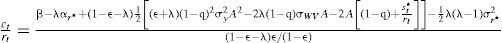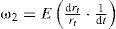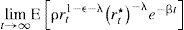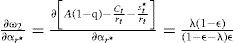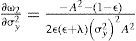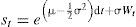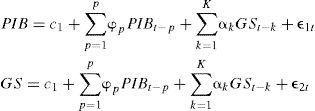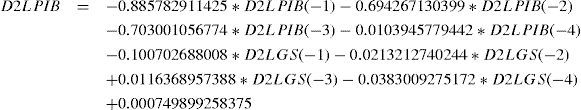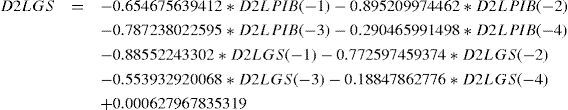El presente trabajo examina el gasto en materia de seguridad asignado a acciones contra el crimen organizado y sus efectos en el crecimiento económico. Para lograr dicho objetivo se emplea un modelo estocástico macroeconómico de equilibrio general, el cual permite analizar la acumulación de recursos asignados a la lucha contra el crimen organizado, así como los efectos de los shocks exógenos correspondientes al producto y al gasto de éste. El modelo muestra que un cambio en el nivel de recursos económicos que el crimen organizado destine en contra del Estado provocará una reacción de este último, lo cual impactará en el crecimiento económico debido a la elasticidad de sustitución intertemporal del consumo. Por último, con base en las relaciones funcionales que proporciona el modelo teórico, se muestra evidencia empírica, mediante un modelo de vectores autorregresivos (var), de si existe una relación entre el gasto presupuestario en materia de seguridad y el crecimiento económico.
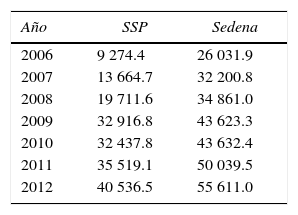
El narcotráfico y el crimen organizado han estado presentes durante mucho tiempo en México. No obstante, en el sexenio pasado (2006–2012) éste se vuelve un tema relevante y prioritario en la política de gobierno, en la cual se adopta una serie de estrategias para delimitar la presencia del crimen organizado en ciertas regiones del país. En el rubro de seguridad los sectores policiaco y militar fueron de los más dinámicos del sexenio anterior. El gobierno emprendió una ofensiva en contra del crimen organizado que se ha equiparado discursivamente con una guerra, y al finalizar el sexenio el gobierno gastó más de 642mil millones de pesos en su estrategia para la pacificación del país, cifra que equivale a más del doble de los 308mil millones de pesos que se erogaron en la administración anterior (2000–2006); esto de acuerdo con cifras del Centro de Estudios de las Finanzas Públicas de la Cámara de Diputados (cefp). Al margen de la polémica teórica de si se trata de una guerra o no, el hecho es que gran parte del Ejército Mexicano se encuentra en las calles, operando y metido de lleno en el combate contra el crimen organizado. El problema del narcotráfico y el crimen organizado ha llegado a un nivel que se compara con el terrorismo en otros países, tal como lo muestran los ataques a la población civil del 15 de septiembre de 2008 en Michoacán. Esto ha creado una preocupación en el gobierno, el cual ha destinado mayores recursos para hacer frente a este problema que ya es considerado un asunto de seguridad nacional. Para el último año de gobierno de la administración 2006–2012, el presupuesto asignado a las Secretarías de Gobernación (Segob), Defensa Nacional (Sedena), Marina (Semar), Seguridad Pública (ssp) y la Procuraduría General de la República (pgr) es superior a los 153mil millones de pesos de acuerdo con el cefp. El cuadro 1 muestra la dinámica del gasto asignado a la ssp y a la Sedena, lo cual refleja la prioridad que tuvieron estos sectores en el sexenio 2006–2012 como parte de la estrategia de combate al crimen organizado. Por último, es importante mencionar que el gasto federal que se destinó exclusivamente a la guerra contra narcotráfico y el crimen organizado durante 2006–2011 fue de alrededor de 174 millones de pesos.
Presupuesto asignado durante el sexenio 2006–2012 a la seguridad pública y la defensa nacional (en miles de millones de pesos corrientes)
| Año | SSP | Sedena |
|---|---|---|
| 2006 | 9 274.4 | 26 031.9 |
| 2007 | 13 664.7 | 32 200.8 |
| 2008 | 19 711.6 | 34 861.0 |
| 2009 | 32 916.8 | 43 623.3 |
| 2010 | 32 437.8 | 43 632.4 |
| 2011 | 35 519.1 | 50 039.5 |
| 2012 | 40 536.5 | 55 611.0 |
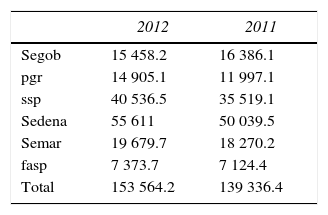
El cuadro 2 muestra el presupuesto por Secretaría en materia de seguridad, así como las contribuciones del Fondo de Aportaciones a la Seguridad Pública de los Estados y del Distrito Federal (fasp) para el año 2011–2012 en el marco del Programa Nacional de Seguridad Pública.
Presupuesto de egresos de la Federación en materia de seguridad nacional, 2011–2012 (en miles de millones de pesos corrientes)
| 2012 | 2011 | |
|---|---|---|
| Segob | 15 458.2 | 16 386.1 |
| pgr | 14 905.1 | 11 997.1 |
| ssp | 40 536.5 | 35 519.1 |
| Sedena | 55 611 | 50 039.5 |
| Semar | 19 679.7 | 18 270.2 |
| fasp | 7 373.7 | 7 124.4 |
| Total | 153 564.2 | 139 336.4 |
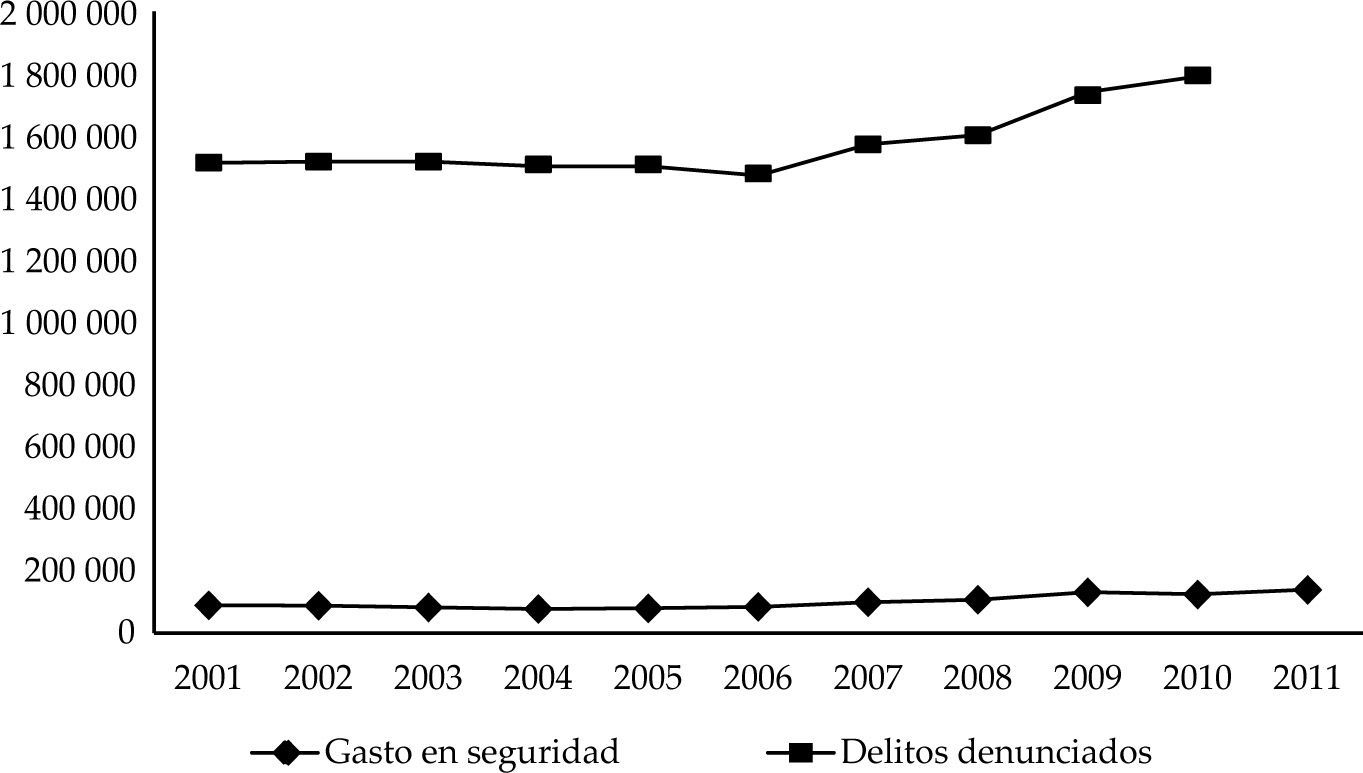
Asimismo, es importante destacar que el incremento significativo del gasto en materia de seguridad en las distintas dependencias que participan también ha llevado a una tendencia a la alza en los delitos “denunciados”, como se muestra en la gráfica 1. De igual forma, dicha gráfica evidencia cómo ha evolucionado el gasto en seguridad en los últimos diez años, el cual se incrementó de 90 mil millones de pesos en 2001 a 139 mil millones en 2011.
El incremento del gasto en materia de seguridad claramente ha sido, en buena medida, utilizado para hacer frente a la amenaza del crimen organizado. Se podría pensar, en principio, que al dirigir mayores recursos en seguridad se afectan otros sectores productivos, lo que llevaría a un deterioro del crecimiento económico en el largo plazo, esto acorde con Yang, Lin y Chen (2012). Landau (1993), en un estudio empírico de regresión para 71 países del nordeste de áfrica para el periodo 1969–1989, muestra una relación no lineal entre el gasto militar y el crecimiento económico. Por otro lado, se tienen los trabajos de Yang, Lin y Chen (2012) que encuentran una relación negativa entre el gasto antiterrorismo y el crecimiento económico, pero una relación positiva entre el gasto antiterrorista y el bienestar social. Asimismo, el trabajo de Lin y Lee (2012) señala que el crecimiento está en función al grado de aversión al riesgo de los agentes. Por último, Deger y Sen (1983) muestran que el gasto en defensa podría estimular la demanda y con ello aumentar el empleo y la producción, lo cual tiene un efecto positivo en el desarrollo económico.
Un tema actual es el impacto de las decisiones del gobierno sobre el incremento en el gasto en materia de seguridad sobre diversas variables macroeconómicas, como la inversión o el crecimiento económico. En esta investigación se desarrolla un modelo, en el marco de la optimización intertemporal, que pretende explicar los efectos del incremento en el gasto en seguridad asignado a acciones contra el crimen organizado, el consumo, la inversión y el crecimiento económico. El modelo incorpora este gasto primero como un bien de consumo y luego como un bien de inversión. De igual forma, toma como punto de partida el trabajo de Gong y Zou (2003), el cual se desarrolla en el marco de la teoría neoclásica para analizar el impacto del gasto en seguridad en el crecimiento económico desde una perspectiva de optimización estocástica.
El modelo teórico que se propone está planteado en un ambiente estocástico, esto es, si bien se establece un gasto presupuestario para combatir los grupos del crimen organizado, las partidas pueden estar cambiando en forma continua en función de las circunstancias en que se encuentre el país. Este problema puede también analizarse como un juego de dos etapas, donde la reacción tanto del gobierno como del crimen organizado está en función de la cantidad de recursos destinados para dicho fin. Es importante hacer notar que si bien el gasto en seguridad pública y el gasto militar no son lo mismo, de ambos se extrae una proporción que representa el gasto que se destina para combatir al crimen organizado y que dicho proporción debe entenderse como el gasto en seguridad en el modelo propuesto. Para resolver el modelo, se parte de los supuestos que se establecen en la ortodoxia neoclásica, individuos maximiza- dores de satisfacción, una función de producción del tipo AK. De esta forma, los resultados macroeconómicos tendrán fundamentos microeconómicos. Además, se considera una función de producción como en Turnovsky (2000) y una función de utilidad cóncava estrictamente creciente. En el marco teórico planteado se examinará el impacto en el crecimiento de los cambios marginales en los recursos que se destinan para combatir al crimen organizado. Un resultado relevante del modelo es que el crecimiento está en función de la elasticidad de sustitución intertemporal de los individuos.
En el apartado empírico, con base en las relaciones funcionales provenientes del modelo teórico, se propone un modelo de vectores autorregresivos (var) para examinar la relación entre el gasto presupuestario asignado a la seguridad y el producto interno bruto (pib). Se observa que aunque el presupuesto en materia de seguridad y el pib tienen comportamientos de crecimiento similares, estás variables no presenta una relación causal, en ambas direcciones, en el sentido de Granger durante el periodo 2000–2012.
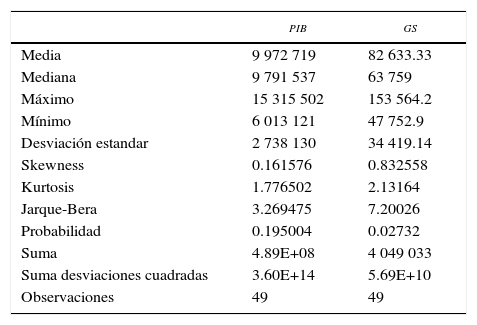
Características de las series trimestrales del pib y del gasto en seguridad (millones de pesos a precios corrientes)
| pib | gs | |
|---|---|---|
| Media | 9 972 719 | 82 633.33 |
| Mediana | 9 791 537 | 63 759 |
| Máximo | 15 315 502 | 153 564.2 |
| Mínimo | 6 013 121 | 47 752.9 |
| Desviación estandar | 2 738 130 | 34 419.14 |
| Skewness | 0.161576 | 0.832558 |
| Kurtosis | 1.776502 | 2.13164 |
| Jarque-Bera | 3.269475 | 7.20026 |
| Probabilidad | 0.195004 | 0.02732 |
| Suma | 4.89E+08 | 4 049 033 |
| Suma desviaciones cuadradas | 3.60E+14 | 5.69E+10 |
| Observaciones | 49 | 49 |
La presente investigación está organizada en cuatro secciones: la primera sección es una introducción; el siguiente apartado incorpora el gasto en materia de seguridad como un bien de consumo; a continuación se incorpora al gasto en materia de seguridad como un bien de inversión, lo que permite explicar la dinámica de la acumulación de armamento y equipo para combatir la amenaza del crimen organizado. En las secciones dos y tres se obtiene una solución a las expectativas de la tasa de crecimiento económico. El cuarto apartado muestra una evidencia empírica sobre la relación del gasto presupuestario en seguridad y crecimiento y, por último, el último apartado presente las conclusiones de la investigación.
Gasto en materia de seguridad como bien de consumoEl modelo está planteado en el contexto donde el Estado mexicano se encuentra en una confrontación militar en contra del crimen organizado. Se parte del supuesto de que las preferencias están definidas por el consumo (ct), el nivel de gasto en materia de seguridad para combatir al crimen organizado (st), y se incluye también el nivel de gasto que el crimen organizado destine a la guerra en contra del Estado (st*), de tal forma que la utilidad queda en función de estas tres variables, es decir: u(Ct,st,st*). Es importante hacer notar que aunque el gasto del crimen organizado está en la función de utilidad, no implica que el agente económico necesariamente decida sobre la misma ni que guarde una relación positiva con la utilidad, de hecho guarda una relación negativa con ella. Para tal efecto, se propone una función de utilidad que no le proporcione satisfacción al agente ante un incremento de dicho gasto, y que cumpla con todas las características teóricas dentro del margen de la ortodoxia neoclásica. Se establece una función de producción con tecnología estocástica del tipo AK como en Merton (1975) y Turnovsky (2000), la cual está dada por:
donde Yt es la producción, A una constante positiva, kt el stock de capital que al multiplicarse por dt define la parte determinista por unidad de tiempo, σy el parámetro de volatilidad del producto, y dWt el elemento estocástico que incorpora los impactos no esperados en la producción. Además, se parte del supuesto de que el gasto del crimen organizado destinado a la guerra en contra del Estado sigue un proceso estocástico de la siguiente forma:Ecuación en la cual α es el nivel medio del gasto que el crimen organizado destina a la guerra contra el Estado (tendencia), σ la volatilidad de dicho gasto y dVt el componente estocástico que se distribuye de forma normal, con media cero y varianza dt. También se supone que Cov(dWt,dVt) = σWVdt, donde σWVdt>0, esto implica que la correlación entre los shocks del gasto tanto del crimen organizado como del Estado son positivos, lo que captura el fenómeno de acumulación de armamento entre ambos.Una vez que se incorpora el gasto en materia de seguridad dentro de los bienes de consumo se tiene que el incremento marginal en la identidad de la renta nacional1 puede expresarse como dϒt=[ctdt+stdt+st*dt]+dkt, donde dk es el cambio marginal del stock de capital. Entonces, la restricción presupuestal se puede reescribir como dkt=dϒt−ctdt−gTdt−st*dt, donde el gasto total de gobierno es Gtdt=g¯dt+stdt, en el cual se incluye el gasto corriente (g¯) y el gasto en materia de seguridad st. En virtud de las ecuaciones [1] y [2] se obtiene el incremento marginal del capital:
Si se considera un gasto corriente nulo, esto es cuando g¯dt=0, con el fin de no realizar cálculos innecesarios para los objetivos que se persiguen se tiene entonces que:Problema de optimización (modelo 1)Se parte del supuesto de que los individuos que habitan esta economía buscan maximizar su utilidad, para ello tendrán que elegir las trayectorias óptimas de consumo y gasto en materia de seguridad. El problema de decisión está supeditado a la dinámica del capital y del gasto del crimen organizado en su lucha contra el Estado, descontada a una tasa subjetiva, 0<β<1, sujeto a [2] y [1], es decir:
Este problema de maximización se aborda desde la teoría del control óptimo estocástico.2 Defiendo:
entonces:Al aplicar a la expresión anterior el teorema de valor medio, ∫abf(x)dx=f(a)(b−a)+o(b−a), y la expansión de Taylor se obtiene:
Equivalentemente a:La diferencial estocástica dJ(k,s*,t) se calcula con el lema de Itô:
Al tomar el valor esperado, los términos estocásticos dWt y dVt se hacen cero. Posteriormente, se divide por dt y se toma el límite cuando o(dt)/dt→0, lo que conduce a la expresión:
donde F(kt)=Akt. Esta expresión se conoce como la ecuación de Hamilton, Jacobi y Bellman (h-j-b).Condiciones de primer ordenSe define la función de valor J(kt,st*,t)=V(kt,st*)e−βt, y se calculan las derivadas parciales respecto a las variables de estado y tiempo, es decir:
Al sustituir las derivadas parciales de la función de valor en la ecuación [3] se tiene que:
Se propone como candidato de solución la función V(kt,st*)=ρk1−δ(st*)−φ, y se calculan las derivadas parciales respecto a las variables de estado. En este caso, φ es la elasticidad de sustitución del gasto del crimen organizado y ρ es un parámetro de la función de valor. Así:
Al sustituir las derivadas parciales de la función V(kt,st*) a partir de [4] se tiene que:
A fin de obtener una solución específica, se propone enseguida una forma funcional adecuada de la utilidad.
Función de utilidad y decisiones óptimasSe considera una función de utilidad de tipo Cobb-Douglas con dos bienes que generan satisfacción, el consumo y el gasto destinado para combatir al crimen organizado, por lo cual se propone:
Ahora bien, si se supone otro factor que no cause utilidad, como lo es el gasto que el crimen organizado destina a combatir al Estado, entonces se obtiene otra función de utilidad tal que:
y si se redefine a λδ=φ, dado que (1/1−δ) es constante, al ser multiplicada por la función de utilidad no altera las preferencias, por lo que la función de utilidad puede expresarse como:Los parámetros satisfacen 0<θ<1; φ>0 cuando 0<δ<1 y φ<0 cuando δ>1, y las restricciones sobre φ y δ son para asegurar que un incremento del gasto que el crimen organizado destina para combatir al Estado no genere bajo ninguna circunstancia utilidad, es decir: ∂ut/∂st*<0, para todos los casos posibles. A partir de [5], y considerando la función de utilidad propuesta, se llega a:
Al aplicar las condiciones de primer orden respecto al consumo y al nivel de gasto en materia de seguridad en la ecuación [6], se obtienen las siguientes expresiones:
Si se define el consumo total (Ct) como la suma del consumo individual y el nivel de gasto destinado a combatir el crimen organizado, es decir, Ct=ct+st, ct=θCt, st=(1−θ)Ct, 0<θ<1. Si se sustituye Ct en [7] se obtiene la razón consumo capital, misma que será útil para evaluar más adelante el crecimiento económico:Así, al sustituir [8] en [6] se obtiene la expresión que conduce enseguida a la razón consumo capital:
Después de dividir la ecuación [9] entre (s*)−φ, descomponiendo el término [•](δ−1)/δ y dividiendo entre k1−δ y ρ la razón consumo capital se puede expresar como:
y dado que ct+st=Ct y F(kt)=Akt, la ecuación dinámica del stock de capital está dada por:Por lo que las expectativas de la tasa de crecimiento del consumo y el stock de capital, denotado por ω1, satisface:
Por lo anterior, se obtiene la ecuación diferencial que conduce al stock de capital, dkt=kt[φ1dt+AσydWt], cuya solución, con condición inicial k(0)=k0, está dada por:
La trayectoria estocástica de gasto del crimen organizado viene dada por la siguiente expresión:
Las condiciones que garantizan una razón consumo-capital positiva están dadas por:
Resultados teóricos y análisisEl análisis se enfoca en los efectos del gasto sobre el crecimiento y el stock de capital. Con relación al gasto medio que el crimen organizado destina para combatir al Estado, el crecimiento en la tendencia media de la amenaza que representan las organizaciones criminales afecta al crecimiento económico de la siguiente forma:
De esta manera, φ>0 cuando 0<δ<1, y φ<0 cuando δ>1. Si δ>1, ∂ω1/∂α>0, y si 0<δ<1, ∂ω1/∂α<0. Esto quiere decir que un alto o bajo crecimiento en la tendencia media del gasto del crimen organizado para combatir al gobierno conlleva a un crecimiento o decrecimiento económico siempre y cuando la elasticidad de sustitución intertemporal en el consumo, dada por 1/δ, sea relativamente pequeña o grande. Cuando el crimen organizado aumenta su nivel promedio de recursos económicos destinados para combatir al gobierno se genera una reacción del Estado, esto es, el gobierno también aumentará su gasto para contrarrestar a los criminales, y dado que el gasto en materia de seguridad del Estado tiene una relación directa con la función de utilidad, entonces la utilidad marginal del agente aumentará el gasto en materia de seguridad. El que el gobierno aumente su gasto para combatir al crimen organizado conduce a una reducción en la inversión de capital cuando la elasticidad de sustitución intertemporal del consumo es relativamente elástica, es decir, cuando 0<δ<1. Por tanto, en el largo plazo, la tasa de crecimiento reducirá. Por otra parte, cuando δ>1, la elasticidad de sustitución de consumo del agente representativo es pequeña, lo que va a reducir el consumo, aumentar la inversión y producir mayor ingreso.En cuanto al impacto estocástico de la amenaza del crimen organizado en el crecimiento económico, este está dado por:
De esta manera, se tiene que ∂ω1/∂σ2>0 cuando 0<δ<1 o cuando φ<−1 y δ>1, y ∂ω1/∂σ2<0 cuando δ>1 y −1<φ<0. Estos resultados sugieren que una alta elasticidad de sustitución intertemporal en el consumo de los individuos que anidan la economía (que no son criminales) va a conducir al crecimiento económico cuando exista una mayor volatilidad en la amenaza que representa el crimen organizado. Sin embargo, se debe tener cierta precaución, ya que se puede presentar el caso de que la amenaza del crimen organizado cause más desutilidad, esto es, que se presente un valor absoluto grande de φ.
Los impactos estocásticos (por la volatilidad de la producción) en el incremento marginal del producto tienen el siguiente efecto sobre el crecimiento económico:
Así, ∂ω1/∂σy2>0 cuando γ>1,y ∂ω1/∂σy2<0 cuando 0<δ<. Lo que se obtiene de esto es que un impacto estocástico en el cambio marginal del producto conlleva al crecimiento económico cuando la elasticidad de sustitución intertemporal en el consumo de los individuos (diferentes a los criminales) es relativamente pequeña.
Gasto en materia de seguridad como bien de inversión (modelo 2)En este apartado se incorpora el gasto en materia de seguridad como un bien de inversión, por lo que puede verse la acumulación de capital como acumulación de armamento (capacidad de las fuerzas del orden público para combatir al crimen organizado). Si se denota al stock de armamento del Estado comost y al stock de armamento del crimen organizado como st*, la riqueza total (rt) del Estado será la suma del stock de capital y armamento, es decir, rt=kt+st; mientras que la riqueza total del narcotráfico y el crimen organizado (rt*) será la suma de su stock de capital y armamento, esto es, rt*=kt*+st*.
La utilidad de los individuos que pueblan la economía están definida por el consumo ct, la riqueza total rt y la riqueza total del crimen organizado rt*, por lo tanto se tiene que u(ct,rt,rt*). Se incluyen ambos niveles de riqueza en la función de utilidad porque representan una visión realista del poder de un gobierno y su estatus en el monopolio absoluto de la fuerza. Y al igual que en el apartado anterior, el hecho de que la riqueza del crimen organizado esté en la función de utilidad no implica que el agente tome decisiones sobre dicha variable. De hecho, la riqueza del crimen organizado se incorpora en dicha función para indicar que un incremento de esta variable genera desutilidad. Por otro lado, un stock de capital elevado siempre conduce a una mayor producción, lo cual lleva a un mayor gasto en materia de seguridad y una mayor acumulación de armamento, pero una acumulación sin una reserva sustancial de capital y expansión de la producción es insostenible en el largo plazo.3
Si se supone una función de utilidad u(ct,rt,rt*), y, asimismo, que la riqueza del crimen organizado sigue una tendencia estocástica de forma que:
Donde αr* es la tendencia media de la riqueza del crimen organizado, αr* es la volatilidad de dicha riqueza y dVt son los cambios inesperados. Observe que el cambio marginal de la riqueza puede expresarse en términos de los cambios marginales de capital y del stock de armamento (o recursos para enfrentar al crimen organizado), lo cual se representa mediante:
La ecuación [10] muestra que el incremento marginal en la riqueza (capital y armamento) es igual al incremento marginal del ahorro (producción menos consumo y gasto paramilitar del crimen organizado). Los individuos ahora elegirán su stock de capital, de armamento y su consumo para maximizar su utilidad descontada a una tasa subjetiva.Al igual que en el primer modelo, se supone que la producción sigue un comportamiento estocástico determinado por:
Si se denota, como antes, F(kt)=Akt y a la proporción del stock de armamento del Estado como q=st/(kt+st) o (1−q)=kt/(kt+st), y en virtud de [11] y [10], se sigue que:
así:Una vez que se establece esta restricción, los individuos pueden optimizar su utilidad.
Problema de decisión (modelo 2)El problema de los individuos consiste en maximizar su utilidad, descontada a una tasa subjetiva β, de tal manera que:
Este problema de control óptimo estocástico se resuelve de manera similar al primer modelo, por lo que se obtiene la siguiente ecuación:
Una vez que se aplica el lema de Itô se obtiene:
La expresión anterior se divide entre dt y, posteriormente, se le toma el límite cuando o(dt)/dt→0, lo cual conduce a la expresión que se conoce como la ecuación h-j-b:
Una vez establecida la función de valor bajo la forma Jrt,rt*,t=Vrt,rt*e−βt, entonces:
que nos lleva a:Solución y tasa de crecimiento de la riquezaSe propone como candidato de solución a V(rt,rt*)=Xr1−ε−λrt*λ, y se supone que la función de utilidad es de la forma uct,rt,rt*=ct1−ε/1−εrt/rt*−λ, así 0<ε<1 cuando −1<λ<0, y ε>1 cuando λ>1, lo que garantiza que un incremento en la riqueza del crimen organizado genera desutilidad.
Sean ct,rt,rt* óptimos, en virtud de la ecuación [12], y considerando la función de utilidad, se obtiene la expresión:
Sí se deriva la ecuación [13] respecto al consumo:
Con el fin de obtener la razón consumo-riqueza, la cual es un factor importante que explica el crecimiento, se tiene que:
De esta manera, se obtiene la expresión que se buscaba, expresada de la forma siguiente para hacer notar que el consumo está en función de la riqueza, la elasticidad del consumo y la elasticidad de la razón de la riqueza del Estado y del crimen organizado:Si se deriva la ecuación [13] respecto al stock de armamento (q) se tiene que:
Si se sustituyen ahora los valores correspondientes de F(•) y F′(•)=−Ar en [13] se obtiene que:
Esta última expresión se reescribe como:
Si se divide entre Xr1−ε−λr*λ, puede observarse que:
A partir de la ecuación [16] se obtiene el stock óptimo de armamento y equipo tecnológico en materia de seguridad, el cual es:
Al incorporarse las ecuaciones [14] y [16] en [13], se deduce que:
De la ecuación anterior, se tiene que:
Al sustituir la ecuación [18] en [14] se obtiene la razón consumo-riqueza, misma que explica el crecimiento de la riqueza y, en consecuencia, la tasa de crecimiento de la economía:
Similar al primer modelo, la tasa de crecimiento de la economía se denotará con ω2, el cual está dado por el valor esperado de la tasa de crecimiento de la riqueza:
En este caso, la condición de transversalidad para que la razón consumo-riqueza sea positiva está dada por:
lo que garantiza que ct/rt>0.Resultados teóricos y análisisEl primer resultado está enfocado en determinar la razón de cambio de la tasa de crecimiento de la economía respecto a los cambios en la tendencia media de la riqueza del crimen organizado, esto es:
Así, se tiene que cuando λ<0 y 0<ε<1, entonces ∂ω2/∂αr*<0. Además, si λ>0 y ε>1, entonces ∂ω2/∂αr*>0. En el primer caso se concluye que un aumento de la tendencia media en la riqueza del crimen organizado conlleva a un decrecimiento económico si el país tiene una elasticidad de sustitución intertemporal en el consumo relativamente alta. En el segundo caso, un aumento en la tendencia media de la riqueza del crimen organizado conlleva a un crecimiento económico si el país tiene una elasticidad de sustitución intertemporal de consumo relativamente baja.
Respecto al impacto estocástico de la riqueza del crimen organizado sobre el crecimiento económico del país, éste está dado por:
Por lo que ∂ω2/∂σr*2<0 cuando ε>1 y 0<λ<1. Asimismo, cuando 0<ε<1 y −1<λ<0 ó cuando ε>1 y λ>1, entonces ∂ω2/∂σr*2>0. De esta manera, si la elasticidad de sustitución intertemporal del consumo es relativamente grande, el efecto que tiene un incremento en la volatilidad en la riqueza del crimen organizado (stock de armamento y capital) consistirá en que el país va a reaccionar reduciendo su consumo, invertirá más tanto en materia de seguridad como en armamento, tecnología, recursos humanos y acumulación de capital, lo que lleva a una tasa de crecimiento económica positiva. Por otro lado, con una elasticidad de sustitución intertemporal de consumo relativamente baja, el país tendrá un gasto en consumo y reducirá la inversión tanto en materia de seguridad como en armamento, tecnologías, recursos humanos y acumulación de capital, lo que inducirá a un decrecimiento económico como resultado de un incremento de la volatilidad de la riqueza del crimen organizado.
En el modelo propuesto, un valor de λ>1 puede también llevar a un crecimiento económico incluso con una elasticidad de sustitución intertemporal relativamente baja (ε>1). El impacto estocástico en el rendimiento del producto del país σy2 sobre el crecimiento económico no parece ser claro, pero cuando se supone que σVW=0, su impacto ante un cambio de σy2 afecta al crecimiento económico de la siguiente forma:
Nótese que si 0<ε>1 y −1<λ<−ε, entonces ∂ω2/∂σy2>0. Asimismo, si 0<ε>1 y −ε<λ<0 ó ε>1 y λ>0, entonces ∂ω2/∂σy2<0. El análisis sobre el impacto estocástico en el cambio marginal del producto es similar a lo que se ha mencionado antes, esto es, el crecimiento está en función de la elasticidad de sustitución intertemporal del consumo; una elasticidad de sustitución relativamente grande lleva a un crecimiento, mientras que una pequeña conduce a un decrecimiento económico.
Evidencia empíricaEstablecer una proporción especifica del gasto que destina el gobierno a combatir al narcotráfico y al crimen organizado y la volatilidad del mismo no es una tarea factible. Si bien para el periodo 2006–2011 el gobierno gastó alrededor de 174 millones de pesos exclusivamente en la guerra contra el narcotráfico y el crimen organizado, los gastos de este último son imposibles de estimar, así que un modelo que involucre ambos aspectos, como se mencionó en el apartado teórico, no es factible; no obstante, para analizar algunas de las relaciones funcionales que provienen del modelo teórico, se propone un esquema var que utilice datos existentes, como los presupuestos en materia de seguridad.
A continuación se pretende mostrar si existe alguna relación empírica entre el presupuesto en materia de seguridad y el crecimiento económico, para esto se utilizan cifras trimestrales del pib a precios corrientes de la base de datos del inegi. Para el gasto en seguridad se empleó el presupuesto anual asignado a las dependencias encargadas de la seguridad nacional, con datos obtenidos del Anuario Estadístico 2012 del inegi; sin embargo, para estimar los datos faltantes se realizó una simulación de Monte Carlo con el fin de homologar la frecuencia de las series. Dada la tendencia de la serie en el gasto en seguridad dicha simulación se realiza bajo el supuesto de que el gasto se comporta como:
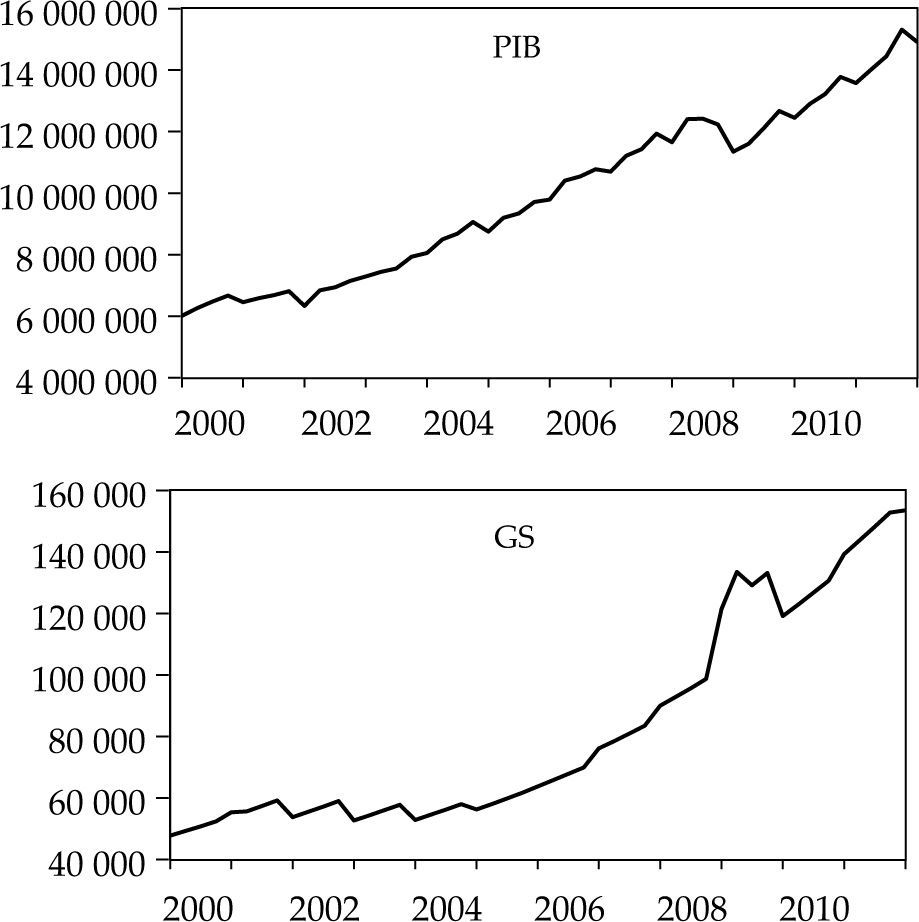
es decir, el gasto en seguridad tiene tendencia exponencial y fluctuaciones normales. Antes de cualquier especificación, se muestran de forma breve, las características básicas en niveles de las series empleadas, donde gs es el gasto en seguridad; las series son trimestrales y se encuentran a precios corrientes para el periodo 2000–2012.Se observa que el comportamiento de las variables de 2000 a 2012 sigue una tendencia creciente, el gasto en seguridad guarda una correlación positiva de forma sustancial con el incremento del producto.
En la gráfica 2, correspondiente al gasto en seguridad, se observa el rápido crecimiento que se tiene en esta materia en el sexenio 2006–2012, lo que muestra la importancia que tuvo en dicha administración. Al respecto, existen diversos análisis empíricos sobre el gasto público (donde se incluye también el gasto en defensa), como Landau (1983), Barro (1990) y Romer (1986), en ellos se establece una relación negativa del gasto en seguridad con el crecimiento económico. La mayoría de los estudios son de sección cruzada, por lo que es relevante observar que sucede con un modelo var. En el modelo sólo se utilizan dos variables, el gasto presupuestario en materia de seguridad y el pib. En lo que sigue se examina qué relación han guardado estas variables de 2000 a 2012 y si ésta es causal.
A continuación se desarrolla un análisis de vectores autorregresivos a fin de caracterizar las interacciones simultáneas de las variables objeto de estudio:
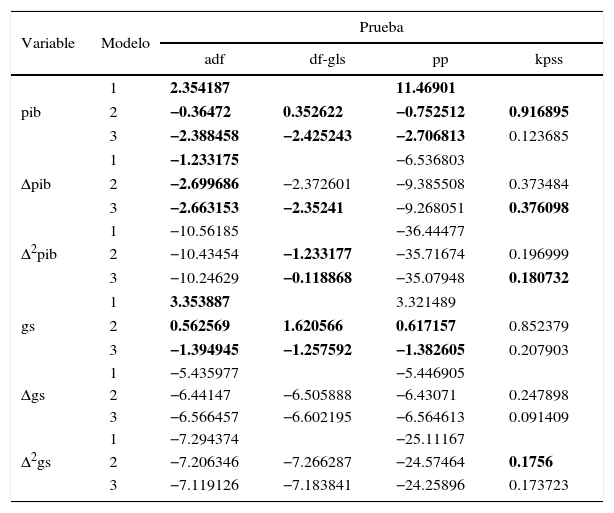
Dado que dicha técnica sólo es útil para series estacionarias, se procede a diferenciar las series de tal forma que no presenten raíz unitaria, esto es, que exista convergencia tanto en media como en varianza, con el fin de ser tratadas con este análisis.Prueba de raíz unitariaEnseguida se muestran las series para elaborar el var y se les realizan distintas pruebas de raíz unitaria con el fin de encontrar su grado de integración.
Prueba de raíces unitarias
| Variable | Modelo | Prueba | |||
|---|---|---|---|---|---|
| adf | df-gls | pp | kpss | ||
| pib | 1 | 2.354187 | 11.46901 | ||
| 2 | −0.36472 | 0.352622 | −0.752512 | 0.916895 | |
| 3 | −2.388458 | −2.425243 | −2.706813 | 0.123685 | |
| Δpib | 1 | −1.233175 | −6.536803 | ||
| 2 | −2.699686 | −2.372601 | −9.385508 | 0.373484 | |
| 3 | −2.663153 | −2.35241 | −9.268051 | 0.376098 | |
| 1 | −10.56185 | −36.44477 | |||
| Δ2pib | 2 | −10.43454 | −1.233177 | −35.71674 | 0.196999 |
| 3 | −10.24629 | −0.118868 | −35.07948 | 0.180732 | |
| 1 | 3.353887 | 3.321489 | |||
| gs | 2 | 0.562569 | 1.620566 | 0.617157 | 0.852379 |
| 3 | −1.394945 | −1.257592 | −1.382605 | 0.207903 | |
| Δgs | 1 | −5.435977 | −5.446905 | ||
| 2 | −6.44147 | −6.505888 | −6.43071 | 0.247898 | |
| 3 | −6.566457 | −6.602195 | −6.564613 | 0.091409 | |
| Δ2gs | 1 | −7.294374 | −25.11167 | ||
| 2 | −7.206346 | −7.266287 | −24.57464 | 0.1756 | |
| 3 | −7.119126 | −7.183841 | −24.25896 | 0.173723 | |
Nota: se aplicaron las pruebas Dickey Fuller Aumentada (adf), Phillips-Perron (pp), Dickey-Fuller con mínimos cuadrados generalizados (df-gls) y Kwatkowsky, Phillps, Schimidt y Shin (kpss) considerando tres modelos diferentes: 1) sin intercepto y sin tendencia, 2) con intercepto y 3) con intercepto y tendencia. Las letras en negritas indican que la prueba de raíz unitaria no es significativa a 95% de confianza.
La estimación correcta del modelo var cumple con ciertas especificaciones, tales como el orden de integración cero de las series, otra característica que presenta es la correcta especificación del término estocástico (error).
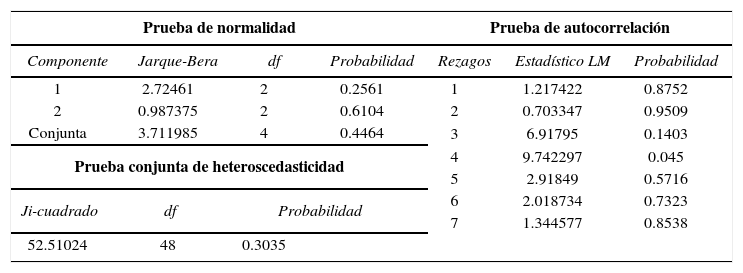
Pruebas sobre el término estocástico
| Prueba de normalidad | Prueba de autocorrelación | |||||
|---|---|---|---|---|---|---|
| Componente | Jarque-Bera | df | Probabilidad | Rezagos | Estadístico LM | Probabilidad |
| 1 | 2.72461 | 2 | 0.2561 | 1 | 1.217422 | 0.8752 |
| 2 | 0.987375 | 2 | 0.6104 | 2 | 0.703347 | 0.9509 |
| Conjunta | 3.711985 | 4 | 0.4464 | 3 | 6.91795 | 0.1403 |
| Prueba conjunta de heteroscedasticidad | 4 | 9.742297 | 0.045 | |||
| 5 | 2.91849 | 0.5716 | ||||
| Ji-cuadrado | df | Probabilidad | 6 | 2.018734 | 0.7323 | |
| 7 | 1.344577 | 0.8538 | ||||
| 52.51024 | 48 | 0.3035 | ||||
El valor de 3.7 del estadístico Jarque-Bera y la probabilidad asociada muestran que el error cumple con la característica de normalidad. En lo referente a la prueba de heteroscedasticidad, dada la probabilidad asociada, no se rechaza la hipótesis nula de homocedasticidad, por lo que la varianza en el término estocástico es constante y, finalmente, dadas las probabilidades asociadas no se puede rechazar la hipótesis nula de no autocorrelación, por lo que el término estocástico no presenta dicha característica.
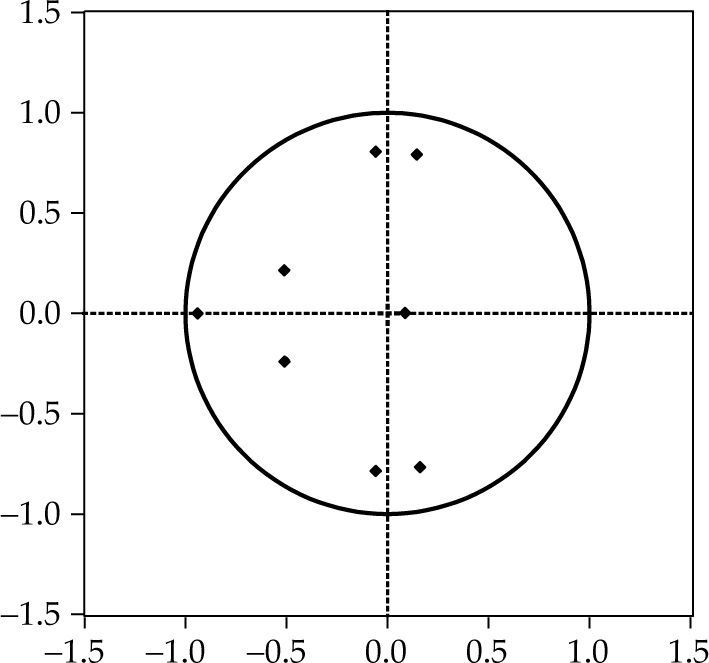
Estabilidad del modeloEn lo que sigue se muestra que el modelo converge y es estable, por lo que el var es invertible.
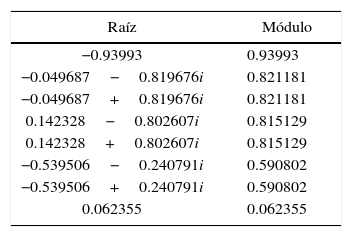
Prueba de estabilidad
| Raíz | Módulo |
|---|---|
| −0.93993 | 0.93993 |
| −0.049687−0.819676i | 0.821181 |
| −0.049687+0.819676i | 0.821181 |
| 0.142328−0.802607i | 0.815129 |
| 0.142328+0.802607i | 0.815129 |
| −0.539506−0.240791i | 0.590802 |
| −0.539506+0.240791i | 0.590802 |
| 0.062355 | 0.062355 |
Nota: ninguna raíz se encuentra fuera del círculo unitario.
var satisface la condición de estabilidad.
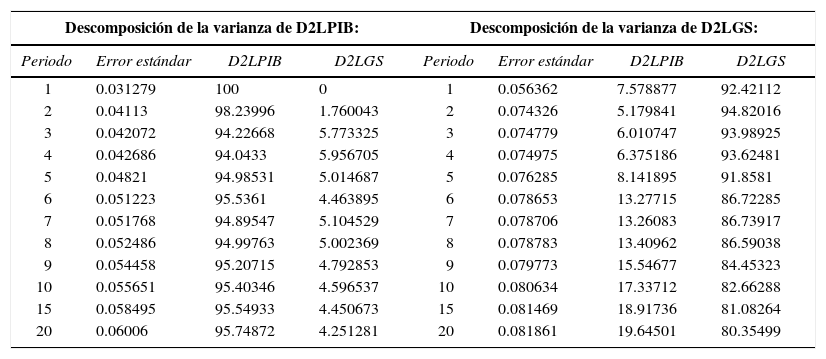
El cuadro siete muestra la descomposición de varianza en el modelo var.
Descomposición de la varianza
| Descomposición de la varianza de D2LPIB: | Descomposición de la varianza de D2LGS: | ||||||
|---|---|---|---|---|---|---|---|
| Periodo | Error estándar | D2LPIB | D2LGS | Periodo | Error estándar | D2LPIB | D2LGS |
| 1 | 0.031279 | 100 | 0 | 1 | 0.056362 | 7.578877 | 92.42112 |
| 2 | 0.04113 | 98.23996 | 1.760043 | 2 | 0.074326 | 5.179841 | 94.82016 |
| 3 | 0.042072 | 94.22668 | 5.773325 | 3 | 0.074779 | 6.010747 | 93.98925 |
| 4 | 0.042686 | 94.0433 | 5.956705 | 4 | 0.074975 | 6.375186 | 93.62481 |
| 5 | 0.04821 | 94.98531 | 5.014687 | 5 | 0.076285 | 8.141895 | 91.8581 |
| 6 | 0.051223 | 95.5361 | 4.463895 | 6 | 0.078653 | 13.27715 | 86.72285 |
| 7 | 0.051768 | 94.89547 | 5.104529 | 7 | 0.078706 | 13.26083 | 86.73917 |
| 8 | 0.052486 | 94.99763 | 5.002369 | 8 | 0.078783 | 13.40962 | 86.59038 |
| 9 | 0.054458 | 95.20715 | 4.792853 | 9 | 0.079773 | 15.54677 | 84.45323 |
| 10 | 0.055651 | 95.40346 | 4.596537 | 10 | 0.080634 | 17.33712 | 82.66288 |
| 15 | 0.058495 | 95.54933 | 4.450673 | 15 | 0.081469 | 18.91736 | 81.08264 |
| 20 | 0.06006 | 95.74872 | 4.251281 | 20 | 0.081861 | 19.64501 | 80.35499 |
El cuadro anterior evidencia la variación porcentual del pib ante un cambio porcentual en el gasto en seguridad. En el primer semestre no hay cambio alguno, sin embargo, del segundo trimestre en adelante se observa un efecto positivo del pib ante un incremento del gasto en seguridad. En lo referente a éste último, se observa un efecto inmediato y creciente que experimenta el mismo ante las variaciones porcentuales del pib. Con base en este cuadro podría concluirse que el gasto en seguridad ha tenido un efecto positivo en el crecimiento del producto, no obstante, la prueba de causalidad en el sentido de Granger indica que estas variables no son causales.
Representación del varEl modelo que se elaboró con el programa EViews6 tiene la siguiente estructura:
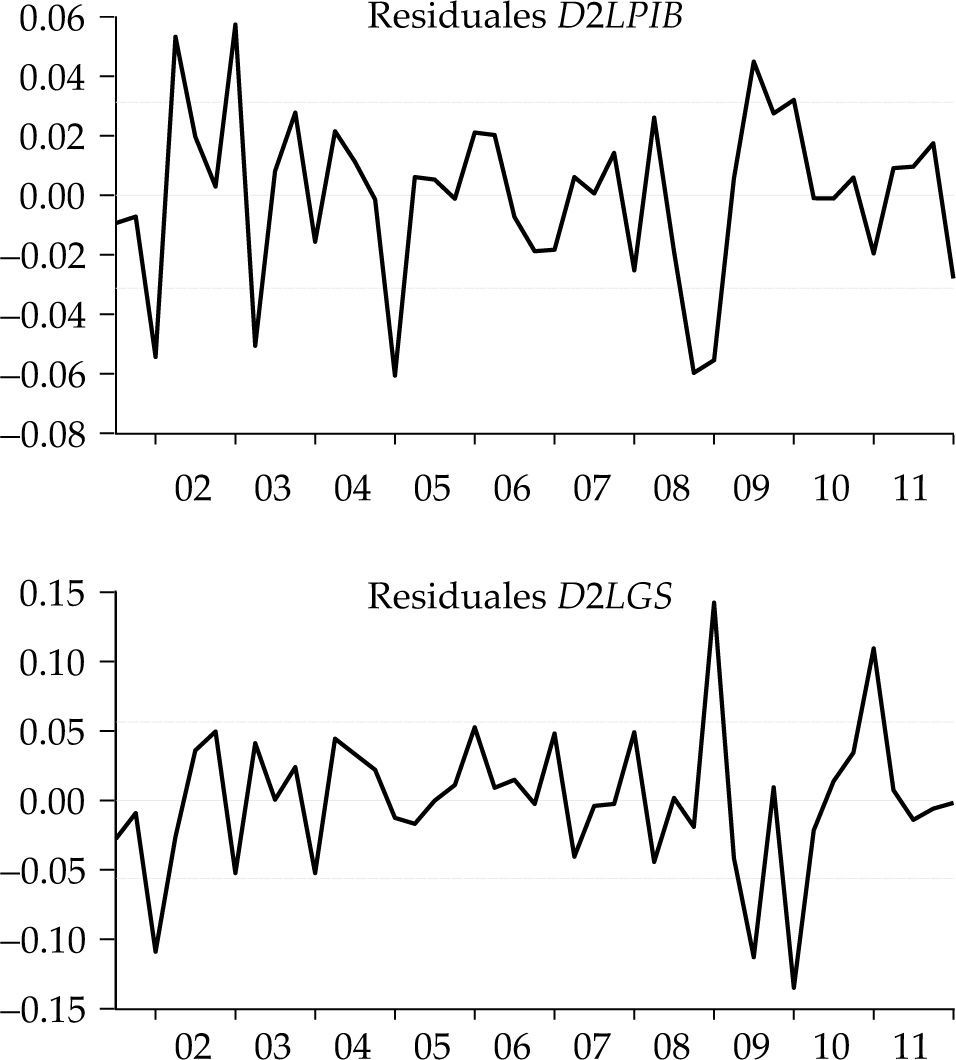
Si bien no hay causalidad en el sentido de Granger en las series estacionarias con las que se elaboró el var, si existe una fuerte relación cuando las series están en niveles, ya que el gasto en seguridad está explicado por el pib hasta por ocho rezagos; por otro lado, cuando las series son estacionarias, se observa que una caída del producto durante 2008–2009 conduce a un incremento significativo en el gasto en seguridad (véase la gráfica 4).
ConclusionesEl trabajo examinó el efecto del gasto en materia de seguridad en el crecimiento del producto mediante un modelo de crecimiento endógeno estocástico con agentes maximizadores de utilidad. Asimismo, se analizó la acumulación de armamento (donde se incluyen todos los recursos tecnológicos para el combate al crimen organizado). El análisis muestra que un alto (bajo) crecimiento en el gasto del crimen organizado en su guerra contra el Estado lleva a una reacción de este último a incrementar (reducir) también su gasto en materia de seguridad, lo cual conlleva a un crecimiento (no crecimiento) de la economía en función de la elasticidad de sustitución intertemporal de consumo del país. El modelo también permite analizar la influencia de la volatilidad en el gasto del crimen organizado, lo que puede llevar a un crecimiento económico cuando la elasticidad de sustitución intertemporal del país es relativamente grande, esto se debe a la inminente reacción del gobierno; además de que el impacto estocástico sobre el rendimiento del producto puede estimular el crecimiento económico. En conclusión, la relación teórica obtenida entre gasto en materia de seguridad y el crecimiento del producto puede guardar una relación tanto negativa como positiva. Por último, a partir del análisis empírico, se destaca que una caída del producto durante 2008–2009 conduce a un incremento significativo en el gasto en seguridad, esto aunado a la idea de que un poco crecimiento provoca mayores niveles de criminalidad y, en consecuencia, un incremento en el gasto en seguridad. Cabe destacar que si bien el gasto en seguridad y crecimiento están positivamente correlacionados, y aunque parece que el crecimiento del producto se pudiera explicar en parte por el primero, la prueba de causalidad de Granger lleva a concluir que no existe ninguna relación causal entre gasto en presupuesto para seguridad y el crecimiento del pib.
Con un gasto en seguridad de 308 mil millones de pesos durante el sexenio 2006–2012, con base en la gráfica 1 se observa que a medida que ha crecido el presupuesto para la guerra se ha incrementado la violencia. En 2011 el inegi publicó su Encuesta Nacional de Victimización y Percepción sobre Seguridad Pública (Envipe) como parte de los trabajos del Subsistema Nacional de Información de Gobierno, Seguridad Pública ε Impartición de Justicia (snigspij), en dicho estudio se consigna que de 2005 a 2011 aumentó la percepción de inseguridad que tienen los mexicanos. En 2005 resultó que 54.2% de los ciudadanos percibió una situación de inseguridad en su entidad federativa. El hecho es que la situación empeoró en 2011, cuando 69.5% de la población considero que vive en condiciones de inseguridad, causa que pone en materia de discusión cuál o cuáles deben ser las prioridades del Estado mexicano.
Los autores agradecen los valiosos comentarios de dos dictaminadores anónimos de la revista.
Por simplicidad se supondrá que la economía es cerrada.
Para una sencilla y rápida compresión sobre dicha metodología véase Venegas-Martínez (2008).
La consideración de la riqueza de un individuo en la función de utilidad ha sido adoptado por varios autores en distintas aplicaciones tal como Gong y Zou (2003).