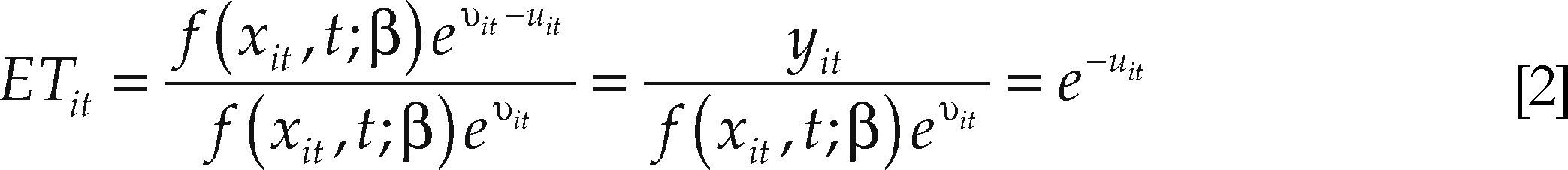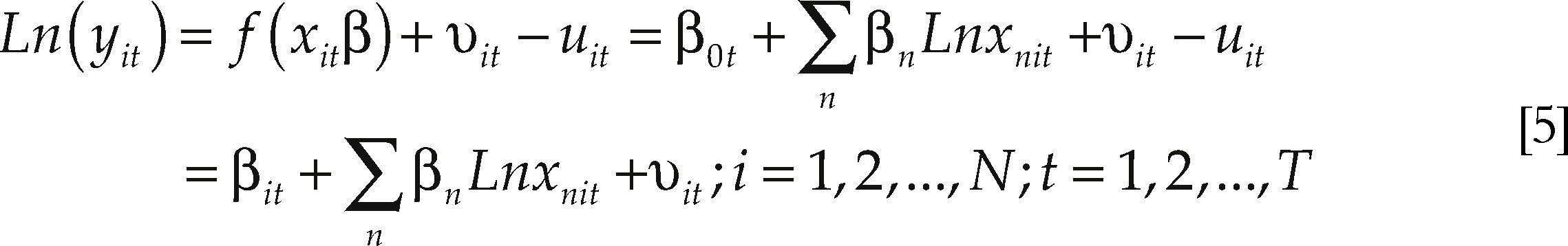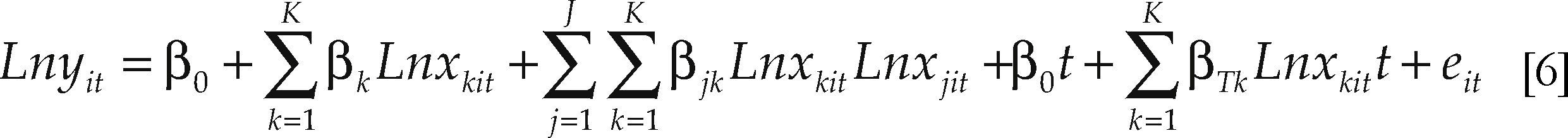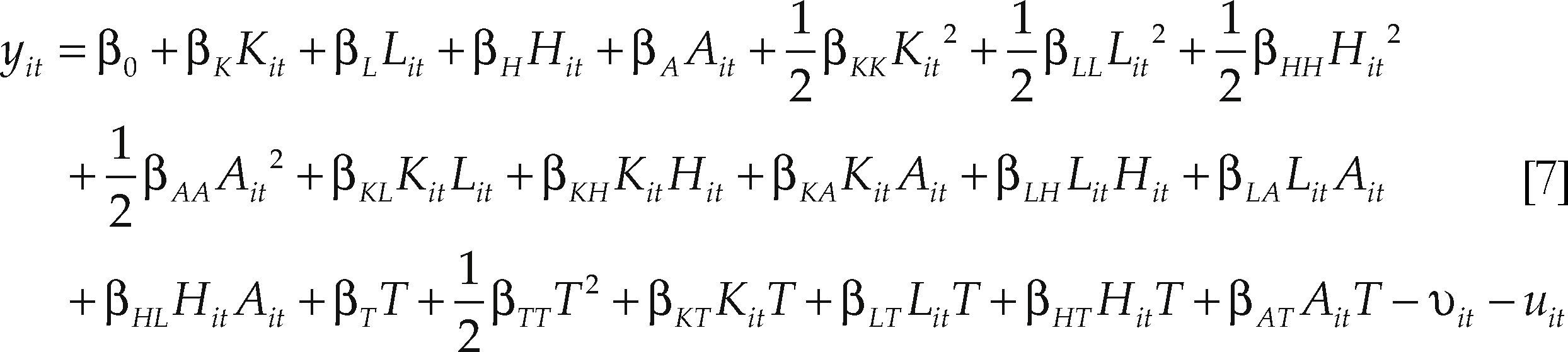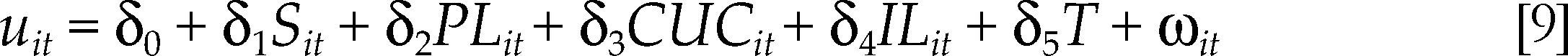El documento estima un modelo de frontera de producción estocástica y un modelo de ineficiencia técnica para 25 industrias manufactureras mexicanas en el periodo 1985-2009. Se determina la relevancia de los insumos en el valor agregado, las variables de ineficiencia, los niveles de eficiencia en cada industria, los grupos de industrias eficientes y los perfiles de las industrias. Los resultados muestran que el capital humano, el personal no calificado y el capital son generadores de eficiencia, mientras que la productividad laboral y el poder de mercado tienden a reducir la ineficiencia técnica. Entre las medidas de política para alcanzar la “mejor práctica” están la provisión adecuada de insumos, el acceso a mercados nacional e internacionales, las facilidades crediticias y los programas de capacitación de personal.
The document estimates simultaneously a model of stochastic production frontier and a model of technical inefficiency for 25 Mexican manufacturing industries from 1985 to 2009. It was determined the relevance of inputs in the aggregated value, the variables of inefficiency, the levels of efficiency en each industry, groups of efficient industries, and the profiles of the industries. The results show that human capital, unqualified personnel and capital boost efficiency, while labor productivity and market power tend to reduce technical inefficiency. Among policy measure aimed to achieve the “best practice” are adequate input provision, access to domestic and international markets, credit facilities and employees training programs.
El crecimiento de la productividad refleja un uso más eficiente de los recursos de una empresa; sin embargo, sólo proporciona una visión parcial de este desempeño. En la literatura existen otras perspectivas que permiten medir el desempeño de las industrias, entre éstas están aquellas que estiman funciones de producción para medir la productividad. La idea detrás es que los productores operan sobre la frontera de posibilidades de producción, es decir, que son técnicamente eficientes. Un enfoque alternativo es el análisis de fronteras de producción estocásticas, que estima funciones de producción aceptando que no necesariamente todas las industrias son técnicamente eficientes. Este documento sigue el enfoque de fronteras de producción estocásticas para medir la eficiencia técnica en las industrias manufactureras mexicanas en el periodo 1985-2009.
Dado el papel central de la eficiencia en aspectos como el crecimiento de la productividad total de los factores o el crecimiento económico, existen numerosos trabajos que estudian los niveles, evolución y determinantes de la eficiencia técnica. Los estudios tienden a realizarse a nivel sectorial, industrial, empresas o planta. Las metodologías empleadas son diversas pero sobresalen los documentos que emplean modelos de fronteras de producción estocásticas. Tanto los resultados como las variables explicativas de la ineficiencia son diversos.
Así, por ejemplo, Kim (2003) estima funciones de producción de frontera estocásticas mediante un panel no balanceado de empresas en seis sectores manufactureros de Corea. Determina que el tamaño de la empresa, las exportaciones y las actividades de investigación y desarrollo tienen efecto positivo y significativo en todos los sectores, mientras que el capital extranjero parece no afectar los niveles de eficiencia.
Batra y Tan (2003) estudian el vínculo entre habilidades, tecnología y productividad en pequeñas empresas manufactureras, así como las diferencias entre ellas. Emplean datos a nivel firma para seis países en desarrollo, entre ellos México, para estimar niveles de eficiencia a partir de una función de producción. Hallan que la eficiencia técnica aumenta con el tamaño de la empresa y que, en general, las pequeñas empresas operan con menores niveles de eficiencia que las grandes empresas. Asimismo, identifican un conjunto de factores que distinguen a las firmas más eficientes, a decir, educación y capacitación, inversión en nuevas tecnologías, automatización y control de calidad, por lo que sugieren la necesidad de una política orientada a mejorar la eficiencia de las pequeñas empresas.
Margono y Sharma (2006) estudian la descomposición del crecimiento de la productividad total de los factores, estimando la eficiencia técnica en cuatro industrias, para el periodo 1993-2000, en Indonesia a través de un modelo de frontera estocástica. Encuentran una eficiencia promedio de 59%. Señalan que el tipo de propiedad contribuye a la ineficiencia en el sector textil, mientras que el tamaño, la propiedad y el tiempo de operar generan ineficiencia en los sectores químico y productos de metales.
Díaz y Sánchez (2008) analizan el desempeño de las pequeñas y medianas empresas manufactureras para 1995-2001, centrándose en el grado de ineficiencia técnica y sus determinantes. Emplean un conjunto de datos de panel para estimar simultáneamente una función de producción de frontera estocástica y los determinantes de la ineficiencia mediante un panel no balanceado. Determinan que las pequeñas y medianas empresas tienden a ser menos ineficientes que las grandes empresas debido a los diversos factores organizacionales. Fu y Gong (2009) estudian los efectos spillovers tecnológicos derivados de la inversión extranjera directa como fuente de eficiencia técnica en China a nivel industrial durante 2001-2005; afirman que el stock de investigación y desarrollo está vinculado con los niveles de eficiencia.
Para el caso de México, son relativamente pocos los estudios de eficiencia en la industria manufacturera. No obstante, existen trabajos que estiman la productividad total de los factores que, al descomponerla en sus componentes, calculan la eficiencia técnica. Así, Grether (1999) mide la eficiencia para un conjunto de empresas manufactureras para 1984-1990. Encuentra que el capital extranjero tiene influencia positiva en la eficiencia a nivel planta; sin embargo, no genera efectos spillovers a nivel sectorial.
Bannister y Stolp (1995) exploran los vínculos entre localización industrial, concentración y eficiencia en la manufactura mexicana por Estado. Encuentran que a nivel agregado existe una relación positiva entre concentración y eficiencia en la producción. También señalan que la eficiencia total está relacionada con la eficiencia de escala. En particular, afirman que factores como escala, urbanización y economías de aglomeración están positivamente relacionados con la eficiencia técnica a nivel regional, mientras que determinan una relación negativa con la propiedad extranjera.
Brown y Domínguez (2004) encuentran que existe un comportamiento inestable de las industrias. Sólo cuatro industrias tienen cambios positivos en la eficiencia entre 1984 y 1993. Señalan que el incremento en el índice de eficiencia es muy bajo, tanto en promedio como por el número de industrias por debajo de la frontera de producción derivado de las políticas ineficientes orientadas a disminuir el rezago tecnológico de las empresas. Por el contrario, Chávez y Fonseca (2012) determinan un aumento en la eficiencia técnica manufacturera a nivel estatal para 1988-2008.
Así, el objetivo de este trabajo es determinar los niveles de eficiencia técnica en las industrias manufactureras mexicanas analizando los factores que la determinan, lo que permite clasificarlas en función de las características que explican los diferentes niveles de eficiencia alcanzados. Se emplea información para 23 industrias de acuerdo a la Clasificación Internacional Industrial Uniforme Revisión 3. Naciones Unidas (CIIU Rev. 3) con dos dígitos para examinar los insumos dentro de la función de producción. Posteriormente, se calcula el nivel de eficiencia técnica, la cual puede originarse por diversas razones que comprenden malos procesos de gestión (toma de decisiones), cuellos de botella tanto en las líneas de producción como en la proveeduría de insumos, uso ineficaz de tecnologías, etcétera. Al mismo tiempo, se determinan las causas de las diferencias entre producto actual y potencial en cada industria. Se parte de dos ideas principales respecto a los determinantes de la eficiencia técnica media, que se prueban empíricamente. La primera es que la acumulación de capital tangible como intangible (capital humano y tecnológico) llevan a una eficiencia técnica mayor. La segunda es que el nivel medio de esta eficiencia es mayor en las industrias más competitivas, puesto que las firmas con prácticas ineficientes (uso subóptimo de insumos) se ven forzadas a mejorar su desempeño o salir del mercado.
Este estudio contribuye a la literatura de los determinantes de la eficiencia técnica para el caso mexicano, pues los resultados permiten, además de analizar los niveles de eficiencia técnica actuales, clasificar a las industrias en tres grupos en función de sus niveles de eficiencia y, en consecuencia, determinar un perfil de las industrias basado en los rankigs de eficiencia y en otras características de las mismas.
El resto del documento se organiza como sigue. En la sección dos se resumen los elementos teóricos para modelar la ineficiencia técnica a través del análisis de fronteras de producción estocástica. En la tercera se aplica esta metodología al sector manufacturero mexicano y se describen las variables relevantes usadas en las estimaciones. La sección cuatro presenta los principales resultados. Las conclusiones se muestran en el apartado cinco.
Eficiencia técnica: elementos teóricosEl desempeño de una industria se evalúa a través del concepto de eficiencia técnica que, en términos generales, se refiere a la capacidad de una firma para producir el máximo producto para un conjunto dado de insumos (Farrell, 1957).1 Una metodología comúnmente utilizada para medirla es la de frontera estocástica (Aigner et al., 1977). Esta técnica asume que, para una combinación de insumos, la máxima producción alcanzable por una industria está delimitada por una función paramétrica de insumos conocidos con parámetros desconocidos y una medida de error. Entre menor sea la distancia del producto actual a la frontera estocástica o de “mejor práctica”, mayor será la eficiencia técnica de la industria. Una frontera estocástica de la función de producción puede expresarse como:2
donde yit es la producción de la i-ésima industria i = 1,2,…,N en el periodo t = 1,2,…,T; f(xit,t;β) representa la tecnología (frontera) de producción; xit es un vector (1×K) de insumos y otros factores que influyen en la producción asociado con la industria i-ésima en el periodo t; β es un vector (K×1) de parámetros desconocidos a estimar que indican la importancia relativa de cada uno de los insumos de producción; t es un indicador de tendencia temporal proxy del cambio tecnológico.
La idea básica de la frontera estocástica es introducir un componente no negativo en el término de error de la función de producción para considerar la posibilidad de la ineficiencia técnica. El término de error en el modelo se divide en dos partes: el componente aleatorio tradicional (νit) y un nuevo componente de ineficiencia (uit), independientes de los regresores. La primera parte, νit, es un vector de errores aleatorios que se asumen iid, N(0,σν2), e independientemente distribuidos de uit, Los νit capturan la variación aleatoria de la producción debido a factores fuera del control de las industrias (cambios en la demanda, huelgas o eventos fortuitos). La segunda parte, uit, es un vector de variables aleatorias independientemente distribuidas y no negativas (uit ≥ 0), representa la ineficiencia técnica en el producto específico a la industria. En particular, uit es el producto combinado de factores no relacionados con el precio y organizacionales que limitan alcanzar la máxima producción posible para los insumos y tecnología existente.
Así, cuando una industria alcanza la eficiencia técnica total (ET = 1), uit toma el valor de 0; cuando la industria enfrente problemas en este sentido (0 < ET < 1), uit toma un valor mayor a cero. La magnitud de los uit determina la brecha de eficiencia, es decir, que tan lejos está una industria de su producción potencial. De este modo, la i-ésima industria enfrenta una frontera de producción estocástica con una parte determinística común a todas las industrias, f(xit,t;β), y una especifica a la industria, eνit–uit.
La eficiencia técnica del i-ésimo productor en el t-ésimo tiempo se expresa como la razón del producto actual al máximo producto potencial:
La especificación de la frontera estocástica [1] permite que la ineficiencia técnica de una industria cambie en el tiempo, midiendo las tendencias en el cambio de productividad. Un aspecto adicional es la identificación de las fuentes de ineficiencia técnica a nivel industrial. Existen en general dos modelos para analizar las diferencias de eficiencia, que varían según la especificación del término de efectos de ineficiencia uit.3
En este documento se sigue el modelo libre de sesgo de Battese y Coelli (1995) para la estimación simultánea de la frontera de producción estocástica y el modelo de efectos de ineficiencia. Este enfoque estima los parámetros que influyen en el nivel de eficiencia técnica al mismo tiempo que los cambios de la eficiencia técnica y técnicos. Incorpora influencias exógenas para explicar variaciones en el desempeño del productor. En consecuencia, los efectos de eficiencia técnica se definen al modelar la media de uit como una función de características específicas a la industria. Se asume que las uit, con media δzit y varianza σu2, son afectadas por la eficiencia técnica. El modelo de ineficiencia se especifica uit = g(zit,δ), donde g(•) es una forma funcional que en general se asume lineal:
zit es un vector (L×1) de variables explicativas relacionadas con la ineficiencia técnica específicas a la i-ésima industria que puede cambiar con el tiempo; δ es un vector (1×L) de parámetros desconocidos a estimar; ηit es un término de error que se distribuye normal, N(0,σω2), truncado en –δzit. En otras palabras, son variables aleatorias no observables, idénticamente distribuidas, obtenidas de la truncación de la distribución normal con media cero y varianza desconocida, σ2, con medias, δzit, i = 1,2,…,N y t = 1,2,…,T. Así, las medias serán diferentes para cada industria y periodos de tiempo pero las varianzas se asumen iguales. De acuerdo con Kumbhakar, Ghosh y McGuckin (1991) las variables específicas a las industrias pueden tener efectos en la eficiencia y, por ende, deben incorporarse directamente en la estimación de la frontera de producción.
De este modo, las ecuaciones [1], de la frontera estocástica, y [3], de ineficiencia técnica, se estiman simultáneamente usando el método de máxima verosimilitud, obteniéndose el nivel de eficiencia técnica (ETit) de la forma:4
Los modelos de frontera estocástica tienden a estimarse con la metodología de datos de panel y a considerar que la eficiencia técnica varía con el tiempo (Fried, Lovell y Schmidt, 1993). De esta manera, se plantea el siguiente modelo de panel:
donde yit representa el producto de la i-ésima industria en el periodo t; xit denota un vector con los valores correspondientes a los insumos y otras variables relevantes; β es un vector de parámetros a estimar. β0t se interpreta como el intercepto de la frontera de producción común a todos los productores en el periodo t y βit = β0t– uit es el intercepto para el productor i en el periodo t. El término νit es el componente de ruido y uit es el componente (no negativo) de ineficiencia técnica variante en el tiempo. νit tiene las mismas propiedades de [1]. Al estimar la ecuación [5] se obtienen los parámetros β de la función de producción y los valores de eficiencia técnica de la industria i en el periodo t.
Especificación del modeloDe acuerdo con Delgado y Álvarez (2003) en el enfoque de la frontera estocástica el análisis de la eficiencia parte de la estimación de la frontera de producción como función de diversos insumos, conjuntamente con la estimación de la ineficiencia técnica asociada. Al respecto, la literatura emplea tres formas funcionales de la función de producción: Cobb-Douglas (C-D), translog y CES (elasticidad de sustitución constante). La forma funcional flexible más utilizada es la translog. Si bien esta especificación requiere de la estimación de más parámetros que la función C-D, no impone las restricciones de ésta y, por tanto, generalmente se prefiere, a menos que una prueba de hipótesis determine lo contrario o que la disponibilidad de datos impida utilizar una función tipo translog (Coelli et al., 2003).
En este sentido, la función translog es una generalización de la C-D, al considerar términos cruzados y cuadrados como elementos. El hecho de que las derivadas parciales no sean constantes hace a la función translog más flexible y preferible que la C-D (Shao y Lin, 2001). Adicionalmente, una ventaja de la función translog es que se ajusta a cualquier tipo de tecnología productiva sin imponer restricciones a priori sobre los rendimientos a escala; también estima las interacciones entre insumos y, al mismo tiempo, las elasticidades se expresan en función de las propias variables, por lo que éstas varían en función del nivel de uso de los factores productivos. En contraste a la función C-D, la translog permite relaciones de complementariedad y de sustituibilidad entre los factores.5
Por ende, dado que la especificación C-D es un caso particular del modelo translog, se parte de la especificación de la segunda. En cualquier caso, se emplean pruebas de razón de máxima verosimilitud para confirmar la forma funcional. Siguiendo a Karagiannis y Tzouvelekas (2001), la expresión [1] o [5] se especifica como una función translog:6
donde k, j = 1,…,K; 1,…,J indican los insumos convencionales usados en el proceso de producción. Con eit = νit–uit, νit es el error aleatorio y uit el término de ineficiencia; y uit representa la producción que se aproxima por el valor agregado para la industria i = 1,2,…,23 y el tiempo t = 1,2,…,25, en millones de pesos de 2003; xit es un vector (1×21) que contiene un término constante; cuatro insumos, capital (K), trabajo (L), capital humano (H) y un elemento de tecnología (A); una variable de tendencial temporal (t) y 15 términos de interacción entre los insumos.
Se emplea el stock de la formación bruta de capital (SFB) como proxy del insumo K, en millones de pesos de 2003 que se construye con el método convencional del inventario permanente,7L es el personal empleado en las manufacturas en millones de personas (PE); el capital humano, H, se aproxima por el trabajo altamente calificado, en millones de personas, que representa las personas con educación de licenciatura más las de posgrado; A es la tecnología que entra en el modelo como el stock del gasto en investigación y desarrollo (I+D) en el sector manufacturero como proporción del producto en esa industria (SID), estimado de igual forma que el stock de capital físico.8
Las variables en el modelo de frontera de producción estocástica se expresan en desviaciones respecto a sus medias muestrales.9 Esto sólo es un cambio en las unidades de medida y no modifica los datos en sí mismos; sin embargo, tiene la ventaja que los parámetros de primer orden estimados se interpretan como elasticidades de producción de los inputs, evaluadas en las medias muestrales (Coelli et al., 2003). Por lo tanto, el modelo tiene J = 4, N = 23 y T = 25, y la forma de la función de producción translog es:
Por otro lado, la ineficiencia técnica se especifica como una función lineal:
donde se supone la influencia de dos factores en el nivel de ineficiencia uit, siendo uno de ellos un término independiente (ηit). Los componentes incluidos en el vector zit se asocian con cuatro variables: capital físico (K), capital humano (H), tecnología (A) y tiempo (T). Como proxy del capital físico se calcula el costo del uso del capital (CUC) en millones de pesos de 2000, puesto que en la medida que el capital sea más caro la producción tiende a desincentivarse.10 El capital humano entra en el modelo como la productividad laboral (PL), pues cabe esperar una relación positiva entre mano de obra con alta calificación y los niveles de productividad, de tal manera que una mayor eficiencia del trabajo pueda acercar a la producción a su nivel potencial. La PL se mide como el producto interno bruto (pib) por horas trabajadas a precios constantes con año base 2003. La tecnología se aproxima mediante los efectos spillover (S) que se miden como la participación de la inversión extranjera directa en las ventas nacionales en la i-ésima industria, ya que teóricamente uno de los beneficios derivados de la existencia de empresas extranjeras es el desbordamiento tecnológico en la economía interna. Por último, se incluye una variable de estructura de mercado (ILi) para controlar las diferencias no observadas entre las industrias, derivadas de estructuras de mercado no competitivas que pueden llevar a ciertas firmas dentro de la i-ésima industria a alejarse del potencial de producción y, en el extremo, salir del mercado.11 De esta manera, el modelo de ineficiencia está dado por:
Cabe esperar que el CUC tenga un efecto positivo en los niveles de ineficiencia técnica. Asimismo, la estructura de mercado y la competencia pueden tener un efecto considerable en dicho nivel. Así, si en un determinado mercado existe competencia intensa, entonces las empresas con niveles de producción actuales por debajo de su capacidad de producción eventualmente pueden salir del mercado (Mayes, Harris y Lansbury, 1994). Dado que las firmas menos eficientes salen del mercado, la eficiencia técnica promedio en esa industria aumenta. En este sentido, se espera una relación positiva entre eficiencia técnica y competencia intensa (mayor concentración).
Alternativamente, a partir de una estructura de mercado de competencia perfecta con un elevado número de pequeños oferentes y un determinado nivel de competencia, un incremento en el poder de mercado puede llevar a una intensificación de la competencia y, en consecuencia, de la eficiencia promedio. Sin embargo, esto puede ocurrir hasta alcanzar cierto nivel de concentración de mercado, a partir del cual una mayor concentración lleva a la reducción de la competencia y genera ineficiencias, pues las pocas empresas que permanecen en el mercado tienen incentivos a disminuir su nivel de producción, creándose así una brecha entre el producto potencial y el efectivo. Por ende, la relación entre estructura de mercado y el nivel promedio de eficiencia técnica en una industria puede tener una forma de U-invertida (Caves y Barton, 1990).
De esta manera, resulta difícil especificar a priori el grado en que el poder de mercado afecta el nivel de eficiencia técnica. En la literatura no existe un consenso respecto al signo en esta relación, esto es, queda indeterminado. Por el contrario, se espera un signo negativo del parámetro CUC, mientras que los efectos spillover tecnológicos y la productividad laboral a nivel industrial pueden incentivar los niveles de eficiencia, por lo que los signos esperados de S y PL son positivos.
Las series se obtuvieron de diferentes fuentes como las bases de datos de la Organización para la Cooperación y Desarrollo Económicos (ocde), del Banco de Información Económica del Instituto Nacional de Estadística y Geografía (inegi) y del Banco de México. Las industrias que se agrupan de acuerdo a la ciiu Rev. 3 a dos dígitos se presentan en el Cuadro 1. Para obtener los precios constantes se emplea el índice de precios implícito en cada industria y, en su caso, el tipo de cambio real para 2003.
Industrias manufactureras, clasificación ciiu Rev. 3
| Código | Industria | Nombre corto |
|---|---|---|
| 15 | Elaboración de productos alimenticios y bebidas | Alimentos y bebidas |
| 16 | Elaboración de productos de tabaco | Tabaco |
| 17 | Fabricación de productos textiles | Textiles |
| 18 | Fabricación de prendas de vestir; adobo y teñido de pieles | Prendas de vestir |
| 19 | Curtido y adobo de cueros; fabricación de maletas,bolsos, talabartería y calzado | Pieles y calzado |
| 20 | Producción de madera y fabricación de productos de madera y corcho, excepto muebles | Madera y productos |
| 21 | Fabricación de papel y de productos de papel | Papel y productos |
| 22 | Actividades de edición e impresión y de reproducción de grabaciones | Edición, impresión y grabaciones |
| 23 | Fabricación de coque, productos de la refinación del petróleo y combustible nuclear | Productos derivados del petróleo |
| 24 | Fabricación de sustancias y productos químicos | Sustancias y productos químicos |
| 25 | Fabricación de productos de caucho y plástico | Caucho y plástico |
| 26 | Fabricación de otros productos minerales no metálicos | Otros productos minerales no metálicos |
| 27 | Fabricación de metales comunes | Metales |
| 28 | Fabricación de productos elaborados de metal, excepto maquinaria y equipo | Productos de metal |
| 29 | Fabricación de maquinaria y equipo n.c.p. | Maquinaria y equipo |
| 30 | Fabricación de maquinaria de oficina, contabilidad e informática | Maquinaria de oficina y cómputo |
| 31 | Fabricación de maquinaria y aparatos eléctricos n.c.p. | Maquinaria y aparatos eléctricos |
| 32 | Fabricación de equipo y aparatos de radio, televisión y comunicaciones | Aparatos de radio, televisión y comunicaciones |
| 33 | Fabricación de instrumentos médicos, ópticos y de precisión y fabricación de relojes | Instrumentos médicos y de precisión y relojes |
| 34 | Fabricación de vehículos automotores, remolques y semirremolques | Vehículos automotores |
| 35 | Fabricación de otros tipos de equipo de transporte | Otros equipos de transporte |
| 36 | Fabricación de muebles; industrias manufactureras n.c.p. | Muebles |
| 37 | Reciclamiento | Reciclamiento |
Nota: n.c.p. = no clasificados en otra parte.
Fuente: elaboración propia con base en la División de Estadísticas de la Organización de las Naciones Unidas (onu).
El conjunto de datos obtenidos representa un modelo de datos de panel no balanceado para 1985-2009 con datos anuales y 5 175 observaciones. Las estimaciones de máxima verosimilitud se obtienen mediante el programa Frontier 4.1, que permite una estimación del modelo de frontera estocástica de un sólo paso, al tiempo que estima los parámetros de las variables incluidas en la explicación de la ineficiencia.
Por otro lado, se realizan distintas pruebas de especificación sobre las estimaciones de la función de producción estocástica y del modelo de ineficiencia para señalar ciertas características de las industrias manufactureras y determinar cuál es el mejor modelo. Estas pruebas pueden realizarse usando la prueba estadística de máxima verosimilitud generalizada (LR), que requiere que el modelo sea estimado bajo la especificación de la hipótesis nula y la especificación de la hipótesis alternativa. La prueba LR se define por:
donde L(H0) y L(H1) son los valores logarítmicos de la función de verosimilitud bajo las hipótesis nula y alternativa, H0 y H1, respectivamente. Si H0 es verdadera, se asume comúnmente que la prueba LR tiene una distribución chi-cuadrada con grados de libertad igual al número de restricciones establecidas en la hipótesis nula. No obstante, si H0: γ = 0 no es cierta, el estadístico LR tiene una distribución asintótica que es una combinación lineal de distribuciones χ2 (Coelli, 1995). Se contrastan cuatro hipótesis: 1) no efectos de ineficiencia técnica, 2) cambio técnico cero, 3) presencia de progreso técnico neutral y 4) forma funcional de la función de producción.
Dado que es posible que no exista ineficiencia técnica o que las variables que supuestamente originan tal ineficiencia no sean significativas, se debe evaluar en la hipótesis nula que dichas variables sean todas iguales a cero. En caso de no rechazar la hipótesis que los parámetros de esas variables sean cero, el modelo se reduce a uno con término de error con distribución normal truncada. Por el contrario, si no se rechaza la hipótesis de que todos los parámetros, aleatorios y determinísticos, del término de error relacionado con la eficiencia sean iguales a cero, indica que este término es redundante en la modelización (Kumbhakar y Lovell, 2000). En ese caso se podría estimar la función promedio tradicional para cada industria, lo que implica que todas las industrias son eficientes.
Formalmente, esta hipótesis se plantea como H0: ausencia de efectos de ineficiencia técnica, por lo tanto el valor de γ es cero, y los coeficientes de la frontera de producción pueden estimarse usando el modelo clásico de mínimos cuadrados ordinarios (MCO), H0: γ= δ0 = δ1 = … = δM = 0, y H1: el valor de γ≠ 0, esto implica la existencia de efectos de ineficiencia, por lo cual la estimación máximo-verosímil propuesta es adecuada, H0: γ > 0.12
Además, puesto que la muestra temporal es relativamente amplia, cabe esperar que exista cambio técnico en las industrias, lo que se prueba mediante la hipótesis nula que supone la no existencia de cambio técnico. En términos formales, H0: βt = βtt = βkt = 0, ∀k, que implica que los parámetros de interacción entre los insumos y el tiempo son cero, y H1: βt ≠ βtt ≠ βkt ≠ 0, ∀k, es decir, que al menos uno de los insumos provoca un cambio técnico con el paso del tiempo. Asimismo, como se pueden tener parámetros asociados a los insumos que sean significativos, pero que no lo sean cuando se considera la tendencia temporal, puede pensarse que existe cambio técnico neutral a la Hicks,13 para ello se prueba que los parámetros de interacción de la tendencia temporal con los insumos sean todos iguales a cero, es decir: H0: βkt = 0, ∀k, frente a H1: βkt ≠ 0, ∀k.14
En la cuarta hipótesis se prueba la validez de la función translog frente a la función C-D. La hipótesis nula señala que la tecnología es Cobb-Douglas, ya que los parámetros de segundo orden son todos cero (H0: βjl = 0, ∀j,l), mientras que la alternativa dice que la tecnología es del tipo translog, pues no todos los parámetros de segundo orden son cero (H1: βjl ≠ 0, ∀j,l).
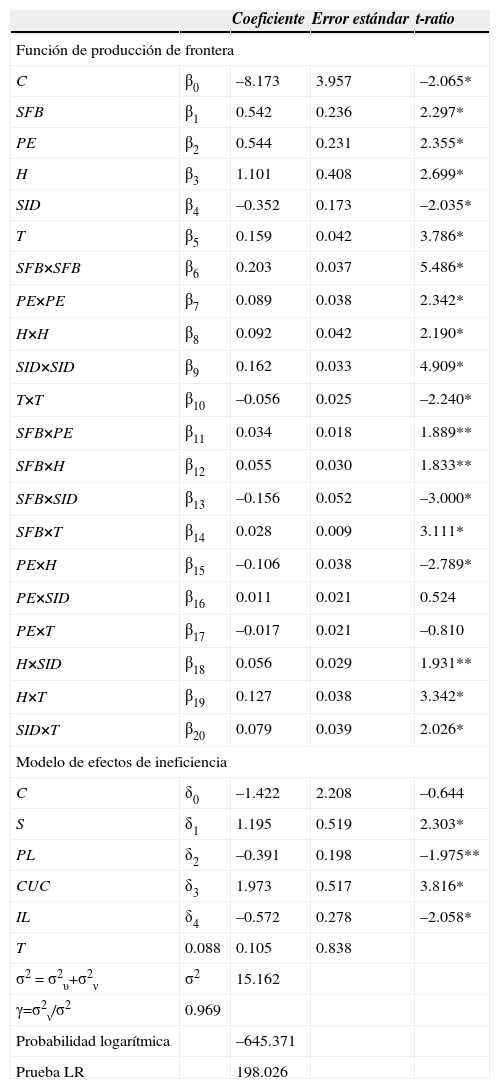
Análisis empíricoLos resultados del modelo de frontera de producción estocástica y del modelo de ineficiencia técnica se muestran en el Cuadro 2. Un signo positivo en los parámetros de la primera ecuación implica que los insumos tienden a aumentar el nivel de producción; un signo negativo en el segundo modelo indica que un aumento en el valor de las variables lleva a una reducción de la ineficiencia.
Estimación de la función de producción de frontera estocástica 23 industrias manufactureras, 1985-2009
| Coeficiente | Error estándar | t-ratio | ||
|---|---|---|---|---|
| Función de producción de frontera | ||||
| C | β0 | –8.173 | 3.957 | –2.065* |
| SFB | β1 | 0.542 | 0.236 | 2.297* |
| PE | β2 | 0.544 | 0.231 | 2.355* |
| H | β3 | 1.101 | 0.408 | 2.699* |
| SID | β4 | –0.352 | 0.173 | –2.035* |
| T | β5 | 0.159 | 0.042 | 3.786* |
| SFB×SFB | β6 | 0.203 | 0.037 | 5.486* |
| PE×PE | β7 | 0.089 | 0.038 | 2.342* |
| H×H | β8 | 0.092 | 0.042 | 2.190* |
| SID×SID | β9 | 0.162 | 0.033 | 4.909* |
| T×T | β10 | –0.056 | 0.025 | –2.240* |
| SFB×PE | β11 | 0.034 | 0.018 | 1.889** |
| SFB×H | β12 | 0.055 | 0.030 | 1.833** |
| SFB×SID | β13 | –0.156 | 0.052 | –3.000* |
| SFB×T | β14 | 0.028 | 0.009 | 3.111* |
| PE×H | β15 | –0.106 | 0.038 | –2.789* |
| PE×SID | β16 | 0.011 | 0.021 | 0.524 |
| PE×T | β17 | –0.017 | 0.021 | –0.810 |
| H×SID | β18 | 0.056 | 0.029 | 1.931** |
| H×T | β19 | 0.127 | 0.038 | 3.342* |
| SID×T | β20 | 0.079 | 0.039 | 2.026* |
| Modelo de efectos de ineficiencia | ||||
| C | δ0 | –1.422 | 2.208 | –0.644 |
| S | δ1 | 1.195 | 0.519 | 2.303* |
| PL | δ2 | –0.391 | 0.198 | –1.975** |
| CUC | δ3 | 1.973 | 0.517 | 3.816* |
| IL | δ4 | –0.572 | 0.278 | –2.058* |
| T | 0.088 | 0.105 | 0.838 | |
| σ2 = σ2υ+σ2ν | σ2 | 15.162 | ||
| γ=σ2ν/σ2 | 0.969 | |||
| Probabilidad logarítmica | –645.371 | |||
| Prueba LR | 198.026 | |||
Nota: * y ** significancia a 1 y 5 por ciento respectivamente.
Fuente: elaboración propia con base en resultados de Frontier 4.1.
Considerando los parámetros de primer orden, βk, se observa que todos tienen el signo positivo esperado y significativo, excepto SID, favoreciendo así el valor agregado manufacturero. La variable que más contribuye a agregar valor es el capital humano. No obstante, el capital y el trabajo contribuyen notablemente a agregar valor. Esta significancia implica la estandarización de procesos de producción y la necesidad de contratar mano de obra de baja calificación y capital.
En contraste, el gasto en I+D muestra signo negativo y significativo, lo que implica que aumentos en el uso de esta variable contraen el valor agregado manufacturero, señalando su ineficiencia. En consecuencia, las empresas del sector pueden generar mayor valor restringiendo la inversión en actividades de innovación. Lo anterior sugiere que su evolución depende fuertemente del uso intensivo de mano de obra con elevada capacitación apuntalado con el uso de bienes de capital. Además, las posibilidades de sustitución entre trabajo cualificado y capital parecen amplias dentro de las estrategias de producción de las empresas, dadas las complementariedades tecnológicas (significancia de parámetros SFB×PE y SFB×H).
Los resultados señalan que la producción manufacturera se caracterizó por rendimientos decrecientes a escala, esto es, aumentos en los insumos llevan a incrementos menos que proporcionales en el valor agregado.15 Sin embargo, existen efectos de escala positivos en el incremento de la productividad total de los factores.16
Por otro lado, se encuentra que no todas las variables explicativas de la ineficiencia técnica tienen el signo esperado aunque si son estadísticamente significativas. En particular, un aumento en la productividad laboral y de la variable asociada con la estructura de mercado (IL) tiende a eliminar la diferencia entre el producto actual y el potencial. De esta manera, existe una correlación negativa entre estas dos variables y la ineficiencia técnica.
El signo y significancia de todas las variables en este modelo es un resultado interesante por distintas razones. Primero, dado el efecto positivo del capital humano —que incluye personal con licenciatura y posgrado, encontrado en la función de producción de frontera, y el impacto favorable de la productividad laboral en la reducción de la ineficiencia—, puede pensarse que la formación de trabajo de alta calificación que se incorpora al sector potencializa las capacidades de estas industrias. Por ende, parece que las políticas educativas han impactado en la competitividad de las empresas manufactureras.
Segundo, se observa que el poder de mercado impacta positivamente en los niveles de eficiencia.17 Además, a pesar de que existen rendimientos decrecientes, puede pensarse que la concentración de mercado está asociada más a la escala de producción, es decir, se relaciona con la conducta de la firma. De este modo, cuando la empresa aumenta su oferta, que le permite ganar poder de mercado, mejora, en última instancia, su eficiencia técnica. Está situación está en línea con la nueva teoría de la organización industrial que argumenta que la conducta puede modificar la estructura y, de esta manera, el desempeño de las firmas (Tirole, 1990).
Tercero, la presencia de empresas extranjeras, a través del efecto de la inversión extranjera directa (ied) en las ventas nacionales (S), parece generar distorsiones en la forma de producción manufacturera, dado el signo positivo de δ1. Esto sugiere que existen limitados efectos de desbordamiento y de aprendizaje derivados de la operación de este tipo de firmas internacionales, ya sea en términos de producto, procesos, encadenamientos, capacitación o difusión de tecnología. Alternativamente, puede pensarse que la operación de las firmas extranjeras es en áreas básicas (ensamble o maquila, sin actividades de diseño o innovación), al tiempo que depende de las decisiones de las matrices, lo que no contribuye a mejorar la eficiencia en las industrias. Esta idea está en línea con el resultado encontrado para el gasto en I+D.
Cuarto, el signo del coeficiente de CUC es el esperado. Esto significa que como el costo de una unidad adicional de capital es más elevado, aquellas firmas que accedan a este insumo lo harán en condiciones menos favorables, limitando así su nivel de eficiencia. Al mismo tiempo, el empleo de nuevas unidades de capital puede no justificar la contratación de trabajo adicional u otros insumos, generándose esa ineficiencia.
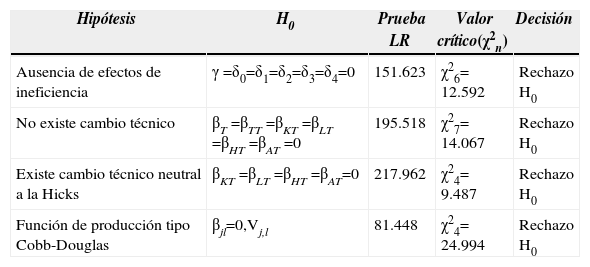
Respecto a los resultados de las pruebas de hipótesis (Cuadro 3) se determina que existen efectos de ineficiencia en el modelo y que, por tanto, la estimación máximo-verosímil es adecuada. La hipótesis nula γ = 0 se rechazó a 1% de significancia. Significa que la mayor parte del error aleatorio explica por la varianza en la ineficiencia técnica de las empresas. Como el parámetro estimado γ es cercano a uno (γ = 0.969), el error estadístico compuesto se debe a los efectos de ineficiencia técnica uit y a que el error aleatorio νit es aproximadamente cero.18 En consecuencia, la ineficiencia técnica es una variable relevante en la explicación del nivel del valor agregado de la manufactura mexicana.
Pruebas de especificación del modelo
| Hipótesis | H0 | Prueba LR | Valor crítico(χ2n) | Decisión |
|---|---|---|---|---|
| Ausencia de efectos de ineficiencia | γ =δ0=δ1=δ2=δ3=δ4=0 | 151.623 | χ26= 12.592 | Rechazo H0 |
| No existe cambio técnico | βT =βTT =βKT =βLT =βHT =βAT =0 | 195.518 | χ27= 14.067 | Rechazo H0 |
| Existe cambio técnico neutral a la Hicks | βKT =βLT =βHT =βAT=0 | 217.962 | χ24= 9.487 | Rechazo H0 |
| Función de producción tipo Cobb-Douglas | βjl=0,Vj,l | 81.448 | χ24= 24.994 | Rechazo H0 |
Nota: el estadístico LR se define como: LR = –2{ln[L(H0)/L(H1)]} = –2{ln[L(H0) – L(H1)]}. LR se distribuye como una chi-cuadrada con grados de libertad igual al número de restricciones establecidas en la hipótesis nula, esto es, igual al número de parámetros que se igual a cero en la hipótesis nula. En el contraste con H0: γ= 0 el estadístico LR sigue una distribución chi-cuadrada mixta. Los valores críticos se obtienen de Kodd y Palm (1986). En todos los casos α= 0.05.
Fuente: elaboración propia con base en los resultados de Frontier 4.1.
En cuanto a la segunda hipótesis, como la variable t es proxy del cambio tecnológico, entonces no habrá cambio técnico si todos los parámetros asociados con el tiempo son cero (βt = βjt = 0, para toda j).19 Así, se rechaza la hipótesis de no cambio técnico a 1% de significancia. Asimismo, se probó la hipótesis de que ese cambio es neutral en el sentido de Hicks, rechazándose el argumento de que el cambio técnico haya favorecido la utilización de uno de los insumos considerados. Por lo tanto, la ineficiencia técnica puede explicarse por la mayor explotación relativa de uno de los factores, posiblemente a favor del personal empleado cuya contribución es menor a la del capital humano.
La última hipótesis señala que la tecnología en las industrias manufactureras es tipo Cobb-Douglas (βJt = 0, para toda j y l), la cual se rechazó a 1% de significancia. Se acepta que la especificación translog representa adecuadamente la tecnología prevaleciente en cada industria, por lo que los términos de interacción son importantes en la determinación del valor agregado. Por lo tanto, las estimaciones se realizan sobre una forma funcional translog que al presentar mayor flexibilidad en los términos permite la sustitución de factores, así como un ajuste instantáneo de los insumos (Díaz-Bautista, 2007).20
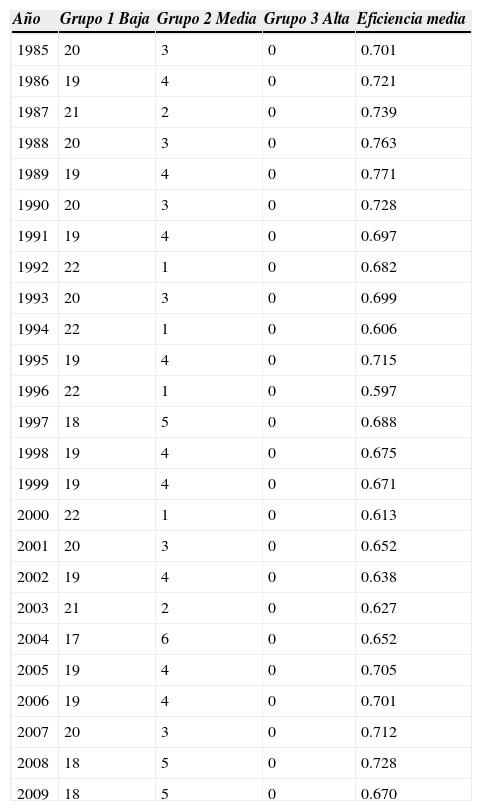
Por otra parte, la eficiencia manufacturera promedio por año se muestra en el Cuadro 5. Se aprecia que se agrupa de forma relativamente simétrica alrededor de la media. El valor más bajo se registró prácticamente a la mitad del periodo muestral (ET1996 = 0.597), mientras que la máxima eficiencia se alcanzó en 1989 (ET1989 = 0.771).
Clasificación de la eficiencia técnica, por año e industria
| Año | Grupo 1 Baja | Grupo 2 Media | Grupo 3 Alta | Eficiencia media |
|---|---|---|---|---|
| 1985 | 20 | 3 | 0 | 0.701 |
| 1986 | 19 | 4 | 0 | 0.721 |
| 1987 | 21 | 2 | 0 | 0.739 |
| 1988 | 20 | 3 | 0 | 0.763 |
| 1989 | 19 | 4 | 0 | 0.771 |
| 1990 | 20 | 3 | 0 | 0.728 |
| 1991 | 19 | 4 | 0 | 0.697 |
| 1992 | 22 | 1 | 0 | 0.682 |
| 1993 | 20 | 3 | 0 | 0.699 |
| 1994 | 22 | 1 | 0 | 0.606 |
| 1995 | 19 | 4 | 0 | 0.715 |
| 1996 | 22 | 1 | 0 | 0.597 |
| 1997 | 18 | 5 | 0 | 0.688 |
| 1998 | 19 | 4 | 0 | 0.675 |
| 1999 | 19 | 4 | 0 | 0.671 |
| 2000 | 22 | 1 | 0 | 0.613 |
| 2001 | 20 | 3 | 0 | 0.652 |
| 2002 | 19 | 4 | 0 | 0.638 |
| 2003 | 21 | 2 | 0 | 0.627 |
| 2004 | 17 | 6 | 0 | 0.652 |
| 2005 | 19 | 4 | 0 | 0.705 |
| 2006 | 19 | 4 | 0 | 0.701 |
| 2007 | 20 | 3 | 0 | 0.712 |
| 2008 | 18 | 5 | 0 | 0.728 |
| 2009 | 18 | 5 | 0 | 0.670 |
Nota: la eficiencia técnica se clasifica en tres grupos: grupo 1, de baja eficiencia, cumple con ET ≤ 0.82; grupo 2, de eficiencia media, cae en el intervalo 0.82 < ET ≤ 0.92, y grupo 3, de alta eficiencia, cuando 0.92 < ET ≤ 1.0. Esta propuesta de clasificación es de Kompas y Nhu Che (2004). Un valor de la eficiencia menor a 0.9 significa que la producción está por debajo de la potencial en 10% o más, clasificándose como de baja eficiencia técnica.
Fuente: elaboración propia con base en resultados de Frontier 4.1.
En general, durante el periodo se aprecia una eficiencia reducida, resultado que también encuentra Aguilar Gutiérrez (2011). En todos los años los valores medios son inferiores a 80%; aún más, para más de la mitad de los años las eficiencias promedio son inferiores a 70%. Antes de la intensificación de la apertura comercial en 1994, la eficiencia técnica promedio fue de 72.2%, mientras que en el subperiodo 1994-2006 ésta fue de 66.6%, señalando el efecto perverso que ha tenido el proceso de integración comercial con el exterior. En otras palabras, la mayor competencia de firmas extranjeras ha distorsionado la producción de las empresas en la economía mexicana.
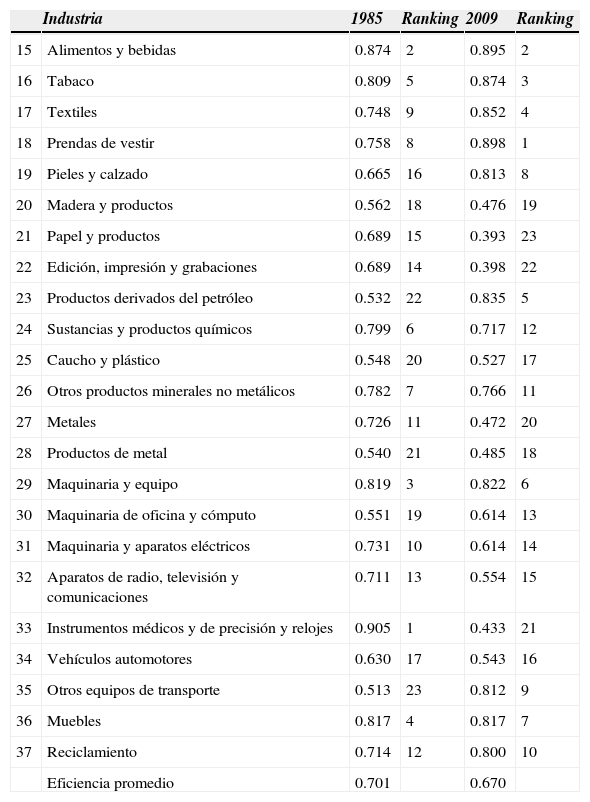
Considerando dos años en particular (inicio y fin del periodo) es posible hacer comparaciones entre las industrias (Cuadro 4). Se registra una baja eficiencia media para 1985, de 0.701. Las industrias más eficientes fueron Equipo, instrumentos médicos y de precisión y relojes (0.905), Alimentos y bebidas (0.874), Maquinaria y equipo (0.819), Muebles (0.817) y Tabaco (0.809), lo que puede deberse, por ejemplo, a que al ser industrias relativamente maduras la necesidad de emplear unidades adicionales de capital (cuyo costo es elevado) es baja y, por tanto, les permitió acercarse a su producto potencial. Por el contrario, las industrias menos eficientes fueron Otros equipos de transporte (0.513), Productos derivados del petróleo (0.532), Productos de metal (0.540), Caucho y plástico (0.548) y Maquinaria de oficina y cómputo (0.551). Los bajos niveles se explican por la naturaleza de estas industrias, que requieren de importaciones de bienes de capital que genera una brecha entre el producto efectivamente alcanzado y el potencial.
Eficiencia técnica en la industria manufacturera mexicana
| Industria | 1985 | Ranking | 2009 | Ranking | |
|---|---|---|---|---|---|
| 15 | Alimentos y bebidas | 0.874 | 2 | 0.895 | 2 |
| 16 | Tabaco | 0.809 | 5 | 0.874 | 3 |
| 17 | Textiles | 0.748 | 9 | 0.852 | 4 |
| 18 | Prendas de vestir | 0.758 | 8 | 0.898 | 1 |
| 19 | Pieles y calzado | 0.665 | 16 | 0.813 | 8 |
| 20 | Madera y productos | 0.562 | 18 | 0.476 | 19 |
| 21 | Papel y productos | 0.689 | 15 | 0.393 | 23 |
| 22 | Edición, impresión y grabaciones | 0.689 | 14 | 0.398 | 22 |
| 23 | Productos derivados del petróleo | 0.532 | 22 | 0.835 | 5 |
| 24 | Sustancias y productos químicos | 0.799 | 6 | 0.717 | 12 |
| 25 | Caucho y plástico | 0.548 | 20 | 0.527 | 17 |
| 26 | Otros productos minerales no metálicos | 0.782 | 7 | 0.766 | 11 |
| 27 | Metales | 0.726 | 11 | 0.472 | 20 |
| 28 | Productos de metal | 0.540 | 21 | 0.485 | 18 |
| 29 | Maquinaria y equipo | 0.819 | 3 | 0.822 | 6 |
| 30 | Maquinaria de oficina y cómputo | 0.551 | 19 | 0.614 | 13 |
| 31 | Maquinaria y aparatos eléctricos | 0.731 | 10 | 0.614 | 14 |
| 32 | Aparatos de radio, televisión y comunicaciones | 0.711 | 13 | 0.554 | 15 |
| 33 | Instrumentos médicos y de precisión y relojes | 0.905 | 1 | 0.433 | 21 |
| 34 | Vehículos automotores | 0.630 | 17 | 0.543 | 16 |
| 35 | Otros equipos de transporte | 0.513 | 23 | 0.812 | 9 |
| 36 | Muebles | 0.817 | 4 | 0.817 | 7 |
| 37 | Reciclamiento | 0.714 | 12 | 0.800 | 10 |
| Eficiencia promedio | 0.701 | 0.670 |
Nota: */ Posición que ocupa en la industria i considerando la eficiencia técnica. Fuente: elaboración propia con base en los resultados de Frontier 4.1.
Para 2009, la eficiencia media fue de 0.670, registrando una tasa de crecimiento negativa de 4.4%. Más de la mitad de las industrias registró reducciones en la eficiencia con tasas de crecimiento promedio de 20.5%; en contraste, sólo 12 muestran tasas positivas, indicando un ambiguo proceso de aprendizaje en las manufacturas, es decir, la existencia tanto de industrias ganadoras como de perdedoras. Asimismo, Productos derivados del petróleo y Otros equipos de transporte registraron un pobre desempeño en el primer año, mejorando sustancialmente sus capacidades al presentar un crecimiento de 57% para 2009. De igual manera, Pieles y calzado y Prendas de vestir registraron tasas de crecimiento promedio de 20%. Como el capital humano es factor esencial para la producción, y la productividad laboral reduce la ineficiencia, una estrategia que emplee intensivamente personal calificado permitió reducir los niveles de ineficiencia en éstas.
En contraste, las industrias con menores niveles de eficiencia fueron Papel y productos (0.393), Edición, impresión y grabaciones (0.398), Metales (0.472) y Madera y productos (0.476). Sobresalen Instrumentos médicos y de precisión con una caída en la eficiencia a menos de la mitad de su nivel en 1989. De nuevo, la apertura comercial o el alto costo de financiamiento para este tipo de industrias, con relativamente baja tecnología, pudieron limitar su nivel de eficiencia. En general, para las industrias con pérdida de eficiencia técnica, el cambio técnico no ha sido asimilado positivamente, por lo que la brecha entre la producción actual y potencial se amplió. Esto es, les ha permitido aumentar el nivel de producción, pero a un ritmo menor que el desplazamiento de la frontera de producción o de mejor práctica.
De igual manera, los valores de la eficiencia permiten clasificar a las industrias en tres grupos: eficiencia baja, media y alta. En el Cuadro 5 se observa una clara concentración de las industrias en el grupo de baja eficiencia técnica; en promedio, para todos los años el 78% de las industrias reflejaron niveles pobres de eficiencia.
Destacan dos hechos. Primero, en cuatro años sólo una industria alcanzó niveles de eficiencia medios (en todos los casos industrias distintas). Segundo, ninguna industria se acercó con el tiempo al nivel de producción de mejor práctica (grupo 3 vacío). Además, en términos agregados, en 2008 y 2009 se tienen más industrias con baja eficiencia que en 1985 y la eficiencia promedio es menor. Este resultado indica un estancamiento de la eficiencia manufacturera, alcanzándose, en consecuencia, un umbral de baja eficiencia.
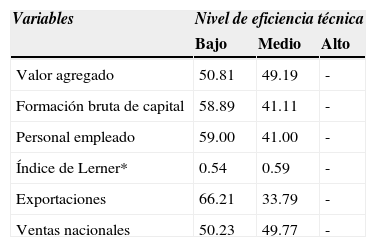
Si se combinan las medidas de eficiencia estimadas con un conjunto de características de las industrias, es posible determinar el perfil de industrias relativamente eficientes. Las características más relevantes para cada grupo de eficiencia para 2009 se muestran en el Cuadro 6. Se consideran las variables más importantes en este documento junto con otras de relevancia (exportaciones, ventas nacionales, tamaño de la firma). El grupo 1 incluye el 72% de las industrias en ese año.
Características de los grupos de eficiencia técnica (participación en el total)
| Variables | Nivel de eficiencia técnica | ||
|---|---|---|---|
| Bajo | Medio | Alto | |
| Valor agregado | 50.81 | 49.19 | - |
| Formación bruta de capital | 58.89 | 41.11 | - |
| Personal empleado | 59.00 | 41.00 | - |
| Índice de Lerner* | 0.54 | 0.59 | - |
| Exportaciones | 66.21 | 33.79 | - |
| Ventas nacionales | 50.23 | 49.77 | - |
Nota: */ Valor del índice de Lerner (poder de mercado).
Fuente: elaboración propia.
Se observan distintos aspectos de interés. Primero, el valor agregado por las industrias de eficiencia media es mayor que en las industrias del grupo de baja eficiencia, lo que implica que entre más cerca se este de la mejor práctica mayor valor puede generarse. Segundo, para ser eficientes se debe invertir intensivamente en capital. Tercero, las industrias intensivas en mano de obra son menos eficientes, puesto que el grupo de menor eficiencia contrata, en términos relativos, trabajo en mayor proporción que el grupo medio. Cuarto, las estructuras de mercado no competitivas generan mayor eficiencia técnica; el índice de Lerner es más alto en el grupo de eficiencia media.
Quinto, de acuerdo con la hipótesis de autoselección, las industrias con baja eficiencia exportan en promedio menos que las industrias con mayor eficiencia. Asimismo, parece que si una industria es más eficiente tiene más capacidad para vender internamente. Por último, cuanto más grande sea una firma menor es la ineficiencia que se encuentra.
ConclusionesEn este documento se estimó una función de producción de frontera estocástica y el modelo de ineficiencia técnica vinculado para determinar la importancia de los insumos en la producción de las industrias manufactureras mexicanas para el periodo 1985-2009. Asimismo, se identificaron características que explican las diferencias entre tres grupos de industrias clasificadas en función de los niveles de eficiencia técnica estimados.
Las estimaciones de la función de producción muestran que todos los insumos incluidos son significativos. La formación bruta de capital, el número de personas con licenciatura o con posgrado y el personal empleado contribuyen positivamente, mientras que el gasto adicional en I+D tiende a contraer la producción. Además, de acuerdo a este modelo, las industrias manufactureras exhibieron en promedio, durante el periodo, rendimientos decrecientes a escala.
Las pruebas de hipótesis realizadas indican que la producción manufacturera se caracterizó por la existencia de efectos de ineficiencia técnica, explicando las desviaciones del valor agregado actual respecto del máximo alcanzable si se siguiera la mejor práctica. No obstante, se determinó que el sector manufacturero no pasó por un proceso de cambio técnico Hicks-neutral. Por último, se estableció que la mejor forma de modelar a estas industrias es la función translog, ya que los términos de interacción son importantes en la determinación del valor agregado.
En cuanto a los efectos de ineficiencia, se tiene que todas las variables explicativas son estadísticamente significativas. En particular, un aumento en la productividad laboral y del poder de mercado tiende a reducir la ineficiencia. Por el contrario, los efectos spillover, derivados de la participación de la inversión extranjera directa en las ventas nacionales de las industrias, y el costo del uso del capital amplían esa ineficiencia.
De igual forma, se observaron los niveles medios de eficiencia técnica. El valor más bajo de la eficiencia se presentó en 1996, mientras que la máxima eficiencia se alcanzó en 1989. En general, la eficiencia es baja aunque con ciertos altibajos, lo que está en línea con el resultado de Brown y Domínguez (2004). Por ejemplo, en 2006, la eficiencia media fue de 0.676, con 13 industrias registrando pérdidas de eficiencia, lo que indica un proceso limitado de aprendizaje. Las industrias más eficientes fueron Pendas de vestir, Alimentos y bebidas, Tabaco y Textiles. Asimismo, los valores de la eficiencia permitieron clasificar a las industrias en grupos de eficiencia baja, media y alta. En el periodo, las industrias tienden a ubicarse en la primera categoría. Al parecer, no obstante la existencia de cambio tecnológico, las industrias no tienden a acercarse al nivel de producción de mejor práctica, lo que sugiere, dados los rendimientos decrecientes, que las industrias parecen haber llegado un umbral máximo de eficiencia.
Finalmente, se determinó el perfil de las manufacturas eficientes, destacándose que entre más cerca se este de la mejor práctica mayor valor puede agregarse; para ser eficientes se debe invertir en capital, tanto físico como humano); las industrias intensivas en mano de obra son menos eficientes; las estructuras de mercado no competitivas generan mayor eficiencia; es necesario alcanzar un nivel mínimo eficiente para participar en mercados internacionales (hipótesis de autoselección de firmas exportadoras); cuanto más grande sea una firma menor es la ineficiencia; los niveles de eficiencia no parecen estar correlacionados con las intensidades tecnológicas en las industrias.
De este modo, los resultados muestran que las industrias manufactureras mexicanas tienen una baja eficiencia técnica promedio menor a 70%, evidenciando altos niveles de ineficiencia que limitan la producción potencial y requieren de políticas para, por un lado, mejorar la eficiencia en el uso de insumos para impulsar a las firmas hacia el nivel de producción de mejor práctica, dado el estado actual de tecnología, y, por el otro, desplazar la frontera actual hacia afuera mediante el uso de tecnología avanzada. Entre las recomendaciones de política aplicables para las industrias manufactureras mexicanas están:
- 1)
El capital humano tiene la mayor correlación positiva y significativa con los niveles de eficiencia técnica, seguido del personal con baja calificación, por lo que las estrategias que promuevan el conocimiento, aprendizaje y capacitación facilitarían la modernización de procesos y así cerrar la brecha con el producto potencial.
- 2)
Promover inversiones estratégicas para incrementar el stock de capital y revertir el efecto negativo de los gastos en I+D. Para ello, las autoridades económicas pueden proveer asistencia en aspectos relacionados con desarrollo de recursos humanos, tecnologías de la información, acceso nacional a insumos de calidad, al mercado nacional e internacional, a fuentes de financiamiento en mejores condiciones, infraestructura general, entre otros; mejorando la productividad laboral, la competitividad, la eficiencia y el crecimiento del sector.
- 3)
Como la inversión extranjera a través del efecto en las ventas nacionales tiende a generar ineficiencia en el sector, el gobierno debe reorientar su interés por atraer capitales de calidad que permitan eliminar esa desventaja. Una opción es el fomento de empresas micro, pequeñas y medianas de propiedad mexicana, ya sea para integrarse a cadenas de valor globales o no.
- 4)
La correlación negativa entre el stock tecnológico y la eficiencia técnica es inesperada. Esto puede deberse a que si bien las firmas actualizan su tecnología no hay mejoras sustanciales en su eficiencia. El uso combinado de esta variable con el trabajo, calificado o no, tiene apenas un reducido efecto en la eficiencia, por lo que la reducción de costos con la nueva tecnología es menos que proporcional a ésta. Al respecto, las autoridades pueden incentivar la creación de redes y articulación entre firmas para alcanzar economías de escala y de alcance, así como para acceder a nuevas tecnologías, al tiempo que se desarrollan capacidades del personal para su uso.
Los autores agradecen los valiosos comentarios de dos dictaminadores anónimos de la revista.
Existen otras definiciones similares; por ejemplo, para Koopmans (1951) la eficiencia técnica representa la capacidad y voluntad de una unidad económica para producir el máximo producto posible dado un nivel de insumos y tecnología.
Suponiendo una función Cobb-Douglas en logaritmos esta ecuación se expresa como: yit= βxit+ (υit– uit).
El primer modelo, sugerido por Battese y Coelli (1992), establece una forma exponencial determinística del tiempo para el componente de ineficiencia y define uit= ute(–η[t–T]), donde ut, i = 1,2,…,N, son variables aleatorias no negativas iid obtenidas de truncar (en cero) la distribución normal; η es un parámetro desconocido a estimar que representa la tasa de cambio en la ineficiencia técnica; η> 0 se asocia con una mejora en la eficiencia técnica a través del tiempo.
Existe una alternativa para determinar la eficiencia técnica entre las industrias que emplea una metodología de dos pasos donde las estimaciones del modelo defirontera estocástica se obtienen en primera instancia y en la segunda etapa los valores estimados de la ineficiencia se regresan en un vector de variables explicativas.
Una desventaja de esta función es la posibilidad de problemas de multicolinealidad (Harris, 1999). Sin embargo, esta situación no es seria en este estudio, puesto que la mayoría de los parámetros estimados, de segundo orden y cruzados, son estadísticamente significativos. Además, la función CES permite la posibilidad de valores de producción cero para un subconjunto de firmas, no obstante, no se adecuada a los intereses de este documento, ya que en la muestra no se presenta ningún valor de producción cero.
Se incorpora cambio técnico no neutral para considerar la posibilidad de que la tasa marginal de sustitución entre los insumos sea no constante, esto es, que existan demandas de insumos asimétricas originadas por la adopción de avances tecnológicos. Por ejemplo, la innovación en procesos gerenciales y productivos, los cambios en la estructura de mercado, nacional e internacional, o las mejoras periódicas en la capacidad de utilización, son fuentes potenciales de ganancias de eficiencia en el tiempo que producen sesgo a favor del capital o trabajo (Machin y Van Reenen, 1998). Asimismo, admitir la posibilidad de cambio técnico no neutral parece ser un supuesto más realista que el enfoque de cambio tecnológico neutral a la Hicks, puesto que no requiere considerar como punto de partida la existencia de rendimientos constantes a escala, lo que es compatible con la función translog empleada.
El stock de capital en t está dado por skt = (1–δ)•skt–1 + It–1, donde δ es la tasa de depreciación lineal e I es la inversión realizada en el periodo anterior. El stock de capital en t–1 se calcula como sktt–1 = It/(k + d), siendo k la tasa de crecimiento promedio del producto de largo plazo y d la tasa de depreciación.
Alternativamente, el modelo se estimó con tres proxies de capital humano: trabajo altamente calificado que representa el número de personas con educación de posgrado, el trabajo con calificación media y la participación del trabajo calificado en el total del trabajo manufacturero; asimismo, se probó el efecto de la variable tecnología aproximándola como el número de patentes concedidas en el sector manufacturero. Los resultados no varían considerablemente, por lo que utiliza la variable H.
Las variables se transforman como: x’ = Ln(x – X¨) = Ln(x) – Ln(X¨), siendo X¨ la media geométrica.
El costo del uso del capital se obtiene como: CUCit = [Vt(δt + rt)]×100, donde Vt es el valor de mercado de un nuevo activo a precios constantes, esto es, el precio relativo de una unidad de capital respecto a la producción; δt la tasa de depreciación de un nuevo activo; rt el costo real del capital financiero, aproximado por el índice de precios implícito de la inversión en capital fijo divida por el deflactor del pib.
El índice de Lerner se calcula como: ILi= (pi – ci)/pi, donde pi representa el precio promedio de la i-ésima industria y ci el costo marginal promedio dentro de esa misma industria; pi se aproxima mediante el índice de precios en la industria i, y ci a través del índice de valor unitario, que se calculan para el año base 2003.
Si se acepta la nula de γ= 0, entonces σu2 = 0 y, por tanto, este término puede excluirse del modelo.
El cambio técnico neutral en el sentido de Hicks se refiere a que las productividades marginales relativas de los factores productivos se mantienen constantes para una proporción dada de factores.
La inclusión del tiempo como variable permite suponer que los cambios de la frontera de producción en el tiempo se originan por el cambio técnico. En el modelo se considera que existe cambio tecnológico ahorrador (empleador) del insumo k si βtj es positivo (negativo). Es neutral si las βtj son todas iguales a cero.
Las elasticidades de producción se calculan a partir de los parámetros estimados en la ecuación [9], es decir, eknt=∂ynt∂xknt=βk+∑i=1kβkixint+βTkt Por lo tanto, se tiene que la suma de los coeficientes asociados es en promedio menor a 1 en el periodo para todas las variables, excepto para SFB.
En promedio, la elasticidad de escala es 1.0012 para la manufactura total en el periodo.
En mercados con barreras a la entrada, los productores disfrutan de algún grado de poder de mercado que les permiten obtener beneficios extraordinarios. En consecuencia, esas firmas pueden no producir en el nivel máximo, dados los insumos y la tecnología. De esta manera, es posible que las estructuras de mercado no competitivas alojen firmas poco eficientes, generando un efecto de ineficiencia a nivel industrial.
Donde el valor del parámetro está dentro del intervalo cerrado [0,1].
El cambio tecnológico puede medirse por los cambios del producto a lo largo del tiempo, manteniendo constante el uso de las variables-insumo. Por ende, la primera derivada parcial de la función de producción respecto al tiempo determina la tasa de cambio tecnológico.
De cualquier manera se realizaron estimaciones de la función Cobb-Douglas, determinándose que la translog produce un mejor ajuste, ya que reduce la magnitud del término compuesto de error.