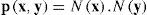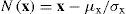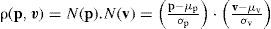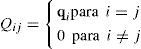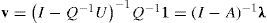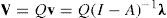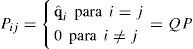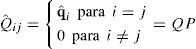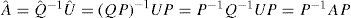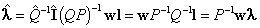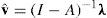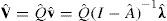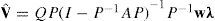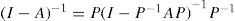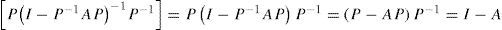El aspecto empírico de la teoría del valor: respuesta a Nitzan y Bichler

Resumen

La teoría del valor trabajo, originada en los clásicos y reformulada por Marx, ha encontrado apoyo empírico en numerosos trabajos en los últimos treinta años. En diversas economías los sectores en términos monetarios están altamente correlacionados con los mismos en términos de valor trabajo. En su libro Capital as Power (2009), y en una subsecuente discusión en línea, Jonathan Nitzan y Shimshon Bichler afirman que tales resultados son inválidos porque los cálculos no obtienen resultados en valor trabajo, sino que se han correlacionado dos variables monetarias. También arguyen Nitzan y Bichler que las correlaciones son espurias por la presencia de una tercera variable. En este artículo se refutan ambas críticas y, consecuentemente, se refuerza el soporte empírico a la teoría del valor trabajo.

Introducción

A lo largo de los años y desde la aparición del trabajo pionero de Anwar Shaikh (1984), los autores del presente artículo y muchos otros investigadores han presentado hallazgos de una estrecha correlación entre los valores monetarios y los valores trabajo de los sectores industriales de muchas economías capitalistas y han afirmado que dichos hallazgos apoyan la teoría clásica del valor trabajo.¹

En su libro Capital as Power (2009), y en una subsecuente discusión en línea,² Jonathan Nitzan y Shimshon Bichler afirman que sorprende lo erróneo de tales investigaciones, sobre la base de dos consideraciones:

• 1.

  Las investigaciones empíricas en cuestión no utilizan datos reales de tiempo de trabajo para estimar el valor trabajo, sino que utilizan datos monetarios de cuadros insumoproducto. Quienes afirmamos que hay evidencia de la estrecha correlación entre valores trabajo y precios somos culpables de un razonamiento circular debido a que suponemos lo que debemos demostrar: que es posible proceder de manera inversa e ir de dinero a tiempo de trabajo.

• 2.

  Las correlaciones que se presentan en los trabajos son espurias puesto que no toman en consideración el tamaño de la industria. Las correlaciones precio-valor observadas, afirman, son una expresión de la desigualdad en el tamaño de las industrias: las indus-trias “grandes” muestran, naturalmente, agregados en precios altos para sus productos y alto contenido de trabajo.

En relación con el primer punto Nitzan y Bichler (2009: 94) señalen que, para examinar la relación entre precios y valores es necesario conocer de antemano dos cosas: los precios y los valores. No obstante, dicen, sucede que no resulta tan sencillo “conocer” estas dos magnitudes aparentemente triviales y que, contrariamente a lo que afirman explícitamente las investigaciones empíricas, éstas dan la impresión de que ni siquiera intentan correlacionar precios y valores. Luego afirman que “hasta donde saben, todos los modelos marxistas que pretenden correlacionar precios con valores no hacen tal cosa; en lugar de eso, de hecho correlacionan precios con… ¡precios!” (Nitzan y Bichler, 2009: 96) [Traducción del texto original en inglés].

Respecto al segundo punto, critican la práctica de correlacionar agregados sectoriales en precios y en valores en los siguientes términos:

Las correlaciones obtenidas de esta forma reflejan no sólo las covariaciones de precios y valores unitarios, sino de las cantidades físicas de las mercancías. Nótese que el valor unitario y el precio unitario de cada sector están multiplicados por el mismo factor (la cantidad física de la mercancía). Este hecho significa que, siendo el resto de los elementos iguales, entre mayor sea la variabilidad de la escala del producto entre distintos sectores, la correlación entre su precio total y su valor total será más estrecha. Y dado que distintos sectores varían en el tamaño de su producto, el resultado común incrementará la correlación general en comparación con la correlación subyacente entre precios unitarios y valores unitarios. Hasta qué punto esto magnifica el resultado queda al descubierto cuando se controlan el tamaño de los sectores o: las correlaciones valor-precio se desploman, generalmente, a niveles insignificantes (Nitzan y Bichler, 2009: 95) [Traducción del texto original en inglés].

En lo que sigue respondemos ambos argumentos. En la sección dos abordamos el señalamiento de que quienes proponemos la teoría del valor trabajo no medimos valores trabajo; en la siguiente sección refutamos la aseveración de que las correlaciones precio sectorial-valor son espurias y, finalmente, en la última sección presentamos una breve conclusión.

Cantidades reales vs magnitudes monetarias

En primer lugar analizamos el argumento de Nitzan y Bichler según el cual los investigadores que hemos afirmado examinar empíricamente la correlación entre precios y valores, en el sentido marxista, de hecho no hacemos tal cosa y que nuestro análisis se limita a correlaciones entre precios en diversos niveles. Son tres las bases sobre las cuales se asienta tal crítica.

• 1.

  Marx define el valor de una mercancía como la cantidad de trabajo abstracto social-mente necesario (directo e indirecto) para producir dicha mercancía. Sin embargo, el tiempo de trabajo abstracto socialmente necesario (ttsn) no es, incluso en principio, una magnitud observable.

• 2.

  Aun si uno comente el disparate de identificar el ttsn con las horas de trabajo medidas con reloj checador, no disponemos de dicho dato, y quienes afirman haber probado la teoría del valor trabajo, lo han hecho usando los talones de recibo de nómina de la industria como sustituto (proxy) de horas de trabajo directo.

• 3.

  Para calcular el tiempo de trabajoindirectamente necesario para la producción de una mercancía se requieren los “coeficientes técnicos” que ligan los sectores de la economía. En principio, estos coeficientes son la cantidad de producto de la industriaj, medido en unidades físicas, necesaria para producir una unidad de producto de la industriai (donde los índicesj ei van de 1 an, siendon el número de industrias que componen la economía). No obstante, los cuadros de insumo-producto disponibles proporcionan coeficientes basados en magnitudes monetarias: insumo monetario de la industriaj necesario para producir el valor monetario de la producción en la industriai.

Nitzan y Bichler hacen explícito el primer punto, si consideramos su afirmación de que “es imposible medir esta cantidad [de tiempo de trabajo abstracto socialmente necesario]” (2009: 96) [Traducción del texto original en inglés].Los otros dos puntos parecen estar implícitos en las afirmaciones que hacen en cuanto a que las investigaciones empíricas en cuestión ni siquiera tratan de correlacionar precios y valores, por lo que se quedan en el nivel de “correlacionar precios con precios”.

Permítasenos examinar cada uno de estos puntos.

Tiempo de trabajo: socialmente necesario y según el reloj checador

La posible discrepancia entre el concepto de tiempo de trabajo abstracto socialmente necesario de Marx y las horas reales de trabajo desempeñado por trabajadores específicos en empresas específicas, en tanto que medido directamente por el reloj checador, tiene dos aspectos. El primero tiene que ver con la variación en la productividad del trabajo (de un nivel dado de calificación) entre empresas, mientras que el segundo con la cuestión de la fuerza de trabajo calificada en oposición a la fuerza de trabajo no calificada.

Supongamos que en una industria determinada algunas empresas utilizan tecnología relativamente avanzada u organizan el proceso de trabajo en una forma relativamente eficiente o ejercen una intensidad de trabajo relativamente alta, mientras que otras se rezagan en una o más de estas condiciones. Entonces, las primeras empresas producirán un determinado producto con menor insumo de tiempo de trabajo según horas de reloj checador, mientras que las últimas empresas lo harán con mayor insumo de esas horas. Ya que las horas reales de trabajo desempeñado en las empresas más eficientes y en las menos eficientes no pueden ser, por igual, “socialmente necesarias” esto establece que las horas de reloj checador no son, en general, equivalentes a las horas socialmente necesarias.

Ahora bien, ¿en qué sentido esto resulta pertinente al cálculo de los valores trabajo a nivel de industria? Desde la concepción de Marx, el tiempo de trabajo socialmente necesario para la producción de un producto dado es la cantidad “normal” o “promedio”. En efecto, habla del “tiempo de trabajo promedialmente necesario, o tiempo de trabajo socialmente necesario” (el subrayado es de Marx), y continua:

El tiempo de trabajo socialmente necesario es el requerido para producir un valor de uso cualquiera, en las condiciones normales de producción vigentes en una sociedad y con el grado social medio de destreza e intensidad de trabajo (Marx, 1982,: 48) [Traducción del texto original en inglés].

De ello se sigue que si nuestros datos cubren la totalidad de la industria, las horas de reloj checador agregadas casi se corresponden con las horas social-mente necesarias, dado que el total es tan sólo el promedio multiplicado por el tamaño de la muestra.

Más allá de esta perogrullada aritmética, también es claro que Marx avizoró un mecanismo que refuerza (aun si es de forma imperfecta) la convergencia de las horas reales de trabajo desempeñado en varias empresas en el promedio socialmente necesario. La idea es que si ciertas empresas requieren del insumo trabajo en una cantidad sustancialmente mayor al promedio, operarán con costos más altos y quedarán fuera del negocio, mientras que aquellas empresas que consigan producir un producto dado con un insumo trabajo sustancialmente menor al promedio operarán con ganancias excedentes y, por lo tanto, atraerán émulos. El grado de convergencia impuesta será mayor cuanto mayor sea el grado en que la lógica de reducción de costos y búsqueda de beneficios del “capitalismo” domine el mercado.

Desde esta perspectiva, la noción de que el tiempo de trabajo socialmente necesario es en principio una magnitud no observable es un obscurantismo. Es cierto, no existe un cronómetro que mida el componente socialmente necesario de las horas de trabajo que desempeña un trabajador en particular en una empresa en particular. No obstante, sí es posible medir estadísticamente el trabajo socialmente necesario, de no ser así, la teoría de Marx carecería de sentido. ¿Y qué hay con respecto a la fuerza de trabajo calificada vs la no calificada? Marx, siguiendo a Smith y Ricardo, pensó en fuerza de trabajo no calificada o “simple” como la línea base, concibiendo a la fuerza de trabajo calificada como cierto múltiplo de la fuerza de trabajo simple. En la concepción clásica, la fuerza de trabajo calificada “crea valor” a una tasa mayor en comparación con la fuerza de trabajo simple, y esa diferencia puede medirse con la diferencia de salario. Hay un fuerte tufo de circularidad en esta noción, da la impresión de dejar fuera la cuestión de si la diferencia de salario refleja correctamente las diferencias en las tasas de “creación de valor”.

En otros trabajos hemos analizado esta cuestión y hemos roto con la circularidad, al tiempo que mantenemos el análisis básico de Marx.³ Desde nuestra perspectiva, todo trabajo “crea valor” (esto es, cuesta un gasto de tiempo humano finito) a una tasa uniforme, sin embargo, la fuerza de trabajo calificada transfiere al producto una porción de una suma de tiempo de trabajo previamente acumulado, siempre y cuando las destrezas en cuestión hayan sido adquiridas vía el trabajo del individuo y su instructor en un determinado proceso de capacitación. Este análisis sigue el modelo de análisis de Marx de la transferencia del valor de los medios de producción al producto: destrezas humanas adquiridas se “deprecian en” el producto tanto como lo hacen las máquinas. Las implicaciones que resultan de este punto las abordamos en el siguiente apartado.

El talón del recibo de nómina vs horas de trabajo

Ahora volvemos a la afirmación según la cual los autores de la correlación precio-valor ni siquiera usan tiempo de trabajo medido por horas de reloj checador en los valores trabajo, en el lado correspondiente de la relación. Si bien es verdad que muchos estudios han utilizado los talones del recibo de nómina en la industria como un sustituto para obtener directamente el insumo trabajo, es falsa la afirmación de que todos los trabajos empíricos que abordan la correlación precio-valor se apoyan en datos salariales. Las cuadros suecos de insumo-producto dan el insumo trabajo no en términos monetarios sino en años persona. David Zachariah ha analizado la relación precio-valor para varias economías y encuentra que las cifras suecas muestran la misma fuerte correlación observada en otros estudios (Zachariah, 2006).

Además, incluso si el cuadro de insumo-producto expresa el insumo trabajo en términos salariales es posible proceder a la inversa para obtener horas si se dispone de datos sobre salario industrial promedio: uno deflacta los números del talón del recibo de nómina usando el salario promedio específico del sector. Esto fue lo que hicieron Cockshott, Cottrell y Michaelson (1995) para su análisis de la economía del Reino Unido, obteniendo tasas de salarios por hora promedio por industria a partir de la encuesta New Earnings Survey. El resultado: la correlación entre precios y valores trabajo permaneció casi tan consistente como cuando se recurrió al talón del recibo de nómina como sustituto del insumo trabajo sectorial. De manera específica, los autores encontraron una correlación precio-valor de 0:98 al usar directamente datos del recibo de nómina en comparación con 0:96 después de ajustar tasas salariales específicas por industria.

Pero permítasenos detenernos en este aspecto por un momento. Es legítimo preguntar si resulta o no lo más apropiado medir las horas persona gastadas en una industria particular o usar el talón del recibo de nómina pagada por ésta para medir el tiempo de trabajo socialmente necesario dedicado a ella (antes de considerar el trabajo indirecto aportado vía los insumos no laborables).

Si la variación en el salario promedio entre industrias sólo es “ruido” en relación con el análisis del valor, entonces estaremos en mejores condiciones si utilizamos datos de los años persona reales cuando estén disponibles o deflactando los recibos de nómina industriales mediante las tasas salariales industriales, si es posible, para obtener cifras en años persona. No obstante, está la posibilidad de que las diferencias entre salarios promedio entre industrias refleje (parcialmente) las diferencias en la composición de calificación de la fuerza de trabajo en dichas industrias y que (como mencionamos en el apartado anterior) éstas estén asociadas con diferencias en la aportación indirecta de trabajo debido a la escolaridad y capacitación de los trabajadores calificados. Sin más investigación no podemos decir nada definitivo respecto a este asunto, pero al menos parece plausible que la cifra para el insumo trabajo teóricamente “correcta” se encuentre entre las horas persona medidas y la cifra del salario relativo que aparece en el recibo de nómina del sector implicado. Pero si estas dos cifras dan apoyo a valores muy similares en la correlación precio-valor entonces, por supuesto, el asunto es discutible.

Trabajo indirecto y coeficientes técnicos

El hecho de que los coeficientes interindustriales se den como proporción de magnitudes monetarias, más que como proporción de flujos de productos en especie, es resultado del grado de agregación de los cuadros de insumoproducto disponibles para las economías capitalistas. Para construir un cuadro de insumo-producto significativo in natura los datos deben estar totalmente desagregados por producto, pese a ello, muchas de las industrias tal y como aparecen en los cuadros existentes producen una amplia gama de productos. Por ejemplo, no puede haber un número significativo en especie para la cantidad de producto de “aeronaves y partes” o de “componentes electrónicos y accesorios” o para el flujo en especie del producto de la segunda industria hacia la primera. En una economía planificada sería posible elaborar flujos de material en términos de identificadores únicos para cada tipo de producto, mediante uso de códigos de barra, por ejemplo. Pero, dado que esta información no está disponible para los departamentos de estadísticas nacionales en las economías capitalistas la solución práctica es presentar los valores monetarios agregados de los flujos entre sectores.

Ahora bien, esto no crea un problema si uno está interesado en comparar el valor monetario agregado del producto de las industrias con el valor trabajo agregado de esos mismos productos, ya que el vector de los valores trabajo sectoriales agregados calculado a partir de cuadros monetarios concordará con el vector calculado a partir de una cuadro físico, conforme a un escalar, independientemente del vector de precio y de la tasa salarial (común) que se usaron para elaborar el cuadro monetario. O, en otras palabras, el vector de valores trabajo sectoriales obtenido es independiente del vector de precio usado. Uno también podría (si fuera prácticamente posible) usar un vector arbitrario para contabilizar precios o pesos para elaborar un cuadro monetario. El hecho de que los precios reales se utilicen en los datos publicados no “contamina” de ninguna manera las cifras de valor que uno obtiene; no se induce una bondad de ajuste espuria entre valores y precios. Aportamos una prueba de esta aseveración en el apéndice a este capítulo.

Los coeficientes de correlación entre dos vectores no cambian bajo una multiplicación escalar de uno de los vectores. Una correlación entre precipitación pluvial y temperatura, por ejemplo, no se ve afectada por el hecho de que la temperatura se mida en grados Fahrenheit o centígrados, tampoco si la precipitación pluvial se mide en centímetros o pulgadas. Así, dado que los valores sectoriales agregados obtenidos a partir de datos monetarios concuerdan, conforme a un escalar, con aquellos que se habrían obtenido a partir de datos in natura, se sigue que los coeficiente de correlación obtenidos de esta forma serán los mismos que aquellos que se habrían obtenido con datos en especie. La única fuente de variación habría sido el supuesto de que la tasa salarial era la misma entre industrias. Empero, como ya lo hicimos notar con anterioridad, se han hecho pruebas donde se efectúan correcciones con diferentes tasas salariales entre industrias, comprobándose que la correlación permanece fuerte.

Correlación espuria

En esta sección abordamos la afirmación de Nitzan y Bichler (2009) de que las correlaciones precio-valor que otros y nosotros hemos obtenido son básicamente espurias, ya que no toman en consideración el tamaño de la industria. Esto tiene que ver con el argumento que esgrimió Kliman (2002).

Respondemos de tres formas a esa parte de su argumento:

• 1.

  Explicando la hipótesis que ponemos a prueba en nuestras investigaciones. Una comprensión clara de esta hipótesis eliminará, creemos, cualquier tentación de pensar en los resultados como un caso de correlación espuria.

• 2.

  Demostrando que la correlación espuria que Nitzan y Bichler dicen demostrar se basa en lo que en ciencias de la computación se denomina error tipo y en física un error dimensional. Este argumento se lo debemos a Valle Baeza (2010) y Fröhlich (2010a).

• 3.

  Citando evidencia empírica adicional para apoyar la idea de que no son espurias las correlaciones observadas entre contenido de trabajo y valor monetario.

La hipótesis básica que se pone a prueba

Hay algo de ironía en la oposición de Nitzan y Bichler a la teoría del valor trabajo. La idea sobre la que basan su propio trabajo, que el “capital es poder” tiene antecedentes clásicos respetables. Hace mucho Adam Smith escribió que la riqueza monetaria es poder. Sin embargo, Smith fue específico: la riqueza monetaria era el poder para comandar el trabajo de otros. Si Nitzan y Bichler tuvieran que buscar un correlato conmensurable del poder harían bien en seguir a Smith, pero al hacerlo tendrían que abandonar su oposición a la teoría del valor trabajo: el poder es poder sobre el trabajo y hay una correlación directa entre montos de dinero y cantidad de trabajo comandada. Nitzan y Bichler niegan esta correlación, privando así a su teoría de las bases factuales que Adam Smith tenía.

El propósito de las investigaciones empíricas que otros y nosotros hemos realizado con respecto a la relación entre precio-valor ha sido verificar esta proposición básica de la economía política clásica, el trabajo es la fuente del valor de cambio de las mercancías. En primer lugar abordamos este asunto porque queremos analizar ingreso nacional en términos de las categorías marxistas: tasa de plusvalor y composición orgánica del capital entre otras. En un inicio los revisores rechazaron nuestro trabajo señalando que utilizábamos cantidades monetarias para medir lo que tendrían que ser razones de valor trabajo. Para establecer la validez de nuestro procedimiento mostramos que incluso si desagregamos la economía más detalladamente, haciendo uso de los cuadros de insumo-producto, hay una correlación estrecha entre magnitudes de valor trabajo y magnitudes monetarias. Por ello, resultaba válido usar datos monetarios para obtener razones como la composición orgánica del capital o la tasa de explotación.

El análisis que Marx hace de la tasa de explotación descansa en la hipótesis de que el trabajo objetivado ―o para ser más precisos, trabajo concurrentemente necesario― es la fuente de valor monetario. Para establecer la validez de esta hipótesis y del análisis de la explotación que se desprende de ella, es suficiente con descomponer la economía en gran número de sectores y mostrar que el valor monetario del producto bruto de dichos sectores se correlaciona estrechamente con la fuerza de trabajo concurrentemente gastada para producir ese producto bruto. Lo cual a su vez requiere que uno calcule dos vectores:

• 1.

  Un vector de flujos monetarios de producción indexado por sector, cada uno de cuyos elementos es de dimensión unidades monetarias por año.

• 2.

  Un vector del número de personas, cuyo trabajo anual se objetiva directa o indirectamente en ese producto monetario, siendo la dimensión de cada uno de sus elementos un número de personas, ya que las horas persona por año se reducen a la dimensión persona. Coincide que éste es exactamente el formato de los cuadros suecos de insumo-producto previamente mencionados.

Si hay una fuerte correlación entre ambos vectores podemos afirmar que los datos son consistentes con la hipótesis de que el trabajo es la fuente de valor. Hay que subrayar que este método examina directamente lo que queremos probar, a saber, si el valor monetario es proporcional o no al trabajo utilizado.

El argumento de que las correlaciones observadas son espurias depende de la idea de que existe un tercer factor independiente que es la causa de variaciones concomitantes en los vectores de flujo de personas y monetarios. Cualquier correlación observada en las ciencias tiene posibilidades de ser espuria, es decir, siempre cabe esa posibilidad. No obstante, en este caso, para sostener que una correlación es espuria uno tiene que identificar ese tercer factor y también mostrar que en efecto induce la correlación observada. De forma que, ¿cuál podría ser este tercer factor?

Kliman (2002) sugiere que es el tamaño de la industria. Las industrias “grandes” emplean más gente y también venden más producto, y la correlación entre precios sectoriales y valores sectoriales surge nada más por ese hecho. Pero para que un tercer factor sea la causa común de la variación en los dos vectores de interés, ese factor debe ser cuantificable. ¿Cómo mediría el tamaño de la indus-tria? Las medidas más obvias del tamaño de una industria ―cuántas personas emplea o su corriente de abastecimiento― quedan fuera debido a que estamos buscando algo que sea independiente. Kliman, Bichler y Nitzan sugieren que hay una especie de tercera forma de tamaño de industria que ocasiona las variaciones tanto en el empleo como en la corriente de abastecimiento.

En efecto, hay otras posibles medidas, por ejemplo el área de terreno que una industria ocupa, el número de toneladas de producto que produce o la cantidad de megavatios-hora que utiliza. En principio cualquiera de ellos podría ser el tercer factor que determine el trabajo utilizado y la corriente de abastecimiento de una industria, sin embargo, sólo tenemos que enlistarlas para ver qué tan poco plausible es que el área de terreno o el tonelaje sea una tercera fuente apropiada de variación.⁴

La agricultura es por mucho la industria “más grande” en el Reino Unido, en términos físicos. Es la que ocupa el mayor espacio, aún así la cantidad de empleo y corriente de abastecimiento no es de ninguna forma proporcional a su tamaño en estos términos. La industria de suministro de agua es la mayor en términos de kilogramos producidos pero, de nueva cuenta, su posición en términos de corriente de abastecimiento y empleo se queda muy corta.

Empero, de hecho, Bichler y Nitzan no proponen ninguna de estas medidas de tamaño antes mencionadas; en su lugar sugieren que la causa común de variación es simplemente el número de unidades de producto creadas. En una hoja de cálculo muestran que si uno toma dos vectores no correlacionados (a y b) y los multiplica a cada uno por un tercer elemento al azar (c), entonces el resultado a o c estará correlacionado con b o c. En términos matemáticos eso está bien, no obstante, no tiene pertinencia para la cuestión en disputa a menos que se les pueda asignar algún significado económico a los vectores a, b y c. Colocar encabezados en las columnas como “precio unitario” y “número de unidades vendidas” no da a su ejemplo ninguna justificación a menos que puedan explicar qué son esas “unidades” en el contexto de los cuadros de insumo-producto.

De forma que si observamos los sectores industriales en el Reino Unido, ¿cuáles serían las unidades de producto? Veamos, para la industria 30 ―calzado― presumiríamos que son pares de calzado. Pero, cuál es la unidad de producto de la industria 47 ―productos de hule― o para la industria 50 ―productos de cerámica― o para la industria 67 ―armas y municiones―, ¿la unidad de producto sería una bala, un tanque o una bomba atómica? En producción de electricidad, ¿la unidad es el kilovatio/hora, el megavatio/hora o qué? ¿En producción lechera sería la pinta, el galón o el litro?

Hay dos cuestiones aquí. Primera, muchas industrias definidas al nivel de detalle de los cuadros insumo-producto nacional generan productos heterogéneos para los cuales no existe una unidad común y, segunda, muchas industrias producen por “volumen”, para cuyo caso la unidad de medida es arbitraria.

Nitzan y Bichler escriben que “la mayor parte de gente” piensa el precio como un atributo de “mercancías individuales”, como el caso del precio del Toyota Corolla, el precio de un saco de trigo, el precio de un vuelo en United Airlines de Nueva York a Tokio (Nitzan y Bichler, 2009: 95). Puede que sea así ―y hay ocasiones en que las unidades pertinentes parecen ser obvias― pero, entonces, la “mayor parte de la gente” no ha pensado respecto a cómo medir la relación que hay entre precio y valor en el total de la economía, y no tiene idea de las cuestiones intrincadas que surgen cuando uno trata de definir “unidades” para todos los bienes producidos.

Una correlación imposible

Ya hemos argumentado contra la idea de que uno puede llegar a establecer un conjunto de “unidades” naturales bien definidas para el producto de cada sector de la economía, de tal forma que uno pueda analizar la relación entre precios por unidad y valor trabajo por unidad. En esta sección dejamos de lado nuestro escepticismo respecto a dichas unidades: por el bien de la argumentación supondremos que hay una unidad natural definida para cada mercancía. Por tanto, hay un vector bien definido de precios (p), donde p_i es el precio del producto de la industria i por unidad natural; un vector bien definido de valores por unidad(v), y un vector bien definido de tamaños de industria (q_i); i = 1,…,n, expresado en términos de unidades naturales.

La cuestión que señalan Nitzan y Bichler es que la correlación “apropiada” a considerar es la que se da entre precio por unidad y valor por unidad, mientras que la correlación que de hecho examinan quienes afirman probar la teoría del valor trabajo es aquella entre precios sectoriales agregados (p_iq_i) y valores sectoriales agregados (v_iq_i) ―y la multiplicación por q_i induce a una correlación espuria. Como ya mencionamos, pretenden ilustrar esta cuestión mediante una hoja de cálculo en la que la correlación original p,v es mínima, pero debido a la variación en el tamaño de la industria la correlación de p_iq_i y v_iq_i es sustancial. ⁵

Nuestra respuesta a ello es que si bien la correlación p_iq_i y v_iq_i es matemáti- camente válida (y no espuria como ya hemos argumentado), la supuesta correlación de p_i y v_i no es matemáticamente válida ni significativa.

Cuando Nitzan y Bichler calculan su correlación p,v inicial se apoyan en la función correl de Microsoft Excel. Pues bien, Excel es en términos de ciencias de la computación un programa “sin dimensiones”, no verifica que la operación matemática que uno corre tiene sentido, dado que no sabe nada respecto a qué es aquello que representan los números en una hoja de cálculo. Sistemas de programación más rigurosos como Fortress (Allen et al., 2005) o Vector Pascal (Cockshott, 2002) permiten al usuario especificar las unidades utilizadas para las variables, para que se pueda efectuar un análisis dimensional. De haber hecho esto, la computadora habría advertido a Bichler y Nitzan del error que estaban cometiendo.

El análisis dimensional es un conjunto de reglas para verificar aspectos básicos de modelos matemáticos; especifica condiciones necesarias (aunque no suficientes) para la validez de un modelo. Las variables, en general, son pares ordenados ―una magnitud x y una unidad de medida [m]―, por ejemplo el precio del petróleo podría ser 90 [$/barril]. Las reglas básicas del análisis dimensional son como sigue: ⁶

• 1.

  Cualquier expresión matemática debe ser dimensionalmente consistente, esto es, las unidades en el lado izquierdo de la expresión deben ser las mismas que las unidades en el lado derecho.

• 2.

  Se permite adiciones o sustracciones de magnitudes con mismas unidades:x[m] + y[m] = (x + y)[m].

• 3.

  No se permiten adiciones y sustracciones de magnitudes con diferentes unidades: no es posiblex[m] + y[t].

• 4.

  Se permiten multiplicaciones de variables con diferentes unidades:x[m]y[t] = (xy)[mt].

• 5.

  También son aceptables divisiones de variables con diferentes unidades:x[m]/y[t] = (x/y)[m/t].

En términos dimensionales, el valor unitario de la mercancía i es v_i[h/ui] y su precio unitario es p_i[$/ui] donde h denota tiempo de trabajo y u_i la unidad física apropiada de producto i.

Ahora el coeficiente de correlación entre dos vectores x e y es el producto interior de los vectores normalizados:

donde la función de normalización N(x) para un vector x sustrae su media(μ_x) y la divide entre su desviación estándar σ_x:

La correlación entre precio por unidad y valor por unidad quedaría dada por la expresión:

Pero, ¿cuál es el problema aquí? Para encontrar μ_p tenemos que sumar los precios por unidad de varias mercancías y para encontrar μ_v tenemos que sumar sus valores unitarios. Sin embargo, la regla 3 no nos permite realizar esta operación. Por ejemplo, la adición del precio de petróleo p_o [$/barril] y el precio de un lápiz p_p [$/lápiz] no es posible, dado que involucra dimensiones incompatibles (independientemente de las reglas, intuitivamente es claro que algo no está bien con la noción del precio promedio de un barril de petróleo y un lápiz, en oposición a, digamos, el precio promedio de petróleo entre distintos mercados o periodos). Dado que la normalización depende de calcular la media de un vector y calcular la media depende del sumar, la normalización sólo queda definida para vectores de dimensión homogénea. Y, de la misma forma, la correlación sólo es válida para vectores de dimensión homogénea.

El intento de calcular p(p,v) por unidad falla porque los vectores p y v no son dimensionalmente homogéneos; no representan n valores de dos variables, sino dos series de n variables distintas. Por otro lado, la correlación de precios multiplicados por cantidades p_iq_i y de valores trabajo multiplicados por cantidades v_iq_i está bien definida porque cada p_iq_i tiene dimensión [$] y cada v_iq_i tiene dimensión [h]. Cada una tiene dimensiones homogéneas y, por lo tanto, la correlación está bien definida entre ellas.

Los críticos que sostienen la correlación espuria confundieron el problema: no hay correlación original de dos variables con n observaciones que se complique al introducir una tercera variable. La alegada correlación espuria es una forma significativa de medir la relación precio-valor, mientras que la correlación de Nitzan y Bichler que se supone no es espuria es un error total.

Algunas cuestiones realmente para investigar

El asunto de la correlación espuria resultó ser un argumento falso. No obstante, hay formas significativas de abordar la sospecha que esconde el argumento. En esta sección discutimos brevemente dos líneas de investigación empírica que pueden arrojar luz adicional sobre la materia.

Primero, el valor trabajo de una mercancía o conjunto de mercancías representa la suma de tiempo de trabajo directo e indirecto necesario para su producción. En la terminología que utiliza Pasinetti (1981), los valores trabajo podrían quedar descritos como coeficientes de trabajo verticalmente integrados. De forma similar, es posible calcular (a partir de los mismos datos de insumo-producto) coeficientes verticalmente integrados para insumos seleccionados distintos al trabajo. Para que tal cálculo sea económicamente significativo, el insumo seleccionado debe ser razonablemente homogéneo; posibles candidatos podrían incluir petróleo, electricidad y acero. Esto es, uno puede definir “valores de petróleo”, por ejemplo, de manera análoga a los valores trabajo. Surge una pregunta: ¿cómo la correlación entre precios sectoriales y valores de petróleo se compara con la correlación entre precios y valores trabajo? Nótese que si tales correlaciones fueran simplemente un artificio resultante de las diferencias en el “tamaño” de las industrias (como sea que se mida), uno esperaría encontrar una correlación similar para cualquier insumo seleccionado.

Este tipo de análisis lo realizaron Cockshott y Cottrell (1997a). Usando datos de insumo-producto para el Reino Unido probamos los candidatos “valor base” petróleo, electricidad y hierro y acero, y encontramos correlaciones contra el precio en el orden de 0.799, 0.826 y 0.576 respectivamente, en comparación con 0.977 para el trabajo. ⁷ Cabe mencionar, que no consideramos que alguna de estas correlaciones sea espuria, el punto es que los valores trabajo producen un ajuste más estrecho con los precios sectoriales en comparación con las otras opciones.

Segundo, hasta aquí nos hemos concentrado en el coeficiente de correlación como la estadística por medio de la cual podemos evaluar la relación precio-valor. Sin embargo, la correlación no es la única herramienta pertinente ―en gran medida nos hemos centrado en ella porque queremos responder al cargo de corre- lación espuria― y vale la pena mencionar un importante enfoque alternativo.

Esto es, uno puede enfocarse en la razón de precio agregado-contenido de trabajo (o a la inversa contenido de trabajo-precio) entre los sectores de una economía. Si la teoría del valor trabajo es correcta, la distribución de estas proporciones debe ser bastante uniforme (si la teoría se mantiene exacta, cosa que por supuesto no pensamos encontrar, todas las razones de precio-valor sectoriales serán idénticas). Este enfoque lo sugirieron a nivel teórico Farjoun y Machover (1983) y en términos empíricos lo siguieron Cockshott y Cottrell (1998). La estadística apropiada aquí es el coeficiente de variación (cv), esto es, la razón de la desviación estándar con respecto a la media. ⁸ La idea es que si los precios están “cercanos” a los valores trabajo el cv del precio con respecto a la razón valor entre sectores debe ser “pequeño”.

Una dificultad con este enfoque es que el cv no es una estadística normalizada (a diferencia del coeficiente de correlación, que satisface –1 ≤ p ≤ 1), de forma que no es inmediatamente obvio qué significa “pequeño”. Empero, uno puede comparar el coeficiente de variación entre distintos candidatos para valor base, como ya lo señalamos con anterioridad. Observando la proporción de x-contenido respecto al precio de 100 sectores de la economía del Reino Unido, Cockshott y Cottrell (1997a) encontraron un cv de 0.198 para x = trabajo; 11.41 para petróleo; 3.69 para electricidad y 7.81 para hierro y acero; la cifra para la base trabajo es claramente mucho menor en comparación con las otras.

Una línea de investigación relacionada sería comparar el cv de las razones precio-valor utilizando cuadros de insumo-producto con diferentes grados de desagregación. La mayor parte de los cuadros de ingreso-producto comprenden entre 50 a 100 sectores; no obstante, el US Bureau of Economic Analysis publicó un cuadro con más de 400 sectores. Uno podría esperar encontrar una dispersión de alguna forma más amplia de razones de precio-valor al usar datos más desagregados, dado que habría menos mezcla y promedios. Qué tanta diferencia haría esto, es una cuestión empírica para la cual aún no contamos con una respuesta. Permítasenos subrayar que este tipo de investigación nos ha proporcionado información adicional útil respecto a la relación precio-valor ―referente a qué tan robusta es en un nivel más “micro”―, en contraste con el cargo estéril y confuso de correlación espuria.

Conclusión

Hemos considerado dos acusaciones presentadas por Nitzan y Bichler contra la investigación que pretende ofrecer apoyo empírico a la teoría del valor trabajo.

En contra de su objeción, en el sentido de que la investigación no descubre valores trabajo y permanece en un círculo de relaciones precio-precio, hemos respondido que los talones de recibo de nómina son un sustituto razonable para el concepto de tiempo de trabajo socialmente necesario que planteó Marx y, más aún, que las cifras del tiempo de trabajo están disponibles para algunos países y que se las ha utilizado en la literatura, y, además, que también es posible obtener, a partir de los talones de recibo de nómina, datos de tiempo de trabajo si hay información sobre la tasa salarial promedio por industria. En este punto también hemos sostenido que el haber utilizado coeficientes interindustriales calculados como proporción de magnitudes monetarias, en lugar de proporción de flujos en especie, de hecho no compromete el análisis.

Contra la acusación de correlación espuria, presentamos una serie de argumentos para refutar la idea de que existe una correlación “correcta” (pero posiblemente nula) entre precios y valores a nivel de la mercancía individual que es artificialmente inflada usando datos a nivel de industria. La supuesta correlación correcta es de hecho no válida, rompe las reglas del análisis dimensional, mientras que hay bastante evidencia auxiliar que apoya la validez de los hallazgos de una relación estrecha entre precios y valores; un hallazgo que también puede expresarse sin recurrir a la correlación. Quedan abiertas preguntas interesantes respecto a la relación precio-valor, sin embargo, la formulada respecto a si es una correlación espuria no es una de ellas.