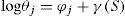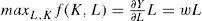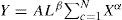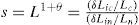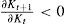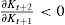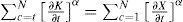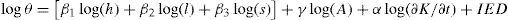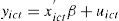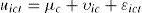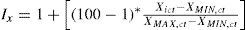El artículo evalúa el impacto del trabajo calificado en la productividad y retornos del trabajo a nivel de subsectores industriales de las zonas urbanas más pobladas del norte para el periodo 2001-2009. Se observó que el porcentaje de trabajadores con escolaridad alta, que labora en los 53 subsectores considerados en el estudio, creció de 9.69 a 14.34 por ciento. Las estimaciones de los modelos de panel fijos, aleatorios y mixtos sugieren que los retornos a escala son crecientes siempre y cuando se tenga la presencia de flujos de capital positivos e inversión extranjera directa. También se destaca que existe una importante variabilidad en los resultados, a nivel de ciudad, aunque ésta deriva más de las características de la actividad económica que de la localización de las ciudades.
La frontera norte de México ha experimentado cambios importantes en su estructura y dinámica económica en los últimos 20 años como consecuencia de la creciente integración económica entre México y Estados Unidos. Frente a ello, se ha observado un importante crecimiento económico y de la población en las ciudades fronterizas, lo que ha generado la expansión urbana de las mismas. Asimismo, se han desarrollado sectores económicos importantes, particularmente el de la manufactura de exportación y las maquiladoras, causando aglomeraciones industriales en la región. Por ello, resulta importante estimar el efecto de estos cambios en el mercado laboral de las zonas urbanas de la frontera norte, ya que esto permitiría conocer si la urbanización, la especialización económica y los niveles de educación de la fuerza laboral han provocado cambios en los niveles de productividad y las remuneraciones de los trabajadores en estas zonas urbanas.
Al respecto, cabe destacar que los incentivos a especializarse, así como las decisiones de mantener un flujo continuo de inversiones en infraestructura física y mejoras tecnológicas en las actividades económicas surgen primordialmente de los retornos crecientes derivados de la inversión en capital humano. El crecimiento tanto de una región económica como de una ciudad o país, o de una determinada industria, depende básicamente de la maximización en el uso intensivo de las habilidades y conocimientos adquiridos por el factor trabajo (Acemoglu, 2002; Henderson, 1974; Rosen, 1983). Además, cabe destacar que la competencia de mano de obra en el mercado de trabajo local también incentiva el aprendizaje (Schultz, 1972; Glaeser, 2011; oecd, 2012).
Por su parte, el surgimiento de las economías de escala en las industrias es un proceso complejo, no sólo porque puede venir de cualquiera de las distintas divisiones del trabajo que se dan dentro de determinada actividad moderna (Henderson, 2003), sino porque, a nivel agregado, puede existir la presencia de dichas economías de escala sin que pueda detectarse concretamente de qué actividades han surgido. A nivel agregado, un derrame (es decir, el beneficio de la interacción dentro o fuera de las empresas entre trabajadores con distintas habilidades y diversas disponibilidades de tecnología) se traduce en el crecimiento de una determinada firma, en el contexto del sector industrial al que se adscribe la actividad económica de dicha empresa.
Se ha señalado que el proceso de ajuste del mercado laboral, particularmente en lo relacionado a los salarios nominales, el empleo y la productividad, es com- plejo y no se limita exclusivamente a una relación como la curva de Phillips (Galindo y Catalán, 2010). Por tanto, en el ámbito macroeconómico, es difícil estimar los efectos de escala generados por derrames de habilidades y conocimiento. En ese sentido, se ha señalado que la existencia de economías de escala se aprecia en áreas geográficas reducidas, ya que en ellas se facilita la libre transmisión de conocimientos entre pares (trabajadores) debido a la proximidad física (Barro y Sala-i-Martin, 2004). En este contexto, tanto la ciudad como las industrias pueden ser un nivel de análisis más adecuado para estimar los efectos de escala surgidos del conocimiento (Barro y Sala-i-Martin 2004: 219).
Desde la perspectiva urbana, el potencial de los individuos y de las empresas que participan en los mercados deriva de la adquisición de habilidades y conocimientos, mediante los cuales es posible la aplicación de métodos y técnicas de producción que permitan desarrollar economías de escala o, en su defecto, aminorar el impacto en el crecimiento económico que pueda derivar de una crisis económica surgida de alteraciones fuera del control de la ciudad y sus agentes económicos (Jacobs 1970; Glaeser y Redlick, 2008; Glaeser, 2011; oecd, 2012).
En este sentido, el presente artículo busca encontrar evidencia de que el trabajo calificado, entendiendo por calificación la escolaridad y especialización, presenta rendimientos a escala mayores que el trabajo poco calificado en las zonas urbanas más densamente pobladas del norte de México entre 2001 y 2009, y que estos retornos no son sólo beneficios individuales, sino que existe un derrame de capital humano, tanto pecuniario como no pecuniario, a nivel subsector industrial y ciudad, entendiendo por pecuniarios los impactos monetarios de tener conocimiento, y no pecuniarios los efectos en la producción misma. Del mismo modo, se pretende estimar los retornos a través del tiempo entre los sectores de la actividad económica y entre las ciudades. Lo anterior basado en la premisa de que la atracción de los trabajadores hacia la ciudad surge de los incentivos de intercambiar habilidades que complementen las ya adquiridas, de aprender de los otros y de beneficiarse de la diversidad de habilidades (Marshall, 1890; O’Flaherty, 2005).
En específico, se analizan las diez zonas urbanas más pobladas del norte de México bajo la luz de las habilidades y conocimientos de los individuos que las integran. Con más de cuatro décadas de cambios en políticas e instituciones que han reestructurado la actividad de la región norte del país (Mendoza Cota, 2002; Urciaga García y Almendarez Hernández, 2008) se espera observar que la dinámica laboral en las ciudades, sus empresas e individuos, haya cambiado, y que el tener habilidades y conocimientos sea un factor decisivo en las diferencias en producción y retribuciones al trabajo.
El trabajo se divide de la siguiente manera: en el apartado dos se esbozan elementos empíricos sobre las condiciones laborales en la actividad econó-mica de las diez zonas urbanas más pobladas del norte de México durante dos cortes de tiempo: 1999 y 2009. Con base en ello, en el apartado tres se presentan las bases teóricas del estudio, en el cuatro se incluye la metodología del estudio, en el cinco que discuten los resultados econométricos y, finalmente, en el seis se exponen las conclusiones.
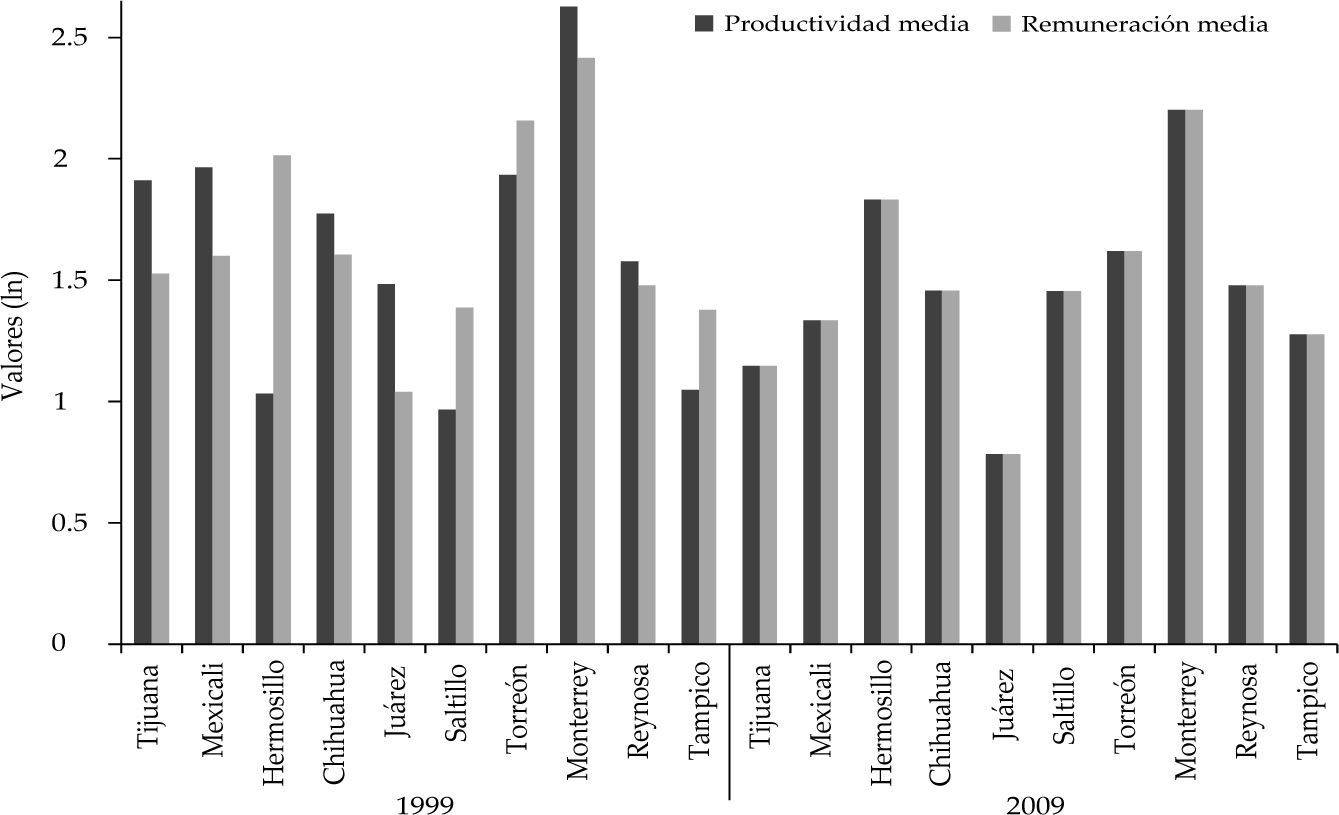
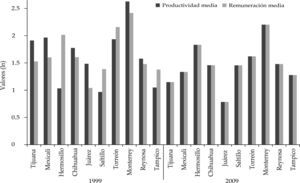
Las particularidades de los mercados laborales urbanos del norte de MéxicoEn esta sección se describe el comportamiento de las variables que caracterizan el mercado laboral de las principales ciudades de la frontera norte de México. En ese sentido, la gráfica 1 muestra la productividad (π)1 y remuneraciones promedio (w) en logaritmos para cada ciudad durante 1999 y 2009. Se aprecia en la mayoría de los casos que ambas variables decrecieron durante los años considerados. En Hermosillo, Torreón, Saltillo y Tampico las remuneraciones sobrepasan a la productividad. En el resto de las ciudades ocurre lo contrario. El único caso que más se acerca a una situación de igualdad entre π y w es Juárez, en 2009. En tal sentido, puede concluirse que no hay igualdad en el comportamiento de las remuneraciones y productividad en los datos analizados, lo que sugiere que existen factores localizados en los centros urbanos que implican una diferenciación en el comportamiento de los mercados laborales.
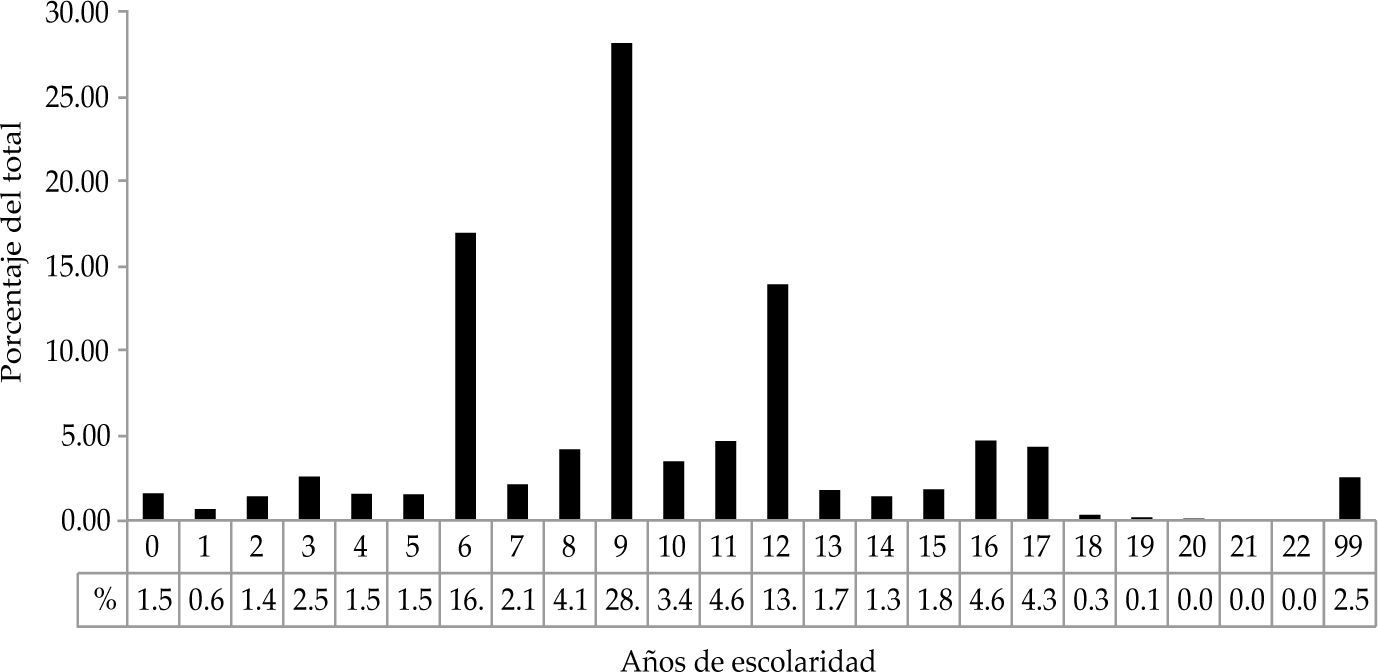
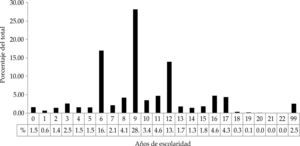
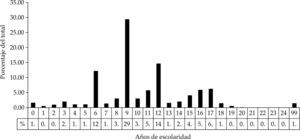
La gráfica 2 muestra los años de escolaridad del personal ocupado de 53 subsectores industriales2 (de acuerdo con la clasificación del Sistema de Clasificación Industrial de América del Norte, scian, del Instituto Nacional de Estadística y Geografía, inegi) para las diez áreas urbanas más pobladas de las seis entidades del norte de México en el año 2000. En concordancia con la escolaridad promedio de los seis estados en su conjunto, la mayoría del personal ocupado en los subsectores mencionados cuenta con nueve años de escolaridad, 28.1% del total del personal.
Los otros dos grupos más grandes son: seis años de escolaridad, que engloba a 16.9% del personal ocupado, y 12 años de escolaridad, con 13.9% del total. Cabe destacar que estos tres grupos (6, 9 y 12 años de escolaridad) representan 58.9% de todo el personal ocupado en dichos subsectores en el 2000. Esta cifra, sumada al 14.43% de los restantes niveles de escolaridad (entre ocho y once años), representan 73.33% del total del personal ocupado. Es decir, 73 de cada 100 empleados tienen entre 6 y 12 años de escolaridad. Por su parte, el total de personal con educación superior (de 16 años de escolaridad en adelante) suman 9.69% del personal total de estas zonas urbanas, mientras que 9.29% cuenta con menos de cinco años de escolaridad, lo equivalente a primaria incompleta o educación nula.
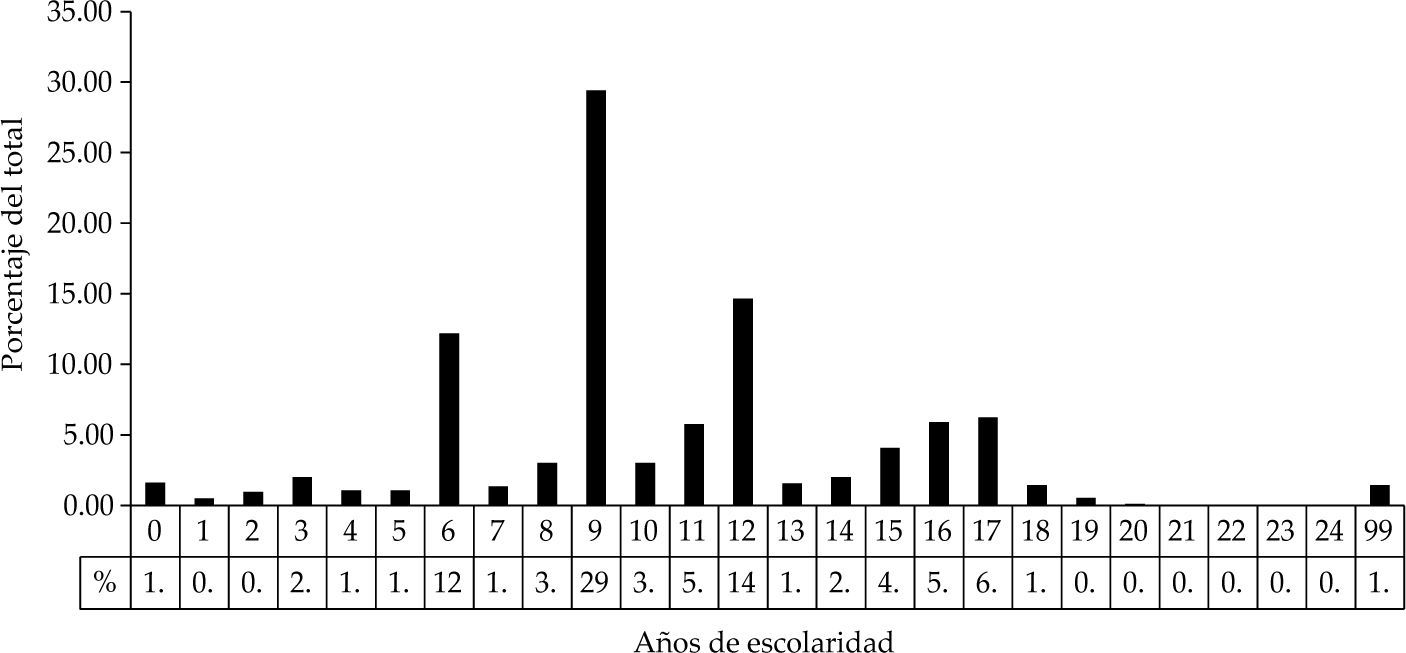
La gráfica 3 muestra los años de escolaridad del personal ocupado de los 53 subsectores económicos para las diez áreas urbanas más pobladas de las seis entidades del norte de México en el 2010. Para el final de la década, 56.1% de los trabajadores tenían nueve años de escolaridad, una caída de 2.8% respecto a 2000. De igual manera, el grupo de 6 a 12 años de escolaridad, que en 2000 sumaban poco menos de tres cuartas partes del total, representa para 2010 sólo 69.21% del total, una caída de poco más de cuatro por ciento.
El personal con primaria incompleta (de 0 a 5 años de escolaridad) también experimento una caída, ya que en 2010 registra 8.3% del total, 1.01% menos que en 2000. La caída generalizada en todos los grupos podría estar indicando una caída en el empleo en general, dadas las condiciones recesivas experimentadas a nivel global durante la década; sin embargo, el grupo de 16 y más años de escolaridad creció, al pasar de 9.69% en 2000, a 14.34% para 2010.
Es de señalar que tanto en la gráfica 2 como en la 3 existen variaciones en la escolaridad, aunque pequeñas. No obstante, las diferencias de 2000 a 2010 en la composición de los estratos con mayor escolaridad se estiman considerables durante el periodo.
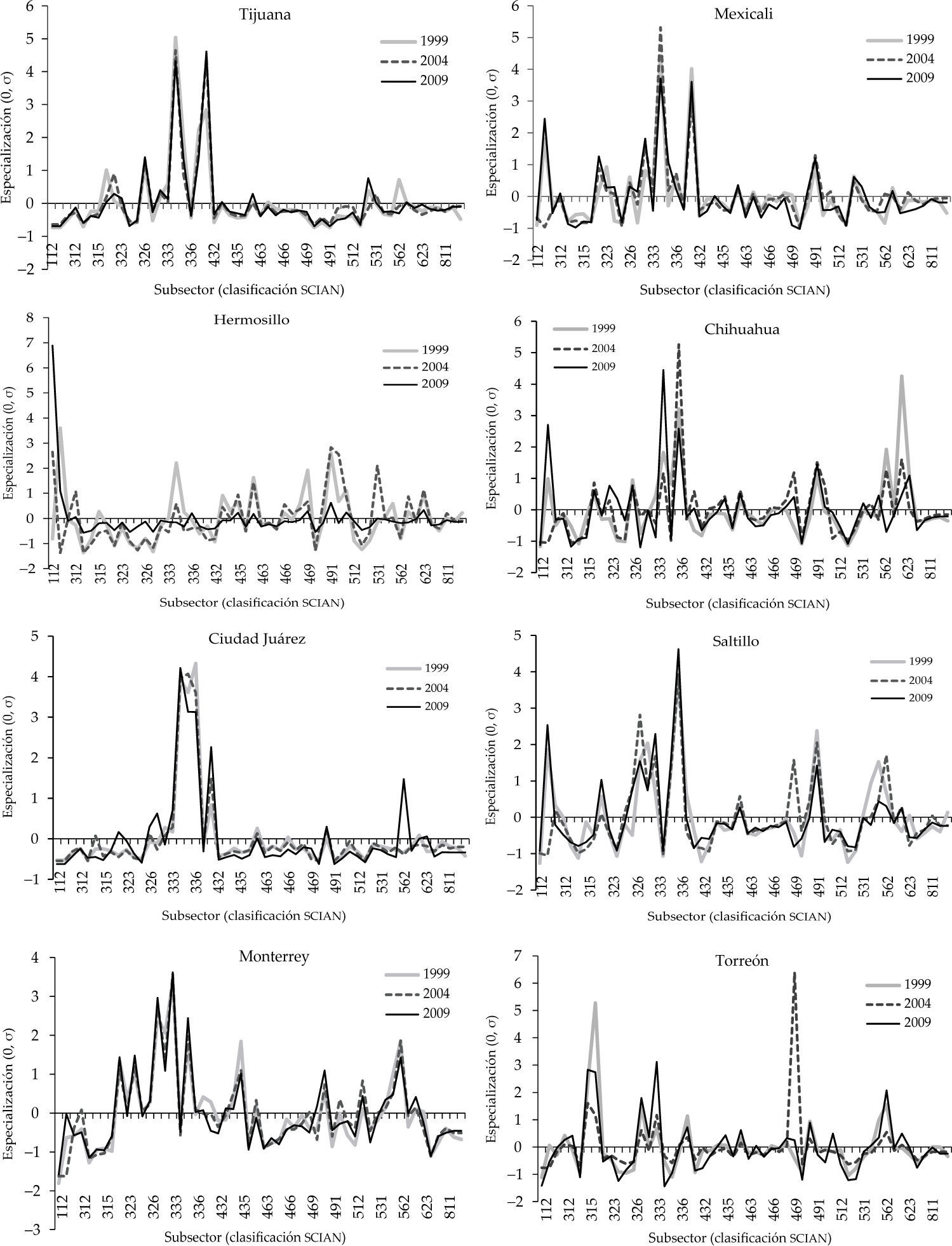
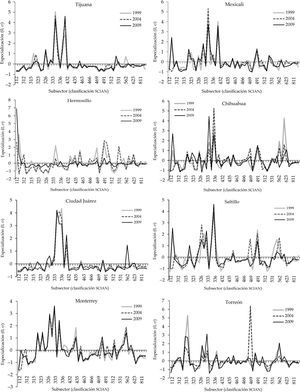
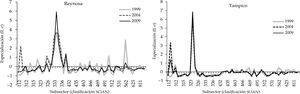
Por lo que corresponde a la especialización laboral, en la gráfica 4 se presenta el índice de especialización construido para cada área urbana de la muestra en los tres momentos en el tiempo que se tienen. El índice hecho fue normalizado (es decir, media cero y desviación constante por año) con el fin tener un punto de comparación en la distribución por año de la utilización de la mano de obra en los 53 subsectores en cada zona urbana. Se optó por incluir en esta gráfica el año 2004, ya que permite ver la transición en actividades dentro de las zonas urbanas estudiadas durante la década.
Se destaca que el subsector de actividad económica en el que se presentan elevaciones por arriba del promedio nacional es el de fabricación de equipo de computación, comunicación, medición y de otros equipos, componentes y accesorios electrónicos (334), el cual constantemente presenta un índice más elevado en varias de las ciudades analizadas para el 2009, salvo en Tijuana y Mexicali, donde ya presentaba picos en 2004 y 1999. De hecho, de 2004 a 2009 cae en Mexicali la intensidad en el uso de población ocupada en dicho subsector.
Dos casos que pudiese decirse se esperaban son los picos presentes en Tampico (221: Generación, transmisión y suministro de energía eléctrica, y 324: Fabricación de productos derivados del petróleo y del carbón) y Hermosillo (112: Ganadería (sólo acuicultura animal), 5los tres años, pero mayor en 2009). Notable es la caída en Tampico del subsector 221 durante 2004-2009, ciudad donde la industria petrolera tiene presencia, caso único entre las diez zonas urbanas analizadas. Dada la fuerte influencia de las actividades primarias en el estado de Sonora, no es raro que Hermosillo muestra especialización en un subsector de dichas actividades, pero sí lo es la creciente especialización durante los tres cortes temporales.
En adición al subsector 334, la presencia del 333: Fabricación de maquinaria y equipo, del 335: Fabricación de equipo de generación eléctrica y aparatos y accesorios eléctricos, del 336: Fabricación de equipo de transporte y del 339: Otras industrias manufactureras, reafirman la importancia de la industria de ensamblaje en la región norte de México. Sin embargo el panorama y la relevancia en el tiempo en cada caso particular es distinta: en Tijuana, por ejemplo, la especialización del subsector 339 creció, al igual que en Juárez. En cambio, en Chihuahua y Juárez la especialización en el subsector 336 cayó durante la década, mientras que en Saltillo repuntó.
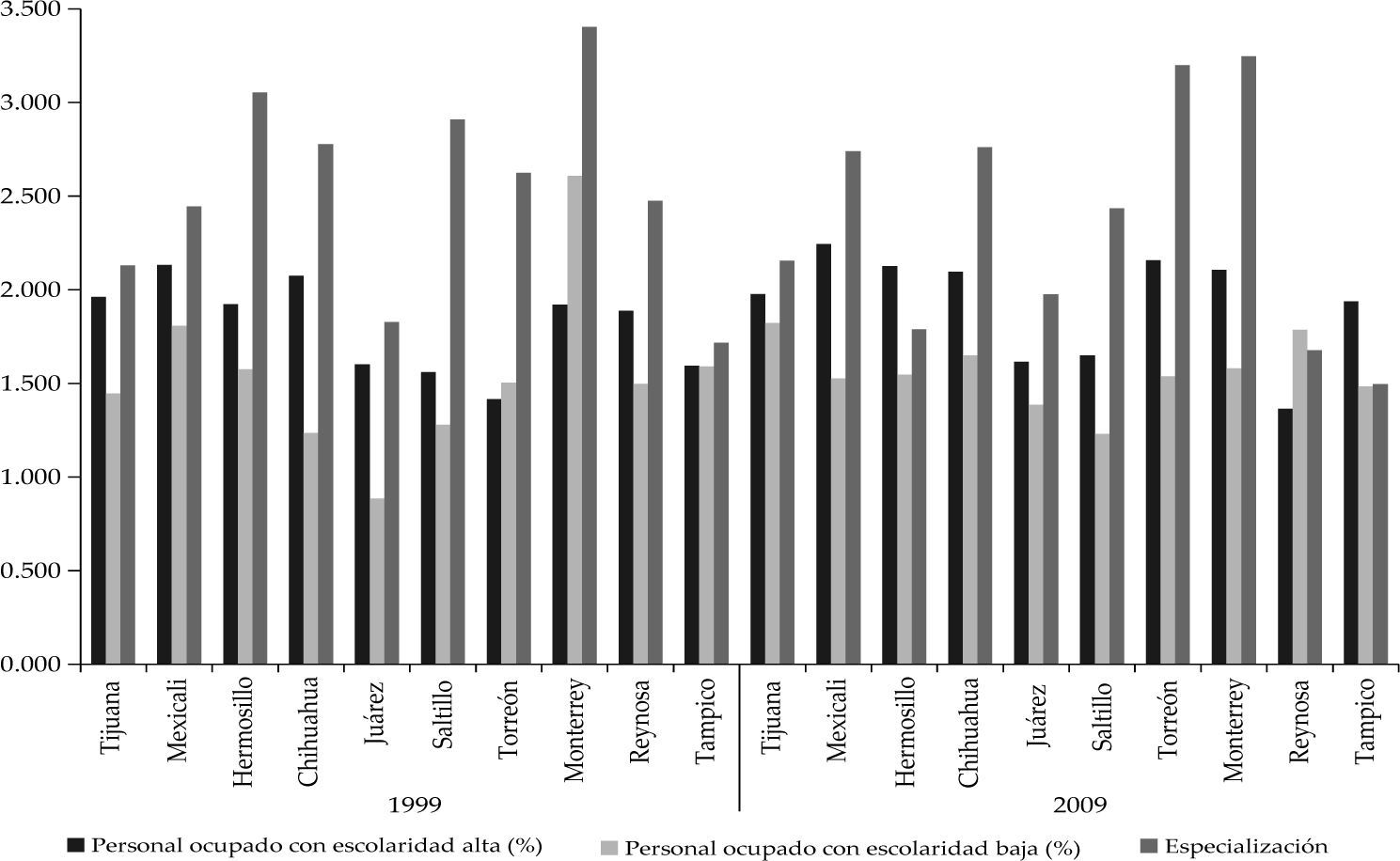
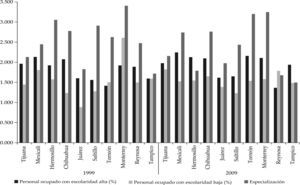
La gráfica 5, al igual que la gráfica 1, permite ver los cambios entre las variables independientes: h (porción de trabajadores con escolaridad alta), l (porción de trabajadores con escolaridad baja) y s (especialización laboral). 3 En la mayoría de los casos h es mayor que l tanto en 1999 como en 2009, las excepciones son Monterrey, en 1999, y Reynosa, en 2009. De 1999 a 2009 es visible la caída en las tres variables consideradas, siendo más evidente en la especialización laboral para casi todos los casos.
En conclusión, el fenómeno que quizá se esté viendo aquí es la reordenación de la masa laboral ante los cambios en los mercados de trabajo, dadas las condiciones recesivas de la década. Empresas van y otras vienen, mientras que la población ocupada se va adaptando a la situación. Asimismo, la gráfica 5 permite concluir que es posible desarrollar un análisis econométrico a fin de encontrar efectos marcados de tiempo en la especialización. En el caso de la escolaridad en el trabajo, las disparidades son quizá más presentes entre ciudades que de un periodo a otro, aunque con la gráfica es posible exhibir que en efecto existen.
Perspectiva teórica del análisis del mercado laboral-urbanoLa perspectiva teórica de la investigación se sustenta en dos vertientes definidas: la teoría del capital humano y las teorías económicas sobre sistemas de ciudades. Dado que las posturas que se adscriben a una o a otra no son mutuamente excluyentes, se busca integrar las dos visiones a manera de síntesis de las recopilaciones teóricas con el objetivo de estar en posibilidad de tener elementos teórico-conceptuales que permitan darle perspectiva a las estimaciones econométricas sobre el efecto del trabajo calificado en la productividad laboral de las áreas urbanas de la frontera norte de México.
Teoría del capital humanoEl capital humano es una categoría económica que considera al trabajo altamente calificado como un factor de la producción, intangible y capaz de generar riqueza, no sólo al individuo que la posee sino a la sociedad en su conjunto. Además, es un rasgo distintivo de quien lo posee debido a que, en la forma de conocimiento y técnica, el trabajador al igual que el capitalista cuenta con un acervo para hacer uso de él (Schultz, 1972: 5-6). Por ello, la inversión en educación es una actividad rentable (Becker, 1993: 17) o, dicho de otra manera, existen retribuciones por su uso que derivan de los rendimientos por la aplicación de dicho capital en el proceso de producción. Así, tanto la escolaridad como el entrenamiento en el trabajo o aprendizaje al hacer4 son importantes para el trabajador (Lucas, 1988). Independientemente de la forma en que dicho conocimiento y las habilidades laborales hayan sido adquiridos (de manera formal o informal), estás elevan las ganancias y productividad (Becker, 1993: 20-1).
Si conceptualmente es posible desglosar al capital humano por lugar de adquisición (escuela y trabajo), en términos técnicos es posible también definirlo como un bien rival y no rival. El capital humano es rival si se le concibe como aquel conocimiento cuya aplicación práctica en la producción no es concebida sin la presencia física del individuo, y no rival si se le asume como el acervo que, si bien es producido por individuos, permanece y puede ser aplicado tanto por el creador del mismo como por otros (Romer, 1990).
Para varios autores (Romer, 1990; Lucas, 2008; Moretti, 2004) es en la no rivalidad del aspecto del capital humano donde se deben buscar derrames de éste. Por derrames debe entenderse la influencia del capital humano por encima y más allá del rendimiento individual que un individuo pueda percibir por tenerlo (Moretti, 2004). En otras palabras, se debe asumir que los factores de la producción funcionan bajo rendimientos crecientes a escala y que el proceso, después de un tiempo, ha madurado lo suficiente como para asumir que la creación de conocimiento, como una externalidad, ha surgido y favorecido la productividad (Barro y Sala-i-Martin, 2004).
Sin embargo, en la literatura no queda claro cuál es esta no rivalidad y de dónde surge. Existe la posibilidad de que surja de la investigación y el desarrollo (Romer, 1990) que una empresa o industria lleve a cabo para la mejora de su proceso productivo. Puede provenir de la interacción entre individuos cuyo nivel de capital humano es el promedio en la economía o del nivel agregado de capital humano (Lucas, 1988; Barro y Sala-i-Martin, 2004; Moretti, 2004).
En el presente trabajo se utiliza la siguiente ecuación:
donde logθj es un parámetro que captura la productividad, φj representa el aporte individual y γ(S) el aporte colectivo de los trabajadores.
Asimismo, se considera que Y=AKα+Lβ, donde K es el capital y L es el trabajo, se asume que α+β=1 (Barro y Sala-i-Martin, 2004). De esta forma, en las economías imitadoras como México, el aporte del capital físico no es total, sino que se comporta como el agregado de lo disponible (Y=ALβ∑c=1NXα). Suponiendo que A (los cambios en productividad) depende de la educación total de los trabajadores en la ciudad, entonces A=γ(S), mientras que L está en función de la escolaridad o aporte marginal de educación, es decir: L=φj.
Así, se obtiene Y=γ(S)φj K, cuya transformación logarítmica genera la ecuación: lnY=lnγ(S)+lnφj+lnK. Retornando la ecuación inicial, el modelo toma la forma de: logθj=φj+γ(S), donde θ es un cambio en la productividad (productivity shifters), φj son efectos de grupo (j) que capturan variaciones de capital humano individuales y S es el stock de capital humano total (Acemoglu y Autor, 2011: 47-50; Moretti; 2004: 2271).
La teoría económica en los sistemas de ciudadesLas economías de escala pueden surgir en distintos niveles de la actividad económica, pero invariablemente, que surjan o no, es un asunto que permanece ligado a las características de la ciudad e individuos que la habitan. En muchos sentidos, la ciudad es la más pequeña unidad geográfica observable, donde la interacción de los agentes económicos puede verse como un sistema interconectado y regido por la heterogeneidad de los individuos que determina el aporte individual a la riqueza generada (Hesham M. y Anas, 2004).
Las habilidades y conocimientos son, en gran parte, esenciales para comprender el porqué de esta heterogeneidad entre agentes y, por ende, un elemento importante para explicar la presencia de economías de escala. Entre muchas otras cosas, la heterogeneidad del factor trabajo urbano, y su capacidad para especializarse o diferenciarse, define el patrón de la vida económica dentro de la ciudad y, a final de cuentas, el desarrollo o deterioro de la misma (Glaeser, 2011; Jacobs, 1970).
Las primeras discusiones sobre la aglomeración económica suelen atribuírsele a Marshall, quien dedica en su obra central un buen espacio a la discusión de la localidad, en específico a cómo los patrones de la aglomeración de la actividad económica divergen entre las distintas ciudades y pueblos, trayendo consigo habilidad y destreza (Marshall, 1890). A partir de ahí surgen dos vertientes claras del estudio de la difusión del conocimiento en las ciudades: la búsqueda de beneficios por aglomeración que generan economías señaladas por Marshall, Arrow y Romer (Henderson, 2003; Glaeser, 1999) y los beneficios por diferenciación en las actividades económicas o las economías señaladas por Jacobs (Jacobs, 1970; Glaeser, 1999).
Cabe destacar que las teorías sobre sistemas de ciudades suelen centrarse en analizar el surgimiento de la aglomeración humana, así como la existencia o desaparición de las ciudades (Hesham M. y Anas, 2004; Glaeser y Redlick, 2008). Entre sus discusiones destaca un concepto clave para el trabajo presente, que es el de la especialización laboral. Tanto aglomeración industrial como polinización de nuevas actividades surgen, inicialmente, de la asimilación de conocimientos no del individuo, sino de la masa laboral en sí (Glaeser et al., 1992; Henderson, 2003). El concepto trastoca lo ya abordado en teoría del capital humano sobre el aprendizaje en el trabajo. Sin embargo, los autores citados lo exponen como inherente a la ciudad, como un fenómeno humano con un patrón geográfico (Bacolod, Blum y Strange, 2009), que refleja la abundancia en la mano de obra capacitada en una actividad en específico dentro de la localidad (Glaeser, 1999; Henderson, 1994).
Finalmente, otro elemento teórico que se introduce en el enfoque analítico del trabajo es la especialización, que surge del tiempo empleado en una actividad. Retomando como punto de partida la ecuación de Duranton y Puga (2004) se obtiene: x(h)=β[l(h)]1+θ, donde x es el producto, β la productividad, h el tiempo que el trabajador l dedica a la producción de x, y θ la intensidad del beneficio individual de especializarse. Si se asume el capital físico como dado al nivel agregado, lo anterior implica que Y=βL1+θ, es decir, que la especialización genera retornos crecientes al trabajo.
Teorías sobre cambios en la productividad y su mediciónEl estudio de la productividad es muchas veces situado bajo la perspectiva de la convergencia o divergencia entre regiones a un nivel agregado. Existe evidencia de una marcada convergencia en el mundo industrializado durante el siglo pasado: los países con baja productividad laboral a finales del siglo xix experimentaron una tasa de crecimiento mayor de dicha convergencia a lo largo del siglo xx (Baumol, 1986). También el entorno ha sido estudiado como elemento que afecta a la productividad laboral (Sveikauskas, 1975), así como los ciclos económicos (Jorgenson y Griliches, 1967).
Las fuentes de los choques de productividad son alteraciones en las posibilidades de producción, como la tecnología, y variaciones en los costos de utilización de los factores, entre los cuales está el factor trabajo. El impacto del conocimiento en el terreno productivo es un choque en la productividad, ya que potencia las posibilidades de producción de una planta, industria o región (Bernanke, 1981). Las teorías antes mencionadas (capital humano y teorías sobre sistemas de ciudades) indagan sobre estos choques y su relación con la adquisición de conocimiento. Cabe destacar que la medición de los choques de productividad como los derrames de conocimiento implica dividirlos en pecuniarios y no pecuniarios (Acemoglu y Autor, 2011). Por ello, el modelo planteado en el apartado anterior, logθj=φj+γ(S), permite una buena aproximación al medir θj, ya sea la productividad misma (Y/L o π) o la percepción monetaria del trabajo por el aporte a la producción, puesto que en equilibrio competitivo
por lo que en teoría el salario o remuneración es una buena proxy para medir la productividad.
Formalización del modelo aplicadoA fin de conciliar las posturas teóricas que componen el marco, la aplicación y la practicidad del modelo empírico aplicado, se parte de unidad regional de análisis a nivel de ciudades, las cuales están enmarcadas en el entorno nacional. Desde esta va, se asume a la economía mexicana como un país que imita la tecnología, lo que puede formalizarse como: Y=ALβ∑c=1NXα, con X como bienes intermedios disponibles (Barro y Sala-i-Martin, 2004: 352) o capital físico K. Es de señalar que la única diferencia entre un país imitador y uno creador de tecnología reside en diferencias entre A y L. En particular, las diferencias en A (ya sea asumido como un parámetro de productividad o el nivel agregado de capital humano) son atribuibles a diferencias institucionales entre países, como el acceso a educación y el entorno productivo en el que las empresas operan (Acemoglu y Dell, 2010: 4). Para México y, en específico, la realidad productiva del norte del país, dos grandes cambios son el modelo de Industrialización por Sustitución de Importaciones (isi) de mediados del siglo veinte y el Programa Nacional de Industrialización Fronteriza de la segunda mitad del mismo siglo (Bataillon, 1988: 39-40), que generó la llamada industria maquiladora de exportación.
El objetivo de este trabajo es analizar los pormenores de los efectos de ambos cambios en los patrones de crecimiento económico. De esta manera, el estudio parte del supuesto de que dichos cambios han ocurrido, es decir, las ciudades en cuestión pasaron dichas etapas y, actualmente, se encuentran en condiciones determinadas que, se esperaría, permitan ver al capital humano y a la especialización como factores clave en la productividad y remuneraciones.
Formalmente, siguiendo a Acemoglu y Autor (2011: 47-8), para las zonas urbanas del norte de México la función de producción estaría determinada como sigue:
donde Lβ=hβ1 sβ2 lβ3, h es el aporte marginal del trabajador en la industria i con mucha escolaridad y l el de poca escolaridad, X representa a los bienes intermedios o capital físico disponible y s a la especialización laboral local entendida como:
o porción (δ) de trabajo en una industria i en la ciudad c respecto a la industria i a nivel nacional (n).
Si una economía es imitadora existe un costo de imitar las innovaciones exteriores (Barro y Sala-i-Martin, 2004: 353-5). En el modelo a aplicar no se toman precios ni se buscan los efectos de mercado por la imitación. Es decir, no se busca determinar un costo explicito en la formalización, por el contario, se asume que el costo va implícito al dividir la participación del trabajo (β) en varios elementos. El trabajo, pues, no exhibe retornos similares a los de una economía innovadora a menos que existan todos los elementos requeridos (trabajo calificado, especialización laboral).
Asimismo, un cambio tecnológico surgido de inversiones en capital físico, K, sucede si la fuerza laboral cuenta con la calificación necesaria (Acemoglu, 2002). Bajo el esquema que se ha construido el modelo, sin embargo, dicho cambio por inversiones en K se internaliza: la fuerza laboral ya tiene una escolaridad y especialización dadas. En una nación imitadora, los flujos de capital son internos y externos, y divisibles, puesto que existen registros de los flujos de inversión extranjera directa (ied), cuyo impacto es considerable, especialmente en las zonas del norte de México (Gallagher y Zarsky, 2007; Feenstra y Hanson, 1995).
Es posible que K (o los insumos intermedios ∑c=1NXα, como se les ha nombrado antes también) se tome como un flujo fijo. Si en el tiempo t tenemos Kt=1, entonces en t+1 tendremos K=0 si:
y en t+2 si:
Es decir, si N es la suma de actividades en la economía (o bienes intermedios disponibles), entonces:
será como se asume formalmente al capital físico cuyos valores son 0 y 1 solamente. También IED=1 si el subsector i, en la ciudad c al año t recibe flujos de inversión extranjera directa, y 0 en otro caso.
Metodología de estimaciónCon base en los aspectos teóricos presentados anteriormente en la ecuación [1] y retomando los supuestos considerados en el apartado anterior, se desarrolló un modelo empírico para medir las variables transformadas en logaritmos, el cual engloba los efectos individuales de capital humano sobre la productividad φj y los efectos globales γ(S), o del capital humano total, y en el cual se esperaría observar derrames de capital humano de la siguiente manera:
Ecuación en la cual:
- 1.
logθ es el parámetro que mide la productividad laboral. En esta investigación, logθ=logπ=logw, donde π es la productividad medida en términos de volumen de producción (valor agregado) yw son las remuneraciones percibidas.
- 2.
φj=[β1 log(h)+β2 log(l)+β3 log(s)] es la parte de efectos individuales, conh como trabajo con escolaridad alta,l como trabajo con escolaridad baja ys un índice de especialización.
- 3.
γ(S)=γ log(A) es la parte de la educación total en la ciudad, la suma de todos los años de escolaridad de todo el personal ocupado en el área urbana, o los efectos globales, de donde se espera surjan los derrames. Con el fin de mantener la notación en minúsculas que se tiene de las variables, se considerará que γ log(A)=a, que no es el mismo que el coeficiente α del capital físico.
- 4.
α log(∂K/∂t)+IED es la parte de capital físico, tanto el flujo existente como el aporte del capital extranjero. Ambas variables son ficticias (valores de cero y uno).
De esta manera, el modelo permite estimar el impacto de los determinantes de la productividad laboral en las ciudades más grandes del norte de México, utilizando diversas variables que afectan las habilidades y calificación de la fuerza de trabajo. En primer término, la variable del punto 2 recoge los efectos marginales de los trabajadores de cada una de las industrias consideradas. Dichos efectos se relacionan con los diferentes niveles educativos de los trabajadores y el grado de especialización laboral que éstos tengan (φj). Adicionalmente, se construyó una variable que incluye el efecto total de la educación y la posibilidad de que esto genere efectos de derrame o difusión de las habilidades laborales debido a la aglomeración de trabajadores en las industrias y ciudades consideradas [γ(S)]. Finalmente, se incluyó una variable que representa el capital físico con valores de cero a uno, con el fin de controlar los efectos del capital en la productividad laboral
Modelo de panel con efectos mixtosDe origen, la estructura del modelo implica que los datos presenten una estructura multinivel de tres dimensiones: ciudad, subsector y tiempo. El modelo deberá entonces tener, matricialmente, la siguiente forma:
donde i denota el subsector económico, c la ciudad, t el tiempo y x es un vector de K variables explicativas (Hsiao, 2003: 302), las cuales se han definido en el apartado anterior.
De acuerdo con Baltagi (2001: 175), el término de perturbaciones tiene también una estructura con errores anidados de la siguiente manera:
Expresión en la cual μc representa el error correspondiente a la ciudad y vic el error correspondiente a la industria.
Por consiguiente, los componentes del error anidado se convierten en estima- dores de la magnitud que aportan a la varianza total las actividades en el subsector i, en la ciudad c y en el conjunto de niveles ict. Se asume que se distribuyen normalmente con media cero y σμ2,σν2,σε2, respectivamente. El modelo contempla una descomposición de la matriz de varianzas y covarianzas del error que permite realizar una regresión de mínimos cuadrados ordinarios (mco) de los datos transformados. Sin embargo, realizarla es similar a realizar una regresión de mínimos cuadrados generalizados (mcg) de la regresión original con pesos basados en la variabilidad entre y por grupos. (Hsiao, 2003: 303). Por ello, también se estimó un modelo de panel con efectos mixtos, que permite la transformación de la varianza del error, controlando así por la jerarquía en el orden de los mismos (Stata Press, 2011; Rabe-Hesketh y Skrondal, 2008). En particular, en la medida que las β del modelo de panel son consideradas como las medias entre grupos, es posible estimar la varianza entre los grupos de los modelos considerados.
De esta manera, dada la naturaleza de la base de datos utilizada, es imposible considerarla como un típico modelo de panel en el que se tienen y años y x observaciones en el territorio u, otra categoría agrupable. Por ello, el término “panel” se utiliza aquí para describir una técnica de estimación econométrica y no porque los datos con que se cuentan se comporten como un panel en sí. Es por ello que se corren las regresiones de efectos fijos y aleatorios con los datos basados en dos variables de grupo diferentes: por ciudad c y por subsector i. Ello puede traer consigo dos consecuencias: que los coeficientes de las variables al nivel 1 (subsector) y nivel 2 (ciudad) se inflen, o salgan no significativos, o que se presenten casos de multicolinealidad entre variables.
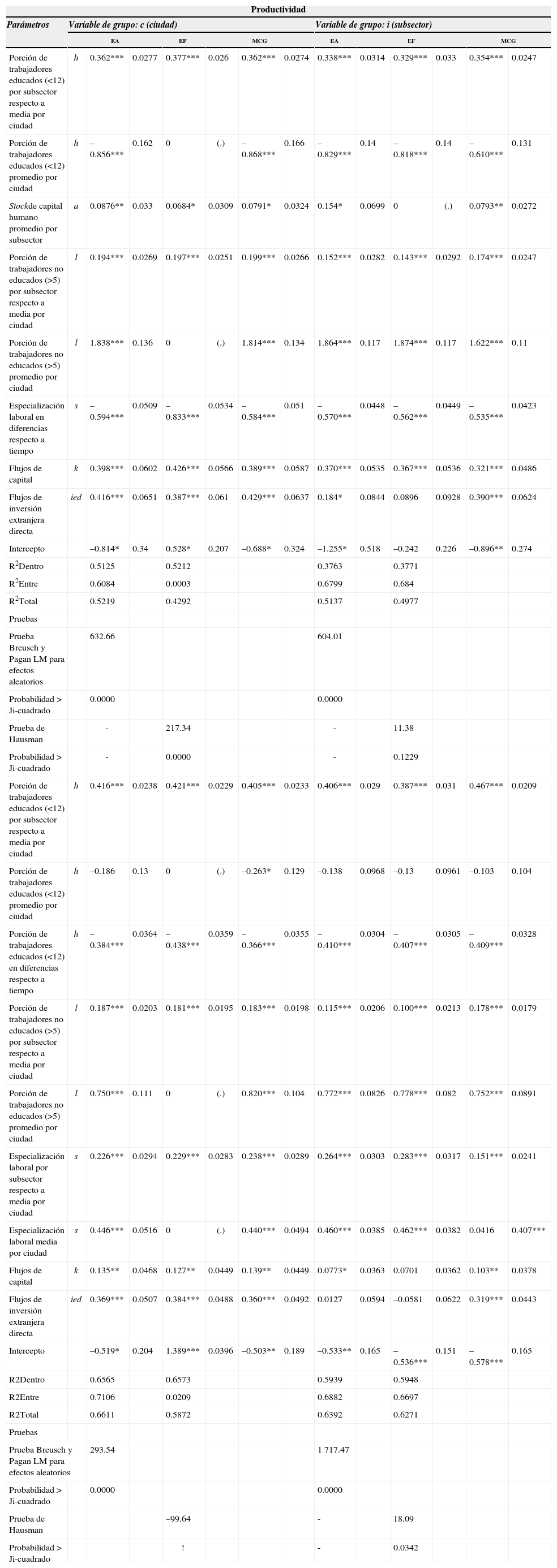
El cuadro 1 muestra los resultados de los modelos de panel estimados. En aquellos donde la productividad es la variable dependiente y se asumen efectos aleatorios, es posible captar efectos por ciudad. Los coeficientes de determinación totales obtenidos rondan ente 0.42 y 0.52, lo cual, para datos de panel, se estima adecuado. Estos modelos asumen una estructura de panel heterocedástica, con el fin de que cualquier resultado que muestre una variabilidad considerable salte a la vista de inmediato. Ese no fue el caso, por lo menos, en las variables relacionadas al trabajo y nivel de educación.
Resultados de los modelos de panel: efectos fijos, aleatorios y mcg por ciudad y subsectore s
| Productividad | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Parámetros | Variable de grupo: c (ciudad) | Variable de grupo: i (subsector) | |||||||||||
| ea | ef | mcg | ea | ef | mcg | ||||||||
| Porción de trabajadores educados (<12) por subsector respecto a media por ciudad | h | 0.362*** | 0.0277 | 0.377*** | 0.026 | 0.362*** | 0.0274 | 0.338*** | 0.0314 | 0.329*** | 0.033 | 0.354*** | 0.0247 |
| Porción de trabajadores educados (<12) promedio por ciudad | h | –0.856*** | 0.162 | 0 | (.) | –0.868*** | 0.166 | –0.829*** | 0.14 | –0.818*** | 0.14 | –0.610*** | 0.131 |
| Stockde capital humano promedio por subsector | a | 0.0876** | 0.033 | 0.0684* | 0.0309 | 0.0791* | 0.0324 | 0.154* | 0.0699 | 0 | (.) | 0.0793** | 0.0272 |
| Porción de trabajadores no educados (>5) por subsector respecto a media por ciudad | l | 0.194*** | 0.0269 | 0.197*** | 0.0251 | 0.199*** | 0.0266 | 0.152*** | 0.0282 | 0.143*** | 0.0292 | 0.174*** | 0.0247 |
| Porción de trabajadores no educados (>5) promedio por ciudad | l | 1.838*** | 0.136 | 0 | (.) | 1.814*** | 0.134 | 1.864*** | 0.117 | 1.874*** | 0.117 | 1.622*** | 0.11 |
| Especialización laboral en diferencias respecto a tiempo | s | –0.594*** | 0.0509 | –0.833*** | 0.0534 | –0.584*** | 0.051 | –0.570*** | 0.0448 | –0.562*** | 0.0449 | –0.535*** | 0.0423 |
| Flujos de capital | k | 0.398*** | 0.0602 | 0.426*** | 0.0566 | 0.389*** | 0.0587 | 0.370*** | 0.0535 | 0.367*** | 0.0536 | 0.321*** | 0.0486 |
| Flujos de inversión extranjera directa | ied | 0.416*** | 0.0651 | 0.387*** | 0.061 | 0.429*** | 0.0637 | 0.184* | 0.0844 | 0.0896 | 0.0928 | 0.390*** | 0.0624 |
| Intercepto | –0.814* | 0.34 | 0.528* | 0.207 | –0.688* | 0.324 | –1.255* | 0.518 | –0.242 | 0.226 | –0.896** | 0.274 | |
| R2Dentro | 0.5125 | 0.5212 | 0.3763 | 0.3771 | |||||||||
| R2Entre | 0.6084 | 0.0003 | 0.6799 | 0.684 | |||||||||
| R2Total | 0.5219 | 0.4292 | 0.5137 | 0.4977 | |||||||||
| Pruebas | |||||||||||||
| Prueba Breusch y Pagan LM para efectos aleatorios | 632.66 | 604.01 | |||||||||||
| Probabilidad > Ji-cuadrado | 0.0000 | 0.0000 | |||||||||||
| Prueba de Hausman | - | 217.34 | - | 11.38 | |||||||||
| Probabilidad > Ji-cuadrado | - | 0.0000 | - | 0.1229 | |||||||||
| Porción de trabajadores educados (<12) por subsector respecto a media por ciudad | h | 0.416*** | 0.0238 | 0.421*** | 0.0229 | 0.405*** | 0.0233 | 0.406*** | 0.029 | 0.387*** | 0.031 | 0.467*** | 0.0209 |
| Porción de trabajadores educados (<12) promedio por ciudad | h | –0.186 | 0.13 | 0 | (.) | –0.263* | 0.129 | –0.138 | 0.0968 | –0.13 | 0.0961 | –0.103 | 0.104 |
| Porción de trabajadores educados (<12) en diferencias respecto a tiempo | h | –0.384*** | 0.0364 | –0.438*** | 0.0359 | –0.366*** | 0.0355 | –0.410*** | 0.0304 | –0.407*** | 0.0305 | –0.409*** | 0.0328 |
| Porción de trabajadores no educados (>5) por subsector respecto a media por ciudad | l | 0.187*** | 0.0203 | 0.181*** | 0.0195 | 0.183*** | 0.0198 | 0.115*** | 0.0206 | 0.100*** | 0.0213 | 0.178*** | 0.0179 |
| Porción de trabajadores no educados (>5) promedio por ciudad | l | 0.750*** | 0.111 | 0 | (.) | 0.820*** | 0.104 | 0.772*** | 0.0826 | 0.778*** | 0.082 | 0.752*** | 0.0891 |
| Especialización laboral por subsector respecto a media por ciudad | s | 0.226*** | 0.0294 | 0.229*** | 0.0283 | 0.238*** | 0.0289 | 0.264*** | 0.0303 | 0.283*** | 0.0317 | 0.151*** | 0.0241 |
| Especialización laboral media por ciudad | s | 0.446*** | 0.0516 | 0 | (.) | 0.440*** | 0.0494 | 0.460*** | 0.0385 | 0.462*** | 0.0382 | 0.0416 | 0.407*** |
| Flujos de capital | k | 0.135** | 0.0468 | 0.127** | 0.0449 | 0.139** | 0.0449 | 0.0773* | 0.0363 | 0.0701 | 0.0362 | 0.103** | 0.0378 |
| Flujos de inversión extranjera directa | ied | 0.369*** | 0.0507 | 0.384*** | 0.0488 | 0.360*** | 0.0492 | 0.0127 | 0.0594 | –0.0581 | 0.0622 | 0.319*** | 0.0443 |
| Intercepto | –0.519* | 0.204 | 1.389*** | 0.0396 | –0.503** | 0.189 | –0.533** | 0.165 | –0.536*** | 0.151 | –0.578*** | 0.165 | |
| R2Dentro | 0.6565 | 0.6573 | 0.5939 | 0.5948 | |||||||||
| R2Entre | 0.7106 | 0.0209 | 0.6882 | 0.6697 | |||||||||
| R2Total | 0.6611 | 0.5872 | 0.6392 | 0.6271 | |||||||||
| Pruebas | |||||||||||||
| Prueba Breusch y Pagan LM para efectos aleatorios | 293.54 | 1 717.47 | |||||||||||
| Probabilidad > Ji-cuadrado | 0.0000 | 0.0000 | |||||||||||
| Prueba de Hausman | –99.64 | - | 18.09 | ||||||||||
| Probabilidad > Ji-cuadrado | ! | - | 0.0342 | ||||||||||
Notas: ea: efectos aleatorios; ef: efectos fijos; mcg: mínimos cuadrados generalizados. h y l (a nivel ciudad) omitidas por colinealidad. a (a nivel subsector) omitida por colinealidad. La matriz de varianzas-covarianzas utilizada en la prueba de Hausman (V_b-V_B) no es definida positiva.
Notas: h, l y a (a nivel ciudad) omitidas por colinealidad.La matriz de varianzas-covarianzas utilizada en la prueba de Hausman (V_b-V_B) no es definida positiva. El modelo ajustado en estos datos no cumple las condiciones asintóticas necesarias para la prueba de Hausman.
Nota: en todos los modelos mcg se asumen paneles heterocedásticos y no autocorrelación entre ellos. Errores estándar en cursivas. Significancia de parámetros: (*) p<0.05, (**) p<0.01 y (***) p<0.001. Fuente: elaboración propia con base en datos de Censos Económicos 1999 y 2009 y Censos de Población 2000 y 2010, inegi.
Los datos se obtuvieron de los censos oficiales de México publicados por el inegi. Se utilizaron en específico los Censos Económicos de 1999 y 2009, y los Censos de población y Vivienda de 2000 y 2010. Los primeros registran datos de la actividad económica ocurrida durante 1998 y 2008. Continuando con el estilo del Censo, se mantendrán los años que éste estipula en el análisis de las variables, así cuando se menciona 1999, en realidad es información sobre 1998, mismo esquema se aplica para 2009.
De los Censos Económicos se extraen cuatro variables: valor agregado censal bruto, remuneraciones totales, personal ocupado y formación bruta de capital fijo. De los Censos de Población se extrae información de los microdatos, en específico sobre la escolaridad acumulada del personal ocupado en las actividades económicas locales de las diez ciudades a considerar. Por último, todos los datos fueron ajustados para que quedaran como números índices, donde el valor más pequeño entre los subsectores, por ciudad, sería 1, y el valor más alto 100. Todas y cada una de las variables aquí descritas fueron tratadas de esta manera. Formalmente, se puede decir que cada variable X se transforma en:
Todo logaritmo natural obtenido se saca de las variables transformadas por este proceso.
Resultados de los modelos de panel y mcgEn los modelos del cuadro 1 se presentan los resultados de los modelos de panel de efectos fijos, aleatorios y mcg, por ciudad y subsectores. En los modelos donde las remuneraciones son la variable explicada, el agrupar por subsector resulta más contundente, dadas las pruebas individuales y conjuntas. Los coeficientes de determinación totales obtenidos (R cuadrada total) rondan ente 0.58 y 0.66, lo cual, para datos de panel, se estima bueno. Las pruebas lm de Breusch-Pagan indican que es pertinente mantener los modelos de efectos aleatorios. La prueba de Hausman para los datos agrupados por subsector también lo confirma. Sin embargo, la prueba de Hausman para los datos agrupados por ciudad no lo confirma, ya que se presenta una situación similar a la de los modelos con productividad como variable dependiente.
Respecto a los resultados de las pruebas de Hausman, se sabe que la estructura de los datos no es de un panel normal y que su comportamiento podía o no ajustarse al de un panel tradicional. Es por ello que no sorprende del todo que pruebas como la de Hausman arrojen resultados no del todo claros. La respuesta está en la naturaleza misma de dicha prueba, ya que se espera que, dado un número infinito de datos, el resultado sea siempre un valor positivo y la matriz de varianza-covarianza (vce) sea definida positiva. Sin embargo, en bases de datos finitas, esto no siempre resulta así. De esta manera, mientras que en la primera prueba de Hausman estimada se tiene que la matriz de varianza-covarianza compuesta para la prueba no es definida positiva, en la segunda prueba el resultado fue completamente negativo. Al respecto, existe evidencia teórica reciente (Schreiber, 2008) que indica que, en caso de un estadístico negativo, es posible tomar el valor absoluto del indicador, aunque la matriz de varianzacovarianza, construida de los parámetros, no sea definida positiva. Lo anterior independientemente de que el indicador obtenido sea positivo o negativo.
Es importante subrayar las características del modelo multinivel con efectos mixtos. Dicho modelo es una regresión de máxima verosimilitud con efectos mixtos: fijos y aleatorios. Los efectos fijos estimados son los mismos que se obtendrían corriendo una regresión de máxima verosimilitud en panel. Los efectos aleatorios no son parámetros en sí, sino el efecto que dicha variable tiene sobre la varianza total del modelo (Stata Press, 2011). Debe recordarse que se está asumiendo que yict=xict'β+uict, donde uict=μc+vic+εict. Es decir, que el resultado obtenido para efectos aleatorios son los componentes del término de error uict (Gutiérrez, 2008).
En el cuadro 2 se construye de la siguiente manera: tres modelos cuya variable dependiente es productividad y tres modelos con remuneraciones como variable explicada. Lo único que varía entre ellos es la construcción de los efectos aleatorios: en el modelo 1 se consideran variables sobre el ordenamiento de los datos (ciudad y subsectores), en el modelo 2 se asumen efectos aleatorios en algunas variables relevantes por subsector, mientras que en el modelo 3 se hace al nivel de ciudad por ciudad.
Modelos de efectos mixtos (datos anidados), productividad y remuneraciones
| Productividad | |||||||
|---|---|---|---|---|---|---|---|
| Parámetros | Modelo 1 | Modelo 2 | Modelo 3 | ||||
| Efectos fijos | |||||||
| Porción de trabajadores educados (<12) por subsector respecto a media por ciudad | h | 0.349*** | 0.0271 | 0.353*** | 0.0277 | 0.360*** | 0.0297 |
| Porción de trabajadores educados (<12) promedio por ciudad | h | –0.789 | 0.643 | –0.74 | 0.634 | –0.697 | 0.625 |
| Stockde capital humano promedio por subsector | a | 0.110** | 0.0342 | 0.111** | 0.0341 | 0.109** | 0.0342 |
| Porción de trabajadores no educados (>5) por subsector respecto a media por ciudad | l | 0.166*** | 0.0251 | 0.161*** | 0.0251 | 0.162*** | 0.025 |
| Porción de trabajadores no educados (>5) promedio por ciudad | l | 1.803*** | 0.538 | 1.779*** | 0.53 | 1.752*** | 0.522 |
| Especialización laboral en diferencias respecto a tiempo | s | –0.812*** | 0.05 | –0.826*** | 0.0555 | –0.842*** | 0.0715 |
| Flujos de capital | k | 0.460*** | 0.0521 | 0.461*** | 0.0519 | 0.441*** | 0.0525 |
| Flujos de inversión extranjera directa | ied | 0.346*** | 0.0647 | 0.333*** | 0.0649 | 0.338*** | 0.0646 |
| Intercepto | –1.077 | 1.056 | –1.132 | 1.041 | –1.128 | 1.027 | |
| Efectos aleatorios | |||||||
| Ciudad | µ | 0.114*** | 0.0551 | 0.110*** | 0.0536 | 0.106*** | 0.0519 |
| Porción de trabajadores educados (<12) por subsector respecto a media por ciudad | h | 0.00135** | 0.00345 | ||||
| Especialización laboral en diferencias respecto a tiempo | s | 0.0205*** | 0.0173 | ||||
| Subsector | ν | 0.186*** | 0.0359 | 0.0223 | 0.102 | 0.188*** | 0.0361 |
| Porción de trabajadores educados (<12) por subsector respecto a media por ciudad | h | 0.0166*** | 0.0151 | ||||
| Especialización laboral en diferencias respecto a tiempo | s | 0.0831*** | 0.0557 | ||||
| Stock de capital humano promedio por subsector | a | 0.00331*** | 0.00241 | ||||
| Residual | ε | 0.532*** | 0.0345 | 0.495*** | 0.0363 | 0.522*** | 0.0341 |
| Criterio de información de Akaike (aic) | 2 670.577 | 2 668.21 | 2 669.696 | ||||
| Criterio de información bayesiano (bic) | 2 730.169 | 2 742.7 | 2 739.22 | ||||
| Likelihood-ratio test | 8.37 | 4.88 | |||||
| Probabilidad > Ji-cuadrado | 0.039 | 0.0871 | |||||
| Efectos fijos | |||||||
| Porción de trabajadores educados (<12) por subsector respecto a media por ciudad | h | 0.615*** | 0.0271 | 0.587*** | 0.0256 | 0.614*** | 0.0271 |
| Porción de trabajadores educados (<12) promedio por ciudad | h | –0.121 | 0.429 | –0.103 | 0.455 | –0.189 | 0.452 |
| Porción de trabajadores educados (<12) en diferencias respecto a tiempo | h | –0.702*** | 0.0312 | –0.744*** | 0.0374 | –0.715*** | 0.0518 |
| Porción de trabajadores no educados (>5) por subsector respecto a media por ciudad | l | 0.0315* | 0.0141 | 0.0346* | 0.0138 | 0.0185 | 0.0137 |
| Porción de trabajadores no educados (>5) promedio por ciudad | l | 0.726* | 0.367 | 0.696 | 0.389 | 0.736 | 0.386 |
| Especialización laboral por subsector respecto a media por ciudad | s | –0.0121 | 0.0232 | 0.0328 | 0.0239 | 0.0314 | 0.0436 |
| Especialización laboral media por ciudad | s | 0.483** | 0.17 | 0.509** | 0.181 | 0.515** | 0.18 |
| Flujos de capital | k | 0.182*** | 0.0235 | 0.176*** | 0.0215 | 0.162*** | 0.0232 |
| Flujos de inversión extranjera directa | ied | 0.119** | 0.0434 | 0.177*** | 0.0417 | 0.122** | 0.0419 |
| _cons | –0.633 | 0.672 | –0.689 | 0.712 | –0.573 | 0.707 | |
| Efectos aleatorios | |||||||
| Ciudad | µ | 0.0415*** | 0.023 | 0.0489*** | 0.0259 | 0.0473*** | 0.0256 |
| Porción de trabajadores educados (<12) por subsector respecto a media por ciudad | h | 2.67E-15 | 5.64E-12 | ||||
| Porción de trabajadores educados (<12) en diferencias respecto a tiempo | h | 0.0166*** | 0.0094 | ||||
| Especialización laboral por subsector respecto a media por ciudad | s | 0.0123*** | 0.00964 | ||||
| Subsector | ν | 0.484*** | 0.0363 | 0.427*** | 0.0341 | 0.476*** | 0.0354 |
| Porción de trabajadores educados (<12) por subsector respecto a media por ciudad | h | 2.60e-08*** | 4.43E-08 | ||||
| Porción de trabajadores educados (<12) en diferencias respecto a tiempo | h | 0.122*** | 0.0268 | ||||
| Especialización laboral por subsector respecto a media por ciudad | s | 0.0158*** | 0.0096 | ||||
| Residual | ε | 0.0870*** | 0.00583 | 0.0512*** | 0.00516 | 0.0784*** | 0.00532 |
| aic | 1 784.748 | 1 721.155 | 1 754.544 | ||||
| bic | 1 849.306 | 1 800.611 | 1 834 | ||||
| Likelihood-ratio test | 69.59 | 36.2 | |||||
| Probabilidad > Ji-cuadrado | 0.0000 | 0.0000 | |||||
Nota: errores estándar en cursivas. Significancia de parámetros: (*) p< 0.05, (**) p< 0.01 y (***) p< 0.001.
En el primer modelo, donde la variable dependiente es la productividad, la varianza total es de 0.832. Se destaca que alrededor de 14% es atribuible a diferencias entre la ciudad de origen de la actividad desarrollada, mientras que 22.3% a las diferencias en la actividad realizada misma (calculo obtenido de los coeficientes del cuadro 2). En los modelos dos y tres, con productividad como variable dependiente, el trabajo con escolaridad alta, h, impacta los términos aleatorios más como efecto por diferencias entre subsector, o actividad realizada, que por diferencias entre las distintas ciudades.
La especialización laboral s, o concentración de mano de obra, resulta significativa y considerable (11.38% de la variabilidad del modelo 2) si se le asume como un cambio en el tiempo (variación en el indicador de 1999 a 2009) cuyo impacto es por subsectores. Es decir, existen cambios considerables en la concentración de trabajo, lo que sugiere un reordenamiento de la distribución de la masa laboral a nivel local en las distintas ciudades, pero el efecto no se puede considerar como significativamente distinto para cada una de ellas, sino que se dio, en general, en las diez áreas urbanas consideradas, o en determinados subsectores independientemente de la ciudad.
Una variable de sumo interés es el acervo de capital humano por subsector, que sólo se incluye en el modelo 2 y únicamente cuando se considera la productividad como variable dependiente. La elasticidad de la productividad a dicho factor es inelástica, el coeficiente obtenido es pequeño, lo que indica que el acervo de conocimiento y habilidades no es un eje determinante de la producción. Sin embargo, se destaca el coeficiente positivo obtenido del acervo de capital humano hacia la productividad. Cambios en el acervo de capital humano por subsector solamente explica 0.45% de la varianza del modelo.
De acuerdo con Moretti (2004), es en esta variable donde debe ponerse atención para evidencia contundente de derrames de capital humano. Se concluye pues, de acuerdo a lo encontrado en los modelos mixtos de productividad, que los derrames no pecuniarios si existen, son muy pequeños y se limitan a la industria que los tiene, no más allá en el resto de las actividades. Dada la elevada significancia de la ied en los modelos, toda evidencia apunta a que los efectos se magnifican en firmas cuyo subsector es receptor de este tipo de capital.
Resultados para las remuneracionesEn el primer modelo, donde las remuneraciones son la variable dependiente (parte inferior del cuadro 2) las diferencias entre ciudades explican sólo 6.77% de la varianza total, mientras que las disparidades entre subsectores explican 79.02%. De esta manera, la mayor parte de la variabilidad se relaciona con las diferencias entre subsectores, a diferencia de los modelos con productividad como variable explicada. La remuneración percibida por el personal ocupado responde al rubro del trabajo, y la diferencias que derivan de la localización en las ciudades en que labora es porcentualmente reducida.
En los modelos 2 y 3 el trabajo con escolaridad alta se insertó como una variación en el tiempo y como una diferencia entre subsectores. Tanto en el efecto aleatorio en la ciudad como en el efecto del subsector la diferencia en el tiempo en los porcentajes de personal con escolaridad alta es más relevante; en el modelo 2, por ejemplo, explica 18.3% de la varianza total. Es decir, que de 1999 a 2009 las remuneraciones percibidas variaron en un rango de±18% y, dado que el signo del coeficiente fijo en el modelo 2 de la misma variable es negativo, se considera posible asumir una caída.
La especialización laboral se inserta como un efecto aleatorio en diferencias en el tiempo. A diferencia de los modelos de productividad, en las remuneraciones la especialización no explica significativamente el porqué de la variabilidad entre subsectores.
Prueba de razón de verosimilitud y criterios aic y bicEn los modelos de efectos mixtos no se puede, tal como se hace en los modelos de panel convencionales, realizar la prueba de Hausman, que implica comparar dos modelos separados. Es común, en estos casos, realizar pruebas lr (razón de verosimilitud) entre un modelo y otro con el fin de ver si la inclusión de parámetros aleatorios es pertinente (Rabe-Hesketh y Skrondal, 2008). Las pruebas lr que se presentan en el cuadro 2 indican que, para el caso de la productividad, el mejor modelo es el 2 (con efectos aleatorios por subsector). Para las remuneraciones, tanto el modelo 2 como el 3 resultan mejores al modelo 1, sin embargo, el 2 arroja un parámetro Ji-cuadrado más alto, por ello también se toma ése como el mejor modelo. Los criterios aic y bic corroboran lo mismo, ya que son medidas que evalúan las ventajas de la bondad del ajuste del modelo con relación a su nivel de complejidad, lo que permite realizar la selección del modelo. Por ello, se puede concluir que tanto la prueba de máxima verosimilitud como los criterios utilizados apoyan la bondad de ajuste de las estimaciones, donde la productividad laboral es la variable dependiente.
ConclusionesLos resultados muestran que el mercado laboral experimentó cambios como consecuencia del crecimiento de la calificación del factor trabajo y la urbanización. De esta manera, se aprecia que la mayoría de la población ocupada de las ciudades más pobladas del norte de México tiene entre 6 y 12 años de escolaridad acumulados. Además, entre 1999 a 2009, la proporción del personal con escolaridad alta empleado en los 53 subsectores considerados creció de 9.69 a 14.34 por ciento. Las tendencias de la información indican que la percepción salarial de los subsectores con mayor proporción de trabajo con escolaridad alta creció en comparación a los subsectores con mano de obra menos educada; sin embargo, la tendencia de la productividad fue opuesta. Lo anterior sugiere que el trabajo más educado pudo haberse relocalizado a sectores con baja productividad.
Por su parte, los resultados obtenidos de las estimaciones econométricas de los modelos de efectos mixtos muestran heterogeneidad. Los coeficientes para la proporción de trabajadores más educados y los coeficientes de la inversión extranjera directa fueron positivos en todos los modelos. No obstante, el coeficiente de la especialización solamente muestra impactos positivos en las remuneraciones al nivel de análisis de ciudad. Por tanto, más allá de las características del periodo analizado, los retornos a escala son crecientes siempre y cuando se tenga la presencia de flujos de capital e inversión extranjera directa positivos en el contexto urbano. Lo anterior sugiere que continúa la presencia de enclaves, cuya repercusión quizá ya trascendió más allá de una sola empresa, pero no ha permeado fuera de los confines del subsector o empresa en cuestión. Dichos resultados concuerdan con el trabajo de Jordaan (2008) en que las estimaciones econométricas sugieren que la ied genera externalidades negativas dentro de las industrias, pero externalidades positivas mediante los encadenamientos hacia atrás.
Otro hallazgo de este trabajo es que las estimaciones muestran que las diferencias entre subsectores son el origen de gran parte de la variabilidad tanto en la productividad como en las remuneraciones. Así, se aprecia que el modelo de efectos mixtos evidencia que en los modelos donde las remuneraciones son la variable dependiente, las diferencias entre ciudades explican en menor grado los cambios en la varianza total. La mayor parte de la variabilidad deriva de los cambios entre subsectores. Esto indica que la locación geográfica no aporta gran variabilidad, sino más bien la actividad a nivel de los subsectores es el determinante de mayor relevancia. Finalmente, si se incluyen efectos de tiempo, el crecimiento de la especialización laboral en las ciudades y subsectores económicos resulta positivo en la dinámica del crecimiento de la productividad laboral y las remuneraciones.
De esta manera, los hallazgos del estudio sugieren que existen algunos aspectos que son favorables para el crecimiento y empleo laboral en el sector manufacturero de las áreas urbanas de la frontera norte de México. En particular, se destacan los efectos positivos en el crecimiento de la educación de la fuerza de trabajo, pero también la especialización laboral, particularmente al nivel de subsectores. Por ello, el desarrollo de políticas de desarrollo de aglomeraciones industriales al nivel de subsectores es potencialmente un factor para el crecimiento de la productividad y salarios manufactureros. En ese sentido, la posibilidad de atraer inversiones que permitan generar las aglomeraciones a un mayor nivel de desagregación, las cuales podrían derivar en economías externas, es un campo de acción de una potencial política industrial. Lo anterior podría tener un papel decisivo en la expansión de la productividad del sector manufacturero en México.
Los autores agradecen los valiosos comentarios y sugerencias de dos dictaminadores anónimos de la revista.
La productividad laboral se obtuvo dividiendo el valor agregado entre el personal ocupado de los 53 subsectores de la actividad productiva urbana.
112 Ganadería, 221 Generación, transmisión y suministro de energía eléctrica, 311 Industria alimentaria, 312 Industria de las bebidas y del tabaco, 313 Fabricación de insumos textiles, 314 Confección de productos textiles, 315 Fabricación de prendas de vestir, 321 Industria de la madera, 322 Industria del papel, 323 Impresión, 324 Productos derivados del petróleo y del carbón, 325 Industria química, 331 Industrias metálicas básicas, 332 Fabricación de productos metálicos, 333 Fabricación de maquinaria y equipo, 334 Equipo de computación, comunicación, componentes y accesorios electrónicos, 335 Generación eléctrica y aparatos, 336 Equipo de transporte, 337 Muebles y productos relacionados, 339 Otras industrias manufactureras, 432 Comercio al por mayor de productos textiles y calzado, 433 Comercio al por mayor de productos farmacéuticos, de perfumería, accesorios de vestir, artículos para el esparcimiento y electrodomésticos, 434 Comercio al por mayor de materias primas agropecuarias, 435 Comercio al por mayor de maquinaria, mobiliario y equipo para actividades agropecuarias, industriales y de servicios, 461 Comercio al por menor de alimentos, bebidas y tabaco, 462 Comercio al por menor en tiendas de autoservicio y departamentales, 463 Comercio al por menor de productos textiles, accesorios de vestir y calzado, 464 Comercio al por menor de artículos para el cuidado de la salud, 465 Comercio al por menor de artículos de papelería 466 Comercio al por menor de enseres domésticos, computadoras y artículos para la decoración de interiores, 467 Comercio al por menor de artículos de ferretería, 468 Comercio al por menor de vehículos de motor y refacciones, 469 Inter-mediación y comercio al por menor por medios masivos de comunicación, 481 Transporte aéreo, 484 Autotransporte de carga, 491 Servicios postales, 492 Servicios de mensajería y paquetería, 511 Edición de publicaciones y de software, excepto a través de Internet, 512 Industria fílmica y del video, 522 Instituciones de intermediación crediticia y financiera no bursátil, 523 Actividades bursátiles cambiarias y de inversión financiera, 531 Servicios inmobiliarios, 541 Servicios profesionales, científicos y técnicos, 561 Servicios de apoyo a los negocios, 562 Manejo de desechos, 621 Servicios médicos de consulta externa, 622 Hospitales, 623 Residencias de asistencia social y para el cuidado de la salud, 721 Servicios de alojamiento temporal, 722 Preparación de alimentos y bebidas, 811 Servicios de reparación y mantenimiento, 812 Servicios personales, 813 Asociaciones y organizaciones.
La variable que refleja la especialización laboral se calculó dividiendo el personal ocupado total (por subsector, por ciudad y por año) entre el personal ocupado total (por subsector y año nacional).
Formalmente:
donde i es el subsector económico; c, la ciudad; t, el año; j, el estrato educativo, y n, la nación (México).