Reflexiones sobre adivinar en preguntas de opción múltiple y cómo afecta el resultado del examen

Resumen

Los exámenes de opción múltiple (EOM) son la herramienta más difundida en educación médica, pero su utilidad está supeditada a la confiabilidad del instrumento y la validez de las inferencias que emanan de la medición. La posibilidad de adivinar, inherente al formato de evaluación, puede introducir varianza irrelevante a la medición y reducir la representación del rasgo latente en la calificación del examen por diferencias individuales respecto a educated guessing, testwiseness y la tendencia a adivinar. En este artículo se presentan brevemente las características generales de la Teoría Clásica de los Tests (TCT) y la Teoría de Respuesta al Ítem (TRI) y su abordaje al problema de adivinar. Asimismo, se propone un modelo teórico dentro de la TCT que integra los mecanismos que afectan la adivinación y se determina la variación de la probabilidad de aprobar un EOM, en función de ciertos supuestos respecto a adivinar a través de un análisis teórico dentro de un modelo TRI. Es posible concluir que algunas características de los ítems propician la adivinación, y cuando ésta ocurre se encuentran inmersas diversas variables, relacionadas o independientes, del rasgo que se pretende medir, que determinan la magnitud de su efecto.

Abstract

Multiple-choice tests (MCT) are the most employed assessment tool in medical education; however, its use is limited to the instrument reliability and validity of the inferences made upon the measurement. Guessing, an inherent element of this evaluating tool, may introduce construct-irrelevant variance and reduce the load of the latent trait in the score of the exam due to individual differences regarding educated guessing, testwiseness and guessing tendency. This article presents an overview of Classical Test Theory (CTT) and Item Response Theory (IRT), including a discussion of how each theory addresses the guessing phenomenon. With respect to the latter, we propose a theoretical model that integrates factors related to guessing within the CTT framework. We further include a theoretical analysis, which displays the variation of the probability of passing a MCT reliant on certain assumptions regarding guessing that are akin to a particular IRT model. In conclusion, various features of the items increase the likelihood of guessing, and, when guessing takes place, the magnitude of its effect is determined by some variables that can be dependent or independent of the latent trait.

Introducción

Los exámenes de opción múltiple (EOM) son la herramienta más utilizada en educación médica al hacer posible una evaluación objetiva, estandarizada, costo-efectiva y eficiente^1–3. Un ítem de opción múltiple (IOM) desarrollado de forma correcta puede evaluar desde memoria hasta procesos cognitivos superiores como razonamiento clínico y toma de decisiones. Otras ventajas incluyen: a) un muestreo más extenso del contenido por evaluar, y b) una administración y calificación en poco tiempo, aun en grandes poblaciones de estudiantes⁴. Esta forma de evaluación se ha utilizado a gran escala internacionalmente y ha sido un tema central en investigación en educación desde el siglo pasado. Lo que se espera de cualquier método de evaluación educativa es que proporcione una medición lo más certera posible del rasgo latente que se pretende medir. La validez del método es especialmente trascendente cuando se trata de exámenes sumativos, donde el puntaje se utiliza para tomar decisiones sobre los sustentantes (en educación médica, concretamente, de éste puede depender la emisión de un título o el acceso a un curso de especialidad). Por ello, es indispensable que los EOM, como instrumento de medición, sean lo más confiables, válidos y justos posible.

Respecto a estas tres características, surge un elemento inherente a este formato de evaluación que siempre se ha cuestionado: la posibilidad de adivinar. Existe la posibilidad de que los sustentantes sumen puntos que no representen dominio sobre el tema e incluso, al menos teóricamente, que aprueben un examen a expensas de una ventaja del propio formato. Esta posibilidad se presenta aunque se adivine a ciegas. Sin embargo, pocas veces el sustentante tiene que adivinar a ciegas. Por un lado, los EOM suelen incluir ítems con deficiencias en su construcción, que permiten descartar una o más opciones o inferir la respuesta correcta, incluso con un bajo nivel de conocimiento^5–7. Este fenómeno se conoce como testwiseness⁸. Por otro lado, es común que, con base en un conocimiento parcial, el sustentante pueda descartar uno o más distractores de un IOM, lo cual se ha denominado informed guessing o educated guessing^9–11. En general, adivinar constituye una fuente de error de medición que puede convertirse en sesgo estadístico¹². Por lo tanto, la decisión sobre el punto de corte entre aprobar y reprobar un EOM debería tomar en cuenta que un porcentaje de los aciertos no refleja el dominio del tema o contenido evaluado por la pregunta, sino que se debe al azar.

Para el análisis de pruebas en general (y EOM en específico), existen dos enfoques psicométricos principales: la Teoría Clásica de los Tests (TCT) y la Teoría de Respuesta al Ítem (TRI). Ambos modelos tienen como objetivo realizar inferencias sobre uno o más rasgos latentes, imposibles de observarse directamente, a partir de las respuestas a las preguntas. Por otro lado, sus supuestos subyacentes difieren de forma notable, incluyendo la forma en que consideran y enfrentan el problema de acertar preguntas por adivinación.

El presente artículo tiene dos objetivos: primero, revisamos brevemente las características de la TCT y la TRI, en general (para una revisión más extensa, véase Leenen¹³) y cómo cada teoría ha abordado el problema de adivinar. Al respecto, incluimos a) un modelo que integra los mecanismos que afectan la adivinación con los conceptos claves de la TCT, y b) una breve descripción de algunos modelos TRI específicos para EOM. Segundo, investigamos, a partir de un análisis teórico enmarcado dentro del modelo Nedelsky, cómo la probabilidad de aprobar un EOM varía en función de ciertos supuestos o estrategias respecto a adivinar. Los resultados de esta investigación aportan evidencia sobre la (baja) plausibilidad de acreditar un examen a expensas de adivinar a ciegas o con base en testwiseness o educated guessing exclusivamente.

Dos marcos psicométricos y cómo tratan al problema de la adivinación

Conceptos generales de la Teoría Clásica de los Tests

Los supuestos y procedimientos de la TCT son relativamente simples y consideran la prueba en su totalidad. Distingue entre dos factores que componen la puntuación observada (comúnmente representada por X) en el examen: la puntuación verdadera (V) y el error de medición (E):

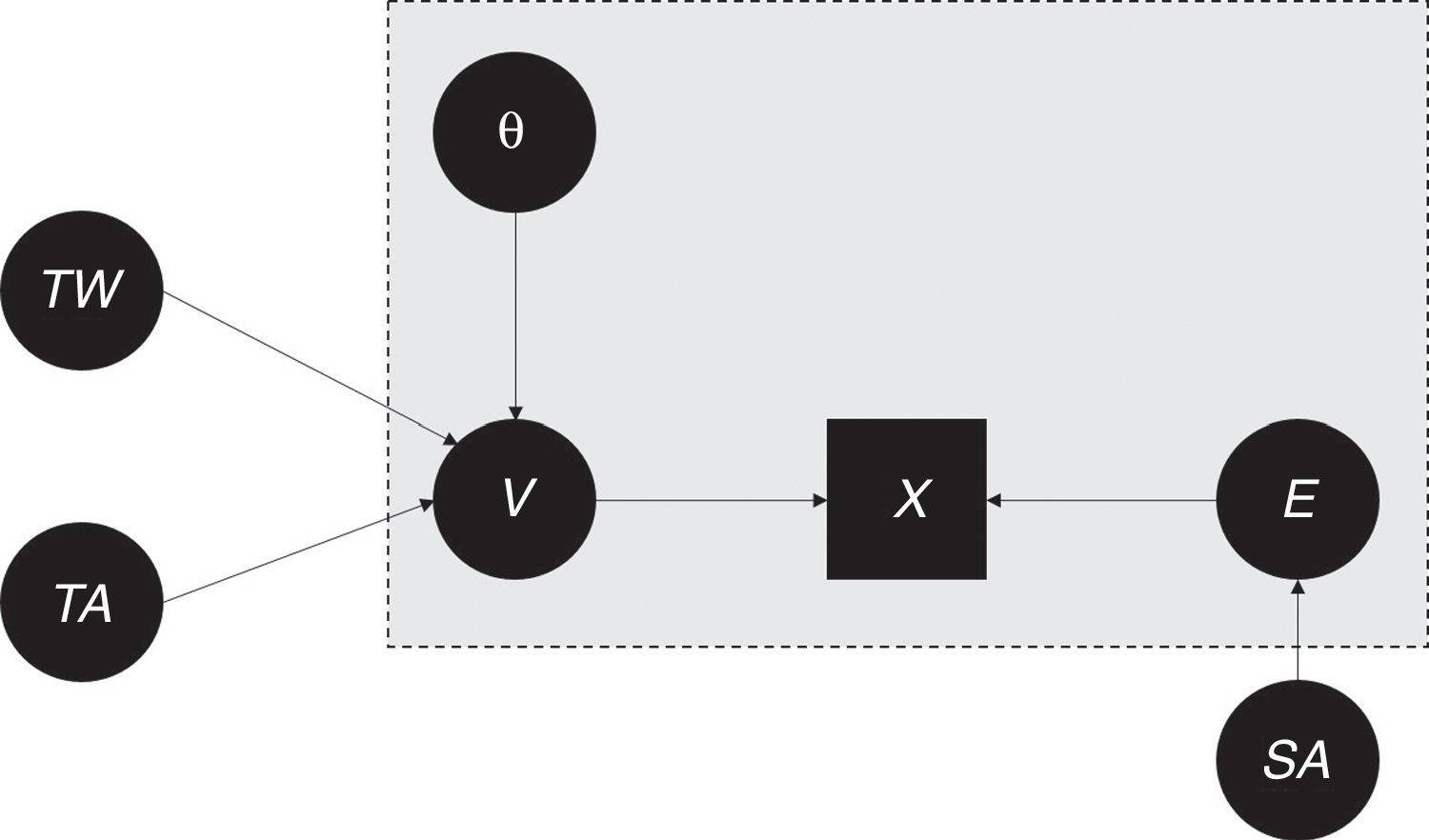
La TCT parte de la concepción teórica e hipotética de que el examen se puede replicar un gran número de veces y que, en cada réplica, las características esenciales (por ejemplo, ciertos contenidos que se deben cubrir según la tabla de especificaciones y el nivel taxonómico de las preguntas) permanecen, mientras que las características incidentales (como las preguntas concretas y las circunstancias de aplicación) varían. La puntuación verdadera, por definición, recoge todos los efectos sistemáticos, es decir, de los factores que permanecen entre réplicas. Ésta incluye el efecto del constructo latente que se pretende medir (habitualmente representado por θ) y de otros factores, como las estrategias para adivinar en caso de incertidumbre o la familiaridad con el formato de respuesta. Como se explicará posteriormente, θ es central al considerar la validez del examen, mientras que los demás factores generan varianza irrelevante para el constructo^14,15. El error de medición reúne los efectos no sistemáticos, o sea aquellos que varían entre las réplicas hipotéticas, como por ejemplo, la mala suerte de equivocarse por la presencia de una distracción (como por ruido excesivo). La parte gris de la figura 1 representa las cuatro variables principales en el modelo clásico y su relación.

Figura 1.

Modelo teórico que integra suerte al adivinar (SA), testwiseness (TW), tendencia a adivinar (TA) con los conceptos centrales de la TCT, puntuación verdadera (V), rasgo latente (θ), error de medición (E) y la puntuación obModelo teórico que integra suerte al adivinar (SA), testwiseness (TW), tendencia a adivinar (TA) con los conceptos centrales de la TCT, puntuación verdadera (V), rasgo latente (θ), error de medición (E) y la puntuación observada (X).

Sigue de la ecuación (1) que las diferencias entre sustentantes respecto de su puntuación observada reflejan tanto diferencias verdaderas como diferencias incidentales; la confiabilidad en la TCT se define como la proporción de diferencias verdaderas en las diferencias observadas. Se puede entender la confiabilidad en términos del efecto relativo que tienen los factores V y E sobre (la varianza en) X. El concepto estrechamente relacionado del error estándar de medición se suele usar para derivar un intervalo de confianza para la puntuación verdadera con base en la puntuación observada^16,17.

El concepto de validez^15,18,19 se refiere al efecto que tiene el constructo latente θ sobre X. Como se muestra en la figura 1, éste se manifiesta a través de V y deja claro que la validez depende de la confiabilidad de un instrumento¹⁶.

Adivinar en la Teoría Clásica de los Tests

Suerte al adivinar, testwiseness, educated guessing y la tendencia a adivinar

Aunque la TCT y sus conceptos centrales refieren a la prueba en su totalidad, es conveniente analizar el proceso interno que ocurre en el sustentante al enfrentarse con un IOM. Al respecto, es razonable suponer que éste realiza un análisis tácito de las m opciones de respuesta, el cual resulta en una valoración sobre la plausibilidad de cada opción. Con base en estas valoraciones, elegirá entre las alternativas ofrecidas, o bien, dejará la pregunta sin responder. La adivinación ocurre si el sustentante decide contestar la pregunta, a pesar de que su análisis no haya conducido a la certidumbre respecto a una de las opciones.

Formalmente, estas valoraciones desembocan en m + 1 probabilidades: una probabilidad para cada opción de que el sustentante la elija, y otra de dejar la pregunta sin responder. En el caso de que la probabilidad asociada con la opción correcta sea diferente de 0 o 1, la puntuación en esta pregunta (y, por lo tanto, la puntuación observada X en el test) está influida por un factor aleatorio que denominamos suerte al adivinar (SA). La SA tiene un efecto no sistemático, por lo cual es parte del error de medición E (véase la figura 1). Obviamente, la SA interviene cuando el sustentante adivina a ciegas. En este caso, por definición, las probabilidades asociadas con las m opciones de respuesta son idénticas. Sin embargo, es vital enfatizar que la SA también interviene, por ejemplo, cuando el sustentante sabe eliminar algún distractor y adivina entre las opciones restantes.

En la introducción se mencionaron dos conceptos relacionados con la adivinación: testwiseness (TW) y educated guessing (EG). Ambos se relacionan con el proceso de valorar la plausibilidad de las opciones de los IOM al implicar valoraciones distintas que, por ende, llevan a probabilidades no uniformes de que se elija cada opción. En el caso de TW, las valoraciones de las m opciones de respuesta se deben a características relacionadas con aspectos gramaticales y sintácticos del ítem, no con el rasgo θ. EG, por otro lado, entra en escena cuando la diferenciación entre opciones de respuesta se debe al rasgo latente. Es importante señalar que los efectos de TW y EG no necesariamente incrementan la probabilidad de acertar el ítem (en comparación con la probabilidad de acertarla al adivinar a ciegas). Puede ser, por ejemplo, que en un ítem concreto, tengan un efecto engañoso, esto es, que lleven al sustentante a bajar la probabilidad que le asigna a la respuesta correcta.

Aunque estos dos conceptos a menudo se consideran de forma simultánea^9,20,21, es básico reconocer que tienen una concepción psicológica distinta. TW refiere a una capacidad del sustentante, es decir, es un constructo que ejerce un efecto sistemático sobre X (véase la flecha directa de TW hacia V en la figura 1), pero sin relación directa con θ (nótese la ausencia de una flecha entre TW y θ). A diferencia de TW, EG es una conducta que se manifiesta cuando θ influye en el proceso de la valoración de las opciones de respuesta, sin que éste lleve al sustentante a la identificación certera de una opción como la correcta. Debe ser claro que EG depende totalmente de θ y que está típicamente asociado con niveles intermedios de θ, donde el conocimiento parcial del sustentante es suficiente para, por ejemplo, descartar un distractor, pero insuficiente para reconocer la respuesta correcta. Puesto que EG es una conducta subordinada totalmente a θ, está implícitamente presente en la flecha que indica el efecto de θ sobre V en la figura 1.

La figura 1 incluye un tercer factor que afecta V: la tendencia a adivinar (TA). Contrario a TW y EG, la acción de la TA no conlleva una distinción entre las m opciones de respuesta, sino afecta la probabilidad de dejar o no en blanco el ítem en caso de incertidumbre. Especialmente cuando se aplica una fórmula de corrección (véase abajo), los sustentantes difieren respecto a la decisión de dejar IOM sin contestar²⁰. La aversión al riesgo y la concepción respecto a la práctica de adivinar son algunos factores que inciden sobre la magnitud de la TA. Por ejemplo, alguien puede opinar que es incorrecto sumar puntos a través de la suerte o que adivinar distorsiona la calificación en el examen; por tanto, la magnitud del efecto de la TA sería baja. Cabe mencionar que el efecto de la TA, al referirse a una tendencia general del sustentante hacia la incertidumbre en los IOM, es sistemático sobre V; se considera una variable moderadora que influye en cómo θ y TW afectan a V.

La regla para calificar

Típicamente, la calificación en un EOM se calcula como el número de ítems en los que el sustentante marcó la respuesta correcta. Esta regla se conoce como number right scoring (NRS) y, bajo la premisa que el sustentante desea maximizar su puntuación, siempre es una invitación a adivinar.

Con el fin de obtener una calificación menos afectada por la adivinación, en algunos contextos se aplica una fórmula de corrección al número de respuestas correctas. Esta regla alternativa castiga—es decir, resta puntos por—las respuestas incorrectas. Si se decide aplicar la fórmula, es esencial mencionarle a los sustentantes, previo al inicio de la prueba, que existirá dicha penalización y que se aplicará a los ítems con respuesta incorrecta (dejando sin penalización los ítems sin responder). La penalización suele depender del número m de opciones de respuesta y en la mayoría de las aplicaciones consiste en restar un valor de 1/(m – 1) por cada respuesta incorrecta. Con esta corrección, la puntuación esperada (en el examen o en cada IOM) bajo el supuesto de adivinar a ciegas es cero²². No obstante, el efecto más trascendente de la fórmula se debe al discurso precautorio y a su potencial de lograr que los sustentantes se abstengan de intentar adivinar, más que a la deducción de puntos^12,22. Así, la fórmula puede reducir la varianza del error en comparación con la calificación obtenida por el NRS, ya que este último cuasi fuerza a los sustentantes a adivinar cuando desconocen la respuesta.

Sin embargo, la fórmula de corrección ha sido criticada porque esta regla introduce varianza sistemática irrelevante para el constructo, debido a que los sustentantes reaccionan de forma diferente a la posible penalización^22–24. Al prevenir a los estudiantes sobre la fórmula, se introducen nuevos elementos, como su personalidad y principalmente su actitud hacia el riesgo, que afectan la estrategia de resolución del examen y distorsionan el puntaje final. En otras palabras, la propensión a tomar riesgos y la tendencia a adivinar se vuelven más trascendentes para los parámetros del examen que la propia fórmula de corrección²⁵.

Es interesante plantear el debate entre defensores y oponentes de la fórmula de corrección dentro del modelo que se presentó en la figura 1. El argumento a favor enfatiza la disminución del efecto de la SA sobre la puntuación observada, la cual beneficia la confiabilidad del examen. El argumento en contra resalta que la fórmula fortalece la influencia de la TA sobre V a expensas de θ y, por ende, atenúa la validez del examen. Según los detractores de la fórmula, la intención de que se reponga la confiabilidad perdida en adivinar no se logra, y se compromete más la validez del instrumento por la varianza irrelevante agregada a la medición.

La Teoría de Respuesta al Ítem

La TRI constituye una familia de modelos que formalizan el proceso de responder a un ítem. En cualquier modelo TRI es central la función característica, la cual relaciona las características de los ítems con los rasgos latentes de los examinados a fin de precisar las probabilidades de observar ciertas (categorías de) respuestas. La TRI tiene un fundamento matemático más robusto, con supuestos más fuertes y precisos e interpretaciones más claras en comparación con la TCT^26,27. Para conocer más respecto a las diferencias entre la TCT y la TRI, véase Leenen¹³, Hambleton y Jones²⁸ y Erguven²⁹.

Dentro de la TRI, se encuentra una diversidad de modelos que difieren en el número de parámetros (cuantificaciones de las características de personas e ítems), y en la función característica que los une para llegar a la afirmación probabilística de acertar el ítem o marcar cierta opción. Por ejemplo, el modelo de Rasch³⁰ —uno de los pioneros de la TRI— supone a) un parámetro para cada ítem (β, su dificultad); b) un parámetro por persona (su nivel θ de habilidad), y c) que la probabilidad de que una persona acierte un ítem (el modelo solo considera dos categorías de respuesta, correcta o incorrecta) crece monótonamente conforme la diferencia θ – β aumenta. El modelo es unidimensional y, como muchos otros modelos de la TRI, asume independencia local.

Adivinar en la Teoría de Respuesta al Ítem

Una propiedad importante del modelo de Rasch es que la probabilidad de acertar un ítem se acerca a cero conforme el nivel θ de la persona disminuye. Por ello, el modelo no se considera muy apropiado para el análisis de EOM, puesto que incluso una persona totalmente ignorante tiene una probabilidad sustancialmente superior a cero de acertar el ítem. Para responder a esta inconveniencia, se han propuesto modelos TRI alternativos que explícitamente consideran la adivinación en los IOM. A continuación, se describen brevemente algunos de éstos.

El modelo logístico de tres parámetros

El modelo TRI más popular y más común para el análisis de EOM es, indudablemente, el modelo logístico de tres parámetros (3PL)³¹. Este modelo incorpora explícitamente la posibilidad de adivinar, al incluir un parámetro (γ, de pseudoadivinación) para cada ítem que representa la probabilidad de acertarlo para personas de un nivel muy/infinitamente bajo. (Cabe mencionar que, a diferencia con el modelo de Rasch, el 3PL incluye otro parámetro para cada ítem, α, su discriminación; sin embargo, éste no es relevante para este artículo.)

La interpretación más común del modelo 3PL supone un proceso en dos pasos: a) el sustentante analiza el ítem y, con base en el resultado de este análisis, b) provee la respuesta correcta (si la conoce) o adivina (si la desconoce). La probabilidad total de acertar el ítem, como está formalizado en la función característica del 3PL, es la suma de dos probabilidades: la de conocer la respuesta correcta, en cuyo caso acierta con certeza, y la probabilidad conjunta de desconocer la respuesta correcta y acertar por adivinación³².

Un modelo Teoría de Respuesta al Ítem en el cual la adivinación depende de la persona

El 3PL restringe el parámetro de pseudoadivinación a ser dependiente del ítem y no de la persona que responde. Sin embargo, es poco plausible suponer que, si el estudiante desconoce la respuesta y adivina, la probabilidad de acertar el ítem es fija, o sea, que no depende de él. Más probable es, entonces, que utilice información parcial durante el proceso de adivinar. Para remediar este inconveniente, San Martin et al.³³ propusieron un modelo en el cual la probabilidad de acertar el ítem por adivinación depende en cierto grado de la variable latente θ.

El modelo de respuesta nominal y sus generalizaciones

Tanto el 3PL como el modelo de San Martín et al. unen los distractores y la no respuesta en una categoría, la “respuesta incorrecta”. Esta práctica, aunque es muy común y refleja la costumbre de otorgar un punto a la respuesta correcta y cero puntos a cualquier respuesta incorrecta, implica pérdida de información. Posiblemente, tomar en cuenta cuál opción incorrecta eligió una persona puede llevar a una estimación más precisa de la θ de ésta, sobre todo para niveles relativamente bajos de la variable latente^34,35.

Se han propuesto varios modelos TRI que permiten analizar las múltiples categorías de respuesta en los IOMs; el primero y más conocido es el modelo de respuesta nominal³⁶, el cual parte del supuesto de que las m opciones de respuesta en un IOM ejercen diferentes grados de atracción sobre el sustentante. Si a₁, a₂, …, a_m son números positivos que cuantifican dicha atracción, entonces el modelo especifica que la probabilidad de escoger la opción j (donde j es un índice entre 1 y m) se da por:

La fuerza de atracción es conceptualmente similar a la valoración de las opciones de respuesta en el modelo que se describió en la sección Adivinar en la TCT. Los valores a₁, a₂, …, a_m de la ecuación (2) son una función (es decir, dependen) tanto de los parámetros de las opciones de respuesta como de la persona.

El modelo de respuesta nominal comprende algunos detalles teóricamente menos deseables. Por ejemplo, la función característica implica que personas totalmente ignorantes siempre estarán atraídas a una opción específica, lo cual es poco plausible; es más verosímil que estas personas sean indiferentes entre las opciones ofrecidas. Los modelos de Samejima³⁷, Thissen y Steinberg³⁴, y más recientemente Suh y Bolt²¹, remedian estos inconvenientes.

El modelo Nedelsky

El modelo Nedelsky³⁸ asimismo distingue entre los distintos distractores de un IOM, pero adopta unos supuestos más simples —y sobre todo psicológicamente diferentes— que los mencionados en el párrafo anterior. Supone un proceso que consiste en dos pasos. Primero, el sustentante realiza de forma independiente una evaluación de cada opción de respuesta; en el caso de que sea un distractor, la evaluación posiblemente le lleva a identificar la opción como incorrecta. La probabilidad de que esto ocurra depende de características de la opción (como su dificultad) y del nivel del sustentante en la variable latente (las personas difieren respecto a su habilidad para identificar distractores). Nótese que el modelo excluye la posibilidad de rechazar la opción correcta en este paso (se supone que en un IOM correctamente desarrollado, ningún nivel de θ puede llevar al rechazo de la opción correcta). En el segundo paso, el sustentante adivina a ciegas entre las opciones que no rechazó en el paso anterior. Si, por ejemplo, en un ítem de cuatro opciones de respuesta, el sustentante sabe identificar dos distractores en el primer paso, entonces en el segundo paso elegirá una de las dos opciones restantes con probabilidad de 0.50.

Nota final sobre los modelos Teoría de Respuesta al Ítem para ítem de opción múltiple

Para concluir esta sección, es importante resaltar que todos los modelos descritos, excepto el 3PL, al permitir que la variable latente θ intervenga en el proceso de respuesta cuando el sustentante adivina, incorporan y formalizan la posibilidad de EG. Al mismo tiempo, siendo modelos unidimensionales, excluyen explícitamente la posibilidad de que otros constructos, como TW o la TA, determinen la probabilidad de acertar el ítem o escoger cierta opción.

La probabilidad de aprobar un exámenes de opción múltiple

En esta sección, se presentan los resultados de un análisis teórico de la probabilidad de aprobar un EOM bajo seis escenarios diferentes. Como estándar de pase tomamos el criterio de obtener el 60% de la calificación máxima, lo cual es habitual en el sistema educativo de México. Todos los análisis refieren a exámenes de hasta 60 ítems, cada uno con cuatro opciones, y se pueden enmarcar dentro del modelo Nedelsky (véase la sección anterior). En particular, se supone que en cada ítem ocurre una de cuatro alternativas: el sustentante puede descartar 0, 1, 2, o los 3 distractores y, enseguida, adivina ciegamente entre las opciones restantes (sin dejar ítems sin contestar). Los escenarios difieren respecto de las probabilidades que se asocian a estas alternativas.

La tabla 1 presenta la distribución de probabilidades para cada escenario. El primer escenario corresponde con adivinar a ciegas todo el examen (en el 100% de los ítems no sabe descartar ningún distractor). En el segundo (y tercer) escenario, se supone que el sustentante puede descartar uno (o dos) distractores de cada ítem. Nótese que esto equivale a adivinar a ciegas en un examen donde los IOM tienen tres (o dos) opciones de respuesta. En contraste con los primeros tres escenarios, los últimos permiten que las cuatro alternativas ocurran en el mismo examen. La distribución de probabilidades en éstos responde a la experiencia de los autores al sustentar exámenes. Por ejemplo, el cuarto escenario especifica que el sustentante adivina a ciegas en el 10% de los ítems, descarta uno o dos distractores en el 40% y 20%, respectivamente, y que descarta los tres distractores en el 30% de los casos. Este escenario se puede relacionar con el desempeño de un estudiante de bajo nivel académico. Por otro lado, los dos últimos escenarios refieren más a estudiantes de nivel académico medio y alto, respectivamente.

Tabla 1.

Probabilidades de eliminar cierto número de distractores en una pregunta de cuatro opciones de respuesta para seis escenarios hipotéticos analizados bajo el modelo Nedelsky

Escenarios		Probabilidad de eliminar x distractores
		x = 0	x = 1	x = 2	x = 3
1	Adivinar a ciegas	100%	0%	0%	0%
2	Descartar un distractor	0%	100%	0%	0%
3	Descartar dos distractores	0%	0%	100%	0%
4	Estudiante nivel bajo	10%	40%	20%	30%
5	Estudiante nivel medio	5%	30%	20%	45%
6	Estudiante nivel alto	1%	10%	19%	70%

En la figura 2, se muestra la probabilidad de aprobar en función del número de ítems que contiene el examen, para cada escenario y bajo dos reglas para calificar: NRS y aplicando la fórmula de corrección (restando 1/(m−1) por respuesta errónea). El gráfico superior izquierdo evidencia que la probabilidad de aprobar un examen con 10 ítems, adivinando a ciegas, es aproximadamente 2%, si la calificación se obtiene por NRS. Desde 20 ítems, la probabilidad de aprobar se vuelve despreciable (< 0.1%) y con 50 ítems aprobar un EOM a ciegas es prácticamente imposible. Con la fórmula de corrección, obviamente, se llega aún más rápido a la asíntota de 0.

Figura 2.

Probabilidad, bajo el modelo Nedelsky, de aprobar un examen en función del número de ítems, con y sin fórmula de corrección, para cada escenario descrito en la tabla 1.

Cuando el sustentante puede descartar un distractor en cada ítem, el patrón de probabilidades es similar: en particular, se evidencia que, para los exámenes comunes (es decir, de 50 ítems o más), la probabilidad de aprobar es despreciable. En cambio, los sustentantes que pueden identificar dos opciones incorrectas en cada ítem y adivinan a ciegas entre las dos restantes, tienen, en un examen de 50 ítems, una probabilidad de 10% de aprobar. Es importante resaltar dos implicaciones de este resultado: a) existe una probabilidad significativa (aunque baja) de que un estudiante apruebe un EOM sin poder identificar la respuesta correcta en ningún ítem, aún si contiene un número habitual de éstos, y b) exámenes donde los ítems tienen sólo dos opciones (como verdadero-falso) son susceptibles a ser aprobados adivinando a ciegas. Las implicaciones anteriores se refieren al caso de NRS; aplicando la corrección por adivinar las probabilidades se reducen a valores despreciables. Así, se ejemplifica la utilidad de la fórmula de corrección para evitar que aquellos que desconocen la respuesta correcta acumulen puntos.

Las gráficas correspondientes al Escenario 4, que corresponde a un estudiante de bajo nivel que no debería pasar el examen, muestran que la probabilidad de aprobar, sin la fórmula de corrección, no es inferior a 30%, incluso con 60 ítems. Si se aplica la penalización, la probabilidad se reduce a aproximadamente 2%. En las gráficas correspondientes al estudiante de nivel medio, se observa un efecto muy pronunciado de la fórmula de corrección: la evolución de la probabilidad de aprobar en función del número de ítems está totalmente supeditada a ésta. Con el NRS, la probabilidad de aprobar tiende a 1 conforme el número de ítems aumenta, mientras que con la fórmula tiende a 0. En un examen de 60 ítems, las probabilidades son de 87% (sin corrección) versus 32% (con corrección). El ejemplo evidencia que la decisión sobre la regla para calificar es transcendental. Bajo las condiciones del último escenario, correspondiente al sustentante de alto nivel, las probabilidades de aprobar el examen exceden 95% aún con un examen de solo 8 ítems, mientras no se aplique la fórmula de corrección. Este escenario muestra que la fórmula generalmente no perjudica al estudiante de alto nivel, siempre que contenga un número suficiente de ítems (a partir de 17 ítems, la probabilidad de aprobar el examen excede 90%).

Discusión y conclusiones

Tras el análisis teórico en la sección anterior, es preciso vincular los resultados con los abordajes de la adivinación según los dos marcos psicométricos. El Escenario 1, donde sólo sucede la adivinación a ciegas, ejemplifica la gran carga que ejercería el efecto de SA sobre la puntuación observada, ya que el resultado dependería directamente de éste. Sin embargo, la adivinación a ciegas es una práctica aislada, que difícilmente se sistematiza como estrategia de resolución, especialmente en exámenes de medianas o altas consecuencias. En los demás escenarios, al descartar una o más opciones, se introducen los efectos de TW y EG. Bajo la condición de unidimensionalidad de la TRI, la identificación de un distractor sólo podría deberse a EG; si el efecto de TW tiene una influencia significativa, las pruebas de ajuste típicamente llevan a un rechazo del modelo y se requieren variantes multidimensionales. Desde la TCT, mientras más influencia ejerce la acción de la TA y TW sobre V, mayor es la varianza irrelevante al constructo, y menos válidas resultan las inferencias realizadas sobre la puntuación observada.

Las propias características de los ítems son las que desencadenan más o menos efecto de EG y TW. Varios autores han identificado que la mayoría de los EOM en ciencias de la salud –especialmente en educación médica de pregrado y posgrado– albergan ítems que violan las directrices de construcción^{7,10,39,40,45}. En general, dos distractores constituyen un límite natural y asequible para un IOM, y se sugiere que sólo se incluyan más si se logra asegurar la calidad y pertinencia de los excedentes^41–43. Además, existe suficiente evidencia sobre exámenes con tres o cuatro distractores en donde al menos uno de ellos es no funcional^{6,10,11,14,39,44,45}, lo cual propicia un aumento del efecto de EG y TW y hace debatibles los juicios que se basan en los resultados del examen, principalmente para puntajes cercanos al estándar de pase y preocupantemente si se trata de un examen de altas consecuencias. Desde el contexto de educación médica, es evidente la preocupación asociada con acertar por adivinación, especialmente cuando se asume correspondencia entre el porcentaje de respuestas correctas y el porcentaje de preguntas en las que el estudiante tiene el conocimiento suficiente para reconocer la respuesta correcta.

La fórmula de corrección tradicional, que resta 1/(m−1) para cada respuesta incorrecta, resulta sustancialmente conveniente para estudiantes de nivel medio (Escenarios 3, 4 y 5), donde es imperativo discriminar entre los que dominan con suficiencia el tema y aquellos que no alcanzan la competencia mínima. Empero, también puede afectar a estudiantes aversos al riesgo y no solo reducir su puntuación, sino mermar su probabilidad de aprobar²². En efecto, adivinar casi siempre es ventajoso, incluso con la fórmula de corrección tradicional, porque es infrecuente que el sustentante sea incapaz de, al menos, descartar un distractor^4,46. Existen dos circunstancias propiciadas por la implementación de la fórmula que contradicen su objetivo: a) la fuerte influencia de ésta hacia el efecto la TA (más la consecuente carga de varianza irrelevante al constructo)^22,24, y b) su utilización para paliar la validez perdida en el contenido¹⁵. Como alternativas a la fórmula de corrección tradicional, se ha sugerido aumentar la penalización por ítem incorrecto para desalentar a los sustentantes que ignoran el discurso precautorio⁴⁷, o modificar el estándar de pase en función al desempeño de los sustentantes y a la probabilidad de adivinar⁴⁸.

Los Escenarios 4, 5 y 6 parecen más plausibles que simplemente asumir que los ítems son uniformes (es decir, que en todos sucede lo mismo: adivinar a ciegas, o descartar determinado número de distractores). En el ámbito de educación médica, especialmente para exámenes de medianas y altas consecuencias, es totalmente verosímil asumir que los estudiantes poseen un cierto nivel de θ y de TW debido a su trayectoria académica y experiencia con EOM, por eso resultan más apropiados los supuestos en los que la asignación de probabilidad varía. Es importante enfatizar que en el análisis teórico se supone que, sin importar la valoración que asigne el individuo a cada opción o su concepción respecto a adivinar, siempre da respuesta a los ítems. En realidad, la decisión sobre responder los ítems introduce otra fuente de incertidumbre que no se investigó en este análisis.

Con base en los resultados de este trabajo, es posible recomendarle a los tomadores de decisiones que consideren los elementos ajenos al rasgo que se pretende medir que influyen en el puntaje obtenido en el examen, o al menos estén conscientes de ellos, de modo que el punto de corte no sea arbitrariamente localizado en un porcentaje de la calificación máxima, y/o que se establezcan estándares para asegurar la calidad de los reactivos que constituyen las pruebas. Finalmente, como futura línea de investigación, sugerimos explorar experimentalmente la pertinencia del modelo teórico propuesto con la intención principal de determinar el efecto de la regla de calificar sobre los factores TA, TW y EG. En específico, podría definirse un método para evaluar cómo la regla para calificar modifica el efecto de la TA, a través de la percepción del riesgo, utilizando ítems que difieran en el grado que permiten la ocurrencia de TW y EG.

Contribución de cada autor

AJN concibió múltiples ideas, desarrolló el trabajo y llevó a cabo los análisis teóricos basados en el modelo Nedelsky. IL concibió las ideas principales del artículo, determinó la estructura de las ideas, y desarrolló el programa informático para el análisis teórico. Ambos autores aprobaron la versión final del artículo.

Presentaciones previas

Ninguna.

Responsabilidades éticas

Protección de personas y animales

Los autores declaran que para esta investigación no se han realizado experimentos en seres humanos ni en animales.

Confidencialidad de los datos

Los autores declaran que en este artículo no aparecen datos de pacientes.

Derecho a la privacidad y consentimiento informado

Los autores declaran que en este artículo no aparecen datos de pacientes.

Financiación

Ninguna.

Conflictos de interés

Los autores declaran no tener conflictos de interés.

Agradecimientos

Ninguno