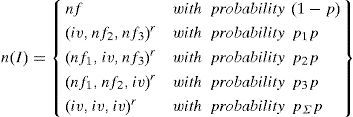Impulse noise reduction or removal is a very active research area of image processing. A nonlinear hybrid filter for removing fixed impulse noise (salt & pepper) noise from color images has been proposed in this study. Technique is based on mathematical morphology and trimmed standard median filter. Proposed filter is composed of a sequence of morphological standard and well known operations erosion-dilation and trimmed standard median filter. It removes the fixed impulse noise (salt & pepper) very well without distorting the image features, color components and edges. It does not introduce blurring and moving effects even in high noise densities (up to 90%). The standard similarity measure peak signal to noise ratio (PSNR) and computation time have been used to evaluate the performance of proposed hybrid filter.
Noise is the most annoying problem in image processing. One way to get rid of this problem is the development of such a robust algorithm that can perform the processing tasks in presence of noise. The other way is to design a filtration process to eliminate the noise from images [1] while preserving its features, edges and details.
Noise introduces random variations into image that fluctuate the original values to some different values. Causes which may introduce noise to images include flaws in data transmission, imperfect optics, sensor malfunctioning, processing techniques and electronic interference [2; 3].
Mathematical morphology is a methodology specifically designed for the analysis of geometrical structures in an image by probing it with small patterns called structuring elements [4]. The resultant image operators are nonlinear and found useful for many applications like edge detection, object segmentation [5], noise suppression [6] and exploring geometrical structures of images [7]. Alternate sequence filters (ASFs) are recognized as one of these important operators and have been widely used and researched [8; 9; 10; 11]. Some other morphological filters include multi structure elements based morphological filters [12; 13], soft morphological filters [14; 15] and hybrid operator-based morphological filters [16].
Median filter [17] having the good denoising power has been the most popular filter. Its variations have been proposed in multistate median filter [18], median filter based on homogeneity information [19; 20] decision based trimmed median filters [21; 22] to improve its performance.
Recently the extensions of mathematical morphology to color images have been proposed in [23; 24; 25; 26; 27]. The proposed hybrid filter combines the strong processing capabilities of mathematical morphology and decision based trimmed median filter for noise suppression or cancellation. By using the concept of ASF, a sequence of erosion and dilation combined with the trimmed median filter is composed with line structuring elements. It not only achieves the outstanding results but produces visually satisfactory reconstructed images even in very high noise densities.
The rest of the paper is structured as follows, section 2 discusses the proposed method in detail, section 3 provides the results and discussion upon those results, section 4 concludes the whole method and section 5 lists the references quoted in this study.
2Materials and methodsDifferent models exist for image de noising including ROF model [28], Total variation model [29], Bias model [30], Affine model [31], Graphical model [32] and Multiplicative noise model [33] etc. These models have proved best for the removal of a variety of noise like salt and pepper noise, Gaussian noise, uniform noise, Rayleigh noise, exponential noise, mixed noise, Gamma noise and poison noise etc.
The noise model used in the paper consists of well known and morphological standard operations known as erosion-dilation and trimmed standard median filter. This noise model is selected because it does not distort the features of image, image edges and image color components while removing the fixed impulse noise (salt & pepper). Further, even in case of high densities of noise, moving and blurring effects are also not introduced by this noise model.
2.1Noise ModelA digital image can be modeled in any of color spaces like RGB, HSV and L*a *b. RGB is most commonly used as basic color space. RGB enables the mixing of red, green and blue light to produce a wide range of colors. Therefore a three dimensional (3–D) vector is used to represent the colors in RGB model, containing the red as first, green as second and blue as the third element. These elements are called three primary components having the range [0, 2d–1], mostly with d=8.
A two dimensional (2D) vector can be used to represent a digital color image I (G, H, 3), in which (x, y) depicts the position of a pixel in I and 1≤x≤G,1≤y≤H. If I (x, y, 1), I (x, y, 2) and I (x, y, 3) denote the red, green and blue components respectively, then occurrence of impulse noise can be modeled as [2].
n(I) is noisy signal, nf=(nf1,nf2,nf3)r is noise free color vector, iv is the impulse value andImpulse value iv can have two values either 0 or 255.
2.2Filtration SchemeThe scheme used in proposed method is component wise filtering. Color space RGB is used and each of its components is passed through the proposed hybrid filter separately.
Erosion and dilation are the most elementary operations of mathematical morphology. Erosion computes the local minima and dilation computes the local maxima of neighbor of the input image, on which they are working. If SE is structuring element then component wise erosion of color image I is defined by
where k=1,2,3 showing R, G, B components Component wise Dilation of image color I is defined by where k=1, 2, 3 showing R, G, B componentsif nk=neighborhood of size (2m+1)x(2m+1), form=1,2,3… then component wise trimmed median of color image I is defined by
Proposition. When image I is eroded or dilated with structuring element or kernel SE, the following inverse relationship holds for the operators erosion and dilation.
Proof. Given two sets Ik and se the erosion can be shown as
and dilation can be defined by by complementing eq(10) and from eq(12) by complementing eq (11) and from eq (12) as dilation is Minkowski addition Ik⊕se¯=Iˆk⊕se¯. (Complement.property.for.addition)From (13) & (14) it can be clearly observed they contain inverse relationship
Therefore Ikϵse¯=Iˆkδse¯
This inverse relationship of erosion and dilation is very useful for removing salt & pepper noise. By using them alternatively salt & pepper noise can be removed very effectively as they are of inverse properties.
The general definition of ASF is given by
Therefore definition of propose hybrid filter for color image I (G,H,3) can be given by
k=1, 2, 3 Showing the primary color components of RGB3Results & discussionPeak signal to noise ratio (PSNR) is used as objective similarity between a filtered image and noise free original image, measured in decibels (dB).
Expression (17) is based on another similarity measure called Mean Square Error (MSE).
I, O are filtered and original images respectively, G,H are dimensions of images, k shows each of primary color components of RGB and R is the maximum intensity having the value 2d−1 where d=8.
We used the three test images Lena, Peppers and Baboon of size 512x512 as given in fig. 2.
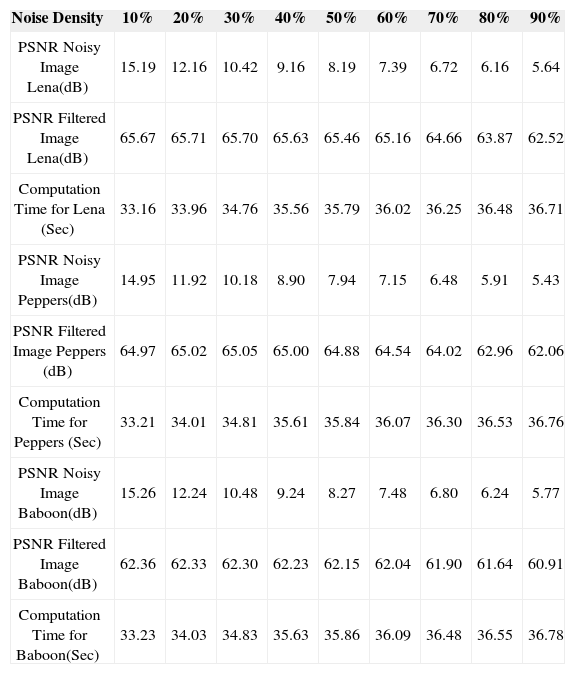
We have found that our method receives the best numerical and visual performance with a window of size m=1 i-e (3x3) for experimental results. Table. 1 shows the PSNR values for test images corrupted by impulse noise up to 90%, filtered images and computation time for showing the effectiveness and strength of proposed method.
PSNR and Computation Time for test Images Lena, Peppers, Baboon Corrupted by 10%–90% of Noise.
| Noise Density | 10% | 20% | 30% | 40% | 50% | 60% | 70% | 80% | 90% |
|---|---|---|---|---|---|---|---|---|---|
| PSNR Noisy Image Lena(dB) | 15.19 | 12.16 | 10.42 | 9.16 | 8.19 | 7.39 | 6.72 | 6.16 | 5.64 |
| PSNR Filtered Image Lena(dB) | 65.67 | 65.71 | 65.70 | 65.63 | 65.46 | 65.16 | 64.66 | 63.87 | 62.52 |
| Computation Time for Lena (Sec) | 33.16 | 33.96 | 34.76 | 35.56 | 35.79 | 36.02 | 36.25 | 36.48 | 36.71 |
| PSNR Noisy Image Peppers(dB) | 14.95 | 11.92 | 10.18 | 8.90 | 7.94 | 7.15 | 6.48 | 5.91 | 5.43 |
| PSNR Filtered Image Peppers (dB) | 64.97 | 65.02 | 65.05 | 65.00 | 64.88 | 64.54 | 64.02 | 62.96 | 62.06 |
| Computation Time for Peppers (Sec) | 33.21 | 34.01 | 34.81 | 35.61 | 35.84 | 36.07 | 36.30 | 36.53 | 36.76 |
| PSNR Noisy Image Baboon(dB) | 15.26 | 12.24 | 10.48 | 9.24 | 8.27 | 7.48 | 6.80 | 6.24 | 5.77 |
| PSNR Filtered Image Baboon(dB) | 62.36 | 62.33 | 62.30 | 62.23 | 62.15 | 62.04 | 61.90 | 61.64 | 60.91 |
| Computation Time for Baboon(Sec) | 33.23 | 34.03 | 34.83 | 35.63 | 35.86 | 36.09 | 36.48 | 36.55 | 36.78 |
Fig. 3 shows the visual performance of proposed method for test images Lena, Peppers and Baboon corrupted by 40%, 60% and 80%.
We can observe from Fig. 3 that our method removes impulse noise in edge regions as well as keeps intact with image features and color components. Fig. 4 gives a graphical representation for values of PSNR and computation time.
First sequence removes the 50% of noise, then trimmed median estimates the original values for noisy pixels 0 and 255 and the final sequence is used to preserve the color features in the whole image after removing noise.
4ConclusionA method for impulse noise removal from color images has been proposed. It has combined the mathematical morphology and trimmed median filter. Method utilizes the inverse property of the most elementary operators of mathematical morphology namely erosion and dilation. A unique sequence of these operators with trimmed median filter has been composed that effectively removes the salt & pepper noise from color images. The results evaluate the performance of proposed hybrid filter. Proposed filter very effectively removes the noise from edge regions and inner regions of noisy images without distorting the features and color components.