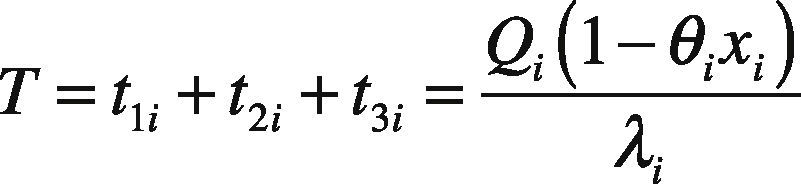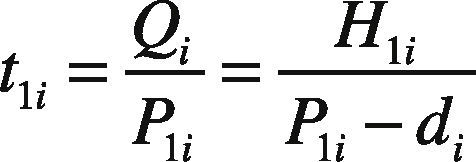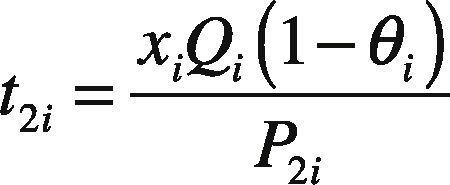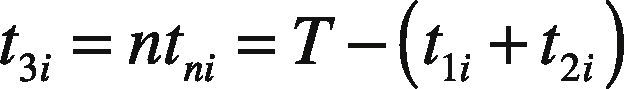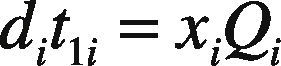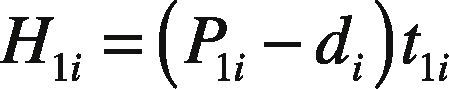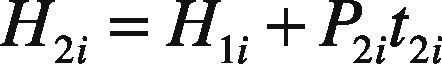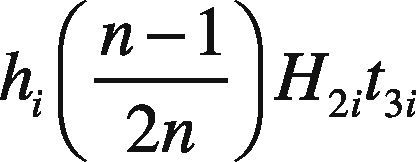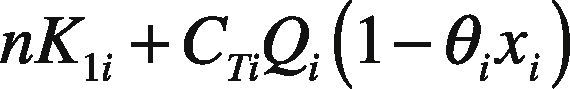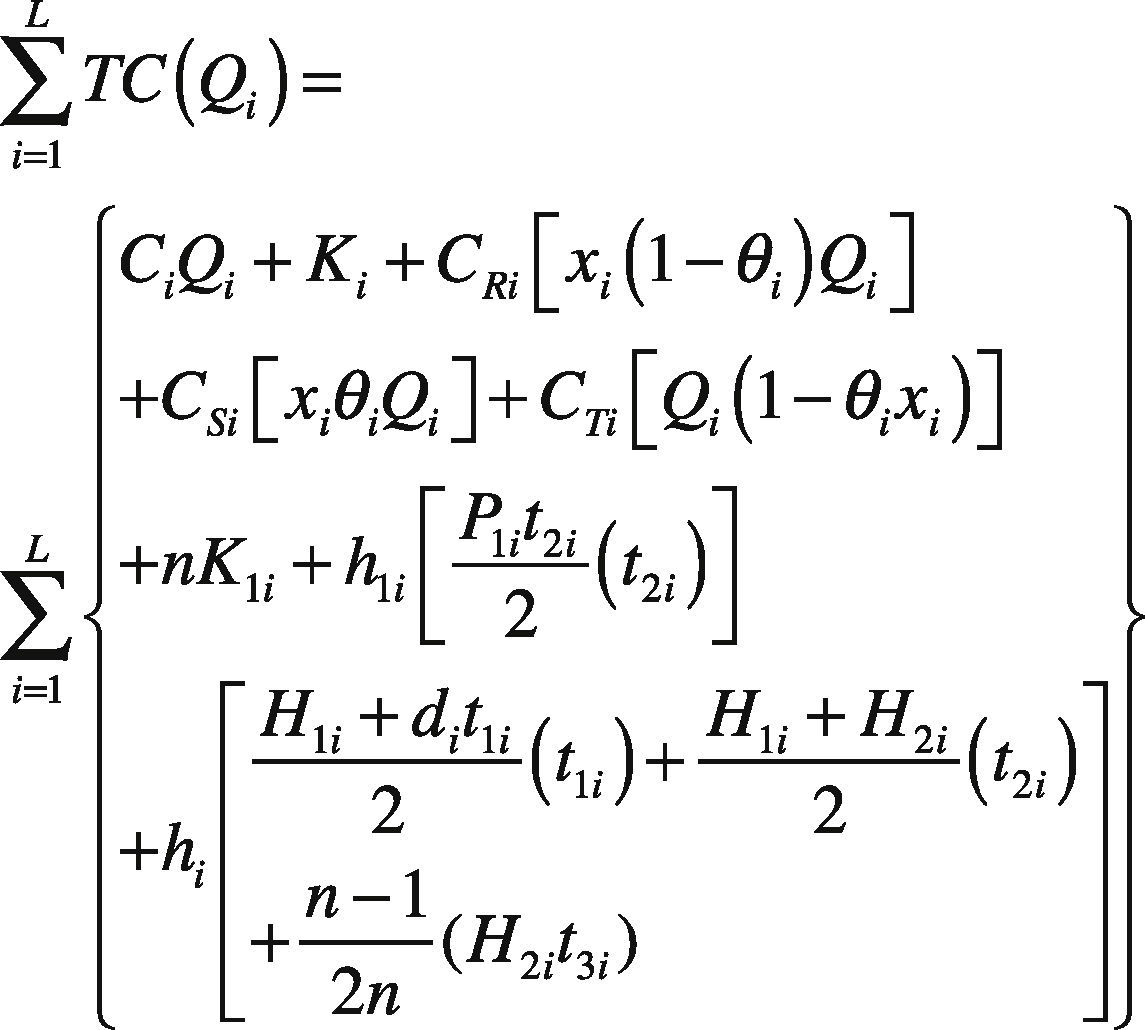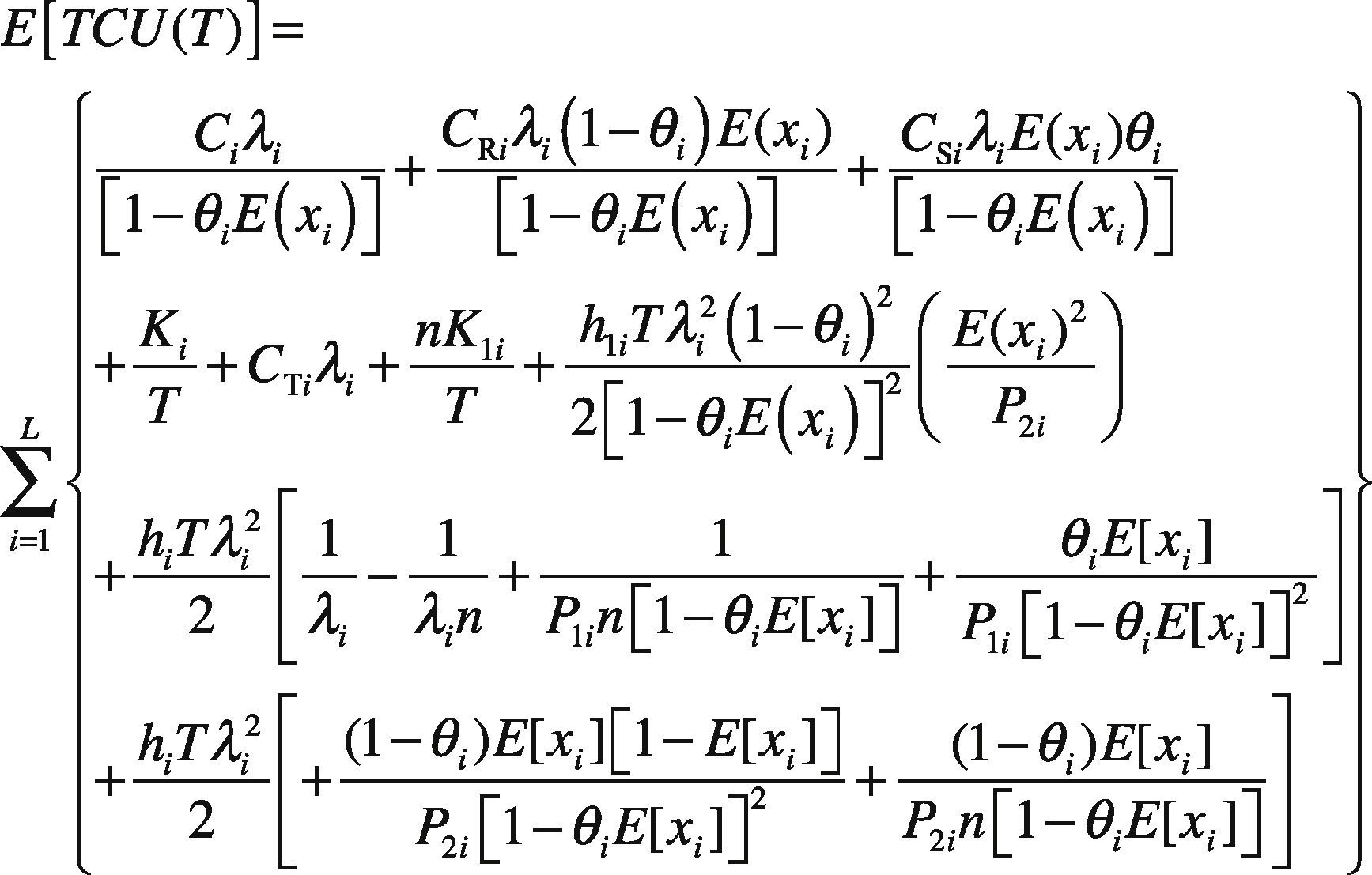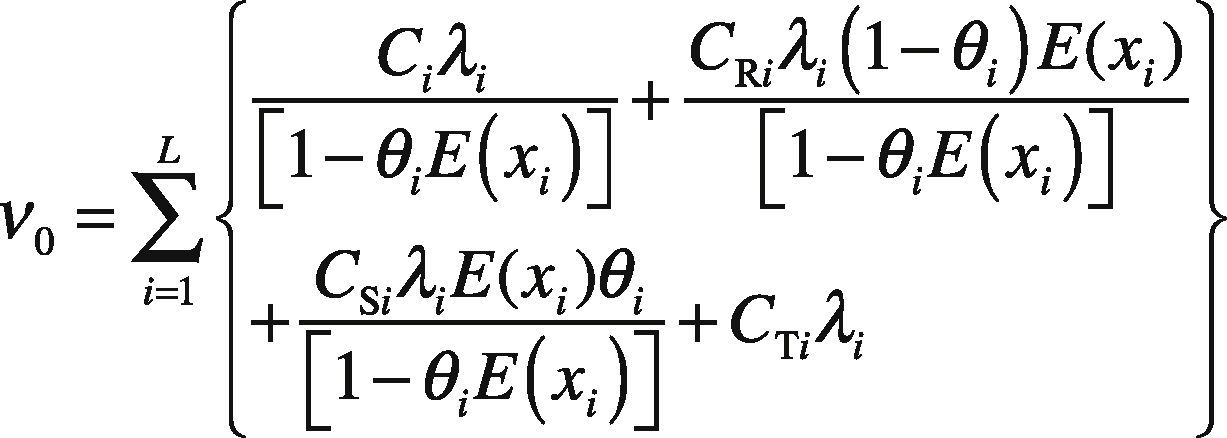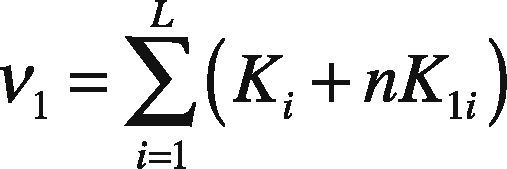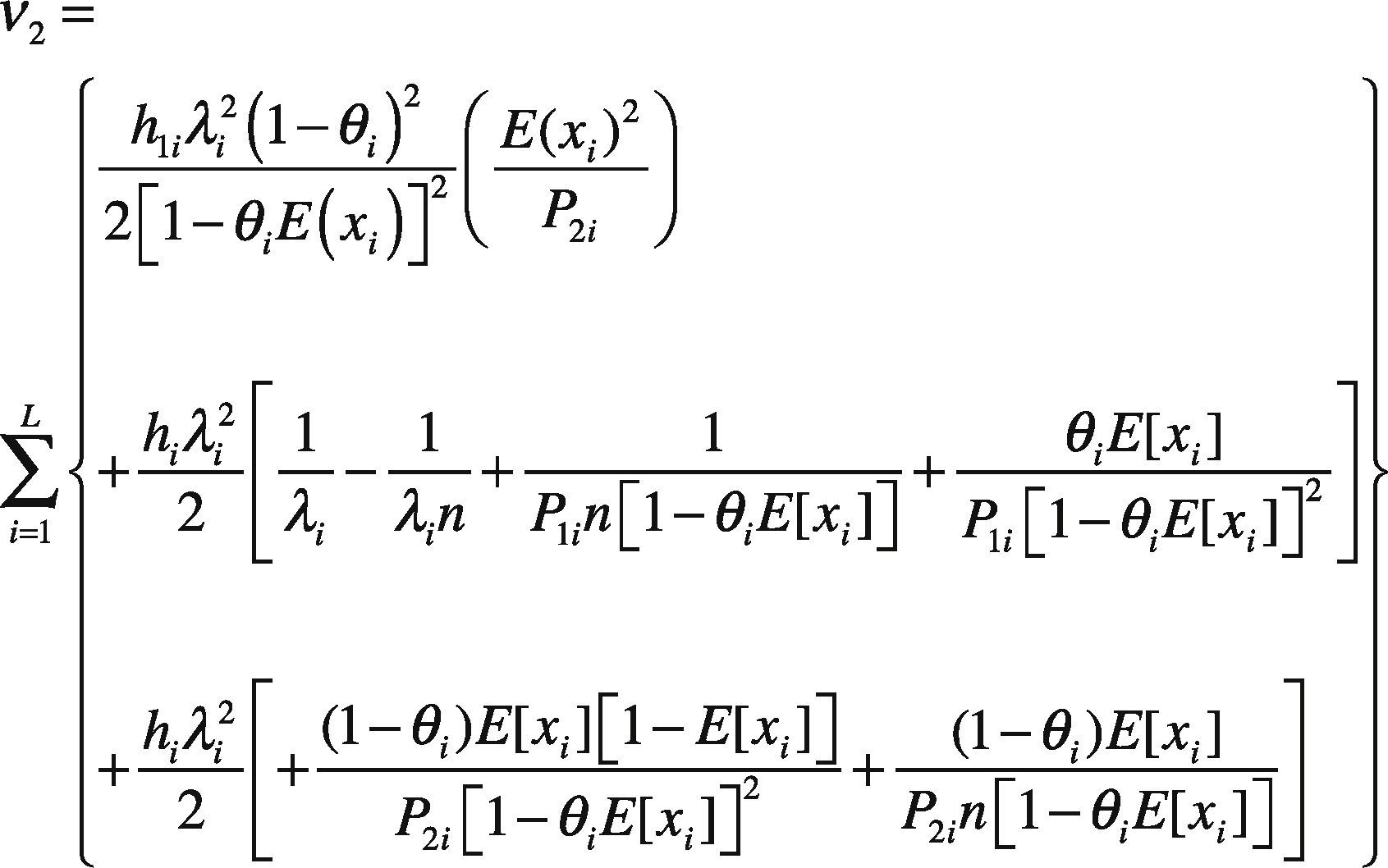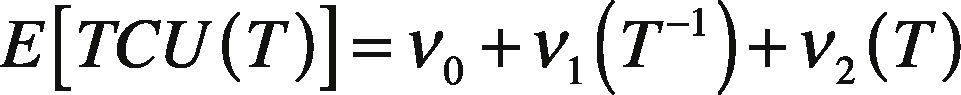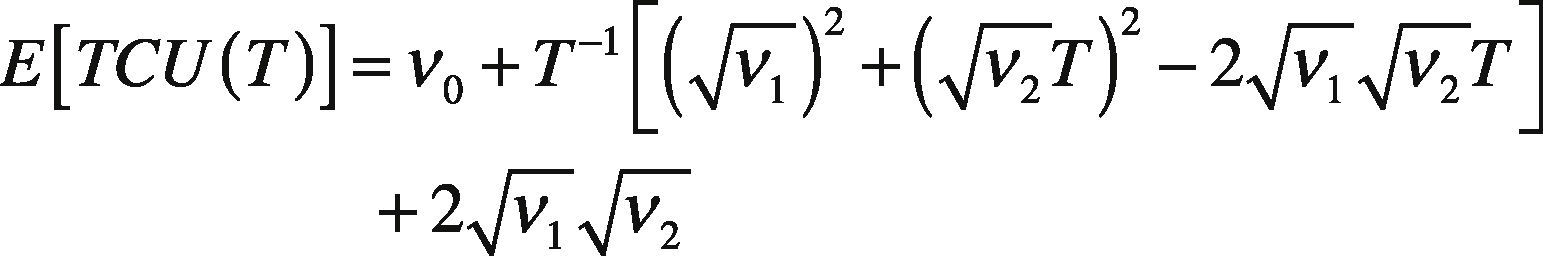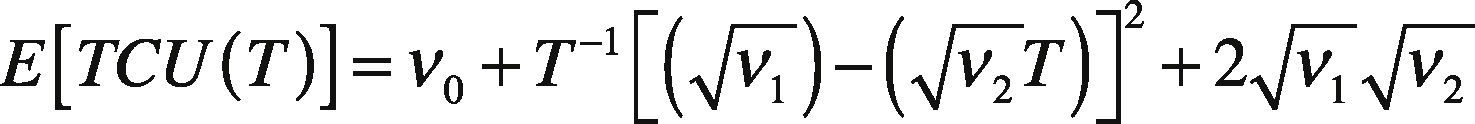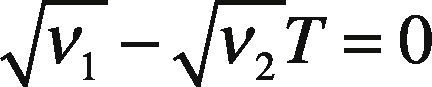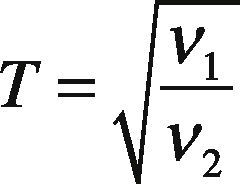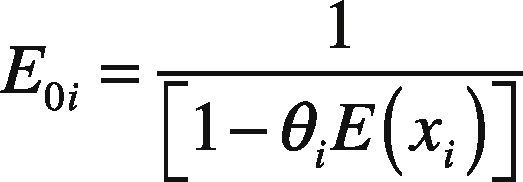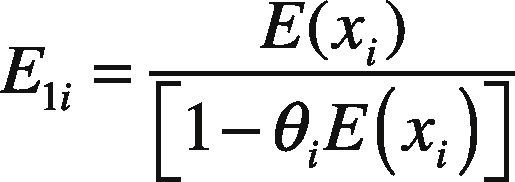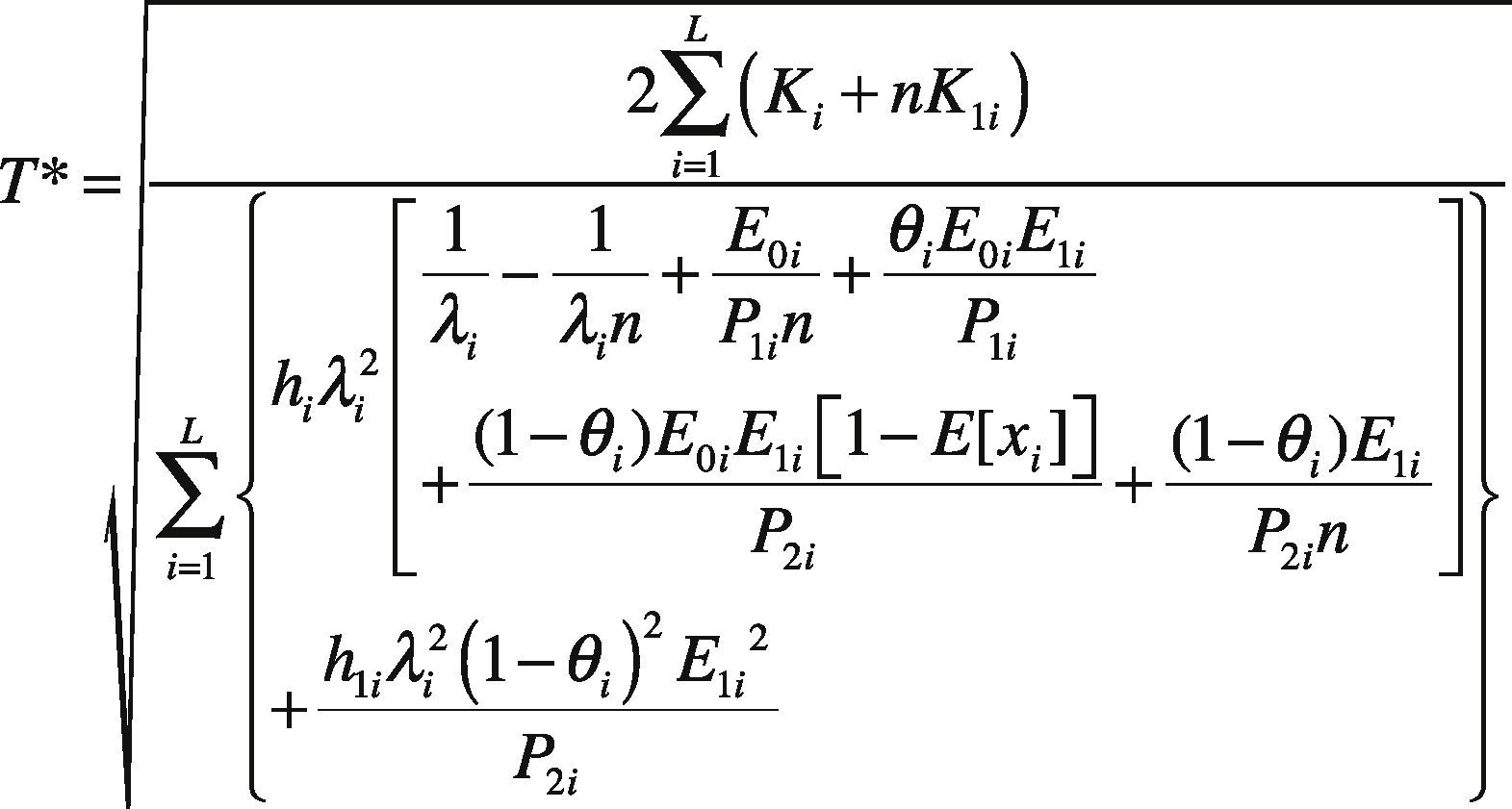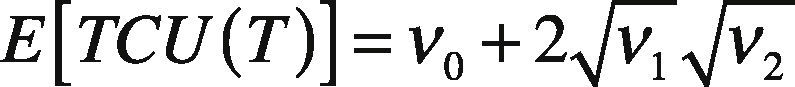In a recent paper, Chiu et al. (2014) utilized mathematical modeling and differential calculus to determine the common production cycle time that minimizes total production, inventory, and delivery costs for a multi-item economic production quantity (EPQ) model with scrap, rework, and multi-delivery. The present study proposes an algebraic approach substituting the use of differential calculus on the system cost function for deriving the optimal common cycle time in the aforementioned multi-item EPQ model. This simplified approach may enable managing practitioners to resolve real multi-item EPQ models more effectively.
In this study, a multi-item economic production quantity (EPQ) model with scrap, rework, and multi-delivery is resolved using a simplified algebraic approach. In real-life production planning, maximizing production equipment utilization is always an important operating goal for manufacturing firms (Nahmias, 2009). Intending to accomplish this goal, production planners frequently propose fabricating multiple products sequentially using a single piece of production equipment (Bergstrom & Smith, 1970; Gaalman, 1978; Rosenblatt & Finger, 1983). Rosenblatt (1985) compared two policies for the joint replenishment problem, both with a general ordering cost function. A fixed-cycle policy was solved using a dynamic programming approach, resulting in partitioning the items into groups. The other basic-cycle policy used a heuristic approach to partition the items into only two groups. A simulation model was developed to compare the effectiveness of the two policies and the economic order quantity (EOQ) approach. Mitchell (1988) examined a problem of single-item service objectives in a multiitem inventory system subject to a system-wide service-level constraint. A computationally efficient algorithm based on the Generalized Knapsack Duality algorithm was developed to find approximately optimal policies for such a system. The result indicates that operating costs can be reduced significantly by applying the proposed model rather than the simpler uniform service model often used in practice.
Sox and Muckstadt (1996) proposed a formulation and solution algorithm for the finite-horizon capacitated production planning problem with random demand for multiple products. They developed a sub-gradient optimization algorithm based on Lagrangian relaxation to solve the formulation, and provided some computational results indicating that this approach works well for rolling-horizon planning compared with the rolling-horizon performance of the corresponding optimal finite-horizon solution. Rizk et al. (2006) studied a multi-item dynamic production-distribution planning problem between a producer and a distribution center. They assumed that the cost of transportation between the manufacturing location and the distribution center offered economies of scale and could be represented by general piecewise linear functions. The production system of the producer is a serial process with a multiple parallel machines bottleneck stage and divergent finishing stages. A predetermined production sequence was maintained on the bottleneck machines. They proposed a tight mixed-integer programming production model with three different formulations representing general piecewise linear functions. Hence, three equivalent mathematical programming models of the manufacturer-distributor flow planning problem were examined. Tests were performed to compare the computational efficiency of these models. Chiu et al. (2014) studied the optimal common production cycle policy for a multi-item EPQ model with scrap, rework, and multiple deliveries. They considered an imperfect production system wherein a portion of nonconforming items is scrap and the other portion can be reworked and repaired in the same production cycle. Their objective was to determine the optimal common production cycle time that minimizes the long-run average cost per unit time for the specific multi-item EPQ model. Mathematical modeling and analysis were used to solve the proposed model, and a closed-form optimal common cycle time for multi-item production planning was obtained. Practical usage of their research result was demonstrated by a numerical example.
Additional studies related to various aspects of imperfect production systems, multi-item production planning, and multi-delivery systems can be found elsewhere (Cedillo-Campos & Sánchez-Ramírez; 2013; Chiu, Y. et al., 2013a; Chiu, S. et al., 2013a; Acosta-Cano & Sastrón-Báguena, 2013; Chiu, Y. et al., 2014). Over a decade ago, Grubbström and Erdem (1999) proposed an algebraic approach to obtain EOQ for an inventory model with backlogging. Their algebraic derivation straightforwardly derived the optimal order quantity without reference to the first- or second-order derivatives. A few studies applied the same or similar methodologies to solve various aspects of EPQ models and vendor-buyer integrated supply chain systems (Lin et al., 2013; Chiu, S. et al., 2013b; Chiu, Y. et al., 2013b; Tseng et al., 2014; Wu et al., 2014). This study extends such an algebraic method to the multi-item EPQ model with scrap, rework, and multiple deliveries [1] and demonstrates that the optimal common replenishment cycle time can be derived without derivatives.
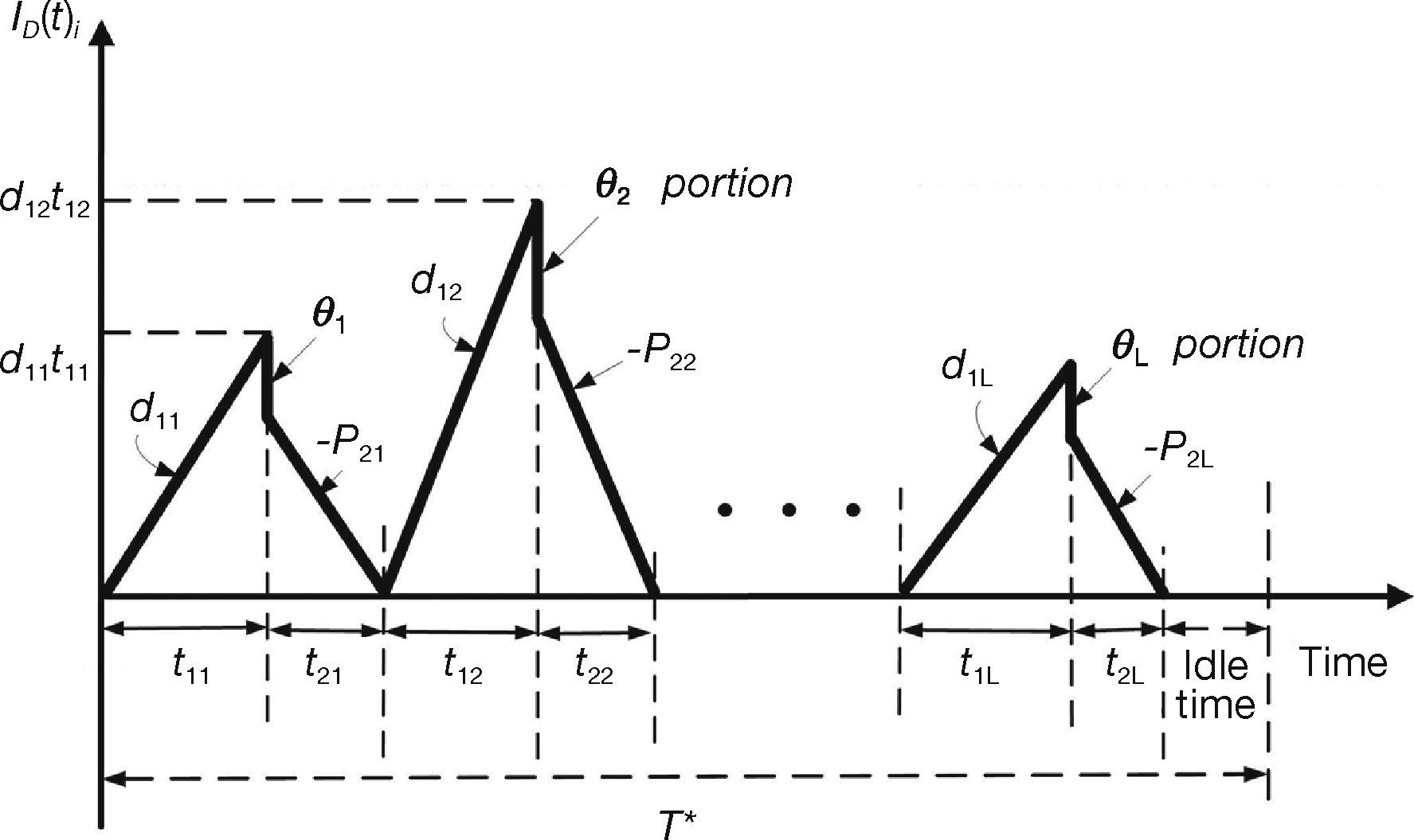
2Model Description and Algebraic DerivationReconsider the multi-item EPQ model with scrap, rework, and multiple deliveries, as examined in [1], wherein L products are manufactured in sequence on a single machine and all items produced are screened with inspection cost included in unit production cost Ci. To ease the comparison efforts for readers, this study employs the same notation used in [1]. In the manufacturing process of each product i (where i = 1, 2, …, L), there is an xi portion of defective items produced randomly at a rate di. Among the defective items, a θi portion is considered to represent scrap items, and the other portion can be repaired at a rework rate of P2i. The rework process starts immediately when the regular production process of each product i is completed in each cycle, with an additional unit rework cost CRi (see the rework time t2i in Fig. 1).
Shortages are not allowed under normal operation; thus, the constant production rate P1i for product i must satisfy (P1i – di – λi) > 0, where λi is the demand rate for product i per year, and di = xiP1i. The level of on-hand inventory of defective items during uptime t1i and the rework time t2i is depicted in Figure 2. Additionally, a practical multi-delivery policy is adopted in the proposed systems to meet customers’ demands. Under the specific delivery policy, finished goods for each product i can only be delivered to customers if the entire production lot is quality assured at the end of the rework process. Fixed quantity n installments of the finished batch are delivered at a fixed interval of time during delivery time t3i (see Fig. 1).
Other notation used in the modeling and analysis of this study is listed as follows:
T = common production cycle length, a decision variable.
Qi = production lot size per cycle for product i.
CSi = disposal cost per scrapped item.
hi = unit holding cost.
Ki = production setup cost.
h1i = unit holding cost for each reworked item.
K1i = fixed delivery cost per shipment for product i.
CTi = unit shipping cost for product i.
t1i = production uptime for product i in the proposed EPQ model.
t2i = the rework time for product i in the proposed EPQ model.
H1i = maximum level of on-hand inventory for product i when regular production ends.
H2i = maximum level of on-hand inventory in units for product i when rework process ends.
n = number of fixed quantity installments of the finished batch to be delivered to customers in each cycle, it is assumed to be a constant for all products.
tni = a fixed interval of time between each installment of finished products delivered during t2i, for product i.
ID(t)i = on-hand inventory of defective items for product i at time t.
I(t)i = on-hand inventory of perfect quality items for product i at time t.
TC(Qi) = total production-inventory-delivery costs per cycle for product i.
E[TCU(T)] = total expected production-inventory-delivery costs per unit time for L products in the proposed system using the common production cycle time T as the decision variable.
The following formulas represent the common production cycle time, production uptime, rework time, and finished items delivery time for each product i (where i = 1, 2, …, L) and can be obtained directly from Figures 1 and 2:
The total number of defective items produced in a given cycle and on-hand inventory levels H1i and H2i can also be obtained directly from Figures 1 and 2 as follows:
The holding costs for finished products in delivery time t3
and total delivery costs for product i in a cycle are as follows [1]:
Total system costs for L products in a given cycle consists of variable production cost, setup cost, rework cost, disposal cost, fixed and variable delivery cost, holding cost during uptime t1i, rework time t2i, and delivery time t3. Thus, total TC(Qi) for L products can be expressed as follows:
Substituting all variables from Eqs. (1) to (9) in Eq. (10), and applying the expected values of x in order to account for its randomness, E[TCU(T)] can be obtained as follows [1]:
Unlike the conventional method, which uses differential calculus on the system cost function E[TCU(T)] to find the optimal common production cycle time [1], this study uses the following simplified algebraic approach.
2.1The Proposed Algebraic DerivationEquation (11) has different forms of decision variable T in its right-hand side (RHS), namely T 0 , T-1, and T1. Let ν0 , ν1, and ν2 stand for the following:
Thus, Eq. (11) can be rearranged as follows:
With further rearrangement, Eq. (15) becomes either
orNote that if the second term of Eq. (17) equals zero, then E[TCU(T)] can be minimized. That is:
orSubstituting Eqs. (13) and (14) in Eq. (11), we obtain the optimal common production cycle time T* as follows:
In order to compare the result with that of (1), we let E0i and E1i represent the following:
Thus, Eq. (20) can be rearranged as follows:
Equation (23) is identical to that obtained using the conventional differential calculus method [1]. Applying the optimal T* —see Eqs. (17) and (18)—, we obtain the following simplified formula for E[TCU(T)]:
3Concluding remarksThe conventional approach to a multi-item EPQ model with scrap, rework, and multi-delivery is to first employ differential calculus to prove the convexity of the system cost function, and to then derive the optimal production cycle time decision [1]. This study presents an alternative algebraic approach to replace the use of differential calculus in the optimization process. Such a simplified approach is a handy solution that may enable managing practitioners to effectively resolve real-life multi-item EPQ models.




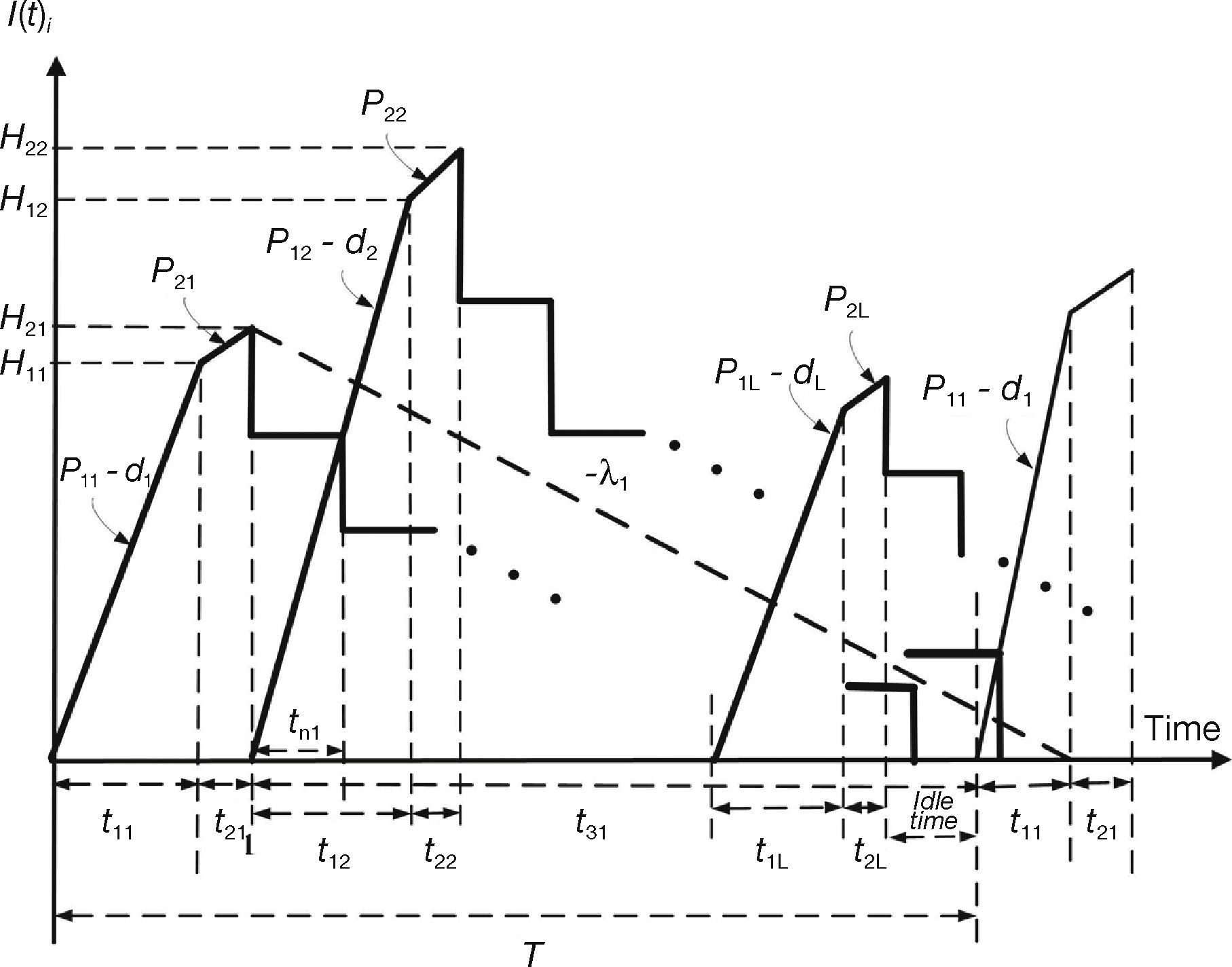
![The level of on-hand inventory of perfect quality items of product i in the proposed multi-item EPQ system using a common cycle policy [1]. The level of on-hand inventory of perfect quality items of product i in the proposed multi-item EPQ system using a common cycle policy [1].](https://static.elsevier.es/multimedia/16656423/0000001300000004/v1_201509302251/S1665642315000474/v1_201509302251/en/main.assets/thumbnail/gr1.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![The level of on-hand inventory of defective items of product i in the proposed multi-item EPQ system [1]. The level of on-hand inventory of defective items of product i in the proposed multi-item EPQ system [1].](https://static.elsevier.es/multimedia/16656423/0000001300000004/v1_201509302251/S1665642315000474/v1_201509302251/en/main.assets/thumbnail/gr2.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)