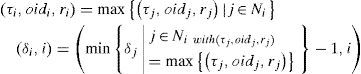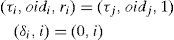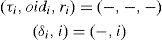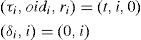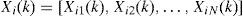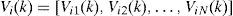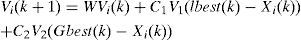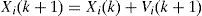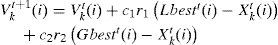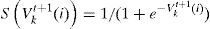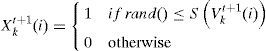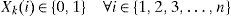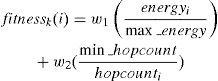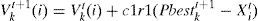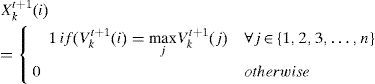An Energy-efficient Routing Protocol for MANETs: a Particle Swarm Optimization Approach

Abstract

Mobile ad hoc networks (MANETs) are infrastructure-free networks created by wireless mobile devices with restricted battery life. This limited battery capacity in MANETs makes it necessary to consider the energy-awareness feature in their design. Since routing protocols have central role in MANETs, their energy-awareness increases network life time by efficiently using of the available limited energy. TORA is one of these routing protocols that offer high degree of scalability. This paper employs the Binary Particle Swarm Optimization algorithm (BPSO) to add the energy-awareness feature to the TORA routing protocol. The proposed protocol considers routes length in its route selection process and also includes routes energy level in its calculations. It formulates the routing issue as an optimization problem and then employs BPSO to choose a route that maximizes a weighted function of the route length and the route energy level. Extensive simulations in ns-2 simulator environment show that the proposed routing protocol, called BPSO-TORA, prolongs the network lifetime remarkably and outperforms TORA in terms of network life time, system life time and total delivered data.

1

Introduction

A MANET is an autonomous collection of nodes mobile users that offers infrastructure-free architecture for communication over a shared wireless medium [1, 2]. MANET nodes have limited processing speed and power, battery, storage, and communication capabilities. One of the most challenging issues in MANETs is their routing algorithms [3, 4 and 5]. Routing protocols for ad hoc networks can be divided into two categories based on when and how the routes are discovered: proactive (table-driven) [6, 7] and the reactive (on-demand) [8, 9]. For the table-driven routing protocols, consistent and up-to-date routing information are maintained at each mobile host. Hence, for the table-driven protocols each mobile host maintains one or more tables containing routing information to every other mobile host in the network. When a network topology changes, the mobile hosts propagate the updated messages throughout the network in order to maintain the routing information about the whole network.

These routing protocols differ in the method by which the topology information is distributed across the network and in the number of routing-related tables. An example of table-driven ad hoc routing protocols is the Destination-Sequenced Distance-Vector (DSDV) routing algorithm [10]. In contrast to the table-driven routing protocols, the reactive routing protocols don't maintain all up-to-date routes at every mobile host. Instead, the routes are created whenever they are required. When a source host wants to send a datagram to a destination, it invokes the route discovery mechanism to find the path. An example is the Ad hoc On-demand Distance Vector Routing (AODV) [11], which is an improvement of the DSDV algorithm. AODV minimizes the number of broadcasts by creating routes on-demand as opposed to the DSDV which maintains a list of all the routes. The Dynamic Source Routing protocol (DSR) [12] and Temporally Ordered Routing Algorithm (TORA) [13] are other on-demand routing protocols.

Much attention has been attracted, due to the limited battery capacity in MANETs energy-aware routing in recent years. Energy-aware routing is an effective solution to prolong the lifetime of energy-constrained nodes in mobile ad hoc networks [14, 15, 16]. As generalized in [17], there are generally two categories of energy-aware routing concepts: Minimum Energy (ME) routing that selects the route with least total energy consumption for packet transmission, and max-min routing that selects the route which bottleneck residual node energy is the maximum. This paper focuses on TORA algorithm which is a highly adaptive, efficient and scalable distributed source-initiated on-demand routing algorithm and tries to make it an energy-efficient routing protocol. To this end the BPSO algorithm is employed to design a TORA-based energy aware routing protocol following the max-min idea.

The rest of this paper is organized as follows. In section 2, TORA routing protocol is described. Preliminaries including Particle Swarm Optimization are given in section 3. The proposed energy-aware routing protocol (BPSO-TORA) is presented in section 4 and its performance is evaluated in section 5 through an extensive simulative study. Finally the paper is concluded in section 6.

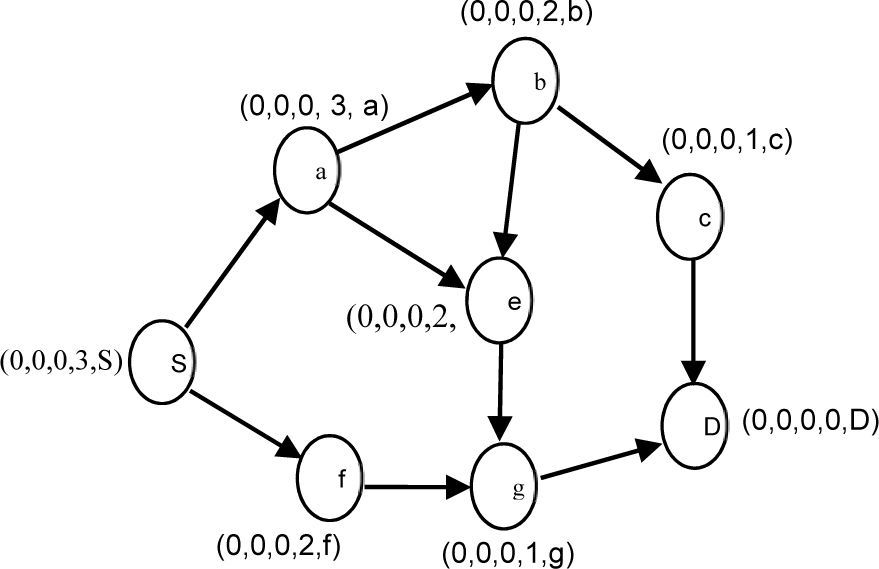
2

TORA Routing protocol

TORA [13] is a highly adaptive distributed routing algorithm that is well-suited for use in mobile ad hoc networks. In TORA, each node has five kinds of information: H_i, N_i, HN_{i, j}, RR_i and LS_i,j. H_i = (τ_i, oid_i, r_i, δ_i, i) is related with each node i ∈ N (N is the set of nodes in network). In this ordered quintuple τ_i, is logical time of a link failure, oid_i is the ID of originator node, r_i is a bit used to divide each of the unique reference into two unique sub-levels, δ_i is a propagation ordering parameter and i is the unique ID of the node. At first the height of each node in the network other than the destination node is set to NULL, H_i =(-, -, -, -, i). The height of the destination node is always ZERO, H_did = (0,0,0,0, did), that did is the ID of destination node. N_i is the set neighbors of node i. HN_i,j is a height array for each neighbor j∈N_i. RR_i is a route-required flag (RR_i) which is initially unset. LS_i,j is a link-state array with an entry for each link (i,j)∈L, where j∈N_i. The state of the links is determined by the heights H_i and HN_i,j. Each link is directed from the higher node to the lower node. If a neighbor j is higher than node i, the link called upstream (UP). If a neighbor j is lower than node i, the link called downstream (DN). If the neighbors height entry, HN_i,j, is NULL, the link is distinct undirected (UN).

TORA can be divided into three phase: creating routes, maintaining routes and erasing routes. Details of these phases are brought from [2] as follow.

2.1

Creating Routes

This phase requires use of the QRY packets and UPD packets. A QRY packet consists of an ID of destination (did), which distinct the destination node that algorithm is running. An UPD packet consists of a did, and the height of the node i which is broadcasting the packet, H_i. When a node that has undirected links and its route required flag is 0, need a route to the destination node, it broadcasts a QRY packet and set its route-required flag with 1. When a node i receives a QRY packet, it operates as follows: (a) if it has no downstream links and its route required flag is 0, it re-broadcasts the QRY packet and sets its route-required flag with 1. (b) If it has no downstream links and its route-required flag is set with 1, it rejects the QRY packet. (c) If it has at least one downstream link and its height is NULL, this node sets its height to H_i = (τ_j, oid_j, r_j, δ_j + 1, i), that HN_i,j = (τ_j, oid_j, r_j, δ_j, j) is the minimum height of its non-NULL neighbors, then broadcasts an UPD packet. (d) If it has at least one downstream link and its height is non-NULL, it first compares the time the last UPD packet was broadcast to the time the link over which the QRY packet was received became active. If an UPD packet has been broadcast since the link became active, it rejects the QRY packet; otherwise, it broadcasts an UPD packet. If a node has the route-required flag with 1 when a new link is established, it broadcasts a QRY packet.

When a node i receive an UPD packet from a neighbor j ∈ N_i, node i first updates the entry HN_i,j with the height contained in the received UPD packet and then operate as follows. (a) If the route required flag is set with 1, node i sets its height to H_i = (τ_j, oid_j, r_j, δ_j + 1, i) that j is its non-NULL neighbor and height of is minimum in between neighbor nodes, then updates all the entries in its link-state array LS, un-sets the route-required flag and then broadcasts an UPD packet which contains its new height. (b) If the route-required flag is 0, node i simply updates the entry LS_i,j in its link-state array.

2.2

Maintaining Routes

Maintaining routes is only performed for nodes that their height is non-NULL. Furthermore, any neighbor's height which is NULL is not used for the computations. A node i is said to have no downstream links if H_i is lower than HN_i,j for all non-NULL neighbors j ∈ N_i. This will result in one of five possible actions depending on the state of the node and the preceding event. Each node (other than the destination) that has no downstream links modifies its height, H_i = (τ_i, oid_i, r_i, δ_i, i), as follows.

Case 1: Node i has no downstream links due to a link failure. In this case:

(τ_i, oid_i, r_i) = (t,i,0) where t is the time of the failure and (δ_i, i) = (0, i).

Case 2: Node i has no downstream links due to a link reversal following reception of an UPD packet and the ordered sets (τ_j, oid_j, r_j) are not equal for all j∈N_i. In this case:

Case 3: Node i has no downstream links due to a link reversal following reception of an UPD packet and the ordered sets (τ_j, oid_j, r)_j are equal with r_j = 0 for all j∈N_i. In this case:

Case 4: Node i has no downstream links due to a link reversal following reception of an UPD packet, the ordered sets (τ_j, oid_j, r_j) are equal with r_j = 1 for all j∈N_i and oid_j = i. In this case:

Case 5: Node i has no downstream links due to a link reversal following reception of an UPD packet, the ordered (τ_j, oid_j, r)_j are equal with r_j = 1 for all j∈N_i and oid_j ≠ i. In this case:

2.3

Erasing Routes

If case 4 of maintaining routes phase are detected, node i sets its height and the height entry for each neighbor j∈N_i to NULL unless the destination is a neighbor, in which case the corresponding height entry is set to ZERO, updates all the entries in its link-state array LS, and broadcast a CLR packet. The CLR packet containing of a did and the reflected level of node i, (τ_i, oid_i). When a node i receives a CLR packet from a neighbor j∈N_i it perform as below. (a) If the reference level in the CLR packet matches the reference level of node i, it sets its height and the height entry for each neighbor j∈N_i to NULL unless the destination is a neighbor, in which case the corresponding height entry is set to ZERO, updates all the entries in its link-state array LS and broadcasts a CLR packet. (b) If the reference level in the CLR packet does not match the reference level of node i, it sets the height entry for each neighbor j∈N_i to NULL and updates the matching link-state array entries. Thus the height of each node in the part of the network which was partitioned is set to NULL and all invalid routes are erased. If (b) causes node i to lose its last downstream link, it perform as in case 1 of maintaining routes.

By using these three phases, TORA discover and modify routes between source and destination nodes. Fig. 1 shows the routes creating process in TORA. When routes created, each node has the height structure. Also each node has an array that keeps information of neighbors. In this way, in each node we have situation of node and neighbors.

Figure 1.

Routes creating process in TORA

3

Particle Swarm Optimization

Particle Swarm Optimization is a search algorithm that has been inspired from bird flocking and fish schooling. This population based algorithm has been designed and introduced by Kennedy and Eberhart [14] in 1995. The basic PSO has found many successful applications in a number of problems including standard function optimization problems [15, 16], solving permutation problems [17] and training multi-layer neural networks [18]. Some applications of PSO are given in [19, 20 and 21]. The PSO algorithm contains a swarm of particles in which each particle indicates a potential solution. The particles fly through a multidimensional search space in which the position of each particle is adjusted according to its own experience and the experience of its neighbors. PSO system combines local search methods (through self experience) with global search methods (through neighboring experience), attempting to balance exploration and exploitation. As in evolutionary computation paradigms, the concept of fitness is employed and candidate solutions to the problem are termed particles, each of which adjusts its flying based on the flying experiences of both itself and its companion. PSO is an approach to problems whose solutions can be represented as a point in an n-dimensional solution space. A number of particles are randomly set into motion through this space. During each iteration they observe the fitness of themselves and their neighbors and emulate successful neighbors (those whose current position represents a better solution to the problem than theirs) by moving towards them. The position and velocity of particle i at iteration k can be respectively expressed by notations (1)–(2).

Particle i keeps track of its coordinates in the solution space which are associated with the best solution that has achieved so far by that particle. This value is called local best Lbest_i. Another best value that is tracked by the PSO is the best value obtained so far by any particle in the neighborhood of that particle. This value is called global best Gbest The basic concept of PSO lies in accelerating each particle toward its local best and the global best locations. Various schemes for grouping particles into competing, semi- independent flocks can be used, or all the particles can belong to a single global flock. This extremely simple approach has been surprisingly effective across a variety of problem domains. The velocity and position of particle i at iteration k+1 can be calculated according to the following equations:

Where w is the inertia weight, c₁ and c₂ are constants which determine the influence of the local best position Lbest_i(k) and the global best position Gbest(k). Parameters r₁ and r₂ are random numbers uniformly distributed within [0,1].

3.1

Binary Particle Swarm Optimization (BPSO)

In 1997 the binary version of this algorithm was presented by Kennedy and Eberhart [6] for discrete optimization problems. In this method, each particle has a position in a D-dimensional space and each element of a particle position can take the binary value of 0 or 1 in which 1 means “included” and 0 means “not included”. The major difference between binary PSO with continuous version is that velocities are defined in terms of probabilities. Using this definition a velocity must be restricted within the range [0,1]. So a map is introduced to map all real valued numbers of velocity to the range [0,1] [4]. The normalization function used typically is a sigmoid function as:

Where the value of rand() drawn from U(0,1) and the function S(v) is a sigmoid limiting transformation. At the beginning of the algorithm, a number of particles and their velocity vectors are generated randomly. Then in some iteration the algorithm aims at obtaining the optimal or near-optimal solutions based on its predefined fitness function. The velocity vector is updated in each time step using two best positions, Lbest and Gbest, and then the position of the particles is updated using velocity vectors.

4

Particle Structure of the Routing Protocol

Although TORA can typically provide multiple routes for any source/destination pair, it always selects a route with fewer hops. Obviously this puts the shorter routes under a heavy load and hence their energy depletes earlier than others. The result is a decreased network life time and consequently a reduced network throughput [22, 23]. To solve this problem a routing protocol is developed that not only considers routes length in its calculations, but also includes routes' energy level in its decisions. The goal is to select a route that in one hand has a short length and on the other hand has a high energy level. This route is not necessarily the shortest one, since the shortest route may has a lower energy level. It is in fact one of the short routes that has a relatively high energy level. To find such a route a multiple objective BPSO algorithm is used. To BPSO-based formulation of the routing problem, two important questions are needed to be answered: (1) Which parameter is considered as the particle position? (2) How the objective function is defined?

Position of particles

One of the key issues in designing a successful PSO algorithm is the representation step which aims at finding an appropriate mapping between problem solution and PSO particle. It is assumed, that each node that forwards packets is equipped with a BPSO algorithm. A representation, in which solutions are encoded in a 1 × n vector, called position vector, in which n is the number of neighbor nodes of the current node is used. The position matrix of each particle has the two following properties:

1) All the elements of the vector have either the value of 0 or 1. In other words if X_k is the position vector of kth node, then:

In each vector only one element is 1 and others are 0. If X_k(i) = 1 then the ith neighbor node will be chosen as next hop of the route. Figure 2 shows a solution representation in a node with 5 neighbors in which node 3 is the selected as the next hop to forward packets.

Figure 2.

Position Vector

Fitness evaluation

In this paper length and energy are used to evaluate the fitness of possible routes, each one getting started from one of neighbor nodes. The fitness value of node k, in case of choosing neighbor node i as the next node of the route, can be given using equation (7).

Where energy_i, refers to the bottleneck node energy level of possible route i, max_energy is the highest bottleneck node energy level among all possible routes starting from the current node, hopcount_i, is the number of hops from neighbor node i to the destination, max_hopcount is the maximum hopcount among the neighbor nodes and finally w₁ and w₂ are weighting factors for route energy and route length respectively.

Particles Velocity, Lbest and Gbest

Velocity of each particle is considered as a 1 × n vector whose elements are in range [-Vmax, Vmax].Lbest and Gbest are 1 × n vectors the same as position vectors. Lbest_k represents the best position that kth particle has visited since the first time step and Gbest_k represents the best position which kth particle has visited from the beginning of the algorithm. For updating Lbest and Gbest in time step, if fitness value of current position is greater than Lbest or Gbest, then they are replaced with the current position.

Particle Updating. First updating of the particles is explained. Equation (9) is used for updating the velocity vector and then Equation (10) for position matrix of each particle. Note that since the network nodes don't distribute routing information among each other, hence any node can only find Lbest and ignores Gbest:

In equation (9)Vkt(i) is ithe element of the kth node's velocity in tth time step of the algorithm and Xkt(i) denotes the ith element of the kth node's position vector in tth time step. Equation (10) means that in each column of position matrix, value 1 is assigned to the element whose corresponding element in velocity vector has the maximum value. If in a velocity vector there is more than one element with maximum value, then one of these elements is selected randomly and 1 is assigned to its corresponding element in the position vector.

The algorithm of BPSO-TORA algorithm can be stated as Fig. 3. This algorithm is run by each node on the route from the source node to the destination.

Figure 3.

BPSO-TORA Algorithm

5

Simulation Results

Now, the proposed algorithm is examined through its implementation in ns-2 [24] environment. This implementation is run by making some modifications over TORA module of ns-2 simulator and then it is evaluated based on the following simulation setup:

• –

  Network space: 1000 m × 1000 m

• –

  Simulation time: 500 second

• –

  Traffic model: CBR

• –

  Primary energy of each node: 25 j

• –

  Packet size: 512 bytes

• –

  Mobility model: random way point

• –

  Medium access protocol: IEEE 802.11

• –

  Speed of mobile nodes: 0–20 m/s

In order to study BPSO-TORA's performance in different operational conditions three different scenarios are considered. In these scenarios BPSO-TORA and TORA are evaluated for wide ranges of “number of nodes”, “nodes' pose time” and “traffic rate”. In each scenario the proposed algorithm is compared with TORA in terms of three basic performance metrics, namely, network life time, system life time and total delivered data [25, 26]. The network lifetime: it is defined as the time when first node of the network finishes its own battery for the first time. The system lifetime: it is defined as the time when 20% of nodes finish their own battery. The total delivered data: it is defined as the total number of data packets that is delivered during of system lifetime.

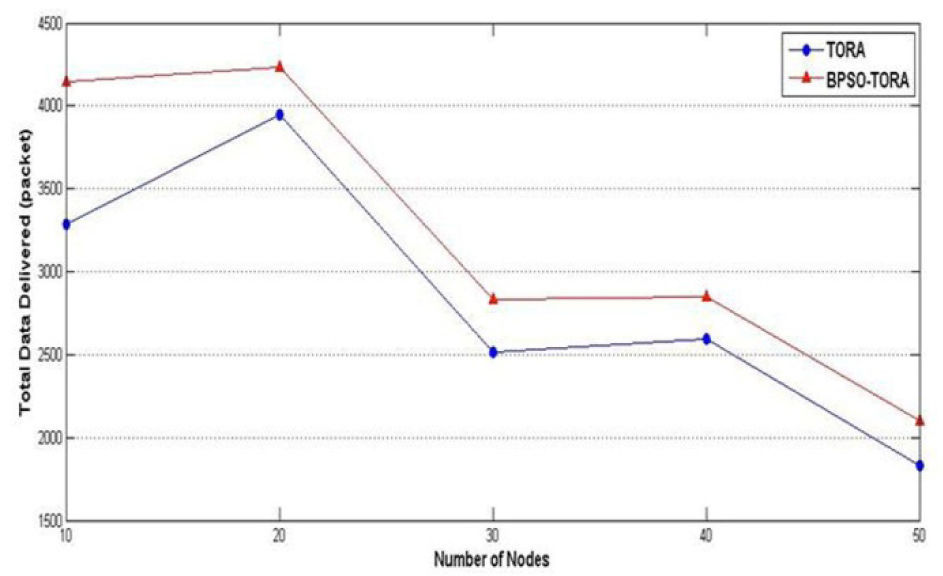
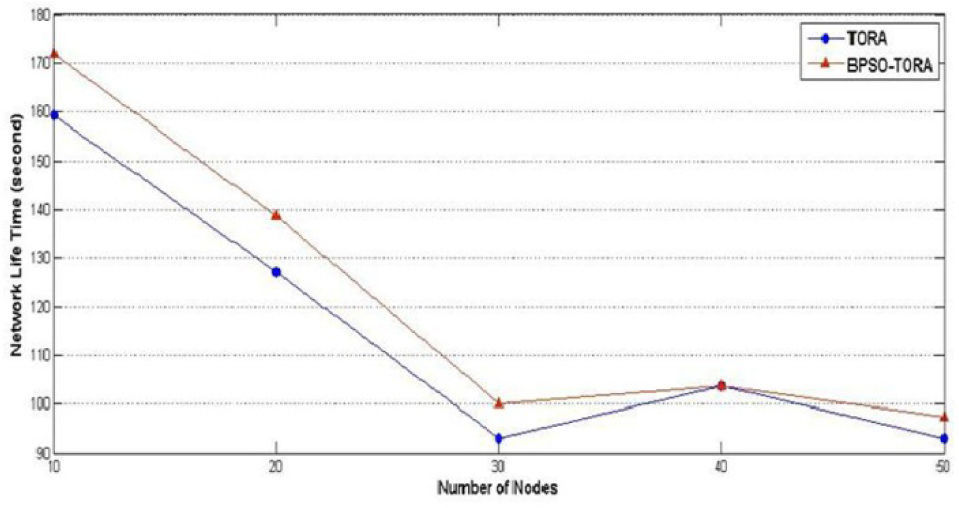
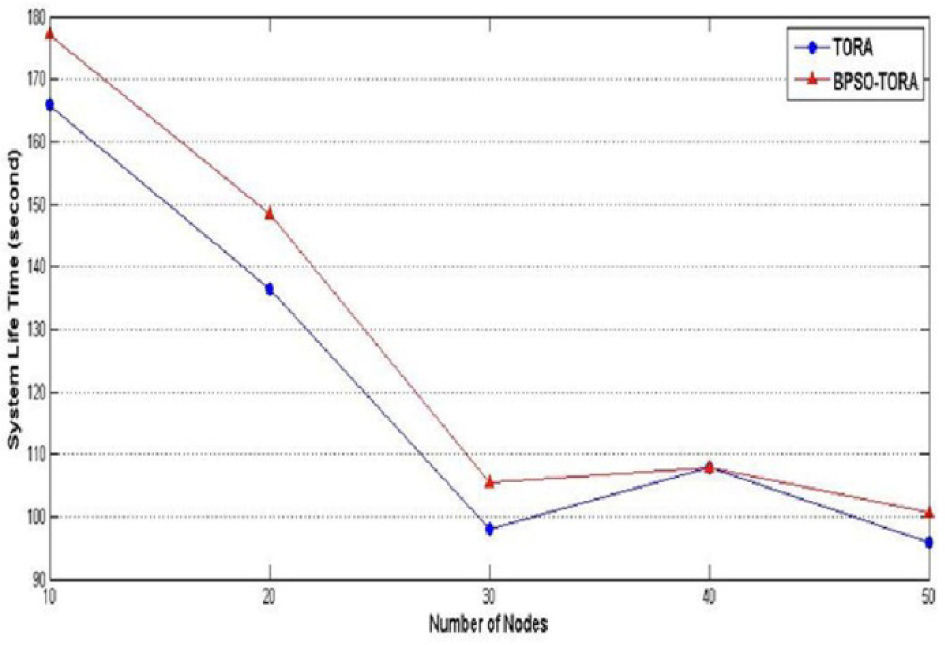
Scenario 1: Impact of number of nodes on BPSO-TORA's performance

In this scenario BPSO-TORA and TORA are simulated under different numbers of nodes to study how these algorithms are affected by the number of nodes. To this end nodes' pause time are fixed at 10 seconds, nodes' sending rate at 10 packets per second and the network simulation is repeated for different numbers of nodes i.e. 10, 20, 30, 40 and 50 nodes. Simulation results are shown in Figs. 4–6. Fig. 4 shows how the total delivered data of these protocols changes as the number of nodes increases. It is observed that the total delivered data of BPSO-TORA is considerably higher than TORA algorithm. On the other hand Figs. 5–6 show that the network life time and system life time of BPSO-TORA are considerably higher than of TORA. This improved performance of BPSO-TORA has roots in this fact that BPSO-TORA includes nodes' energy level in the route selection process. According to equation (8) since BPSO-TORA considers both the route length and the route energy level in its decisions, it doesn't select the route with lower energy level and hence the network life time increases. Obviously this increased network life time leads to improved packet delivery rate.

Figure 4.

Total delivered data versus number of nodes

Figure 5.

Network life time versus number of nodes

Figure 6.

System life time versus number of nodes

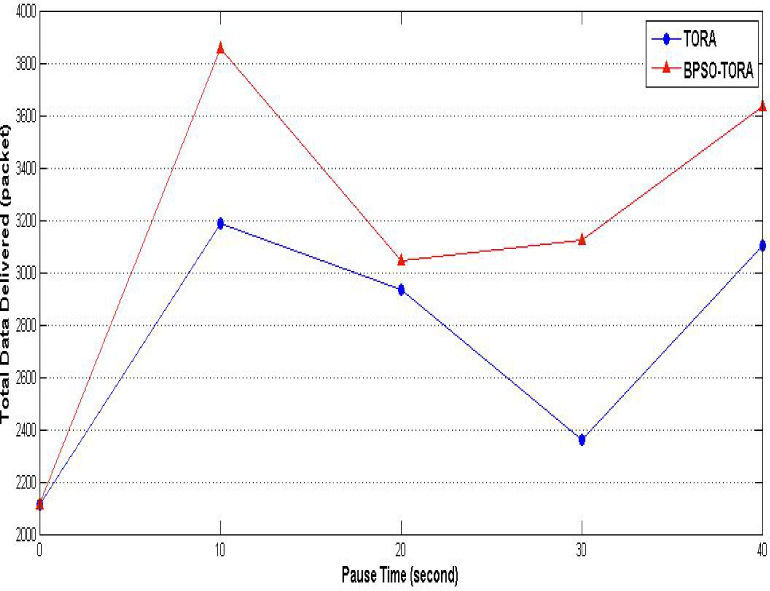
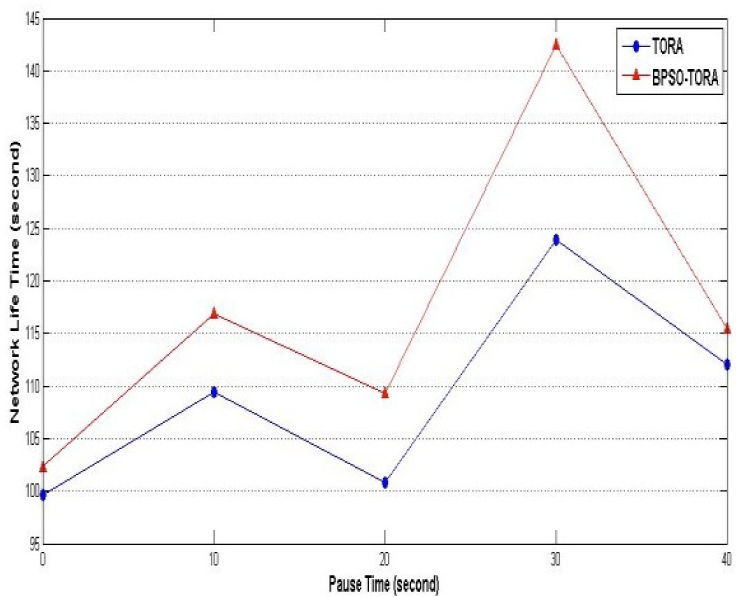
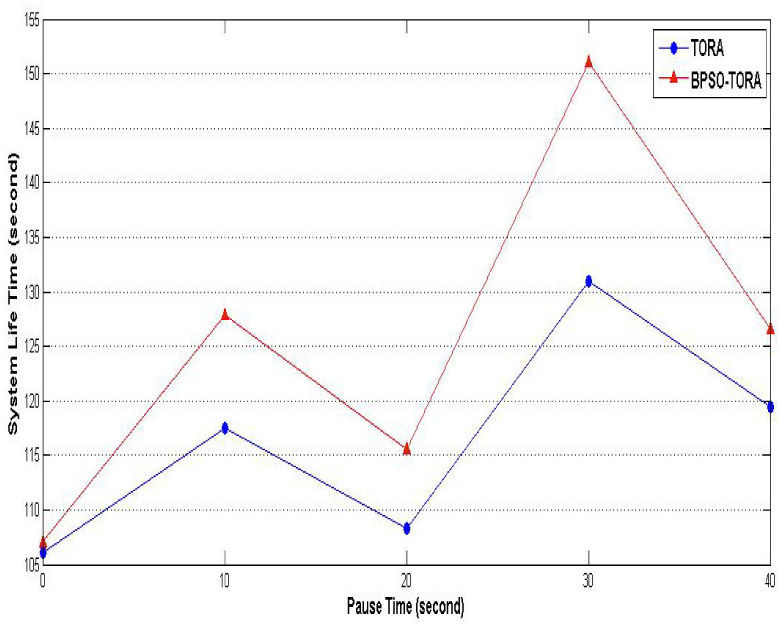
Scenario 2: Impact of pause time on BPSO- TORA's performance

In this scenario BPSO-TORA and TORA are simulated under different pause times to study how these algorithms are affected by it. To this end nodes' count are fixed at 25, nodes' sending rate at 10 packets per second and the network simulation is repeated for different pause times i.e. : 0, 10, 20, 30 and 40 seconds. Simulation results are shown in Figs. 7–9. Fig. 7 shows how the total delivered data of these protocols changes as the nodes' pause time changes. According to this figure it is observed that the total delivered data of BPSO-TORA is considerably higher than TORA algorithm. On the other hand Figs. 8–9 show that the network life time and system life time of BPSO-TORA are considerably higher than of TORA for different values of pause time. The reason of this improved performance can be found taking into account the equation (8) according to which BPSO-TORA considers both the route length and the route energy level in its decisions. It selects a route that not only has shorter length but also has an acceptable energy level. This leads to balanced distribution of the network traffic among different routes that causes in turn to an increased network life time. Obviously when the network life time increases more packets can be sent through it and hence the packet delivery rate will be increased.

Figure 7.

Total delivered data versus pause time

Figure 8.

Network life time versus pause time

Figure 9.

System life time versus pause time

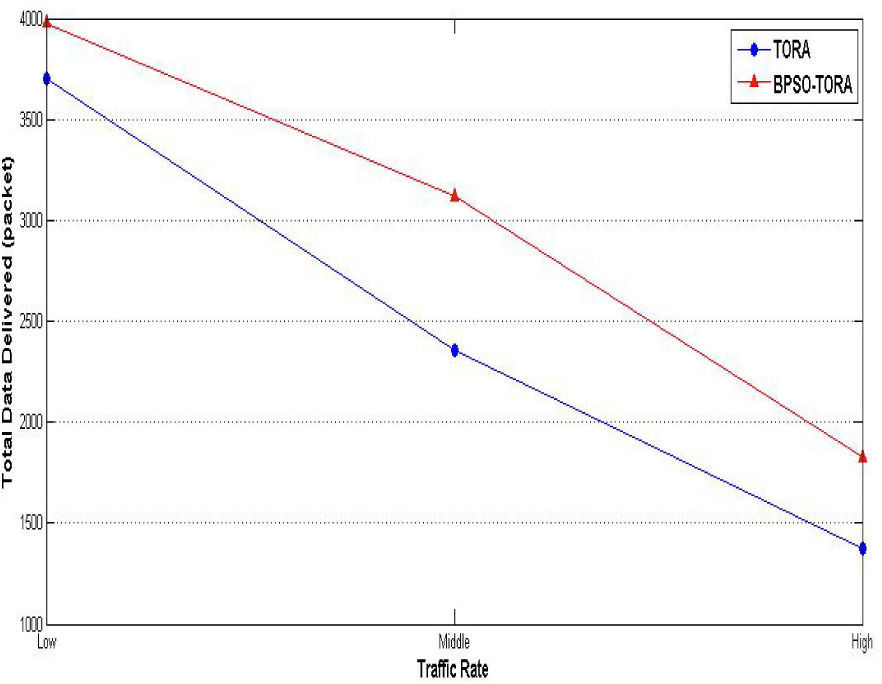
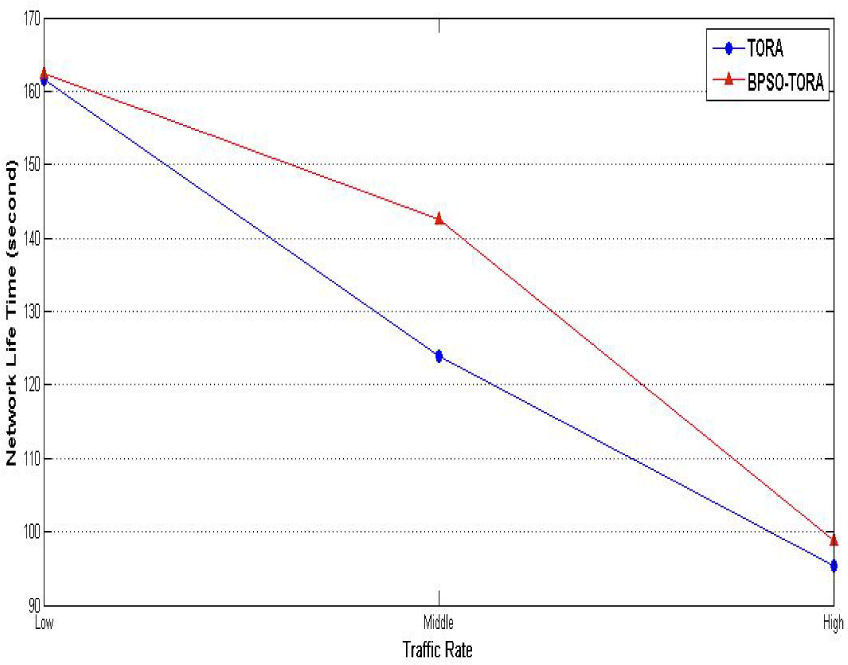
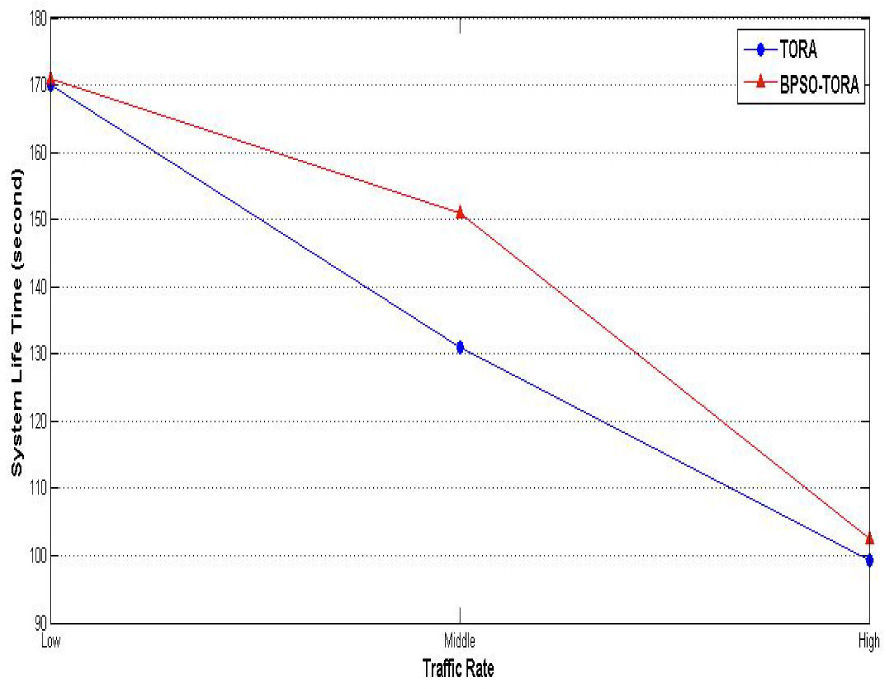
Scenario 3: Impact of traffic rate on BPSO-TORA's performance

In this scenario how the proposed algorithm behaves under different amount of the network load is studied. For this purpose 3 different levels of traffic rates are considered for each node i.e. Low (5 packets per second), Medium (10 packets per second), High (15packets per second) and then behavior of TORA and BPSO-TORA is examined under each one of these traffic intensity. The simulation results are shown Figs. 10–12. Same as previous scenarios, in this scenario BPSO-TORA outperforms TORA in terms of packet delivery rate, network life time and system life time. As discussed above the reason for this improved performance is behind the fitness function of (8).

Figure 10.

Total delivered data versus traffic rate

Figure 11.

Network life time versus traffic rate

Figure 12.

System life time versus traffic rate

From these simulations it is concluded that BPSO-TORA has better performance in comparison with TORA algorithm. Better performance of BPSO-TORA is due to this fact that it uses those routes that have higher level of energy and short length. This leads to balanced consumption of energy in various routes and nodes; hence BPSO-TORA experiences less route breakages and achieves better performanc

6

Conclusion

In this paper BPSO-TORA, a novel energy-aware routing protocol for mobile ad hoc networks has been presented. It redefines the routing algorithm as an optimization problem and then employs BPSO algorithm to solve it. The main feature of BPSO-TORA is that it distributes load among routes considering energy of routes. This causes the load to be distributed uniformly among routes and leads to long life of network. The simulation results indicated that the total delivered data, network life time and system life time in BPSO-TORA are remarkably better than TORA routing protocol.