An Implementation of the Task Algebra, a Formal Specification for the Task Model in the Discovery Method

Abstract

This paper describes an implementation of the Task Algebra, a formal model of hierarchical tasks and workflows, in the Haskell programming language. Previously we presented the Task Algebra as a formal, unambiguous notation capturing the kinds of activity and workflow typically seen in business analysis diagrams, similar to UML use case and activity diagrams. Here, we show how the abstract syntax for the Task Algebra may be parsed and then semantically analysed, by a suite of Haskell functions, to compute the execution traces of a system. The approach is illustrated with a case study of a journal management system. The results show how it is possible to automate the semantic analysis of requirements diagrams, as a precursor to developing a logical design.

1

Introduction

There has been a steady take up in the use of formal calculi for software construction over the last 25 years [1], but mainly in academia. Although there are some accounts of their use in industry (basically in critical systems), the majority of software houses in the “real world” have preferred to use visual modelling as a kind of “semi-formal” representation of software.

A method is considered formal if it has well-defined mathematical basis. Formal methods provide a syntactic domain (i.e., the notation or set of symbols for use in the method), a semantic domain (like its universe of objects), and a set of precise rules defining how an object can satisfy a specification [2]. In addition, a specification is a set of sentences built using the notation of the syntactic domain and it represents a subset of the semantic domain.

Spivey says that formal methods are based on mathematical notations and “they describe what the system must do without saying how it is to be done” [3], which applies to the non-constructive approach only. Mathematical notations commonly have three characteristics:

• •

  conciseness - they represent complex facts of a system in a brief space;

• •

  precision - they can specify exactly everything that is intended;

• •

  unambiguity - they do not admit multiple or conflicting interpretations.

Essentially, a formal method can be applied to support the development of software and hardware. This paper shows the results the implementation of a particular process algebra using the Haskell language to build the kernel of a framework. There are some implementations of process algebras such as JACK [4], a Java implementation of a process algebra, which is offered as a Java extension package with CSP operators embedded in the language; Foster [5] describes a plug-in extension for Eclipse translating BPEL4WS models to Finite State Process (FSP) algebra able to perform equivalence verification process. We are applying our particular process algebra, called Task Algebra, to characterise the Task Flow models in the Discovery Method. The advantage is that this will allow software engineers to use diagram-based design methods that have a secure formal underpinning.

2

The task flow model

The Discovery Method is an object-oriented methodology proposed formally in 1998 by Simons [6]; it is considered by the author to be a method focused mostly on the technical process. The Discovery Method is organised into four phases; Business Modelling, Object Modelling, System Modelling, and Software Modelling. The Business Modelling phase is task-oriented. A task is defined in the Discovery Method as something that has the specific sense of an activity carried out by stakeholders that has a business purpose. This task-based exploration will lead eventually towards the two kinds of Task Diagrams: The Task Structure and Task Flow Diagrams.

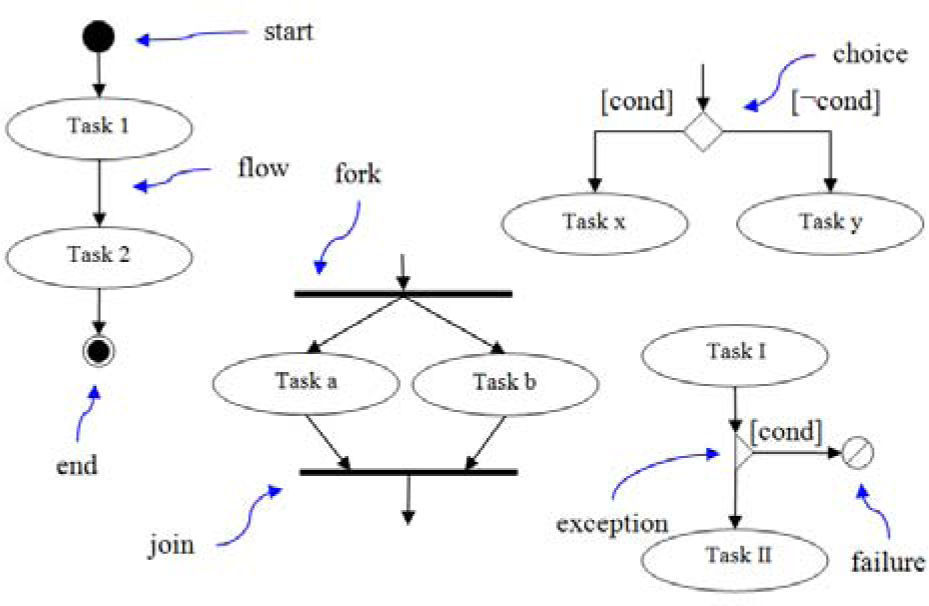
The business workflow is represented in the Discovery Method using the Task Flow Diagram. It depicts the order in which the tasks are realised in the business, expressing also the logical dependency between tasks. While the notation used in the Discovery Method is largely based on the Activity Diagram of UML, it maintains consistently the labelled ellipse notations for tasks. Figure 1 shows the notation for the Task Flow Diagram.

Figure 1.

Elements of the Discovery’s Task Flow Diagram.

2.1

The task algebra for task flow models

Even though Task Flow models could be represented using one of the process algebras described above, a particular algebra was defined with the aim of having a clearer translation between the graphical model and the algebra. One of the main difficulties with applying an existing process algebra was the notion that processes consist of atomic steps, which can be interleaved. This is not the case in the Task Algebra, where even simple tasks have a nonatomic duration and are therefore treated as intervals, rather than atomic events.

A simple task in the Discovery Method [6], [7] is the smallest unit of work with a business goal. A simple task is the minimal representation of a task in the model. A compound task can be formed by either simple or compound tasks in combination with operators defining the structure of the Task Flow Model.

In addition to simple tasks and compound tasks, the abstract syntax also requires the definition of three instantaneous events. These may form part of a compound task in the abstract syntax.

2.2

The task flow metamodel

The basic elements of the abstract syntax are the simple task, which is defined using a unique name to distinguish from others; ϕ representing the empty activity; and the success σ and failure φ symbols, representing a finished activity.

Simple and compound tasks are combined using the operators that construct the structures allowed in the Task Flow Model. The basic syntax structures for the Task Flow Model are sequential composition, selection, parallel composition, repetition, and encapsulation:

• •

  Sequential composition defines the chronological order of execution for a task or a group of tasks from the left to the right and ‘;’ is used as the operator.

• •

  Selection is represented with the symbol ‘+’ and it means that there is a choice between the operands.

• •

  Parallel composition defines the simultaneous execution of the elements in the expression. It is represented by the symbol ‘||’.

• •

  Repetition allows the reiteration of an expression in the form of an until-loop and while-loop structure. It is represented using the μx fixpoint notation.

• •

  Finally, encapsulation is used to group a set of tasks and structures. This constructs a compound task and is represented using curly brackets‘{‘ ‘}’.

The abstract syntax has the following definition in Backus Naur form:Activity ::= ε

- empty activity

| σ

- succeed

|ϕ

- fail

| Task

-- a single task

| Activity ; Activity

-- a sequence of activity

| Activity + Activity

-- a selection of activity

| Activity || Activity

-- parallel activity

| μx.(Activity ; ε + x)

-- until-loop activity

| μx.(ε + Activity ; x)

--while-loop activity

Task::= Simple

-- a simple task

| { Activity }

-- encapsulated activity

A task can be either a simple or a compound task. Compound tasks are defined between brackets ‘{‘ and ‘}’, and this is also called encapsulation because it introduces a different context for the execution of the structure inside it. Curly brackets are used in the abstract syntax to represent diagrams and sub-diagrams but also have implications for the semantics that will be explained later. Also, parentheses can be used to help comprehension or to change the associativity of the expressions. Expressions associate to the right by default.

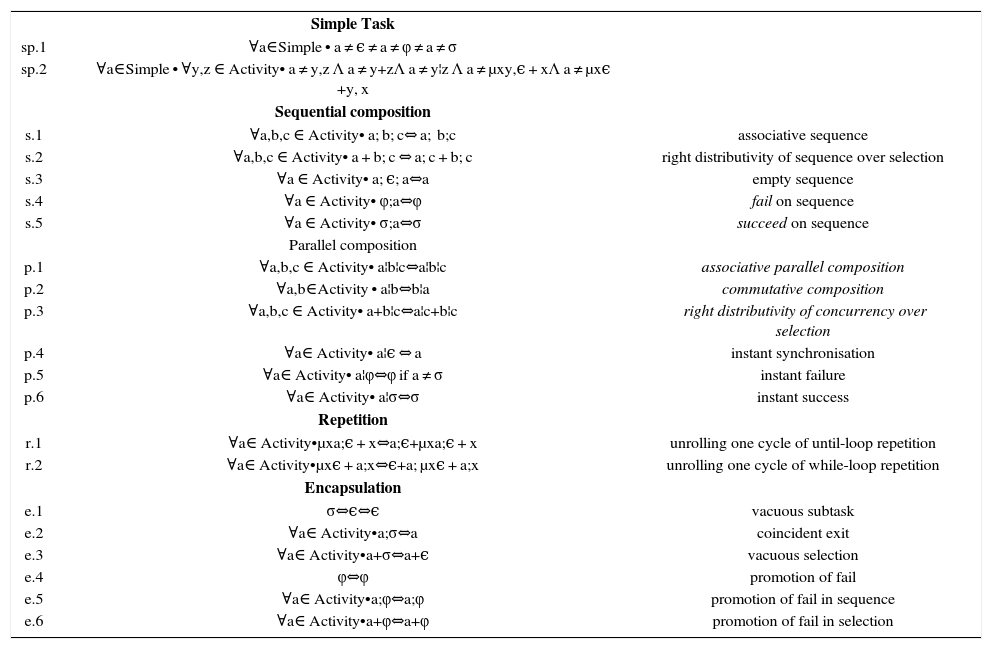
2.3

Task model constructions

Just as the graphical structures of the Task Flow Model can be composed, basic definitions in the abstract syntax may form complex expressions. The abstract syntax definition can be considered like a Universal Algebra which, to accomplish an accurate representation of the diagram syntax, has to be limited by axioms. The abstract syntax definition and its axioms form an Ideal or Quotient Algebra. Table 1 presents the set of constructions for the algebra. More details of the axioms can be seen in [8], [9].

Table 1.

Task Algebra constructions.

	Simple Task
sp.1	∀a∈Simple • a ≠ ϵ ≠ a ≠ φ ≠ a ≠ σ
sp.2	∀a∈Simple • ∀y,z ∈ Activity• a ≠ y,z Λ a ≠ y+zΛ a ≠ y¦z Λ a ≠ μxy,ϵ + xΛ a ≠ μxϵ +y, x
	Sequential composition
s.1	∀a,b,c ∈ Activity• a; b; c⇔ a;  b;c	associative sequence
s.2	∀a,b,c ∈ Activity• a + b; c ⇔ a; c + b; c	right distributivity of sequence over selection
s.3	∀a ∈ Activity• a; ϵ; a⇔a	empty sequence
s.4	∀a ∈ Activity• φ;a⇔φ	fail on sequence
s.5	∀a ∈ Activity• σ;a⇔σ	succeed on sequence
	Parallel composition
p.1	∀a,b,c ∈ Activity• a¦b¦c⇔a¦b¦c	associative parallel composition
p.2	∀a,b∈Activity • a¦b⇔b¦a	commutative composition
p.3	∀a,b,c ∈ Activity• a+b¦c⇔a¦c+b¦c	right distributivity of concurrency over selection
p.4	∀a∈ Activity• a¦ϵ ⇔ a	instant synchronisation
p.5	∀a∈ Activity• a¦φ⇔φ if a ≠ σ	instant failure
p.6	∀a∈ Activity• a¦σ⇔σ	instant success
	Repetition
r.1	∀a∈ Activity•μxa;ϵ + x⇔a;ϵ+μxa;ϵ + x	unrolling one cycle of until-loop repetition
r.2	∀a∈ Activity•μxϵ + a;x⇔ϵ+a; μxϵ + a;x	unrolling one cycle of while-loop repetition
	Encapsulation
e.1	σ⇔ϵ⇔ϵ	vacuous subtask
e.2	∀a∈ Activity•a;σ⇔a	coincident exit
e.3	∀a∈ Activity•a+σ⇔a+ϵ	vacuous selection
e.4	φ⇔φ	promotion of fail
e.5	∀a∈ Activity•a;φ⇔a;φ	promotion of fail in sequence
e.6	∀a∈ Activity•a+φ⇔a+φ	promotion of fail in selection

3

Task algebra implementation

The implementation for the task algebra was developed in the Haskell language [10], which is a lazy functional language based on lambda calculus. The application in Haskell is a compiler that transforms a task algebra expression and, if the expression is correct, generates the corresponding traces for the expression. The process will be similar to a one-pass compiler [11]. Figure 2 shows the process for a task algebra expression in the implementation to generate the set of traces.

Figure 2.

Structure of the Task Algebra implementation.

From the BNF definition for the task algebra described in [8], [9], there are just a couple of changes that have been made with the aim of facilitating the analysis of the input string representing an expression in the algebra:Activity ::= Epsilon

-- empty activity

| Sigma

- σ succeed

| Phi

--ϕ fail

| Task

-- a single task

| Activity ; Activity

-- a sequence of activity

| Activity + Activity

-- a selection of activity

| Activity || Activity

-- parallel activity

| Mu.x(Activity ; Epsilon + x)

- until-loop activity

| Mu.x(Epsilon + Activity ; x)

- while-loop activity

Task::= Simple

-- a simple task

| { Activity }

-- encapsulated activity

Evidently, the Greek symbols used in the algebra had to be converted into machine-readable tokens in the Latin character set. Also, the Mu symbol was separated from the variable x using a dot to simplify their identification in the lexical analyser (the bound expression is then contained in parentheses). Table 2 shows the correspondence between the expression written in the original algebra syntax and the machine-readable syntax for the Haskell application.

Table 2.

Comparison between original Task Algebra syntax and the Haskell implementation.

Task Algebra	Task Algebra implementation
a;ϕ c	a; Phi; c
a + ε + b	a + Epsilon + b
a || b || σ	a || b || Sigma
μx.(a ; ε +x)	Mu.x(a ; Epsilon + x)
μx.(ε + a ; x)	Mu.x(Epsilon + a ; x)

Additionally, the traces for the expression are generated executing the function tr. For instance, the execution of tr “a; Phi; c” creates the traces for the expression a; Phi; c. Consequently, the expressions depicted above have the following set of traces, in which semantic tokens denote the execution of corresponding syntactic tokens, apart from “!”, which denotes the commit-action:tr “a; Phi; c”

{[a,Phi]}

tr “a + Epsilon + b”

{[!],[!,a],[!,b]}

tr “a || b || Sigma”

{[Sigma]}

tr “Mu.x(a ; Epsilon + x)”

{[a,!],[a,!,a]}

tr “Mu.x(Epsilon + a ; x)”

{[!],[!,a,!],[!,a,!,a]}

As can be seen, traces are produced following the semantics defined in [9] with the exception of the repetition structures. Traces for the until- and while-loops are generated for a finite number of cycles, setting an arbitrary maximum limit of two repetitions for each loop. The while- and until-loops show, as expected, different trace sets due to the position of the condition (e.g., the trace [!] is produced in the while-loop as a result of the possibility of doing nothing). Minor differences in the trace notation are the syntax for commit ‘!’ instead of ‘↓’, and the use of square brackets to delimit traces as a substitute for the angle brackets used originally. In addition, simple task names should begin with a lowercase; uppercase is reserved for compound tasks and the algebra keywords.

The implementation takes a string as an input for the expression in the algebra, which is translated into the corresponding functions to generate the resulting trace semantics. The parser was built using the Happy parser generator for Haskell. In addition, a simple hand-written lexical analyser was built. Together, the parser and the lexical analyser are responsible for linking each input subexpression to the appropriate constructor for the corresponding Activity data type.

Model : Activity { $1 }

| CompoundTask Model Model

$1 $2 }

CompoundTask :

‘let’ taskName ‘=‘

Encapsulation { CompoundTask $2 $4 }

Encapsulation:

‘{‘ Activity ‘}’ { Task

(Encapsulation $2) }

Activity :

Activity ‘;’ Activity {

Sequence $1 $3 }

| Activity ‘+’ Activity {

Selection $1 $3 }

| Activity ‘||’ Activity {

Parallel $1 $3 }

-- Until-loop

| ‘Mu’ ‘.’ simple ‘(‘ Activity

‘;’

‘Epsilon’ ‘+’ simple ‘)’ {

UntilLoop $5 (Simple $3) (Simple $9 }

-- While-loop

|’Mu’ ‘.’ simple ‘(‘ ‘Epsilon’

‘+’ Activity’;’ simple ‘)’ {

WhileLoop $7 (Simple $3) (Simple $9)}

| ‘(‘ Activity ‘)’ { Task

(Brackets $2) }

| Encapsulation { $1 }

| ‘Epsilon’ { Epsilon }

| ‘Phi’ { Fail }

| ‘Sigma’ { Succeed }

| simple { Task (Simple

$1) }

| taskName { Task

(Compound $1) }

The definition of the Activity data type is as follows:-- Activity

data Activity

= Epsilon

| Fail

| Succeed

| Task Task

| Sequence Activity Activity

| Selection Activity Activity

| Parallel Activity Activity

| UntilLoop Activity Task Task

| WhileLoop Activity Task

Task

| CompoundTask String Activity

| Model Activity Activity

deriving (Eq, Ord)

Then, we define Show for each datatype defined in order to see the syntactic structure. Subsequently, we define the function trace for each datatype, to be able to construct traces for any kind of compound syntax. Finally, we define Show for each kind of event defined for the set of traces, in order to see the results.

The definition of the function trace is as follows:trace :: Activity -> DataDictionary -> SetOfTraces

where SetOfTraces is declared as a set of the Trace type. Trace is declared as a list of Event elements:type Trace = [Event

type SetOfTraces = Set Trace

Event is a data type defining the trace elements:data Event = Ident String | Phi |

Sigma | Commit

deriving (Eq, Ord)

From here, the use of the function trace, by pattern matching, calls the appropriate functions implementing the semantics from [9]. For example, for sequence composition the function trace is called as follows:trace (Sequence a b) dict

which is equal to:trace a dict #* trace b dict

meaning that the trace of a sequence of a followed by b is equal to the trace of a concatenated with the trace of b, using the concatenated product operation (#*). As defined in [9], the concatenated product works over the set of traces:(#*) :: SetOfTraces -> SetOfTraces ->

SetOfTraces

setA #* setB

| setA == empty = empt

| setB == empty = empty

| otherwise

= union (insert (findMin

setA # findMin setB)

(singleton (findMin setA) #*

(difference setB (singleton (findMin

setB)))))

((difference setA (singleton

(findMin setA))) #* setB)

which uses the concatenation function to append the traces. The semantic function for concatenation of traces implemented in Haskell:(#) :: Trace -> Trace -> Trace

[Sigma] # (item:rest) = [Sigma] #

rest

[Phi] #(item:rest)= [Phi]# rest

[Commit] # trace@(item:rest)

| item == Commit = trace

| otherwise = Commit : trace

(item:rest) # trace = item : (rest #

trace)

epsilon#trace = trace

The next section introduces a case study to show how this implementation can be used.

4

An electronic journal

An interesting case study was developed by Adams [12] working with the Discovery Method for modelling a web based electronic journal. The study models an electronic journal, which is offered free to all subscribers, where the authors submit their articles and pay towards the costs of their online publication by conducting peer reviews of articles submitted by other authors.

There are four actor roles identified in the system. Reader is the role denoting someone who wants to browse the journal, read articles or search for information in the journal. The role of Author defines someone who wants to publish his/her articles. The Reviewer is the role of an author who is required to review other unpublished papers with the aim of paying towards the cost of publishing his/her own paper. The last role is that of the Editor, the administrator of the system. The editor role is subdivided into a master editor and sub-editors, who can be assigned their role by any master editor. In the study, a Task Structure diagram is developed for each of the four main roles, describing the tasks they individually perform.

Here, we focus on the Task Flow analysis, which is the part of the Discovery Method where Task Flow Diagrams are constructed in order to determine the workflows linking the identified tasks. For every Task Structure Diagram in the case study, there is a corresponding Task Flow Diagram, illustrating the order in which the tasks are carried out for each role. In general, Task Flow diagrams are constructed from the viewpoint of the principal users of a system.

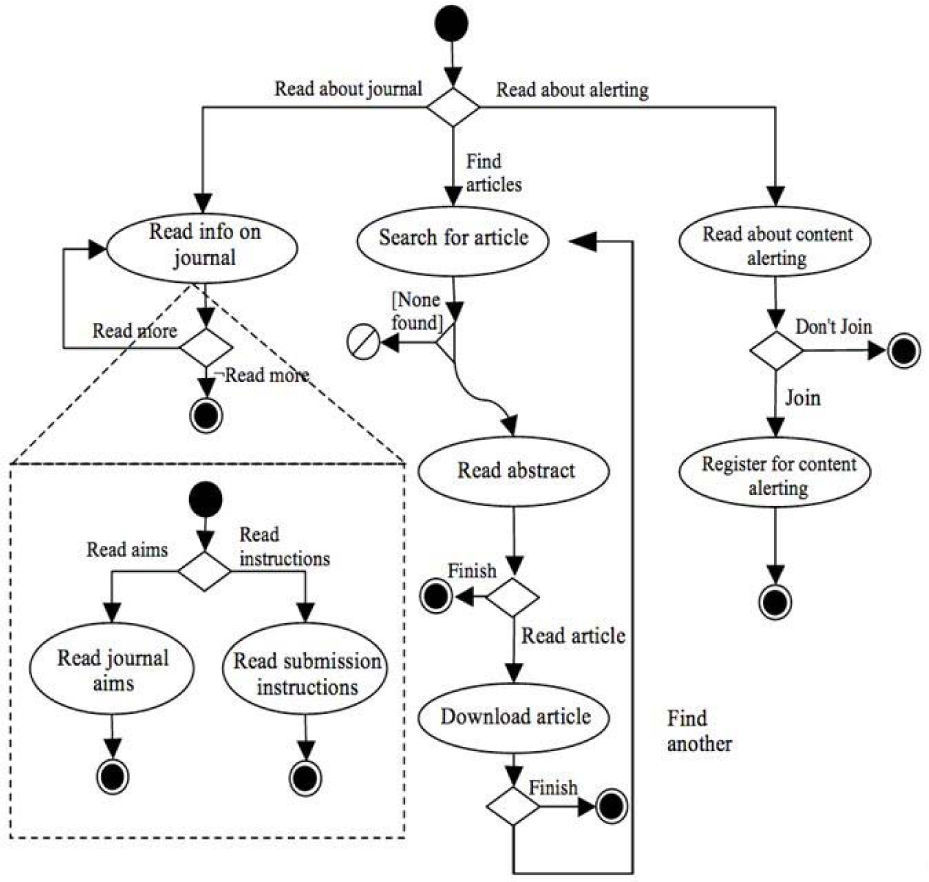
Figure 3 shows the Task Flow Diagram for the reader role. The diagram describes the choice the reader has initially, to decide between reading information about the journal, searching for an article, or reading about content alerting before subscribing to the content alerting service.

Figure 3.

Reader Task Flow Diagram.

The diagram is formed by six tasks: Read Info on Journal, Search for Article, Read Abstract, Download Article, Read about Content Alerting, and Register for Content Alerting. The first task is clearly defined as a compound task, which is formed by the subtasks Read Journal Aims, and Read Submission Instructions.

The task algebra expression for the diagram from Figure 3 should be as follows:Mu.x(ReadInfoOnJournal; Epsilon+x)

+Mu.x((searchForArticle; Phi+readAbstract;

downloadArticle+Epsilon); Epsilon+x)

+(readAbourContentAlerting;

Epsilon+registerForContentAlerting)

Additionally, the compound task ReadInfo On Journal can be defined like this:

let ReadInfo On Journal = {read Journal Aims+read Submission Instructions}

In the trace semantics only simple tasks and events are represented in the traces. The compound task ReadInfo On Journal is unpacked and its subtasks’ traces are spliced into the system’s global traces, as defined by the semantics. After the task algebra expression is defined, it may be processed by the tr function to generate the set of traces. For this case, 17 possible paths form the set of complete traces; we are presenting here only partial results as an example:{ [!,readAboutContentAlerting,!],

[!,readAboutContentAlerting,!,

registerForContentAlerting],

[!,readJournalAims,!],

...

[!,searchForArticle,!,readAbstract,!,

searchForArticle,!,Phi],

[!,searchForArticle,!,Phi] }

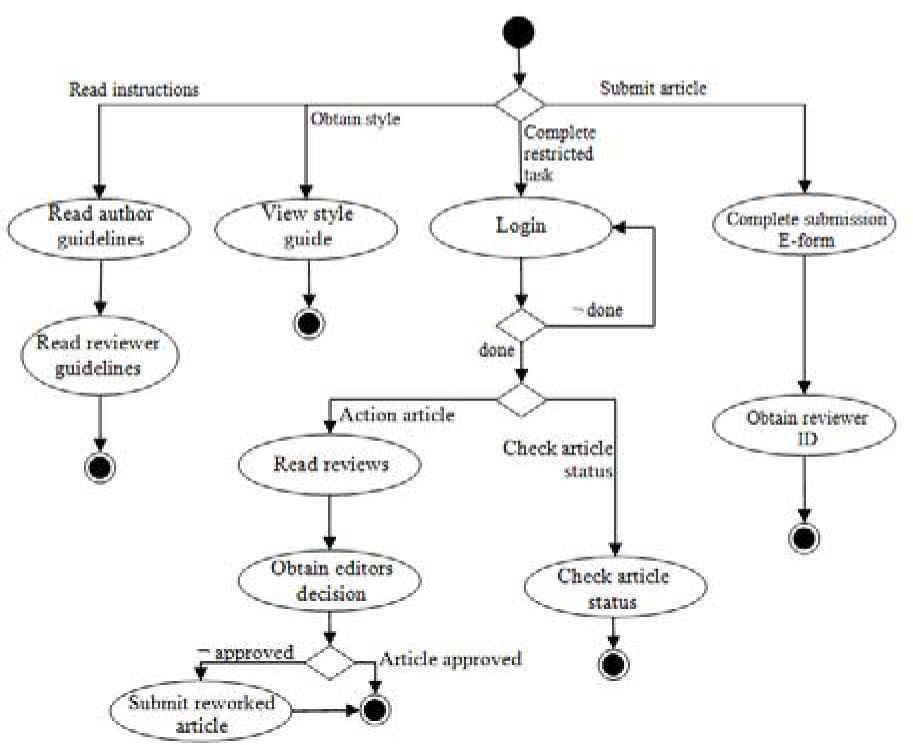
4.1

Author task flow diagram

The role of Author is used for someone who wants to publish his/her articles. It involves the options of Read Instructions, Obtain Style, Complete Restricted Task (such as Read Reviews or Check Article Status), and Submit Article. Figure 4 shows the Task Flow Diagram for the author role. All tasks in the diagram are simple tasks with the exception of Login, which is defined later.

Figure 4.

Author Task Flow Diagram.

The Task Algebra expression for the Author diagram is represented as follows:(readAuthorGuidelines; readReviewerGuidelines) +

viewStyleGuide + (Mu.x(Login; Epsilon + x);

(readReviews; obtainEditorsDecision;

submitReworkedArticle+Epsilon)+checkArticleStat

us) + (completeSubmissionEform;

obtainReviewerID)

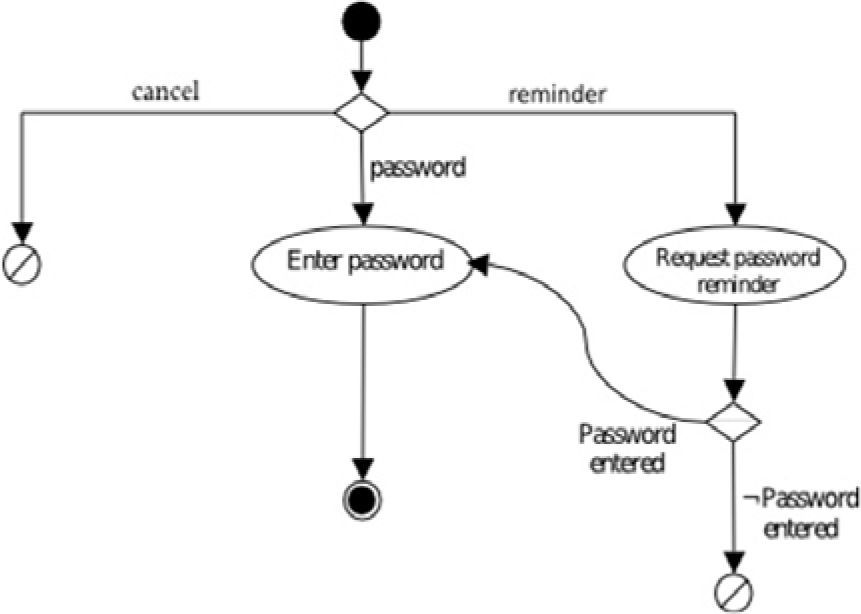
The compound task Login contemplates the complete process for login into the system, including the case when the user fails to remember the password, with the possibility to activate a password reminder. Figure 5 presents the Task Flow diagram for this task. The resultant expression in the task algebra is:

let Login = {(Phi + Epsilon + (requestPassword; Epsilon + Phi))}

Figure 5.

Login Task Flow Diagram.

The set of complete traces resulting from the task algebra expression includes the task Login which, as was mentioned above, manages the success and failure cases of logging into the system by entering the password. Because Login is in a cycle to allow multiple opportunities to gain entry into the system, an until-loop structure Mu.x(Login; Epsilon + x) is needed. The set of traces from Login is unpacked within the set of traces in the general expression to generate the complete set of traces (27 possible paths); again, we are presenting here only partial results as an example:{[!,completeSubmissionEform,obtainRev

iewerID],

[!,enterPassword,!,checkArticleStatus

],

...

[!,requestPassword,!,enterPassword,!,

requestPassword,!,enterPassword,!,rea

dReviews,obtainEditorsDecision,!,subm

itReworkedArticle],

[!,requestPassword,!,enterPassword,!,

requestPassword,!,Phi],

[!,requestPassword,!,enterPassword,!,

Phi],

[!,requestPassword,!,Phi],

[!,viewStyleGuide],

[!,Phi]}

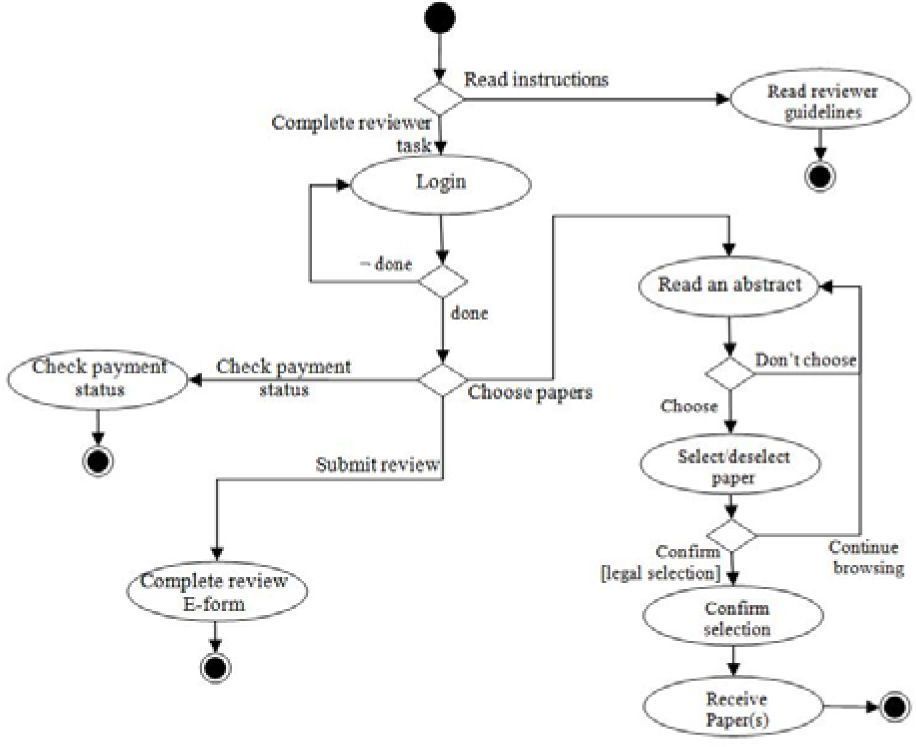
4.2

Reviewer task flow diagram

The Reviewer role defines the behaviour in the system for a user who wants to write a review of an article or perform some related activity, such as read an abstract in order to choose a paper, check his/her payment status (authors “pay” by doing reviews), or simply checking the guidelines for the reviewers. Figure 6 shows the Task Flow Diagram for this role where, as for the previous role, Login is the only compound task in this diagram. The flow for Login is the same defined earlier in Figure 5.

Figure 6.

Reviewer Task Flow Diagram.

In a similar manner to the section above, the content of the Reviewer Task Flow Diagram may be expressed directly in the syntax of the task algebra, incorporating as unitary wholes any tasks that encapsulate further flows, such as the Login task:

readReviewerGuidelines + (Mu.x(Login; Epsilon + x); checkPaymentStatus + completeReviewForm + (Mu.x((Mu.y(readAnAbstract; Epsilon+y); selectPaper); Epsilon+x); confirmSelection; receivePapers))

From applying the trace function to the task algebra expression above, the set of complete traces is obtained (34 paths), in which once again the behaviour of the Login task is unpacked; we are presenting here only partial results as an example:{[!,enterPassword,!,checkPaymentStatus,[!,enterPassword,!,completeReviewEform,

[!,enterPassword,!,enterPassword,!,ch

eckPaymentStatus],

[!,enterPassword,!,enterPassword,!,co

mpleteReviewEform],

[!,enterPassword,!,enterPassword,!,re

adAnAbstract,!,readAnAbstract,

selectPaper,!,confirmSelection,receiv

ePapers],

...

[!,requestPassword,!,enterPassword,!,

requestPassword,!,enterPassword,!,rea

dAnAbstract,!,selectPaper,!,readAnAbs

tract,!,selectPaper,

confirmSelection,receivePapers],

[!,requestPassword,!,enterPassword,!,

requestPassword,!,Phi],

[!,requestPassword,!,enterPassword,!,

Phi], [!,requestPassword,!,Phi],

[!,Phi]}

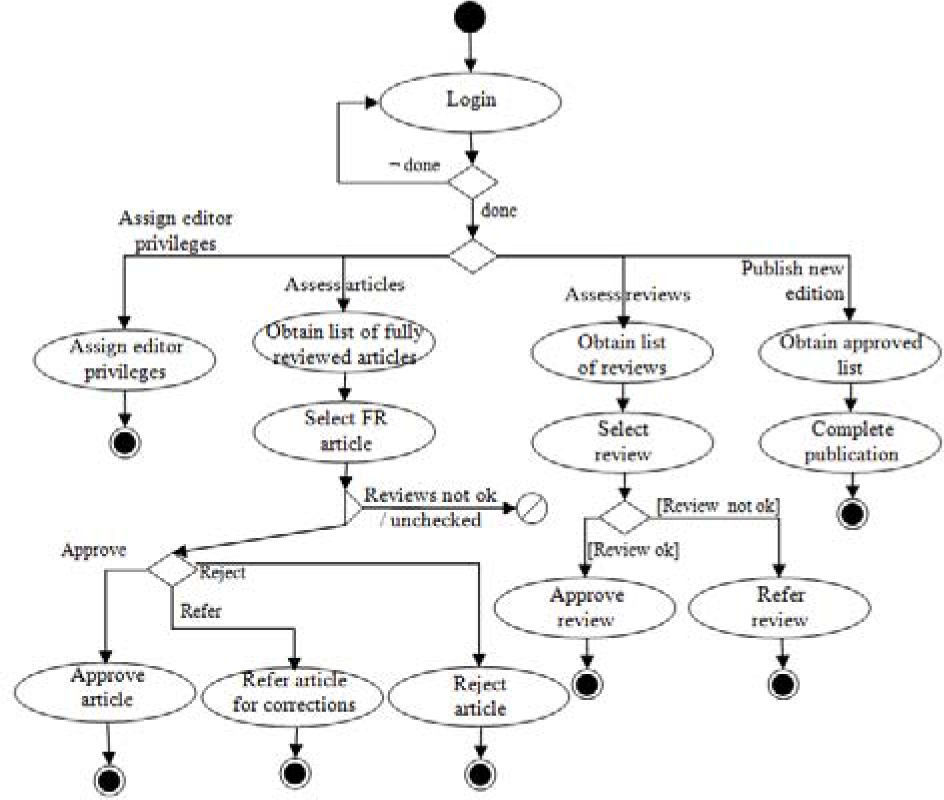
4.3

Editor task flow diagram

The Editor role’s behaviour is specified in Figure 7. As can be seen, an editor is able to evaluate articles and reviews, publish a new edition of the journal, and even to assign sub-editor privileges. The Task Flow Diagram shows the different tasks involved for the execution of this role and, like the other roles, but with the exception of the Reader role, the compound task of Login is required. The rest of the tasks used in this diagram are considered simple tasks.

Figure 7.

Editor Task Flow Diagram.

The expression in the Task Algebra includes the until-loop for the verification of the login before carrying out the remaining tasks. After the editor has logged in, s/he has to choose which of the activities want to perform. The task algebra expression is presented here:

Mu.x(Login; Epsilon+x); (assignEditorPrivileges + (obtainListFRArticles; selectFRArticle; Phi + (approveArticle + referArtForCorrections + rejectArticle)) + (obtainListReviews; selectReview; approveReview + referReview) + (obtainApprovedList; completePublication)

The many different executions of this Task Algebra expression may be obtained by applying the tr tracing function, which obtains the set formed by 53 traces; again, we are presenting here only partial results as an example:{[!,enterPassword,!,assignEditorPrivi

leges],

[!,enterPassword,!,enterPassword,!,as

signEditorPrivileges],

[!,enterPassword,!,enterPassword,!,ob

tainApprovedList,

completePublication],

...

[!,requestPassword,!,enterPassword,!,

requestPassword,!,enterPassword,!,obt

ainListReviews,selectReview,!,referRe

view],

[!,requestPassword,!,enterPassword,!,

requestPassword,!,Phi],

[!,requestPassword,!,enterPassword,!,

Phi],

[!,requestPassword,!,Phi],

[!,Phi]}

These examples show how it is possible to express realistic Task Flow diagrams in the Task Algebra and convert them to traces, illustrating the possible executions of the diagrams. These traces are potentially verifiable by equivalence checking and model checking [13]. We think Flow Task diagrams could potentially be used to create formal models of a variety of applications (e.g., objectoriented software [14], flow diagram of algorithms as in [15]), depending of the use of flow diagrams; whether its use represents an advantage or not is a matter for future research.

5

Conclusions

The work presented in this paper extends the earlier theoretical presentation of the Task Algebra [8] by providing a reference implementation in the Haskell programming language. Haskell was chosen, because of the transparency with which the algebra’s constructors and recursive tracing function could be implemented in the functional style. The capability of this implementation was demonstrated using an extended case study analysing tasks and workflow in a journal management system, distributed over several task diagrams and consisting of both simple and compound tasks. The tracing function was shown to produce all the complete traces of the system, as a measure of the system’s behaviour. Such traces may be used to answer questions about the semantic properties of a system. For example, the equivalence of two sets of traces may be used to prove that two different ways of modularising a system as a set of hierarchical diagrams actually denote systems with the same behaviour; while non-equivalence would reveal that they are in fact different. A further use for the traces may be found when checking for arbitrary temporal logic properties of a system, by verifying LTL or CTL theorems against the traces. This is the subject of current and future work.