Automated Multi-Contrast Brain Pathological Area Extraction from 2D MR Images

Abstract

The aim of this work is to propose the fully automated pathological area extraction from multi-parametric 2D MR images of brain. The proposed method is based on multi-resolution symmetry analysis and automatic thresholding. The proposed algorithm first detects the presence of pathology and then starts its extraction. T2 images are used for the presence detection and the multi-contrast MRI is used for the extraction, concretely T2 and FLAIR images. The extraction is based on thresholding, where Otsu's algorithm is used for the automatic determination of the threshold. Since the method is based on symmetry, it works for both axial and coronal planes. In both these planes of healthy brain, the approximate left-right symmetry exists and it is used as the prior knowledge for searching the approximate pathology location. It is assumed that this area is not located symmetrically in both hemispheres, which is met in most cases. The detection algorithm was tested on 203 T2-weighted images and reached the true positive rate of 87.52% and true negative rate of 93.14%. The extraction algorithm was tested on 357 axial and 443 coronal real images from publicly available BRATS databases containing 3D volumes brain tumor patients. The results were evaluated by Dice Coefficient (axial: 0.85 ± 0.11, coronal 0.82 ± 0.18) and by Accuracy (axial: 0.96 ± 0.05, coronal 0.94 ± 0.09).

1

Introduction

Nowadays, the issue of automatic analysis of brain tumors is of great interest. It is the first step in surgical and therapy planning. The very first step of the automatic analysis of brain tumor is its detection and subsequent segmentation. The detection of brain tumors is generally a more complex task than the detection of any other image object. Pattern recognition usually relies on the shape of the required objects [1] or on the object movements in video sequences [2]. Since the tumor shape varies in each case, other properties have to be used.

The aim of the proposed method is the presence detection of the brain tumor in 2D MR image and subsequent extraction of the whole pathological area including active tumor and edema.

Several different and interesting methods have been developed in recent years. The existing algorithms can be classified into semi- and fully- automatic methods from a user viewpoint and into region- and contour-based methods from a technical viewpoint.

The semi-automatic [3–4] require some user interaction, e.g. to select the starting point lying inside the tumor or to select several points of foreground and several points of background. The automatic [5–6] methods do not require any interaction and are usually based on prior knowledge of the human brain structure, either tissue atlas or left-right symmetry, or their combination.

The region-based methods [7–10] usually search for pixels or regions with similar properties that create connected regions. This includes e.g. region growing, classification etc. The contour-based methods [11] use image gradient in particular area to boundary detection and region creation or for subsequent boundary evolution. The most famous method of this group is active contours [12]. Some works [13–15] use combination of region-based and contour-based methods and try to combine the advantages of both of these groups.

At present, multi-parametric image analysis is frequently discussed within the scientific community [16]. This technique, even though it can be based on traditional segmentation methods (thresholding, active contours), exploits information obtained from more images or modalities at the same time.

Fully automatic exact segmentation of the tumor is still an unsolved problem, as the accurate image segmentation itself. The method proposed in this paper analyzes 2D magnetic resonance images and is fully automatic.

The tumor extraction methods usually rely on other contrast images, such as T1-weighted contrast enhanced images [17]. This is the image that we are trying to avoid, since it requires contrast enhanced agent (usually gadolinium) to be injected into the patient blood.

The great advantage of the symmetry approach is that the process does not need any intensity normalization, human work etc.

2

Methodology

The purpose of the proposed method is a fully automatic extraction of pathological areas from stand-alone 2D MR image of brain, where no neighbor slices are considered. Hence, for the better performance, the usage of multi-contrast MR is suitable. The reason for multi-contrast MRI is the much better distinguishing of particular tissues than in case of using only one contrast image. E.g. the edema reaches similar intensities as CSF (Cerebro-Spinal Fluid) in T2-weighted images, while in FLAIR images, the intensities are absolutely different. On the other hand, the differentiation between necrosis and white matter is much better in T2-weighted images. The example of the described problem is shown in Figure 1, where the normalized values in T2-FLAIR intensity space are depicted.

Figure 1.

Distinguishing of particular tissues in multi-contrast T2-FLAIR MRI. Red: WM, Yellow: GM, Green: CSF, Violet: Tumor, Blue: Edema. (b) and (c) show the source T2 and FLAIR images, respectively. The images were taken from simulated images of BRATS database.

In this work, FLAIR and T2-weighted images are used. In both images, the pathological areas are well visible.

The method consists of two main steps: the detection and the extraction of the pathological area. Both are based on multi resolution symmetry analysis.

The tumor detection process consists of several steps. The flow chart can be seen in Figure 2.

Figure 2.

Brain tumor presence detection flow diagram.

The first step is the skull extraction followed by image cutting. For this cut image, the probabilistic map of anomalies is computed, and features are extracted from this map. These features are used for the decision, whether a pathological area is present in the image. If so, this area is located and then the decision, which half contains the tumor, is made. If no pathological area is present, the image shows a healthy brain and no other computation is needed.

2.1

Preprocessing

The preprocessing consists of brain extraction, image registration and the symmetry axis detection. None of these parts is the aim of this work, but for this purpose, the existing algorithms described in [18], [19] and [20] can be used for brain extraction, image registration and symmetry axis detection, respectively. Addition of such methods as a preprocessing step is the aim of future work to complete the whole system.

2.2

Symmetry Analysis

The most important part of the presence detection process is the detection of symmetry anomalies, which are usually caused by a brain tumor, whose detection is the main purpose of this article. The first step of this process is dividing the input image into two approximately symmetric halves.

Assuming that the head is not rotated and the skull is approximately symmetric, the symmetry axis is parallel to the vertical axis and divides the image of the detected brain into two parts of the same size. Since the method is not pixel-based, the precision of the determined symmetry axis does not have significant influence.

Since the features are extracted from the computed asymmetries, the size of the image has to be normalized. Hence, every cropped image is resized into the same size, concretely 256 × 256 pixels.

A squared block, with the side length computed as one quarter of the cropped image side length, is created. The algorithm goes through both halves symmetrically by this block.

The step size is smaller than the block size to ensure the overlapping of particular areas. These areas are compared with their opposite symmetric part. In this case, the step size of one eighth of the block size was set.

A comparison is done by the Bhattacharya Coefficient [21]. Normalized histograms with the same range are computed from both parts and the Bhattacharya Coefficient (BC) is computed from these histograms as follows [21]:

where N denotes the number of bins in the histogram, l and r denote histograms of blocks in the left and the right half, respectively. The range of values of BC is <0;1>, where the smaller the value, the bigger the difference between histograms. For the next computation, the asymmetry is computed as:

This asymmetry is computed for all blocks. Since the step size is smaller than the block size, the overlap exists and more values of asymmetry are present for most pixels. To obtain the appropriate asymmetry map, the mean of all values computed for a particular pixel is computed. The computed values of asymmetry create the asymmetry map, which expresses the probability of tumor presence in a particular location. The higher the asymmetry is, the higher is the probability of the tumor presence in a given location.

2.3

Multi-resolution map

The whole cycle of symmetry checking is repeated four times but with different block size. Height and width of the block are iteratively reduced to the half of the previous value. So the size of the block is 1/1, 1/4, 1/16, and 1/64 of the initial size, respectively. The purpose of smaller areas is more precise detection of asymmetry. This approach corresponds to the multi resolution image analysis described in [22]. A block size of 1/256 of the initial size was tested as well, but the results were not improved and the maximum of asymmetry coefficient for this block size was equal to 1 for every image in database.

The output of each cycle is a probabilistic map of anomalies. The product of values corresponding to a particular pixel is computed. The output is the new multi resolution probabilistic map. The examples of particular probabilistic maps are shown in Fig. 3.

Figure 3.

Asymmetry probabilistic maps for block side length equal to 1/4, 1/8, 1/16, and 1/32 of shorter side of cut image are shown in (a), (b), (c) and (d), respectively. In (e) and (f), input image and total probabilistic map are shown, respectively.

2.4

Feature extraction

In the next step, features are extracted from computed probabilistic maps. These features are used for the decision whether the particular image contains a pathological area. According to experiments, the relative and absolute thresholding can help in distinguishing between the images of healthy brain and brain with tumor. The thresholding creates a given number of regions with a given size, and both of these values differ for healthy and brain tumor patients. The extracted features are as follows:

• •

  global maximum of the total probabilistic map,

• •

  maximum of each probabilistic map for a particular block size,

• •

  number of regions created by absolute value thresholding the multi-resolution probabilistic map and the sum of their size,

• •

  number of regions created by relative value thresholding the multi-resolution probabilistic map and the sum of their size.

Global maximum of the total probabilistic map:

Since the proposed method is based on searching the pathological area by symmetry checking, the maximum of asymmetry coefficient is the main feature, which can be used for classifying the image.

Maximum of each probabilistic map for a particular block size:

Other usable features are maxima of each probabilistic map computed in the previous step. Functional dependency of the anomaly coefficient on the block size is non-ascending; it means that for a smaller block, the anomaly coefficient is greater or equal to that of a larger block. For images with large tumors, this value is high even for a large block, while for small tumors, the anomaly coefficient descends earlier and it reaches small values for a large block. For healthy brains, this function is even more shifted.

The maximum asymmetry for multi-resolution asymmetry map and for particular block sizes is shown in Figure 3.

Number of regions created by absolute value thresholding of the total probabilistic map and the sum of their size:

This feature assumes that the anomaly probabilistic map of healthy brain contains a smaller value compared to the brain with tumor.

When the thresholding is done, in case of healthy brain, the result is a smaller number of regions and also a smaller sum of their size. In most healthy cases, both numbers are equal to zero.

Number of regions created by relative value thresholding of the total probabilistic map and the sum of their size:

For the extraction of this feature, the total probabilistic map is thresholded by relative value computed from the maximum of this map. Here, it is assumed that for brain with tumor, there is a significant peak in the part where a tumor is situated. So for thresholding by a value computed from this maximum, healthy areas are filtered out, because they are usually much more symmetric. Moreover, the tumor is in most cases concentrated in one location, therefore a small number of regions is created by thresholding. In case of a healthy brain, the situation is inverse.

The maximum is comparable to values in other parts, so more regions are created by thresholding; moreover, they are spread into the whole brain. For large tumors, the sum of areas is comparable to the one of healthy brain, but the number of regions is smaller.

For both relative and absolute thresholding, 10 different levels of threshold are set, so 10 values are extracted for each feature. Statistical graphs of number of region and sum of their size for both relative and absolute thresholding for different threshold levels are shown in Figure 4 and Figure 5, respectively.

Figure 4.

Number of regions and the sum of their sizes for different absolute threshold levels. Blue: healthy brains, Red: brains with tumor.

Figure 5.

Number of regions and the sum of their sizes for different relative threshold levels to maximum in a particular image. Blue: healthy brains, Red: brains with tumor.

2.5

Tumor presence detection

The part of the proposed method, which detects the presence of a pathological area in a particular brain, uses a supervised machine learning algorithm Support Vector Machine (SVM), invented by Cortes and Vapnik in 1995 [22], with linear kernel function. The features described in the previous section are used for image classification.

2.6

Pathological area extraction

After the detection of symmetric anomalies and the image classification, the pathological area can be extracted. The pathological area extraction is based on the method described in [23], but multi-contrast images, concretely T2 and FLAIR, are involved in this task, now. In T2-weighted images, glioma and potential edema produce much stronger signal than the white matter, in which they are mostly located. For this reason, the thresholding is employed here. Since the intensities in image can differ from case to case depending on the data acquisition, it has to be computed from the particular image. Moreover, only pixels in the most asymmetric parts have to be involved in the threshold computation. Otherwise, the threshold would be computed incorrectly in case of small tumors. For this purpose, the asymmetry mask is computed. This mask includes the regions, where the asymmetry reached at least 10% of the maximum asymmetry for particular image.

Since the result is both-sided mask, healthy and pathological areas are included.

The threshold is determined automatically by Otsu's algorithm [25], but any other automatic method can be also used.

Even though, the threshold is determined only from the image points in the most asymmetric parts, the thresholding process is applied to the whole image.

Since some incorrect areas could be extracted, only the regions that have the intersection with the asymmetry mask are labeled as pathological. Regions with the size smaller than 10% of the largest segment are eliminated as well.

Since CSF appears hyper-intense in T2-weighted images as well, the FLAIR volume is employed. In FLAIR the CSF produces much weaker signal than the white matter and the tumor or edema itself.

Hence, the areas with the lower intensity than the median intensity (which is most likely the intensity of the white matter) in FLAIR image are eliminated.

3

Experiments and results

3.1

Datasets

Two different datasets were used for the algorithm evaluation. The first dataset consists of 203 T2-weighted images of brain with various image sizes. The smallest image has the size of 256 × 256 px, while the largest one has the size of 630 × 630 px. Since the cropped images are resized into the same size of 256 × 256 px, the image size does not matter. 131 of test images are the images of healthy brain from 11 patients. 72 images from 13 patients are the images of brain containing a tumor, a tumor with an edema or only an edema. These images are of various resolutions and contain pathological areas of various shape, size and location. In the database, there are images of 12 small tumors, whose size is less than 2% of the skull size, 30 medium tumors, whose size is between 2 and 9% of the skull size, and 30 large tumors, whose size is more than 10%.

The second dataset was obtained from the MICCAI 2012 Challenge on Multimodal Brain Tumor Segmentation organized by B. Menze, A. Jakab, S. Bauer, M. Reyes, M. Prastawa, and K. Van Leemput. The challenge database contains fully anonymized images from the following institutions: ETH Zurich, University of Bern, University of Debrecen, and University of Utah.

For each patient, T1, T2, FLAIR, and post-gadolinium T1 MR volumes are available. All volumes are linearly co-registered to the T1 contrast image, skull stripped, and interpolated to 1 mm isotropic resolution.

The data used in algorithm evaluation contains real volumes of 15 high-grade and 7 low-grade glioma subjects.

From each case, several slices with pathological area in axial and coronal plane were taken. In total, the extraction algorithm was tested on 357 images with resolution 256 × 256 pixels in axial plane and on 443 images with resolution 256 × 181 in coronal plane. Since the proposed method is fully automatic and independent on image intensities, each image of the database can be considered as unique and independent on others.

All the simulated images are in BrainWeb space [27]. The information about the simulation method can be found in [28].

3.2

Evaluation Criteria

For the evaluation of a pathological area extraction, Dice Coefficient and Accuracy were used. The Dice Coefficient (DC) [28], in some works called Similarity Index, is computed according to the equation:

where A and B denotes the ground truth and the extraction result masks, respectively. This criterion compares the intersection of two sets with their union. The range of values of DC is <0;1>, where the value 1 expresses the perfect agreement. According to [29], the DC > 0.7 indicates an excellent similarity.

Another widely measure employed for segmentation evaluation is Accuracy (A) defined as follows:

where TP, FP, FN and TN stand for “True Positive”, “False Positive”, “False Negative”, and “True Negative”, respectively [30]. This measure is in the same range as DC and the higher value indicates the better performance as well.

3.3

Results

At first, the detection of a pathological area presence in the particular image was tested by a five-fold cross-validation process on 203 T2 axial images. It means that the samples in the database were randomly ordered and split into five groups. In five cycles, each of these groups was once used as the validation set, while the remaining four sets as training data.

The confusion matrix of the classification is summarized in Table 1. The algorithm achieved 87.52% of true positive rate and 93.14% of true negative rate.

Table 1.

Tumor presence detection performance.

	Tumor present	Tumor absent
Test positive	87.52%	6.86%
Test negative	12.48%	93.14%

To avoid dependency on the order of samples, the cycle of random ordering and five-fold cross-validation was repeated one hundred times.

After the decision whether the image contains a tumor the tumor location is found. This method was tested on 357 axial and 443 coronal images.

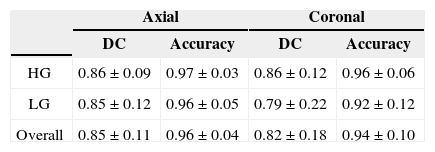
The summary of the extraction process results is in Table 2. The results are separated according to the tumor type and the slice plane. Slightly better results were achieved for high grade gliomas (HG) than for low grade gliomas (LG).

Table 2.

Segmentation evaluation by Dice Coefficient and Accuracy.

	Axial		Coronal
	DC	Accuracy	DC	Accuracy
HG	0.86 ± 0.09	0.97 ± 0.03	0.86 ± 0.12	0.96 ± 0.06
LG	0.85 ± 0.12	0.96 ± 0.05	0.79 ± 0.22	0.92 ± 0.12
Overall	0.85 ± 0.11	0.96 ± 0.04	0.82 ± 0.18	0.94 ± 0.10

The worst results were achieved for LG in coronal planes, while in other cases the results are comparable and achieved the value 0.86 for DC and 0.96 for Accuracy.

The several results for both planes, both types of glioma and several intervals of resulting DC are shown in Figures 6–9.

Figure 6.

The average (a) and above-average (b) results for axial slice of high grade glioma. Red: segmentation, Blue: ground truth.

Figure 7.

The average (a) and above-average (b) results for axial slice of low grade glioma. Red: segmentation, Blue: ground truth.

Figure 8.

The average (a) and above-average (b) results for coronal slice of high grade glioma. Red: segmentation, Blue: ground truth.

Figure 9.

The average (a) and above-average (b) results for coronal slice of high grade glioma. Red: segmentation, Blue: ground truth.

4

Conclusion

The aim of this work was a detection of images containing an abnormality caused by tumor and its subsequent location. Therefore the evaluation was divided into 2 parts: detection of a tumor presence and its subsequent extraction. The tumor presence detection reaches the true positive rate of 87.52% and the true negative rate of 93.14%. The overall accuracy of this part of the proposed system is 91.15%.

The second part includes the extraction of a pathological area in both axial and coronal planes. In axial and coronal plane, the DC coefficient reached value 0.85 ± 0.11 and 0.82 ± 0.18, respectively. Considering the statement that the DC > 0.7 indicates an excellent similarity, the achieved result can be evaluated as very good. Moreover the algorithm considers only information from 2D image and it is fully automated. It is expected that the performance will be improved in future using the neighbor slices information.

The extraction accuracy reached values 0.96 ± 0.04 and 0.94 ± 0.10 for axial and coronal plane, respectively. This indicates that in average 95% of pixels were correctly labeled either as pathological or as healthy tissue.

The proposed method can be also used for detection of tumor in 3D volume, but particular axial and coronal slices would be evaluated separately. Hence, the attention in the future work will also be paid on the relations between neighbor slices and after that, the work will go on to extending the proposed algorithm to 3D.

The future work will also consist of implementing the automatic symmetry axis detection, based on literature referred in section 2, and the separation of the tumor and the edema.

In overall evaluation, the proposed system can automatically detect the presence of a tumor in 2D MR image of brain with accuracy of 91.15% and subsequently extract the whole pathological area with the Dice Similarity Coefficient of 0.85 ± 0.11 and 0.82 ± 0.18 for axial and coronal plane, respectively, compared to the manual expert segmentation.

Acknowledgements

Research described in this paper was financed by the National Sustainability Program under grant L01401, by the Czech Science Foundation under grant no. 102/12/1104, and by the Czech Ministry of Education under grant no. LD14091. For the research, infrastructure of the SIX Center was used.