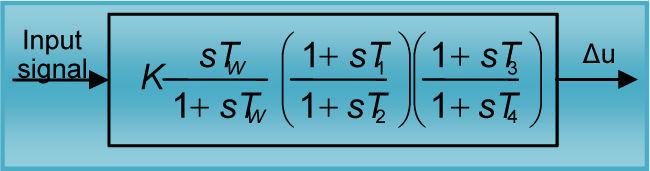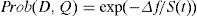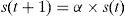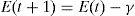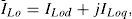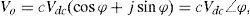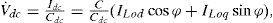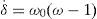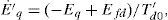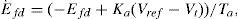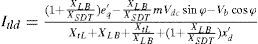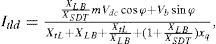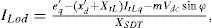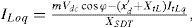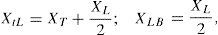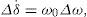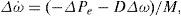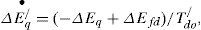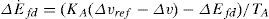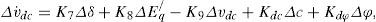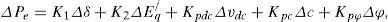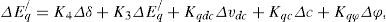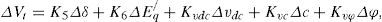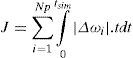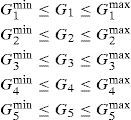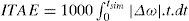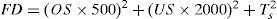Controller Design of STATCOM for Power System Stability Improvement Using Honey Bee Mating Optimization

Abstract

Damping of low frequency electromechanical oscillations is very important for a safe system operation. The fast acting, of a static synchronous compensator (STATCOM) which is capable of improving both steady state and dynamic performance permits newer approaches to system stabilization. This paper presents a novel methodology for tuning STATCOM based damping controller in order to enhance the damping of system low frequency oscillations. The design of STATCOM parameters are considered an optimization problem according to the time domain-based objective function solved by a Honey Bee Mating Optimization (HBMO) algorithm that has a strong ability to find the most optimistic results. To validate the results accuracy, a comparison with Genetic Algorithm (GA) has been made. The effectiveness of the proposed controller is demonstrated through nonlinear time-domain simulation and some performance indices studies over a wide range of loading conditions. The simulation study shows that the designed controller by HBMO performs better than GA in finding the solution. Moreover, the system performance analysis under different operating conditions shows that the φ based controller is superior to the C based controller.

Nomenclature

DC	DC Direct current
E’q	Internal voltage behind transient reactance
Efd	Equivalent excitation voltage
FACTS	Flexible alternating current transmission systems
FD	Figure of demerit
GA	Genetic algorithm
GTO	Gate turn off thyristor
HBMO	Honey bee mating optimization
ITAE	Integral of time multiplied absolute value of the error
K	Proportional gain of the controller
KA	Regulator gain
M	Machine inertia coefficient
Pe	Electrical output power
PI	Proportional integral
Pm	Mechanical input power
PSO	Particle swarm optimization
SMIB	Single machine infinite bus
STATCOM	Static synchronous compensator
SVC	Static var compensator
TA	Regulator time constant
T’do	Time constant of excitation circuit
Te	Electric torque
Ts	Settling time of speed deviation
Vdc	Dc capacitor voltage
V	Terminal voltage
VSC	Voltage source converter
ω	Rotor speed
δ	Rotor angle
φ	Excitation phase angle
ΔPe	Electrical power deviation
ΔVdc	DC voltage deviation

1

Introduction

Leading in recent years, flexible alternative current transmission systems (FACTS) devices are one of the most effective ways to improve power system operation controllability and power transfer limits. Through the modulation of bus voltage, phase shift between buses, and transmission line reactance, the FACTS devices can cause a substantial increase in power transfer limits during steady state [1]. These devices are an addition to normally steady-state control of a power system but, due to their fast response, the FACTS can also be used for power system stability enhancement through improved damping of power swings [2]. The real power flow with primary function of FACTS devices can be regulated to reduce the low frequency oscillation and enhance power system stability. Recently, several FACTS devices have been implemented and installed in practical power systems [3-5]. STATCOM is a member of the FACTS family that is connected in shunt with the system. From the viewpoint of the power system dynamic stability, the STATCOM provides better damping characteristics than the SVC. It is able to exchange transiently reactive power with the system, it can improve oscillation stability better than SVC [6, 7]. The STATCOM is based on the principle that a voltage source inverter generates a controllable AC voltage source behind a transformer-leakage reactance hence, that the voltage difference across the reactance can produce active and reactive power exchange between the STATCOM and the transmission network. Several trials have been reported in the literature of dynamic models of STATCOM in order to design suitable controllers for power flow, voltage and damping controls [8]. Wang [9] established the linearized Phillips–Heffron model of a power system installed with a STATCOM and demonstrated the application of the model in analyzing the damping effect of the STATCOM. Furthermore, seems that no efforts have been made to identify the most suitable STATCOM control parameter, in order to arrive at a robust damping controller. Intelligent controllers have the potential of overcoming the above mentioned problems. Fuzzy-logic-based controllers, for example, have been used for controlling a STATCOM [7, 10, 11]. The performance of such controllers can be improved by adaptively updating their parameters. Although using the robust control methods [12], the uncertainties are directly introduced to the synthesis. Due to the large model order of power systems, the order resulting controller will be very large in general which is not feasible because of the computational economical problems when implementing. Thus, one important issue, in this respect, is the tuning of the controller parameters of the STATCOM. For this reason, usually a linearized model of the system around a single operation is used for STATCOM controller design.

Many of the optimization techniques such as PSO [13, 14], GA and HBMO are used for optimization problems. The HBMO algorithm can be used to solve many of the same kind of problems as GA [15] and does not suffer from of GA’s problems. Though GA methods have been employed successfully to solve complex optimization problems, a recent research has identified deficiencies on its performance [16, 17]. In order to overcome these drawbacks, the HBMO algorithm is proposed to optimal tune of controller parameters to improve power system stability in this paper. The HBMO algorithm is a very strong method for optimization and has emerged as a useful tool for engineering optimization. Hence, this method is efficient in handling large and complex search spaces [18, 19].

In this study, the problem of designing a robustly STATCOM based damping controller is considered as an optimization problem and both, HBMO and GA techniques are used for searching optimized parameters. The effectiveness and robustness of the proposed controller are demonstrated through nonlinear time-domain simulation and some performance indices studying the damp low frequency oscillations under different operating conditions. Evaluation results show that the HBMO based tuned damping controller achieved good performance for a wide range of operating conditions and is superior to the controller designed using GA technique.

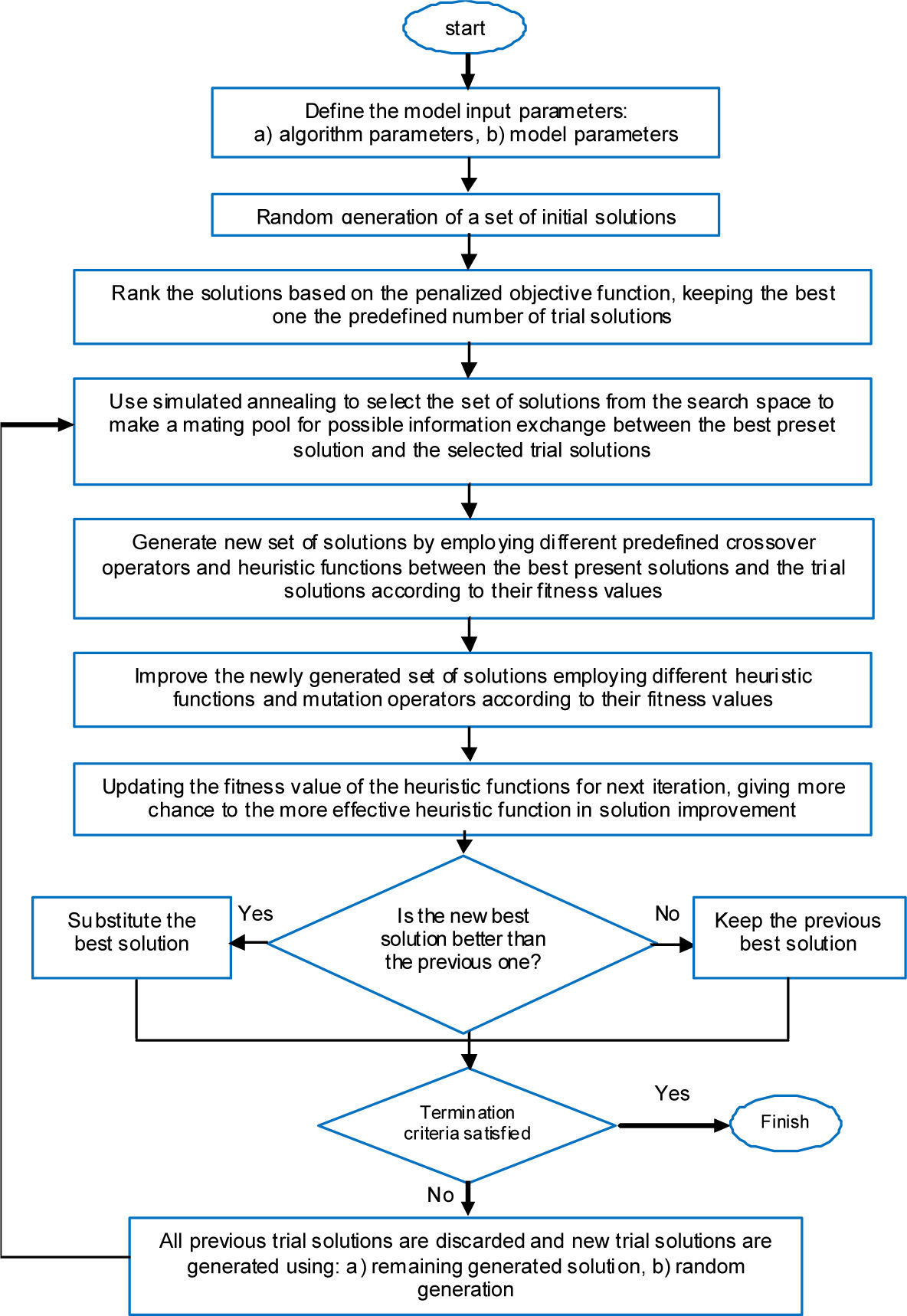
2

Honey bee mating optimization

The honey bee is one of the social insects that only can survive as a member of a colony. The activity of honey bee suggests many characteristics such as; team work and communication. A honey bee colony is normally compossed by a single egg-laying queen whose life-span is longer than that of any other bee; and depending on the season, regularly lays around 60,000 workers. A colony may contain only one queen during its life-cycle. That is called monogynous. Only the queen is fed with “royal jelly.” “Nurse bees” take care of this gland and feed the queen with it. The royal jelly allows the queen bee to become the biggest bee in the hive [20].

Several hundred drones live with the queen and its workers. Queen bee’s life-span is about 5 or 6 years, whereas for the rest of the bees, specially worker bees, their life-spam do not reach 1 year. The drones die after the mating process.

The drones play the father role in the colony that are haploid and amplify or multiply their mother’s genome without changing their genetic combinations, except for mutation. Hence, drones are agents that anticipate one of the mother’s gametes and by the sake of that female can play genetically the males´s role. Broods, cared by workers, improve from fertilized or unfertilized eggs. They represent potential queens and prospective drones, respectively. In the marriage process, the queens in mating period, fly from the nest to far places. Insemination ends with the gradual death of drones, and by the sake of those queens receive the “mating sign.” Any drone can take part in the mating process just onece, but the queens mate several times. These features make bee mating process very interesting among other insects.

2

Working principle and mathematical presentation

The queen plays the most important role in the mating process in nature likewise the HBMO algorithm. The spermatheca is a place for sperm of drones and queen’s, all drones, however are originally haploid; after successful mating, the drone’s sperm is stored in the queen’s spermatheca. A brood is reproduced by coming of some genes of drone’s into the brood genotype. A brood has only one genotype [21].

Therefore, an HBMO algorithm would be constructed by the following five important stages:

• 1.

  The algorithm starts with a mating flight, where a queen selects drones probabilistically from the spermatheca. A drone is selected from list randomly for the generating broods.

• 2.

  Generating new broods by combining drone’s with queen´s genotypes.

• 3.

  Using workers to carry on local searching on broods.

• 4.

  Adaptation of worker’s ability, based on the improvement of broods.

• 5.

  Substitution of queen’s workers by stronger and aptitude broods.

When all queens have completed their mating flights, the breeding begins. All the broods after the generation are sorted according to fitness, i.e. their weakness or health. The best brood is replaced by the worst queens until all queens will be the best and there is no need of broods. After the completion of mating, the remaining broods finally are killed hence, a new mating process begins.

2.2

Original HBMO algorithm

A drone mates with a queen probabilistically using an annealing function like this:

Where Prob(D,Q) is the probability of adding drone’s sperm D to queen’s spermatheca Q, Δ(f) is the perfect difference of fitness D of queen, and s(t) is the speed of the queen at time t. The mating is high whether queen’s speed level is high, or drone’s fitness is equal to queen’s. After every transition, the speed of queen will decrease according to the following equations:

Where: α is a factor ε(0,1) and γ is the amount of energy, E(t) reduction after each transition.

The algorithm starts with three user-defined parameters and one predefined parameter. The predefined parameter is the number of workers (W), representing the number of heuristics encoded in the program. The three user-defined parameters are the number of queens, the queen’s spermatheca size representing the maximum number of mating per queen in a single mating flight, and the number of broods that will be born by all queens. The energy and speed of each queen at the beginning of each mating flight is initialized at random. A number of mating flights are realized. At the commencement of a mating flight, drones are generated randomly and the queen selects a drone using the probabilistic rule in Equation (1). If the mating is done successfully, the storage of drone’s sperm in queen’s spermatheca occurs. The combination of drone’s and queen’s genotypes, generate a new brood, which can be improved later on by employing workers to carry on a local search. One of the main differences between HBMO algorithm and classic evolutionary algorithms is that by storing many different drone’s sperm in the spermatheca for the queen to use it, some of them create a new solution for the fittest broods, and gives the possibility to have the fittest broods.

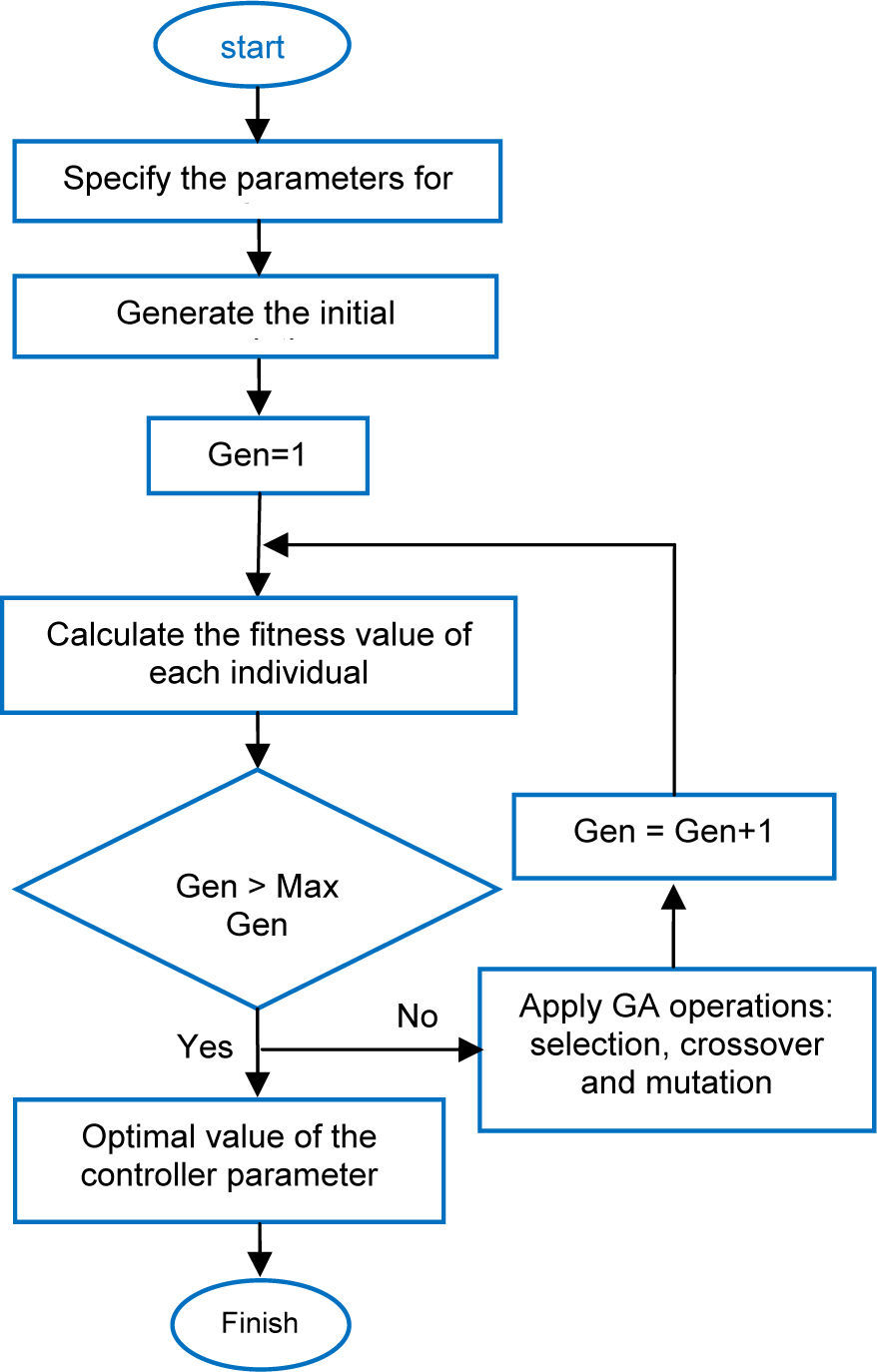
The role of the workers is brood caring and for the sake of it, they are not separated from the population and are used to grow the broods generated by the queen. Every worker has different capability for producting in solutions. The computational flow chart of HBMO algorithm is shown in Figure 1.

Figure 1.

Flowchart of the HBMO algorithm.

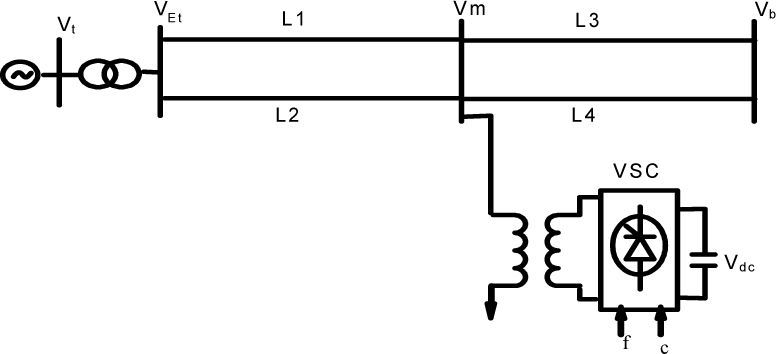
3

Power system modeling

A SMIB power system installed with a STATCOM shown in Figure 2, is widely used for studies of power system oscillations, it is adopted in this paper to demonstrate the proposed method. The synchronous generator delivers power to the infinite-bus through a double circuit transmission line and a STATCOM. The system data is given in the appendix. The system consists of a step down transformer with a leakage reactance X_SDT, a three phase GTO-based voltage source converter, and a DC capacitor [9].

Figure 2.

SMIB power system equipped with STATCOM.

The VSC generates a controllable AC voltage source behind the leakage reactance. The voltage difference between the STATCOM bus AC voltage, v_L(t) and v_0(t) produces active and reactive power exchange between the STATCOM and the power system, which can be controlled by adjusting the magnitude V₀ and the phase angle φ. The dynamic relation between the capacitor voltage and current in the STATCOM circuit are expressed as [9]:

Where for the PWM inverter c = mk and k is the ratio between AC and DC voltage depending on the inverter structure, m is the modulation ratio defined by the PWM and the magnitude c is also defined by the PWM. The C_dc is the dc capacitor value and I_dc is the capacitor current while i_Lod and i_Loq are the d-and q-components of the STATCOM current, respectively.

The dynamics of the generator and the excitation system are expressed through a third order model given as [9, 15]:

The expressions for the power output, terminal voltage, and the d-q axes currents in the transmission line and STATCOM, respectively, are:

X_T, x’_d and x_q are the transmission line reactance, d-axis transient reactance, and q-axis reactance, respectively. A linear dynamic model is obtained by linearizing the nonlinear model round an operating condition.

3.1

Power system linearized model

A linear dynamic model is obtained by linearizing the nonlinear model around an operating condition. The linearized model of power system is given as follows:

Where, K₁,K₂,...,K₉, K_pu, K_qu and K_vu are linearization constants. The state space model and block diagram of the linearized dynamic model of SMIB power system with STATCOM is given by [15, 22].

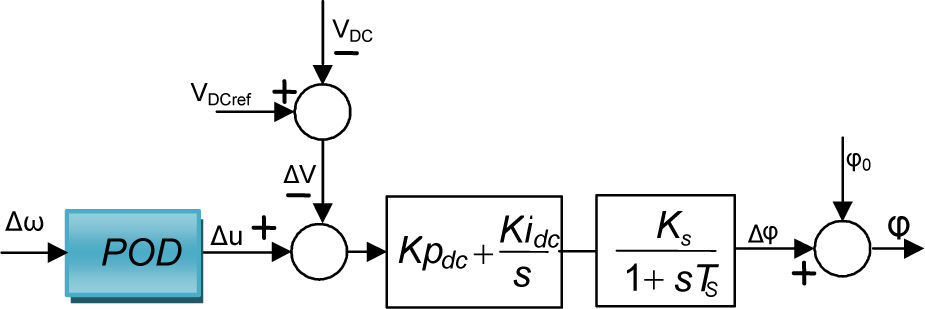
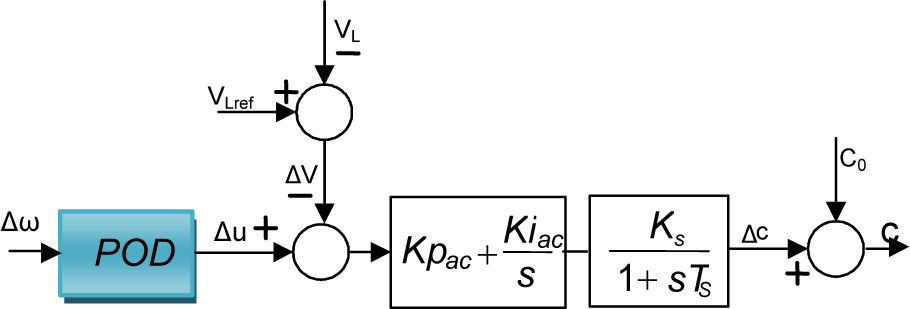
3.2

STATCOM based controllers

The POD controller, that is better than the PID controller [23], is designed to produce an electrical torque in phase with the speed deviation according to the phase compensation method. The speed deviation Δω is considered as the input to the damping controller. The structure of the POD controller is given in Figure 3. This controller may be considered as a lead-lag compensator. It comprises gain block, signal-washout block and lead-lag compensator. The block diagram of STATCOM dc voltage PI controller with power oscillation damping stabilizer (φ based controller) is shown in Figure 4. Setting of capacitor voltage is on the controlling part, which in relation to capacitor reference voltage and in comparison to the capacitor voltage, the amount of the angle phase of the converter can be computed.

Figure 3.

Power oscillation damping controller.

Figure 4.

STATCOM PI controller for dc voltaje.

The DC-voltage regulator controls the DC voltage across the DC capacitor of the STATCOM. Figure 5 illustrates the block diagram of STATCOM ac voltage PI controller with a power oscillation damping stabilizer (C based controller).

Figure 5.

STATCOM PI controller for ac voltaje.

3.3

STATCOM controllers design using HBMO

In the proposed method, we must tune the STATCOM controller parameters optimally to improve overall system dynamic stability. The two signal control of the STATCOM (φ and c) can be modulated in order to produce the damping torque, since the selection of the parameter for STATCOM based damping controller is a complex optimization problem. To acquire an optimal combination, this paper employs the HBMO to improve optimization synthesis and find the global optimum value of objective function. For our optimization problem, the objective function is a time domain-based objective function:

Where, the t_sim is the time range of simulation and N_p is the total number of operating points for which the optimization is carried out. It is aimed to minimize this objective function in order to improve the system response in terms of the settling time and overshoots. The design problem can be formulated as the following constrained optimization problem, where the constraints are the controller parameters bounds:

Minimize J Subject to:

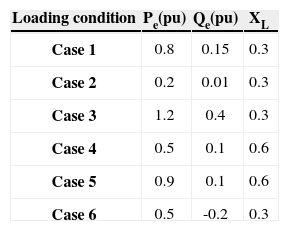
The proposed approach employs HBMO to solve this optimization problem and search for an optimal set of controller parameters. The optimization of controller parameters are carried out by evaluating the objective function as given in Equation 24, which considers a multiple of operating conditions. The operating conditions are given in Table 1.

Table 1.

Loading conditions

Loading condition	Pe(pu)	Qe(pu)	XL
Case 1	0.8	0.15	0.3
Case 2	0.2	0.01	0.3
Case 3	1.2	0.4	0.3
Case 4	0.5	0.1	0.6
Case 5	0.9	0.1	0.6
Case 6	0.5	-0.2	0.3

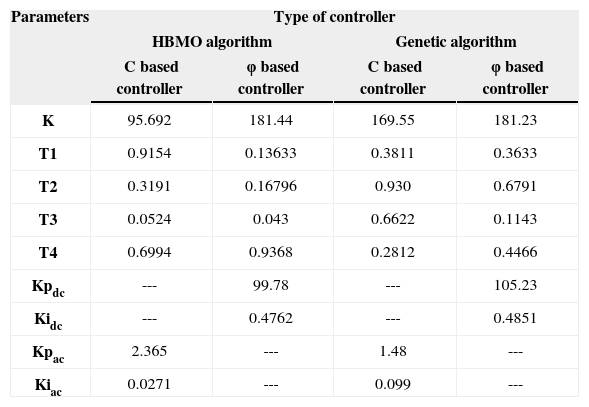
In order to acquire a better performance, the number of queen, N_drone, N_brood, the size of the queen’s spermatheca, the decreasing factor and N_workers are chosen as 1, 100, 100, 50, 0.98 and 1000, respectively [21]. In order to facilitate the comparison with genetic algorithm (see appendix B), the design and tuning of the damping controller for STATCOM are used. The final values of the optimized parameters with objective function, J, are given in Table 2.

Table 2.

The optimal parameter settings of the proposed controllers

Parameters	Type of controller
	HBMO algorithm		Genetic algorithm
	C based controller	φ based controller	C based controller	φ based controller
K	95.692	181.44	169.55	181.23
T1	0.9154	0.13633	0.3811	0.3633
T2	0.3191	0.16796	0.930	0.6791
T3	0.0524	0.043	0.6622	0.1143
T4	0.6994	0.9368	0.2812	0.4466
Kpdc	---	99.78	---	105.23
Kidc	---	0.4762	---	0.4851
Kpac	2.365	---	1.48	---
Kiac	0.0271	---	0.099	---

4

Nonlinear time domain simulation

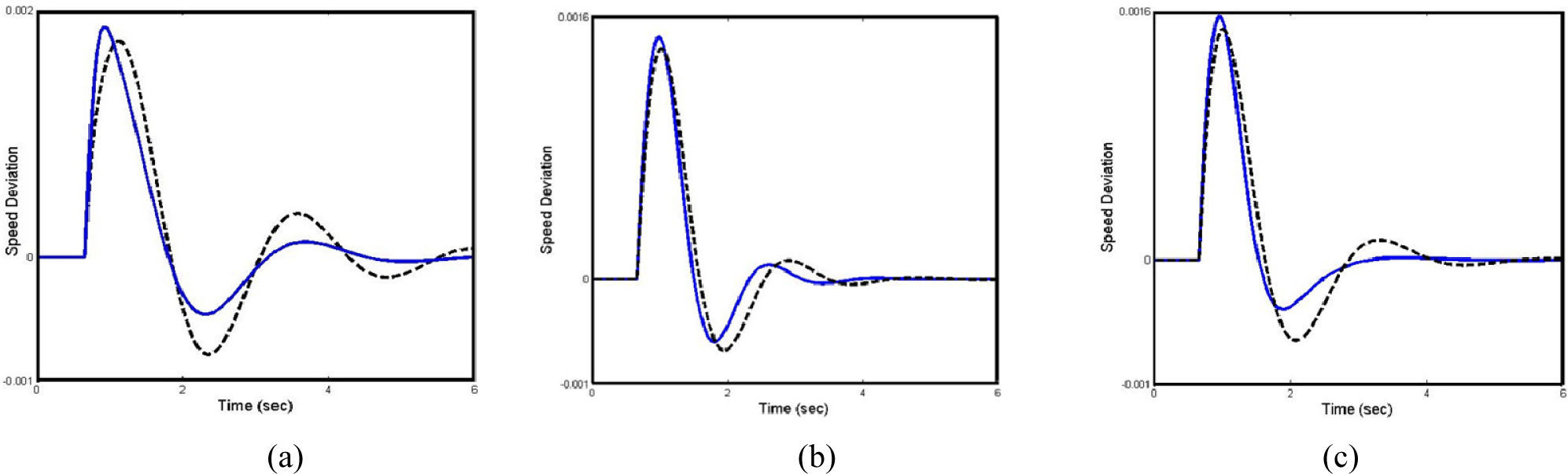
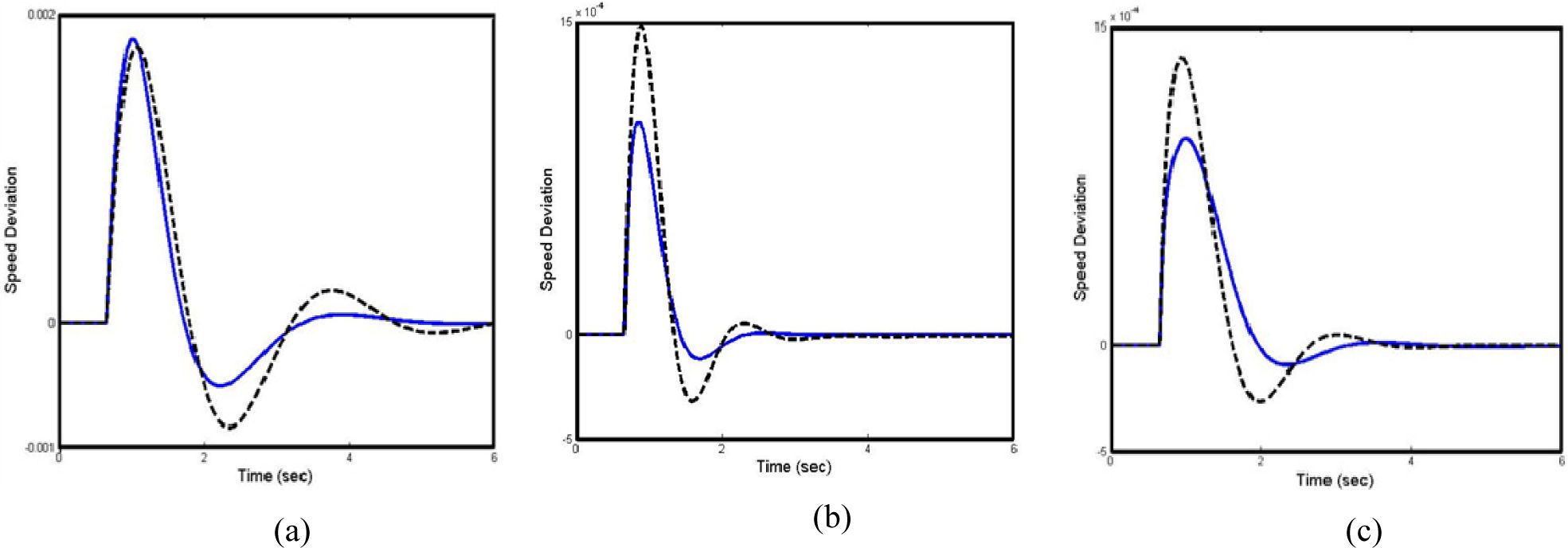
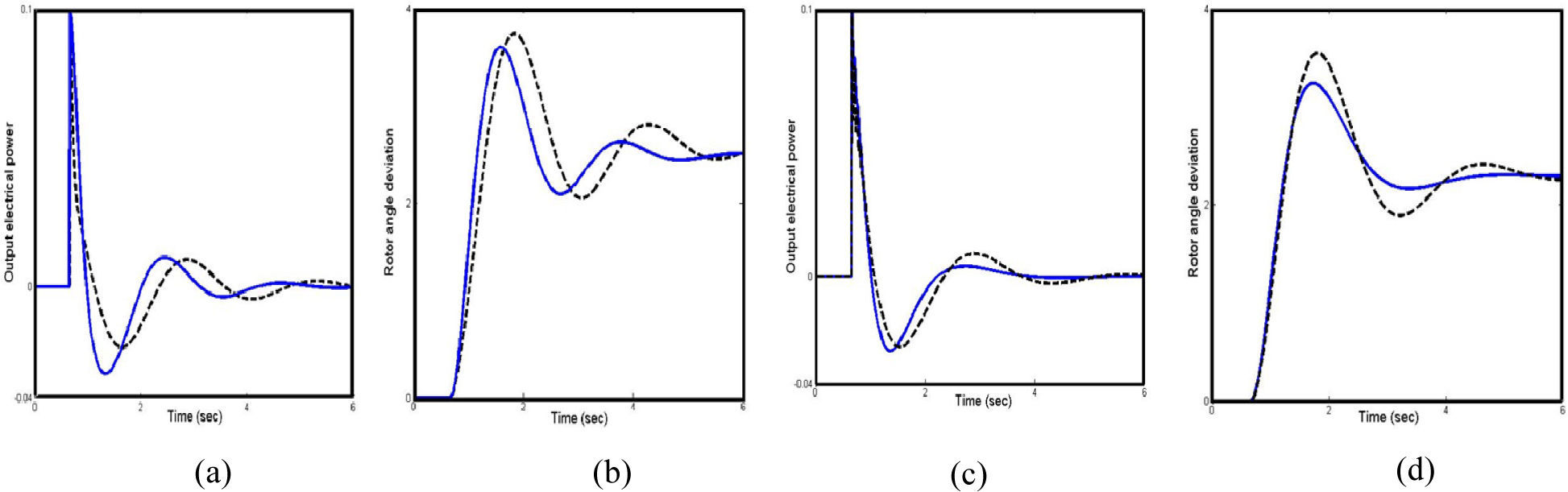
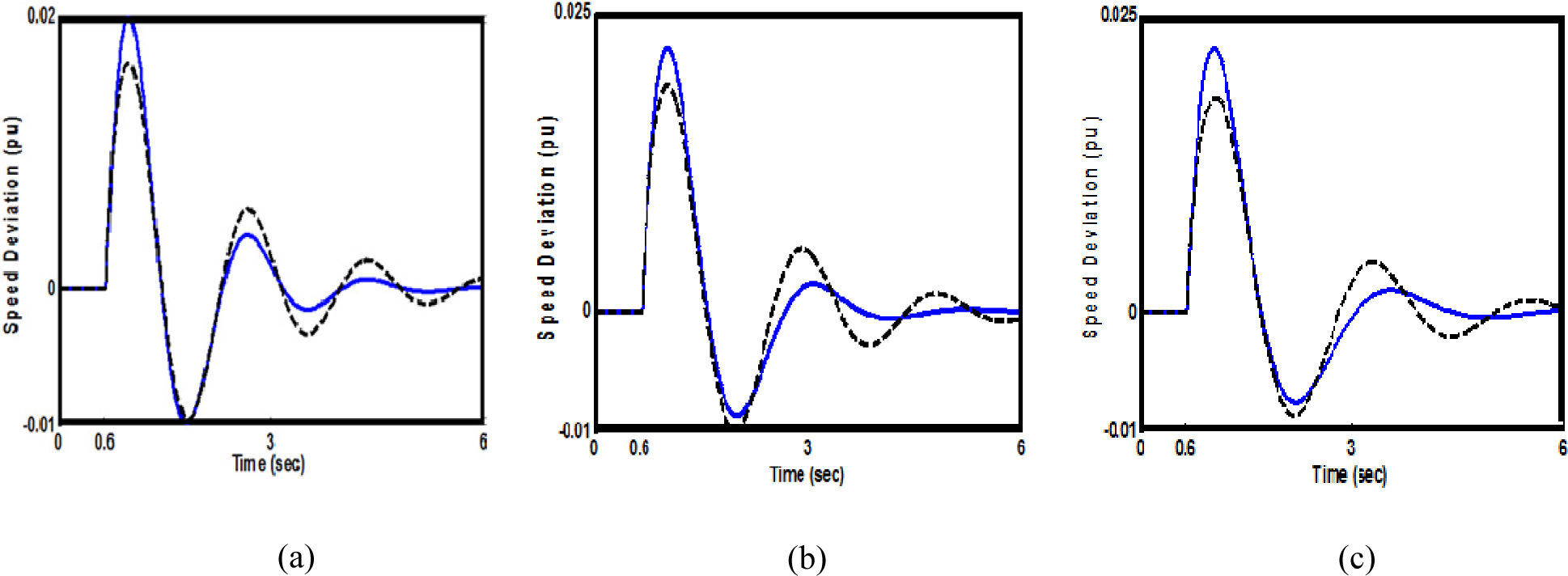
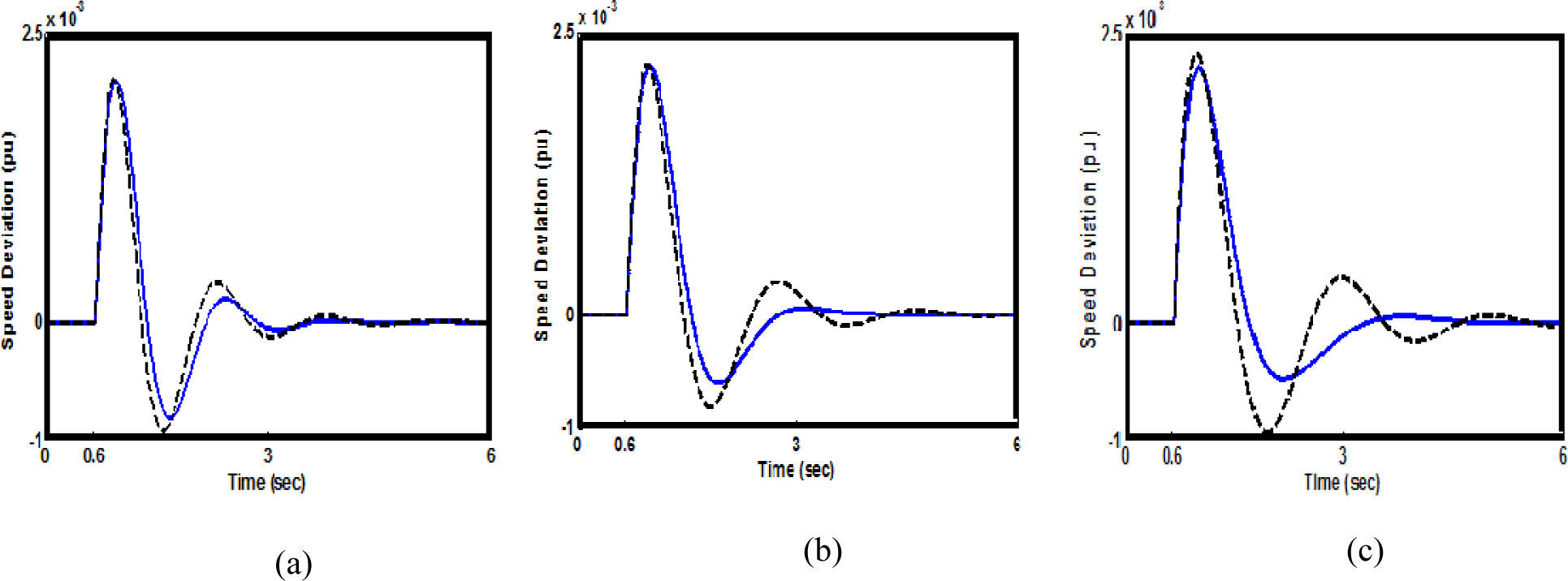
In this section, the performance of the proposed controller under transient conditions is verified by applying a 6-cycle three-phase fault at t = 0.6 sec, at the middle of the L₃ transmission line. The fault is cleared by permanent tripping of the faulted line. The performance of the controllers when the HBMO is used in the design is compared to that of the controllers designed using the GA. The simulation results at all cases loading conditions due to designed controller based on the φ based controller and C based controller are shown in Figures 6-11. It can be seen that the proposed controller has good performance in damping low frequency oscillations and stabilizes the system quickly. Moreover, from the above conducted tests, it can be concluded that the φ based controller is superior to the C based controller.

Figure 6.

Dynamic responses for Δω at (a) case 1, (b) case 2, (c) case 3, loading conditions; solid (HBMO based C controller) and dashed (GA based C controller).

Figure 11.

Value of performance index with C controller: a) ITAE and b) FD.

To demonstrate performance and robustness of the proposed controller, two performance indices: ITAE and FD based on the system performance characteristics are defined as:

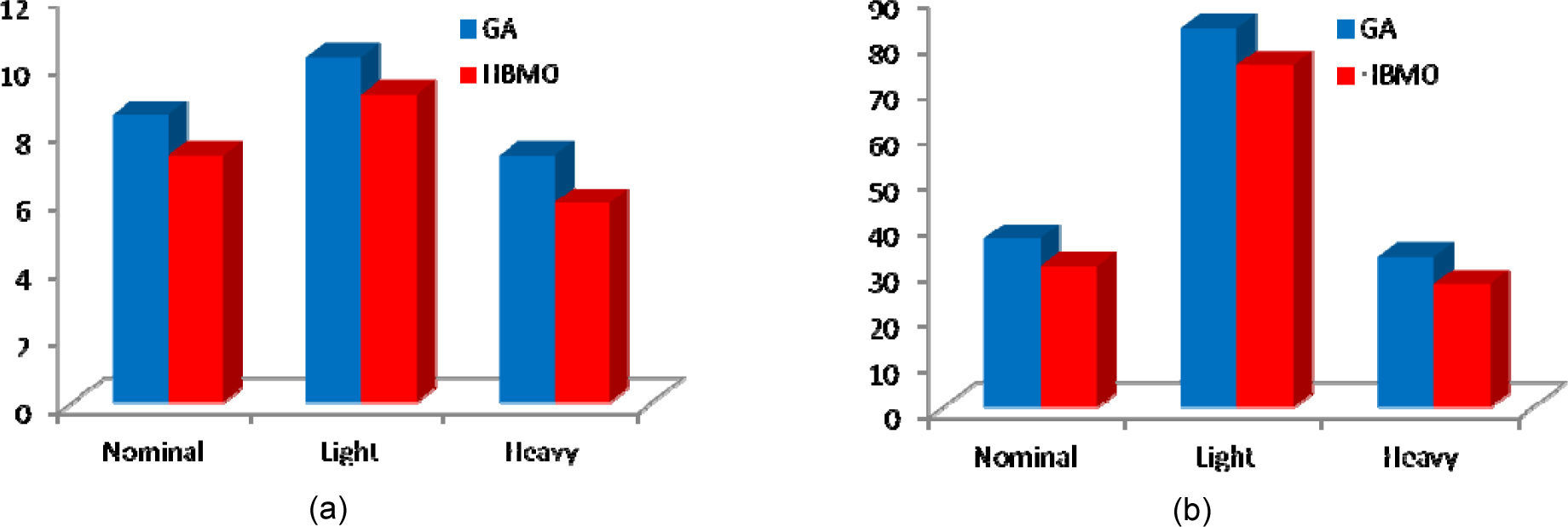
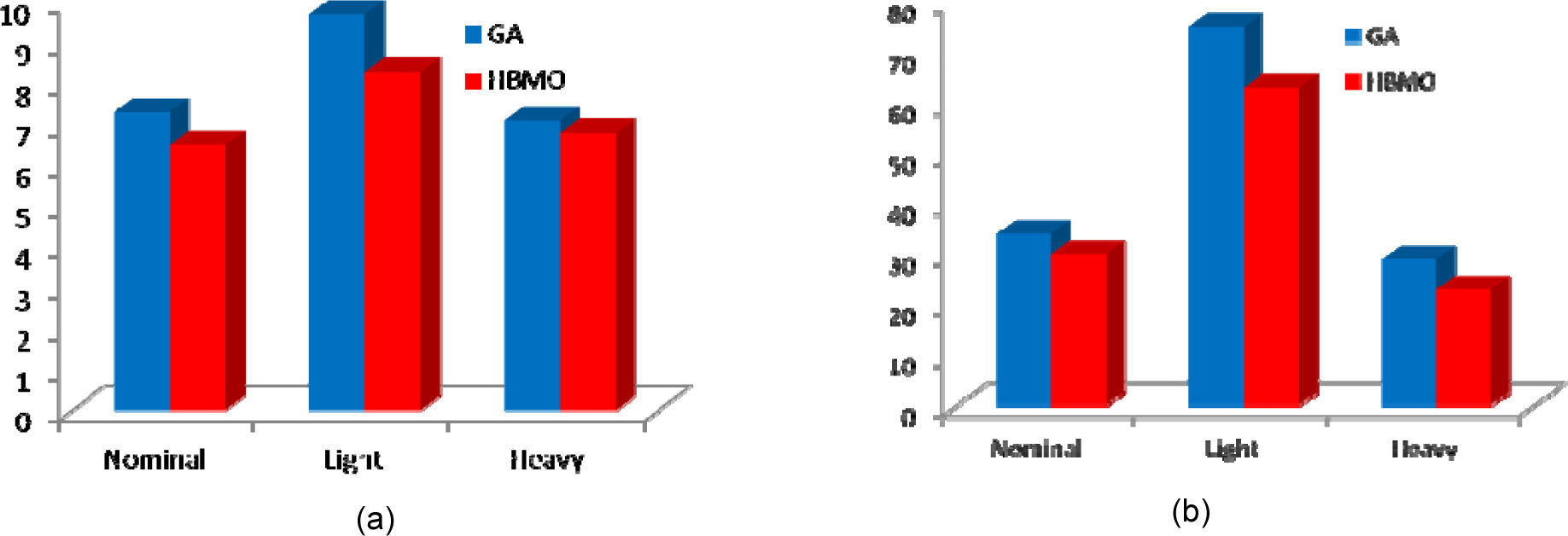
Where, speed deviation (Δω), Overshoot (OS), Undershoot (US) and settling time of speed deviation of the machine is considered for evaluation of the ITAE and FD indices. It is worth to mention that, the lower the value of these indices, the better the system response in terms of time-domain characteristics. Numerical results of the performance and robustness for all system loading cases are shown in Figures 11 and 12. It can be seen that the application of both PSS and STATCOM damping controllers where the controllers are tuned by the proposed coordinated design approach which gives the best response in terms of overshoot, undershoot and settling time.

Figure 12.

Value of performance index with φ controller: a) ITAE and b) FD.

5

Conclusions

The honey bee mating optimization (HBMO) algorithm has been successfully applied to the optimal design of STATCOM based damping controllers. The design problem of the controller is converted into an optimization problem which is solved by a HBMO technique with the time domain-based objective function. The robust design has been found to be very effective for a range of operating conditions of the power system. The effectiveness of the proposed STATCOM controllers for improving transient stability performance of a power system are demonstrated by a weakly connected example system subjected to severe disturbance. The system performance characteristics in terms of ITAE and FD indices revealed that using both, the proposed HBMO and the GA based controllers, the overshoot, the undershoot, the settling time and speed deviations of the machine are greatly reduced at various operating conditions. The nonlinear time domain simulation results show the robustness of the proposed controller and their ability to provide good damping of low frequency oscillations. It can be seen that the HBMO based STATCOM controller achieves good robust performance, provides superior damping in comparison with the GA based STATCOM controller and greatly enhances the dynamic stability of power system. Moreover, the φ-based controller provides better damping characteristics and greatly enhances the first swing stability compared to the C-based controller.

Acknowledgements

The authors would like to thank the anonymous reviewers for their helpful criticisms and suggestions for improving the earlier version of this paper.