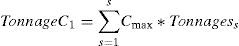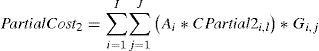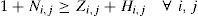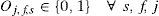The importance of efficient logistics management for chemical industry considered to be one of the important issues in process industries. Motivated from a chemical factory operating in Turkey, cost efficient daily logistics planning using multiple third party logistics providers (3PL) with different contracting schemes are analyzed. In order to reduce planning time and maximize the physical vehicle capacity utilization, problem of the company is formulated as a mixed integer mathematical model, and a two-phase solution approach is proposed. Using the real life daily shipment requirement data the proposed model and the solution methodology is tested. Furthermore, impact of various company practices and types of different transportation pricing schemes are analyzed to better design 3PL contracts. The initial results are very promising where optimum solution for large scaled problem can be obtained in seconds and the daily shipment planning can be updated dynamically whenever it is necessary. The analysis indicates that cost savings through holistic planning is robust to contracting schemes and specific clauses are not always needed to guarantee certain service quality. We believe that the efficiency achieved through the integration of such techniques can become highly attractive for further applications in the industry.
Process sectors are the leading sectors in most of the countries. In Europe, the chemicals sector contributes 2.4% of EU GDP [1]. Recent studies report that logistics operations are key aspect of the chemical industry as production and consumption locations are mostly separated and estimated to be as high as 15 % of the GDP in some of the developing countries [2]. Thus, supply chain in process industry needs to be improved in terms of efficiency and responsiveness. The study is motivated from one of the leading chemical products factory in Turkey, which produces raw material to different manufacturing sectors as well as sell directly to individual consumers or retailers. Company produces a large number of products for a set of customers that are dispersed all over Turkey. As most of the producers in the chemical sector, the company outsourced its final product delivery to multiple third party logistics providers. The problem on hand is to develop a decision support tool that assigns the daily orders to appropriate shipments, deciding on the 3PL company, vehicle type as well as the respective load compositions and stop-over points of the vehicles, in order to reduce the total transportation cost and prevent late deliveries.
The simplest version of this problem can be modeled as “one dimensional bin-packing” problem such that some ‘objects’ of different size, in our setting delivery orders have to be packed into a set of bins, i.e. vehicles with given capacities. The objective is to minimize the cost associated with using the bins. Even for identical capacity bins, bin-packing problem can be shown to be NP-hard [3], so that in most decision support systems heuristics are suggested. There are various solution approaches for the bin packing problem. Ghiani et al. [3], summarizes the common greedy approximation algorithms while Scholl et al. [4] offer a good survey of existing solution procedures, as well as a good exact algorithm that they have developed. Different than heuristic approaches, Carvalho [5] used exact solution methodologies like column generation and branch-and-bound for the bin-packing problem. However the daily logistics planning problem is much more complex than bin-packing problem, since vehicle types may not be identical. Moreover, most of the 3PL contracts include restriction on the maximum number of locations that should be visited and objective function may include cost elements other than unit vehicle cost.
The study most similar to our case belongs to Çetinkaya et al. [6]. In order to improve the outbound supply chain activities of Frito-Lay, a leading firm on the FMCG sector, Çetinkaya et al. [6] conducted a study to optimize Frito-Lay’s inventory and transportation decisions simultaneously. At first, they develop a mixed integer programming (MIP) model which considers inventory lot-sizing and vehicle routing decisions, including inventory holding, truck loading, dispatch and mileage costs, as well as, production, storage, and truck capacity constraints. Furthermore, direct and partial shipment options are also taken into account while constructing the MIP model. In our study, inventory costs are not incurred by the producer. Thus we do not need to consider inventory related costs. Instead, different cost structure of different 3PL companies will be taken into account to minimize the outbound transportation costs. Likewise, González-Ramírez et al. [7] considered a real-life problem of a parcel company, serving in Monterrey, Mexico; where the service region of the parcel company is divided into districts and each district is served by a single vehicle. They formulated a mathematical model and used a heuristic approach to solve this problem.
The remainder of the paper is organized as follows: In the following section, we introduce the daily logistics planning problem. The notation used in the paper together with the formulation of the daily logistics planning problem as MIP is explained in section 3. We propose a two-stage the solution technique in section 4. We will illustrate our solution approach with a case study and discuss the initial findings in section 5. We conclude with final remarks in section 6.
2Problem definitionOne of the leading chemical product factories in Turkey produces raw material to different manufacturing sectors as well as products for individual consumers or retailers. The company produces a large number of products for a set of customers that are dispersed all over Turkey. As most of the producers in the chemical sector, the company outsources its final product delivery to third party logistics providers. Company cooperates with four different 3PL providers to send their items. These companies have various conditions on pricing. These different pricing structures are as follows:
Company # 1 has two types of unit transportation price per kilogram for each final delivery location. If the order is more than certain amount, 3PL is required to deliver the order directly to customer and charges for “direct delivery” price per kg (cost type 1). If the order is less than the pre-determined threshold, 3PL takes the order to its local distribution center and distribute the order from there. If this is the case, company # 1 charges for “partial shipment” price per kilogram which is typically more than the unit “direct delivery” price for identical delivery location (cost type 2). For partial deliveries the maximum number of delivery location (on city center basis) is limited to 4. For shipments that requires more than 4 stop-overs, 3PL company charges extra “stop-over fee”. Having extra stop over points also delays the delivery of the orders. Thus, it is undesirable for the chemical company. The company # 1, has a minimum shipment load condition (minimum tonnage per vehicle), i.e. if the total load of the vehicle is less than the agreed minimum tonnage, chemical company pays a unit fee per kilogram for the weight difference to complete the tonnage (cost type 3).
Company # 2 and 3 use similar pricing structure. If there is only one delivery point for the shipment, i.e. single order is enough for full truckload, the pricing is per vehicle per location (cost type 4). Otherwise, if there are orders with different delivery points “partial delivery” pricing is charged per kilogram per location (cost type 5). When only one order is enough for shipment, actually there is no decision that needs to be made. As long as direct shipment (cost type 4) is cheaper, company prefers to send the order to its final location directly. Even if there are more than one agreed 3PL carriers that can serve for the order, we can calculate the threshold weight for each final delivery location that will provide the minimum cost for the company. These threshold weights for each location and the 3PL company that provides the cheapest direct service for the location is determined. The direct delivery cost for 3PL companies # 2 and 3 (cost type 4) are excluded from the model to decrease the size of the model.
For deliveries to regional locations, company # 4 is contracted. Company # 4 distributes the local deliveries with small vans and fixed fee per route per van (cost type 6) is charged.
Except cost type 4, all the 5 different cost entries are included in the model. Other less common cost items such as stop-over fees, extra fee for loading and/or unloading, overnight parking fees for long-haul transportation routes that requires more than one day on the road are all excluded for simplification.
3PL companies use different types of vehicles with limited capacity on weight. The items are loaded in pallets so instead of volume capacity of the vehicles, base area limitation of the vehicles can be binding for shipment.
3Mathematical modelThe daily logistics planning problem is formulated as a mixed integer linear programming model. As it can noticed from section 2, the discussed problem on hand is more complicated than one dimensional bin packing problem. Proposed model reflects the practical issues that are important for chemical factory. The objective function of the model is to minimize the total shipment cost for a given list of orders. The formulated objective function also provides the maximum usage of available physical capacity of the vehicles.
3.1NotationFollowing indices, parameters and decision variables are used throughout the paper:
i = (1…I) set of orders that needs to be shipped.
l = (1…L) set of final delivery locations.
Note that each order has one final delivery location so we use order-location pair (i,l) index together without loss of information.
f = (1,…,4) 3PL companies that any shipment can be assigned.
s = (1…S) set of shipments that are scheduled.
j = (1, 2) where vehicle type 1 denotes the truck and type 2 denotes the long-truck.
Throughout the paper we use the following parameters:CDirect1(i,l)
Unit direct cost per kilogram for 3PL company # 1, for final delivery location l. (cost type 1)
CPartial1(i,l)Unit partial cost per kilogram for 3PL company # 1, for final delivery location l. (cost type 2)
CmaxTonnage completion fee per kilogram for 3PL company # 1. (cost type 3)
CPartial2j,lUnit partial cost per kilogram for 3PL company # 2, for vehicle type j and final delivery location l. (cost type 5)
CPartial3j,lUnit partial cost per kilogram for 3PL company # 3, for vehicle type j and final delivery location l. (cost type 5)
C4Unit transportation cost per shipment for 3PL company # 4. (cost type 6)
WjWeight capacity of vehicle type j.
AreajBase area of the vehicle type j.
AiWeight of order i.
BiBase area requirement of order i
DjThe minimum tonnage (shipment weight) of vehicle type j which is set by company # 1.
TjThe weight threshold limit for company # 1 for an order to be considered as partial shipment in vehicle type j. (in kilograms.)
MA positive large number used for modeling purposes.
Two basic decisions need to be made for each shipment s: assigning each i with final delivery location l to one shipment s and assigning each shipment s to the 3PL company f with vehicle type j. The associated variables are the following:X(i,l)s
A binary variable that takes the value of 1 if order i with final delivery location l is assigned to shipment number s and 0 otherwise.
Oj,f,sA binary variable that takes the value of 1 if shipment s is assigned to 3PL company f using vehicle type j and 0 otherwise.
The cost scheme of each order i should be decided. The associated decision variables are as follows:Zi,j
A binary variable that takes the value of 1 if order i is assigned to partial delivery shipment in vehicle type j and 0 otherwise. (valid for 3PL company # 1.)
A group of auxiliary variables are defined for modeling purposes. These auxiliary variables are as follows:Hi,j
A binary variable that takes the value of 1 if both X(i,l)sand Oj,1,s are assigned to 1 and it is 0 otherwise. (valid for 3PL company # 1.)
Gi,jA binary variable that takes the value of 1 if both X(i,l)s and Oj,2,s are assigned to 1 and it will be used to assign partial cost to order i and 0 otherwise. (valid for 3PL company # 2.)
Ri,jA binary variable that takes the value of 1 if both X(i,l)s and Oj,3,s are assigned to 1 and order i is assigned to partial delivery cost and 0 otherwise. (valid for 3PL company # 3)
Ni,jA binary variable that takes the value of 1 if both Zi,j. and Hi,j. are assigned to 1 and it is 0 otherwise. (valid for 3PL company # 1)
Qi,jA binary variable that takes the value of 1 if Zi,j is assigned to 0 and Hi,j is cost and 0 otherwise. (valid for 3PL company # 3)
3.2Mathematical formulationThe daily logistics planning problem explained above is modeled as follows:(Full Mathematical Model)
where constraints (1) through (6) are used to calculate different cost entities belong to different pricing scheme of the 3PL companies. Constraints (1), (2), and (3) account for the total direct and partial delivery costs and tonnage completion fee, respectively paid to 3PL company # 1. Similarly, constraints (4) and (5) are the total partial delivery cost for 3PL companies # 2 and 3, respectively. Finally constraint (6) is the total cost for regional shipment assigned to 3PL company # 4.Constraint set (7) guarantees that each customer order is assigned to one and only one shipment. Constraint set (8) ensures that each shipment is assigned to only one vehicle type to one 3PL company. While constraint set (9) ensures that each shipment will have at least one order in it. Constraint sets (10) and (11) ensure that weight and base area capacity of the vehicles are not violated. Constraint set (12) assigns partial delivery cost to orders that are assigned to 3PL company # 1 and weight of the order is less than the shipment weight threshold.
Constraint set (13) ensures to assign direct cost (cost type 1) if order is not pricing partially and shipped by 3PL company # 1. Constraint sets (14) and (15) determine the amount of tonnage that is under the minimum tonnage (shipment load) weight, Dj. Maximum number of stop-over location (which is set to 4, for our case) is guaranteed at constraint set (16). Constraint sets (17), (18) and (19) are auxiliary constraints that set the logical connection between order variables X(i,j),s and 3PL company assignment variables Oi,f,s for 3PL companies # 1, 2, and 3, respectively. Constraint set (20) is also an auxiliary constraint set ensures that the orders are shipped by only one 3PL company. Auxiliary constraint sets (21) and (22) assign either direct delivery or partial delivery cost to each item assigned to 3PL company # 1.Finally constraint sets (23a-23d) are for binary variable declarations. In the next section, our solution approach will be discussed.
4Solution methodologyAs mentioned before, the proposed model to plan the daily logistics requirement includes additional constraints and binary variables compared to traditional bin-packing problem. For an average day, if there are approximately 140 orders and 20 shipments, this will be translated into approximately 4600 decision variables and approximately 1450 constraints in the model. Such a large scale problem cannot be solved within short time that is necessary for fast planning, so we propose a two-stage hierarchical solution approach. As it is illustrated in Figure 1, the proposed solution algorithm provides a near optimum solution to the problem in two stages.
On the first stage, delivery orders that belong to the same final locations are aggregated and the final locations are tried to be assigned to 3PL companies and shipments. When all the orders that have identical delivery location cannot be assigned to the same vehicle (because of the vehicle capacity) then in the second stage these orders are assigned to vehicles with available capacity optimally.
Moreover, when various criteria of the large-scale real-life problems are included into the mathematical models the complexity of the problem increases and accordingly, the optimal solution of the model cannot be reached in reasonable short time. In those cases, decomposition of the whole mathematical program into various smaller sub-programs is a good approach. For instance, one of the examples in the literature in which the whole mixed integer problem is decomposed into sub (mixed-integer) problems can be seen in the study of Rezazadeh et al. [8]. Similar approach is adapted in the proposed solution algorithm. Data set is partitioned into mutually exclusive and collectively exhaustive smaller problems using geographical proximity and service agreement regions of different 3PL companies.
4.1Solution algorithmThe algorithm can be summarized as follows:
Step 0. (Initialization) Retrieve the daily delivery requests from ERP system. These orders form the unassigned order set, I.
Step 1. (Pre-process)
- 1.1
Aggregate all delivery requests that will go to the same customer and the same delivery point. (Some customers may have multiple delivery points)
- 1.2
Check if there are full truckload (FTL) delivery requests, if so assign the order to cheapest available 3PL company with appropriate sized vehicle, remove it from unassigned order list. This step also assigns all possible direct delivery shipments for 3PL company # 2 and 3.
- 1.3
For each order, determine base area requirement (i.e. number of standard pallets needed) and potential 3PL companies that serve to its final delivery location.
- 1.4
Based on geographical proximity and 3PL company contracts, all final delivery locations can be clustered into 4 exclusive subsets:
Then for region 1 the MIP reduces to subproblem,(SP1-IP)
min DirectCost1 + PartialCost1 + TonnageC1 + PartialCost2 s.t. (1-4), (7-18), (20-23)
For region 2 : (SP2-IP)min DirectCost1 + PartialCost1 + TonnageC1 + PartialCost3 s.t. (1-3), (5), (7-17), (19-23)
For region 3 : (SP3-IP)min DirectCost1 + PartialCost1 + TonnageC1 s.t. (1-3), (7-17), (21-23)
and for region 4, the problem reduces to subproblem, (SP4-IP) min Cost4s.t. (6-11), (23a), (23c)- 1.1
Step 2. For aggregated delivery orders, relax the constraint set (23a), i.e., solve subproblem for each region for divisible demand in order to assign final delivery locations to vehicles and 3PL companies. Solving each subproblem relaxing the constraint set (23a), thus letting X(i,l)s be continuous variable (where i=l is the aggregated orders of location l) will allow the model to divide the order of a final delivery point more than one vehicle. More specifically, in Step 2 instead of X(i,l)s X(l,l)s is where X(l,l)s denotes the percentage of all orders whose final delivery location is l assigned to shipment s. As a result, the new subproblems that will assign final delivery locations to shipments will be the linear relaxations.
Step 3. For all final locations l∈l, If optimum Xl,l,s*=1 for any l, then assign all orders with final location l to associated shipment ŝ. Subtract total weight and total area requirement of orders with final location l from vehicle capacity to calculate remaining vehicle capacity for shipment ŝ. Remove all order i with final location l from unassigned order list.
If for any final location l∈l optimum Xl,l,ŝ*<1 keep all orders with final location in the unassigned order list.
Step 4. For all orders remained in unassigned list, solve all subproblems for each region (SP1-/P, SP2-/P, SP3-/P, and SP4-/P) assuming indivisible demand (i.e. keep constraint set 23a). In this step, the vehicle type and company of each shipment is already known (decided in step 2) and the mixed integer problem is solved only for a small subset of delivery orders, in order to assign these unassigned orders to shipments with leftover capacity.
Step 5. For each shipment s, if 67% of the vehicle weight capacity is filled (sector standards due to loading with pallets), shipment is approved and vehicle is taken to ramp for loading. If assigned weight for shipment is less than 67% of potential vehicle capacity, shipment is postponed until next planning cycle with new delivery requests.
During a day, new delivery requests may arrive to planning department. A user-friendly decision support system (DSS) to aid planning daily shipment assignments is supposed to have a positive impact. With this idea in mind, a DSS was developed using MS EXCEL to accommodate two-phase solution approach to the daily logistics planning problem and reporting the findings in interactive manner.
The DSS requires the amount, product code, final delivery address of delivery requests that can be retrieved from ERP program as input parameters. After calculating pallet requirement i.e. the area needed within vehicle base using the amount and product code data, the decision support tool solves the decision making problem using the modeling approaches explained in section 4. Finally, for each 3PL company the system reports total number and type of vehicle that should be used and which delivery order should be loaded to which vehicle so that total cost will be minimized while satisfying all sector specific requirements. The use of the DSS is demonstrated in the next section through a case study.
5Computational studySeveral experiments were performed in order to assess the performance of the proposed method as well as to study the impact of various problem parameters on problem complexity.
5.1Computational performanceIn order to demonstrate computational efficiency of the proposed solution algorithm, our solution algorithm is compared with solving the full model in an existing mixed integer optimizer. The performance of the full mathematical model presented in section 3. B, is assessed via running the model for problems with different sizes using lp-solve version 5.5.2.0 [9] in a Windows 7 laptop with Intel Core i5-3317U CPU 1.7GHz processor and 8GB RAM.
Table 1 reports the run time (in seconds) of planning problems with different number of delivery requests starting from 5 requests to 25 requests. Since optimal solution couldn’t receive in 24 hours for even 15 requests, the computational performance of the full mathematical model for larger instances are not reported. For the instances, with 5 delivery requests, the full mathematical model results in optimality almost instantaneously. When the delivery request number reached to 25, the full mathematical model cannot provide even a feasible solution in 24 hours and the algorithm is stopped. Since in real life application, we have on the average 125 delivery requests per day, instead of solving the full model with brute force optimization, using the decomposable structure of the problem is essential. In the next section more detailed computational results are reported for real-size problem.
5.2Case studyIn order to evaluate the performance of the proposed methodology we conducted a computational study on an historical data of the company. The DSS described previously was implemented using historical data of one of the largest chemical products company in Turkey. The company offers a wide portfolio input material to different sized companies from various manufacturing sectors. Company also offers consumer products to individual customers via large retailers and its own depots. Their demand level changes quite often during a month where a peak at the end of the months is expected, and accordingly, their planning efforts increase at the end of each month. Company issues most of its delivery requests on Monday to Friday but sent shipments on Saturdays as well. They do not work on Sundays and holidays. In this section, historical demand data for a representative month is analyzed. One representative month with one holiday during weekdays is chosen and the daily shipment requests are retrieved from the database. In total around 3000 tons of orders with 3500 separate delivery request are received by logistics department in a representative month of 24 working days. On the average 125 shipment requests are received per day with daily shipment size of 104 tons. The number of daily delivery request of the company shows drastic changes with minimum 5 orders in total 11 tons and maximum 434 orders in total 212 tons.
For each working day, logistics planning is executed using the proposed solution algorithm. The algorithm reported the shipment plans for small sized days within 10 seconds and for the days where number of delivery request is more than 150; the optimum solution is achieved in 15 minutes. Since the previous ad-hoc planning was taking up about an hour of the planner, the computation time is within reasonable limits.
In order to measure the efficiency of the solution algorithm, the plans suggested by the solution algorithm is desired to be compared to the historical plans executed by the company for the same set of deliveries. Even though the objective of the company as well as our study is to minimize total cost for shipment of daily delivery requests, due to confidentiality clauses, we cannot report the exact savings obtained through the proposed modeling approach. However, to give a flavor of the efficiency of the proposed planning tool, we compare the vehicle utilizations realized in the company and the potential vehicle utilizations that should be obtained if our proposed method would have been used. Figure 2 visualizes the vehicle utilization for each day of the month.
The historical data of the company indicates no significant pattern reflecting the performance of vehicle utilization with respect to neither on the number of delivery requests nor on total amount of delivery in kilograms. On the average vehicle utilization is observed as 68% which is the minimum industry standard. It is also observed that company performed below the industry standard both with intense planning load (e.g. 4th day of week 4 with 136 tons of total product sent) or with light planning load of 5 delivery requests. However, by using the proposed method, on the average 82% of vehicle utilization can be achieved. Higher vehicle utilization is observed when total delivery in kilograms is low. With the proposed algorithm shipments below 67% of vehicle utilization is postponed to the next working day. Thus the higher efficient shipments are achieved. For example, 6th day of week 2, total delivery request is less than 2/3 of a truck capacity, thus instead of delivering with 55% vehicle utilization, our approach suggests to do the delivery next day with additional truckload.
Our proposed approach achieves efficient vehicle utilization as high as 94.5% (for 6th day of week 4) where number of delivery requests which is 21, is lower than average value. As it can be seen in Figure 2, our proposed approach improved the vehicle utilization for all days of the representative month. The cost savings due to better planning is in similar lines as the vehicle utilization.
5.3Impact of contractsAs mentioned before 3PL companies # 2 and 3 use similar pricing structure. In this study these pricing structures are referred as contract type 1. Also company 1’s pricing structure is referred as contract type 2. For each working day, logistics planning is executed using the proposed solution algorithm for three scenarios. First it is planned using current contracting structure i.e. company # 1 on contract type 2, and companies # 2 and 3 on contract type 1, This is used as a benchmark to compare with two hypothetical scenarios where all 3PL companies are identical contract term, either on contract type 1 or type 2. The resulting vehicle utilization for each day of the month under each contracting can be seen in Figure 3.
It is observed that there is no single dominating contract type that has higher average vehicle utilization for the historical data. For the first three Fridays (days 5, 12, and 19) where number of delivery requests and total amount of goods that need to be send is over average, contract type 2 seem to achieve higher average vehicle utilizations with respect to other scenarios, while for the last Friday (day 26) as well as the other most loaded days (days 24 and 30) contract type 1 provides higher average vehicle utilization. On the overall, current contracting scheme with one major company with one type of contacting scheme and other two companies on another contracting scheme seems to be a good policy to benefit from advantages of both cost structures. Also we observed that vehicle utilizations are quite high on this hybrid approach, as on heavy loaded days such as days 16 and 17 as well as quite light workload days such as day 2 and day 27. On day 13 the total amount of delivery request is so low that none of the contracting schemes produced a feasible shipment and the delivery request of day 13 is postponed to the next working day, which is day 15.
6Final remarksIn this work, motivated from a large scale chemical products company, cost efficient daily outbound logistics planning of a firm is modeled as a mixed integer problem. When the delivery of final products to customers are under financial responsibility of the producer, outbound logistics activities can be as high as 15% of total operational expenses and even a slightest improvement on any of these cost components will reflect significant absolute savings. Especially multiple 3PL companies are used with different contracting schemes, allocating the delivery requests to vehicles of different logistics companies becomes no more a trivial task and with ad-hoc methods, efforts for a feasible plan may require long man-hour. The efficiency of the plan with respect to cost performance cannot be guaranteed. Thus, formulating the problem of the company as a mixed integer mathematical model with the objective of minimizing the total delivery cost provides a solution to this planning problem within reasonable time. Such a solution will let to savings in both aspects.
In addition to the mathematical formulation, a two-phase solution approach is proposed to solve the problem in short time. The proposed model and the solution methodology were applied in the daily shipment planning problem in the company. The model is in process of implementation and tested by one of the major chemical factories in Turkey. The preliminary results indicate that the efficiency achieved through the integration of such techniques can become highly attractive for further applications in the industry.
The authors are grateful to the people from the company, who prefer to remain anonymous, for their continuous support for this project.