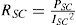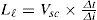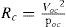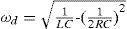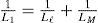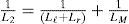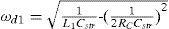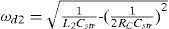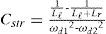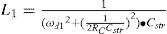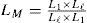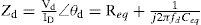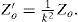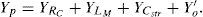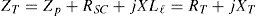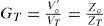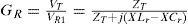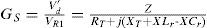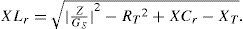Design of Plasma Generator Driven by High-frequency High-voltage Power Supply

Abstract

In this research, a high-frequency high-voltage power supply designed for plasma generator is presented. The power supply mainly consists of a series resonant converter with a high-frequency high-voltage boost transformer. Due to the indispensable high-voltage inheritance in the operation of plasma generator, the analysis of transformer need considering not only winding resistance, leakage inductance, magnetizing inductance, and core-loss resistance, but also parasitic capacitance resulted from the insulation wrappings on the high-voltage side. This research exhibits a simple approach to measuring equivalent circuit parameters of the high-frequency, high-voltage transformer with stray capacitance being introduced into the conventional modeling. The proposed modeling scheme provides not only a precise measurement procedure but also effective design information for series-load resonant converter. The plasma discharging plate is designed as part of the electric circuit in the series load-resonant converter and the circuit model of the plasma discharging plate is also conducted as well. Thus, the overall model of the high-voltage plasma generator is built and the designing procedures for appropriate selections of the corresponding resonant-circuit parameters can be established. Finally, a high-voltage plasma generator with 220V, 60Hz, and 1kW input, along with a 22 kHz and over 8kV output, is realized and implemented.

1

Introduction

High-voltage plasma generating is widely used in industry applications, such as static charge remover, ozone generator for sterilizing, and plastic and metal (ex. Aluminum sheet) surface imprinting processing, and so on. Ozone generator makes use of high-voltage plasma generating to ionize the air and generate Ozone [1]. Static charge remover utilizes high-voltage plasma generating to eliminate static charges in the air. High-voltage plasma generator changes the surface feature under the high-voltage plasma generating process to increase the adhesion of the material surface or the oily ink to fortify the printing quality [2].

In general, a high-voltage plasma generator necessitates a high-voltage electric source and a pair of electrodes. To improve the plasma quality, high-frequency operation is essential for the promotion of plasma stability. A transformer is featured with easy voltage transformation and the resonant converter can definitely lower the switching losses and reduce the EMI (Electromagnetic interference) by using voltage-switching techniques. Thus, it is extremely suitable for the design of high-voltage plasma generator [3-4].

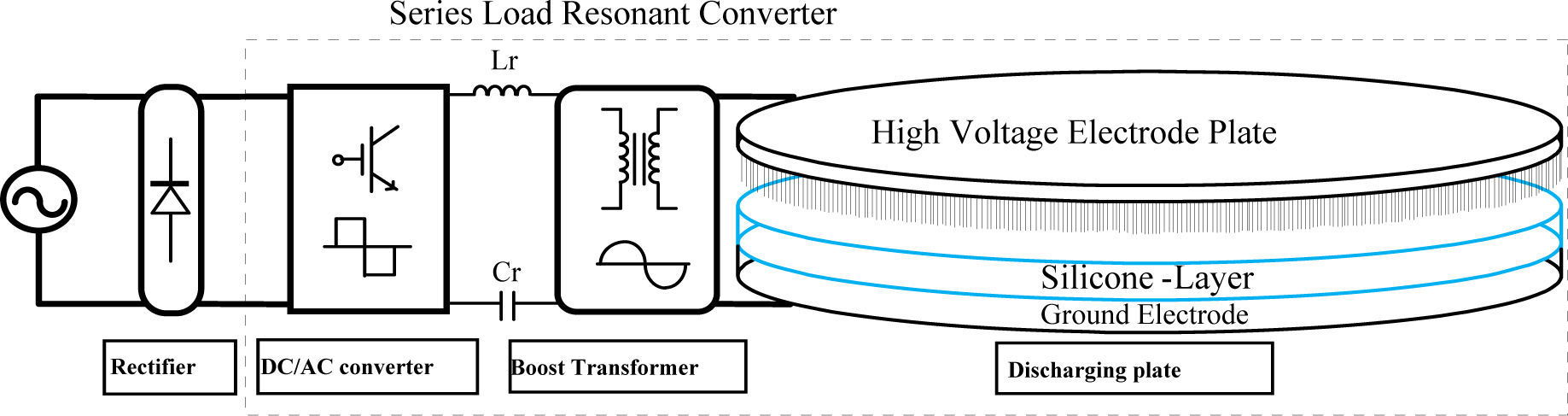
In this study, a series load-resonant converter configuration is selected to design and realize a high-voltage plasma generator. The circuit, comprising a half-bridge inverter switching circuit in series with an inductor, capacitor, and a high-frequency, high-voltage transformer resonant combination, is connected to the discharging electrodes via the high-voltage terminal of the transformer. The transformer and discharging electrodes, therein, are looked upon as parts of the resonant circuit. Consequently, it turns out to be a prerequisite for the designing of a well-performed series load-resonant converter to analyze and model the equivalent circuits of transformer and discharging electrodes in advance. In so doing, the appropriate values of the resonant inductor and capacitor can be determined accordingly [5-8].

Due to the indispensable high-voltage inheritance in the operation of plasma generator, the analysis of transformer need considering not only winding resistance, leakage inductance, magnetizing inductance, and core-loss resistance, but also parasitic capacitance resulted from the insulation wrappings on the high-voltage side [2]. In this study, the voltage is as high as 8 kV and even more with 22 kHz high frequency, thus easily invoking the resonant fluctuation problem. Therefore, the parasitic capacitance must be taken into account during the operation and analysis of the proposed series resonant circuit. [9-11]. In analyzing the high-voltage plasma generator load, the discharger is looked upon as a capacitive load [12-15]. In general, high-voltage discharging equipment is considered as a nonlinear capacitive load and will play as an important role in the resonant stage.

This research employs a series-load resonant converter circuit configuration to produce a high-frequency electric source to accomplish a high-frequency, high-voltage output for a plasma generator via a step-up transformer. The stray capacitance was included in the equivalent circuit of transformer. Besides, the various operating characteristics of the transformer-electrodes combination will be analyzed. The accuracy and validity will be examined by comparing the practical test results with the IsSpice simulating outcomes. Hopefully, a design procedure for series-load resonant converter can be established for future research.

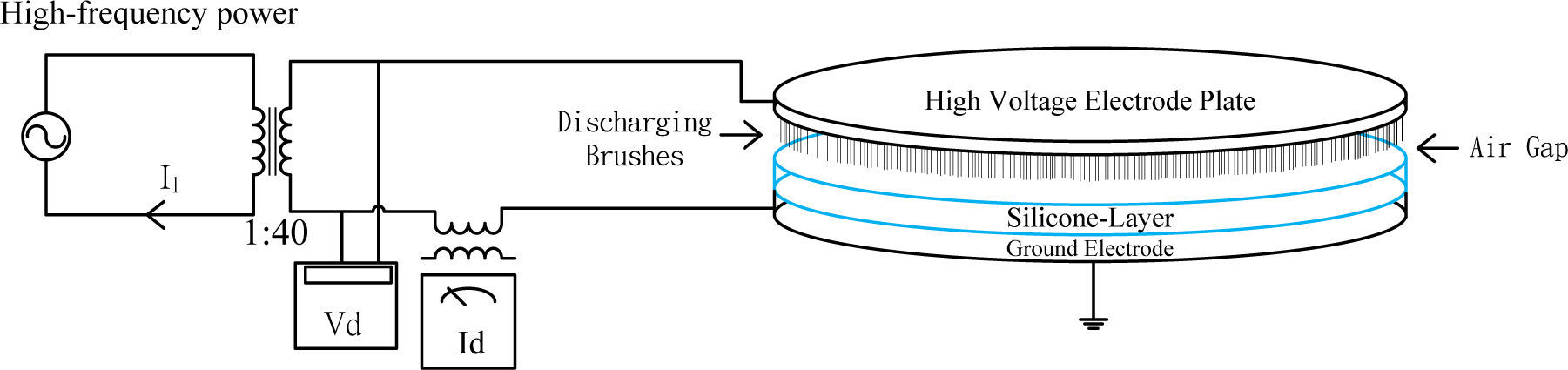
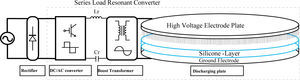
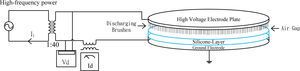
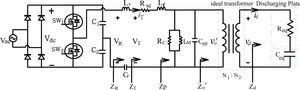
2

Series-Load Resonant Plasma generator

In this paper, the proposed series-load resonant plasma generating configuration is shown in Figure 1. At the first stage, a rectifier is employed to convert 220V, 60Hz AC grid voltage into DC. Next, the half-bridge DC/AC converter with power switches in the resonant circuit being turned ON and OFF in 22 kHz switching frequency and generating a high-frequency square wave is implemented. The appropriately assigned resonant inductor Lr and resonant capacitor Cr constitute the resonant circuit to supply the primary side of transformer with high-frequency sinusoidal voltage. With the step-up transformation, a high-voltage output with peak value as high as 8kV~10kV, and 22 kHz frequency AC sinusoidal voltage is created. If the driving circuit of resonant converter is designed to possess inductive feature. The switching pattern of power switches can be aimed at zero-voltage-switching to reduce the switching losses effectively [16].

Figure 1.

The configuration of series load resonant plasma generator

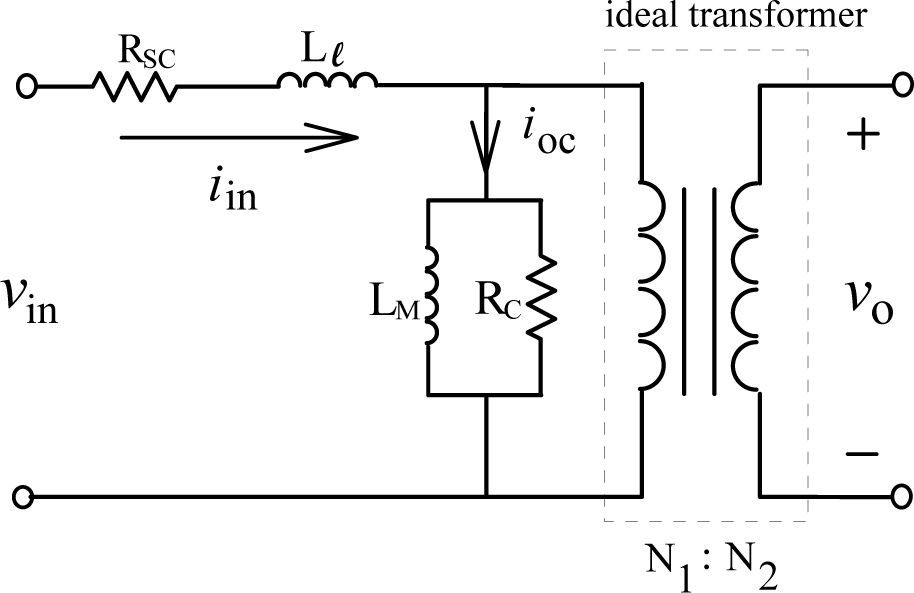
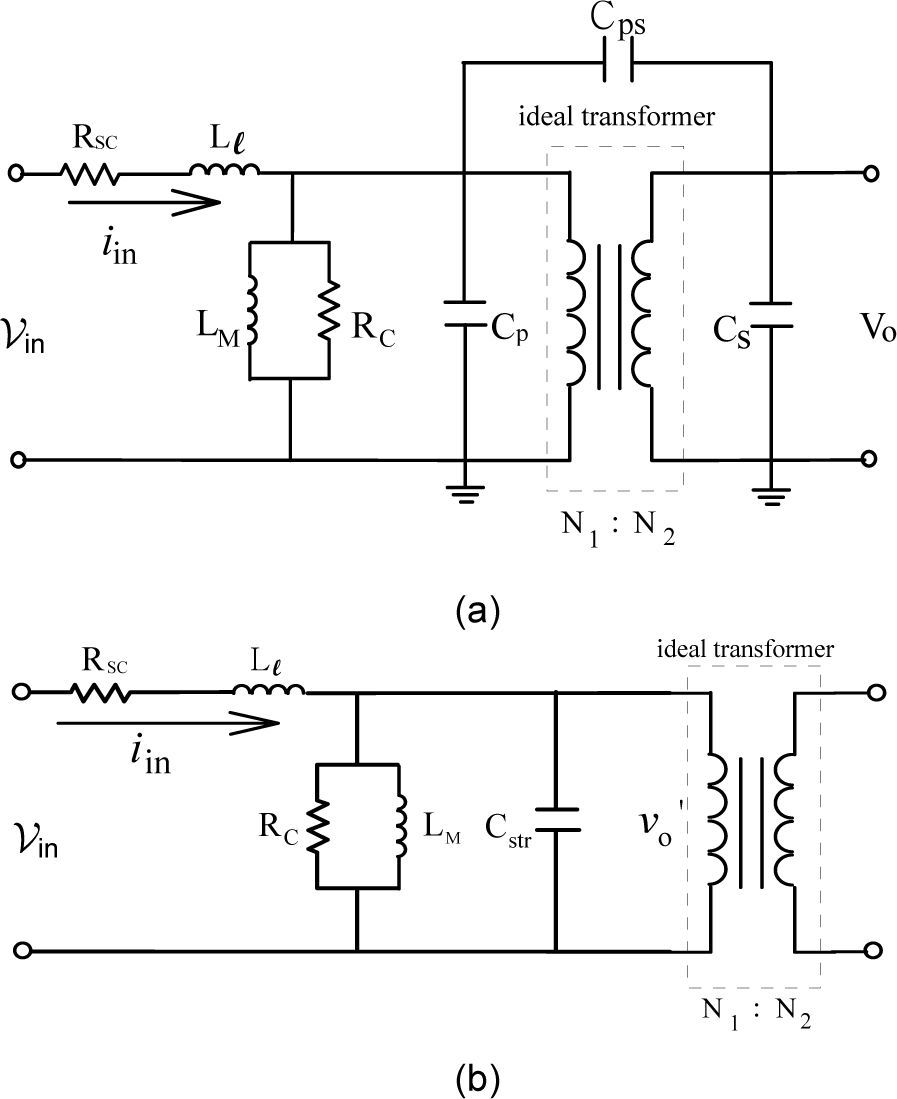
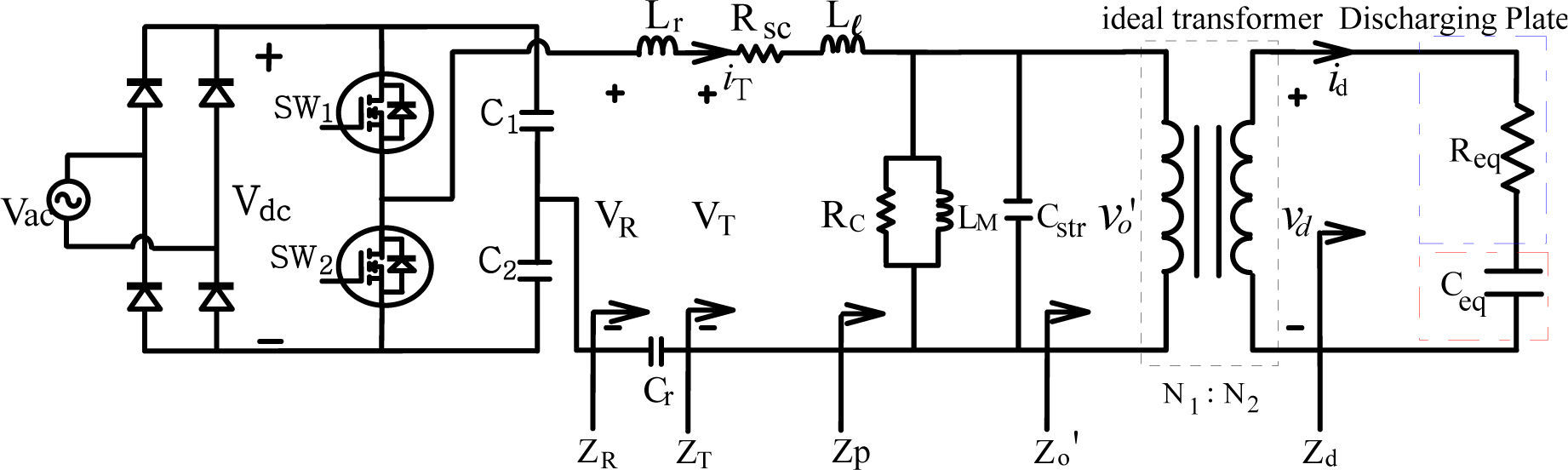
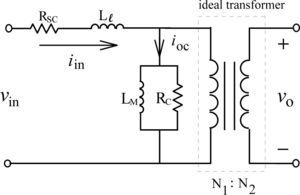
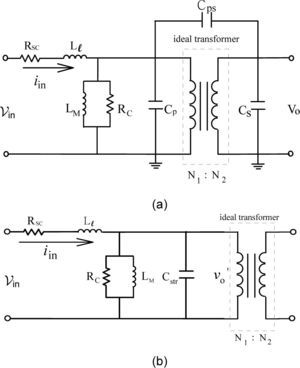
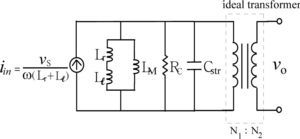
3

The Equivalent Circuit of the High-Frequency, High-Voltage Transformer

Unlike the general-use power transformer, the modeling of high-frequency, high-voltage transformer is a quite different scenario. Due to the insulation design of transformer under high-voltage application, the parasitic capacitance existing between insulating papers can no more be neglected and plays an important role in the design of resonant circuit. Traditionally, the equivalent circuit of general-purpose transformer is illustrated in Fig. 2. Observing from the primary side, the core loss resistance R_c, magnetizing inductance L_M, line copper resistance R_sc, and leakage inductance L_l constitute the whole circuit.

Under the high-frequency, high-voltage operating condition, the proposed modeling method can be described as follows:

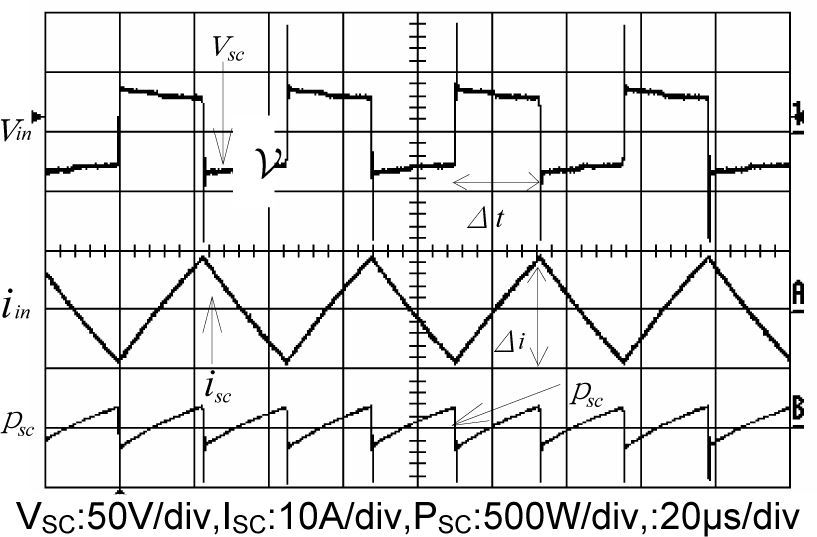
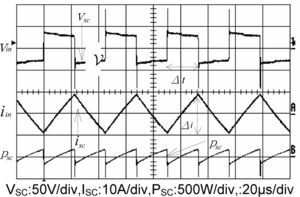
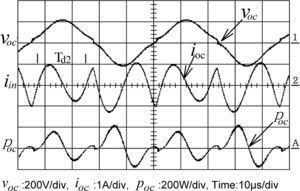
3.1

Short-circuit test

Because of the shortage of high-frequency sinusoidal power supply, in this paper, a high-frequency square-wave generator is built instead and employed to perform the short-circuit test of transformer. With the secondary side being short-circuited, the input voltage Vin is adjusted to achieve rated current for the primary side. When the current I_sc in the primary-side reached rated value 5A, the square wave with peak value about 33.5V is measured. Simultaneously, the input power was read to be 2W. Displayed in Figure 3 are the corresponding waveforms of input voltage, input current, and input power, respectively. By utilizing Eq. 1, the line resistance R_sc can be easily calculated. In this case the R_sc is only 0.08Ω. Due to the line resistance R_sc is very small; the voltage drop can be neglected. The total input voltage can, therefore, be considered applying on the leakage inductance L_l. Based on Eq. 2 and inspecting the waveforms in Figure 3, both the rising time and falling time of current are read to be Δ_t=22.7μs and current deviation is 18.06A with voltage change of 33.5V. The leakage inductance L_l can be computed to be equal to 42.1μH.

Figure 3.

The measured waveforms with transformer being short-circuited.

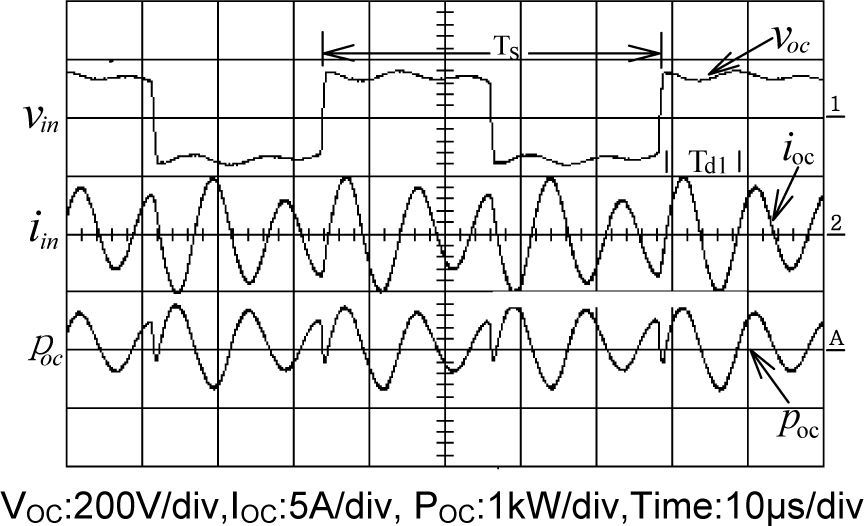
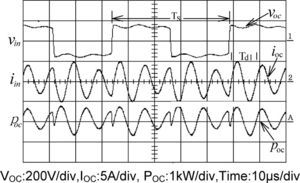
3.2

Open circuit test

With the secondary side being left open, the rated voltage is applied to primary side of transformer as designated as Vin Figure 2. In the meanwhile, the input current and input power can be measured. When the square waveform voltage is applied, the resulting current waveform is measured. Figure 4 demonstrates the waveforms of voltage and current simultaneously. It can be clearly observed that the resonant frequency of current is around 4.5 times that of voltage, and the peak value of current reaches even more than 6 A. This unusual phenomenon implies that there must exist unexpected resonance inside the transformer. The possible reason is that the parasitic capacitance existing between insulating paper layers leads to resonant occurrence because of the mutual energy transfer with the inherited inductance. Therefore, the conventional model of transformer shown in Figure 2 can no longer meet the practical operation of high-frequency, high-voltage transformer.

Figure 2.

The equivalent circuit of general-purpose transformer.

Figure 4.

The measured waveforms with transformer being open-circuited.

Owing to the high voltage and high frequency of the step-up transformer, the parasitic capacitances inevitably exist between the insulating paper layers and affect, to some extent, the performance of corona discharger. In general, the transformer with stray capacitance included can be modeled as the equivalent circuit shown in Figure 5(a). The stray capacitance comprises primary-side stray capacitance C_p, secondary-side stray capacitance C_s, and the stray capacitance C_ps in between layers of primary and secondary windings. The stray capacitances C_s and C_ps can be referred to the primary side and are combined with the primary ones. The equivalent circuit of transformer is illustrated in Figure 5(b) with capacitances being simplified into single one.

Figure 5.

The equivalent circuit of transformer with stray capacitance (a) three stray capacitances (b) with a total equivalent stray capacitance.

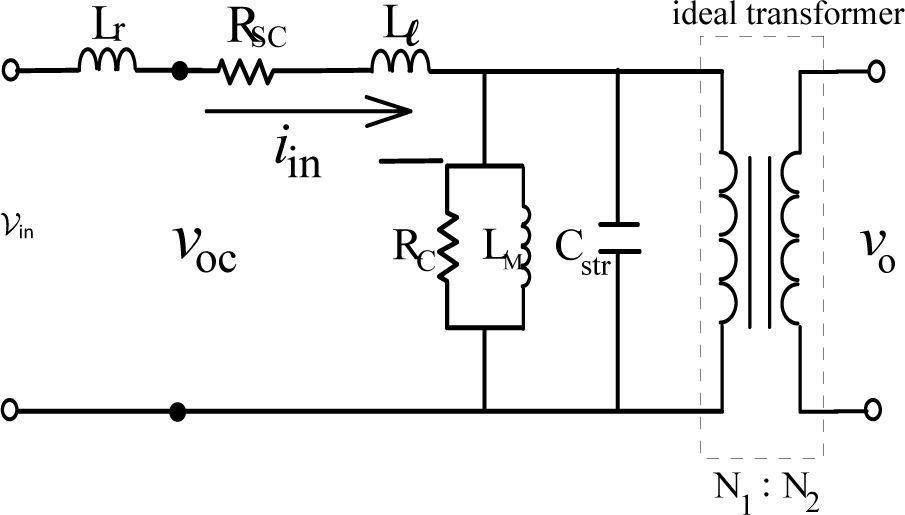
For measuring the total equivalent stray capacitance C_str in Figure 5(b), an expensive and high-grade measuring L_CR instrument is indispensable, and the values of L_M and R_C are unavailable, nonetheless. Alternatively, a measuring method using simple instruments and open-circuit test are proposed to accomplish the measurement of circuit parameters in Figure 5(b). To prevent the possible over-current phenomenon due to the resonance effect, a 200μH inductor will be added to limit the current value. Figure 6 shows the test with a series external inductor L_r. Figure 7 demonstrates the measuring waveforms of open-circuited transformer with external inductor incorporated. The test voltage is 140V and the measured input power is equal to 8W. By using Eq. 3, the core-loss resistance R_c is calculated to be 2450Ω approximately.

Figure 6.

The open-circuited test with a series external inductor Lr.

Figure 7.

The measured waveforms of the open-circuited test with a external inductor L_r=200uH.

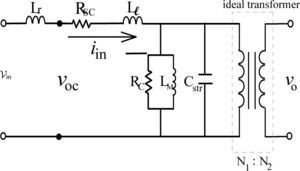
During the open-circuit test period, the primary-side current exhibits obvious oscillating phenomenon. The possible reason is the stray capacitance and transformer leakage inductance constituting a resonant combination. To arrive at the magnetizing inductance LM and stray capacitance C_str in Fig. 5(b), the measured waveforms shown in Fig. 4 and Fig. 7 can be utilized to contrast with the R_LC parallel-resonant equivalent circuit in Fig. 8 to accomplish the calculation and estimation of L_M and C_str.

Figure 8.

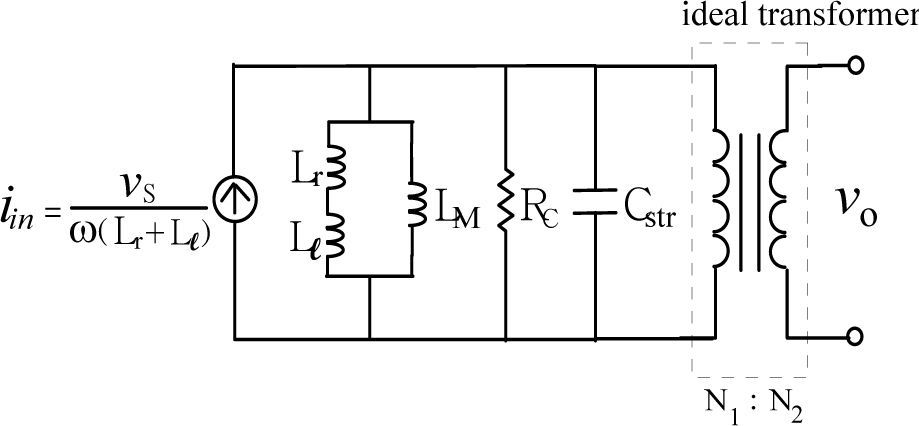
The Norton equivalent circuit of Figure 6 for ignoring Rsc.

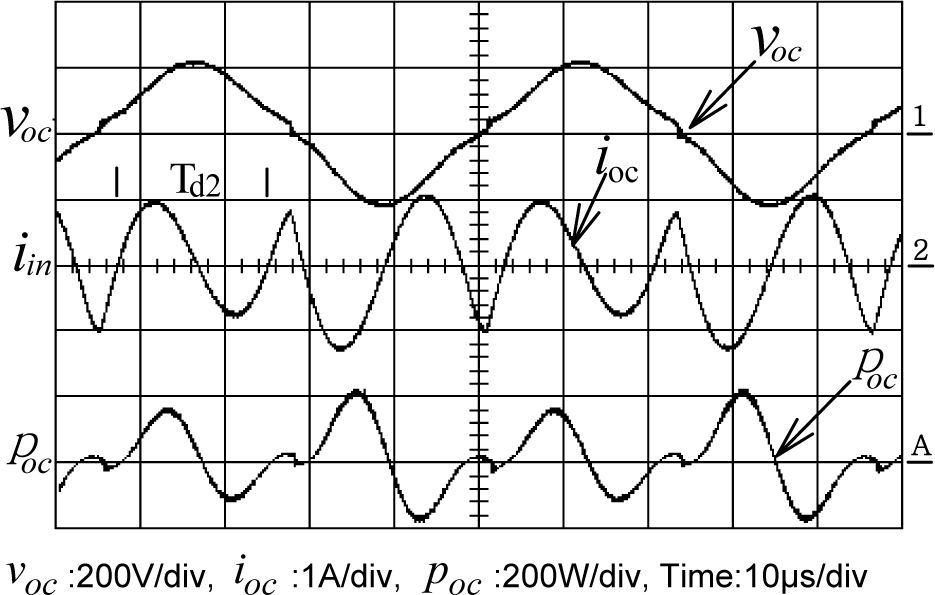
Suppose that the equivalent transformer model in Fig. 5(b) is simplified into the Norton equivalent circuit of R_LC resonant configuration of Fig. 8, the winding resistance Rsc is small enough to be neglected and inductances L_M, L_r and L_l can be merged into a single inductance L₁. The resonant frequency ω_d of the R_LC resonant circuit is expressed as Eq. (4), L₁ and L₂ in Eq. (6) are the total inductance including magnetizing inductance L_M without added inductor and with added inductor, respectively. The corresponding resonant frequencies are conducted to be Eq. (7) and Eq. (8), respectively. With different values of (L_l +L_r), the test results show different waveforms as displayed in Figs. 4 and 7. The natural periods T_d1 and T_d2 in Figs. 4 and 7 are 9.8 μs and 17.8 μs, respectively. The resulting resonant natural frequencies ω_d1 and ω_d2 of current waveforms are 641k (rad/s) and 353k (rad/s), correspondingly. By solving the Eq. (7) and Eq. (8), the stray capacitance C_str can be expressed by Eq. (9) and the equivalent inductance L₁ without current-limiting inductor is conducted as Eq. (10). The magnetizing inductance L_M is, therefore, derived to be as shown in Eq. (11). Based on the abovementioned measurements and calculations, the parameters of high-frequency and high-voltage transformer can be computed and listed in Table 1.

Table 1.

The parameters of the high- frequency high-voltage transformer.

Rsc	Ll	Rc	LM	Cstr
0.08Ω	42.1μH	2.45kΩ	226.8μH	68.5nF

4

Equivalent circuit of plasma generating plate

The plasma generating plates constitute one of the loads of resonant circuit. Consequently, it is very important to take into account the plasma generating effect in designing the resonant circuit and selecting device parameters. In this paper, the study case is based on the plasma generating electrodes used in printing industry. The modeling of equivalent circuit of the plasma generator of the proposed printing machine is essential in this design. The proposed discharging brushes in Figure 9 are clung to the 50cm-radius Aluminum electrode plate. Commonly, plasma generating is looked upon as a high-voltage discharging phenomenon. Under the high-voltage discharging condition, the discharging electrode is considered as a capacitive load [12-13].

Figure 9.

The schematic diagram of plasma generating plate.

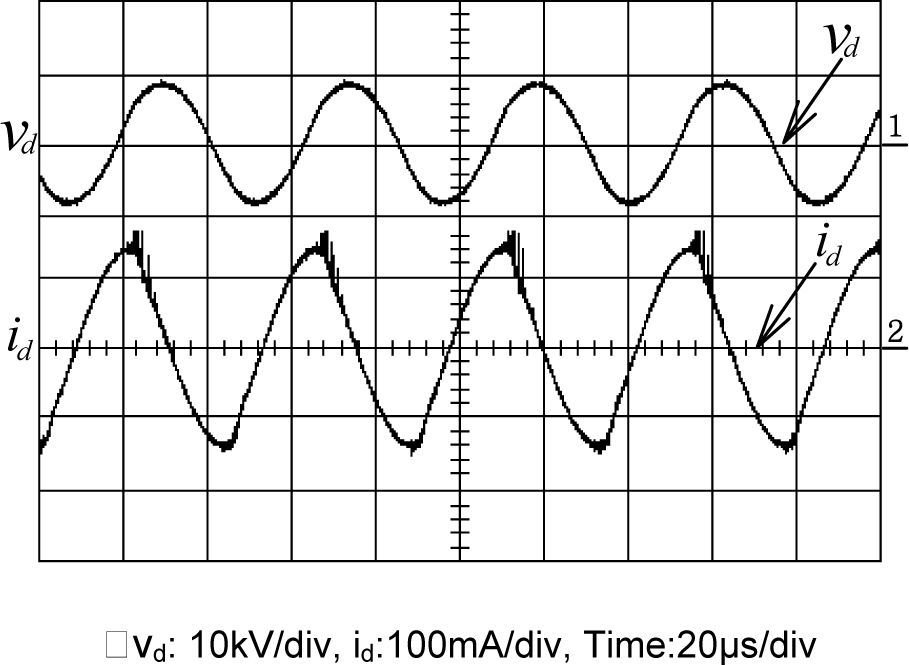
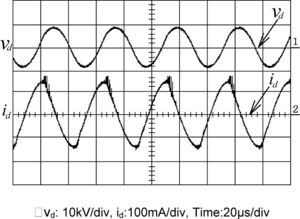
Fig. 10 indicates the equivalent circuit of series-load resonant plasma generator of Fig. 1. The plasma brushes electrode stage illustrates the equivalent circuit of the plasma generating plate, where C_eq and R_eq are in series and regarded as a capacitive load existing in the gap between electrodes. As the discharging gap between brushes and electrode is adjusted to around 3mm, the discharging generator operates very near to the rated condition. Fig. 11 illustrates the measured results under rated condition with rated voltage being applied to the brushes discharging electrodes. It is obvious that the load voltage and load current waveforms display the phase difference θ_d is about 75°, while effective voltage V_d is 5.51kV and the effective current I_d is 105.5mA. The equivalent impedance Z_d of plasma discharger can be expressed in Eq. (12). Next, Table 2 illustrates the associated rating parameters of discharging Plate in Fig. 10.

Figure 11.

The voltage waveform v_d and current waveform i_d with 3mm discharging gap under rating operation.

Table 2.

The parameters of the Discharging plate plasma.

Zd	θd	Req	Ceq
52.2(kΩ)	75o	13.5(kΩ)	143.4(pF)

5

The procedures in designing the resonant circuit

In designing the series-load resonant converter, the determination of parameters of resonant capacitor and inductor plays the crucial role. The equivalent circuit for the series-load resonant converter under rated load has been established in Table 2. Nonetheless, an indeed criterion still needed to find out appropriate values of resonant inductor and capacitor to satisfy the expected performance.

The equivalent circuit of the series-load resonant converter is indicated by Figure 10. Wherein, Z_o′ is the referred value of Z_o in Figure 10 after turn-ratio-square transformation and can be represented by Eq. 13. The total admittance Y_p is expressed as Eq. 14 and the Z_T in Figure 10 is identical with the sum of Z_p (the reciprocal of Y_p), winding resistance R_SC, and leakage reactance X_Ll, as is expressed by Eq. 15. The voltage gain G_T of electrode voltage v_o’ with respect to transformer input voltage V_T is written in Eq. 16. Through the resonant impedance, the output voltage of DC/AC converter V_R is fed to the step-up transformer by powering the transformer with input voltage V_T. The voltage gain G_R can be expressed by Eq. 17. Therefore, the system gain G_s of electrode load voltage with respect to converter output fundamental voltage V_R1 can be expressed in Eq. 18.

Figure 10.

The equivalent circuit of plasma generator.

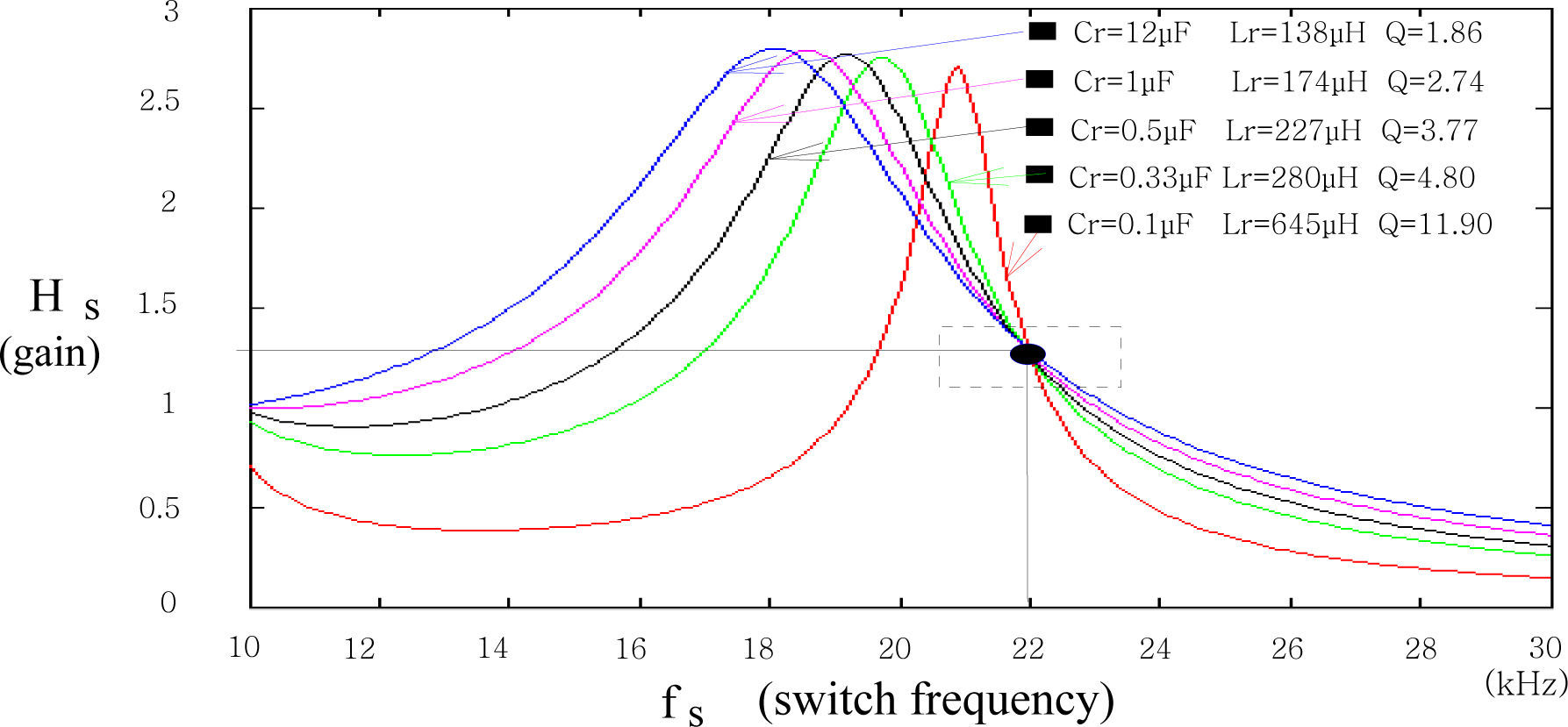
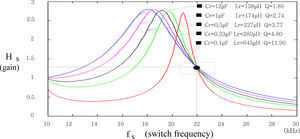
The capacitors available in the market possess only some specified values and cannot cover any required ones. Therefore, in the stage of analyzing and designing a resonant circuit, the capacitor parameter is normally specified at first and the inductor is tuned to observe the influence and response in the experiment. Eq. 19 exhibits the relationship between resonant inductive reactance and capacitive reactance for a specific gain |G_s|. Figure 12 illustrates the alteration profile of five chosen capacitive reactances and their corresponding inductive reactances when operating frequency is 22kHz and system gain is |G_s|=1.3.

Figure 12.

The frequency responses for the particular capacitance Cr and the relative Inductance Lr with |Gs|=1.3 at operation frequency =22kHz.

The designing procedure of the proposed power converter circuit can be demonstrated as shown in the following procedures. Firstly, the required specification, including operating frequency, voltage gain and the like, must be itemized. Next, by employing open-circuit test, the equivalent circuit of the high-frequency step-up transformer is constructed with parameters such as core-loss resistance, magnetizing inductance, winding resistance, leakage reactance, and stray capacitance being included. Accordingly, the complete circuit model of the whole system is established. The frequency response of the voltage gain is, in turn, calculated. By envisaging the relationship between voltage gain and different combinations of resonant devices, the most suitable arrangement of resonant capacitors and inductors that meet the required Q can be determined. In general, it meets the requirement when Q falls between 2.5 and 5. In Figure 12, it can be seen that there are 3 combinations of capacitor and inductor which are qualified. At last, the entire circuit with given resonant device parameters is simulated with software and the results are used to modify and validate the circuit design. The practical experiment is, in turn, utilized to contrast and verify the whole design. After all, this design process can provide a procedure for engineers and researchers in designing high-frequency, high-voltage resonant converters.

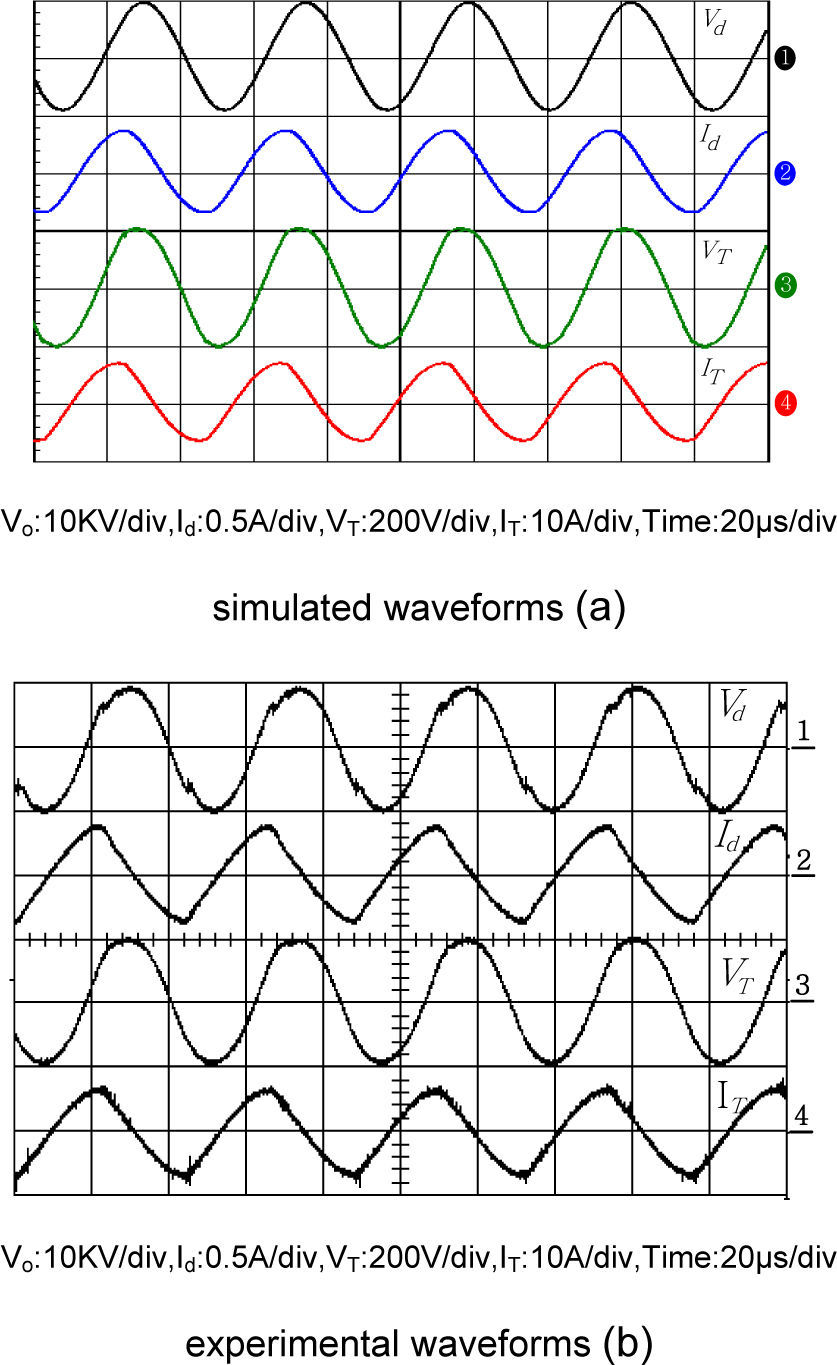
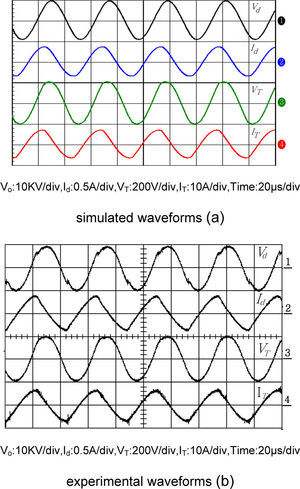
In this paper, the proposed case and referred device parameters being entirely based on a plasma-generator-using print factory and the half-bridge resonant converter has been working until now. Figure 13(a) and Figure 13(b) display the simulation and experiment results of transformer secondary voltage V_d, secondary current I_d, primary voltage V_T and primary current I_T waveforms, respectively. In contrast, the corresponding waveforms are shown in Figure 13(b), as is based on the practical field measurements of the series-load resonant converter. It is obviously inspected that the simulated and measured results are in good agreement each other.

Figure 13.

The practical waveforms of the series-load resonant converter with C_r=0.5uF and L_r=227Uh.

6

Conclusions

In this research, a plasma generator composed of high-frequency, high-voltage transformer, discharging electrodes, and zero-voltage-switching resonant converter is proposed with their associated equivalent circuit being constructed, respectively. Moreover, the entire equivalent circuit of the plasma generator is established by integrating the individual stages. Accordingly, a serial-load resonant converter plasma generator is realized and a valuable and accessible design procedure is set up and presented. The proposed modeling scheme provides effective design information for series-load resonant converter. The feasible derivation can further provide the fast calculation of voltage gain and determine the proper parameters of resonant inductor and capacitor. Based on IsSpice, the simulated results confirm the validity and effectiveness of the proposed approach. The practical measurements also support the availability of this research.