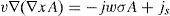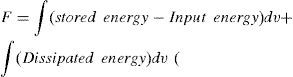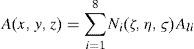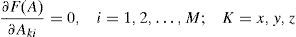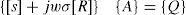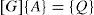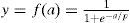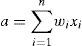Dimension Estimation of Rectangular Cracks Using Impedance Changes of the Eddy Current Probe with a Neural Network

Abstract

In this paper a method for estimating the dimension of rectangular cracks is proposed. The use of Eddy current (EC) nondestructive testing (NDT) based on probe impedance changes on the crack regions is considered. The artificial neural network estimates the dimension of new cracks using impedance changes of the eddy current probe. The experimental results and finite element method (FEM) results are used for training the artificial neural network. By increasing the number of experiments, the results of the finite element method are not necessary. The simulation results are very promising.

1

Introduction

The non-destructive testing technique has been used for a long time to secure the structural integrity of complex mechanical systems such as nuclear power plants. Until about ten years ago, it was mainly based on an empirical approach, this is, supported by human experience combined with simplified knowledge of physical principles behind observed phenomena [1]. Its general goal can be described as finding a defect in a specimen under test without destroying it in order to decide its acceptance or the necessity/possibility of repair. The physical phenomena used for this purpose are different: ultrasounds, the rmography, radiography, etc. [2]. The electromagnetic techniques (E-NDT) are less widespread in industry, but they are drawing growing attention from the international scientific community. Such techniques are particularly effective in several applications, including inspection of tubes for fluid transport or of parts of airplanes. In these cases, it is possible to exploit all the benefits of these methodologies such as velocity, cheapness, possible absence of contact with the inspected body and the possibility of investigating inaccessible defects [2].

In the eddy-current method of non-destructive testing, current-carrying excitation loops of various shapes are commonly used for the induction of eddy currents in a conducting specimen [3]. The existence of flaws or the variations in physical properties of the specimen will perturb the eddy-current flow, and the resultant electromagnetic variations are monitored and analyzed using appropriate sensors [3].

The theoretical prediction of eddy-current probe output signals for various non-destructive testing applications usually involves the solution of the electromagnetic field problem due to a current-carrying loop in the vicinity of a flawless conductor. A general solution for this problem can be sought in the use of various numerical techniques, including the finite element method [4], the boundary element method [5] and the volume integral method [6].

2

Non-destructing testing with eddy current

In this section the experimental results and the finite element method are used for training the artificial neural network.

For training the network, we need data sets with specific targets. Some of these data were obtained from experiments; others were obtained from Maxwell’s equations by the finite element method.

Numerical methods can be viewed as a generic approach for the approximation of the solution over a solution domain by creating an analogy between a system consisting of discrete elements and the original continuous system. The finite element method is used to solve the problem by considering it in the real discrete system. Thus, to establish the global behavior of the problem, the local element description must be integrated over the entire domain to take account of the boundary and interface conditions. The general characterization of the finite element method is that the solution minimizes a global scalar function known as the energy function F. The used formulation of the field equation for the eddy current problem is written in terms of the magnetic vector potential A. From Maxwell’s equations the governing differential equation of the eddy current can be written as follows [8]:

Where v is the reactivity, and J, is the source current density. Function F represents the volume integration of three energies given as:

Where stored energy due to magnetic field, input energy is derived from the impressed current densities and the dissipated energy arises from the eddy current densities in the conducting parts. Hence, the energy function equation can be written

The nodal FE equation (3) is obtained by writing field A inside each element in terms of the nodal values of the field, such that

Where Ni is a shape function equals to one at node i and to zero at all other nodes. The summation is performed on eight nodes where hexahedral elements are used. The two-point Gauss quadrature volume integration method in each direction of the element is used when combining the variational method with the finite element method to obtain a FE solution to the problem. The energy functional minimization is achieved by applying the following equation at each node:

Where M is the total number of nodes in the solution region. A complex elemental matrix in the form:

is then obtained. Where [S] is the real part, [r] is the imaginary part, {A} is the unknown vector, and {Q} is the source vector. Then, the glob-system in 3 x M unknown components of A is obtained by summing the elemental matrices over the total number of elements, which has the form:

Lu-decomposition and back-substitution are used to solve Equation 7. Having done that, the coil impedance and the magnetic flux density are then calculated.

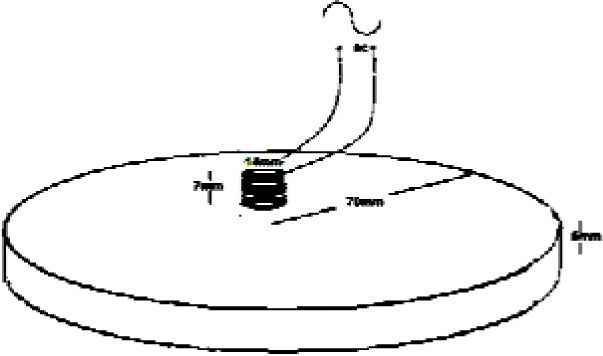
In this paper, the considered specimen is a cylindrical conductive plate with these dimensions: radius=70 mm, height=5 mm. The physical characteristics of the plate are relative magnetic permeability (μ_r =500), electric conductivity (σ=l.0×10⁷ S/m).

The coil specification is as follows: the interior radius of the coil is 6 mm, the exterior radius is 7 mm, and the coil height is 7mm. (Figure 1). The exciting coil has 700 turns, with a current density of 1×10⁸ A/m2 and the relative permeability of an amorphous core which is used in coils is 2000. The exciting frequency is 10Hz.

Figure 1.

Schematic of the Plate Used.

In this study, a rectangular crack backside of the plate was created in each simulation and experiment. For each data the dimension of the crack was changed in each specimen; as the minimum dimension of cracks is (1 mm, 0.05 mm, 0.5 mm), and the maximum of that is (20 mm, 0.5 mm, 3 mm). 63 specimens were examined.

The creation of the data sets required the determination of the impedance changes of the coil. This parameter was evaluated by subtracting the impedance obtained for the plate without crack from the impedances obtained for the plate with the crack. For each crack the coil moves parallel to the x-axis at 1 mm of distance from the surface of the plate, placed along the crack length direction and scanned the crack in 45 different points. (For each data we carried out simulations 45 times: starting from x = -12 mm till x = 32 mm at every 1 mm along the crack direction).

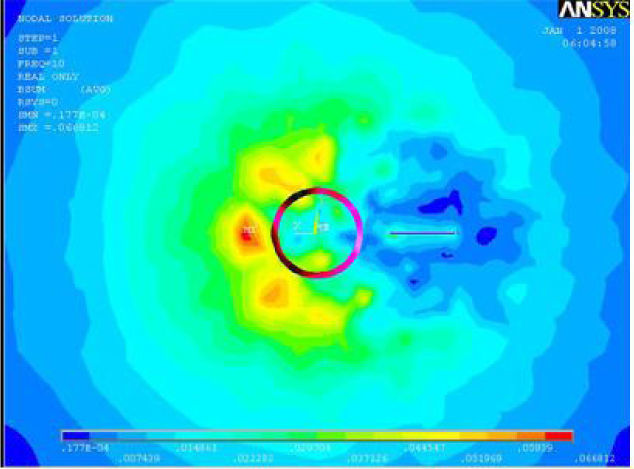
In each stage the voltage and current of the coil resulted from the simulations and experiments, and the impedance and impedance changes of the coil were finally calculated from them. In this study, the imaginary part of impedance changes was used for training the artificial neural network. Figure 2 demonstrates the flux density of the coil in the plate. It can be seen that the magnetic flux density reduced in the environs of crack.

Figure 2.

Flux Density in Plate and Around the Crack in a Specific Crack.

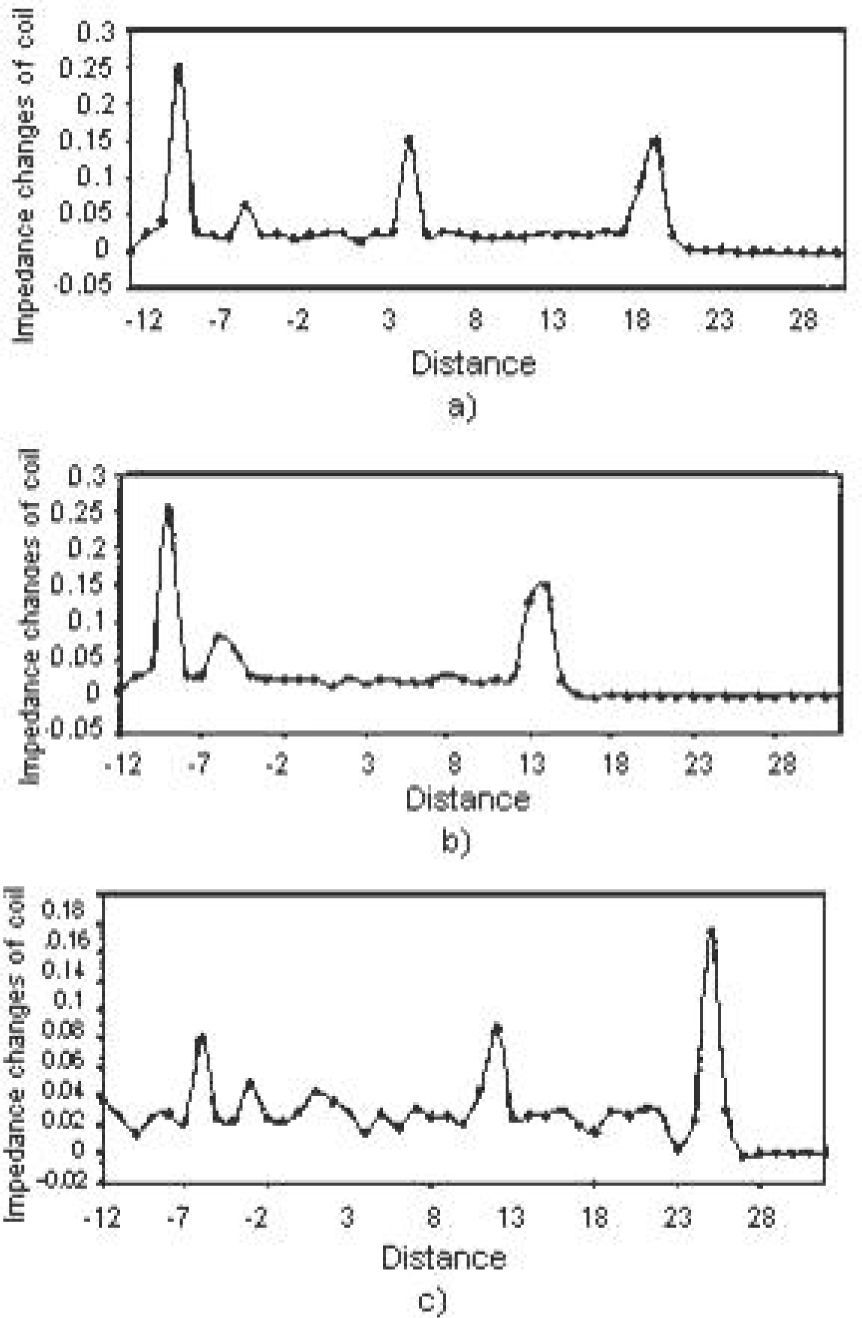
As you see, Figure 3 demonstrates some of the imaginary parts of the impedance changes used for training the artificial neural network.

Figure 3.

Some of the Imaginary Parts of Coil Impedance Changes Resulted From a) Crack With (10, 0.4, 1) mm dimension, b) Crack With (4, 0.5, 1) mm Dimension, c) Crack With (13, 0.4, 3) mm Dimension.

3

A review on artificial neural networks

A neural network is an information processing system composed of an interconnected assembly of simple processing units called neurons [7]. Each neuron has a non-linear transfer function (activation function) and is connected to other neurons via weighted interconnections. Figure 4 is a block diagram of a simple neuron showing the input signals {x₁, x₂,…x_n}, the weighted interconnects {w₁, w₂,…w_n}, and the non-linear activation function.

Figure 4.

Block Diagram of a Simple Neuron.

A common activation function is the sigmoid:

where a is the sum of the weighted interconnections to a particular neuron and is given by

The interconnection weights are determined by training the neural network. A neural network is trained by using a known set of input and output patterns. A known input pattern is applied to the neural network and then the interconnection weights are adjusted until the output of the neural network matches the desired output to within a certain tolerance.

Once trained, neural networks have several properties that make them attractive for use in cracks dimension estimation problems. These properties include:

• 1.

  The ability to generalize from the training set.

• 2.

  The output signal is insensitive to noise appearing at its inputs.

• 3.

  Trained neural networks have fast execution times.

4

Simulation Results

Here the imaginary part of the impedance changes was used for training an artificial neural network; the output of network was a vector with three elements: (length, wide, deep).

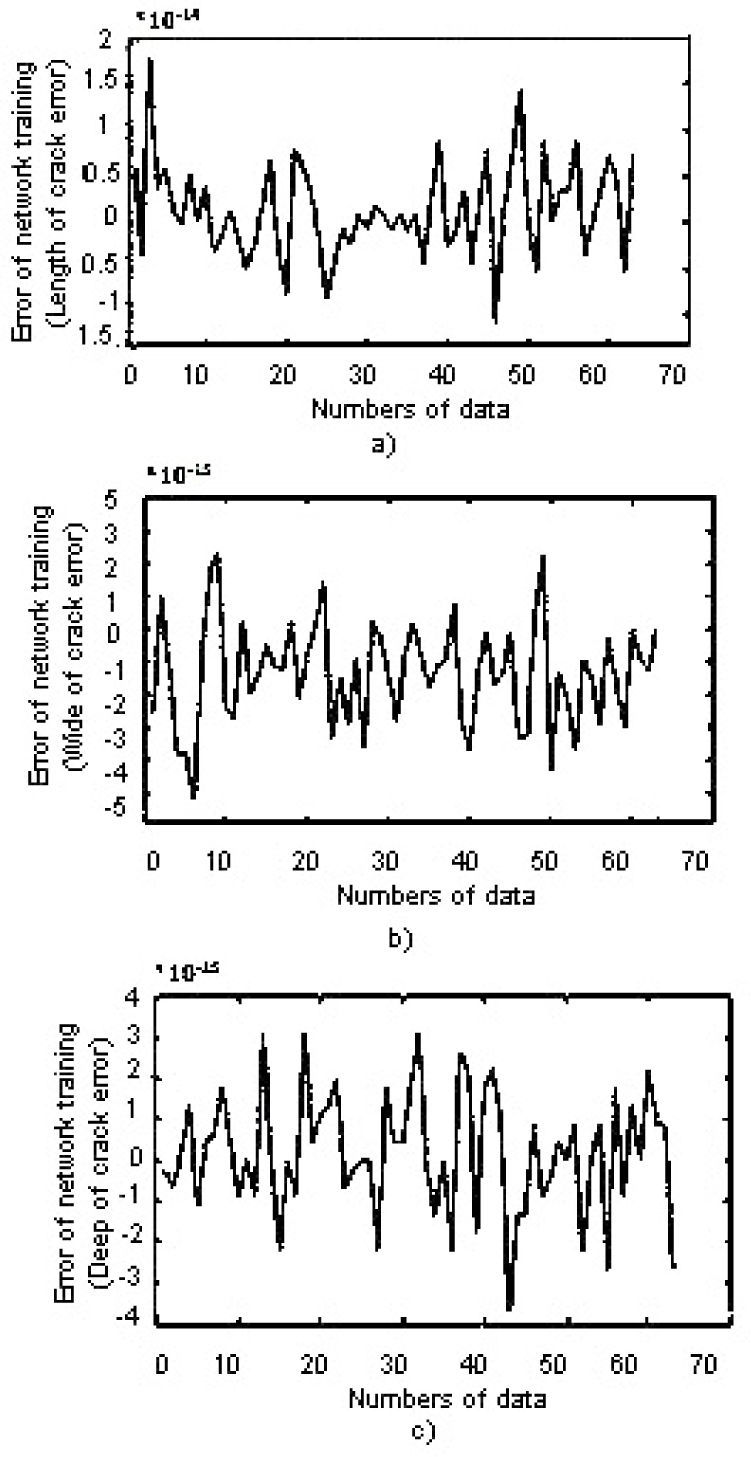
The network used in this research was feed forward 3-5-4 neural network that the LevenburgMarquardt method used for training (Figure 5). By training this network, the error of the neural network was obtained about (10^-15). The curve of the neural network error can be seen in Figure 6.

Figure 5.

Neural Network Used for Detection.

Figure 6.

Error of Network: a) Error of Crack Length Vector, b) Error of Crack Wide Vector, c) Error of Crack Deep Vector.

Some data unavailable in training data sets were used for simulating and testing the network. For example, Figure 7 shows some of these specimens that were used for testing the neural network. The target data and outputs of network are shown in Table 1. After comparing the outputs of network with the targets, the results of the neural network are very promising.

Figure 7.

Two Test Data: a) Crack With (1, 0.1, 2) mm Dimension, b) Crack With (8, 0.4, 1) mm Dimension.

Table 1.

Result of Network for Two Between Data.

Input data	Fig7. a	Fig7. b
Output of network	(1.01, 0.119, 2.01)	(8.1, 0.39, 0.97)
Target data	(1, 0.1, 2)	(8, 0.4, 1)