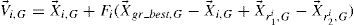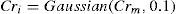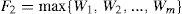Differential evolution (DE) is a simple, powerful optimization algorithm, which has been widely used in many areas. However, the choices of the best mutation and search strategies are difficult for the specific issues. To alleviate these drawbacks and enhance the performance of DE, in this paper, the hybrid framework based on the adaptive mutation and Wrapper Local Search (WLS) schemes, is proposed to improve searching ability to efficiently guide the evolution of the population toward the global optimum. Furthermore, the effective particle encoding representation named Particle Segment Operation-Machine Assignment (PSOMA) that we previously published is applied to always produce feasible candidate solutions for solving the Flexible Job-shop Scheduling Problem (FJSP). Experiments were conducted on comprehensive set of complex benchmarks including the unimodal, multimodal and hybrid composition function, to validate performance of the proposed method and to compare with other state-of-the art DE variants such as jDE, JADE, MDE_pBX etc. Meanwhile, the hybrid DE model incorporating PSOMA is used to solve different representative instances based on practical data for multi-objective FJSP verifications. Simulation results indicate that the proposed method performs better for the majority of the single-objective scalable benchmark functions in terms of the solution accuracy and convergence rate. In addition, the wide range of Pareto-optimal solutions and more Gantt chart decision-makings can be provided for the multi-objective FJSP combinatorial optimizations.
Optimization algorithms have become a useful technique in all-major disciplines and engineering applications [1–2]. Many practical engineering design or decision making problems involve single-objective or multi-objective optimization. In single-objective optimization, the goal is to find the best design solution as to the minimum or maximum value of the objective function. On the contrary, the multi-objective optimization gives rise to Pareto-optimal solutions [3] because of the interaction among different conflicting objectives. Differential Evolution (DE) algorithm is a population-based and stochastic optimizer first developed by Storn and Price [4]. With the advantages of simplicity, less parameter and robustness, the DE algorithm has been given increasing attention and widely used in many fields, such as data mining [5], structural optimization [6], biogeography [7], and so on [8–9]. DE is considered the most recent studies for solving constrained optimization problems, multi-objective global optimizations, and other complex real-world applications. More details on the state-of-the-art investigation within DE can be found in two surveys [10–11] and the references therein.
For the classical DE, the setting of three control parameters: population size Np, the crossover rate Cr and the scale factor F, is very sensitive to the parameter setting and the choice of the best parameters is always problem-dependent [12]. In addition, for a given specific problem, it may be better to adopt different parameter settings during different generation stages of the evolution than use a single mutation strategy with fixed parameter settings [11]. In 2006, Brest et al. [12] presented a self-adaptive method for DE fixes the population size during the evolution process while adapting the control parameters Fi and CRi associated with each individual. The jDE reproduces new Fi and CRi values according to uniform distributions on [0.1, 1] and [0, 1], respectively. And experimental results demonstrated that jDE performs remarkably better than the classic DE/rand/1/bin. Later, Zhang et al. presented “DE/current-to-pbest” with optional archive and controls F and CR in an adaptive manner named JADE [13], to track the historical record of success status for mutation factors and crossover probabilities with adaptive parameters in generations, and the external archive to store recently inferior solutions and their difference from current population provides promising directions toward the optimum. In 2012, Islam et al. proposed the MDE_pBX [14], which adds a variation to the classical “DE/current-to-best/1” mutation scheme by perturbing the current target vector with the best solution in a group of randomly selected individuals. The crossover operation is performed between the current donor vector and any other individual from p top-ranked individuals in the present generation. Simulation results demonstrate that MDE_pBX enhances the ability of the basic DE for finding solutions in search space and helps alleviating the tendency of premature convergence or stagnation.
In the recent studies [12–15], various mutation and controll parameters setting strategies have been presented for DE algorithm. Although a number of works can advance the search ability of DE, there is still much room for improving the performance of DE. Motivated by these results, the modified mutation scheme based on MDE_pBX, in which the mutation operator can be adjusted dynamically on the solution searching status, is presented to bring several individuals appropriately to find new possible solutions. Meanwhile, a wrapper local search (WLS) strategy via trying to increase or decrease current moving vector by the Cauchy distribution is proposed to improve the local search ability and to balance exploration and exploitation in the search space. Moreover, the proposed hybrid DE framework incorporated with PSOMA method that we previously published to produce feasible solutions for the multi-objective Flexible Job-shop Scheduling Problem (FJSP), is designed for finding optimal solutions of multi-objective FJSP.
Competitive experimental results are observed with respect to 15 CEC 2005 benchmark functions for single-objective optimizations, and the three benchmark instances based on practical data were employed as multi-objective FJSP verifications.
The remainder of this paper is organized as follows.
Section 2 describes the typical MDE _pBX, FJSP and external repository. The PSOMA scheme, adaptive mutation method, WLS and the hybrid DE model are presented in Section 3. Experiment and comparison results are provided in Section 4. Conclusions remarks are made in Section 5.
2Related Works2.1Classical Differential Evolution AlgorithmDE algorithm is one of the population-based global optimization algorithms, has two stages including initialization and evolution. After randomly initializs, evolution process evolves from one generation to the next through mutation, crossover and selection operations until the termination criteria are reached. The core of DE algorithm is the mutation operation, which uses a weighted, random vector in each step, to replace the target vector with the better trial vector in the next generation. The main steps of the classical DE are summarized as follows.
2.1.1InitializationThe DE begins by creating an initial population of target vectors consisting of parameter vectors are denoted X→i,G=[xi,G1,xi,G2,⃛,xi,GD]T, i=(1,2,⃛,Np), where i is the index for individuals, G indicates the current generation, Np is the population size, D is the dimension of the parameters, and xi,Gj denotes the j-th component of the i-th individual at the G-th generation. The initial individuals are randomly determined within a predefined search space considering the lower and upper bounds of each parameter as follows.
where xminj and xmaxj denote the lower and upper bounds, respectively, and rand(•) is a uniformly distributed random number between 0 and 1.
2.1.2MutationFor the “DE/rand/1/bin” classical mutation strategy, three different vectors consisting of a base vector (X→r1i,G) and two difference vectors (X→r2i,G and X→r3i,G) are randomly chosen from the populations. The scale factor F is a constant and the effective range is usually taken from the range between 0.5 and 1 as pointed out in [4]. Mutation operation is then carried out by perturbing the base vector via a difference vector scaled by a scalar factor Fi. The donor vector V→i,G=[vi,G1,vi,G2,...vi.GD]T,i=(1,2,...,NP) is expressed as Eq. 2.
where r1, r2, r3 are random and mutually different integers, and they are also different with the vector index i.
2.1.3CrossoverTo increase the diversity of the solutions, the trial vector U→i,G=[ui,G1,ui,G2,⃛ui,GD]T,i=(1,2,⃛,Np) is created by means of crossover operation and is realized between each pair of target vector X→i,G and its corresponding donor vector V→i,G. In a trial vector, elements are inherited from a donor vector and a target vector. The scheme can be simply formulated for the binomial uniform crossover that is widely used in the literature as shown below.
where ui,Gj,vi,Gj and xi,Gj are trial, donor and target vectors from the i-th vector, j-th dimension at G-th generation. Cr is a user-defined probability in the range [0, 1]. jrand is a randomly chosen integer in the range [1, D], which ensures that the trial vector does not duplicate the target vector.
2.1.4SelectionThe selection operation is achieved from the target and trial vectors by comparing their fitness values through the objective function f(•) to select the better individual. In case of minimization problems, the trial vector and the target vector competes in their fitness and the winner has the chance to survive to the next generation.
In the current population, target vector is updated when the newly generated trial vector gets better fitness value than its target vector; otherwise, the target vector is retained in the population.
DE algorithm works through a simple cycle of the stages, and the pseudo-code of the classical DE is given below as Algorithm 1.
2.2Typical MDE_pBX ApproachIslam et al. developed an adaptive DE algorithm based on novel mutation and crossover strategies called MDE_pBX [14] for global optimizations. They presented a p-best crossover operation to improve the accuracy in search space by a large extent. Moreover, the Cauchy distribution and Gaussian distribution are also incorporated into the generation for scale factor F and crossover rate Cr. The new mutation operator named “DE/current-to-gr best/1” scheme is as follows.
X→gr_best,G is the best solution from 15% of individuals selected randomly in current generation. Then, normal binomial crossover is performed between the donor vector and the randomly selected p-best vector to generate the trial vector at the same index. Parameter p is linearly reduced by generations in the following formula.
G is the current generation number, Gmax is the maximum number of generation set up, and ceil(y) is the “ceiling” function returning the lowest integer greater than its argument y. Finally, the parameter adaptation schemes in MDE_pBX is independently generated as follows.
Eq. 7 is a random number sampled from a Cauchy distribution with location parameter Fm formulated as Eq. 8, and the scale parameter is 0.1. Location parameter Fm of Cauchy distribution is initialized to be 0.5 and updated at the end of each generation.
A weight factor wF is a positive constant number between 0.8 to 1. The meanPOW(•)represents a power mean given by Eq. 10. The adaptation of crossover probability Cri is similar with the scale factor Fi, and the detailed description as follows.
where wCr is set between 0.9 to 1, Crm is initialized to be 0.6, and the Gaussian distribution as shown in Eq. 11 substitutes for the Cauchy one in Eq. 7.
2.3FJSP Problem DefinitionFJSP [16] is a generalization of the classical JSP, in which operations are allowed to be processed by any machine from agiven set of available machines. It is quite difficult to achieve an optimal solution due to the high computational complexity and well-known a NP-hard problem. Xia et al. [17] proposed a method which hybridized PSO and simulated annealing (SA). It involved a variable inertia weight w and adopted a weighted concept to transform triple objectives into single objective problems. Ho et al. [18] later proposed a method to estimate bounds of different types of schematic may exist corresponding to the Pareto-optimal fitness value, but Ho’s method did not deal with the diversity under the same Pareto-optimal solutions.
The three minimization objectives addressed in [19] including the total workload of all machines, the workload of critical machine and the completion time of critical job are considered simultaneously. The problem is to organize the execution of n jobs J(i = 1,2,...,n)on m machines Mk(k = 1,2,...,m), where each job Ji needs Oi operations on the order of restraint and each working procedure of job can be processed by multiple processes of M machines. The total number of operations in all jobs is Ot, Ot=∑i=1nOiMij means the collection of the useable machines about j-th operation of i-th job, Mij∈{1,2,...,m}, Oi,j,k means the j-th operation of the i-th job can use k-th machine, pi kmeans the required time of j-th operation of i-th job on the k-th machine, 1≤i≤n,1≤j≤oi,1≤k≤m. The task is to find a set of solutions and three criteria of FJSP are considered and described as follows:
- (a)
The total workload of all machines
where the element pi,j,k denotes the processing time of j-th operation of i -th job in k-th machine.
- (b)
The workload of the critical machine
where Wk denotes the workload of the k-th machine Mk (the summation of pi,j,k on Mk).
- (c)
The completion time of the critical job
where CTi is the completion time of the i-th jobJi.
The main difference between Single-Objective Problem (SOP) and Multi-Objective Problems (MOP) is that MOP contains more than one objective that needs to be accomplished simultaneously. In [20], the authors presented an external repository (or archive) to keep the historical record of the non-dominated solutions found along the search process. In Fig.1, the basic external repository is also adopted in our proposed hybrid DE algorithm for solving the multi-objective FJSP. The reservation process of non-dominated solutions is described as follows.
Case 1.If an external repository is empty, any non-dominated solution found currently is inserted.
Case 2.If a solution is dominated by any individual in external repository, the solution will be discarded.
Case 3.If a solution is non-dominated by all individuals or equaled by any individual in external repository, the solution will be stored.
Case 4.If a solution dominates at least one solution in external repository, those dominated solutions are removed from the external repository, and this solution will be stored.
All new solutions are compared with solutions in the external repository, and one of four cases is corresponded each time. NS means one of new solutions. k in Sk means there exists k solutions in external repository. Sk- means a modified Sk after some dominated solutions are removed by NS.
3The Proposed MethodsAs above mentioned to the adaptive DE variants, the parameters updated iteratively according to their successful experience in the generations, such as JADE [13], MDE_PBX [14]. In this work, the proposed DE model based on self-adaptive mutation (SAM) and wrapper local search (WLS) to enhance the performance of DE. In addition, the effective PSOMA [21] that we previously published is successfully merged into DE model for solving the multi-objective FJSP.
3.1Self-adaptive Mutation (SAM) ApproachThe original DE mutation is “DE/rand/1/bin” in [4]. Islam et al. proposed the mutation of MDE_pBX, although the effect of the method performs better results than many other algorithms, this diversity of solution searching scheme is getting premature convergence at local optima within a smaller number of generations. Taking into consideration of these facts and to overcome the limitations of this feature, the extension of modified mutation searching strategy in [14], which is abbreviated as SAM approach, can be shown below.
In Eq. 18, X→i,G is known as the target vector, V→i,G is known as the donor vector, the scaling factor Fi is a positive scaling parameter for difference vectors. The X→r1i,G and X→r2i,G are two distinct vectors picked up randomly from the current population, and none of them is equal to X→gr_better,G or the target vector. The X→gr_better,G is dynamically chosen from top w% individuals of each population. The linearly decreasing inertia weight is set as Eq. 19, where imax is the current iteration, imax is the user-defined maximum iteration, and the pre-defined lower and upper bounds of w described as wmm≤w≤wmax.
This new proposed self-adaptive mutation operator is a variant of the MDE_pBX. It dynamically uses the best of a group (whose size is w% of the linearly decreasing population size) of randomly selected solutions, from current generation to perturb the parent vector, and unlike in [14] that the X→better,G always picks the best vector from the entire population fixed-ratio to perturb the target vector. This new simple self-adaptive mutation approach can drive the population to the better direction instead of convergence to the best individual in the iteration and help DE not to fall into local optimum quickly in smaller generation.
3.2Wrapper Local Search (WLS) StrategyAccording to related works, it can be found that classical DE can perform well performance on widely search for exploring unsearched solution space but weakly on searching depth. In 2010 [22] we published the efficient wrapper-based hybrid model for solving the biomedical problem and is capable of producing high prediction accuracy and fewer number of features selection simultaneously. In this study, the wrapper-based feature selection framework is properly adopted to enhance the local search performance for DE, named Wrapper Local Search (WLS) strategy, is involved to adjust the scale of moving vector via trying to increase or decrease current moving vector by the Cauchy distribution. In Figure 2, the proposed WLS method utilized these random wrapper-based selected dimensions (“1” indicates selected, “0” denotes excluded) to identify a suitable balance tradeoff of DE search and local search. It can save much time than one by one the single dimension search [23], and will fine tune the searching direction for finding the global best solution.
The pseudo-code of the proposed DE algorithm is described as Algorithm 2.
3.3PSOMA SchemeThe effective particle encoding representation that we previously published and detailed in [21], each dimension contains three components: integer part (machine selection), decimal part (priority order) and real-value number (operation number). In Fig.3 is the structure of PSOMA representation on each dimension. This encoding representation is flexible enough for solving the FJSP to satisfy the precedence constraints and operations in each job by using the structure of the proposed DE model with real-value number.
An example of FJSP (3 jobs, 3 machines, and 6 operations) is considered and illustrated in Table 1. Three Jobs J1, J2 and J3 need to be processed by at least one of three machines M1, M2 and M3. Each job contains several operations such as Job 1 is split into O1.1, O1.2, O1.3 ; Job 2 is split into O2.1, O2.2 etc. The executing times for each machine to execute each job is given, such as O1.1 assigned to M1 is 3 units; O1.2 assigned to M2 is 4 units, etc.
To explain the PSOMA scheme, one possible candidate encoding representation of the individual shown as Figure 4, to give the detailed description of the decoding procedure for FJSP as follows.
Step 1.O2.1 is assigned to M1.
Operation set O1= {O1.1, O2.1, O3.1 }.
Assignment set C1= {O1.1- M3, O2.1- M1, O3.1- M3}.
Max(O1.1, O2.1, O3.1)=Max(0.81, 0.92, 0.37)=0.92.
Then the {O2.1- M1} is assigned from C1.
Step 2.O1.1 is assigned to M3.
Operation set O2= {O1.1, O2.2, O3.1}.
Assignment set C2= {O1.1- M3, O2.2- M2, O3.1- M3}.
Max(O1.1, O2.2, O3.1)=Max(0.81, 0.68, 0.37)=0.81.
Then the {O1.1- M3} is assigned from C2.
Step 3.O2.2 is assigned to M2.
Operation set O3= {O1.2, O2.2, O3.1}.
Assignment set C3= {O1.2- M1, O2.2- M2, O3.1- M3}.
Max(O1.2, O2.2, O3.1)=Max(0.26, 0.68, 0.37)=0.68.
Then the {O2.2- M2} is assigned from C3.
Step 4.O3.1 is assigned to M3.
Operation set O4= {O1.2, O3.1}.
Assignment set C4= {O1.2- M1, O3.1- M3}.
Max(O1.2, O3.1)=Max(0.26, 0.37)=0.37.
Then the {O3.1- M3} is assigned from C4.
Step 5.O1.2 is assigned to M1.
Operation set O5= {O1.2}.
Assignment set C5= {O1.2- M1}.
Max(O1.2)=Max(0.26)=0.26.
Then the {O1.2- M1} is assigned from C5.
Step 6.O1.3 is assigned to M2.
Operation set O6= {O1.3}.
Assignment set C6= {O1.3- M2}.
Max(O1.3)=Max(0.53)=0.53.
Then the {O1.3- M2} is assigned from C6.
As shown in Figure 5, the operations of all jobs are assigned to each machine done and one of the feasible Gantt chart solution is provided. The precedence constraints are {O1.1 before O1.2 before O1.3} from job 1, {O2.1 before O2.2} from job 2, and {O3.1} from job 3. The operation order should be preserved by the different machine selection. It is obvious that each scheduling candidate solution generated by any encoding representation based on PSOMA should be feasible. The pseudo-code of the proposed hybrid DE model with PSOMA scheme for solving FJSP is shown as Algorithm 3.
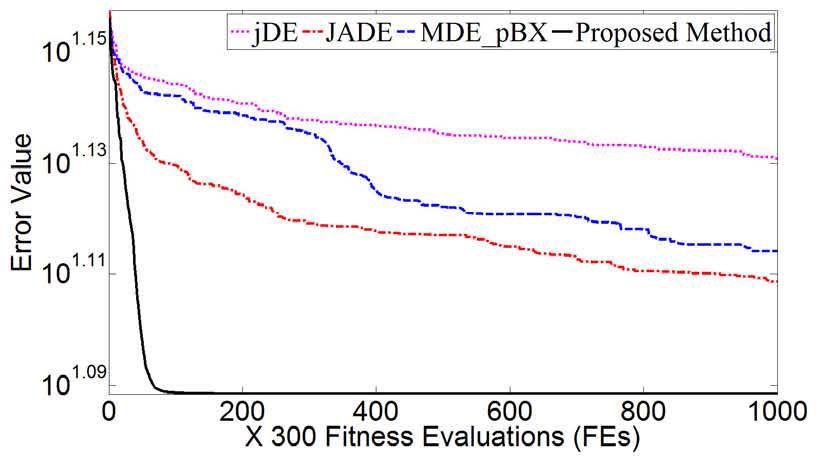
4Experimental Results4.1Single-objective numerical benchmarksIn order to verify the performance of our approach, a selected set of standard test functions from the special session on real-parameter optimization of the IEEE Congress on Evolutionary Computations, CEC 2005 [24] were adopted for testing to related works. The global optimum (equal to function bias), search range, initialization range and function types of each test function are illustrated in Table 2. These functions 1 to 5 are unimodal, functions 6 to 12 are basic multimodal, functions 13 to 14 are expanded multimodal, and the hybrid composition is function 15. In the experiments, 15 numerical test functions with 30 dimensions are conducted for comparing the proposed method with other five related works as jDE, JADE and MDE_pBX reported in [14]. The initial population size is set as 100. The fitness evaluation (FEs) is 500,000. All the DE variants algorithms are implemented on Matlab 2013a. The mean values and standard deviation are calculated. The mean and standard deviation of error values are optimized and recorded by 25 independent runs.
The numerical benchmarks on CEC 2005 [23].
| Functions | Global Optimum | initialization Range | Search Range | Function Types |
|---|---|---|---|---|
| F1 | −450 | [−100, 100]D | [−100, 100]D | Unimodal |
| F2 | −450 | [−100, l00]D | [−100, 100]D | Unimodal |
| F3 | −450 | [−100, 100]D | [−100, 100]D | Unimodal |
| F4 | −450 | [−100, 100]D | [−100, 100]D | Unimodal |
| F5 | −310 | [−100, 100]D | [−100, 100]D | Unimodal |
| F6 | −390 | [−100, 100]D | [−100, 100]D | Basic multimodal |
| F7 | −180 | [0, 600]D | No Boundary | Basic multimodal |
| F8 | −140 | [−32, 32]D | [−32, 32]D | Basic multimodal |
| F9 | −330 | [−5, 5]D | [−5, 5]D | Basic multimodal |
| F10 | −330 | [−5, 5]D | [−5, 5]D | Basic multimodal |
| F11 | 90 | [−0.5, 0.5]D | [−0.5, 0.5]D | Basic multimodal |
| F12 | −460 | [−π,π]D | [−π,π]D | Basic multimodal |
| F13 | −130 | [−5, 5]D | [−5, 5]D | Expanded multimodal |
| F14 | −300 | [−100, 100]D | [−100, 100]D | Expanded multimodal |
| F15 | 120 | [−5, 5]D | [−5, 5]D | Hybrid Composition |
The experiment results of 15 test functions with 30 dimensions numerical functions are listed in Table 3 to Table 5. The best results among the four DE approaches are shown in bold. The convergence characteristics of the proposed method and related works are shown in Figure 6-1 to Figure 6-15.
Experimental results of F1 to F5 test functions.
| Methods | Results | F1 | F2 | F3 | F4 | F5 |
|---|---|---|---|---|---|---|
| jDE | Mean Std. | 0.0000E+00 | 3.4050E−04 | 1.1385E+06 | 2.3619E+00 | 1.2669E+03 |
| 0.0000E+00 | 3.3856E−04 | 5.8794E+05 | 3.7264E+00 | 5.4111E+02 | ||
| JADE | Mean Std. | 0.0000E+00 | 0.0000E+00 | 2.2179E+04 | 2.8565E−03 | 4.8115E+02 |
| 0.0000E+00 | 0.0000E+00 | 1.9635E+04 | 1.3994E−02 | 3.0154E+02 | ||
| MDE_pBX | Mean Std. | 0.0000E+00 | 0.0000E+00 | 8.9062E+04 | 2.2087E−07 | 3.5956E+02 |
| 0.0000E+00 | 0.0000E+00 | 8.4137E+04 | 9.0879E−07 | 2.1233E+02 | ||
| Proposed Method | Mean Std. | 0.0000E+00 | 0.0000E+00 | 2.8032E+04 | 1.3652E+02 | 3.5172E+02 |
| 0.0000E+00 | 0.0000E+00 | 1.5638E+04 | 3.1828E+02 | 1.6625E+02 |
Experimental results of F6 to F10 test functions.
| Methods | Results | F5 | F7 | F8 | F9 | F10 |
|---|---|---|---|---|---|---|
| jDE | Mean Std. | 3.4270E−03 | 8.4743E−03 | 2.0951E+01 | 0.0000E+00 | 6.2726E+01 |
| 3.8188E−03 | 7.1033E−03 | 5.3160E−02 | 0.0000E+00 | 3.6205E+01 | ||
| JADE | Mean Std. | 4.5077E+01 | 1.1313E−02 | 2.0937E+01 | 0.0000E+00 | 4.8916E+01 |
| 1.6687E+02 | 1.134EE−02 | 5.4487E−02 | 0.0000E+00 | 9.3953E+00 | ||
| mde_pbx | Mean Std | 1.7541E+00 | 9.1607E−03 | 2.0114E+01 | 1.6332E+01 | 2.3322E+01 |
| 2.0197E+00 | 7.4285E−03 | 3.0952E+01 | 4.4084E+00 | 5.8728E+00 | ||
| Proposed Method | Mean Std. | 1.5946E−01 | 1.6129E−02 | 2.0161E+01 | 4.6274E−01 | 3 047BE+01 |
| 7.9732E−01 | 1.3326E−02 | 2.3085E−01 | 1.3571E+00 | 6.8312E+00 |
From the simulational results, the proposed hybrid DE model gets better results such as F2, F5, F11, F12, F14 and F15 functions and F1 archive the same results which the real optimum solutions are found. In summary, according to the results shown in Tables 3 to 5, the proposed DE model is highly competitive to the above-mentioned state-of-the-art DEs. The results of the proposed DE are better than, or comparable to, those of the state-of-the-art DEs in terms of the quality of the final solutions.
4.2Multi-objective FJSP benchmarksTo illustrate the effectiveness and performance of the hybrid DE for the multi-objective verification, three FJSP representative benchmarks which are problem 8×8, 10×10, 15×10 have been conducted, and to compare with other related works, such as the PSO-SA [17] and MOEA-GLS [18]. For each problem, the obtained results are reported in table contains three objectives: F1 (total workload), F2 (critical machine workload), F3 (makespan), are mentioned in Section 2. The solutions found from three methods are shown in Table 6 to Table 8.
For example, two new non-dominated solutions (77, 12, 14) and (77, 11, 16) can be obtained by the proposed hybrid DE compared with the PSOSA, and more diversity Gantt chart solutions can be obtained by the hybrid DE compared with the MOEA-GLS. From the simulation results of Gantt chart diversity, the proposed hybrid DE approach performs significantly better than the other two PSO-SA and MOEA-GLS methods in solving all benchmarks. Afterward, three of the Gantt charts from the solution (75, 12, 15) for problem 8×8 are exhibited solutions diversity in Figure 7 to Figure 9 as giving an illustration.
5ConclusionIn this paper, an improved Differential Evolution hybridized adaptive mutation (SAM) and wrapper local search (WLS) is proposed to improve both single-objective and multi-objective optimization performances of DE, and guide the evolution of the population toward the global optimum. Meanwhile, the WLS can disturb individuals to help individuals avoid trap into local minimum in evolution progress. Compare the proposed method with the published algorithms, the experimental results show that the proposed method exhibits better performance for solving most of the test functions from CEC 2005 benchmarks for the single-objective verifications. In addition, the wide range of Pareto-optimal solutions and the more Gantt charts diversity can be obtained for the multi-objective FJSP problems.
This work was partially supported by the National Science Council, Taiwan, under Grant NSC 101-2218-E-254-001.