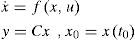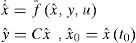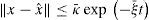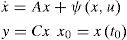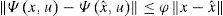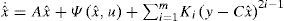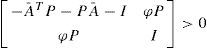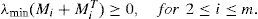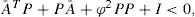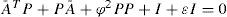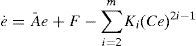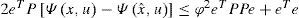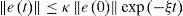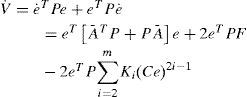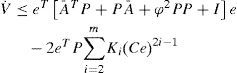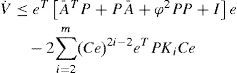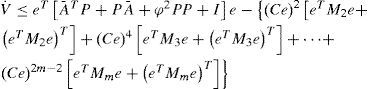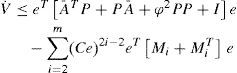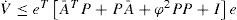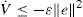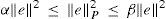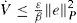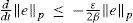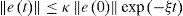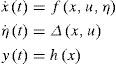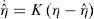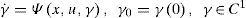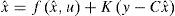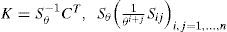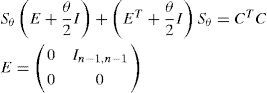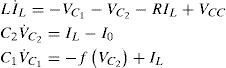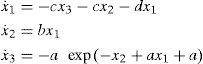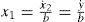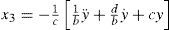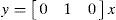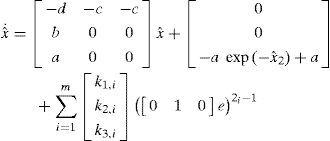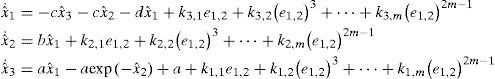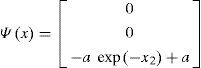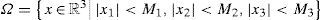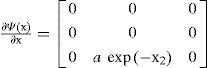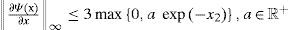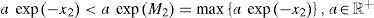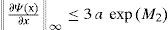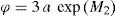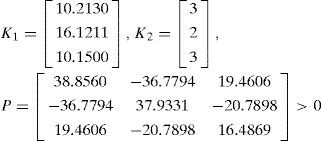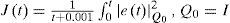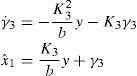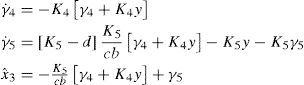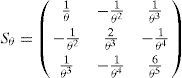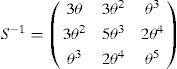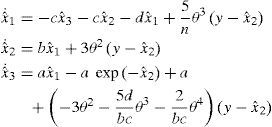In this paper we deal with the experimental synchronization of the Colpitts oscillator in a real-time implementation. Our approach is based on observer design theory in a master-slave configuration thus, a chaos synchronization problem can be posed as an observer design procedure, where the coupling signal is viewed as a measurable output and a slave system is regarded as an observer. A polynomial observer is used for synchronizing the Colpitts oscillator employing linear matrix inequalities. Finally, a comparison with a reduced order observer and a high gain observer is given to assess the performance of the proposed observer.
En este artículo se aborda la sincronización experimental del oscilador de Colpitts en tiempo real. Nuestra aproximación se realiza mediante la teoría de diseño de observadores en una configuración maestro-esclavo, por lo que el problema de sincronización caótica puede plantearse como el diseño de un observador. Se utiliza un observador polinomial para la sincronización del oscilador de Colpitts empleando desigualdades matriciales lineales. Se realiza una comparación con el observador de orden reducido y con el observador de alta ganancia con la finalidad de verificar el desempeño del observador propuesto.
Synchronization in chaotic systems has been investigated since its introduction paper of Pecora and Carrol [1]. This research area has received a great deal of attention among scientist in many fields due to its potential applications mainly in secure communications [2]–[7].
During the last years (almost two decades), many different approaches related to chaos synchronization have been proposed. See for instance, [8]–[10] in which the authors propose the employment of state observers, where the main applications pertain to the synchronization of nonlinear oscillators; in references [11]–[13] use feedback controllers, which allow to achieve the synchronization between nonlinear oscillators, with different structure and order; in [14], [15] use nonlinear backstepping control; in papers [16], [17] consider synchronization time delayed systems; in works [18], [19] consider directional and bidirectional linear coupling; papers [20], [21] use nonlinear control; in [12] use active control; in [13], [22] use adaptive control; in [23]–[24] employ adaptive observers and so on.
Now, we will mention a brief note about observer theory. The design of observers for nonlinear systems is a challenging problem that has received a considerable amount of attention. Since the observers developed by Kalman [25] and Luenberger [26], several years ago for linear systems, different state observation techniques have been propose to handle the systems nonlinearities. A first category of techniques consists in applying linear algorithms to the system linearized around the estimated trajectory. These are known as the extended Kalman and Luenberger observers. Alternatively, the nonlinear dynamics are split into a linear part and a nonlinear one. The observer gains then are chosen large enough so that the linear part dominates over the nonlinear one. Such observers are known as, high gain observers [27]. And many other approaches such as [28]–[30].
In this work the synchronization method is based on a master-salve configuration [1]. The main characteristic is that the coupling signal is unidirectional, that is, the signal is transmitted from the master systems (transmitter) to the slave system (receiver), the receiver is requested to recover the unknown (or full) state trajectories of the transmitter. Therefore, the terminology transmitter-receiver is also used. Thus, a chaos synchronization problem can be regarded as observer design procedure, where the coupling signal is viewed as the output and the slave system is the observer [31]–[33].
As we can notice, there are several methods to solve the synchronization problem from the control theory perspective, in this work, we study the synchronization in master-salve configuration [1] by means of state observers based on differential algebraic approach. These proposals are applied in this paper to a Colpitts oscillator [34]. The Colpitts oscillator has been widely considered for the synchronization problem, see for instance [24], [35].
In this paper an exponential observer of polynomial type for the synchronization problem is proposed. We also have designed an asymptotic observer of reduced order. Finally, for comparison purposes, we construct a high-gain observer.
2Receiver operating principleLet us consider the following nonlinear system,
where x ∈ ℝn, is the state vector;u∈ℝm′, is the input vector, m′ ≤ n; f·:ℝn×ℝm′→ℝn is locally Lipschitz on x and uniformly bounded on u; y ∈ ℝ is the output of the system. To show the relation between observers for nonlinear systems and synchronization we give the following definition.Definition 1 (Exponential synchronization)The dynamical system with state vector xˆ∈ℝn
is in state of exponential synchronization with system (1) if there exist positive constants κ¯ and ξ¯ such thatIn the master-slave synchronization scheme, x is viewed as the state variable of the master system and xˆ is considered as the state variable of the slave system. Hence, the master-slave system synchronization problem between systems (1) and (2) can be solved by designing and observer for (1). In order to solve the synchronization problem as an observation problem we introduce the following observability property.
Definition 2 [40] (Algebraic observability condition-AOC)A state variable xi ∈ ℝ is said to be algebraically observable if it is algebraic over ℝ 〈u, y〉1 that is, x satisfies a differential algebraic polynomial in terms of {u,y} and some of their time derivatives, i.e.,
with coefficients in ℝ〈u, y〉.The system (1) can be expressed in the following form,
Where Ψ(x,u) is a nonlinear vector that satisfies the Lipschitz condition with constant φ that is:
The observer for system (4) has the next form
Where xˆ∈ℝn, and Ki ∈ ℝn for 1 ≤i ≤ m.
Let us consider the following assumptions:
Assumption 1. For Ā:= A −K1C there is a unique symmetric positive definite matrix P ∈ ℝn×n which satisfies the following linear matrix inequality (LMI):
where φ is the Lipschitz constant.Assumption 2. Let us define Mi:=PKiC, then:
Remark 1. By using the Schur complement (see Chapter 11 in [38]) the LMI in Assumption 1 can be represented as an algebraic Riccati equation:
or for some ε> 0Remark 2. Assumption 2 is used to improve the rate of convergence of the estimation error by injecting additional terms (from 2 to m) which depend upon odd powers of the output error.
In order to prove the observer convergence, we analyze the observer error which is defined as e=x−xˆ. From Equations 4 and 6, the dynamics of the observer error is given by:
where Ā:=A −K1C, and F:=Ψx,u−Ψxˆ,uNow, we present a lemma which will be useful in the convergence analysis.
Lemma 1 [39]: Given the system (4) and its observer (6) with the error given by e=x−xˆ. if P=PT > 0 then:
The following proposition proves the observer convergence.
Proposition 1. Let the system (4) be algebraically observable and Assumption 1 and Assumption 2 hold. The nonlinear system (6) is an exponential polynomial observer of the system (4); that is to say, there are constants κ>0 and ζξ0 such that:
where κ=βα,ξ=ϵ2β,α=λminP, and β=λmax (P).Proof. We use the following Lyapunov function candidate V=eTPe
using Lemma 1 we obtain:Making some algebraic manipulations on the last term of the above inequality, and taking into account that Ce ∈ ℝ, we obtain:
For simplicity, we define Mi:=PKiC, for 2≤i≤m, then we have:The above expression can be rewritten in a simplified form:
From Assumption 2, the second term in the right hand side of above the inequality always will be positive or zero, therefore:
by Assumption 1 (and remark 1), we have:We write the Lyapunov function as V=eP2, then by the Rayleigh-Ritz inequality we have that:
where α:=λmin(P), and β:=λmaxP∈ℝ+ (because P is positive definite).By using (9) we obtain the following upper bound of (8):
Taking the time derivative of V=eP2 and replacing in inequality (10), we obtain:
Finally, the result follows with:
where κ=βα and ξ=ϵ2β3Asymptotic reduced order observerNow, let us consider the nonlinear system described by (1). The unknown states of the system can be included in a new variable η(t) and the following new augmented system is considered:
where Δ(x,u) is a bonded uncertain function. The problem is to reconstruct the variable η(t). This problem is overcome by using a reduced order observer. Before proposing the corresponding observer we introduce some hypotheses:Assumption 3η(t) satisfies the AOC (Definition 2).
Assumption 4γ is a C1 real-valued function.
Assumption 5 Δ is bounded, i.e., |Δ| ≤ M < ∞.
Assumption 6. For t0 sufficiently large, there is K > 0, such that, limsupt→t0MK=0.
The following lemma describes the design of a proportional reduced order observer for system (1).
Lemma 2. If Assumptions 3 to 6 are satisfied, then the system:
Is an asymptotic reduced order observer of free-model type for system (12), where ηˆ denotes the estimate of η and K ∈ ℝ+ determines the desired convergence rate of the observer.
Remark 3. To reconstruct η(t) by using an auxiliary state ηˆt sometimes we need to use the output time derivatives, but these may be unavailable. To overcome this fact, an auxiliary function completely artificial γ is defined in such a way that it cancels out all nonmeasurable terms. This action defines a differential equation for γ. This equation is solved, then, γ is substituted in the differential equation of the estimated state and finally the estimate of η is obtained.
We give the following immediate corollary.
Corollary 1. The dynamic system (13) along with
constitute a proportional asymptotic reduced order observer for system (12), where γ is a change of variable which depends on the estimated state ηˆ and the state variables.4High gain-observerWe present a well-known estimation structure (high gain observer) as a comparison with our proposed schemes. Consider the class of nonlinear systems given by (1). In this case, to estimate the state vector x, we suggested a nonlinear high gain-observer with the following structure:
Where xˆ∈ℝn, xˆ0=xˆt0 and the observer high-gain matrix is given by:
and the positive parameter θ determines the desired convergence velocity. Moreover, Sθ=Sθ>0, should be a positive solution of the algebraic equation:5Experimental resultsAs was previously mentioned, the integrated These proposals are applied to a Colpitts oscillator [34]. The Colpitts oscillator has been widely considered for the synchronization problem, see [24, 35].
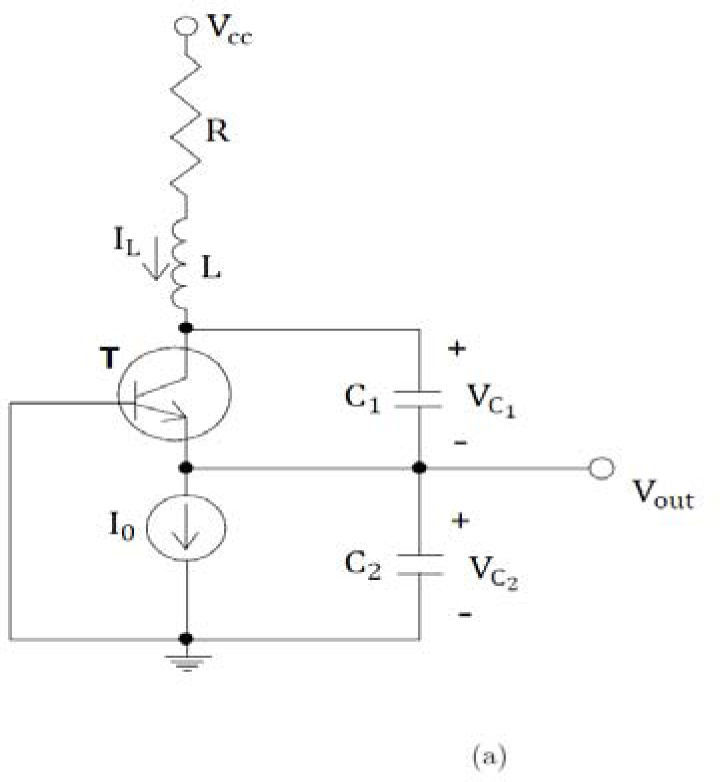
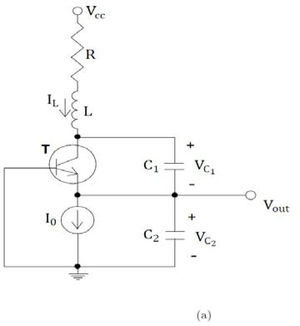
In this work we considered the classical configuration of the Colpitts oscillator [36]. The circuit contains a bipolar junction transistor 2N2222A as the gain element (Figure1(b)), and a resonant network consisting of an inductor and two capacitors (Figure 1(a)).
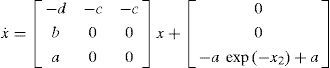
The Colpitts circuit is described by a system of three nonlinear differential equations, as follows:
where f(•) is the driving-point characteristic of the nonlinear resistor, this can be expressed in the form IE=fVC2=f−VBE. In particular, we have fVC2=Isexp−VC2VTWe introduce the dimensionless state variables (x1x2,x3), and choose the operating point of (16) to be the origin of the new coordinate system. In particular, we normalize voltages, currents and time with respect to Vref=VT, Iref=I0 and tref=1/ω0, respectively, where ω0=1/LC1C2/C1+C2 is the resonant frequency of the unloaded L-C tank circuit. Then, the state equations for Colpitts oscillator can be rewritten in the following form:
where, a=bc2c1,b=I0ω0C2VT,c=VTω0LI0,d=RLω0According to Definition 2, it is evident that system (17) is algebraically observable with respect to the output y=x2, because the unknown states can be rewritten as:
hence, Colpitts oscillator is algebraically observable with respect to the selected output y=x2.5.1Synchronization of the Colpitis oscillator employing the exponential polynomial observerFor the implementation of the observer we first rewrite (17) in the form (4),
Applying Proposition 1, we have
hence, the state observer is rewritten as.we verified the real time performance of the exponential observer by using the WINCON platform. To achieve the synchronization in real time, in WINCON the scheme (21) in the master-slave configuration was implemented.Figure 2 shows the real implementation of the Colpitts circuit. The circuit parameters are:
L=100 µH; C1=C2=47nF, R=45Ω, I0=5mA. Using the circuit parameter we obtain a=b=6.2723, c=0.0797, and d=0.6898.
The nonlinear term Ψ(x) in (20), satisfies the Lipschitz condition and is considered as follows
It is necessary to calculate the Lipschitz constant φ introduced in (5) over the bounded set
considering the Jacobian of Ψ(x) asit can be concluded that2From (22), it is obvious that the following conditions hold for all the points in the bounded set Ω.
hence:With (22)–(26) a Lipschitz constant that satisfies the Lipschitz condition (5) is defined as follows
In this case M1=3, M2=0.1, M3=6, and a=6.2723, φ=20.7959
Following the observer (21), for m=2, and solving the LMI given by assumption 1, the observer gains K1 and K2 and positive definite matrix P are as follows
With eigenvalues λ1(P)=1.3151, λ2(P)=5.2514, and λ3(P)=86.7095.
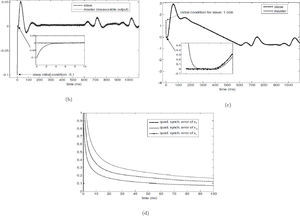
The performance index (quadratic synchronization error) of the corresponding synchronization process is calculated as
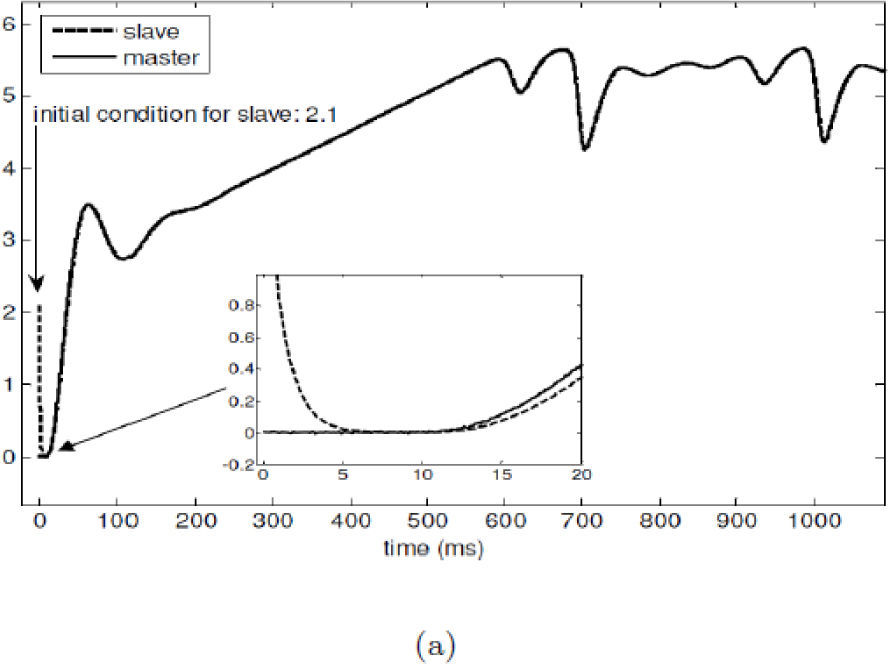
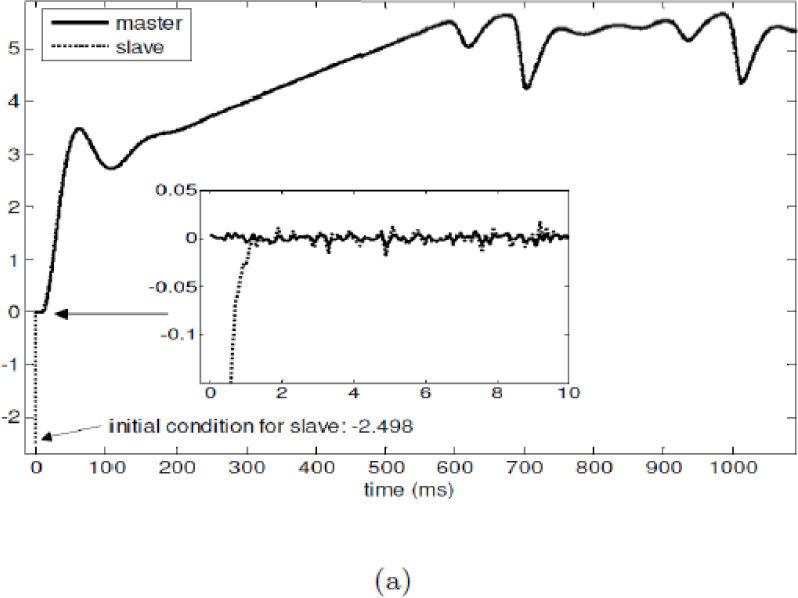
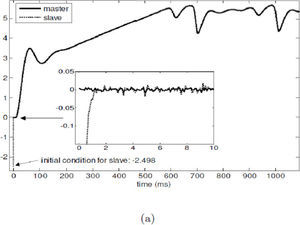
Figures. 3(a) and (c) show the obtained results by using the exponential polynomial observer (21), it is clear that the synchronization is achieved fairly acceptable even with the noisy measurements. The Colpitts circuit starts in x(0)=[0 0 0]T and the arbitrary initial conditions for the observer are xˆ0=2.1−0.11,506T. Figure 3(d) shows the performance index of the synchronization, which depicts an exponential behavior.
Real-time synchronization of Colpitts oscillator employing observer (21): (a) variables x1 and xˆ1, (b) synchronization of variables x2 and xˆ2, (c) synchronization of variables x3 and xˆ3, and (d) performance index
Let us consider the normalized system of the Colpitts oscillator. We assume that the output system is y=x2, therefore, the slave system consists in two estimation structures to achieve synchronization with the master system. Such structures are obtained as follows: Firstly, verify that the master system (Colpitts oscillator) is algebraically observable, and second, by using (13), we construct the observer for the unknown states. Previously, we have verified that master system (Colpitts oscillator) is algebraically observable (see Equations (18) and (19). Then, both unknown states of the master system are algebraically observable, and therefore, we can construct the observers based on Lemma 2 and Corollary 1.
For x1 the observer is given by:
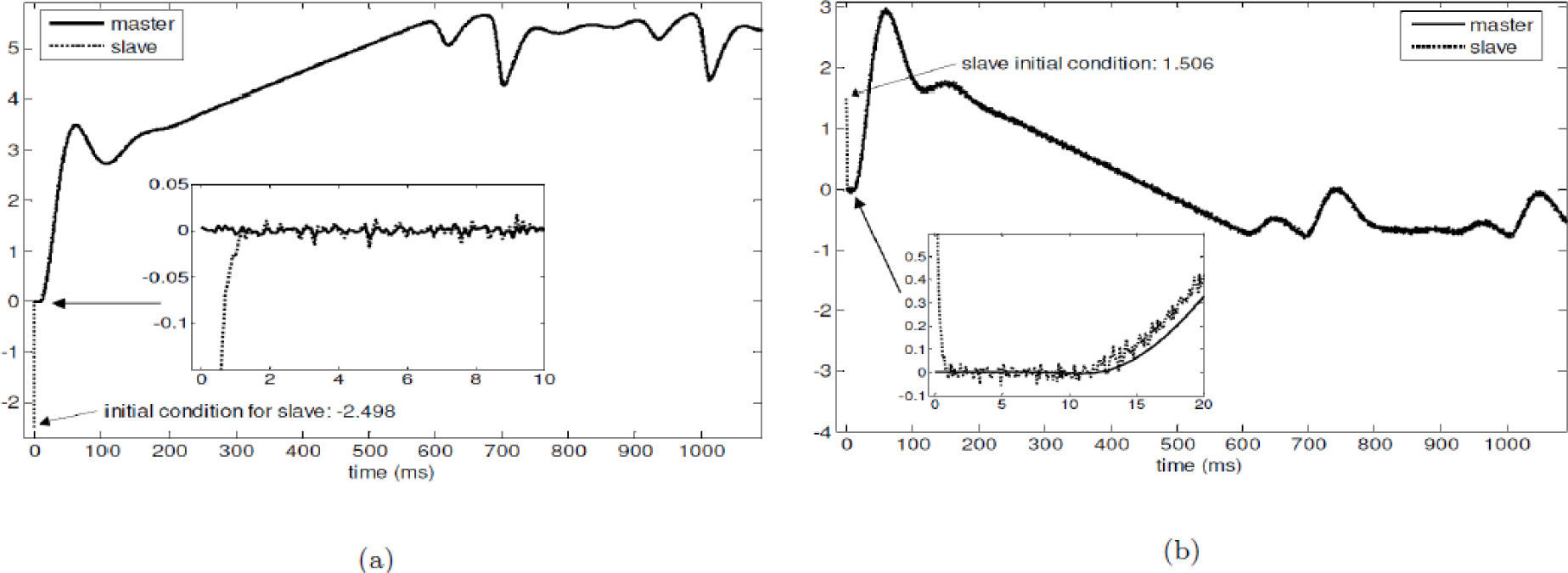
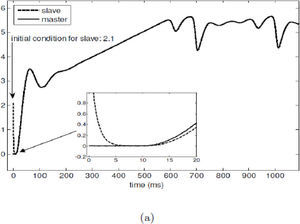
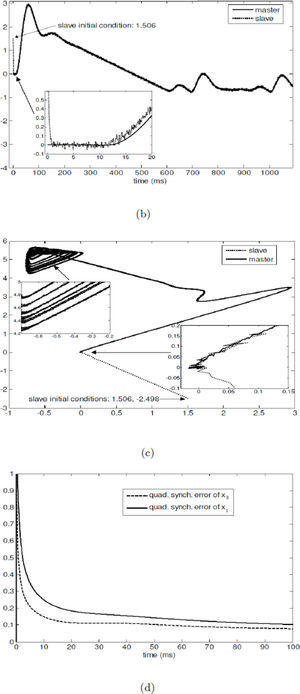
and for x3, we haveTherefore, (27) and (28) constitute the slave system. Now, we present some experimental results for the synchronization of the Colpitts oscillator by using the asymptotic reduced order observer (27) and (28). Figures 4(a) and (b) show the obtained results for the initial conditions xˆ1=−2.498 and xˆ3=1.506 in the schemes (27) and (28), respectively. As we can notice, the synchronization results achieved with the reduced order observer are good. Figure 4(c) presents the phase portrait, where the chaotic behavior of the Colpitts oscillator can be clearly observed. Finally, Figure 4(d) illustrates the performance index, which tends to decrease.
Real-time synchronization of Colpitts oscillator using reduced-order observer (28) and (27): (a) synchronization of coordinates x1 and xˆ1, (b) synchronization between x3 and xˆ3, (c) Phase portrait of the master system (x3 (horizontal) versus x1 (vertical)) and the slave system (xˆ3 and xˆ1), and (d) performance index
The matrix Sθ>0,Sθ=SθT, that satisfies the algebraic Riccati equation (15) for a third order system (n=3), is given by:
and its corresponding inverse matrix is,Then the high gain-observer for Colpitts system (17) is as follows:
Figure 5 depicts the synchronization between Colpitts oscillator (17) and its high gain observer (31). In order to obtain exponential convergence we have used θ=100. As we can notice, the performance on the high-gain observer is not good in comparison with the exponential polynomial observer and with the proportional reduced-order observer. An important advantage of the proposed methodologies is that the magnitudes of the observer gains are smaller than the ones used in the high-gain observer.
Synchronization between Colpitts oscillator and its high-gain observer: (a) synchronization of coordinates x1 and xˆ1, (b) synchronization between x3 and xˆ3, (c) Phase portrait of the master system (x3 (horizontal) versus x1 (vertical)) and the slave system (xˆ3 versus xˆ1), and (d) performance index
In this paper we tackled the synchronization problem based upon observer's theory. As well as, its main contributions, we show the real-time synchronization in the Colpitts oscillator by using two observer structures: An exponential polynomial observer and an asymptotic reduced order observer. For comparison purposes we implemented a high-gain observer. Finally, some experimental results show the effectiveness of the proposed methodologies.