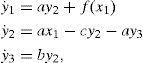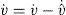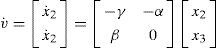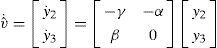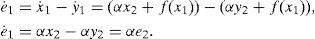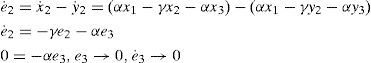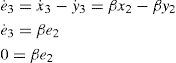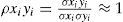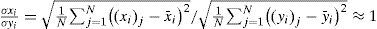Chaotic oscillators have been implemented with a wide variety of discrete electronic devices and quite few realizations using integrated circuit technology. This article describes the synchronization of two chaotic oscillators already fabricated with complementary metal-oxide-semiconductor (CMOS) integrated circuit technology of 0.5um and generating 3- and 5-scrolls. In order to attain the synchronization, we use a master-slave topology with unidirectional coupling. Within this context, a system parameter iterates until the correlation coefficient computed between the chaotic signals generated by the master and slave systems approximates to unity. For the following parameter, its value depends on the standard deviations from the individual signals contrary to previous one. By combining those statistical relationships according to the number of system parameters, we can synchronize integrated chaotic oscillators. Theoretical model simulations of two chaotic oscillators generating 3- and 5-scrolls, and experimental results for two integrated 3-scroll chaotic oscillators validate this approach. Stability and error analysis are also included.
Los osciladores caóticos se han implementado con una variedad amplia de dispositivos electrónicos discretos y muy pocos con tecnología de circuitos integrados. Este artículo describe la sincronización de dos osciladores caóticos fabricados con tecnología de circuitos integrados CMOS de 0.5um que generan 3- y 5-enrollamientos. Se utiliza la configuración maestro-esclavo para obtener la sincronización. A partir de esta configuración, se itera un parámetro del sistema hasta que el coeficiente de correlación entre las señales caóticas del maestro y el esclavo respectivamente, se aproxima a la unidad. Posteriormente, se calcula la razón de las desviaciones estándar para obtener el valor del siguiente parámetro, esto de forma inversa a la determinación del primero. Es posible sincronizar osciladores caóticos integrados al combinar estas medidas estadísticas en relación al número de parámetros del sistema. Simulaciones del modelo teórico de dos osciladores caóticos exhibiendo tres y cinco enrollamientos, además de resultados experimentales para tres enrollamientos confirman el método propuesto. Son incluidos los análisis de error y estabilidad.
Carroll and Pecora verified the experimental synchronization of two chaotic oscillators by using operational amplifiers (opamps) [1]. They pointed out that if two independent chaotic systems were started with the same initial conditions, any arbitrarily small perturbation in those conditions would grow exponentially. After some time, the trajectory evolution of the two systems will be uncorrelated. However, if the two chaotic oscillators were synchronized, both systems will evolve to the same chaotic behavior, e.g., in a master-slave topology [2-6], the slave system behaves as the master system despite their chaotic motion, provided they are both driven with a proper signal. In this manner, the general scheme for synchronizing dynamical systems is to take a (nonlinear) system, duplicate some subsystem of that system and drive it with a control signal from the unduplicated part. This is a self-synchronization where the two sub-systems couples by some technique [1-6], [13]. As a function of the synchronized states, we can classify the synchronization approaches as complete synchronization, phase synchronization, lag and intermittent lag synchronization, imperfect phase synchronization, and almost synchronization [14-17, 20-26]. However, those approaches have been generally proved on chaotic systems depicted by either theoretical relationships or electronic circuits designed with discrete devices opposed to the integrated circuit (IC) case [2-6].
Related to multi-scroll chaotic oscillators, they have been implemented using several approaches, such as opamps, operational transconductance amplifiers (OTAs), and current-feedback opamps (CFOAs) [7]. Note that by interconnecting and superimposing unity-gain cells (UGCs) [8-9], one could design those active devices with complementary metal-oxide-semiconductor CMOS IC technology. This approach was previously reported in [10-11], demonstrating that chaotic oscillators can be realized with IC technology. An integrated chaotic oscillator provides key advantages such as; it reduces the form factor (passive and active device count) contrary to the discrete realizations, and the bandwidth of the chaotic signals increases as a function of the time-constants that can be reached with different IC fabrication technologies.
This issue is quite important in an actual encryption scheme based on chaos, which needs high-rate data transmission, as mentioned in [14]. Finally, having ICs one can tune or select the chaotic behavior using a few external passive elements or exploiting the programming capabilities of current mirrors or logic gates. Another advantage in having integrated chaotic oscillators, is that one can develop custom designs that can derive in realizing custom synchronization approaches, thus allowing to realize integrated designs for communication systems, which are in the state-of-the-art [21-24].
In this manner, to the best of our knowledge, this paper is the first one reporting a systematized algorithm to synchronize two chaotic oscillators at integrated circuit level. The novel contribution to the field consists on a systematic algorithm to synchronize integrated chaotic systems with multiple scrolls by using the correlation coefficient (CoCo) and standard deviation (STD) of the numerical time series to reduce the synchronization error iteratively. Besides, the stability conditions are based on conditional Lyapunov exponents computed only once before the first iteration. Therefore, the synchronization is achieved no matter the values of the initial conditions in the synchronization scheme. This approach can be considered as an extension of the complete synchronization technique based on unidirectional coupling [2, 6, 13].
The main idea of this method consists on sending a chaotic signal from the integrated nonlinear system (master) to another (slave). Then, the slaved system tracks the dynamics of the master system. This means that the behavior of the second system does not have any influence on the first one. Additionally, a 45-degree straight line, on the phase space portrait, is a well-accepted criterion to confirm the synchronization. This results when the same state-variables taken from the integrated master and slave dynamical systems are compared. Note that the dynamical evolution of the chaotic signals is theoretically identical after the synchronization is attained. Within this context, we computed CoCo between the time series of both the master and slave systems. When the data are correlated, the synchronization can be ensured. In a similar way, we used STD of independent chaotic signals to verify the synchronization error, i.e., when this measure converges to the same value implies that chaotic signals are close related and synchronized. Additionally, we can adjust a positive lineal approximation for both statistical measures by varying the parameters in the slave system. It is also proved that this approach is asymptotically stable by computing the conditional Lyapunov exponents. Several numerical simulation results for 3- and 5-scroll chaotic attractors confirm the synchronization approach. Finally, experimental results for two 3-scroll integrated chaotic oscillators are also shown.
2Integrated chaotic oscillatorRecently, a modified Chua’s system was designed and fabricated with CMOS IC technology of 0.5um [10-11]. That IC can generate 3- and 5-scrolls, and its chaotic behavior was demonstrated by computing the maximum Lyapunov exponent [12].
We take that chip as the core of chaotic behavior for our approach. Therefore, the dynamics of the Chua´s system is governed by
being [α,β,γ] constant parameters, x1, x2, x3 the state-variables, and f(x1) a nonlinear function approximated by
for 3-scrolls case, and
for 5-scrolls case, where ξ defines the dynamic range of the sawtooth function, Bp are the breakpoints and k is a multiplier factor. By selecting α =3, β =4, γ =1, ξ =0.8 V, Bp=147 mV, and k=1; the chaotic behavior arises [3].
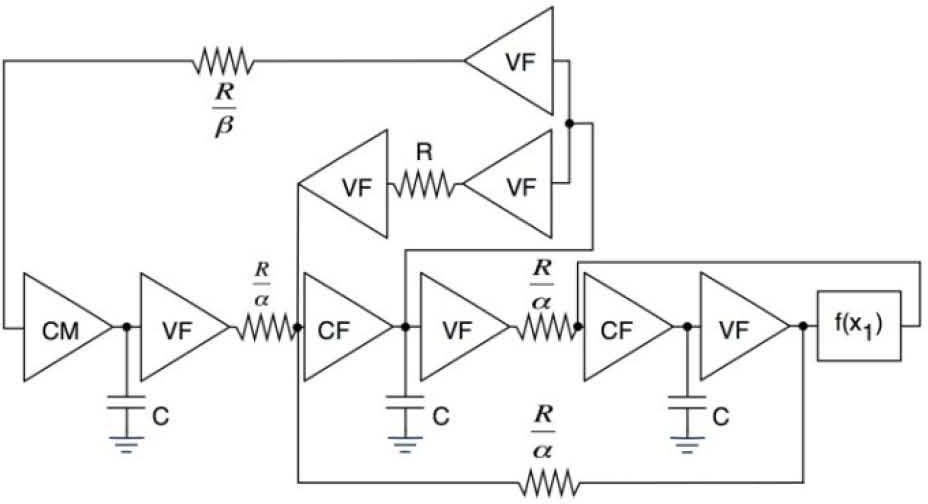
Basically, the integrated chaotic oscillator consists of UGCs like, voltage followers (VFs), current followers (CFs) and current mirrors (CMs), as shown in Fig. 1.
Integrated chaotic oscillator taken from [10-11].
All those UGCs were designed using floating gate MOS (FGMOS) transistors [10-11]. From Figure 1, R and C define the gain of the integrator blocks (τ = t/RC); with R=120kΩ and C chosen according to the desired operating frequency. Note that C is the sum of the external capacitance plus the parasitic capacitance [10]. As the integration is performed externally, we can add a control signal, with a proper impedance coupling, to the slave system; e.g., using opamps as shown herein. This signal could be injected as a current at the nodes connecting the integration capacitors (C). Therefore, the gain of the opamp must be equal to 1/R and multiplied by the gain of the signal to be transmitted. A chip microphotograph is shown in [10].
3Synchronization of integrated multi-scroll chaotic oscillatorsIt is well known that the Pearson CoCo measures the strength and direction of a linear relationship between two variables. As this coefficient approaches unity, we can state that the chaotic signals of master and slave systems have a strong positive correlation, and so are synchronized. The STD was computed to compare two chaotic signals. If the signals from the master and slave are synchronized, we expect that they have the same STD. Synchronization error being minimized when both statistical measures approach unity.
Taken into account those concepts, this section presents the synchronization method for integrated chaotic systems. The proposed approach could be considered as enhanced version of paper in [13]. From the chaotic system described by (1), we select to be the master state controlling the dynamics of the slave system. That way, the slave system becomes
The values for [a, b, c] are randomly selected at the beginning of our approach. A significant remark is that the behavior of the sub-system [y2,y3], depends on x1; nevertheless the behavior of x1 is not influenced by [y2,y3], We select x1 as the driving signal because the resulting conditional Lyapunov exponents have a negative magnitude [14]. This is a necessary and sufficient condition for the integrated chaotic oscillators to be synchronized, as shown herein.
3.1Synchronization conditions: Conditional Lyapunov exponentsLet us consider a state-variable subsystem defined by
where v represents the state variables [x2,x3] of the master integrated chaotic system, and vˆ the state-variables of the slave [y2,y3] By integrating (5), we have
and the differentiation of v and vˆ, according to (1) and (4) becomes
By substituting (6), (7) and (8) in (5), we obtain
This subsystem represents the dissipative part of the modified Chua’s system in (1). It is known that if matrix P has a pair of complex conjugated roots with negative real parts, the synchronization error is asymptotically stable [14]. For our case, the eigenvalues of the matrix P are λc1,2−0.5±3.4j.
Thus, all conditional Lypunov exponents of integrated chaotic oscillators must be negative to guarantee the synchronization. Note that the maximum Lyapunov exponent remains being positive in order to generate chaotic behavior.
3.2Synchronization conditions: Error analysisThis subsection shows that the synchronization error minimizes (it converges to zero ideally) as time tends towards infinity. Let us define the state errors for the master and slave systems as e1 = x1−y1, e2 = x2-y2 and e3 = x3−y3. By using (1) and (4), and considering that α = a, it leads us to
If the synchronization error e1 is designed to vanish gradually, then its differentiation is ė2→0 in (10). This means that the synchronization error e2 tends to zero in order to accomplish this equality. As a result, e2→0 and ė2→0
Therefore, we have the following expression for the synchronization error ė2.
with c = γ. Finally, the synchronization error ė3 implies that b = β, as follows
That way, since e1 tends towards zero, then e2 ≈ 0 and e3 ≈ 0 does. The previous analysis, although intuitive, is linked to a rigorous mathematical treatment based on the idea that the synchronization of entire coupled chaotic systems can be realized by synchronizing only partial states of that chaotic systems [14-15].
3.3Systematic approach to synchronize integrated chaotic systemsIn the context of synchronization, a key remark is that matrix P representing the dissipative part of the integrated chaotic oscillators must have negative conditional Lyapunov exponents with form of λc1,2 − Σ ± jΩ. Therefore, neither the same initial conditions nor belong to the same attraction region are required. Thus we propose that by giving an integrated nonlinear chaotic system x˙=f(x), with parameters m, m ∈ ℜ; we can determine the signal from the master to control the slave system only if this satisfies the necessary and sufficient condition in (9).
Once the output has been decided, the parameters of the slave system are swept linearly in the interval Ψ = {m, m ∈ ℜ: min < m < max}, being min and max, the minimal and maximum values where the chaotic regime remains. For the first parameter, the CoCo is computed until ρxiyi ≈ 1. Similarly, for the second parameter, the SDT is obtained until σxi / σyi ≈ 1. The resolution for each parameter can be adjusted by increasing the number of iterations of CoCo and STD.
Both statistical measures are intercalated for the remaining parameters. By satisfying (10), (11), (12), we obtains limt→∞ e(t) = x(t) −y(t) = 0. In this manner, an algorithm with five iterative steps is summarized herein:
-Step. Considering α = 3, β = 4, γ = 1 in the master chaotic oscillator, choose a random value for the parameters (a,b,c) of the slave system.
-Step 2. Letting (b, c) fixed, compute the solution of (1) and (4) simultaneously while a is being modified each cycle until the CoCo between the numerical time series approximates to unity, i.e.,
-Step 3. Set the best value for a from the previous step and letting now (a,c) fixed, compute the solution of (1) and (4) simultaneously while b is being modified each cycle until the rate of STD of the numerical time series approximates unity, i.e.,
-Step 4: Similarly, setting the best value for (a,b), compute the solution of (1) and (4) simultaneously while c is being modified each cycle until the CoCo between the numerical time series approximates to unity, i.e., ρxiyi=σxiyiσxiσyi≈1.
-Step 5. If the precision of the CoCo and STD does not meet with the required specifications, use the best values found for (a,b,c) and repeat the algorithm. This is considered as a round.
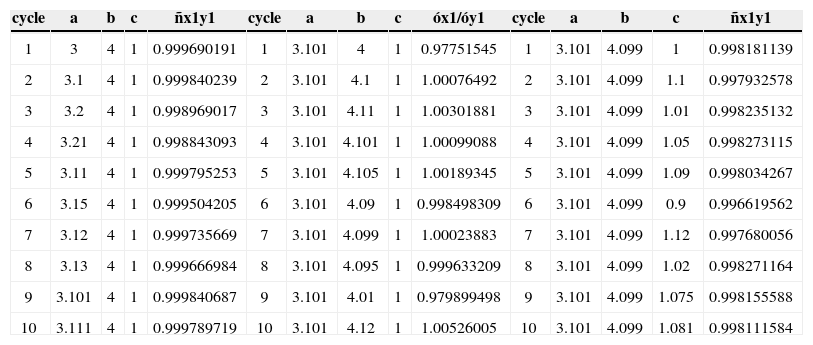
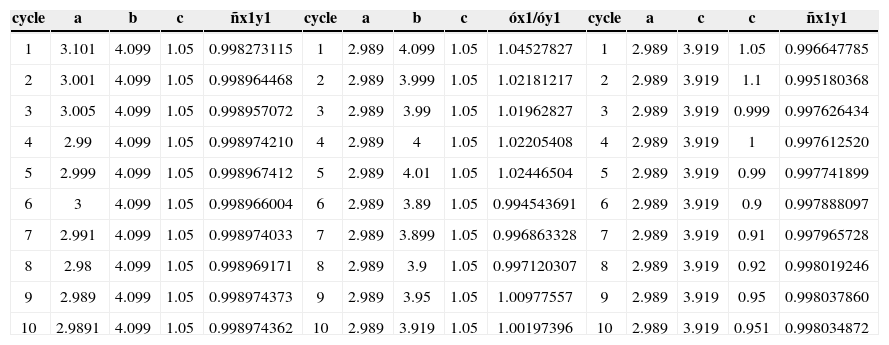
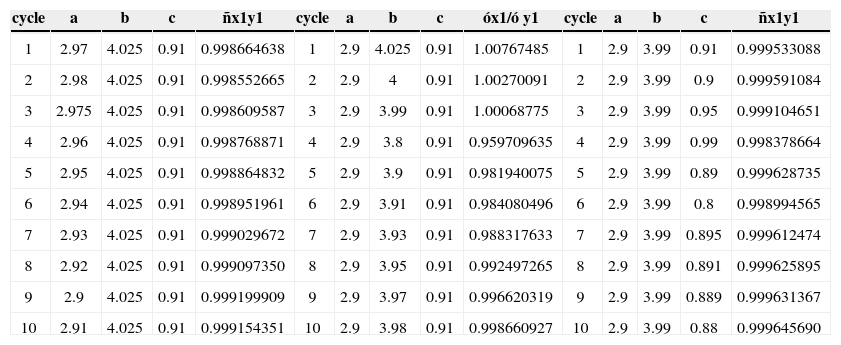
4Numerical Simulation ResultsBy using the aforementioned algorithm, we synchronize the integrated chaotic attractors in (1) and (4) with (x1,x2, x3) = (0.1,0,0) and (y1, y2, y3) = (0.01,0,0) as initial conditions, respectively. The computation of the first rounds to generate 3- and 5-scrolls is shown in Tables 1, 2 and 3. In this work, we complete ten cycles for each one of parameters (a,b,c) using the Adams-Moulton algorithm with a step-size h=0.01 as numerical solver [18]. The vectors containing the time series have a length of 10000 data, which is equivalent to be considered as a long-term evolution; a necessary condition to capture the chaotic behavior of those systems [14]. Those values (cycles and data) can be increased as needed for the user; however, it could be a negative impact in the simulation time [19].
Computing the best values (a,b,c) to generate 3-scrolls (round=1).
| cycle | a | b | c | ñx1y1 | cycle | a | b | c | óx1/óy1 | cycle | a | b | c | ñx1y1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 4 | 1 | 0.999690191 | 1 | 3.101 | 4 | 1 | 0.97751545 | 1 | 3.101 | 4.099 | 1 | 0.998181139 |
| 2 | 3.1 | 4 | 1 | 0.999840239 | 2 | 3.101 | 4.1 | 1 | 1.00076492 | 2 | 3.101 | 4.099 | 1.1 | 0.997932578 |
| 3 | 3.2 | 4 | 1 | 0.998969017 | 3 | 3.101 | 4.11 | 1 | 1.00301881 | 3 | 3.101 | 4.099 | 1.01 | 0.998235132 |
| 4 | 3.21 | 4 | 1 | 0.998843093 | 4 | 3.101 | 4.101 | 1 | 1.00099088 | 4 | 3.101 | 4.099 | 1.05 | 0.998273115 |
| 5 | 3.11 | 4 | 1 | 0.999795253 | 5 | 3.101 | 4.105 | 1 | 1.00189345 | 5 | 3.101 | 4.099 | 1.09 | 0.998034267 |
| 6 | 3.15 | 4 | 1 | 0.999504205 | 6 | 3.101 | 4.09 | 1 | 0.998498309 | 6 | 3.101 | 4.099 | 0.9 | 0.996619562 |
| 7 | 3.12 | 4 | 1 | 0.999735669 | 7 | 3.101 | 4.099 | 1 | 1.00023883 | 7 | 3.101 | 4.099 | 1.12 | 0.997680056 |
| 8 | 3.13 | 4 | 1 | 0.999666984 | 8 | 3.101 | 4.095 | 1 | 0.999633209 | 8 | 3.101 | 4.099 | 1.02 | 0.998271164 |
| 9 | 3.101 | 4 | 1 | 0.999840687 | 9 | 3.101 | 4.01 | 1 | 0.979899498 | 9 | 3.101 | 4.099 | 1.075 | 0.998155588 |
| 10 | 3.111 | 4 | 1 | 0.999789719 | 10 | 3.101 | 4.12 | 1 | 1.00526005 | 10 | 3.101 | 4.099 | 1.081 | 0.998111584 |
Computing the best values (a,b,c) to generate 3-scrolls (round=2).
| cycle | a | b | c | ñx1y1 | cycle | a | b | c | óx1/óy1 | cycle | a | c | c | ñx1y1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3.101 | 4.099 | 1.05 | 0.998273115 | 1 | 2.989 | 4.099 | 1.05 | 1.04527827 | 1 | 2.989 | 3.919 | 1.05 | 0.996647785 |
| 2 | 3.001 | 4.099 | 1.05 | 0.998964468 | 2 | 2.989 | 3.999 | 1.05 | 1.02181217 | 2 | 2.989 | 3.919 | 1.1 | 0.995180368 |
| 3 | 3.005 | 4.099 | 1.05 | 0.998957072 | 3 | 2.989 | 3.99 | 1.05 | 1.01962827 | 3 | 2.989 | 3.919 | 0.999 | 0.997626434 |
| 4 | 2.99 | 4.099 | 1.05 | 0.998974210 | 4 | 2.989 | 4 | 1.05 | 1.02205408 | 4 | 2.989 | 3.919 | 1 | 0.997612520 |
| 5 | 2.999 | 4.099 | 1.05 | 0.998967412 | 5 | 2.989 | 4.01 | 1.05 | 1.02446504 | 5 | 2.989 | 3.919 | 0.99 | 0.997741899 |
| 6 | 3 | 4.099 | 1.05 | 0.998966004 | 6 | 2.989 | 3.89 | 1.05 | 0.994543691 | 6 | 2.989 | 3.919 | 0.9 | 0.997888097 |
| 7 | 2.991 | 4.099 | 1.05 | 0.998974033 | 7 | 2.989 | 3.899 | 1.05 | 0.996863328 | 7 | 2.989 | 3.919 | 0.91 | 0.997965728 |
| 8 | 2.98 | 4.099 | 1.05 | 0.998969171 | 8 | 2.989 | 3.9 | 1.05 | 0.997120307 | 8 | 2.989 | 3.919 | 0.92 | 0.998019246 |
| 9 | 2.989 | 4.099 | 1.05 | 0.998974373 | 9 | 2.989 | 3.95 | 1.05 | 1.00977557 | 9 | 2.989 | 3.919 | 0.95 | 0.998037860 |
| 10 | 2.9891 | 4.099 | 1.05 | 0.998974362 | 10 | 2.989 | 3.919 | 1.05 | 1.00197396 | 10 | 2.989 | 3.919 | 0.951 | 0.998034872 |
Computing the best values (a,b,c) to generate 5-scrolls (round=5).
| cycle | a | b | c | ñx1y1 | cycle | a | b | c | óx1/ó y1 | cycle | a | b | c | ñx1y1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2.97 | 4.025 | 0.91 | 0.998664638 | 1 | 2.9 | 4.025 | 0.91 | 1.00767485 | 1 | 2.9 | 3.99 | 0.91 | 0.999533088 |
| 2 | 2.98 | 4.025 | 0.91 | 0.998552665 | 2 | 2.9 | 4 | 0.91 | 1.00270091 | 2 | 2.9 | 3.99 | 0.9 | 0.999591084 |
| 3 | 2.975 | 4.025 | 0.91 | 0.998609587 | 3 | 2.9 | 3.99 | 0.91 | 1.00068775 | 3 | 2.9 | 3.99 | 0.95 | 0.999104651 |
| 4 | 2.96 | 4.025 | 0.91 | 0.998768871 | 4 | 2.9 | 3.8 | 0.91 | 0.959709635 | 4 | 2.9 | 3.99 | 0.99 | 0.998378664 |
| 5 | 2.95 | 4.025 | 0.91 | 0.998864832 | 5 | 2.9 | 3.9 | 0.91 | 0.981940075 | 5 | 2.9 | 3.99 | 0.89 | 0.999628735 |
| 6 | 2.94 | 4.025 | 0.91 | 0.998951961 | 6 | 2.9 | 3.91 | 0.91 | 0.984080496 | 6 | 2.9 | 3.99 | 0.8 | 0.998994565 |
| 7 | 2.93 | 4.025 | 0.91 | 0.999029672 | 7 | 2.9 | 3.93 | 0.91 | 0.988317633 | 7 | 2.9 | 3.99 | 0.895 | 0.999612474 |
| 8 | 2.92 | 4.025 | 0.91 | 0.999097350 | 8 | 2.9 | 3.95 | 0.91 | 0.992497265 | 8 | 2.9 | 3.99 | 0.891 | 0.999625895 |
| 9 | 2.9 | 4.025 | 0.91 | 0.999199909 | 9 | 2.9 | 3.97 | 0.91 | 0.996620319 | 9 | 2.9 | 3.99 | 0.889 | 0.999631367 |
| 10 | 2.91 | 4.025 | 0.91 | 0.999154351 | 10 | 2.9 | 3.98 | 0.91 | 0.998660927 | 10 | 2.9 | 3.99 | 0.88 | 0.999645690 |
It is significant to observe from Tables 1 and 2 that the values for the parameters (a,b,c) are chosen with more digits as the number of cycles increases.
This is related to the required precision for the CoCo and STD in order to satisfy the synchronization error in (10), (11) and (12). As a function of the synchronized states, we search for the best values for the parameters.
After five rounds, we found (a,b,c) = (3.17, 4.23,1.12), which are quite similar as the ones used in references [10-11] for (1), where (α,β,γ) = (3,4,1). To generate 5-scrolls, the values computed after five cycles were (a, b,c) = (2.90,3.99,0.88) as given in Table 3. In addition, by using the ideal values (α,β,γ) = (3, 4,1) in both the master and slave systems, the CoCo and STD are given in Tables 4 and 5.
From Tables 4 and 5, we observe that the behavior between the numerical time series continues similar although the high-resolution is a few lost. For the case under study, this fact does not matter because we can adapt those relationships using some external electronic device as will be shown in the next section.
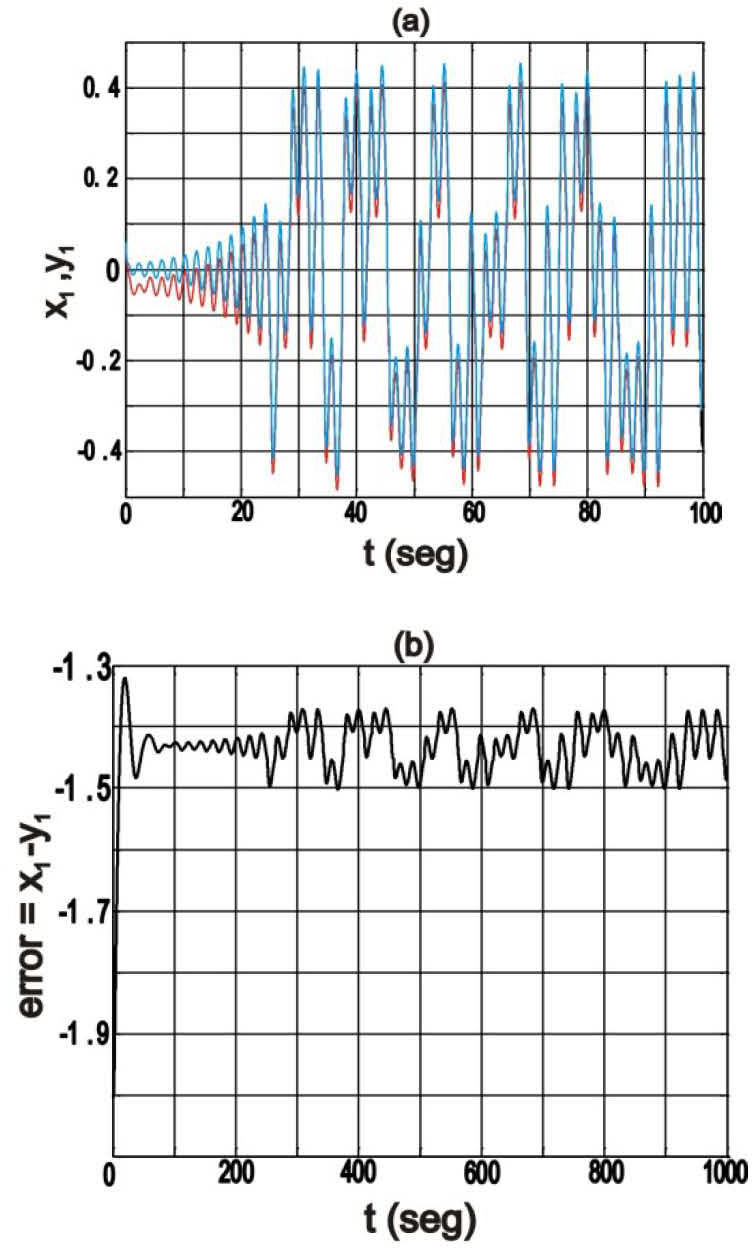
In Figure 2, we show the 3-scroll chaotic attractors of the master and slave systems already synchronized. Additionally, Figure 3(a) shows the time evolution of the state-variables (x1, y1).
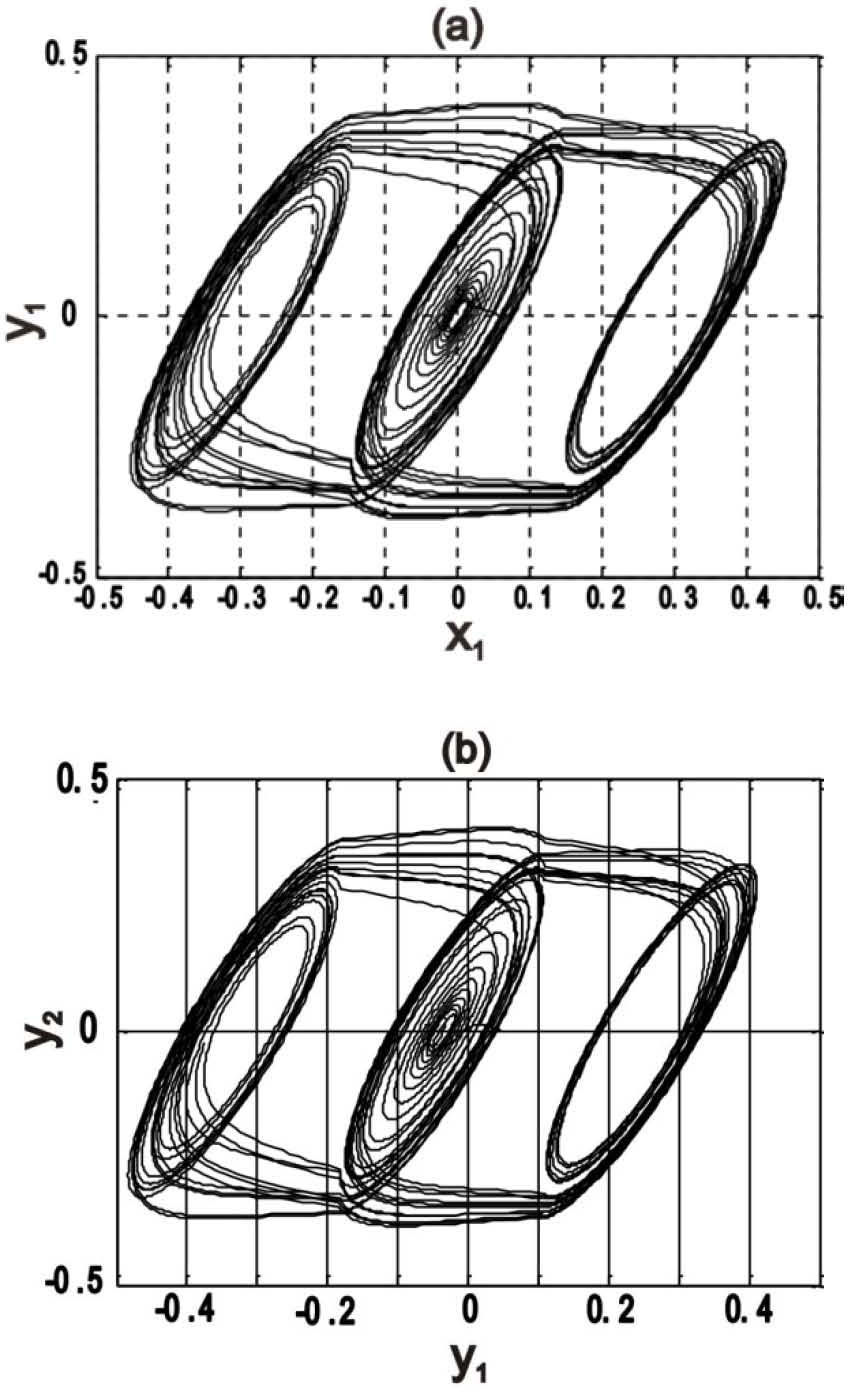
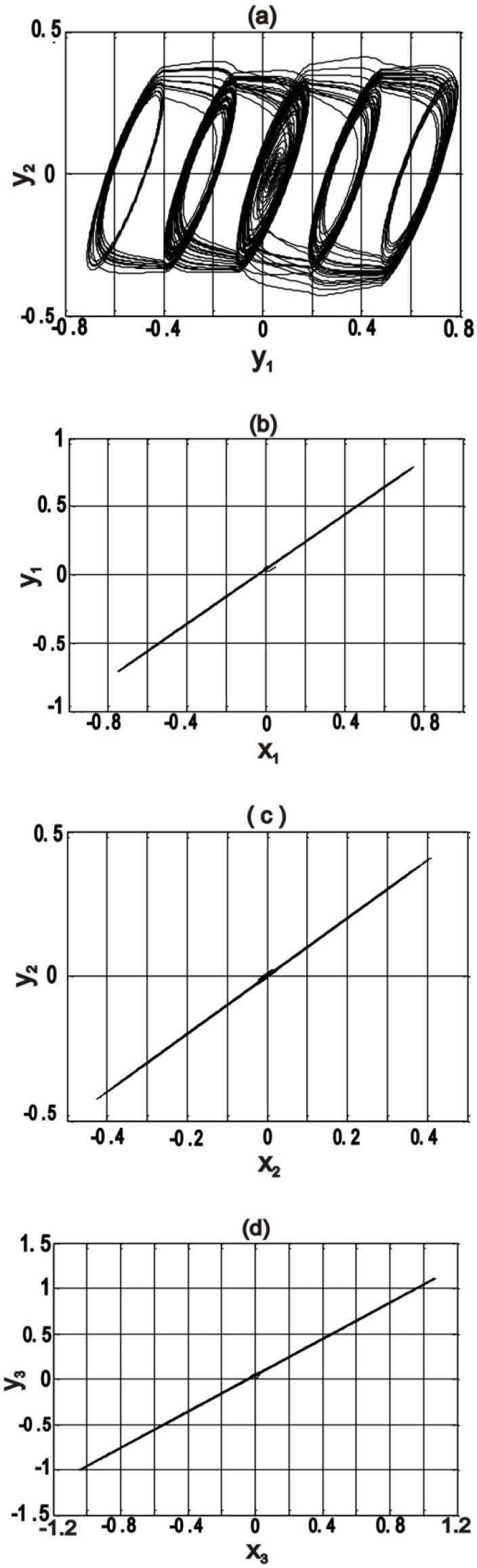
Considering that this simulation was computed using the normalized Chua’s system, we obtain the synchronization after 20 seconds. Also, the synchronization error for this case is shown in Figure 3(b), where its magnitude is suitable. Related to 5-scrolls case, Figure 4(a) shows its chaotic attractor.
Figures 4(b), 4(c) and 4(d) show the synchronization in the phase space for (x1, y1), (x2, y2) and (x3, y3), respectively.
A straight line on those phase space diagrams represents a minimum synchronization error. Therefore, our algorithm is appropriate to synchronize integrated chaotic systems as previously shown.
5Experimental RealizationThe experimental results of synchronizing two double scroll Chua’s chaotic oscillators were given in [2], but by using the commercially available CFOA AD844 in CCII+ configuration. Contrary to that, in this section we show the synchronization results using the IC introduced in [10-11] for the case with 3-scrolls.
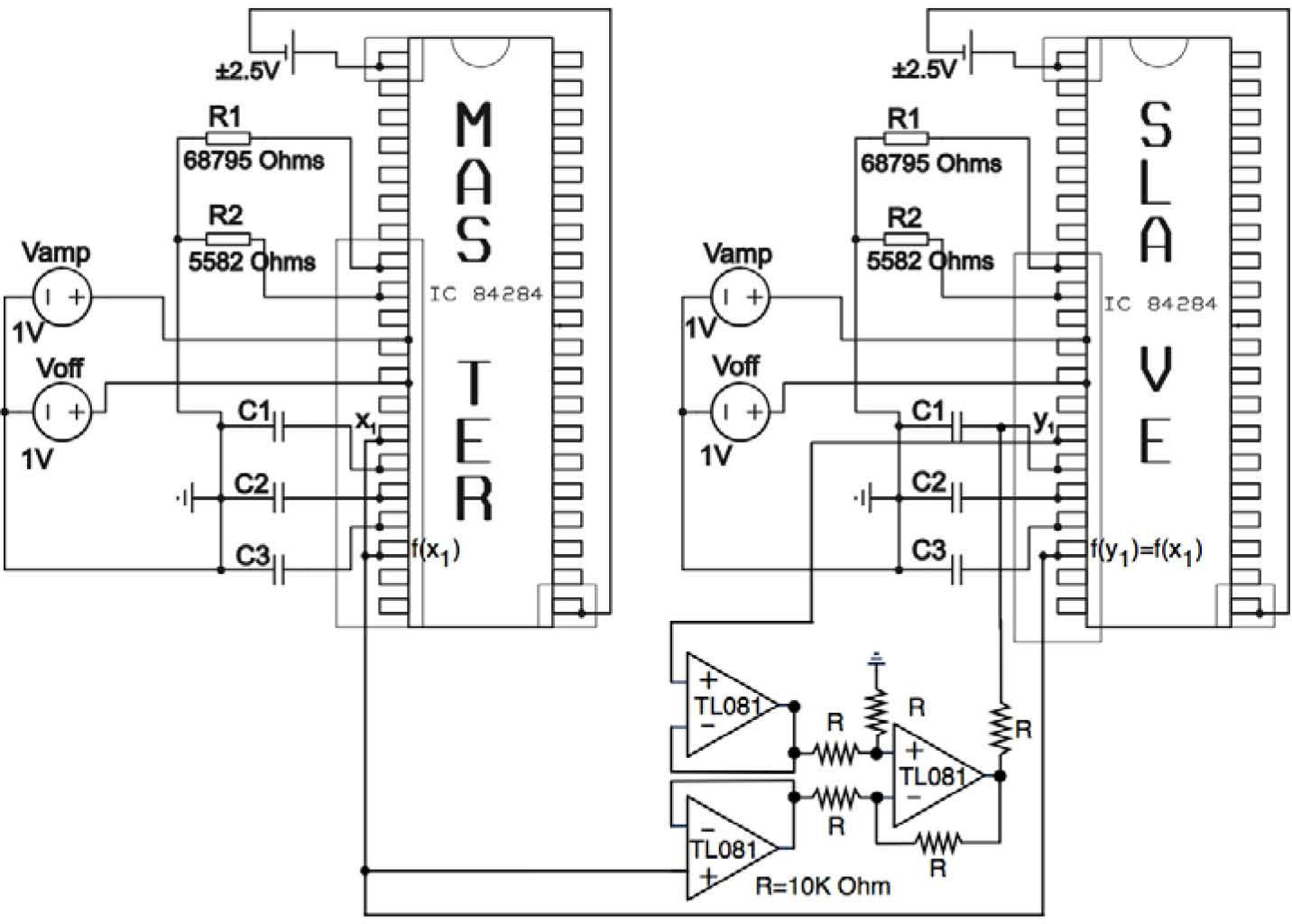
Henceforth, we propose the experimental setup of the synchronization approach as shown in Figure 5. The values of the external elements, as well as the chip pinouts, are setting as given in [10-11]. As was demonstrated in section 3, the synchronization error is asymptotically stable when the nonlinear function of the slave-system is controlled directly by a state from the master. According to that, we take from an integrated analog output buffer, a sample of the chaotic signal of the state x1 (master) marked in Figure 5. Note that this output controls the nonlinear function of slave system f(y1).
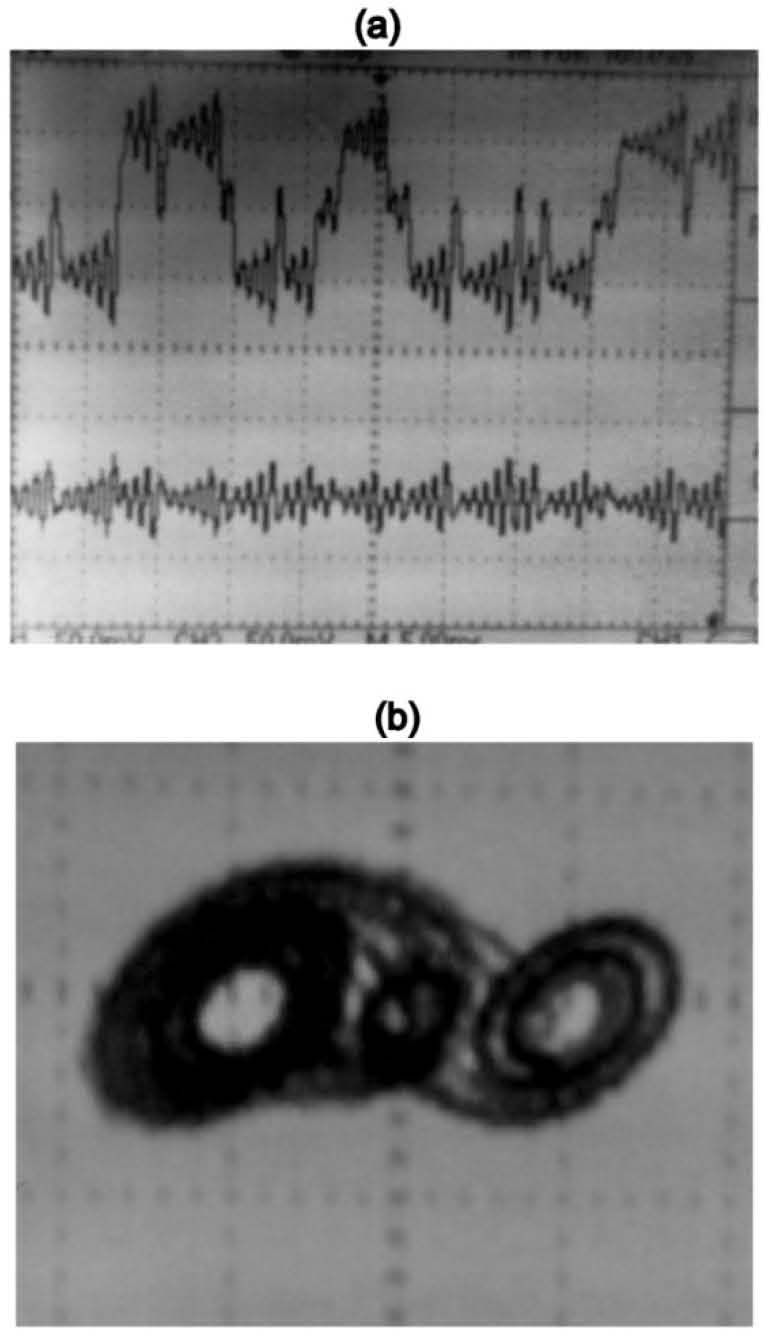
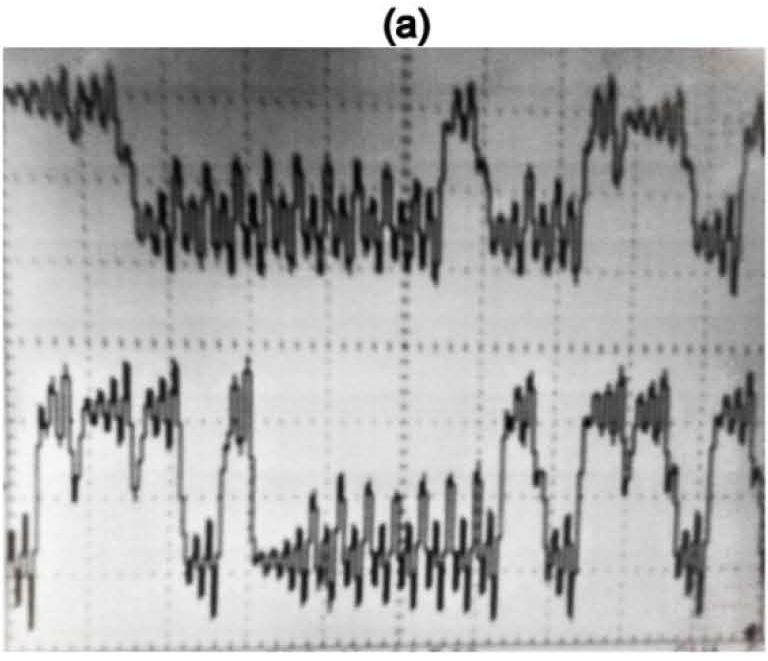
The differential amplifier compares the voltages generated from states x1 and y1. This difference is injected as a current by the voltage-to-current converter resistor at the bidirectional current pin of the integration capacitor C1. This means that the voltage variation in the integration capacitor at the slave system depends on two voltages, one from itself and another from the master system. In this manner, the synchronization is possible when the error (x1−y1) tends towards zero as the feedback current reduces. Figure 6 shows two states (x1, x2) of the master system and their chaotic attractor.
Figure 7 shows the states (x1, y1) and (x2, y2), respectively. Finally, the phase space diagram for (x2, y2) and its synchronization noise are shown in Figure 8.
Figure 8(a). Phase diagram for the synchronization of Figure 7(b) with 20mV/div, (b) Synchronization noise between master and slave systems with 50mV/div.
From those experimental results, we observe a suitable synchronization because of the synchronization error agrees with (10), (11) and (12). At experimental level, the noise-level of the reported synchronization scheme is negligible (<5mv); which is suitable for voltage-mode signal processing of several engineering applications.
6ConclusionWe showed the synchronization of two multi-scroll chaotic oscillators by applying a straightforward method [13]. Contrary to traditional methods, it was demonstrated that the proposed approach is useful to synchronize integrated chaotic systems if the conditional Lyapunov exponents have negative real parts. Therefore, the synchronization is achieved no matter the values for the initial conditions of the synchronization scheme. The synchronization approach was based on a master-slave topology with unidirectional coupling.
The optimal parameters for the synchronization were found from the correlation coefficient and standard deviations computed between the chaotic signals generated by the master and slave systems. Although using a low-resolution for those statistical measures, we found that the synchronization is possible. This is vital because integrated circuits can have variations that could alter the ideal values of system parameters causing losing the synchronization. The numerical simulation results were presented for the chaotic oscillators generating 3- and 5-scrolls, while the experimental results were presented for the chaotic oscillators generating 3-scrolls. In this last case, we used the IC already designed and fabricated with technology of 0.5um of [10-11]. Both, the numerical simulations and the experimental results show a correct synchronization between two integrated chaotic oscillators.
This work has been partially supported by SEP PROMEP and VIEP-BUAP under Projects BUAP-PTC-359 and 2014-VIEP Grants, respectively.
The authors would like to gratefully acknowldege CONACyT for the support under grant 131839-Y.







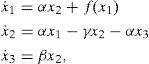
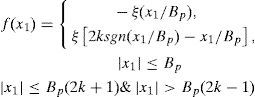

![Integrated chaotic oscillator taken from [10-11]. Integrated chaotic oscillator taken from [10-11].](https://static.elsevier.es/multimedia/16656423/0000001200000003/v2_201505081651/S1665642314716268/v2_201505081651/en/main.assets/thumbnail/gr1.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)