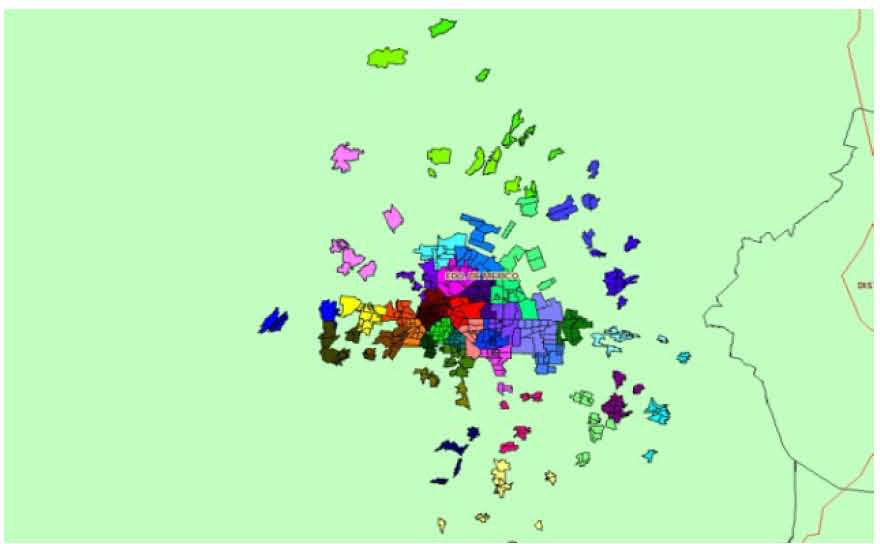
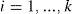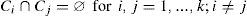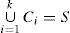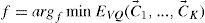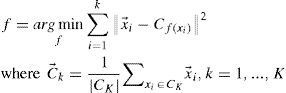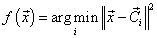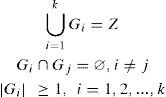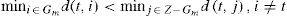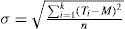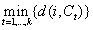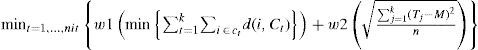The zones design occurs when small areas or basic geographic units (BGU) must be grouped into acceptable zones under the requirements imposed by the case study. These requirements can be the generation of intra-connected and/or compact zones or with the same amount of habitants, clients, communication means, public services, etc. In this second point to design a territory, the selection and adaptation of a clustering method capable of generating compact groups while keeping balance in the number of objects that form each group is required.
The classic partitioning stands out (also known as classification by partition among the clustering or classification methods [1]). Its properties are very useful to create compact groups.
An interesting property of the classification by partitions resides in its capability to group different kinds of data. When working with geographical data, such as the BGU, the partitioning around medoids algorithms have given satisfactory results when the instances are small and only the objective of distances minimization is optimized. In the presence of additional restrictions, the K-medoids algorithms, present weaknesses in regard to the optimality and feasibility of the solutions.
In this work we expose 2 variants of partitioning around medoids for geographical data with balance restrictions over the number of objects within each group keeping the optimality and feasibility of the solution. The first algorithm considers the ideas of k-meoids and extends it with a recursive constructive function to find balanced solutions. The second algorithm searches for solutions taking into account a balance between compactness and the cardinality of the groups (multiobjective). Different tests are presented for different numbers of groups and they are compared with some results obtained with Lagrange Relaxation. This kind of grouping is needed to solve aggregation for Territorial Design problems
El diseño de zonas ocurre cuando pequeñas áreas o unidades geográficas básicas (UGB) deben ser agrupadas en zonas que resulten aceptables según los requerimientos impuestos por el problema estudiado. Estos requerimientos pueden ser la generación de zonas conexas y/o compactas o con la misma cantidad de habitantes, clientes, medios de comunicación, servicios públicos, etcétera. En este punto, es exigido para el diseño de un territorio, la selección y adaptación de un método de agrupamiento que genere grupos compactos satisfaciendo también balanceo en el número de objetos que integran los grupos.
Dentro de los métodos de agrupamiento o clasificación, destaca el particionamiento clásico (llamado también clasificación por particiones [1]). Sus propiedades son muy útiles en la creación de grupos compactos.
Un aspecto importante de la clasificación por particiones reside en su capacidad para agrupar distintos tipos de datos. Si de datos geográficos se trata, como lo son las UGB, los algoritmos particionales alrededor de los medoides han dado resultados satisfactorios cuando las instancias son pequeñas y solo el objetivo de minimización de distancias es optimizado. En presencia de restricciones adicionales, los algoritmos K medoides, presentan debilidades en la optimalidad y factibilidad de la solución.
En este trabajo exponemos 2 variantes de particionamiento sobre medoides para datos geográficos con restricciones de balanceo en el número de objetos que forman los grupos manteniendo optimalidad y factibilidad. El primer algoritmo considera los principios de k-medoides y lo extiende con una función recursiva y constructiva para encontrar solucione balanceadas. El segundo algoritmo se ocupa en la búsqueda de soluciones considerando un esquema de equilibrio entre compacidad y balanceo (multiobjectivo). Se presentan distintas pruebas para el tamaño de los grupos y se comparan con algunos resultados obtenidos por Relajación Lagranjeana. Este tipo de agrupamiento se hace necesario en la resolución de agregación con homogeneidad en la cardinalidad de los grupos para problemas de Diseño de Territorio.
The zones design problem can be approached as a combinatory optimization problem, where the objective function searches for the best combination between the balance for a certain property of the zones and geometrical compactness whereas the restrictions guarantee the connectivity within the zones. Many efforts about the solution of TD problems have been reported: The zones design appears in diverse application such as districts design [2, 3, 4, 5], sales territories [6, 7], service and maintenance areas [8, 9] and use of lands [10, 11, 12].
In the algorithms implicit to solution of TD problems, is desired that all the zones are balanced in regard to one or many properties of the geographic units that form them. For example, zones that have the same workload can be designed, same transfer times or the same ethnic or socio-economical representation percentage. In general, it isn’t possible to achieve the perfect balance; therefore the deviation with respect to the ideal arrangement is calculated. The bigger the deviation, the worse the balance of the zone or the generated zoning plans.
On the other hand, geometric compactness is understood as a condition that tries to avoid the creation of zones with irregular shapes and pursuits the generation of zoning plans with clear boundaries. In the practice it has been observed that the compact zones are easier to manage and to analyze due to the fact that the transfer times and the communication issues are decreased (sampling, districting, location-allocation, etc.). It must be observed that the population balance and the geometric compactness are objectives that are opposed, because an improvement in one of them can cause the other to deteriorate.
Attaining homogeneity in TD is very important in diverse applications that demand an equal resources proportion allocated to every zone. For example, in our population sampling the homogeneity is related to the samplers’ effort, in sales this is understood as the fair demand of the salespeople for every sale point, in logistics, as the effort to distribute the products to the clients.
In TD problems, the clustering algorithm has the job to create groups of compact and balanced zones with regards to the specific same number of geographic units in every group (zone) criterion. The procedure to group data is also known as cluster analysis.
The importance of cluster analysis resides in finding clusters directly in the data without using any previous knowledge. The use of clustering in diverse areas is beneficial, however, in order to have efficient cluster analysis techniques; there must be some kind of similarity between the data. Several researchers propose its use in spatial data, given the existence of distance notions and partitioning around medoids algorithms, they are adapted with ease to this kind of data [13]. In particular, the model PAM (Partitioning Around Medoids), has been important in the latest works about territorial partitioning [14]. PAM achieves this purpose determining an object, representative for each cluster to find k clusters (groups) [14]. This representative object, called medoid, is the one located closer to the center of the cluster. Once the medoids have been selected, each unselected object is grouped with the medoid that is more similar to itself. In this point, an evident weakness of PAM is the process of repeated and long local searches in the solution space; however, it obtains a good “optimum” solution. On the other hand, when additional restrictions are incorporated, the complexity nature increases considerably.
In this work, we have adapted to PAM a homogeneity restriction to balance the number of objects in each cluster. Two algorithms have been implemented: 1) PAM-RH (Algorithm 1): Recursive PAM with homogeneity, where the objects are assigned as usual to the medoids (the closest one) and once every object is assigned, a recursive and constructive procedure is run over this compact solution to adjust it to the desired balance restriction, this implies that the stronger the restriction the higher the complexity of this procedure will be and therefore the computing time will increase considerably in exchange for a well-balanced solution. This adjust looks for the clusters which size is under the ideal size (the number of geographical units, divided by the number of groups to form) and proceeds move objects from the closest group to the group that needs them to achieve balance, but if this group is also under the ideal size then the algorithm will have to move objects from another nearby group to this group. This implies a recursive procedure that will be executed until there is a balance in the number of objects assigned among the clusters.
2) Bi-Objetive PAM (ALGORITHM 2): This algorithm uses a multiobjective function, following the principle of the weighted sum, where each of the objectives has a weight or priority. The extension to PAM is over the objective function that now employs a heterogeneity minimization strategy, this is, the minimization of the standard deviation of the number of objects in each groups to the ideal size of the groups. This will be further explained later in the paper. In accordance to above the present work is organized as follows: this introduction as section 1, section 2 deals with the general aspects of partitioning around the medoids, in section 3 a partitioning algorithm around medoids under a recursive scheme is exposed to continue with section 4 that covers the partitioning with a multiobjective perspective: geometric compactness and balance. Section 5 gathers the final results of the computational experience. Finally the conclusions are presented.
2Preliminaries: PartitioningClustering is the process of grouping a set of objects into classes or clusters so that objects within a cluster have similarity in comparison to one another, but are dissimilar to objects in other clusters. K-means clustering and Partitioning Around Medoids (PAM) are well known techniques for performing non-hierarchical clustering [14].
Let us describe the clustering problem formally. Assume that S is the given data set x→1,...,x→n, where x→i∈Rn. The goal of clustering is to find K clusters C1, C2,..., Ck such that Ci ≠ Ø for
and the objects belonging into same cluster are similar in the sense of the given metric, while the objects belonging into different cluster are dissimilar in the same sense. In other words, we seek a function f:S → {1,...,k} such that for i = 1,..., k: Ci= f−1(i), where ci satisfy the above conditions.
Therefore instead of function f directly, one can search for the centers of the clusters, i.e, vectors c→1,...,c→K, and implement the function f as
that is, assign the point to the cluster corresponding to the nearest center [15].
2.1Sensibility of the partitioning in K-MedoidsWhen the clustering is not of the hierarchical kind, it is known as automatic classification or group analysis. The partitioning methods are also known as optimization methods due to the fact that they reach a unique classification that optimizes a predefined criteria or objective function, without producing a series of nested groups.
One of the most known methods in the literature is k-medoids, and just like dynamic clouds, they are based on the principle that a class can be represented by an object, being this an average point, and individual or group of individuals of the class, a set of parameters, etc; this representative is usually known as kernel. The first algorithm of this kind was proposed by Forgy (1965) [16]. The underlying idea is that given a set of kernels, the following steps must be done: • assign the individuals to the closest kernel, thus forming the classes to proceed with the calculation of the new kernels with the formed classes, • iterate the previous steps until stability is achieved. It parts from an initial configuration of kernels, and the method converges to a partition that doesn’t improve the criteria anymore. Depending on the context and the kind of kernel, a criterion to be improved is defined.
In general, k-medoids is fragile in regard to: 1) the sensibility of the initial selection of the centroids, 2) the prior selection of the value of k, 3) Handling of non-numerical attributes, 4) poor efficiency in the groups of different size, different density and non-convex clusters and 5) with the use of a measure to calculate the centroids, the method is sensitive to outliers.
2.2K-Medoids algorithmOne of the answers to the weaknesses of k-means has been the proposals of algorithms over medoids: instead of using the vector of means as centroids, a vector corresponding to a real data (a representative) is used where k-medoids uses medians instead of means to limit the influence of the outliers.
Due to fact that the K-means algorithm is sensitive to outliers since an object with an extremely large value may substantially distort the distribution of data. How could the algorithm be modified to diminish such sensitivity? Instead of taking the mean value of the objects in a cluster as a reference point, a Medoid can be used, which is the most centrally located object in a cluster. Thus the partitioning method can still be performed based on the principle of minimizing the sum of the dissimilarities between each object and its corresponding reference point. This forms the basis of the K-Medoids method. The basic strategy of K-Mediods clustering algorithms is to find k clusters among n objects by first arbitrarily finding a representative object (the Medoids) for each cluster. Each remaining object is clustered with the Medoid that is the most similar. K-Medoids method uses representative objects as reference points instead of taking the mean value of the objects in each cluster. The algorithm takes the input parameter k, the number of clusters to be partitioned in a set of n objects. A typical K Mediods algorithm for partitioning based on Medoids or central objects is as follows:
Input:
K: The number of clusters
D: A data set containing n objects
Output:
A set, of k clusters, that minimizes the sum of
the dissimilarities of each object to its
nearest medoid.
Method: Arbitrarily choose k objects in D as
the initial representative objects;
Repeat:
Assign each remaining object to the cluster
with the nearest medoid;
Randomly select a non medoid object Orandom;
compute the total points S of swap point Oj
with Oramdom
if S < 0 then swap Oj with Orandom to form the
new set of k medoid
until no change
Like this algorithm, a Partitioning Around Medoids (PAM) was one of the first k-Medoids algorithms introduced. It attempts to determine k partitions for n objects. After an initial random selection of k medoids, the algorithm repeatedly tries to make a better choice of medoids [17].
3Recursive partitioning around medoidsThe majority of the problems of territorial design TD demand geographical clustering. This kind of clustering pursues the compactness, contiguity, convexity and homogeneity of the groups to be created for restrictions that define a specific problem [18, 19, 20]. Different authors have adapted clustering algorithms to solve the TD problems, however, we have focused on taking advantage of the properties of the partitioning around medoids to solve the compactness and in this section we present a partitioning algorithm over medoids that considers in the clustering, geographical data known as Agebs. To answer to the compactness, each geographical unit i is assigned to the closest group representative (medoid). Seen as an optimization problem, the objective function is minimizing the total distance, that is, the sum of the distances of each geographical unit to its respective centroid [20]. Treating the problem in this way the formation of compact groups of geographical units is achieved, however, some problems require a balance on the number of objects that form the groups (groups with the same amount of elements). Then, for n geographical units and k groups to form, each group must have n/k members when n can be split exactly into k groups or |n/k| + 1 otherwise. We denominate this problem as homogeneity in the number of elements. The combination of compactness and homogeneity is treated in this section in an algorithm around medoids with a recursive approach.
3.1PAM-Recursive Homogeneous: Algorithm for compactness and homogeneity in the number of objects (PAM-RH)Considering the capabilities of PAM an algorithm has been built that acts as a post-process in the objective function of PAM, this is, a process that will rearrange the solutions obtained to force the desired balance in the solution.
For n elements to group and k groups to form, having each group with nk elements is desired when these n elements can be split exactly into k groups or in a maximum of nk+1 otherwise. For a group j ∈ {0,...,k − 1} let size Ej be the expected size of j which is calculated with the principle of homogeneity described above. If sizej is the current size of the group j, the group with the least amount of elements is selected (in order to choose the group that will need the most elements to achieve its expected size) to continue with the procedure recursiveHomogeneityAdjust() that is described in the following algorithm:
ALGORITHM 1PAM RECURSIVE HOMOGENEOUS (PAM-RH)
INPUT the centroid j of the group found with
the least elements
INPUT array of centroids
INPUT toSteal – the amount of elements that the
group j needs to “steal” to become of the
expected size.
INPUT cost – the current cost (compactness) of
the unbalanced solution
PROCEDURE recursiveHomogeneityAdjust(j,
centroids, toSteal, cost)
Get the centroid i closest to j;
surplus←sizei – sizeEi;
IF toSteal< surplus THEN
Stack.push(j, toSteal);
WHILE !stack.empty() DO
Node ←stack.pop();
FOR h ← 0 TO h
Move an object from i to j;
//The closest one. Update the cost of the
solution;
END LOOP
END LOOP
ELSE
Stack.push(j, toSteal);
toSteal = toSteal – surplus;
recursiveHomogeneityAdjust(i, centroids,
toSteal, cost);
END IF
END PROCEDURE
The algorithm does the following: It takes as input, the centroid j of the group found with the least elements (this will ensure the complete balance of the solution after the procedure ends), the array of centroids (the current solution), the elements that the cluster j needs (to reach the ideal size) and the current cost of the solution. The first step is to find the closest centroid to the cluster j, this will tell us which one is the closest cluster. Then the surplus of i will be calculated, if the expected size is bigger than the current size of cluster I (sizei – sizeEi) then we’ll have a surplus of elements in that group, otherwise the value will be negative and therefore this group will need to get more elements from another group as well. Next if the elements that cluster j needs to “steal” are less than the surplus of cluster i then we employ an auxiliary stack to store the number of cluster (centroid) and the number elements it needs, this step is done so when the recursion occurs we will have the clusters that need elements stored in here. The following step is a cycle that will finish when this stack is empty. Inside this cycle we take out the element at the top of the stack to move the elements from i to j that are needed and then the cost of the solution is updated.
This is the basic case if the procedure is executed once, the other case is when the elements needed by j can’t be taken from the closest group i, and in this case we store the cluster j and the elements needed. Note that with a negative surplus the new value of toSteal will be increased, this means that cluster i will need to get enough elements from another group to satisfy its own need and the need of cluster j but when the value of surplus is positive but still less than toSteal, this last one decreases because now cluster i will give its surplus of elements to cluster j but will need some more to keep its balance. After this calculation the recursion takes place, now cluster i will be the new cluster used as parameter along with its elements needed. Following this example, let’s assume that we have a total of 3 clusters, so the next cluster, closest to i, let’s call it h has the biggest surplus and therefore has enough elements to give to i and j, this means that toSteal is less than surplus and now we push cluster i to our stack, the cycle will run two times (the size of our stack that right now contains clusters j and i). We take out cluster i and move enough elements from cluster h to i so i can have enough to give to cluster j and remain balanced. Finally cluster j is removed from the stack and we assign the nodes needed to j from the surplus of cluster i and we finish by updating the cost of the solution accordingly.
A vulnerable aspect of this algorithm lies in the dispersion of elements due to those cases where a group that contains many elements (in a much bigger proportion to the other groups) must lend a great percentage of objects to other groups. The implication of this conflict is centered in this big group that will give away many of its objects and until after several iterations the problem seems to invert itself due to the fact that the centroid starts to be surrounded by objects that now belong to other clusters because a cluster can’t give away its own centroid. This case is distinguished as the group formed by objects taken from other groups that in the first iterations had more objects than the rest of the groups. The problem of dispersion occurs usually for cases of 40 groups or more and it is possible to notice that the computational cost increases in function of the number of groups. For this algorithm PAM-RH, good optimal and feasible results have been achieved with a satisfactory homogeneity for no more than 40 groups but the homogeneity achieved has a precise balance over the cardinality of the groups.
The following Table 1 concentrates the results between 4 and 40 groups where 469 objects were grouped; the results that don’t go beyond 800 seconds. The data correspond to the Metropolitan Zone of the Toluca Valley in Mexico (ZMVT). In this table we included two results obtained with PAM alone for 14 and 40 groups to show that PAM on its own can’t reach a satisfying balance or homogeneity. In this table the nomenclature is the following: G (number of groups), Smallest (The size of the smallest group obtained), Biggest (The size of the biggest group obtained), Time (Execution time of the algorithm in seconds).
Test runs for algorithm PAM-RH (Algorithm 1) and two example runs with PAM.
| G | Smallest | Biggest | Cost | Time | Algorithm |
|---|---|---|---|---|---|
| 4 | 117 | 118 | 27.385883 | 4.107 | PAM-RH |
| 8 | 58 | 59 | 21.229193 | 17.174 | PAM-RH |
| 12 | 39 | 40 | 15.595103 | 53.385 | PAM-RH |
| 14 | 34 | 35 | 15.056902 | 79.536 | PAM-RH |
| 16 | 29 | 30 | 15.912905 | 54.236 | PAM-RH |
| 20 | 23 | 24 | 13.539497 | 175.536 | PAM-RH |
| 24 | 19 | 20 | 13.045602 | 240.692 | PAM-RH |
| 28 | 16 | 17 | 11.656398 | 229.474 | PAM-RH |
| 32 | 14 | 15 | 10.739399 | 337.512 | PAM-RH |
| 36 | 13 | 14 | 9.507203 | 483.711 | PAM-RH |
| 40 | 12 | 11 | 10.689795 | 715.477 | PAM-RH |
| 4 | 51 | 172 | 27.17601 | 0.0257 | PAM |
| 14 | 10 | 64 | 12.985695 | 3.604 | PAM |
The hardware used for the tests has the following characteristics:
CPU: Dual Core AMD E-350 at 1.6 Ghz.
RAM: 2GB DDR3.
HDD: SATA-II 320GB 5400 RPM
The algorithmic proposals around the Medoids with restrictions over the cardinality of the clusters that we have exposed have produced good results for small instances.
4Partitioning around medoids with Bi-Objective Function (BI-Objective on the standard deviation)The PAM-RH algorithm has many limitations, mainly its complexity for bigger problems because it forces the solutions to be balanced, therefore we can say that it works under hard restrictions and this implies a high computing cost. Due to the fact that we are trying to reach a small fragment of the solution space that contains the desired feasible homogeneous solutions, we have decided to turn this hard restriction into a soft one in order to improve the computing times and to actually guide the search process towards this fragment of the solution space but of course this change implies a penalization over the homogeneity objective since it won’t be a demanded characteristic of the solutions attained [21]. Now our combinatory problem will have two objectives and we have taken the model proposed in [20] to revise it and adapt it to our new need for homogeneity and below we present the definitions of interest along with the adapted model.
Definition 1. Compactness
If we denote Z = {1,2,..., n} as the set of n objects to classify, it is wished to divide Z into k groups {G1, G2,...,Gk} with k < n in such a way that:
A group Gm with |Gm| > 1 is compact if for every object t ∈ Gm meets:
A group Gm with |Gm| = 1 is compact if its object t meets:
The criterion of neighborhood between objects to achieve compactness is given by the pairs of distances described in 1.
Definition 2. Homogeneity (in the number of elements)
Let Ti = |Gi| for i = 1, 2,..., k y M = n/k where n is the number of geographical units and k the number of groups to form. M is the mean or the average amount of elements that correspond to each group (±1 when the n objects can’t be split into k groups exactly). Then the standard deviation is given by:
The standard deviation indicates how deviated from the average size M are the values of the set Ti. Therefore by minimizing the standard deviation, we minimize the unbalance of the solution rather than building already balanced solutions as it is done in the PAM-RH algorithm. The algorithm standard deviation is shown below:
4.1Algorithm standard deviation a (SD)This algorithm can be seen as a complement or extension that can be used with several algorithms, for our work we chose PAM because of reasons explained in section 1. It can be deduced from our previous section (our definitions) that this algorithm is an implementation of a Bi-objective function formed by equation (7) and (8).
The following procedure is the new proposal itself; it is a simple calculation of the standard deviation of an array that contains the sizes of the entire cluster in the partition.
Procedure CalculateSD (procedure 1)
Input: array T that stores the sizes of the
groups.
Input: M average size of the groups (n/k).
Output: σ the standard deviation of the array T
op = 0
fori = 0 hasta k do
op = (Ti – M)2
end for
S2 = op / n
Return √S2
This algorithm can be incorporated to any objective function as a homogeneity measure, for example a tabu search algorithm for clustering could add this procedure as an objective of the objective function. This means that with the proper strategies: initial solution and neighborhoods and search techniques this small procedure could be exploited to achieve even better solutions. In the following section we present our implementation with a simple PAM algorithm to show how it can be embedded in any algorithm and the results we achieved.
4.2Bi-Objective Proposal for compactness + homogeneity partitioning around medoidsLet UG be the total number of Agebs. Let G = {x1, x2,..., xn} be the initial set of geographical units, where: xi is the ith geographical unit, (i is the index of the UG), and k is the number of zones (groups). Given that it is wished to form groups and to refer to these, we define:
Zi as the set of UG that belong to the zone I and Ct is the centroid, and d(i, j) is the Euclidean distance from node i to node j (from one Ageb to another).
Then we have as restrictions: Zi ≠ ø for i = 1, ..., k (the groups are empty), Zi ∩ Zj= ø for i ≠ j (there no repeated Agebs in different groups), and ∪i=1kZi=UG (the union of all the groups is all the Agebs).
Once the number k of centroids has been decided ct, t = 1, ..., k, to use they must be selected in a random way and next assign the Agebs to the centroids in the following way: for each Ageb i
Each Ageb is assigned to the closest centroid ct. To achieve homogeneous cardinality in the groups to form, a weighted sum is done where each value of k is calculated in accordance to the sum of the distances of the AGEBS assigned to each centroid. The obtained value is weighted with w1 and the standard deviation of the sizes of each group represented by Ti is weighted with a value w2 such that the minimum of the sum of both weighted values is chosen. This can be expressed as the equation (9):
This weighed objectives strategy is common in the multiobjective literature, usually the weights of all the objectives should add up to 1. The values of each weight can be determined by means of experiment designs, shadowing, manual setting, etc. [21]. In our case we have experimented with manual tuning to determine that the most adequate weights for our desired goals are .7 for the homogeneity objective and .3 for compactness.
With this new strategy, in each movement, we achieve a minimization of the unbalanced groups and at the same time the compactness. It can be seen as a process that tries to locate the homogeneous solutions in the space where the compactness plays a tie breaker role to determine the best solution from very similar ones in regard to the standard deviation value. The only extension in this case is only over the objective function; therefore the usual assignation of objects to medoids that PAM employs remains the same.
Based on equation (9) (The multiobjective function of compactness plus homogeneity) the following algorithm is built (procedure 2), which is the calculus of the weighted sum of the distances between objects and medoids plus our new homogeneity measure proposal, the standard deviation (procedure 1).
Procedure Bi-objective PAM Function (Procedure
2)
Input: array T that stores the sizes of the
group.
Input: array C of centroids.
Input: weights w1 y w2.
Output: cost the cost of the weighted sum of
objectives.
cost = 0
for i = 0 until n do
j = ClosestCentroid(i,C)
cost = cost + d(i,j)
Tj = Tj + 1
end for
return w1*CalculateSD(T) + w2*cost
The algorithm returns the value of the weighted sum, over which a search procedure like PAM can be guided towards the desired homogeneous solutions without overlooking the compactness needs of many TD problems.
We show bellow how we incorporate this strategy to a PAM algorithm.
ALGORITHM 2Algorithm PAM with Standard Deviation σ: Bi-
Objetive PAM
Input: Dissimilarity matrix of size n x n.
Input: integer k number of groups to form.
Output: A compact and balanced solution.
1: Initialize: Select k of the n objects
as medoids
2: Associate each object to the closest
medoid
3: for each medoid m do
4: for each object no-medoid o do
5: exchange m with o and
compute the total cost of
the configuration using
Bi-Objetive Function.
6: end for
7: end for
8: Select the configuration with the
lowest cost
9: Repeat 2 and 8 until there is no
change in the medoids
It’s easy to observe that algorithm 2 is the same as PAM but in line 5 we employ Procedure 2 as an objective function (line 5), this will make the search process to revolve around this value and will lead the process to balanced solutions eventually.
The following table 2 gathers some important test runs of our Bi-Objective PAM approach in the standard deviation assuming that it makes sense to grant to the weighted sum a partial treat to the homogeneity. In this table 2 a value of .9 for homogeneity has been specified and .1 for compactness. Even though an experiment design wasn’t done, some tests were, taking into account some values for the weights that could be important for a decision maker with regards to each criterion.
Test runs for PAM with Standard Deviation with weights .9 and .1 respectively: Bi-Objective PAM (ALGORITHM 2).
| G | DH | CC | T | LB | BFS |
|---|---|---|---|---|---|
| 2 | 1 | 37.36047363 | 0.03 | 36.09367 | 36.0995 |
| 4 | 3 | 31.2165947 | 0.24 | 27.21939 | 27.2244 |
| 6 | 3 | 31.01499748 | 0.776 | 22.74695 | 22.8878 |
| 8 | 7 | 25.82069206 | 1.311 | 18.97615 | 19.4539 |
| 10 | 14 | 26.65379524 | 1.456 | 16.25054 | 16.3904 |
| 15 | 7 | 14.69729328 | 8.547 | 13.1308 | 13.7122 |
| 20 | 10 | 16.01709747 | 6.059 | 11.222 | 11.3802 |
| 40 | 9 | 7.332001686 | 142.823 | 7.1723 | 8.9053 |
| 60 | 7 | 5.056399345 | 382.308 | 5.55026 | 6.6463 |
| 80 | 10 | 3.856300831 | 672.112 | 4.45614 | 6.4801 |
| 100 | 10 | 3.037899256 | 1047.046 | ||
| 120 | 8 | 2.572799206 | 1258.085 | ||
| 140 | 8 | 2.191200495 | 1745.663 | ||
| 160 | 8 | 1.880400062 | 2427.552 | ||
| 180 | 6 | 1.622200251 | 2334.863 | ||
| 200 | 6 | 1.41950047 | 2552.976 |
It was assumed that due to the important role of homogeneity in this study case, that it should have a bigger weight. It’s important to note in this table that the difference of homogeneity (DH) consists in subtracting the size of the smallest group to the size of the biggest one.
Compactness cost (CC) is the compactness cost and time (T) is the time that the algorithm needed to find a solution and is given in seconds. Lower bound (LB) is the lowest bound obtained with Lagrange Relaxation and Best feasible solution (BFS) is the best solution found [22].
5Compilation of results of the computational experiments.For the test runs of the algorithm, the map ZMVT has been chosen and a Lagrange Relaxation (LR) approach has been used to obtain the lower boundaries of the optimal solution, based on a 10% tolerance of unbalance in the number of elements in each group, this tolerance represents the elements above or below the ideal mean permitted in any given group.
For example, if we have a problem with 500 geographical units and we want to form two groups, this means that the ideal size should be 500 divided by 2 which is 250, then the 10% tolerance means that any of the groups could have a size of ±%10 of 250, this is, one group could have 225 elements and the other one 275.
Thereafter that the optimal values found by the LR are feasible only for this tolerance restriction. The scheme of LR considered was developed for the p-median problem and to get lower boundaries and it was developed in previous works and it is used in this paper due to the strong similarities between the p-median problem and the partitioning problem, not even in the model but also in the results found [22].
In table 3 the test runs for PAM-RH (Algorithm 1) and Bi-Objective PAM (algorithm 2) have been gathered. It’s possible to assume that by assigning .9 as a weight to the homogeneity objective, the results could be better, just as we did on the experiments exposed in table 2, but the randomness of the solutions doesn’t help to emit a safe conclusion like that.
Test runs for Algorithms 1 and 2.
| G | PAM RH (Algorithm 1) | Bi-Objetive PAM (Algorithm 2) | LR | |||||
|---|---|---|---|---|---|---|---|---|
| CC | Gap % | D H | CC | Gap % | DH | LB | BFS | |
| 2 | 36.73 | 1.76 | 1 | 37.22 | 3.12 | 1 | 36.09 | 36.09 |
| 4 | 27.38 | 0.63 | 1 | 30.95 | 13.75 | 5 | 27.21 | 27.22 |
| 6 | 24.32 | 6.88 | 1 | 29.46 | 29.46 | 6 | 22.75 | 22.77 |
| 8 | 21.22 | 11.54 | 1 | 24.44 | 28.44 | 6 | 19.03 | 19.30 |
| 10 | 17.86 | 9.64 | 1 | 17.12 | 5.11 | 12 | 16.29 | 16.30 |
| 15 | 14.67 | 11.54 | 1 | 14.32 | 8.92 | 4 | 13.15 | 13.78 |
| 20 | 13.53 | 19.96 | 1 | 13.08 | 15.91 | 4 | 11.28 | 11.91 |
| 40 | 10.68 | 47.71 | 1 | 7.520 | 3.93 | 8 | 7.236 | 7.96 |
| 60 | 8.894 | 61.65 | 1 | 5.113 | -7.06 | 7 | 5.502 | 6.47 |
| 80 | 6.156 | 39.83 | 1 | 3.888 | -11.69 | 10 | 4.403 | 5.12 |
| 100 | 8.454 | 126.3 | 1 | 3.049 | -18.35 | 9 | 3.735 | 4.88 |
| 120 | 2.588 | 8 | ||||||
| 140 | 2.194 | 8 | ||||||
| 160 | 1.878 | 6 | ||||||
| 180 | 1.621 | 6 | ||||||
| 200 | 1.420 | 4 | ||||||
| 220 | 1.241 | 4 | ||||||
| 240 | 1.089 | 4 | ||||||
| 260 | 0.949 | 4 | ||||||
| 280 | 0.807 | 4 | ||||||
| 300 | 0.680 | 4 | ||||||
Then, after diverse experimental trials for the map that has been used, it has been decided that a good balance for the values of the weighted sum is .7 for homogeneity and .3 for compactness. The results are presented in the following table.
This table deserves different explanations: The gap value is calculated as the compactness cost of the solution minus the lower boundary and this is divided by the lower boundary again.
This value indicates how worse the solution in regard to the lower boundary is. In general, the gap is used to measure the improvement that a boundary cost has over another. In the literature in a wide sense, GAP means Generalized Assignment Problem and to be able to do a numerical study for algorithms like the ones we have developed, the GAP adapts in order to incorporate the LR boundaries and to compare the relationship between the quality of the boundaries and the feasibility of the solution with regards to the exact optimal solution. The value of the boundaries is previously calculated and they are included in the quotient of the gap equation for this purpose. In previous works we obtained the boundaries for compactness [22]. In this article we have included the homogeneity and the compactness gap. In our study case, we have focused on the upper and lower boundaries through the formula gap = (z* − zLP)/zLP ∗ 100, where z* denotes the solution and zLP denotes the lower boundary that corresponds to the linear relaxation of the problem (measures the quality of the solutions found). A very interesting postgraduate document shows good details about LR and GAP [23].
The contrast between Algorithm 1 and LR with respect to compactness indicates that they are very close to the lower boundary and it’s also possible to observe that the homogeneity or balance difference for PAM-RH is only of one object between the groups. On the other hand, as it was explained above, the values obtained with LR obey a 10% tolerance of unbalance for all of the tests; therefore we don’t know the optimal values for a less flexible tolerance like the results generated by Algorithm 1. In other words a first look to the results seems to show that Algorithm 1 reaches to a solution far from the lower boundary in some cases, however it achieves the “perfect” balance for this case due to the fact that the 469 objects can’t be split into equally sized groups, otherwise the homogeneity difference for this algorithm would be 0. With these results we suggest PAM-RH as an algorithm for small problems where the balance is not an option but a necessity.
For bigger problems we have designed a faster but flexible approach, a homogeneity measure that can be implemented in any clustering optimization algorithm to minimize the unbalance of the solutions. Up until 40 groups the results found are within the 10% tolerance boundaries and as the problem grows it seems that the compactness cost improves with respect to the results of Algorithm 1 and the most important feature is the capability to work with bigger problems, unlike Algorithm 1 that was problematic to keep testing for more than 100 groups due to the heavily increased computing times. With this we conclude that algorithm 2 is a very strong option when a decision maker needs to work with a big clustering problem and a greater tolerance for unbalanced solutions is acceptable. The issues with the unbalance are not unexpected, it is known that in multiobjective problems, a constant struggle between the objectives exists and some will be affected and others benefited.
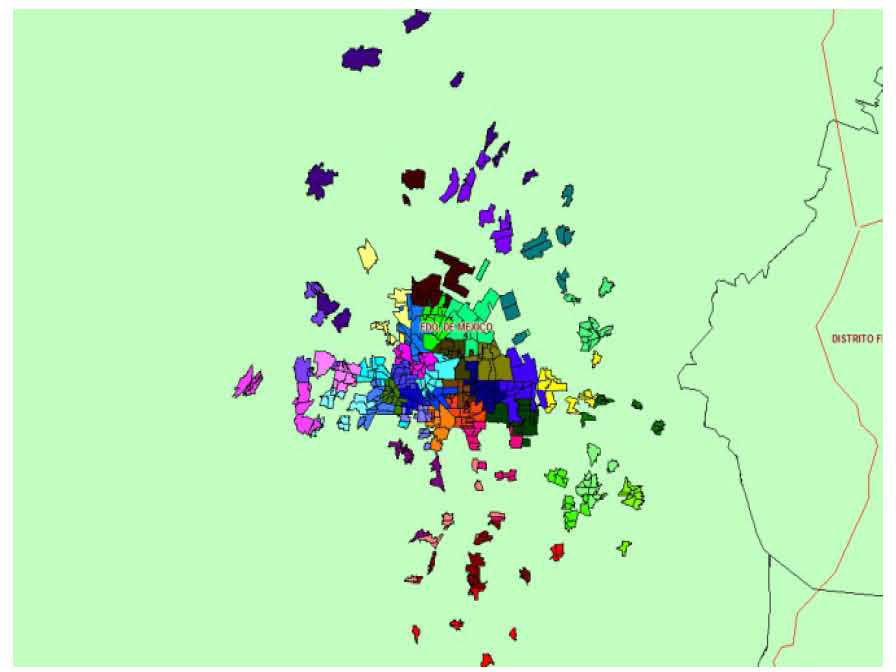
The following figure shows a graphical representation of a solution for 40 groups obtained with Bi-Objective PAM.
This map in figure 2 reveals the problem of homogeneity over 10%. Some groups lose balance not only because of the conflict between the two objectives but also due to the geographical conditions of the data complicate the clustering with the two objectives (compactness and homogeneity), some of the objects are dispersed and not connected
Map for 40 groups (Algorithm 2).
The compactness implied in the classification by partitions has been discussed due to its high computational cost, and in this work we have proven that the complexity is greater when additional restrictions are incorporated to this kind of partitioning. Therefore we propose two solutions, one to deal with the problem in a strict way and another to deal with the high complexity of this problem.
Both algorithms, 1 and 2, are better than the original PAM in regard to homogeneity, attaining compactness just above the ones that PAM obtains without balancing restrictions and in general terms Bi-Objective PAM compared to PAM-RH can work with problems that require a number of groups higher than 100 in an instance of 469 objects.
Algorithm 1 employs PAM improving its objective function with a post-processing of the solution to rearrange it in a balanced one in an iterative and recursive way. This procedure is complex and requires a high computing time as can be observed in table 1. For this, algorithm 2 was developed, that uses a combined objective function where the homogeneity restriction becomes a soft requirement to obtain better solutions for bigger problems in a smaller time (the maximum time is just over 2500 seconds for the biggest instance with an exhaustive algorithm like PAM). This second algorithm can be extended easily to applications with more than 2 criteria; this makes it a very flexible approach.
A not serious flaw from both algorithms is that they barely reach the compactness cost given by LR, however LR has issues to work with the instances of 100 or more groups as well, and in this point our algorithm 2 is a good contribution to achieve bigger groupings. Furthermore algorithm 2 reaches a better compactness for more than 40 groups sacrificing the homogeneity a little.
From the results obtained we have concluded that it is possible to obtain better results in both aspects (compactness and homogeneity) with algorithm 2 if we implement it along with a custom clustering algorithm based on a metaheuristic technique, due to the fact that PAM works with a random initial solution and its search strategy is exhaustive but not necessarily fit to find balanced solutions. Better strategies and techniques adapted to our study case promise better results for our algorithm 2 that has obtained promising solutions with a basic algorithm such as PAM. Also for PAM-RH there’s room for improvement through coding optimization to reduce its complexity.
Currently, we are working with other peers to compare our results with other approaches.