Through introducing two piecewise-linear triangular wave functions in a three-dimensional spiral chaotic Colpitts oscillator model, a four-dimensional grid multiscroll hyperchaotic system is constructed. Interestingly, by adjusting a build-in parameter in a variable of one triangle wave function, the control of the gradient of the multiscroll grid is achieved. Whereas by deploying the zero points of the two triangular wave functions to extend the saddle-focus equilibrium points with index-2 in phase space the scroll numbers do not only increase along with the number of turning points, but they can also generate arbitrary multiples of products. The basic dynamical behaviors of the proposed four-dimensional multiscroll hyperchaotic system are analyzed. Finally, the hardware experimental circuit is designed and the interrelated circuit implementation is realized. The experimental results are in agreement with both theoretical analyses and numerical simulations, which verify the feasibility of the design methods.
In recent decades, chaos theory has been extensively researched in many fields, such as secure communication, synchronization, binary signals transmission and so on [1–3]. Given that chaos can be exploited for potential engineering applications, it is important to develop techniques for designing chaotic attractors with complicated topological structures and complex shapes [4]. Compared with one-direction (1-D) multiscroll chaotic attractors, the grid multiscroll chaotic attractors have become a research hotspot in recent years because of the scrolls in the grid multiscroll chaotic attractors present in two- or multidirection distribution plane, and stereo or multidimension grid shape in phase space [5], which makes the chaotic dynamic behavior more complex.
At present, different kinds of grid multiscroll chaotic attractors are generated by introducing different piecewise-linear (PWL) functions into Chua’s circuit, Jerk system, Colpitts oscillator, piecewise generalized Lorenz system families, and other mode frameworks, and is no longer a very difficult task [6–13, 15–17]. For example, Muñoz-Pacheco et al. [7] introduced the guidelines to synthesize two-direction (2-D) n×m-grid scroll chaotic systems based on saturated functions with multisegments. Lü et al. introduced the hysteresis and saturated functions series approaches for generating 1-D n-scroll, 2-D n×m-grid scroll, and three-direction (3-D) n×m×p-grid scroll chaotic attractors, with rigorously mathematical proof [8] and physical realization [9] for the chaotic behaviors. As is well known, the intrinsic dynamics of the generalized Lorenz system families are confined in the positive half space with respect to the vertical axis because of a limiting threshold effect. In order to break such a threshold effect, Yu et al. [10] introduced a piecewise Lorenz system equipped with a staircase function and an even symmetric PWL function, which could generate various grid multiwing butterfly multiscroll chaotic attractors without requiring any external forcing. Compared with the general chaotic systems, hyperchaotic systems can generate multiple positive Lyapunov exponents, implying that their dynamics are expanded in several different directions simultaneously. It means that hyperchaotic systems have more complex dynamical behaviors that can be used to improve the security of chaotic communication systems. In 2010, Bao et al. [11] constructed a four-dimensional multiscroll hyperchaotic system. By introducing two triangular functions, the system could generate (2M+1)×(2N+1)-scroll chaotic and hyperchaotic attractors. The scroll numbers could increase along with the number of turning points, but the gird of the multiscroll could only generate odd multiples of products by the introduced triangular functions and could not produce arbitrary multiples of products.
In the aforementioned literatures on grid multiscroll chaotic attractor generation, the authors are all concerned with the generation research of standard vertical grid shape in phase space. In order to further improve the complicated topological structures and complex shapes of chaotic attractors. Recently, the oblique grid multiscroll chaotic attractors began to attract the attention among researchers. Yu et al. [12] proposed an approach for generating three-dimensional oblique grid multiscroll chaotic attractors via triangular wave series. The triangular wave series developed here can adjust the swings, widths, equilibrium points, breakpoints, and slopes so as to generate a large number of scrolls with adjustable sizes and shapes. Zhou et al. [13] constructed an oblique grid multiscroll chaotic system by using triangular wave series and step function sequence. However, it can be seen that the gradient of the multiscroll grid cannot be adjusted continuously, and the oblique grid multi-scroll attractors proposed above are not hyperchaotic attractors.
In this paper we propose a new approach for oblique grid multiscroll hyperchaos generation. Through introducing two PWL functions in a four-dimensional linear system and deploying the zero points of the introduced PWL functions, the saddle-focus equilibrium points with index-2 in phase space can be extended. The scroll numbers do not only increase along with the number of turning points, but they can also generate arbitrary multiples of products. Whereas an internal parameter is selected in a variable of one triangle wave function by adjusting the built-in parameter, the distribution of equilibrium points is changed and then the control of the gradient of the multiscroll grid is achieved. The dynamical behaviors of oblique grid multiscroll hyperchaotic system are further investigated, including equilibrium points, the function relation between the built-in parameter and the grid gradient, Lyapunov exponents spectrum and bifurcation diagram. Based on analyses of theory and numerical simulation, the hyperchaotic circuit is designed and the hardware experimentation is realized. The experimental results are in agreement with both theoretical analyses and numerical simulations.
The rest of this paper is organized as follows. In Section 2, a simple grid multiscroll hyperchaotic system is proposed based on a three-dimensional Colpitts oscillator mode. The basic dynamical behaviors of the new system are then investigated in Section 3. In Section 4, a block circuit diagram is constructed for hardware implementation of the oblique grid multiscroll hyperchaotic attractors. Conclusions are finally drawn in Section 5.
2Grid multiscroll hyperchaotic systemThis section introduces a simple four-dimension grid multiscroll hyperchaotic system based on a three-dimensional spiral chaotic Colpitts oscillator model. The numerical simulations of vertical grid multiscroll chaotic attractors and oblique grid multiscroll hyperchaotic attractors are also given.
2.1Chaotic system mathematical modelBecause the three-dimensional spiral chaotic Colpitts oscillator [14] is simple in structure and easy to realize, different kinds of multiscroll chaotic attractors based on its model have proposed by many researchers in recent years [11, 15, 16].
In this paper we have made some improvements on the basis of [11] and [14] in two aspects.Firstly, by introducing two PWL triangular wave functions into the three-dimensional spiral chaotic Colpitts oscillator model, a simple four-dimension hyperchaotic system is constructed. The two PWL functions can generate (2M+1)-scroll and (2N+2)-scroll respectively, then by combining both functions in different ways, which makes it possible to create arbitrary multiples of products grid multiscroll chaotic and hyperchaotic attractors.Secondly, an internal parameter is selected in a variable of one triangle wave function. By adjusting the built-in parameter, the distribution of equilibrium points is changed and then the control of the gradient of the multiscroll grid is achieved. The system dimensionless state equation is given by
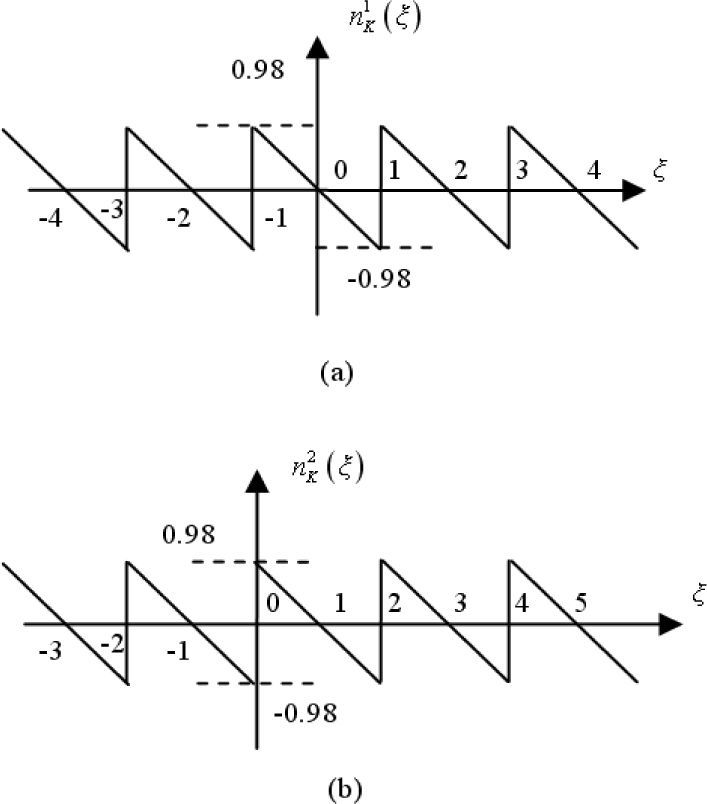
where σ, ρ are control parameters assuming that σ, ρ>0 and x, y, z, u are the state variables. Here, parameter σ determines the dynamical behavior of System (1), whereas parameter ρ is the built-in parameter which can control the gradient of the multiscroll grid. nM(y-ρu) and nN(u) are two triangular wave functions, and M, N=0, 1, 2, …. We use n1,2K(ξ) to express as the general triangular wave functions, the mathematical expression as follows [17]:
and
where a=0.02 and k is positive integer and ξ is variable. It is easy to verify that triangular wave functions n1,2K(ξ) can create 2M+1-scroll and 2N+2-scroll, respectively, for M, N=0, 1, 2, …. Figure 1 shows the phase portrait of triangular wave functions series with k=2. It is noticed that triangular wave functions series (2) and (3) are PWL functions and have better analytical properties such as the existence of solution and stability. From Figure 1, it is very easy to determine the zero points of each linearity range, hence by deploying the zero number points of triangular wave functions n1,2K(ξ), the scroll numbers of chaotic attractors which generated by System (1) can be controlled and then System (1) can generate arbitrary multiples of products grid scroll.
System (1) can be also described as
where
And by following this structure the stability of the system may be explained as in Reference [18]. Then we can get that this system is an unstable dissipative system (UDS) and present scrolls depending on the conditions of the equilibrium points [19].
2.2Vertical grid multiscroll chaotic attractorsIt has been shown that parameters σ and ρ are very important, that one can determine and control the system’s dynamical behavior and the gradient of the multiscroll grid, respectively. According to Formulas (2) and (3), System (1) can generate vertical grid multiscroll chaotic attractors when σ=0.95 and ρ=0 as follows.
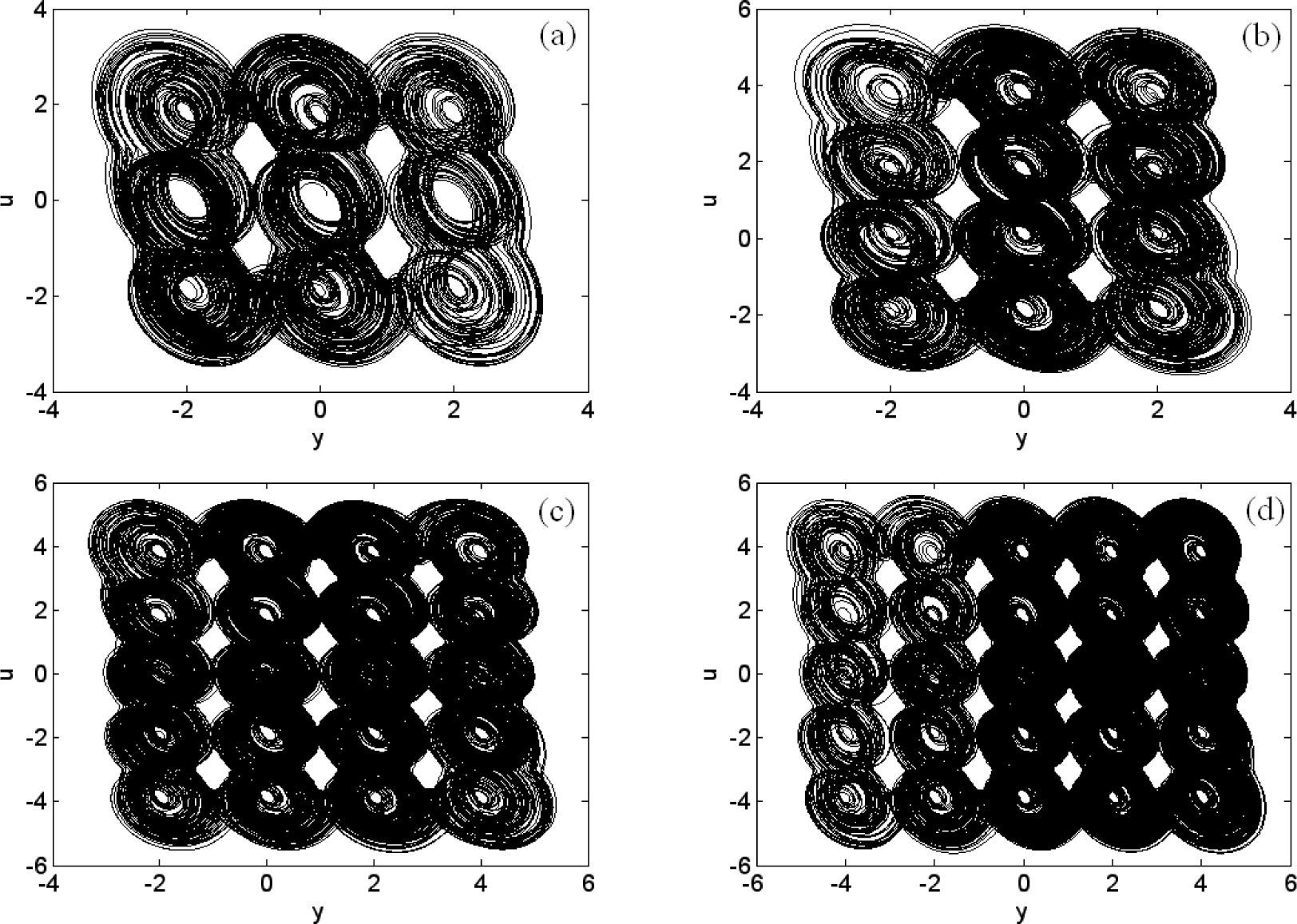
Let both nM(y) and nN(u) be n1K(ξ). System (1) can generate (2M+1)×(2N+1) couple of vertical grid multiscroll chaotic attractors. The 3×3 and 5×5-grid multiscroll attractor are described as the two examples in Figures 2(a) and 2(d).
Let nM(y) and nN(u) be n1K(ξ) and n2K(ξ) respectively. The chaotic system can generate (2M+1)×(2N+2) couple of vertical grid multiscroll attractors, and the 3×4-grid multiscroll attractors is depicted as an example in Figure 2(b).
Let nM(y) and nN(u) be n2K(ξ) and n1K(ξ) respectively. The chaotic system can generate (2M+2)×(2N+1) couple of vertical grid multiscroll attractors, and the 4×5-grid multiscroll attractors is depicted as an example in Figure 2(c).
From Figure 2, it can be seen that all the attractors present standard vertical grid shape in phase space. The Lyapunov exponents spectrum of 3×3-grid scroll attractors includes L1=0.2949, L2=0, L3=-0.5820 and L4=-0.7177.
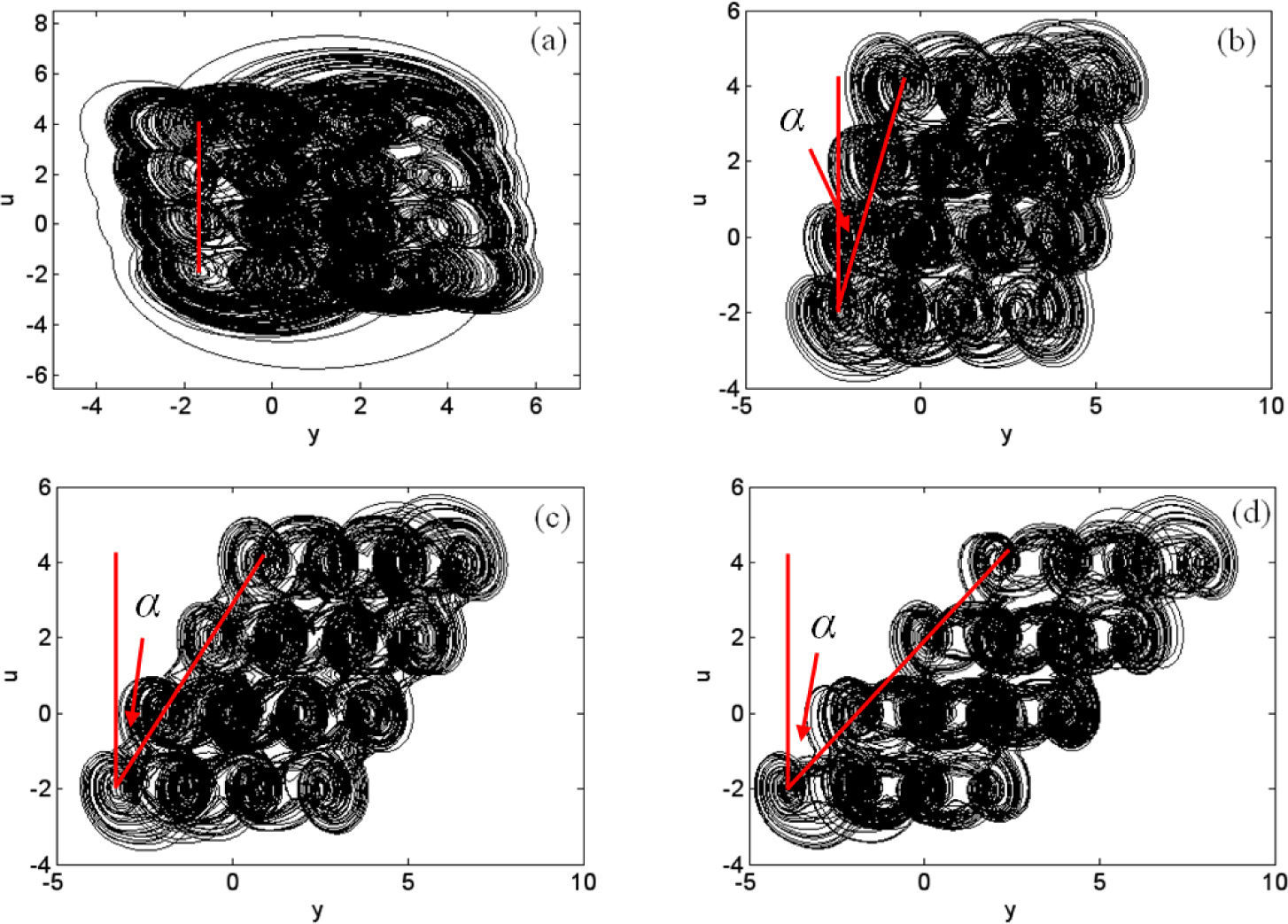
2.3Oblique grid multiscroll hyperchaotic attractorsWhen σ=2.75, ρ varies. Let nM(y) and nN(u) be n2k(ξ), System (1) can generate (2M+2)×(2N+2) couple of grid multiscroll hyperchaotic attractors. Figure 3 shows 4×4-grid multiscroll hyperchaotic attractors when ρ=0, 0.35, 0.7, 1, respectively. It can be observed that the attractors present oblique grid shape in phase space and the gradient α of the grid increases as parameter ρ increases. Simultaneously, it can be seen that compared with chaotic attractors, each scroll of the hyperchaotic attractors connects a whole plane gradually, implying that the hyperchaotic attractors are separated in more directions. It means that the hyperchaotic system has more complex dynamical behaviors. The Lyapunov exponents spectrum of 4×4-grid scroll attractors when ρ=1 includes L1=0.7707, L2=0.7441, L3=0 and L4=-2.5175. Having two positive Lyapunov exponents, it is obvious that the system is a hyperchaotic system when σ=2.75.
3Basic dynamical behaviorsIn this section, the basic dynamical behaviors of the oblique grid multiscroll hyperchaotic attractors are further investigated.
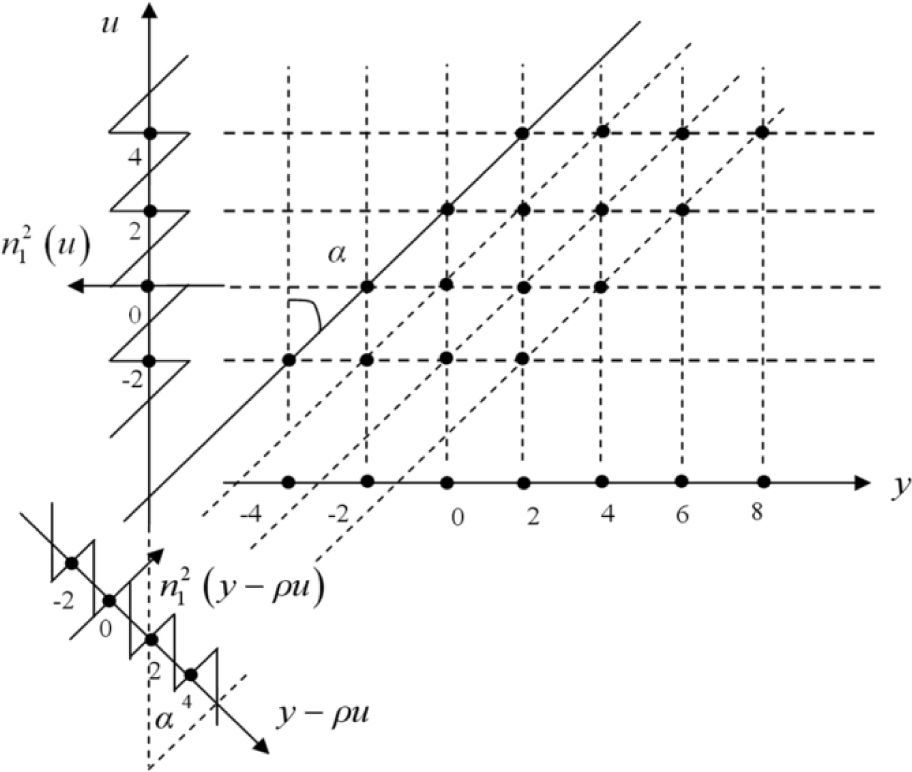
3.1Distribution of index-2 equilibrium pointsIn order to obtain the system equilibrium points, let the right-hand side of System (1) equal to zero. We can obtain x=-y, z=0, nM(y-ρu)=0. This suggests that the system equilibrium points are entirely up to the zero points of the PWL functions nM(y-ρu) and nN(u). If nM(y-ρu)=n2M(y-ρu) and nN(u)=n2N(u), System (1) has (2M+2)×(2N+2) equilibrium points Sij=(i, 0, j) which are on y - u plane, where z=0, i=0,±2, …,±2M and j=0,±2, …,±2N. Note that the equilibrium points in u axis are easily obtained by n2N(u)=0, whereas the equilibrium points in y-axis are determined by n2N(u)=0 and n2M(y-ρu)=0 together. Let M=N=1, then the 4×4 couple of grid multiscroll attractors in y - u plane can be obtained as shown in Figure 4, where “•” denotes the equilibrium points of index-2. Thus, the number of the equilibrium points of index-2 is 4×4. Each equilibrium point can generate one scroll, therefore the number of scroll is 4×4.
According to Formulas (1)-(3), the Jacobi matrix of the equilibrium points Sij of index-2 can be obtained
where
Because the derivative of the absolute value function is the sign function, it is easy to get nM*y*=nM*u*=nN*u*=-1 for scroll equilibrium points Sij. When ρ=1, System (1) are linearized near the equilibrium points, and the corresponding characteristic equation is
Note that the coefficients of Equation (5) are all positive numbers when σ>0. Thus, as long as λ>0, then f(λ)>0. According to Routh-Hurwitz stability criterion, the sufficient and necessary condition for holding the system stability is σ>0.5444. Hence, when σ>0.5444, System (1) is unstable. At this time, Equation (5) has two negative eigenvalues (or one pair of complex conjugate eigenvalues with negative real parts) and one pair of complex conjugate eigenvalues with positive real parts, this means that System (1) undergoes a Hopf bifurcation at σ=0.5444. Moreover, all equilibrium points are two-dimensionally unstable equilibrium points when σ>0.5444, called equilibrium points with index-2. When σ=0.5444, the four eigenvalues of the scroll equilibrium points of System (1) are λ1,2 ≈ 0.3360±2.5639i, λ3 ≈ -0.7268 and λ4 ≈ -0.9453.
3.2Function relation between parameter ρ and the grid gradient αFrom the analyses in the previous subsections, we know that the equilibrium points in the y-axis are mainly determined by n2N(u)=0 and n2M(y-ρu)=0 together and the shape of the grid is directly decided by the distribution of the scroll equilibrium points. From Figure 4, it is very easy to draw the function relation between the control parameter ρ and the grid gradient α which is α=arctanρ. The function relation illustrates the grid gradient α is in proportion to the parameter ρ, which means implementation of the scroll grid gradient α direct control.
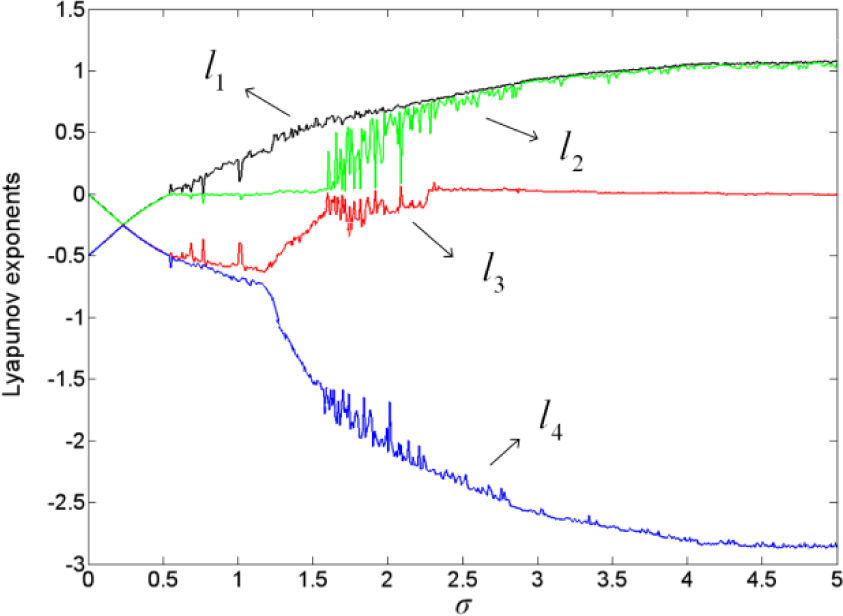
3.3Lyapunov exponents spectrum and bifurcation diagramTo further prove the existence of chaos and hyperchaos in System (1), taking 4×4 scrolls chaotic attractors as an example. When ρ=1, the Lyapunov exponents spectrum is obtained as shown in Figure 5. Whereas σ increases, the system undergoes some representative dynamical routes, such as stable fixed points, Hopf bifurcation, chaos and hyperchaos, which are summarized as follows:
- (1)
when 0<σ<0.5444, L1, 2, 3, 4<0, the system is stable.
- (2)
when σ=0.5444, L1, 2=0, L3, 4<0, System (1) has a Hopf bifurcation at this point.
- (3)
when 0.544<σ<1.712, L1>0, L2=0, L3, 4<0, System (1) is chaotic.
- (4)
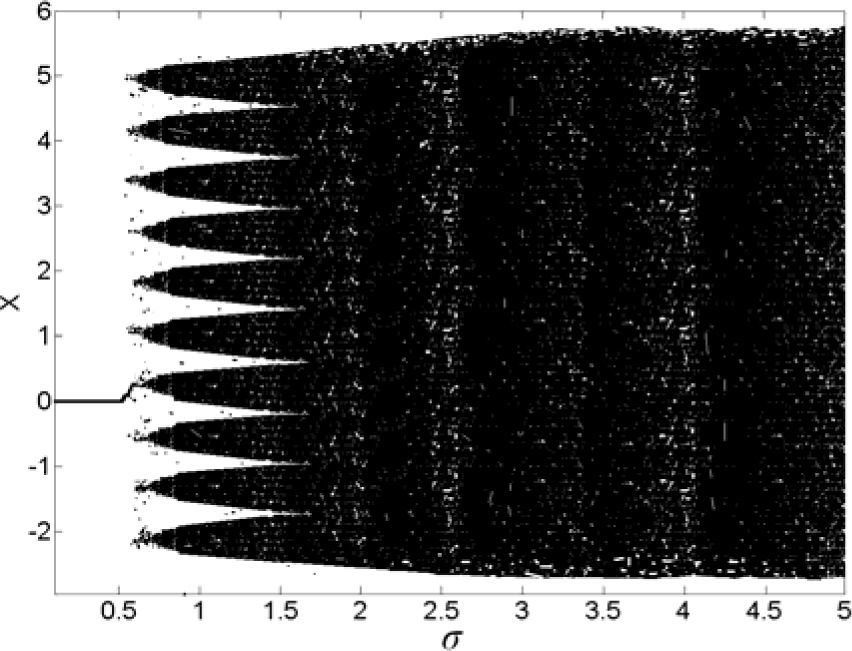
when 1.712≤σ<5, L1, 2>0, L3≤0, L4<0, System (1) evolves from the chaos state to the hyperchaos state. The bifurcation diagram of parameter σ is also found as shown in Figure 6, with increasing parameter σ, several chaos area gradually migrate in close together and finally form an integer.
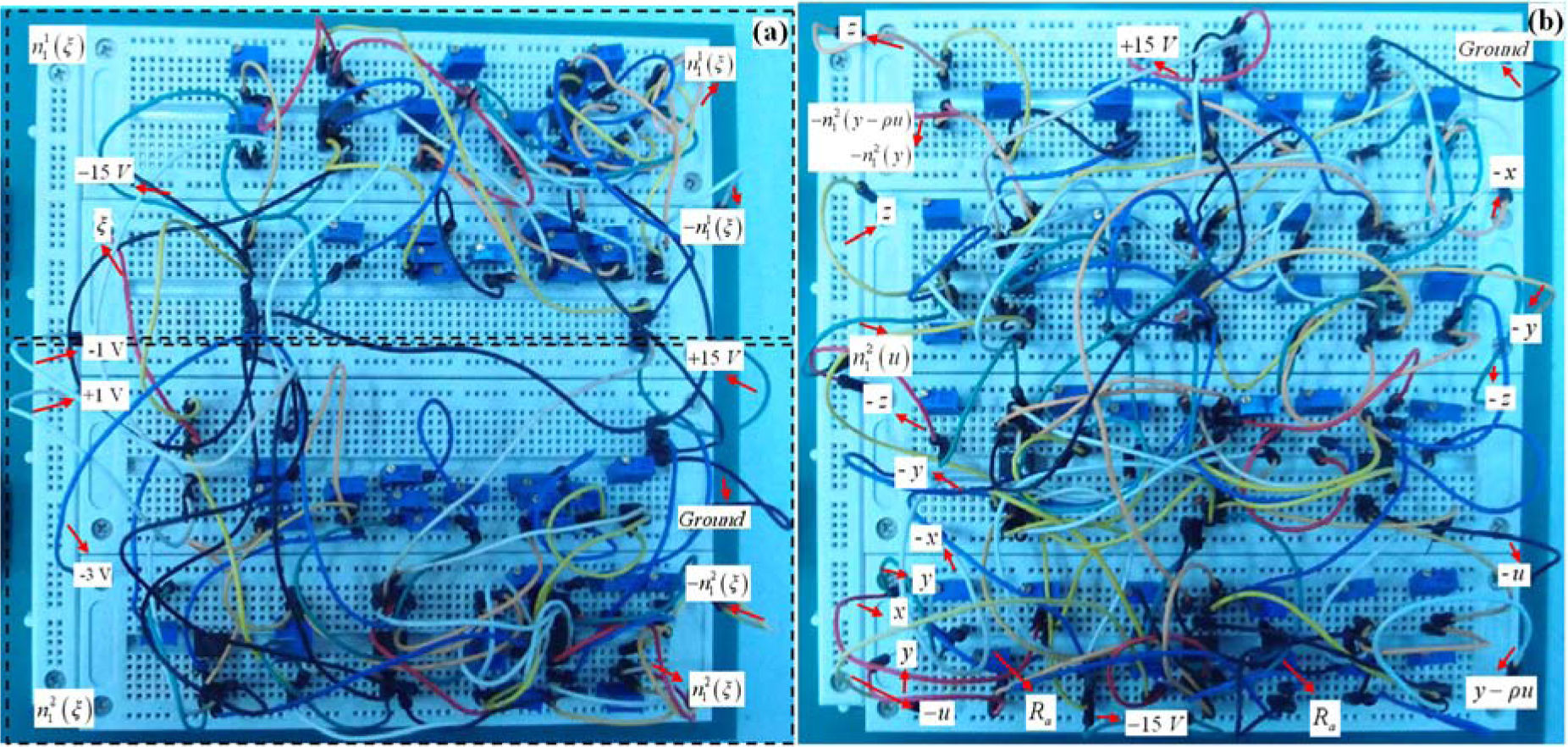
In this section, the oblique grid scroll hyperchaotic attractors are obtained by circuit design and experimental results, respectively. The operational amplifiers and associated circuitry perform the basic operations of addition, subtraction, and integration. All the operating amplifiers are of type TL082CP and their saturation value is |Vsat|=13.5 V. The voltage of power supply is E=±15 V.
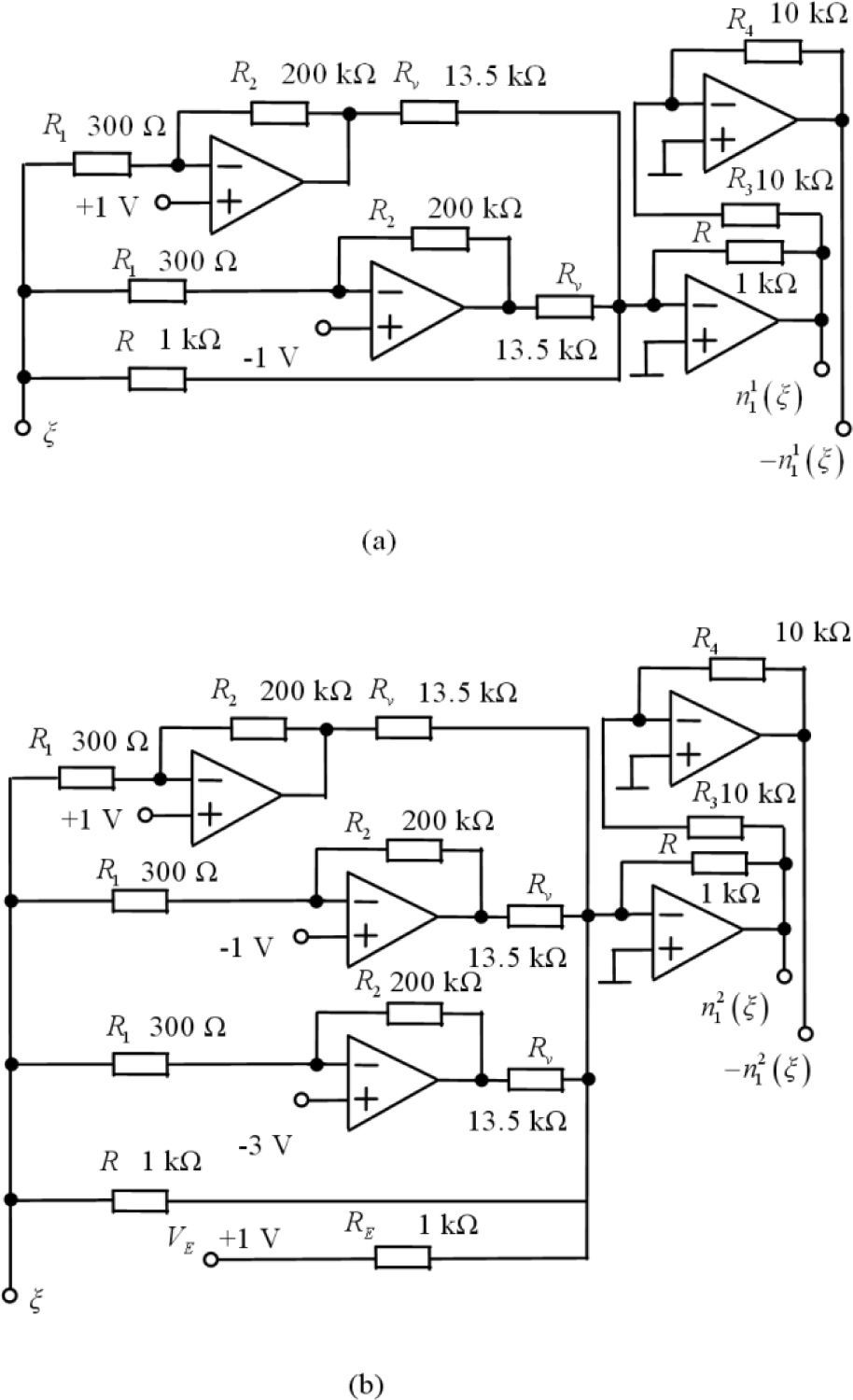
4.1Circuit design of triangular wave functionsAccording to Formulas (2) and (3), let k=1. The triangular wave functions n1,2K(ξ) are designed as shown in Figure 7. In Figure 7, Rv=13.5 KΩ is the resistance for voltage-current conversion, RE is a balance resistance under the additional voltage VE, with RE=1 KΩ, VE=1 V. The parameter q is determined by R1, R2 and their conjoint amplifier, q=R1×|Vsat| / R2=0.02. For |Vsat|=13.5 V, we choose R1=300 Ω, R2=200 KΩ. R1, R2 and linear resistance R are used for producing positive slope line of the triangular wave, whereas linear resistance R is used also for producing negative slope line of the triangular wave.
When the input be ξ, and the output can be n11(ξ) or -n11(ξ) in Figure 7(a). The same, if the input be ξ, and the output is n21(ξ) or -n21(ξ) in Figure 7(b).
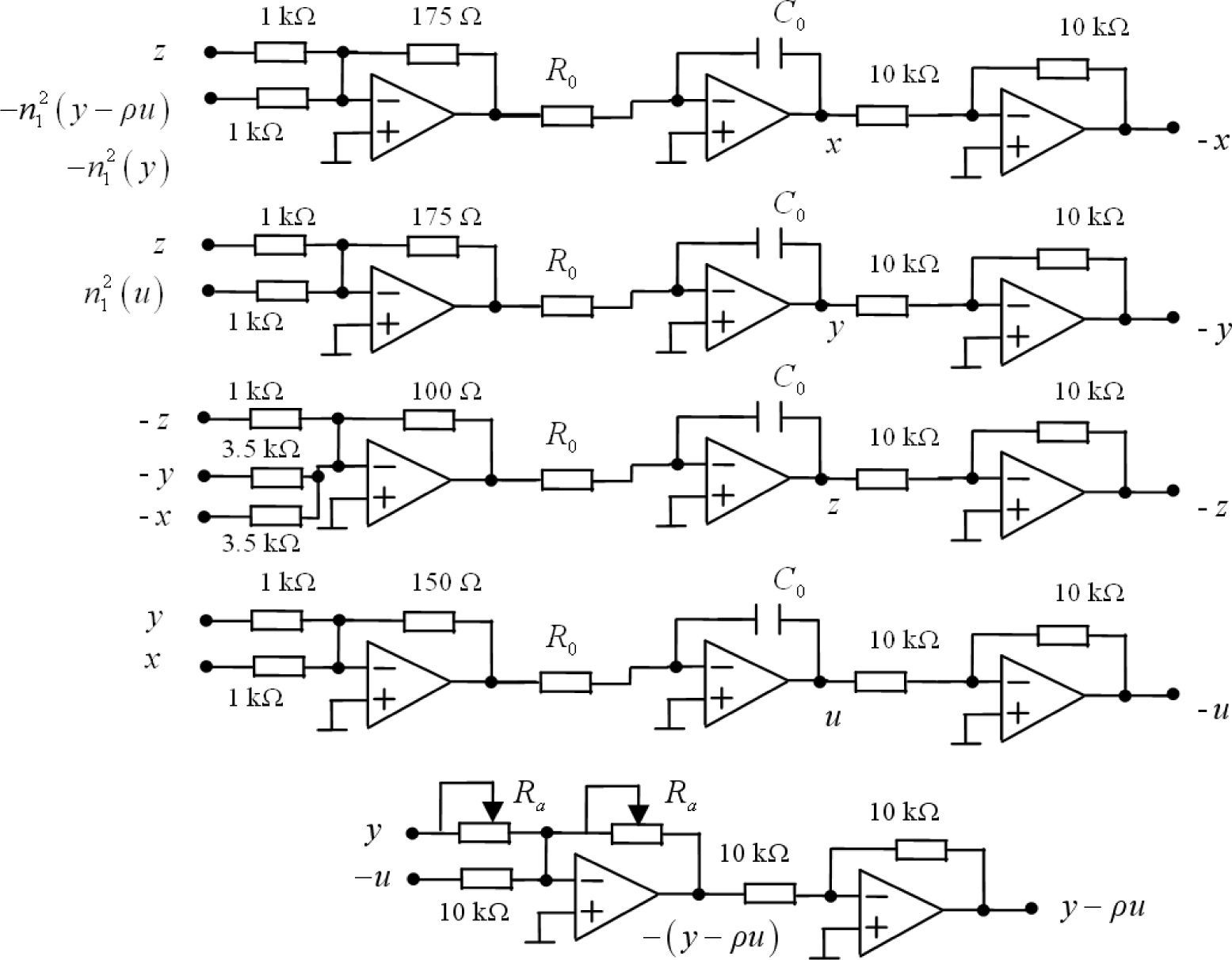
4.2Circuit design of the oblique grid multiscroll hyperchaotic system based on dimensionless state equationFigure 8 illustrates the oblique grid multiscroll hyperchaotic circuit based on dimensionless state equation. The time constant of the integrator is determined by R0C0, which can change the spectrum range of the chaotic signal. Let R0=1 KΩ and C0=33 nF. In Figure 8, we also design the circuit of (y-ρu), where Ra is an exactly adjustable resistor, used to adjust control parameter ρ. The value of control parameter σ of System (1) is 1.75 in Figure 8.
4.3Experimental resultsIn this subsection, the vertical and oblique grid multiscroll hyperchaotic attractors are experimentally confirmed via oscilloscope observations. To assist readers, a circuit implementation of the multiscroll hyperchaotic attractors is shown in Figure 9, based on the circuit diagrams and circuit implementation shown in Figures 7, 8 and 9, we have performed the following real physical experiments.
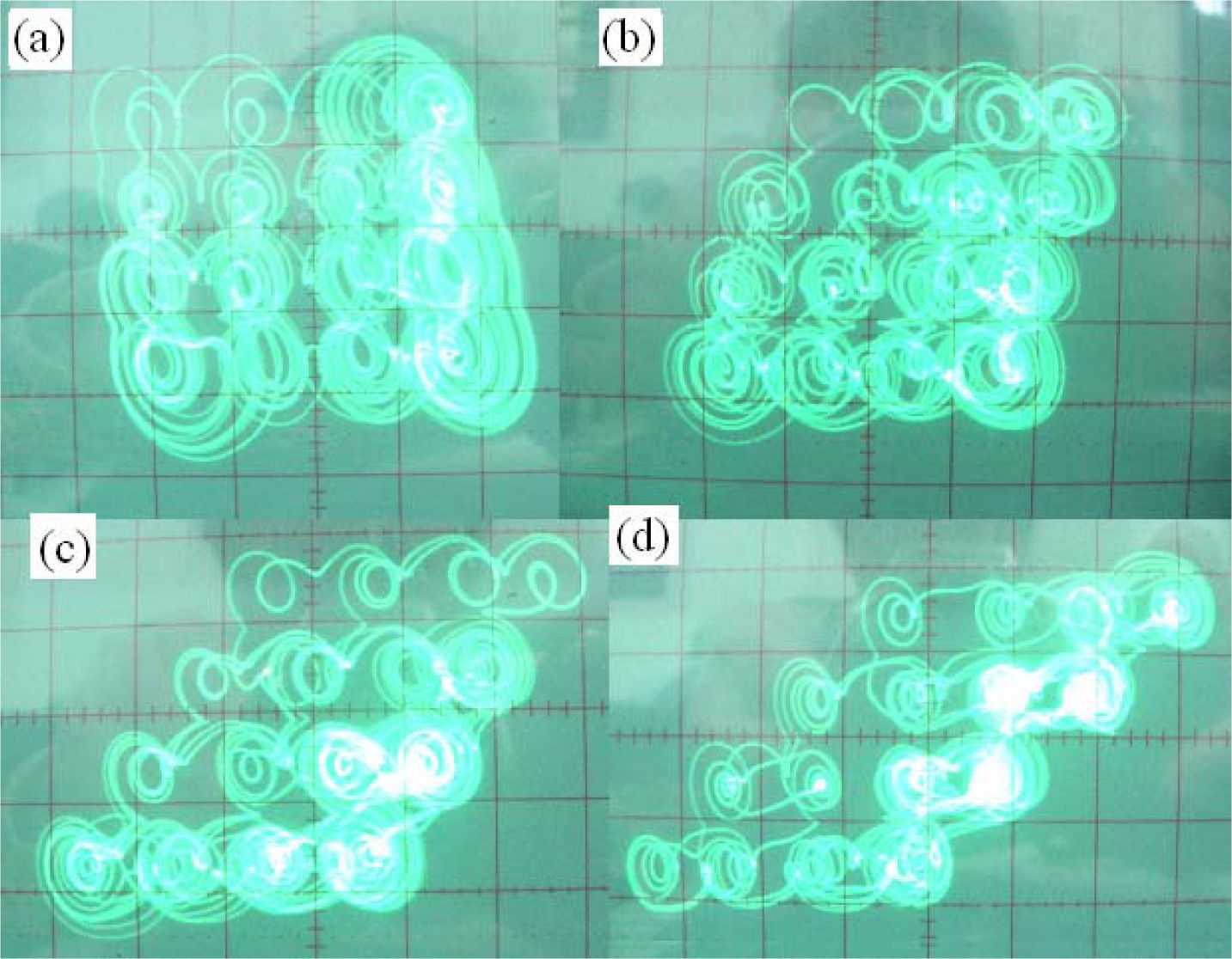
Let the input signal in Figure 7(b) be u, the output is n21(ξ) connected to the input signal n21(u) in Figure 8. Whereas, if we let the input signal in Figure 7(b) be y, the output is -n21(ξ), connected to the input signal -n21(y) in Figure 8. And then we get the standard 4×4 vertical grid multiscroll hyperchaotic chaotic attractors. Figure 10(a) shows the oscilloscope-observed result.
If let the input signal in Figure 7(b) be (y-ρu), the output is -n21(ξ), connected to the input signal -n21(y-ρu) in Figure 8. And then we can get the 4×4 oblique grid multiscroll hyperchaotic chaotic attractors when Ra equal to 3.5 KΩ, 7 KΩ and 10 KΩ, respectively. Figures 10(b)-(d) show the oscilloscope-observed results. From above analyses, the experimental results are in agreement with numerical simulations.
5ConclusionsThis paper has developed a nonlinear modulating function approach for oblique grid multiscroll hyperchaotic attractors based on third-order spiral chaotic Colpitts oscillator model. By introducing two triangle wave functions and adjusting a built-in parameter, the proposed hyperchaotic system does not only generate arbitrary multiples of products scroll numbers but it can also create oblique grid multiscroll chaotic attractors. Moreover, the basic dynamical behaviors are also investigated, confirming the chaotic nature of the presented system. Based on dimensionless state equations and module-based method, the success of the design has been demonstrated by circuit experiment. Theoretical analysis and experimental results confirm the effectiveness and feasibility of the presented scheme.