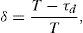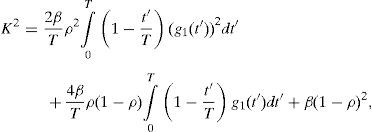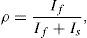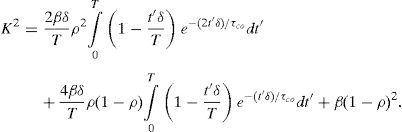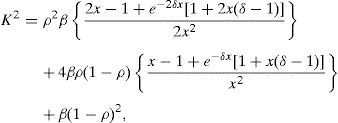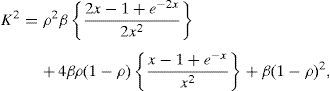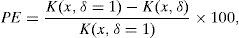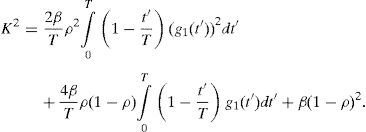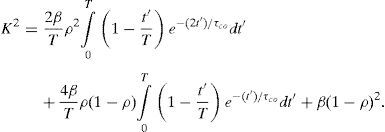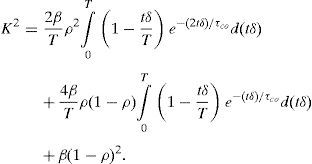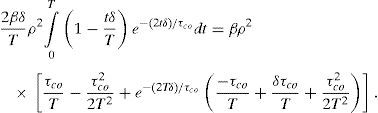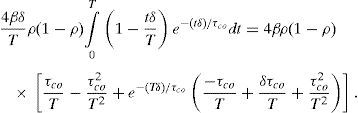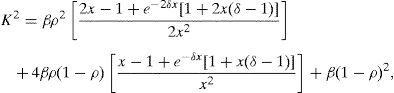Influence of photo-detector's dead-time on the speckle contrast for blood flow measurement

Abstract

The statistics of temporal integration of dynamically scattered light is commonly employed to calculate the correlation time of the light and related physical properties of the object that produce it, i.e. scatterer's speed. Recently, studying the statistics of time-averaged fluorescence intensity, it was reported that a small dead-time (1% of the exposure time) of the photo-detector increases the correlation time by one order of magnitude compared with an ideal photo-detector. Applying the same theory to the speckle contrast calculation for blood flow measurement, we found that the effect of dead-time is negligible compared to an ideal photo-detector for contrast calculation.

1

Introduction

When a diffuse object, e.g., biological tissue, is illuminated by coherent light, a random interference pattern, called speckle, can be observed in the reflected or transmitted light. When the object is static, the speckle pattern is static too. However, if the object moves with a certain speed, the individual grains of the speckle move and change their shape. The speed of the object (for example the blood cells) is inversely proportional to the correlation time (τ_co) of the reflected or transmitted light through the object (Fercher & Briers, 1981; Ohtsubo & Asakura, 1976). For this reason, a proper calculation of τ_co is essential for the object's speed calculation. Laser Speckle Contrast Imaging (LSCI) is a non-invasive optical technique (Boas & Dunn, 2010) that employs the contrast of integrated intensity of the reflected/transmitted light to calculate τ_co and, therefore, the speed of blood flow. In the LSCI community, different research groups had proposed theoretical and experimental improvements for the better calculation of τ_co, i.e., Bandyopadhyay, Gittings, Suh, Dixon, and Durian (2005) showed that the original LSCI theory proposed by Fercher and Briers (1981) did not account for the triangular averaging of the integrated intensity. Parthasarathy, Tom, Gopal, Zhang, and Dunn (2008) proposed a robust LSCI model and a MESI instrument (Multi-Exposure Speckle Imaging) and showed that their instrument improves the calculation of τ_co compared to the traditional LSCI instrument. Kirkpatrick, Duncan, and Wells-Gray (2008) showed that a spatial sub-sampling of the speckle pattern has a detrimental effect of reducing the speckle contrast and, therefore, the measured τ_co. Ramirez-San-Juan, Ramos-Garcia, Martinez-Niconoff, and Choi (2014) proposed a correction factor to solve this problem. Recently, studying the statistics of time-averaged fluorescence intensity, Turgeman and Fixler (2013) found that even a small dead-time (1% of the exposure time) of the photo-detector yields higher measured τ_co, as much as one order of magnitude compared with an ideal photo-detector. The aim of this work is to review the effect of the dead-time on the estimation of contrast and τ_co in the LSCI theory.

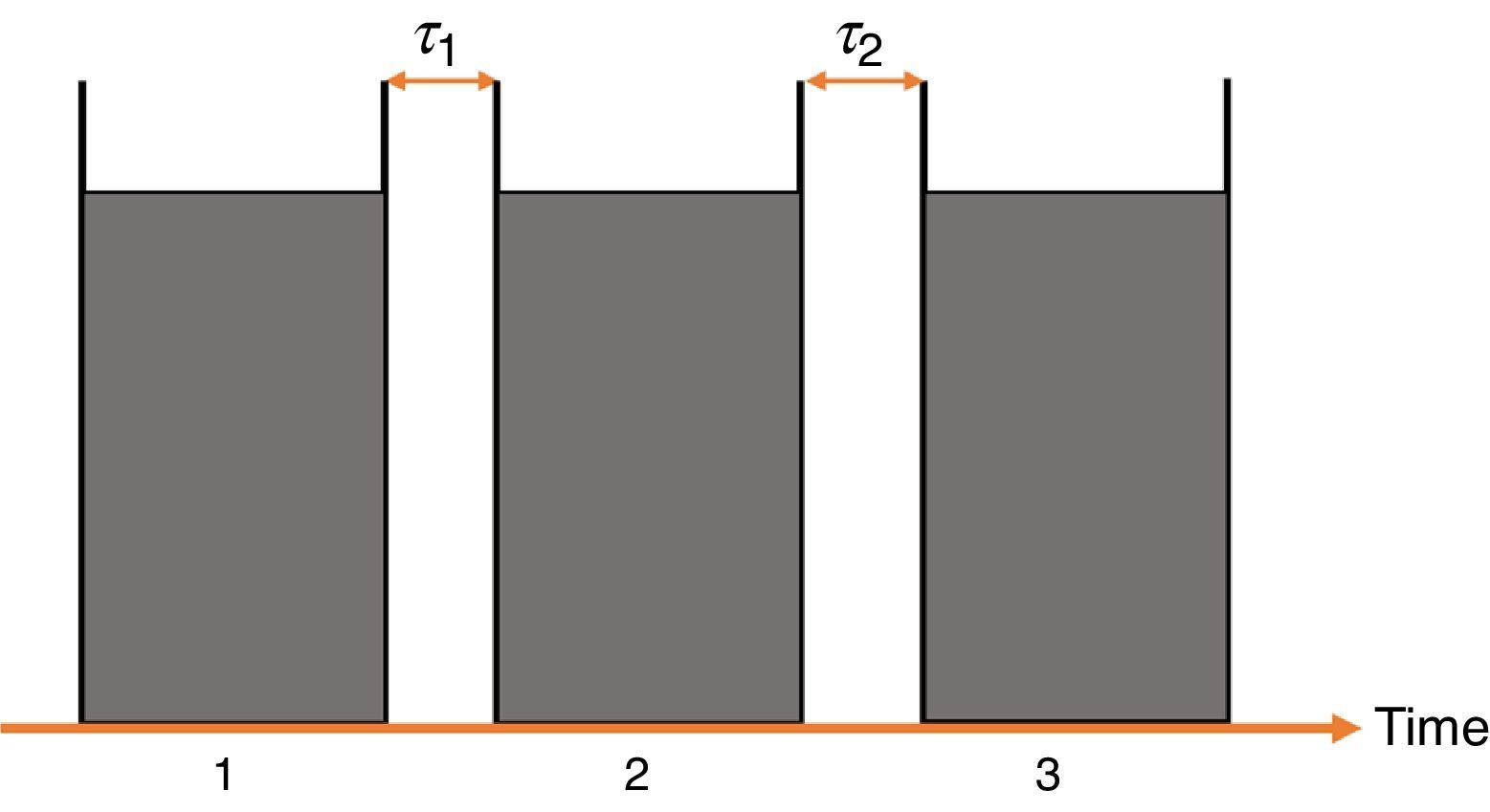
2

Dead-time effect in photo-detectors

In an ideal detection process, the photoelectric emissions in a detector are statistically independent of each other. Nevertheless, in practice, this condition is not strictly satisfied (Cummins & Pike, 1974). In most detectors, some radiation events may not be accounted, either because the system is busy processing a previous pulse or because the system is transferring data (Radiation Solutions, 2007). During this period of time, so-called dead-time or recovery time τ_d, no radiation events can be registered. Therefore, an actual detector registers a smaller number of events during the integration time (T) compared to an ideal detector.

For simplicity, we assume that the time response of the photo-detector can be described by a pulsed function as shown in Figure 1. During a certain time interval, the detector switches from a detection period (illustrated in Fig. 1 as a grey area) to a dead-time period (empty area, τ₁, τ₂). During these time intervals, the detector is insensitive to radiation (Karabıdak, Çevik, & Kaya, 2009).

Figure 1.

Schematic representation of a possible sequence of detection periods (1, 2, 3, …) and dead-time (τ₁, τ₂, …). Each detection period is followed by a dead-time interval during which the detector is inactive.

In Turgeman and Fixler (2013), the influence of the dead-time on the fluorescence variance is analyzed and the following equation is proposed to describe such influence:

where δ is the fraction of the integration time during which the photo-detector is active.

3

Influence of dead-time on integrated speckle contrast

The random interference pattern produced by the coherent addition of scattered laser light with slightly different path lengths produces laser speckle patterns. Such speckle patterns produced by motion of scattering objects, i.e. blood cells, can be used to estimate its speed due to the spatial and temporal variations of the speckle pattern.

For the case of spatial variations, its effect is observed as a blurring in the image.

LSCI quantifies the extent of this localized spatial blurring by calculating the speckle contrast K of the image. The speckle contrast K can be expressed using the following equation (Parthasarathy et al., 2008),

where

is the fraction of dynamically scattered light, I_s and I_f are the contribution from the static and dynamic light, respectively, β is a normalization factor that accounts for spatial integration of the speckle and g₁ (t) is the normalized correlation function of the electric field reflected/transmitted by the sample.

Given that tδ is the effective time that the photo-detector is active during an exposure time t, and assuming that the velocities of the scatterers have a Lorentzian distribution (Ramirez-San-Juan, Ramos-Garcia, Guizar-Iturbide, Martinez-Niconoff, & Choi, 2008) i.e., g1(t)=exp (−t/τco), K2 can be expressed by

After some calculations (see Appendix A), it is possible to express Eq. (3) as

where x=T/τco is the number of correlation intervals captured during the exposure time.

For an ideal detector (δ = 1 or τ_d = 0), Eq. (5) reduces to:

which is the well-known expression for the contrast of light in presence of dynamic and static scatterers (Boas & Dunn, 2010).

In Figure 2, we plotted the percentage error (PE) of contrast obtained for an actual detector (0 < δ < 1) compared with an ideal detector (δ = 1) and given by:

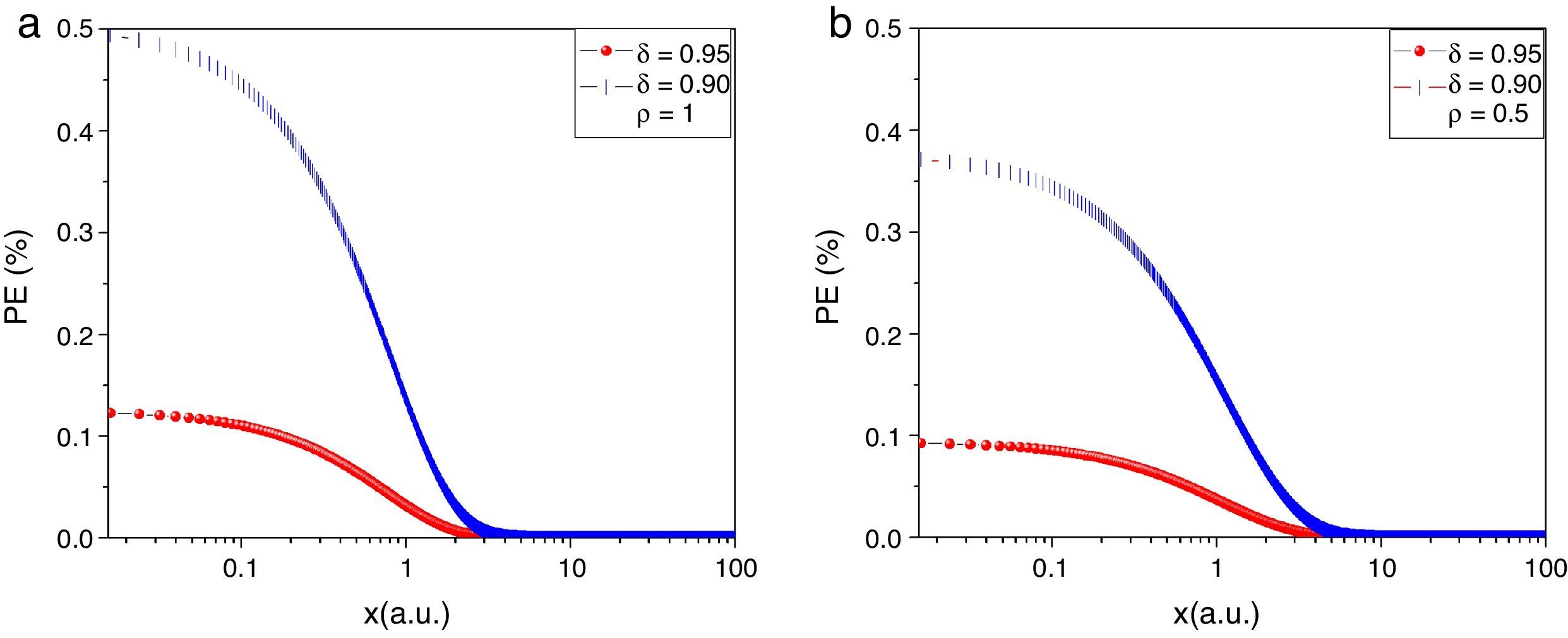
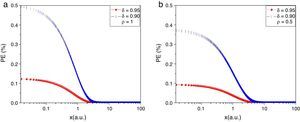
where K(x,δ=1) is the contrast for the ideal detector (τ_d = 0) and K(x,δ) is the contrast for a δ given by Eq. (1). Two different values of δ were employed: 0.95 and 0.9, which correspond to dead-time of 5 and 10% of T, respectively. These values are well beyond the actual photo-detector's dead-time.

Figure 2.

PE as function of the number of coherent interval captured by the photo-detector for a 5% dead-time (• lines) and 10% dead-time (| lines), for (a) ρ=1 i.e., superficial blood vessel, and (b) ρ=0.5 i.e. deep blood vessel. In any case, the PE was smaller than 5% under the conditions described in this work.

Figure 2a shows PE vs x=T/τco for a superficial blood vessel (ρ=1), i.e. all the light is dynamically scattered by the blood vessel and therefore the second and third terms of Eq. (5) drop to zero. Figure 2b shows the corresponding results for a deep blood vessel (ρ=0.5) (Parthasarathy et al., 2008). In this case, 50% of the light reaching the photo-detector is dynamically scattered by the blood vessel and the remaining 50% is statically scattered by the tissue lying over it. In both cases, we can observe that in the short exposure regime (x≤1), the error of the contrast obtained with an actual photo-detector compared with an ideal one is smaller than 0.5%, and for the long exposure regime (x>1), the error rapidly drops to zero. Here, it is important to remark that most of the LSCI experiments are developed in the long exposure regime (Ramirez-San-Juan et al., 2008).

It should be emphasized that there are important differences between the work presented in (Turgeman & Fixler, 2013) and this work which explain the influence that small dead-time has on the calculated correlation time. For example, in (Turgeman & Fixler, 2013), the authors calculated rotational correlation times of fluorescein molecules. In this manuscript, the correlation time of the backscattered light from a blood flow model was calculated. The correlation time of fluorescein molecules is in the order of ns and the integration times reported in (Turgeman & Fixler, 2013) are in the order of tens of ns. Under this regime, the signal captured by the photo-detector is more likely to be influenced by the dead-time. However, for the case of LSCI, the correlation time of dynamic speckle is in the order of tens or hundreds of μs (Parthasarathy et al., 2008), and the integration time is in the order of ms, far away from the dead-time values.

4

Conclusions

Following Turgeman and Fixler (2013) methodology, we have incorporated the dead-time in the LSCI theory. Even when it was reported that this factor is crucial for fluorescence imaging correlation calculations, it was found that the dead-time does not play such an important role in LSCI. In this manuscript, we have confirmed that given that the correlation time and the integration time are much longer than the dead-time of the photo-detector under this regime, the influence of it on the contrast calculation of dynamically scattered light for blood flow measurement is negligible.

Conflict of interest

The authors have no conflicts of interest to declare.

Acknowledgements

This research was funded in part by CONACYT (CB-2010-156876-F). In addition, R. Porras-Aguilar acknowledges the support of the Mexican Science Council, CONACyT through the Catedra-2066.