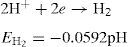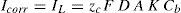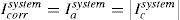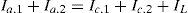Mathematical model for galvanic corrosion of steel–copper couple in petroleum waste water in presence of friendly corrosion inhibitor

Abstract

Galvanic corrosion of steel–copper couple in saline petroleum wastewater in the absence and presence of curcuma extract as corrosion inhibitor was studied as a function of temperature, velocity, and inhibitor concentration. The electrochemical polarization technique was used to evaluate the corrosion parameters. Corrosion currents densities increase with temperature and velocity, while it decreases with inhibitor concentrations. In this investigation, a theoretical model equation was used to analyze the shape of polarization curves. Microsoft Excel program was used to find the galvanic current and galvanic potential. Theoretical results agreed with experimental one.

1

Introduction

Corrosion is a chemical or electrochemical reaction between a metal and its environment that produce degradation of material. There are several kinds of corrosion such as uniform corrosion, galvanic corrosion, crevice corrosion, pitting, intergranular corrosion, etc. Galvanic corrosion happens when a metal or alloy is electrically coupled to another metal in same the environment. There are many methods of corrosion control such as material selection, coatings, inhibitors, and cathodic protection. Corrosion inhibitor is organic or inorganic component that can be added in small amounts to reduce corrosion problems (Khadom, Yaro, AlTaie, & Kadum, 2009a; Khadom, Musa, Kadhum, Mohamad, & Takriff, 2010; Musa, Khadom, Kadhum, Takriff, & Mohamad, 2012). Recently the using of friendly and the natural materials where the aim of researchers that concentrated on studying the kinetics parameters, such as, activation parameters and adsorption behavior of the corrosion inhibition process (Yaro, Khadom, & Ibraheem, 2011a; Yaro, Khadom, & Wael, 2013; Yaro, Khadom, & Wael, 2014). Application of mathematical modeling was rarely used. Mathematical modeling is a powerful tool for increasing the availability of electrochemical data for a number of materials and environmental systems for industrial applications that enable chemical and materials engineers to predict corrosion potentials and corrosion rates using equations derived from electrochemical principles (Khadom & Yaro, 2011; Khadom, Yaro, Altaie, & Kadhum, 2009b). The present work was a step in the direction of application a mathematical model for galvanic corrosion – saline water – inhibitor system at different operating conditions.

2

Mathematical model

For activation control and to determine the potential of a system, in which the reduced and oxidized species are not at unit activity, the familiar Nernest equation can be employed (Cifuentes, 1987; Fontana, 1987):

or written as:

where E is the equilibrium half-cell potential, E^o the standard equilibrium half-cell potential, R is the gas constant (8.314 J/K mol), T is the absolute temperature (K), n is the number of electrons transferred, F the Faraday constant (96,487 coulomb/equiv.), a_red and a_oxid are activities or (concentrations) of oxidized and reduced species. Hydrogen ion activity is commonly expressed, for convenience, in terms of pH. This is defined as (Uhlig & Revie, 1985):

Hence, for the half-cell reaction

Tafel slopes (Tafel constants) are determined from the following equations (Fontana, 1987):

for anode and cathode reaction, respectively, where α is the symmetry coefficient, which describes the shape of the rate controlling energy barrier. The relationship between reaction rate and overvoltage for activation polarization is:

where η^A is overvoltage, β as before, and i is the rate of oxidation or reduction in terms of current density. This equation is called the Tafel equation. The reaction rate is given by the reaction current or current density, so the high field approximation gives (Uhlig & Revie, 1985):

and

The effect of temperature is to change the value of the exchange current density i_o as follows (Uhlig & Revie, 1985):

Corrosion current for anodic reaction rate can be obtained as (Uhlig & Revie, 1985):

and the cathodic one is:

For the case of diffusion control, the reaction current is given by Fick's law (Liberati, Nogueira, Leonel, & Chateauneuf, 2014):

or its equivalent

The limiting current, i.e. the maximum current under diffusion control is obtained when C_s = 0, so

or

where the mass transfer coefficient is defined as

The corrosion current is then

z_c is used in Eqs. (15)–(20) because in corrosion processes the cathodic reaction is the one likely to be controlled by diffusion. C_b solubility of oxygen in water. The bulk concentration of oxygen changes with pressure, for barometric pressures other than 101.325 kPa (sea level), the bulk concentration of oxygen can be computed from the following equation (Truesdale, Downing, & Lowden, 1955):

where C_b is the bulk concentration of oxygen, C_101.325 is a saturation value at 101.325 kPa (tested experimentally, Table 1), P_T is total pressure (kPa), p is the vapor pressure of water. The mass transfer coefficient (K) in Eq. (19) varies with the flow or relative speed between metal and the environment, the geometry of the system and the physical properties of the liquid. To calculate the variation of K in dynamic environment, dimensionless group are used such as (Yaro, Al-Jendeel, & Khadom, 2011b):

Table 1.

Solubility of oxygen in 1% MgCl₂.

Temperature (°C)	Concentration of inhibitor (ppm)	Solubility of oxygen (mg/l)
30	Blank	6
	90	5.9
	180	5.8
	270	5.8
	360	5.8
35	Blank	5.8
	90	5.6
	180	5.6
	270	5.5
	360	5.5
40	Blank	5.6
	90	4.6
	180	4.6
	270	4.6
	360	4.5

All are often applied. For the smooth rotating cylinder electrode, the mass transport correlation is given by Eisenberg, Tobias, and Wilke (1954) relationship applies in the case of turbulent regime.

The value of K from Eqs. (22)–(25) can be expressed as:

This correlation is valid within the following range: 1000 < Re < 100 000 and 850 < Sc < 11 490. The effect of temperature and pressure on diffusion coefficient is shown in the following equation:

where the exponent n varies from 1.75 to 2.0, T_o reference temperature in K, D_o diffusion coefficient at the reference temperature and pressure, P_o reference pressure. For galvanic corrosion under activation control (Hassan, Abdul Kader, & Abdul-Jabbar, 2011) at (E_g):

And

for one metal

for two metals

or in terms of current densities and areas

Or

if I_a.1 ≫ I_a.2, Eq. (31) reduce to

E_e.c1 = E_e.c2 = E_e.c and α_c1 = α_c2 = α_c

for diffusion control (Hassan et al., 2011):

for one metal

for two metals

where f₁ and f₂ are the anodic and cathodic electrode area fractions.

Eq. (47) became

For binary galvanic system under activation control (acidic medium) and mass transfer (diffusion) control (neutral medium),

for one metal:

when two metals at (E_g):

3

Experimental work

3.1

Preparation of plant extracts

Fresh Curcuma longa (turmeric) were washed under running water, sliced into small pieces before drying in a hot air oven at 50 °C for about 6 h. Dry slice was collected and ground into fine powder using a high-speed blender. The dry, Curcuma longa was packed in a plastic bag, sealed, and kept until used. The slice (25 g) was blended with distilled water (250 ml) in a reflux heater with conical flax (500 ml) for 3 h at 70 °C. The conical flax was supplied with mixer for homogenous solution and uniform temperature distribution. The solution is then cooled, followed by filtration to extract solid particles free inhibitor solution. Each 1 cm³ of extract yield a powder 0.0045 g of solid material.

3.2

Polarization tests

A total of 90 test runs was carried out in the presence and absence of inhibitor at different experimental conditions using potentiodynamic polarization technique. Tests were carried out using a beaker of 500 ml. The cell containing working electrode, lugging capillary probe, thermometer, counter graphite electrode. All potential values were measured in reference to a saturated calomel electrode (SCE). The lugging capillary prob was adjusted such that it was at a distance not more than 1 mm from the working electrode. The working electrode were 2 samples from carbon steel type (ASTM A 106/A) and copper type (ASTM B-111-443). The working electrode was (2.4 cm outside diameter x 1.35 cm long) carbon steel (type ASTM A 106/A) and copper (type ASTM B-111-443) cylinder; this cylinder was fixed on brass zone on the shaft. Graphite electrode was used as a counter electrode has a dimension of (9.5 cm diameter × 8 cm. long), two wires were connected to a cylindrical concentric graphite electrode. The chemical compositions (% wt) of working electrodes were for steel alloy 0.25%C, 0.5%Mn, 0.025%P, 0.025%S, 0.1%Si, 0.4%Cr, 0.15%Mo, and the balance is Fe. The copper alloy compositions are 70–73%Cu, 0.007%Pb, 0.0006%Fe, 0.001%Sb, 0.0.009%Sn, and the balance is Zn. Mild steel and copper specimens were cleaned using emery paper of grade number 220, 320, 400, and 600, then washed with running tap water followed by distilled water, then dried with a clean tissue, degreased with benzene, dried, degreased with acetone, dried, and finally left in desiccator over silica gel. The electrode was mounted directly to the working electrode. (SCE) was used as a reference electrode. To ensure that KCl solution was saturated, a small amount of KCl (solid) was kept in the solution of (SCE) as long as the test. The cathodic polarization is carried out beginning from the highest negative potential of −900 mV until reaching the corrosion potential. The potential was changed in scan rate of 10–15 mV/min, then the current is recorded. The anodic polarization readings start of a potential resulting in a zero current density and is increased in a step of 10–15 mV with recording of the current at each step for one minute interval until a potential of about −100 mV. The galvanic corrosion rate of steel–copper couple in the absence and presence of inhibitor concentration of 0, 90, 180, 270 and 360 ppm, area ratio of cathode to anode 1:1, at different temperature 30, 35, and 40 °C was evaluated in aerated 1% (wt) MgCl₂ and pH 6.

4

Results and discussion

4.1

Electrochemical polarization studies

The corrosion behavior of Fe and Cu in 1% MgCl₂ solution with and without inhibitor was studied using polarization techniques. The inhibitor was tested in different conditions of temperature, velocity and inhibitor concentration. A total of 90 test runs is carried out. Electrochemical parameters for each metal individually were calculated using polarization curves similar to Figures 1 and 2 that obtained for Fe and Cu in 1% MgCl₂ solution. While galvanic parameters were calculated by superimposing the anodic branch of the less noble material (mild steel) to the cathodic branch of the most noble material (copper alloy) as shown in Figure 3. Similar figures are obtained at all operating conditions. From polarization curves, the free corrosion current I_corr, corrosion potential E_corr, limiting current density, i_L, and galvanic corrosion, I_g were obtained. A plateau corresponding to a limiting current density (i_l) is observed in the cathodic region of the polarization curves between −800 and −600 mV SCE. Therefore, the cathodic reaction seems to be controlled by diffusion. It was shown that the values of I_corr and I_g increased with temperature and velocity, while it decreased with inhibitor concentration. Maximum inhibitor efficiency was around 90% at 360 ppm and 30 °C. The average values of inhibitor efficiency were approximately 55, 72, 76, and 83% at inhibitor concentration of 90, 180, 270, and 360 ppm respectively. The increasing in corrosion protection with addition of inhibitor may be attributed to increase in metal surface coverage. Increasing inhibitor concentration beyond 380 ppm may yield further reduction in galvanic corrosion current, but economical considerations have to be taken into account. Figures 4 and 5 show the variation of galvanic corrosion as a function of different operating conditions.

Fig. 1.

Polarization curves for the corrosion of Fe in 1% wt MgCl₂ at temperature 30 °C and different rotation speed.

Fig. 2.

Polarization curves for the corrosion of Cu in 1% wt MgCl₂ at temperature 30 °C and different rotation speed.

Fig. 3.

Polarization curves for the corrosion of Fe–Cu coupling at speed of rotation 50 rpm, temperature 40 °C and 180 ppm inhibitor concentration.

Fig. 4.

Galvanic current as a function of speed of rotation at different temperature in absence of inhibitor.

Fig. 5.

Galvanic current as a function of temperature at different inhibitor concentration.

4.2

Theoretical and modeling studies

A mathematical model has been developed based on the ordinary galvanic corrosion model and fluid dynamics analysis model. The calculation is divided into two types. Activation control and mass transfer control. Simplifications leading to analytic solutions of the model equations are so complex, so numerical solutions must be attempted. As an example, a numerical method implemented on a microcomputer. The sweeping method and algorithm are as follows:

• 1.

  Estimate equilibrium potentials for metals and for hydrogen from Eq. (1) at T of 30, 35 and 40 °C. For pH values use Eq. (3) to calculate hydrogen ion concentrations.

• 2.

  Tafel slopes for anodic and cathodic reactions are established from Eqs. (4) and (5) at α = 0.5 and T of 30, 35 and 40 °C.

• 3.

  The exchange current density is calculated from Eq. (10) for three values of temperatures (30, 35 and 40 °C).

• 4.

  Bulk concentration of oxygen in water is calculated from Eq. (21) at different temperatures 30, 35 and 40 °C, by using, Table 1.

• 5.

  The value of oxygen diffusivity is estimated from Eq. (27) at different temperatures 30, 35 and 40 °C. The mass transfer coefficient K is calculated by using Eq. (26).

• 6.

  The limiting current is estimated from Eq. (20) at different temperatures 30, 35 and 40 °C.

• 7.

  It is necessary to realize that the galvanic corrosion potentials (E_g) of the reactions involved are chosen between the more negative (or less positive) equilibrium potential of the metals and the equilibrium potential of hydrogen evolution.

• 8.

  The values of E_eq, β, i_o, E_g (=E_a = E_c) are substituted in Eqs. (11) and (13) to determine anodic and cathodic currents.

• 9.

  For activation control:

• 10.

  The summations of the anodic and cathodic currents are compared to determine the absolute value of their difference.

• 11.

  A new value of E_g is assumed as in step 8 and the program is executed again, showing the difference between the summation of the anodic and cathodic currents to decrease

• 12.

  Step 11 is repeated until a minimum difference current is found. The minimum will be detected when the sweeping procedure goes beyond the true galvanic potential value as the difference starts increasing. The precision will be greater the smaller the potential step while the processing time will increase accordingly.

• 13.

  For mass transfer control:

• 14.

  The difference between the summation of the anodic currents and limiting currents, Eq. (42), are calculated and compared to determine the absolute value of their difference.

• 15.

  A new value of E_g is assumed as in step 8 and the program is executed again, showing the difference between the summation of the anodic and limiting currents to decrease

• 16.

  Step 11 is repeated until a minimum difference is found. The minimum will be detected when the sweeping procedure goes beyond the true galvanic potential value as the difference starts increasing. The precision will be greater the smaller the potential step while the processing time will increase accordingly.

• 17.

  For cathode reaction under activation control complicit with mass transfer:

• 18.

  The difference between the summation of the anodic and cathodic currents and limiting currents Eq. (49), are calculated and compared to determine the absolute value of their difference.

• 19.

  A new value of E_g is assumed as in step 8 and the program is executed again, showing the difference between the summation of the anodic and cathodic currents and limiting currents to decrease

• 20.

  Step 11 is repeated until a minimum difference is found. The minimum will be detected when the sweeping procedure goes beyond the true galvanic potential value as the difference starts increasing. The precision will be greater the smaller the potential step while the processing time will increase accordingly.

A program written in Microsoft Excel 2010 for free corrosion rate of single metal and binary galvanic system under activation control (acidic medium) and mass transfer (diffusion) control (neutral medium) and also to calculate the galvanic corrosion rate when the system is under both activation and mass transfer control. Table 2 that shows the effect of temperature on the corrosion current and corrosion potential of copper and iron, limiting current was calculated from Eq. (44), corrosion current of metals were calculated from Eq. (53). Figures 6 and 7 show a comparison of the galvanic current density obtain from polarization curve and theoretical calculation. Figures 8 and 9 show a comparison of the galvanic current density obtain from polarization curve, weight loss and theoretical calculation.

Table 2.

Galvanic corrosion of Cu/Fe couple versus temperature under the following conditions: [Fe²⁺] = [Zn²⁺] = 10⁻⁶ M, f_Fe = 0.5, f_Zn = 0.5, alpha of H₂ = 0.5, alpha of Cu = Fe = 0.5.

T (°C)	rpm	Eg (mV)	ICu (μA/cm^2)	IFe (μA/cm^2)	IH2/Cu   (μA/cm2)	IH2/Fe   (μA/cm2)	ILimiting (μA/cm^2)
30	0	−0.79537	1.094E−11	57.332	3.23710	0.9141	53.1813
35		−0.83150	2.555E−12	59.644	1.91495	1.1058	56.6239
40		−0.83578	8.056E−12	66.779	1.71268	0.8241	64.2429
30	50	−0.82944	2.062E−12	65.240	4.25687	1.7317	59.2514
35		−0.83656	2.957E−12	64.116	3.31561	1.1878	59.6125
40		−0.83968	9.196E−12	62.836	1.45716	0.8992	60.4799
30	200	−0.79930	7.466E−12	158.870	1.59136	0.8795	156.399
35		−0.80699	1.663E−11	159.46	1.48002	0.6337	157.352
40		−0.81276	3.079E−11	160.84	0.72399	0.4773	159.642

Fig. 6.

Comparison of the galvanic current density obtains from polarization curve and theoretical calculation at temperature 30 °C different rpm.

Fig. 7.

Comparison of the galvanic current density obtains from polarization curve and theoretical calculation at temperature 35 °C different rpm.

Fig. 8.

Comparison of the galvanic current density obtains from polarization curve, weight loss and theoretical calculation at different temperature.

Fig. 9.

Comparison of the galvanic current density obtains from polarization curve and theoretical calculation at different temperature and rpm.

5

Conclusion

Galvanic current and the corrosion current densities increase with increasing temperature and velocity, and decrease with increasing inhibitor concentrations. The addition of inhibitor reduced the galvanic corrosion current. A mathematical model equation was very effective tool to analyze the shape of polarization curves. Theoretical results agreed with experimental one.

Conflict of interest

The authors have no conflicts of interest to declare.

Acknowledgment

The authors would like thanks Prof. Dr. Apreal S. Yaro (Baghdad University – Chemical Engineering Department) for his continuous encouragement and assistance.