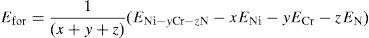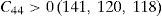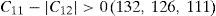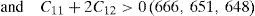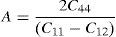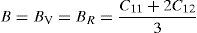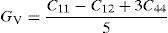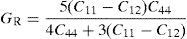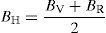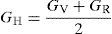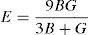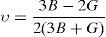Mechanical properties of Ni-based solid solution alloys: A first principles study

Abstract

Present work describes the structural stability and mechanical properties of Ni-based binary and ternary alloys. These alloys have been evaluated using first principles density functional theory (DFT) within generalized gradient approximation (GGA). The equilibrium lattice constant values of the γ phase in these alloys are in good agreement with the experimental data obtained by X-ray diffraction. The values of formation energy per atom of the ternary alloys are considerably lower than the Ni–16Cr binary alloy. These alloys satisfy the mechanical stability criteria in terms of elastic constants and possess ductile behaviour based on shear to bulk ratios.

1

Introduction

The main alloying elements of the important commercial Ni-based solid solution strengthened alloys are Cr, Mo, W and Fe (Bradley, 1988; Davis, 2000; Donachie, 1984; Sims, 1987). Among these, Ni–Cr and Ni–Mo binary alloys appear to be ideal systems for solid-solution strengthening in terms of atomic size and valency difference (Δz) (Delehouzee & Deruyttere, 1967). The Ni–Cr and Ni–Mo alloys display high and low stacking fault energy (SFE) values, respectively. In addition, the Ni–Cr system shows lower degree of solid solution strengthening than the Ni–Mo (Mehta, Mukhopadhyay, Mandal, & Singh, 2015a). The large difference in SFE has marked influence on strengthening mechanism and flow behaviour of these alloys.

A correlation among microstructure, texture and mechanical behaviour of a ternary Ni–16Cr–16Mo has been established recently (Mehta, Mukhopadhyay, Mandal, & Singh, 2015b). It is to be noted that the alloy Ni–16Cr–16Mo possesses an optimized effect of both the factors i.e. SFE and degree of solid solution strengthening. Two other alloys namely Ni–16Cr–8Fe and Ni–16Cr–4W have also been investigated recently which have modest values of SFE lie between Ni–16Cr–16Mo and Ni–16Cr alloys (Mehta et al., 2015b). Interestingly, the atomic size and valency difference of Ni–Mo and Ni–W are more or less same (Delehouzee & Deruyttere, 1967). It is important to mention here the atomic size of Fe is similar to Ni and its addition to Ni–16Cr alloy has marginal effect on SFE. In contrast, the valency difference between Ni–Cr and Ni–Fe is quite large.

The first principles calculations of Ni-based alloys have been carried out by several investigators (Chandran & Sondhi, 2011; Pathak, Mehta, & Singh, 2017; Tsi, Morozov, Yu, Merinov, & Goddard, 2016). These studies have been focused on different alloys as well as on different aspects. Pathak et al. (2017) have recently studied first principles calculation of Ni–Cr and Ni–Mo binary alloys. They have observed that the γ phase of both the alloys are stable and follow Born stability criteria in terms of elastic constants. Both the alloys are ductile and display anisotropic behaviour.

Present work is thus concerned with a first principles study of the Ni–16Cr, Ni–16Cr–16Mo, Ni–16Cr–8Fe and Ni–16Cr–4W alloys. It is to be noted that this study is an extension of the Ni–16Cr binary alloy (Pathak et al., 2017). The major alloying elements of the present alloys are Cr, Mo, W and Fe which impart different degree of solid-solution strengthening and SFE. The two commercial alloys, Hastelloy C-276 and Inconel 600 comprise these elements. The selected alloys are the part of a program to develop new alloys with similar/better properties of the commercial alloys as mentioned above. The comparative stability of the γ (fcc matrix) in these alloys has been explained. The lattice parameter values have been compared with those observed by X-ray diffraction technique. The mechanical properties in terms of elastic constants of these alloys except Ni–16Cr–4W are also evaluated.

2

Methodology

The Quantum Espresso software based on first principles density functional theory (DFT) utilizing pseudopotential technique has been employed (Giannozzi et al., 2009; Hohenberg & Kohn, 1964; Kohn & Sham, 1965; Vanderbilt, 1990). The generalized gradient approximation (GGA) with Perdew–Burke–Ernzerhof formulation has been used to include exchange-correlation effects (Perdew, Burke, & Ernzerhof, 1996). The plane wave cut-off energy has been verified for convergence for all the alloys and accordingly plane wave cut-off energy of 40 Ry has been used. Afterwards, fast fourier transform algorithm has been taken up for the conversions of wavefunctions between real and reciprocal lattices (Goedecker, 1997). In view of that, conjugate gradient algorithm (Gonze, 1996; Payne, Teter, Allan, Arias, & Joannopoulos, 1992) has been used within the frame work of self-consistency. The integration over the Brillouin zone (BZ) has been carried out with the Monkhorst-Pack scheme (Monkhorst & Pack, 1976). The convergence with respect to k-points has been verified for different alloys. The optimum values used for the present calculations are 10 × 10 × 10 for Ni–16Cr, Ni–16Cr–8Fe, Ni–16Cr–8Mo alloys while 4 × 4 × 4 for Ni–16Cr–3W. The structural optimizations of all the alloys for obtaining the minimum energies have been performed by relaxing the lattice constant of corresponding fcc lattice. In order to capture the disordered structure effectively, alloying elements (Cr, Mo, Fe and W) have been placed randomly at different locations within the supercell and the system energies have been computed. All the alloys with minimum system energy have been considered for further calculation. Convergence in present calculation has been obtained when the differences between energies in two consecutive steps are less than 1.36 × 10⁻⁴ meV.

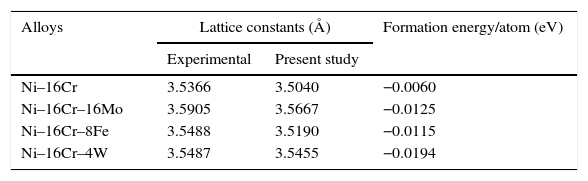
Both the formation energy per atom and the lattice constants of all the alloys have been computed and given in Table 1. The energy of formation per atom has been defined as

where, E_{Ni–yCr–zN} is the total system energy of Ni–yCr–zN alloy, Ni–yCr–zN having ‘x’ Ni-atoms, ‘y’ Cr-atoms and ‘z’ N-atoms, E_Ni, E_Cr, E_N are the total energy per atom in their ground states for Ni, Cr and N (Mo, Fe or W) atoms, respectively (x + y + z) denotes the total number of atoms considered in the super cell. The number of atoms considered in the present calculations for Ni–16Cr, Ni–16Cr–8Fe, Ni–16Cr–8Mo and Ni–16Cr–3W are 12, 12, 12 and 32 atoms, respectively. The ElaStic code has been utilized to calculate the elastic constants (Golesorkhtabar, Pavone, Spitaler, Puschnig, & Draxl, 2013).

Table 1.

Equilibrium lattice constants and formation energy/atom for Ni–16Cr, Ni–16Cr–16Mo, Ni–16Cr–8Fe and Ni–16Cr–4W alloys.

Alloys	Lattice constants (Å)		Formation energy/atom (eV)
	Experimental	Present study
Ni–16Cr	3.5366	3.5040	−0.0060
Ni–16Cr–16Mo	3.5905	3.5667	−0.0125
Ni–16Cr–8Fe	3.5488	3.5190	−0.0115
Ni–16Cr–4W	3.5487	3.5455	−0.0194

3

Results and discussion

The common alloying elements with large wt.% in Ni-based solid-solution alloys are mainly Cr and Mo. The contents of Cr and Mo lie in the range of 10–20% in most of the commercial Ni-based solid solution alloys apart from other alloying elements. It is known that around 16% of both the Cr and Mo in Ni improves the alloy thermal stability, fatigue life, high temperature strength, low expansion characteristics, oxidation and corrosion resistance (Tawancy & Al-Hadhrami, 2012). Based on this, the Ni–16Cr and Ni–16Cr–16Mo have been considered for the present study. It has been mentioned in literature that the optimum compositions of the Ni-based alloy should consist of an equal amounts of Cr and Mo (Tawancy & Asphahani, 1984). In addition, the two other ternary alloys i.e. Ni–16Cr–4W and Ni–16Cr–8Fe have also been investigated in the present study which has moderate values of SFE that lie between Ni–16Cr–16Mo and Ni–16Cr alloys. The amount of W is kept 4 wt.% due to its limited solid solubility in Ni. Interestingly, these alloys also form the compositional subset of several commercial alloys such as Hastelloy C-276, Inconel 600 etc. (Bradley, 1988; Davis, 2000; Donachie, 1984; Sims, 1987).

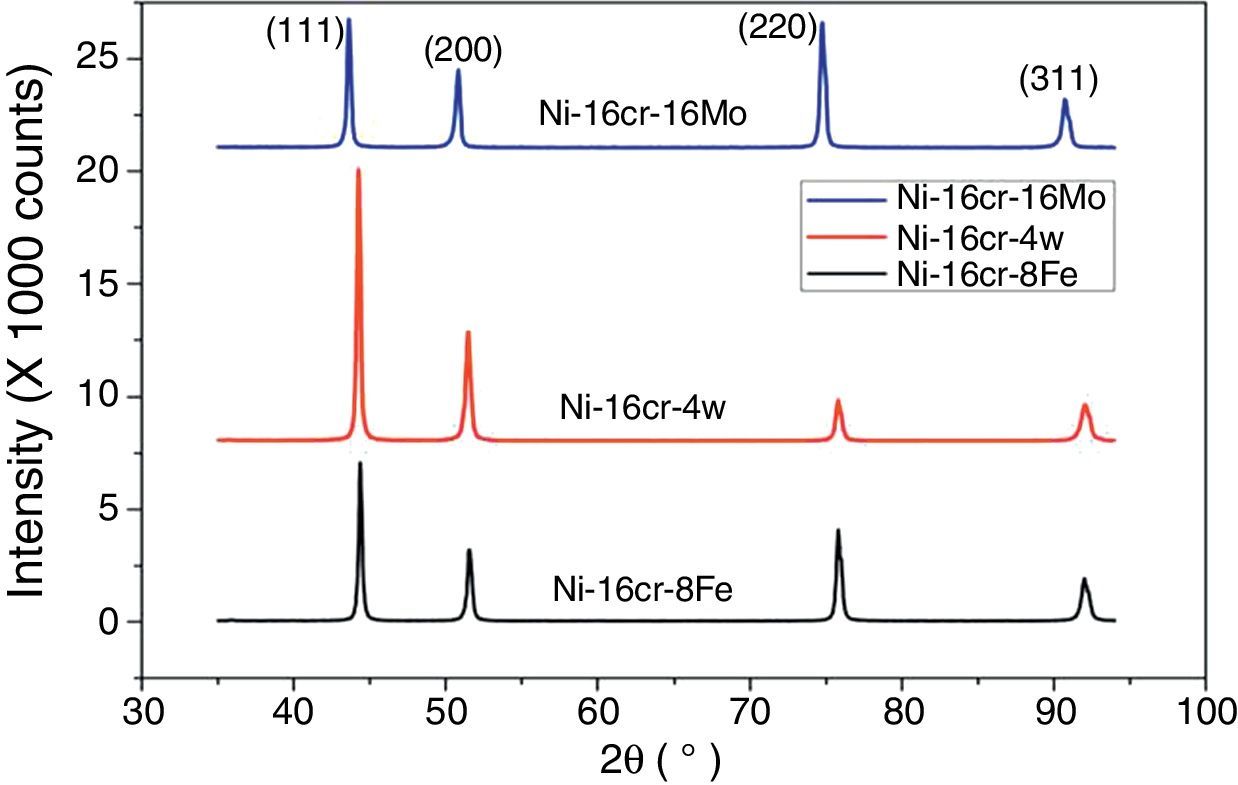
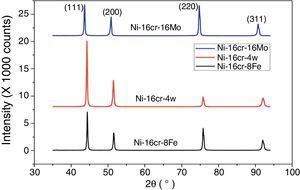
A first principles total energy calculation has been carried out for both the binary Ni–16Cr and ternary (Ni–16Cr–16Mo, Ni–16Cr–8Fe and Ni–16Cr–4W) alloys. The fcc structure of these alloys has been initially optimized by varying the lattice constant value as a function of energy. The corresponding equilibrium lattice constant for each alloy has been obtained with minimum energy. The lattice constants of all the ternary alloys have been measured using XRD technique and corresponding XRD patterns are exhibited in Figure 1. The XRD patterns reflect marginal shift in peak positions indicating change in lattice parameter with different alloys. The equilibrium lattice constant values (Table 1) are in good agreement with the available experimental data (Mehta et al., 2015a, 2015b).

Fig. 1.

XRD patterns of the ternary alloys: (a) Ni–16Cr–16Mo, (b) Ni–16Cr–4W and (c) Ni–16Cr–8Fe.

The lattice constant values of the present solid solution alloys display an increase from the pure Ni (3.5239 Å) although the extent of increase varies with the atomic radii as well as the content of alloying elements. The atomic radii of the elements Ni, Cr, Mo, Fe and W are 1.62, 1.85, 2.01, 1.72 and 2.02 Å, respectively. The marginal increase in lattice parameter of Ni–16Cr alloy can therefore be ascribed to the size of Cr. The alloy Ni–16Cr–16Mo exhibits largest value of lattice constant among the present alloys. This can also be attributed to a combined contribution of atomic sizes of both the alloying elements i.e. Cr and Mo in solid solution. As mentioned above, the atomic radii of these elements are larger than the Ni. It is to be noted that the atomic radii of W is slightly higher than the Mo. The lattice parameter of the alloy Ni–16Cr–4W is smaller than that of the Ni–16Cr–16Mo. It is known that the size difference of Ni and W is quite large (10.4%) but its effect on lattice constant of the alloy Ni–16Cr–4W is small due to small content of the W.

The values of formation energy per atom of the alloys obtained by first principle calculation are given in Table 1. These are negative for all the binary and ternary alloys. This indicates that the γ phase of the present alloys is stable. The values of formation energy per atom of ternary alloys are significantly lower than the Ni–16Cr alloy. It is important to mention here that the ternary phase diagrams of Ni–Cr–Mo, Ni–Cr–Fe and Ni–Cr–W systems exhibit reasonably wide solubility range of γ phase (Bloom & Grant, 1953; Nash, 1991; Turchi, Kaufman, & Liu, 2006). The formation energy per atom values also reflect that the alloy Ni–16Mo–4W is more stable than all other alloys having lowest among others.

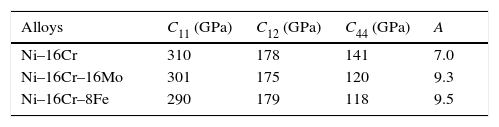
The elastic properties of a single crystal of all the alloys having fcc crystal structures are described by elastic constants C₁₁, C₁₂, C₄₄ and given in Table 2. The values of elastic constants of Ni–16Cr–4W could not be calculated due to large system size as well as with limited computational resource. The elastic constants values except C₁₂ reflect a marginal decrease from binary to ternary alloys. The values of C₁₁ are significantly higher than those of C₁₂ and C₄₄ in all the alloys. The nature of metallic bonding of cubic phases can be predicted based on Cauchy pressures (Olijnyk & Jephcoat, 2000). These are defined as C₁₂–C₄₄ < 0 for cubic materials. The negative Cauchy pressure indicates more directional bonding whereas positive value exhibits metallic bonding. The calculated values of Cauchy pressures for the Ni–16Cr, Ni–16Cr–16Mo and Ni–16Cr–8Fe alloys are 37, 55 and 61, respectively. These values clearly points towards the presence of predominant metallic bonds in present alloys. The extent of metallic bonding increases from binary to ternary alloys and is the highest for Ni–16Cr–8Fe.

Table 2.

Elastic constants and anisotropy factor (A) for ternary Ni–16Cr–16Mo and Ni–16Mo–8Fe alloys.

Alloys	C11 (GPa)	C12 (GPa)	C44 (GPa)	A
Ni–16Cr	310	178	141	7.0
Ni–16Cr–16Mo	301	175	120	9.3
Ni–16Cr–8Fe	290	179	118	9.5

The values of elastic constants can be utilized to envisage the mechanical stability of the γ phase. The Born stability criterions for cubic materials are given in Eqs. (2)–(4) (Born, 1940; Fedorov, 1968). The corresponding calculated values in units of GPa are given in parenthesis for Ni–16Cr, Ni–16Cr–16Mo and Ni–16Cr–8Fe alloys.

The values of elastic constants of these alloys given in parenthesis suggest that mechanical stability of the γ phase in these alloys is quite high. This is also in agreement with available experimental phase diagram wherein these phases have been observed either in single or two and/or three phase field regions (Bloom & Grant, 1953; Nash, 1991; Turchi et al., 2006).

The anisotropy factors (A) for all the alloys are given in Table 2.

For cubic materials

The values of anisotropic factors should be 1 for isotropic materials and away from 1 point towards the presence of anisotropy in elastic constants. The values of anisotropic factors obtained in present alloys are far away from 1. This indicates that the elastic anisotropy is present in these alloys. It is to be noted that the single crystal with fcc structure has different atomic arrangements along different crystallographic directions. The atomic packing is maximum along 〈111〉 which is most close packed direction. The extent of anisotropy increases from binary to ternary alloys. Both the ternary alloys exhibit comparable values of A. Interestingly, these alloys also exhibit the presence of plastic anisotropy in polycrystalline form in hot rolled condition (Mehta et al., 2015a, 2015b).

The effective elastic modulus of isotropic polycrystalline cubic materials can be predicted from the elastic constants by following two approximations. These are namely, the Voigt (Voigt, 1928) and Reuss (Reuss and Angnew, 1929) that provide information about the upper and lower limits. These are defined as

where B is bulk modulus while G_V and G_R are shear modulus values obtained by Voigt and Reuss approximations, respectively.

The average value of these two estimates as mentioned above is given by Hill (1952) approximation for all the alloys. The Voigt–Reuss–Hill (VRH) average values are given by

where B_H, G_H, E and ν are bulk modulus, shear modulus, Young's modulus and Poisson's ratio, respectively.

The calculated values of bulk, shear and Young's modulus of all the alloys are given in Table 3. The binary Ni–16Cr alloy exhibits maximum values. Modulus values decrease from binary to ternary alloys. The alloy Ni–16Cr–8Fe displays lower values of B, G and E than the Ni–16Cr–16Mo. It appears that the values of bulk modulus obtained in present alloys follow Hill's approximation since these are same in Voigt and Reuss approximations. On the other hand, shear modulus values of all the alloys obey VRH approximation wherein Voigt and Reuss describe upper and lower bounds of the shear modulus. The Hill's approximation on the other hand provides the average of these two.

Table 3.

Polycrystalline elastic constants such as bulk modulus (B), shear modulus (G) and Young's modulus (E) and Poisson's ratio (υ) for Ni–16Cr and Ni–16Mo alloys.

Alloys	B (GPa)	GV (GPa)	GR (GPa)	G (GPa)	E (GPa)	G/B	υ
Ni–16Cr	223	111	96	104	270	0.47	0.30
Ni–16Cr–16Mo	213	100	83	92	240	0.43	0.31
Ni–16Cr–8Fe	209	99	80	89	235	0.42	0.31

The values of shear and bulk modulus can also be utilized to predict the brittle and ductile behaviour of materials (Pugh, 1954). This can be visualized by taking the ratios of shear to bulk modulus. The ratio G/B and < 0.57 is associated with brittle and ductile behaviour, respectively. The G/B ratios of present alloys are smaller than that of 0.57. This reflects that these alloys are ductile. It is to be noted that all the three alloys have shown reasonably good ductility (large uniform elongation values) in hot rolled and annealed conditions (Mehta et al., 2015a, 2015b). The larger decrease in the values of G/B ratios in present study can be ascribed to the presence of Cr and Mo elements that decreases SFE significantly in Ni-based solid solution alloys (Table 3). It is known that the decrease in SFE increases the ductility of the alloys.

4

Conclusions

• 1.

  The structural stability and mechanical properties of Ni-based binary and ternary alloys have been evaluated for the first time using first principles density functional theory (DFT) within generalized gradient approximation (GGA).

• 2.

  The values of formation energy per atom of the ternary alloys are significantly lower than the Ni–16Cr binary alloy.

• 3.

  The equilibrium lattice constant values of the γ phase in these alloys are in good agreement with the experimental data.

• 4.

  These alloys satisfy the mechanical stability criteria in terms of elastic constants.

• 5.

  The G/B ratios of these alloys indicate the presence of reasonably good ductility.

Acknowledgements

Authors are grateful to Ministry of Defence, Government of India for financial support. The authors are indebted to The Director, Defence Metallurgical Research Laboratory (DMRL), Hyderabad for his encouragement. They intend their thanks to Director Anurag, Hyderabad for the provision of computational facilities and Dr. R. Sankarasubramanian and Dr. K.K. Mehta for technical support.

Conflict of interest

The authors have no conflicts of interest.