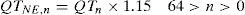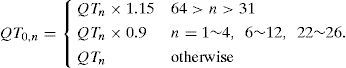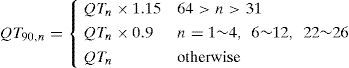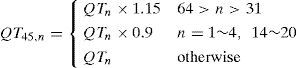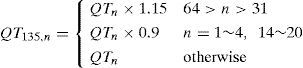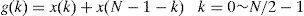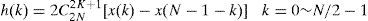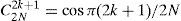Perceptual Zero-Tree Coding with Efficient Optimization for Embedded Platforms

Abstract

This study proposes a block-edge-based perceptual zero-tree coding (PZTC) method, which is implemented with efficient optimization on the embedded platform. PZTC combines two novel compression concepts for coding efficiency and quality: block-edge detection (BED) and the low-complexity and low-memory entropy coder (LLEC). The proposed PZTC was implemented as a fixed-point version and optimized on the DSP-based platform based on both the presented platform-independent and platform-dependent optimization technologies. For platform-dependent optimization, this study examines the fixed-point PZTC and analyzes the complexity to optimize PZTC toward achieving an optimal coding efficiency. Furthermore, hardware-based platform-dependent optimizations are presented to reduce the memory size. The performance, such as compression quality and efficiency, is validated by experimental results.

1.

Introduction

Image compression technology has become a common research subject of digital image processes in recent years [1] because of handheld devices and wireless networks [2]. Transform coding plays an important role in reducing redundancy and maintaining high coding quality and efficiency in image compression in an image-coding scheme. Discrete cosine transform (DCT) is one of the most common forms of transform coding. It uses coding and static Huffman coding techniques for transformation and entropy coding in prevailing image- and video-coding standards [3][2]. These standards include the Joint Photographers Expert Group (JPEG) [5], JPEG2000 [6], Motion Pictures Expert Group (MPEG), MPEG-1/2 [7][8], MPEG-4 [9], H.261/3 [10], and H.264/AVC [11]. Several of the proposed and applied DCT-based coding approaches include arithmetic coding (AC), embedded zero-tree DCT coding (EZDCT) [12], embedded zero-tree coding in hierarchical DCT (EZHDCT) [13], set partition in hierarchical tree (SPIHT) [14], zero-tree entropy coding (ZTE) [15], embedded block coding with optimized truncation (EBCOT) [16], and warped discrete cosine transform (WDCT) [17]. Although these coders achieve high compression efficiency, they have substantially higher computational costs and memory requirements than other techniques. These disadvantages form a hardware implementation bottleneck in mass-market consumer electronic products.

Zhao et al. [18] proposed a highly efficient method referred to as the low-complexity and low-memory entropy coder (LLEC). The LLEC provides block-based transform coding such as the DCT and is suitable for embedded and hardware implementations. Chang et al. presented a block-edge-based method for adaptively adjusting the quantization table [19]. Block-edge detection (BED) provides useful information on edge features and has applications in digital image/video processing, pattern recognition, and computer vision. Determining an efficient and quick method for identifying edge features is an essential step in the detection and segmentation of objects of interest. Although integrating the LLEC technique with DCT is an efficient approach for producing a low-computation and low-memory-cost image codec, it does not provide a perceptual strategy to improve the visual quality of compressed images. Therefore, this study proposes a block-edge-based perceptual zero-tree coding (PZTC) method that integrates and improves these two image-coding techniques efficiently. Furthermore, this paper presents an adaptive quantization table adjustment scheme based on the statistical analysis of DCT blocks in various types of images. Therefore, the proposed combinative coding scheme adaptively adjusts the quantization tables based on edge feature detection. Thereafter, the LLEC codes the quantized coefficients by using a predetermined quantization table to preserve the highest visual quality in the compressed images.

The proposed PZTC was implemented and evaluated on both PC-based and DSP-based embedded platforms. A multicore system was chosen as the development platform for objectively evaluating and observing the coding efficiency of PZTC for use in embedded and portable handheld devices [20]. This study uses the OMAP3530 platform, which is a dual-core system provided by Texas Instruments (TI) and commonly adopted in various consumer products of embedded and handheld devices as the targeted embedded platform [21]. Moreover, this study presents several efficient optimizing techniques (regarding OMAP3530) including software- and hardware-based optimizations [22][23]. The proposed optimizations were designed according to the targeted platform (OMAP 3530) and achieve coding efficiency improvements and reduce the consumed memory. Therefore, the coding complexity of PZTC is analyzed in this study, and the most complex module of PZTC is obtained and optimized based on the OMAP3530 platform facilities. Experimental results indicated that the proposed approach provides satisfactory image compression performances in both the peak signal-to-noise ratio (PSNR) and visual quality. Compared to other coding techniques, the PZTC achieves adequate and effective image compression for various images. Furthermore, PZTC is a single-pass coding algorithm that requires a short computational duration. Experimental results on the PC and DSP platforms show that PZTC provides a promising performance in both computational efficiency and image-coding results.

The features and contributions of this study are as follows:

• 1)

  The proposed PZTC improves two novel methods, which are LLEC and BED. PZTC adopts the edge information of DCT blocks to perform adaptive and perceptual image coding. PZTC is a high-efficiency and high-quality image coder because it uses the proposed effective combinative coding scheme.

• 2)

  The proposed architecture is suitable for embedded and portable applications because of the low complexity of PZTC. This study presents the effective implementation of PZTC on the DSP-based platform and optimizes PZTC by using software- and hardware-based optimizations of the targeted platform to achieve optimal coding and computational efficiency. Moreover, the optimized PZTC is evaluated on the dual-core OMAP3530 to demonstrate the feasibility of its use in embedded and handheld devices.

The remainder of this paper is organized as follows: Section 2 introduces the combinative scheme of the PZTC. Section 3 presents the optimization methods of PZTC for the DSP-based platform. Section 4 shows the experimental results, and Section 5 offers a conclusion.

2

The proposed methods

Reviews of the LLEC and fast BED-based on DCT are described in [18] and [19]. These two methods have a common distinguishing feature, which is based on DCT. Because of this common feature, this section presents the combination of the LLEC and BED to perform a decent coder for image compression.

The flowchart of the proposed coder is shown in Figure 1. First, the input image is processed with the macroblock DCT and transformed into DCT coefficients. After the forward DCT is completed, three specific coefficients on each block can be used to determine the directional edge of this block; thus, the directional edge of each block in the entire input image is obtained. The combinative scheme is described in [24]. The DCT coefficients are quantized by the adaptive quantization tables by adopting the proposed combinative scheme, and the coefficients are expressed as Eqs. (1)–(5). Thereafter, the quantized coefficients are coded by the LLEC with good coding efficiency and quality.

Figure 1.

The flow chart of the proposed encoder.

3

The proposed methods

3.1

Platform-independent implementation

PZTC is implemented with a fixed-point version for simplification to allow porting the proposed PZTC onto the embedded system. The fixed-point PZTC is a platform-independent coder that can be easily ported to various embedded systems. In this paper, the proposed fixed-point PZTC is implemented into TI OMAP3530 [21], which contains a 520 MHz DSP and a 720 MHz ARM. Table 1 shows the performance on the DSP [25], and the coding efficiency of the encoder and decoder can achieve 10.63 and 11.56 fps on average, respectively.

Table 1.

The compression efficiency on DSP.

Fixed-point PZT	Coding efficiency (fps)	Memory consumption (Bytes)
Encoder	10.63	25920
Decoder	11.56

3.2

Profiling the proposed coder

Table 1 shows that, although the proposed PZTC on the DSP performs at a decent coding efficiency, it can be improved to provide an even better coding efficiency. The architecture of OMAP3530 is the focus, and platform-dependent optimizations are adopted. The goal of optimizing the PZTC is to increase the coding efficiency and prevent any extra memory consumption. Furthermore, the coding quality and accuracy must be precise. This simple experiment ensures that PZTC maintains a reasonable coding quality when the optimization level is set to –O3; thus, the coding efficiency is increased by 21.4% for encoding and 10.3% for decoding.

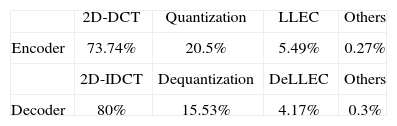
Profiling PZTC and checking its most complex module is necessary before optimization [26]. Table 2 shows the results of profiling the PZTC encoder and decoder. The 2D-DCT and IDCT are the most complex parts in the PZTC encoder and decoder, respectively. Although the proposed fixed-point PZTC adopts fast DCT by Lee [27], numerous loops, multiplications, and additions result in coding complexity. Therefore, the 2DDCT and IDCT modules are the focus to reduce the coding complexity.

Table 2.

Analysis of the coding complexity of modules in the encoder and decoder.

	2D-DCT	Quantization	LLEC	Others
Encoder	73.74%	20.5%	5.49%	0.27%
	2D-IDCT	Dequantization	DeLLEC	Others
Decoder	80%	15.53%	4.17%	0.3%

3.3

Platform-independent implementation

This study uses the integrated functions provided by TI for the software-based platform-dependent optimizations. For example, the bandwidths of the input coefficients and cosine tables are 16-bit width for encoding. Therefore, there are several 16 x 16 and 16 x 32 multiplications. OMAP3530 uses the TMS320C64x+ DSP core, and its 16 x 16 and 16 x 32 multiplications can be substituted with intrinsic functions “_mpy” and “_mpylill”, respectively. Each stage of fast DCT by Lee consists of additions and subtractions with multipliers, which is similar to fast Fourier transform (FFT). The stages are shown as Eqs. (6) and (7), where x denotes the input coefficient, g and h denote the results of each stage, N denotes the number of input points, and k is the index of x, g, and h. is expressed as Eq. (8). The coefficients in the fixed-point 2D-DCT are 32-bit width in maximum; thus, the intrinsic function “_addsub” is used to execute the addition and subtraction simultaneously. The complexity of 2DDCT/IDCT is decreased by approximately 25% when using the intrinsic function.

This study uses CODE_SECTION and DATA_SECTION to locate the most frequently used functions and memory buffers to the internal cache memory for hardware-based platform-dependent optimizations (i.e., L2 RAM). The 2D-DCT and IDCT functions are defined by CODE_SECTION and transferred to L2 RAM, and the 8 x 8 DCT block is defined as DATA_SECTION and is also transferred to L2 RAM. By using the software- and hardware-based optimizations, the total coding complexity of the encoder and decoder can achieve significant reductions of 49.83% and 46.52% in computational costs, respectively, compared to the original platform-independent PZTC.

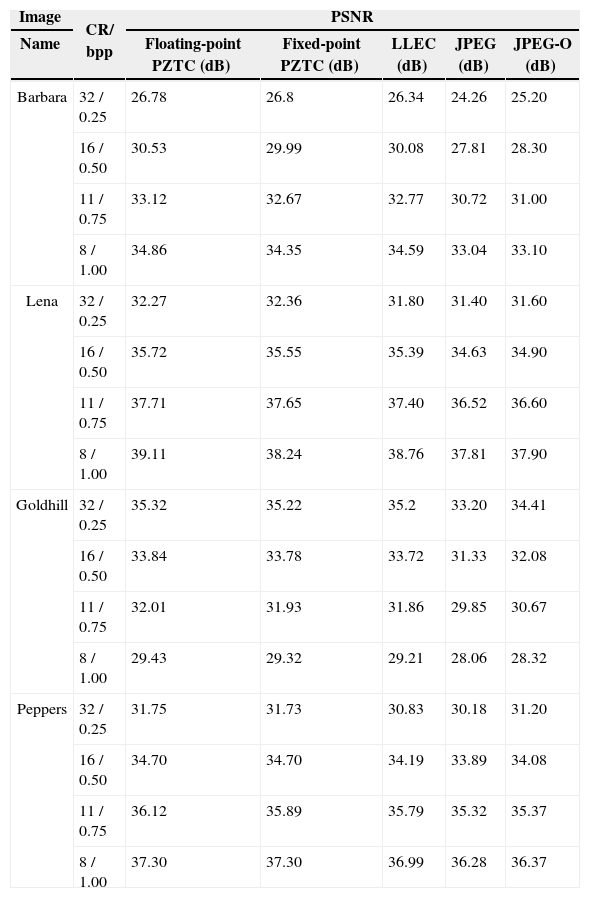
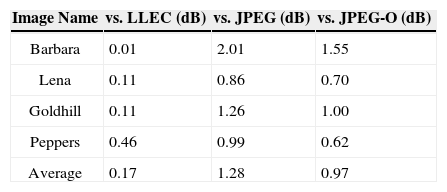
4

Experimental results

The 512 × 512 grayscale sample images were tested at different bit rates (0.25 - 1.00 bpp). This study simulates all experiments introduced in this section using a PC platform with an Intel Duo Core 1.67 GHz processer and 2 GB RAM. The deadzone width of a midtread quantizer was set as 30%–50% larger compared to the regular step size in the proposed architecture. The measuring method of the image quality is PSNR, which is computed from the original image and decoded images. Table 3 shows a comparison of the experimental results from the LLEC, JPEG (using a default Huffman table), and JPEG-O (using adaptive Huffman coding) for testing the performance of the proposed approach. Both the floating-point and fixed-point versions of PZTC are evaluated and discussed in the experiments. The comparison of the compression performances by the PZTC and other three coders (i.e., LLEC, JPEG, and JPEG-O) is shown on Tables 4 and 5 to reveal the advantages of the proposed PZTC in coding quality.

Table 3.

The compression performance at different bit rates (CR denotes the compression ratio).

Image	CR/ bpp	PSNR
Name		Floating-point PZTC (dB)	Fixed-point PZTC (dB)	LLEC (dB)	JPEG (dB)	JPEG-O (dB)
Barbara	32 / 0.25	26.78	26.8	26.34	24.26	25.20
	16 / 0.50	30.53	29.99	30.08	27.81	28.30
	11 / 0.75	33.12	32.67	32.77	30.72	31.00
	8 / 1.00	34.86	34.35	34.59	33.04	33.10
Lena	32 / 0.25	32.27	32.36	31.80	31.40	31.60
	16 / 0.50	35.72	35.55	35.39	34.63	34.90
	11 / 0.75	37.71	37.65	37.40	36.52	36.60
	8 / 1.00	39.11	38.24	38.76	37.81	37.90
Goldhill	32 / 0.25	35.32	35.22	35.2	33.20	34.41
	16 / 0.50	33.84	33.78	33.72	31.33	32.08
	11 / 0.75	32.01	31.93	31.86	29.85	30.67
	8 / 1.00	29.43	29.32	29.21	28.06	28.32
Peppers	32 / 0.25	31.75	31.73	30.83	30.18	31.20
	16 / 0.50	34.70	34.70	34.19	33.89	34.08
	11 / 0.75	36.12	35.89	35.79	35.32	35.37
	8 / 1.00	37.30	37.30	36.99	36.28	36.37

Table 4.

The floating-point PZTC versus other methods.

Image Name	vs. LLEC (dB)	vs. JPEG (dB)	vs. JPEG-O (dB)
Barbara	0.38	2.37	1.92
Lena	0.37	1.11	0.95
Goldhill	0.22	1.37	1.11
Peppers	0.52	1.05	0.71
Average	0.37	1.48	1.17

Table 5.

The fixed-point PZTC versus other methods.

Image Name	vs. LLEC (dB)	vs. JPEG (dB)	vs. JPEG-O (dB)
Barbara	0.01	2.01	1.55
Lena	0.11	0.86	0.70
Goldhill	0.11	1.26	1.00
Peppers	0.46	0.99	0.62
Average	0.17	1.28	0.97

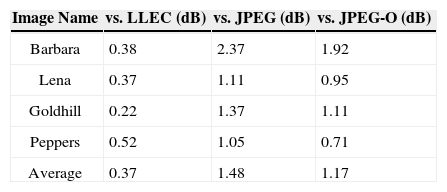
The proposed PZTC method has a far superior performance compared to the LLEC, JPEG, and JPEG-O at a 0.25 bitrate. Table 4 shows that the compression performance of the floating-point PZTC consistently outperforms those of the LLEC, JPEG, and JPEG-O. It is on average superior to the LLEC by 0.37 dB, the JPEG by 1.48 dB, and the JPEG-O by 1.17 dB. Furthermore, Table 5 shows the comparative data between the fixed-point PZTC and other coders. Although the fixed-point PZTC may not provide high PSNR measures compared to those of the floating-point version, it represents higher PSNRs than the LLEC by 0.17 dB, the JPEG by 1.28 dB, and the JPEG-O by 0.97 dB on average. A comparison of the results indicates that the fixed-point PZTC may not provide high PSNR measures of the floating-point version, especially for the “Barbara” test image. The fixed-point PZTC achieves a slightly lower PSNR than that of the LLEC when the compression ratio is set to the 1.0, 0.75, or 0.5 bitrate. Nevertheless, fixed-point PZTC achieves better PSNR values than those of the LLEC when the compression ratio is set to the 0.25 bitrate, which is due to the fixed-point DCT computation removing a detailed fractional portion of the DCT coefficients. The “Barbara” test image contains numerous DCT blocks that distribute sufficient DCT coefficients at a high frequency. Therefore, the removal of the fractional portion of the DCT coefficients may have a significant effect when handling these types of pictures. However, most compression results of fixed-point PZTC are still superior to those of the LLEC, JPEG, and JPEG-O.

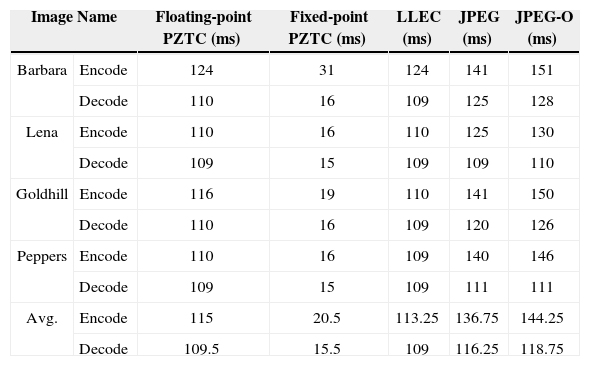
Table 6 shows a comparison of the computational costs of the four coders, which are PZTC (floating-point and fixed-point), LLEC, JPEG, and JPEG-O. Table 6 shows that both floating-point and fixed-point PZTC provide better computational efficiencies than the JPEG and JPEG-O, especially fixed-point PZTC. Floating-point PZTC can save approximately 20 ms for encoding and 10 ms for decoding, compared to those of the standard JPEG codec. Furthermore, fixed-point PZTC has a significantly improved computational complexity compared to floating-point PZTC because the fixed-point version optimizes the fixed-point DCT computation. An examination of the results on Tables 5 and 6 indicates that fixed-point PZTC performs extremely well for computational efficiency with satisfactory visual quality and compression performance.

Table 6.

The comparisons of computational efficiency.

Image Name		Floating-point PZTC (ms)	Fixed-point PZTC (ms)	LLEC (ms)	JPEG (ms)	JPEG-O (ms)
Barbara	Encode	124	31	124	141	151
	Decode	110	16	109	125	128
Lena	Encode	110	16	110	125	130
	Decode	109	15	109	109	110
Goldhill	Encode	116	19	110	141	150
	Decode	110	16	109	120	126
Peppers	Encode	110	16	109	140	146
	Decode	109	15	109	111	111
Avg.	Encode	115	20.5	113.25	136.75	144.25
	Decode	109.5	15.5	109	116.25	118.75

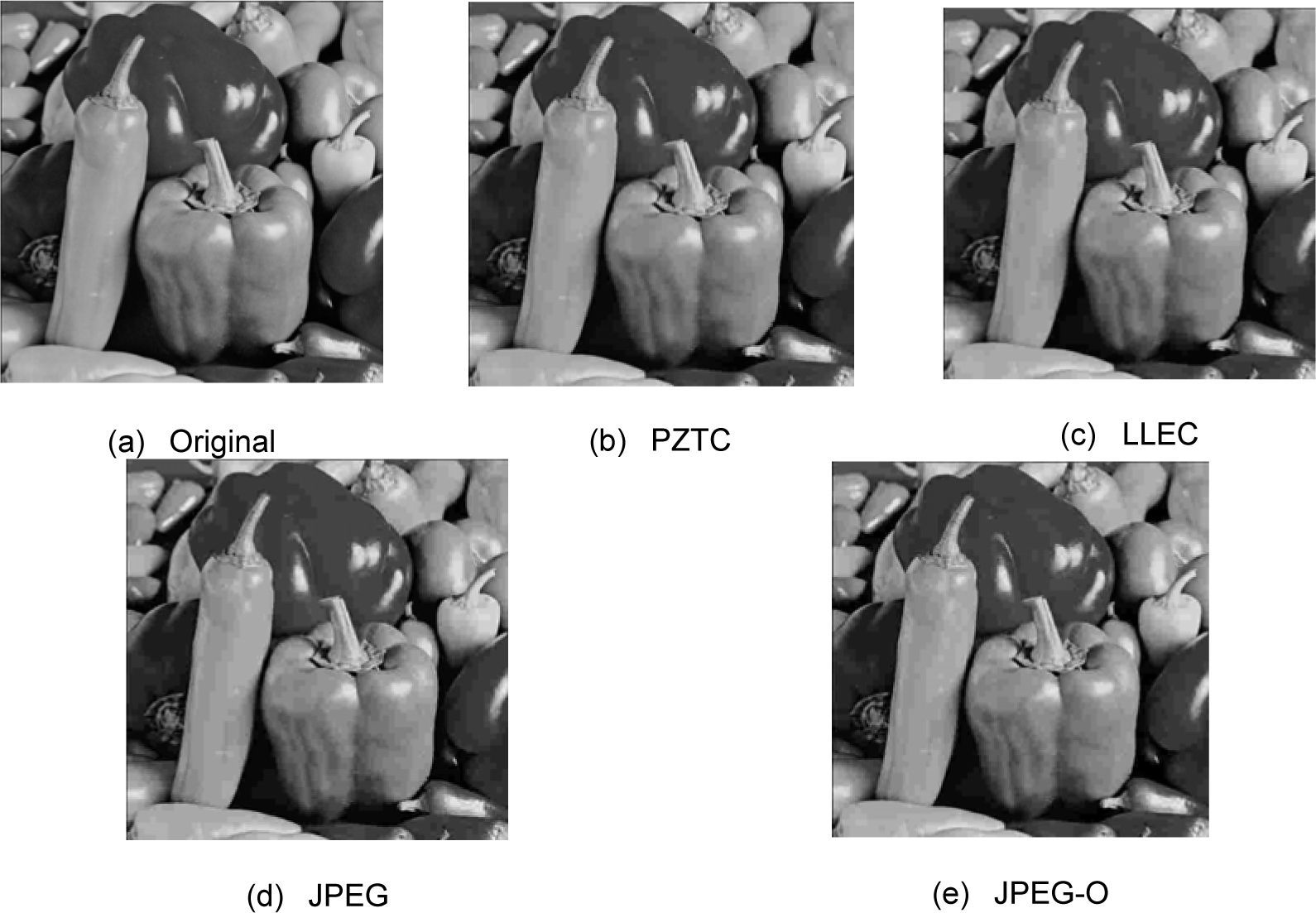
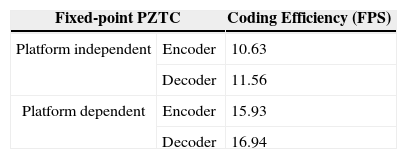
In Section 3, this study presents the numerous optimizing techniques of the PZTC for OMAP3530, where the implementation of PZTC for OAMP 3530 is shown as Figure 2. Table 7 shows the performances of fixed-point PZTC on OMAP3530. We provided the results of platform-independent PZTC on OMAP3530 in a previous study [24]. The software- and hardware-based platform-dependent optimizations in this study are shown in Section 3. Using these optimizations, the PZTC encoder and decoder on OMAP3530 operated at 15.93 and 16.94 fps, respectively. The results in Table 7 show that the improved fixed-point PZTC on the DSP has superior computational and compression efficiencies for both the encoding and decoding processes. Figures 3 to 6 show the visual comparisons of the images at a 0.25 bitrate. The proposed approach can provide an improved visual effect in the smooth regions. The analyses of Figures 3 to 6 are summarized as follows:

Figure 2.

Visual comparison results of Lena at 0.25 bit rates.

Table 7.

The performances of the fixed-point PZTC on OMAP3530.

Fixed-point PZTC		Coding Efficiency (FPS)
Platform independent	Encoder	10.63
	Decoder	11.56
Platform dependent	Encoder	15.93
	Decoder	16.94

Figure 3.

Visual comparison results of Goldhill at 0.25 bit rates.

• •

  In the proposed approach, PZTC provides an improved visual effect in the smooth regions. For example, PZTC performance is of good standard for coding human skin, as shown in Figures 3 and 4.

  
  

  Figure 4.

  Visual comparison results of Peppers at 0.25 bit rates.
• •

  Although PZTC consistently outperforms JPEG and JPEG-O in PSNR measures, it quantizes more coefficients in the median- to high-frequency bands to reduce visual quality in the sharpness regions (i.e., the lines of pants in the Barbara image, as shown in Figure 3).

• •

  Table 3 shows that the increase in compression ratio is significantly greater than the decrease in coding quality. Therefore, PZTC is effective for further promoting the resulting PSNR performance.

  • •

    Because the quantization tables of the JPEG and JPEG-O preserve more edges of the image than step quantization, they provide an improved visual quality in the sharpness- varying regions.

• •

  PZTC has improved and overcome the drawbacks of the original LLEC because PZTC exploits the block-edge information and varies the quantization tables adaptively to perform perceptual image coding. PZTC performance is considerably superior to the performance of the original LLEC for the edge regions (i.e., the edges of the roots in Figure 5).

5

Conclusion

This study proposed a mixed coder that combines the BED and LLEC methods, and implemented them in a dual-core DSP-based platform. These two methods are based on DCT. Therefore, they can be integrated into a coder for DCT coefficients. Section 3 detailed PZTC being ported to TI OMAP3530. Platform-dependent optimizations were proposed to achieve an advanced coding efficiency. Compared to the previous version of PZTC on DSP, the proposed PZTC can achieve a 49.83% and 46.52% reduction in computational complexity. Section 4 showed the experimental results of the proposed encoder. The proposed PZTC (floating-point and fixed-point) achieves better compression quality and coding efficiency compared to other existing coders, such as the LLEC, JPEG, and JPEG-O. Furthermore, fixed-point PZTC was implemented on the DSP, operating at 15.93 FPS on encoding and 16.94 FPS on decoding. Furthermore, the proposed approach can provide an improved visual effect for smooth regions. The experimental results of compression quality, coding, and computational efficiency on the DSP indicate that the proposed PZTC is highly practical for embedded and handheld applications. Because of the superior performances in low bitrate coding and coding efficiency for the applications of embedded computing systems, the proposed PZTC can be adapted for various consumer electronic applications such as real-time video streaming and surveillance usages.

Acknowledgements

This work is supported by the National Science Council of the Republic of China under Contract No. NSC-100-2221-E-027-033, NSC-101-2219-E-027-006.