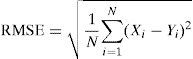Prediction of solar radiation for solar systems by using ANN models with different back propagation algorithms

Abstract

Global solar radiation (GSR) is an essential parameter for the design and operation of solar energy systems. Long-standing records of global solar radiation data are not available in many places because of the cost and maintenance of the measuring instruments. The major objective of this work is to develop an ANN model for accurately predicting solar radiation. Two ANN models with four different algorithms are considered in the present study. Meteorological data collected for the last 10 years from five different locations across India have been used to train the models. The best ANN algorithm and model are identified based on minimum mean absolute error (MAE) and root mean square error (RMSE) and maximum linear correlation coefficient (R). Further, the present study confirms that prediction accuracy of the ANN model depends on the complete set of data being used for training the network for the intended application. The developed ANN model has a low mean absolute percentage error (MAPE) which ascertains the accuracy and suitability of the model to predict the monthly average global radiation so as to design or evaluate solar energy installations, where the meteorological data measuring facilities are not in place in India.

1

Introduction

Kalogirou (2013) stated that solar radiation is the fundamental source of the Earth's energy, providing almost 99.97% of the heat energy needed for various chemical and physical processes in the atmosphere, ocean, land, and other water bodies. It plays a vital part as a renewable energy source. Yadav and Chandel (2014) explained that global solar radiation is considered as the most essential parameter in meteorology, renewable energy and solar energy conversion applications, especially for the sizing of standalone photovoltaic systems. Chen, Duan, Cai, and Liu (2011) reported on the solar radiation measurements which are employed to evaluate the potential power levels to design some of the solar energy applications such as solar water heating, agricultural studies, wood drying, photovoltaic, thermal load analysis on buildings, atmospheric energy balance studies and meteorological forecasting. Benghanem (2012) discussed about the importance of the prediction model to calculate the average of long-term global solar radiation. However, measuring this parameter is possible only in a limited number of places because of the cost and maintenance of the measuring instruments. A common practice is to assess this parameter using suitable empirical correlations through the measured data at some selected places where the measuring facilities are installed. Many researchers have developed various empirical models to estimate the value of global radiation by using other known meteorological parameters such as temperature, sunshine hours, relative humidity, latitude and longitude.

Besharat, Dehghan, and Faghih (2013) reviewed the extensive global solar radiation models available in the chronologically collected literatures. They classified the empirical models discussed in collected literatures into four categories as sunshine-based, cloud-based, temperature-based and other meteorological parameter-based models, based on the employed meteorological parameters as model input. Furthermore, in order to evaluate the accuracy and applicability of the models reported in the literature for computing the monthly average global solar radiation on a horizontal surface, the geographical and meteorological data of Yazd city, Iran was used. The developed models were then evaluated and compared on the basis of statistical error indices and the most accurate model was chosen in each category. Results showed that all the proposed correlations have a good estimation of the monthly average daily global solar radiation on a horizontal surface in Yazd city. However, they reported that the El-Metwally sunshine-based model predicts the monthly averaged global solar radiation with higher accuracy. Quansah et al. (2014) proposed a sunshine hour-based empirical model and an air temperature-based empirical model for the global solar radiation estimation in the Ashanti region of Ghana. Seven models were used for the evaluation process, by exploiting the Angstrom–Prescott model and Hargreaves–Samani model. The experimental analysis showed that the suggested Angstrom–Prescott model underestimated the global solar radiation in April–June and October–November. However, it overestimated the global solar radiation in August, September and December. As the input data for the suggested models were site specific, the estimation of the global solar radiation was complex. Further, the suggested models were not suited for measuring the long-term solar radiation. Because of this, most of the researchers attempted to develop numerous approaches, using the meteorological parameters for solar radiation prediction. One of the prediction or forecasting approaches being followed in recent times is the artificial intelligent techniques to predict the solar radiation.

Yacef, Benghanem, and Mellit (2012) explained that one of the prediction or forecasting approaches being followed in recent times is the artificial intelligent technique to predict the solar radiation. Fadare (2009) designed an artificial neural network-based model for forecast of solar energy potential in Nigeria. The outcome exhibited that the correlation coefficient between the ANN predictions and measured data exceeded 90%, thereby projecting a superior consistence of the model for assessment of solar radiation for locations in Nigeria. Solmaz and Ozgoren (2012) initiated the technique of artificial neural network to determine the hourly solar radiation of six chosen provinces in Turkey. According to the results, an artificial neural network model is capable for quick prediction of hourly solar radiation of the selected cities in Turkey. Sözen, Arcaklioglu, Ozalp, and Kanit (2004) developed an artificial neural network model to determine the solar energy potential in Turkey. The results from training and testing data confirm the ability of the neural network model to predict the solar energy potential as compared to the regression models. An artificial neural network model to predict the mean daily global solar radiation in China was developed by Jiang (2009), who reported that the ANN model has higher accuracy as compared to other regression models. Pandey and Katiyar (2013) presented a brief discussion about the renewable energy and its future, measurement techniques and models of solar radiation for efficient utilization of solar energy.

In the present work, the prediction of monthly average global solar radiation was made by using two different ANN models, each with four different algorithms. Nine inputs were used in both ANN models I and II. The inputs are latitude, longitude, altitude, year, month, mean ambient air temperature, mean station level pressure, mean wind speed and mean relative humidity. Only one output, monthly average global solar radiation was predicted. In ANN model I, 4 stations (Chennai, Kolkatta, New Delhi and Mumbai) data are used for training and testing is done for a new station (Bangalore) data. Nevertheless, in ANN model II, all the five stations (Chennai, Kolkatta, New Delhi, Mumbai and Bangalore) data are used for training and testing. Both ANN models are trained and tested by using the following four different back propagation algorithms: gradient descent (GD), Levenberg–Marquardt (LM), resilient propagation (RP) and scaled conjugate gradient (SCG). Among the two models, an accurate ANN model and the best algorithm were selected based on the minimum mean absolute error (MAE), minimum root mean square error (RMSE) and maximum linear correlation coefficient (R). The mean absolute percentage error (MAPE) value of the present work was computed and compared with other similar works.

2

Artificial neural networks

Artificial neural networks (ANNs) can be used for numerous functions such as prediction, curve fitting and regression. In this work, artificial neural networks are used to formulate the solar radiation prediction models. The fundamental unit of an artificial neural network is a neuron that uses a transfer function to formulate the output. Each input is multiplied with a weight that serves as an association between an input and the neuron and also between the several layers of neurons. In the final stage, the neuron applies a transfer function to obtain the result. Figure 1 shows the general architecture of the ANN. The advantage of ANN techniques is that they do not need the knowledge of mathematical calculations between the parameters but they involve lesser computational effort and provide a compact solution for multi-variable issues.

Fig. 1.

General architecture of artificial neural network.

In the present work, an artificial neural network (ANN) model was developed to predict the monthly average global solar radiation values in India using meteorological data for a period of 10 years from five different locations (Bangalore, Chennai, Kolkata, New Delhi and Mumbai) with diverse climatic condition across India. The commonly used four algorithms, like gradient descent (GD), Levenberg–Marquardt back propagation (LM), resilient back propagation (RP) and scaled conjugate gradient (SCG) were used in the present work to predict the monthly average global solar radiation.

3

Methodology

3.1

Data collection

In India, a minimum number of meteorological stations are installed to monitor the solar radiation because of maintenance and higher cost of the measuring equipment. Monthly data for mean ambient air temperature, mean station level pressure, mean wind speed, mean relative humidity and average global solar radiation of five different locations (Bangalore, Chennai, Kolkata, New Delhi and Mumbai) with diverse climatic condition across India were collected, for a period of 10 years (2000–2009) from Indian Meteorological Department, Pune. Values of the various parameters like latitude, longitude and altitude and range of monthly global solar radiation values of five stations are as shown in Table 1. After collecting the data, the entire dataset is divided into two categories such as training set and testing set. It is further processed with the help of the ANN model.

Table 1.

Geographical location of stations.

S. no	Name of the station	Latitude N (deg min)	Longitude E (deg min)	Altitude (m)	Range of monthly GSR (MJ/m^2)
1	Bangalore	12°57′	77°38′	897	6.45–25.80
2	Chennai (Minambakkam)	13°00′	80°11′	16	10.62–25.44
3	Kolkatta (Dum Dum)	22°39′	88°27′	06	9.83–21.49
4	New Delhi (Safdarjang)	28°35′	77°12′	216	9.50–25.45
5	Mumbai (Santacruz)	19°07′	72°51′	14	11.90–26.71

3.2

Artificial neural network implementation

The design of the ANN model is essential for predicting global solar radiation, where solar radiation measuring instruments are not installed. This ANN model will be very useful for successful utilization of a great amount and free ecological solar power for abundant practical applications.

The ANN structure consists of three layers. Generally an input layer which receives collected data, an output layer which produces computed information and one or more hidden layers useful to connect input and output layer with the help of processing unit neurons. In an artificial neural network model, the value of an output can be estimated by training a set of input–output data. The following most commonly used algorithms such as gradient descent (GD), Levenberg–Marquardt back propagation (LM), resilient back propagation (RP) and scaled conjugate gradient (SCG) are employed for training in a multilayer feed forward network.

In the present analysis, the ANN model was developed in MATLAB version 2012, based on three layers feed forward network with tangent sigmoid activation function in hidden layers and linear activation function in output layer. The following nine parameters, such as latitude, longitude, altitude, year, month, mean ambient air temperature, mean station level pressure, mean wind speed and mean relative humidity, are used as inputs and only one parameter monthly average global solar radiation was predicted as an output. Table 2 presents the performance parameters used to train all the four algorithms in the present research work.

Table 2.

Performance parameters used for training.

GD algorithm
Maximum number of epochs to train	1000
Performance goal	0
Generate command-line output	False
Show training GUI	True
Learning rate	0.01
Maximum validation failures	6
Minimum performance gradient	1e−5
Epochs between displays	25
Maximum time to train in seconds	Inf

LM algorithm
Maximum number of epochs to train	1000
Performance goal	0
Maximum validation failures	6
Minimum performance gradient	1e−5
Initial mu	0.001
Mu decrease factor	0.1
Mu increase factor	10
Maximum mu	1e10
Epochs between displays	25
Generate command-line output	False
Show training GUI	True
Maximum time to train in seconds	Inf

RP algorithm
Maximum number of epochs to train	1000
Epochs between displays	25
Generate command-line output	False
Show training GUI	True
Performance goal	0
Maximum time to train in seconds	Inf
Minimum performance gradient	1e−5
Maximum validation failures	6
Learning rate	0.01
Increment to weight change	1.2
Decrement to weight change	0.5
Initial weight change	0.07
Maximum weight change	50.0

SCG algorithm
Maximum number of epochs to train	1000
Epochs between displays	25
Generate command-line output	False
Show training GUI	True
Performance goal	0
Maximum time to train in seconds	Inf
Minimum performance gradient	1e−5
Maximum validation failures	6
Determine change in weight for second derivative approximation	5.0e−5
Parameter for regulating the indefiniteness of the Hessian	5.0e−7

The schematic diagram of the artificial neural network model for the present work is shown in Figure 2.

Fig. 2.

Schematic diagram of ANN model for the present work.

3.3

Normalization, training and testing

In an ANN, the training set is used for learning by adjusting the weights on the neural network. In other words, the artificial neural network model should be able to predict new data (which is not in the training set) with minimum error. The testing set is used only to assess the performance of a developed ANN model.

In the present work, monthly data collected for five different locations (Bangalore, Chennai, Kolkata, New Delhi and Mumbai) with different climatic condition across India for the period of 10 years, both input and output data sets, were normalized to the range between −1 and +1 according to Solmaz and Ozgoren (2012) before the training process.

where

• X_N: normalized value;

• X_R: value to be normalized;

• X_max: maximum value among all the values for related variable; and

• X_min: minimum value among all the values for related variable.

After completing the normalization process, the entire dataset was divided into two categories for training (80%) and testing (20%) of an artificial neural network model.

3.4

Selection of optimum number of hidden layer neurons

It is very complicated to select the number of neurons in a hidden layer and to choose the number of hidden layers for any artificial neural network model. Usually, one hidden layer is enough for most of the complex applications (Karoro, Ssenyonga, & Mubiru, 2011). Generally the training of an ANN model starts with a random initial weight. It is essential to find the optimal number of neurons in the hidden layer to reach the minimum possible error in ANN model output. An appropriate number of neurons in hidden layer is selected based on the results obtained for MSE and R. Finalization of number of neurons in hidden layer was done, when the mean square error was minimum and the linear correlation coefficient (R) was maximum.

To find the optimal number of hidden neurons in hidden layer, the training of ANN model I was done by increasing the number of neurons one by one until it converged into a minimum mean square error. Among the four algorithms, the Levenberg–Marquardt (LM) algorithm produced the R value in the range of 0.9000. When the R value is greater than 0.9000, it means that a higher number of predicted values are consistent with the measured values. Therefore, in the present work, the LM algorithm was considered to finalize the optimal number of neurons in hidden layer.

In ANN model I, the minimum MSE and maximum R value for training and testing was found at 24 neurons and 20 neurons, respectively. Hence, ANN model I is suitable for training but not good for testing. Thus, it is very difficult to finalize the optimal number of neurons from ANN model I. Now, the same procedure was repeated for ANN model II. From the performance results of ANN model II, a minimum MSE and a maximum R value were observed at 24 neurons, at both training and testing stage. So it can be concluded that, this model performs well at both training and testing. The value of R for both training and testing of ANN models I and II is shown in Table 3.

Table 3.

Selection of optimal number of neurons.

Number of neurons in hidden layer	ANN model I		ANN model II
	R value for training	R value for testing	R value for training	R value for testing
1	0.8961	0.8839	0.9012	0.8978
2	0.8916	0.8894	0.9109	0.9006
3	0.8701	0.8703	0.9317	0.9043
4	0.8996	0.8856	0.9203	0.9084
5	0.8840	0.8761	0.9061	0.9114
6	0.9105	0.8994	0.9146	0.9063
7	0.9091	0.8949	0.9084	0.9190
8	0.9034	0.8976	0.9096	0.9187
9	0.9003	0.9046	0.9071	0.9014
10	0.9054	0.9057	0.9031	0.9042
11	0.8925	0.9082	0.9168	0.9077
12	0.8953	0.9096	0.9183	0.9086
13	0.9018	0.9133	0.9207	0.9095
14	0.9078	0.9165	0.9215	0.9106
15	0.9083	0.9174	0.9291	0.9127
16	0.9115	0.9181	0.9357	0.9134
17	0.9155	0.9209	0.9388	0.9145
18	0.9202	0.9213	0.9412	0.9167
19	0.9287	0.9297	0.9452	0.9174
20	0.9289	0.9383	0.9463	0.9189
21	0.9305	0.9351	0.9497	0.9197
22	0.9313	0.9275	0.9508	0.9203
23	0.9359	0.9256	0.9523	0.9247
24	0.9363	0.9223	0.9545	0.9272
25	0.9311	0.9035	0.9512	0.9236
26	0.9286	0.9031	0.9418	0.9208
27	0.9255	0.8974	0.9386	0.9165
28	0.9216	0.8917	0.9311	0.9100
29	0.9178	0.9005	0.9216	0.9094
30	0.9018	0.8976	0.9189	0.9032

Optimum results are distinguished by Bold.

Based on the above discussion, 24 neurons in hidden layer were found to be the best ones to predict the monthly average global solar radiation with minimum mean square error and also used to compare the performance of all the four algorithms used in the present work.

4

Results and discussion

4.1

Selection of data for ANN models

The main objective of the present work is to develop the most suitable ANN model to predict the monthly average global solar radiation in India by using commonly available metrological parameters. The input and output target dataset was collected from five different locations (Chennai, Kolkata, New Delhi, Mumbai and Bangalore) with diverse climatic condition across India, for a period of 10 years (2000–2009). The collected input and target datasets were randomly divided into two subsets: training and testing datasets. Vital care was taken to avoid the repetition of data in any stage.

Two different ANN models were designed and developed in MATLAB version 2012, by using the following nine input parameters: latitude, longitude, altitude, year, month, mean ambient air temperature, mean station level pressure, mean wind speed and mean relative humidity, and only one output parameter monthly average global solar radiation was predicted by using the following four back propagation algorithms: gradient descent (GD), Levenberg–Marquardt (LM), scaled conjugate gradient (SCG) and resilient back propagation (RP) algorithm. The training and testing stations used for ANN models I and II are given in Table 4.

Table 4.

Training and testing stations used for ANN models I and II.

Name of the ANN model	Training			Testing
	Number of station	Number of data used from each station	Name of the station	Number of station	Number of data used from each station	Name of the station
ANN model I	4	120	Chennai, Kolkatta, New Delhi and Mumbai	1	120	Bangalore
ANN model II	5	96	Chennai, Kolkatta, New Delhi, Mumbai and Bangalore	5	24	Chennai, Kolkatta, New Delhi, Mumbai and Bangalore

In an ANN model I, 4 stations (Chennai, Kolkatta, New Delhi and Mumbai) data are used for training. Testing was done for only one station (Bangalore) data. Among the collected data, 80% of data (totally 480 data – 120 data each from the 4 stations) was used for training. Testing was done for 20% of data (totally 120 data – from Bangalore station – which is not already used for training).

In an ANN model II, all the five stations data are used for training and testing. Training was done by using 80% of data (totally 480 data – 96 data from all the 5 stations) and testing was done for 20% of data (totally 120 data – 24 data from all the 5 stations) which is not already used during training.

4.2

Performance of ANN models

The performance of each of the ANN models was evaluated by using the MAE, RMSE and R. According to Solmaz and Ozgoren (2012), the mean absolute error (MAE) and the root mean square error (RMSE) are expressed by the following equations:

where

• N: total number of data;

• X_i: measured monthly average global solar radiation; and

• Y_i: ANN predicted monthly average global solar radiation.

The mean absolute error (MAE) is defined as a quantity which is used to measure how close the predicted values are with measured values. The root mean square error (RMSE) indicates the level of scatter that ANN model produces. Lower RMSE indicates that the developed ANN model is having good prediction accuracy. The linear correlation coefficient (R) value is used to find the relationship between the measured and predicted values. If R = 1, it means that there is an exact linear relationship between measured and predicted values. However an ANN model with lower values of MAE, RMSE and higher values of R is selected as the best model for prediction.

Table 5 shows the ANN model I performance in terms of mean absolute error (MAE), root mean square error (RMSE) and linear correlation coefficient (R) between the measured target and predicted artificial neural network output. Training and testing of ANN model I was done by four various algorithms for various numbers of neurons. As seen in Table 3, the R value, greater than 0.90, was found only for the LM algorithm in both training and testing.

Table 5.

Performance of ANN model I (at 24 neurons).

Name of the algorithm	ANN model I – training			ANN model I – testing
	MAE	RMSE	R	MAE	RMSE	R
GD	5.7325	6.8223	0.6755	8.6860	11.2127	0.5202
LM	0.8278	1.0819	0.9363	3.4979	4.5497	0.9223
RP	2.4004	3.0722	0.7662	4.1531	5.0187	0.7616
SCG	1.4672	1.8922	0.8715	4.4588	5.1477	0.7990

Optimum results are distinguished by Bold.

The most suitable algorithm to predict the accurate monthly average global solar radiation, for artificial neural network model I, was selected based on the results shown in Table 3. As seen in the table, the best results for training and testing of the LM algorithm were obtained in terms of minimum MAE values of 0.8278, 3.4979 and minimum RMSE values of 1.0819, 4.5497, respectively. The maximum R values of 0.9363, 0.9223 for training and testing data were found. From the analysis of the results, it is very clear that for ANN model I, Levenberg–Marquardt back propagation (LM) is suitable for predicting accurate monthly average global solar radiation.

The performance of ANN model II for training and testing with the statistical values such as MAE, RMSE and R for the most suitable neurons in the hidden layer are given in Table 6. From the analysis of the results, shown in Table 6, it is perfectly understandable that the MAE, RMSE values are minimum and the R value was maximum in both training and testing of LM algorithm as compared to other mentioned algorithms. Thus, Levenberg–Marquardt back propagation (LM) proves the best algorithm for training and testing of ANN model II also in the present work.

Table 6.

Performance of ANN model II (at 24 neurons).

Name of the algorithm	ANN model II – training			ANN model II – testing
	MAE	RMSE	R	MAE	RMSE	R
GD	6.1556	7.7928	0.4550	9.0903	10.7656	0.4844
LM	0.7800	1.0416	0.9545	3.0281	3.6461	0.9272
RP	2.4558	3.1033	0.7113	3.9474	4.9601	0.5852
SCG	1.3038	1.7137	0.8964	3.3172	4.0794	0.8332

Optimum results are distinguished by Bold.

4.3

Selection of the best ANN model

The comparison study between the two artificial neural network models suggest that both models can be employed to estimate the monthly average global solar radiation perfectly when training and testing was done by using the Levenberg–Marquardt back propagation (LM) algorithm. Nonetheless, the latitude, longitude, altitude and other meteorological input data used in the present work were site specific. Therefore, it is necessary to find the best ANN model to predict the monthly average global solar radiation with minimum error. The performance results of two artificial neural network models I and II by using LM algorithm are given in Table 7. When the results obtained from training and testing are compared, an ANN model II consisting of 24 neurons and Levenberg–Marquardt back propagation (LM) algorithm are most suitable for the prediction of monthly average global solar radiation accurately for the present work.

Table 7.

Selection of best ANN model (at 24 neurons).

Name of the model	LM algorithm
	Training			Testing
	MAE	RMSE	R	MAE	RMSE	R
ANN model I	0.8278	1.0819	0.9363	3.4979	4.5497	0.9223
ANN Model II	0.7800	1.0416	0.9545	3.0281	3.6461	0.9272

Optimum results are distinguished by Bold.

In ANN model I, four stations data were used for training. Testing was done for a new station data; whereas, for an ANN model II, all five stations data were used both for training and testing. The best ANN algorithm and model was found on the basis of the minimum mean absolute error, minimum root mean square error and maximum linear regression coefficient. From the analysis of the results, it was found that the predicted values are in good agreement with the measured values in the Levenberg–Marquardt (LM) algorithm and for ANN model II. The reason for the accurate forecasting ability of ANN model II is the quantity and the variety of data used during the training session covering all the stations which spread over the selected region, i.e., India. Because in ANN model II all the five stations data were used for training as well as testing unlike in ANN model I which did not use data of one station during training.

Figure 3 shows the performance of the measured and ANN predicted monthly average global solar radiation for the best model (ANN model II) and the best algorithm (LM) in the present work. From the figure, it can be seen that the ANN predicted values are very close to the measured global solar radiation values for almost all the datasets.

Fig. 3.

Performance of measured and ANN predicted monthly GSR.

Regression plot for the measured and ANN predicted values of training and testing data for the best model (LM-ANN model II) is shown in Figure 4. If the linear correlation coefficient R = 1, it means that there is an exact linear relationship between measured and predicted values. The R value greater than 0.90 shows that there is a good agreement between the measured and predicted values. The best ANN model for the present work has an R value for training and testing data as 0.9545 and 0.9272, respectively. In general, the R values obtained from Figure 4 clearly indicate that the proposed LM-ANN model II was best to predict the monthly average global solar radiation in India.

Fig. 4.

Regression plot for training and testing dataset for LM-ANN model II.

4.4

Error analysis

From the above discussion of the result of the analysis, the prediction of the monthly average global solar radiation is extremely simple by using the best ANN model, however for each station there may be some differences between measured and predicted values. This difference for each station can be accurately quantified by using the following statistical error analysis terms, coefficient of determination (CD2) and mean absolute percentage error (MAPE). The formula for calculating the value of CD2 and MAPE are given below,

where

• N: total number of data;

• X_i: measured monthly average global solar radiation; and

• Y_i: ANN predicted monthly average global solar radiation.

The result of the statistical error analysis for ANN model II with LM algorithm for the five stations are given in Table 8. Generally, the coefficient of determination represents the percentage of data closest to the line of best fit of overall dataset for a particular station. The calculated results (Table 8) show that the minimum and maximum CD2 is 0.9808 and 0.9934 for Mumbai and Bangalore station respectively. The CD2 results clearly denotes the 98–99% of the predicted global solar radiation values are very close to the measured values for almost all the stations by the chosen ANN model II. The mean absolute percentage error (MAPE) expresses accuracy as a percentage in terms of number of data used. The results of MAPE show higher accuracy that almost all the five stations perform well within the range of 0.11–4.24%. Therefore from the above statistical error analysis also, it can be concluded that the LM algorithm and ANN model II perform well for all the five stations used in the present work. Also, the present work confirms the ability of ANN to forecast solar radiation values precisely for all the stations across India which is having the similar meteorological data. The MAPE values of other similar studies and the present work are presented in the decreasing order in Table 9. The MAPE_max value is minimum with 4.24% for LM algorithm in the present work relative to the similar works carried out for other places in the world. Therefore ANN model developed in the present work has accurately predicted the monthly average global radiation.

Table 8.

Testing data results of MAPE and CD2.

Name of the station	CD2	MAPE (%)
Bangalore	0.9934	0.11
Chennai	0.9912	2.16
Kolkata	0.9902	1.02
New Delhi	0.9877	3.18
Mumbai	0.9808	4.24

Table 9.

Comparison of MAPE_max.

Study	Station	MAPEmax (%)	Method/algorithm
Mohandes, Rehman, and Halawani (1998)	Kwash (Saudi Arabia)	19.1	ANN/MLFF
Rehman and Mohandes (2008)	Abha (Saudi Arabia)	11.8	ANN/MLFF
Alawi and Hinai (1998)	Majees (North Oman)	7.30	ANN/MLFF
Sözen, Arcaklio¿lu, Özalp, and Caglar (2005)	Sirt (Turkey)	6.78	ANN/SCG
Sözen et al. (2004)	Mugla (Turkey)	6.73	ANN/LM
Present study	Mumbai (India)	4.24	ANN/LM

Optimum results are distinguished by Bold.

Statistical error analysis for coefficient of determination clearly indicated that the predicted global solar radiation values (98–99%) were close to the measured values for almost all the stations by ANN model II. MAPE values in the present work showed higher accuracy for all five stations model and were also lower than that of the other similar studies. The superior feature of the developed ANN model with LM algorithm in the present research work is, it converges well within a shorter period of time among the four algorithms used in the present work to provide an accurate solution with minimum error.

5

Conclusion

In the present work, ANN model was developed to predict the monthly average global solar radiation in India. Two different artificial neural network models each with four back propagation algorithms viz. gradient descent (GD), Levenberg–Marquardt (LM), scaled conjugate gradient (SCG) and resilient back propagation (RP) algorithm were trained and tested. Meteorological data from five stations covering the geography of India were collected for a period of 10 years for training and testing the network.

In ANN model I, four stations data were used for training. Testing was done for a new station data, whereas, for an ANN model II, all five stations data were used both for training and testing. The best ANN algorithm and model was found on the basis of minimum mean absolute error and root mean square error and maximum linear regression coefficient. From the analysis of results, it was found that the predicted values are in good agreement with measured values in Levenberg–Marquardt (LM) algorithm and for ANN model II. Further, the present work confirms the accurate forecasting ability of ANN model dependence on the quantity and the variety of trained data in a particular application. Because in ANN model II all the five stations data were used for training as well as testing unlike in ANN model I which did not use data of one station during training.

The statistical error analysis for coefficient of determination clearly indicated that the predicted global solar radiation values (98–99%) were close to the measured values for almost all the stations by ANN model II. MAPE values in the present work showed higher accuracy for all five stations and were also lower than that of the other similar studies. The superior feature of the developed ANN model with LM algorithm in the present research work is, it converges well within a shorter period of time among the four algorithms used in the present work to provide an accurate solution with minimum error. Finally, the results obtained indicated that the artificial neural network model can be used to accurately predict the monthly average global solar radiation in India where monitoring facilities are not available. In addition, the ANN model can be used to find the missing data due to the faulty operation of already installed measuring devices. With this ANN model, solar energy potential as required to design solar energy systems can be precisely estimated in India

Conflict of interest

The authors have no conflicts of interest to declare.

Acknowledgement

The authors gratefully acknowledge the Indian Meteorological Department (IMD), Pune, India for providing the 10 years meteorological data of five key locations in India for the research work.