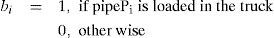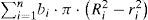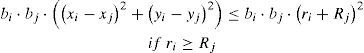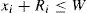Problem for Light Pipes and a Solution Proposal

Abstract

This work deals with the light pipe problem. In this problem it is necessary to both put circles inside circles and circles inside a rectangle. A mathematical model that considers the thickness of the pipes is introduced. This generates a new optimization problem that is harder to solve than other packing problems. The mathematical description of the problem is introduced and some ideas of how to solve the problem are explained.

1

Introduction

The distribution of products from the factory to the consumers is a very important issue in logistics [1]. In fact, the transportation of a product represents 40% of its cost [2]. This means that a more efficient packing and route tracing have a great impact in the competitiveness of a company.

The light pipes distribution problem has some special characteristics that make it different from classics distribution problems. For example, the weight of the pipes does not represent a constraint. Therefore, many pipes can be stacked one over the other without damaging the pipes at the bottom. Another characteristic of this problem is that the pipes can be introduced one inside the other when the internal radius of one of them is greater than the external radius of the other one. This can be done several times, in such a way that it can be a pipe inside another pipe that, at the same time, is inside a greater pipe and so on.

Another important point to consider is that the truck carrying the pipes may be loaded with pipes of several different clients from different locations. Then, whether the pipes for the first client are at the bottom of the truck, an additional cost for relocations of pipes must be considered. Furthermore, an additional way to reduce the cost of transportation is to load the truck in such a way that the reload is minimized.

In this work, the problem of maximizing the load of pipes in a truck is analyzed, disregarding other aspects of the problem that will be treated in a future work.

The main goals of this paper are to introduce a mathematical model for this problem, and to propose some potential ways to solve it. In the next Section, a mathematical formulation of the problem is presented. In Section 3, a description of Evolutionary Strategy, a powerful optimization algorithm, is explained. In Section 4, the result of the experiments are reported. Finally, in Section 5 the conclusion and some ideas for future work are presented.

2

Materials and methods

2.1

The packing problem

Packing a set of light pipes is related to several other problems in literature, for example the Circle Packing in a Square (CPS) [3]. In CPS, there is a set of n circles whose centers have coordinates (x_i, y_i), for i = 1, 2, 3, n. All circles have the same radius r_n, but this radius is unknown a priori. The centers of the circles are located inside a square whose sides have a length S. The solution of the problem consists of locating the centers of the circles in such a way that the radius r_n is maximal, the circles do not overlap and all circles are contained inside the square of side S.

Another similar problem is packing Unequal Discs in a Circle (UDC) [4]. In this problem, there are n disks of different fixed radius r_iand centers with coordinates (x_i, y_i), for i = 1, 2, 3, …,n. The solution of the problem consists of locating the center of the circles in such a way that the radius r_n of a circle that contains all disks is minimized.

In this work, we study the case where the transversal area of the pipes is used in the optimization, ignoring the length of the pipes. The objective is to maximize the sum of the transversal areas of the pipes that are loaded in the truck. The rear view of the box of the truck is rectangular. So, the light pipes packing problem (LPP) has characteristics of both CPS and UDC. For example, it is necessary to put several circles inside a rectangular area, and at the same time to put circles inside other circles.

The LPP has differences with respect the other problems. For example, in the LPP the radii of the circles are fixed from the start and cannot be modified like in CPS. Another difference is that in the LPP, when circles are put inside a circle, the radius of the containing circle is fixed, unlike the UDC. Moreover, in the LPP it is needed to carry the set of pipes is as small as possible, but in this work the focus is in the problem possible that not all the pipes can be loaded in the truck, and must be loaded in another truck. The ideal result is that in which the number of trucks of loading a single truck with as many pipes as possible. Figure 1 shows an example of a truck loaded with a light pipes. The rectangle represents the rear view of box of the truck. The circles represent the transversal view of the pipes loaded in the truck.

Figure 1.

An example of a truck loaded in the LPP problem.

2.2

Mathematical model for LPP

In this subsection, a mathematical model for the LPP problem is presented. There is some terminology that will be used for the rest of the paper. First, the transversal area of a pipe is a ring, so the terms ring and transversal area of a pipe are used as equivalents, and the demonstrations and definitions given for one of them is valid for the other one.

A ring is a geometric figure formed by two concentric circles of different diameter. In this paper, a ring is represented with the letter P. For a set of n rings the i-th element is called P_i. The radius of the greater circle of P_i is denoted by R_i and the radius of the smaller circle of P_i is denoted by r_i (see Figure 2). The greater circle of P_i is denoted by PR_i and the smaller circle of P_i is denoted by Pr_i.

Figure 2.

Radius of a ring.

A general description of the LPP is as follows: given a set of n rings P_i with an external radius R_i and an internal radius r_i and centers (x_i, y_i) for i=1,2,3,…, n, and a rectangular box B of width W and height H. Put as many rings inside B in such a way that there is not intersections between the rings and the area of B occupied by the circles is maximal.

The description above gives a clear idea of what the LPP consist of, but in order to use an optimization procedure, a mathematical model is necessary. In order to have a more precise definition of the problem and create a mathematical model, further concepts and calculations must be introduced. First, the area A_i of a ring P_i can be calculated with the formula:

Where R_i and r_i are the external and internal radius of P_i respectively. Another important calculation that will be very useful in this work is the area of intersection of two rings. In order to make this calculation, consider Figure 3.

Figure 3.

The intersection of two rings.

In Figure 3 there are two rings, P_i (solid lines) and P_j (discontinuous lines). The intersection of these rings defines several regions of interest. Let call these regions a, b, c, d and e. The intersection of the two rings is regions b and c, so calculating the area of these regions is necessary to obtain the area of intersection of two rings. An explicit formula to calculate these areas is very complicated to obtain, but a formula based in the intersection of two circles can be deduced. In order to deduce this formula, the following definitions are introduced.

Define the PR_i as the external circle of P_i, Pr_i as the internal circle of P_i, PR_j as the external circle of P_j, Pr_j as the internal circle of P_j. Finally, let A(x) denotes the area of region x, for example A(d) represents the area of region d, A(Pr_j) represents the area of the internal circle of ring P_j, etc.

Regions b and c can be obtained with the following formula:

Where ? denotes intersection and ∩ denotes union. The demonstration of the formula above is easy to figure out. From Figure 2, it is evident that:

In a similar way:

When (2), (3), (4), (5) and (6) are combined:

The formula above allows us to calculate the intersection of a pair of rings using the intersection of four pairs of circles. The formula to calculate the intersection of two circles with radii R_i and R_j is:

Where:

And d_ij is the Euclidean distance between the centers of the circles. Another important calculation is if two circles have an intersection. This calculation is very simple: if

then the circles do not intersect. An important characteristic of the LPP is that not necessarily all the pipes will be put inside the truck. This is evident when the area of the box of the truck (W·H) is smaller than the sum of the transversal areas of the pipes that must be distributed. Even in some cases where the area in the box is greater, it will not be possible to put all pipes inside the truck. It is important to introduce a way to reflect this inside the model of the problem. A way to do this is to introduce some artificial variables b_i for i = 1, 2,…, n, where n is the number of pipes to distribute, with the following property:

This variable is an artifact that allows us to activate and to deactivate a pipe in order to avoid violating a constraint. The utility of this can be seen in following example: Figure 4 shows a set of pipes inside a truck. The arrangement of the pipes is not feasible, because two of the pipes (the ones in discontinuous lines) intersect other pipes. But if these pipes are deactivated, an arrangement as the one shown in Figure 4 is obtained, where the solution is feasible. This mechanism is a way to “left pipes out of the truck”, if b_i=0 then the pipe P_i is not loaded in the truck.

Figure 4.

Intersections in a solution can be avoided eliminating pipes.

Now, a mathematical model for the LPP problem is presented. Given a set of n rings P_i with an external radius R_i and an internal radius r_i and centers (x_i, y_i) for i=1,2,3,…,n, and a rectangular box B of width W and height H:

Maximize

Subject to:

Or

for i = 1, 2, …, n - 1and j = i + 1, …, n.

for i = 1, 2, …,n

Formula (13) is the objective function to maximize, and it consists of the sum of the areas of the rings inside the box. In (14), the constraint for no overlapping circles is presented. A ring can be completely contained inside another ring; this situation is expressed in (15) and (16). Constraints (17), (18), (19), (20) and (21) impose the condition that all circles must be contained inside the box.

In constraints (14), (15) and (16), the term b_i b_j is present in both sides of the inequality. The reason to have this term is to prevent the evaluation of intersections between rings that are not loaded in the truck. If b_i is equal to zero, or b_j is equal to zero, then both sides of the inequality in (14), (15) and (16) are equal to zero and the constraint is not violated.

The model for the LPP is very complex to solve; the objective function is not linear and contains binary variables. Constraints are both linear and no linear and contain binary variables. It is difficult to adapt this model to gradient methods or other classical optimization techniques. A viable option is to use evolutionary strategies (ES), because these optimization methods are able to work with very complicated objective functions. In the next section an introduction to ES is provided.

3

Evolutionary strategies

Evolutionary Strategies (ES) [5] is a paradigm of Evolutionary Computation (EC)[6]. Other paradigms are Genetic Algorithms [7], Differential Evolution and many others [8]. Evolutionary Computation has been used to solve several problems in the industry. For example, in [9] the authors use a Particle Swarm Optimization Algorithm to optimize networks of mobile devices. In [10] the author uses a Memetic Algorithm to solve mixed-integer constrained optimization problems.

EC is inspired in the Theory of Evolution of Species by Natural Selection, and takes many concepts such as mutation, the survival of the fittest, population, etc, in order to create powerful methods of optimization. In EC a candidate solution for the problem is coded as a vector of numbers, and several of these vectors are generated at random. A set of these vectors is known as a population and a single vector is usually known as an individual. The elements of a population are mutated and recombined in order to obtain new vectors that represent a better solution of the problem. The vectors that are mutated and recombined are a selection of the best elements of the population. The idea is that the best elements of a population can be used to obtain new solutions that are even better than their “parents”. The methods used to represent a solution as a vector of numbers, to select the best individuals, to mutate them and recombine them differ among the different Evolutionary Algorithms.

In Evolutionary Strategies, a candidate solution for the problem is coded as a vector of real numbers, the process of mutation is more important than the process of recombination. Mutations are performed adding a random vector to an individual; this random vector is generated based on exponential functions. The recombination process consists on a weighted sum of two individuals. In order to select the best individuals of a population, the value of the objective function of the optimization problem is used. The elements of the population are sorted and those with the highest value of the objective are chosen. The general algorithm for ES is as follows:

• 1.

  Generate an initial population randomly.

• 2.

  Evaluate the objective function for each element of the population.

• 3.

  Select the best individuals of the population.

• 4.

  Recombine the best elements of the population.

• 5.

  Mutate the recombination of the best elements of the population to create a new population.

• 6.

  Substitute the old population with the new population.

• 7.

  Repeat from Step 2 until the stop criterion is reached.

Every cycle in which new population is created from the old one is called a generation. The number of individuals selected for recombination is usually 1/7^th of the original population. The stop criterion is a maximum number of generations.

Evolutionary Strategy was designed for unconstrained global optimization. In order to work with problems with constraints, several approaches have been proposed. One of the most successful approaches is Stochastic Ranking (SR) [11]. In SR, in order to select the best individuals of a population, the population is sorted either based in the objective function and in the degree of violation of the constraints, based on chance. Two individuals are compared based on the objective function or based on the constraint depending on a random number. This method has been very successful solving complicated problems with constraints.

ES combined with SR is used in order to optimize the LPP problem. The experiments are presented in the next section.

4

Experiments and results

In order to test the effectiveness of the ES combined with SR, three instances of the LPP problem were used. A box with width of 400 cm. and height of 300 cm. was considered. There are three sizes of pipes: pipe one with external radius of 50 cm. and internal radius of 45 cm. pipe two with external radius of 25 cm. and internal radius of 20 cm. and pipe three with external radius of 10 cm. and internal radius of 8 cm. The differences between the instances of the problem are the number of pipes. The numbers of pipes for each instance of the problem are shown in Table 1.

Table 1.

Number of pipes for each instance of the problem.

Instance	# Pipe one	# Pipe two	# Pipe three
1	3	5	5
2	5	5	10
3	10	10	15

ES is a stochastic algorithm, as a consequence of that different results may result for different runs of the algorithm. For this reason, 30 runs were performed for each instance of the problem in order to check the consistency of the algorithm. The parameters for the algorithm are the following: size of the population = 40, number of individuals chosen for reproduction = 6, maximum number of generations = 2000. The results of the experiments are presented in Table 2.

Table 2.

Results of the experiments.

Instance	Total number of Runs	Number of feasible solutions found
1	30	27
2	30	15
3	30	0

Table 2 shows that the number of feasible solutions reported by the Evolutionary Strategy depends on the size of the problem. For the fist instance of the problem, the ES is time. But, in the second instance the algorithm, ES finds feasible solutions in half of the runs. For the most difficult instance of the problem (the third instance), no feasible solution was found. Figure 5 shows an example of a solution for the second instance of the problem obtained by ES.

Figure 5.

A solution reported by an experiment.

5

Conclusions

In this work, the light pipe packing problem LPP is studied. This problem has important applications in practice. A mathematical model for the problem was elaborated in order to handle it as an optimization problem. This mathematical model can be useful both to solve the practical LPP problem and to be use as a benchmark to test new optimization algorithms.

An Evolutionary Strategy was used, combined with Stochastic Ranking in order to find a solution for the problem. The results were not satisfactory, because the optimization algorithm is not consistent finding feasible solutions. For the most complex of the instances of the problem it was not able to find a feasible solution. And it is important to note that practical problems are more complex than the ones tested here. In practice there may be more than one hundred pipes to distribute.

It is also important to remark that this is a research in progress and very little has been tried yet. These are the initial experimentations and many more approaches can be used to solve the problem. Some ideas to solve the problem are presented in the next paragraph.

We conjecture that one of the reasons the ES cannot find better solutions is the design of the objective function. Formulas (13)-(21) were used directly in the algorithm, but it is possible to use some modification to objective function and constraints can be done in order to guide the exploration to the desire solution. It is desirable to give a stronger penalization to circles that intersect with other circles, and that the objective function must be designed to give a better score to solutions that completely contain rings inside another one.

Another idea for research is the use of other algorithms, such as Genetic Algorithms, Simulated Annealing, etc. There are many options to test and to evaluate their performance. Moreover, a combination of different algorithms and heuristics may result in better solutions. For example, an evolutionary algorithm can be used to find the best arrangement for the pipes with the greatest radius, to fix their position and then to use again the evolutionary algorithms to arrange the pipes with the second to the biggest radius, avoiding intersection with the pipes already in the box. This procedure may be repeated until all the pipes are located.

The efficiency of the algorithm can be improved too. In order to calculate the value of the constraints, each pipe is compared with all the rest of them. This procedure is quadratic with respect to the number of pipes and is very expensive in computational time. Looking for a faster way to calculate the intersection may be very useful. A possible solution is the use of a Voronoi diagram in order to be able to identify what ring is closer to the other and calculate intersection only with the closest rings.