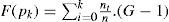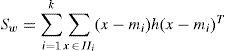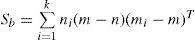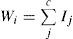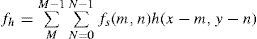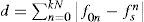Face recognition is one of a complex biometrics in the field of pattern recognition due to the constraints imposed by variation in the appearance of facial images. These changes in appearance are affected by variation in illumination, expression or occlusions etc. Illumination can be considered a complex problem in both indoor and outdoor pattern matching. Literature studies have revealed that two problems of textural based illumination handling in face recognition seem to be very common. Firstly, textural values are changed during illumination normalization due to increase in the contrast that changes the original pixels of face. Secondly, it minimizes the distance between inter-classes which increases the false acceptance rates. This paper addresses these issues and proposes a robust algorithm that overcomes these limitations. The limitations are resolved through transforming pixels from non-illumination side to illuminated side. It has been revealed that proposed algorithm produced better results as compared to existing related algorithms.
Face recognition is a very challenging research area because even the images of same person seem different due to occlusion, illumination, expression and pose variation [1; 2; 3; 4; 5]. Advanced research in the field of face recognition shows that varying illumination conditions influence the performance of different face recognition algorithms [6; 7]. On the other hand, training or testing is also sensitive under varying illumination conditions. These are the factors that make face recognition difficult and have gained much attention for the last so many decades. A large number of algorithms have been proposed in order to handle illumination variation. Categorically these algorithms are divided into three main distinctions. The first approach deals with image processing modelling techniques that are helpful to normalize faces having different lighting effects. For that purpose histogram equalization (HE) [8; 9], Gamma intensity correlation [9] or logarithm transforms [10] work well in different situations. Various proposed models are widely used to remove lighting effects from faces. In [11] authors eliminate this dilemma by calculating similarity measure between the two variable illuminated images and then computing its complexity.
Similarly in [12] authors try to remove illumination by exploiting low curvature image simplifier (LCIS) with anisotropic diffusion. But the drawback of this approach is that it requires manual selection with less than 8 multiple parameters due to which its complexity is increased. Secondly, uneven illumination variation is too tricky even by using these global processing techniques. To handle uneven illumination, region based histogram equalization (RHE) [9] and block based histogram equalization (bhe) [13] are used. Moreover, their recognition rates are much better than the results obtained from HE. In [9] the author suggested a method called quotient illumination relighting in order to normalize the images.
Another approach which handles face illumination is 3D face model. In [14; 15] researcher suggested that frontal face with different face illumination produces a cone on the subspace called illumination cone. It is easily estimated on low dimensional subspace by using generative model applied on training data. Subsequently, it requires large number of illuminated images for training purpose. Different generative models like spherical harmonic model [16; 17] are used to characterize low dimensional subspace of varying lighting conditions. Another segmented linear subspace model is used in [18] for the same incentive of simplifying the complexity of illuminated subspace. For this purpose the image is divided into parts from the region where similar surface appears. Nevertheless, 3D model based approaches require large ingredients of training samples or need to specify the light source which is not an ideal method for real time environment.
In the third approach, features are extracted from the face parts where illumination occurs and then forward them for recognition. In general, a face image I (x,y) is regarded as a product I(x,y)=R(x,y) * L(x,y), where R (x,y) is the reflectance and L (x,y) is the illuminance at each point (x,y) [19]. Nonetheless, it is much complicated to extract features from natural images. The authors in [20] proposed to extract face features by applying high-pass filtering on the logarithm of image. On the other hand, the researcher in [21] introduces Retinex model for removing illumination problem. This Retinex model is further enhanced to multi scale Retinex model (MSR) in [22]. One more advancement of this approach is extended in [23] which introduces illumination invariant Quotient image (QI) and removes illumination variation for face recognition. Similarly in [24; 25] QI theory is enhanced to self-quotient image (SQI) using the same idea of Brajovic [26]. Another way to obtain invariant illumination is to divide the same image from its smoothed version. However, this system is complicated due to the appearance of sharp edges in low dimension feature subspace by using weighted Gaussian filter. The same problem is solved in [27] that uses logarithm total variation model (LTV) to obtain illumination invariant through image factorization. Likewise, the author in [28] reveals that there is no illumination invariant; however it is obtained from aforementioned approaches.
According to [29], the illumination variant algorithms are categorized into two main classes. The first class of algorithms deals with those facial features which are insensitive to lighting conditions and are obtained using algorithms like edge maps [30], image intensity derivatives [31] and Gabor like filters [32] etc. For this type of class bootstrap database is mandatory while it increases error rate when gallery set and probe set are comparatively misaligned.
The second class believes that illumination is usually occurring due to 3D shape model under different poses. One of the limitations of model based approach is that it requires large training set of different 3D illuminated images. Due to this drawback its scope is limited in practical face recognition systems.
2Materials and methodsLarge number of techniques has been proposed for illumination invariant face recognition where each method reveals good result in specific conditions and environment. After eliminating lighting condition from the face, it can be easily visualized by human beings. The limitation across geometric based face recognition is that it only works on limited frontal face databases. These methods are traditional but nowadays variety of subspace methods are used like Principal Component Analysis (PCA), Independent Component Analysis (ICA), Support Vector Machine (SVM) and Linear Discriminant Analysis (LDA) etc. These are the subspace methods that depend on pixel level information because this pixel level information is used to convert high dimensional input data into low dimensional feature subspace. Low dimensional data are arranged according to inter class and intra class mean. Histogram equalization is the most popular and powerful approach to remove illumination from images. The main drawback of this approach is that though it is a reliable method to eradicate lighting from images but it can destroy the actual density value of the face. The actual pixel values are changed in a sense that during inter and intra class mean estimation of histogram equalization, some noise is added that changes the pixel value. In this paper, a technique is proposed which handles produced noise with highest recognition rate. More discussion is provided in later section.
2.1Histogram EqualizationA brief description of histogram equalization is provided in this part. The superior property of histogram is that it provides general formula for contrast enhancement so that the information which is hidden due to illumination factor becomes visible. Let us consider that G is the grey level image while ni shows grey pixels appearance in the image ith times.
Similarly N is the total number of pixels in the image. Mathematically it can be depicted as:
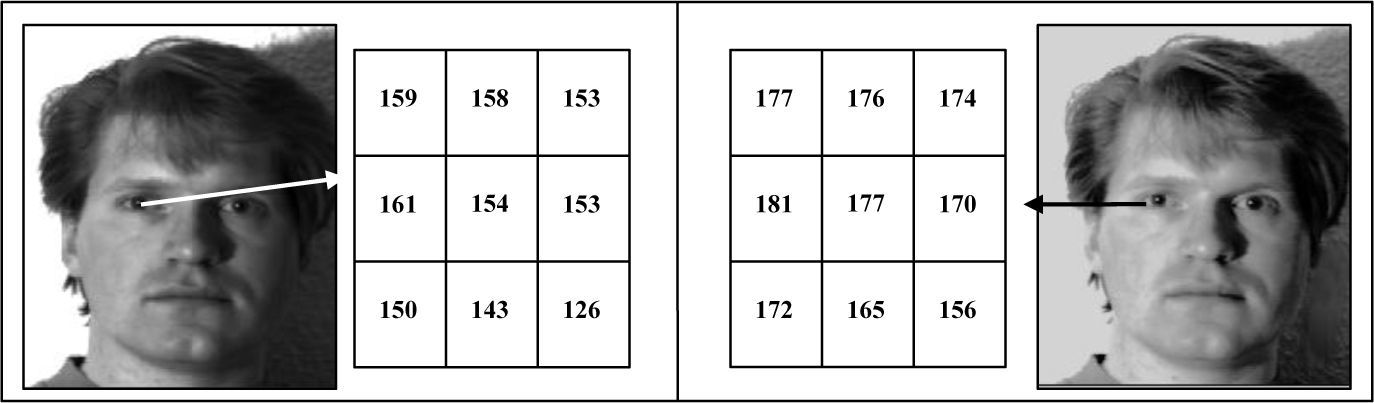
The function of histogram spreads out most intensive frequency pixel value. As a consequence the original pixel information is lost that changes the appearance of the face as shown in Figure 1.
2.2Types of Facial FeaturesThis section illustrates the various characteristics of local and global features. Eyes, nose, mouth etc. are considered to be the most discriminating facial features. These constitute local features that are not greatly affected by the application of histogram. The reason is that each local feature has approximately same geometrical correspondence on every face. But major geometrical variation occurs when global features are taken into consideration. Since the pixel intensities vary when histogram is applied, hence giving rise to increased sharpness of facial contours, edges and hairstyles. Because of dissimilar global facial features, different subspace classifiers mistakenly interpret the image of same person as different. On the other hand, some classifiers only consider local facial features which are suitable enough to report them as the same person. The reason behind this act is that local components of two images of the same person are approximately the same. The contradictory results of two subspace classifiers reveal awful outcomes which suggest that an ideal classifier should be a combination of above mentioned subspace methods.
As already disclosed that local and global facial features behave differently in person identification, LDA based feature extraction processes the whole face because every pixel of the face plays a key role in face representation. Let us consider the mathematical representation of within and between classes as:
Where mi=1ni∑x∈IIix is the mean of the ith classand m=1n∑ki=1∑x∈IIx is the global mean.Global class mean totally depends on pixel x. Te variation in pixel value decreases the distance between intra classes while increasing the distance of interclass scatter matrices. As a result the core features are not followed.
2.3Original Pixel Preservation Model (OPPM)Here the proposed OPPM model is discussed step by step. The very first step is to find the illumination direction. For this let us denote the face by F(x, y) where size of the face is represented by M × N rows and columns. Initially categorize the whole face into C columns as:
where h is the size of column that can be defined according to the datasets. Now the weight W for curve distribution can be calculated as:Here W is used to find the direction of illumination and also the visualization of illumination direction that can be calculated by plotting W via the curve distribution. Now the second step is to apply histogram equalization onto the processed image. The next step is to divide the face on the basis of following parameters as i) midpoint of face according to the illumination direction and ii) the outer boundary of face. For edge detection executes the following steps: Initially, convert histogram equalized image into hexagonal image (as shown in Figure 2) by using the following mathematical equation.
where an original image fs (m,n) represents square pixel image with M × N rows and columns, fh(x,y) is the preferred hexagonal image while h shows interpolation kernel for reconstruction method. Similarly (m, n) and (x, y) are the sample points of original square image and the desired hexagonal image respectively.Hexagonal image is used due to it's inherit property of edge enhancement. Once the edges are highlighted, next phase can be proceeded which leads to the edge detection of OPPM model. Sample edge detection process is illustrated in Figure 3. The main reason of using hexagonal image is i) to enhance the edges with minimum error rate and 2) to divide the image into two equal halves.
Finally, mapping is applied between non-illumination parts to illumination part of the face. This step is usually the marking of facial feature points to compensate on illumination part. Basically, this final step is performed in a two-step process. Firstly, N face markers are applied to point marks on the face as depicted in Figure 4.
Although there are different illumination conditions but in this paper left and right sides of light or black lighting effects are handled. At present, divide the face into two halves with respect to centre of the face. Center position of the face is estimated on the basis of nose tip. At the end, fiducially mesh points are mapped from non-illuminated segment to illuminated segment.
The advantage of aforementioned approach is to provide abrupt and good classification of facial features. As discussed above, with image enhancement the actual pixel value is changed due to increase of pixel brightness. In the next section, analysis of proposed system will be conducted on the basis of experimental results.
3Experiments and AnalysisThe proposed method is tested on most popular datasets of faces like Yale-B and CMU-PIE databases. For feature extraction, Linear Discriminant Analysis (LDA) and Kernel Discriminant Analysis (KDA) are used to represent frontal faces in low dimension. In Yale-B database [9] there are 10 different persons of nine poses with 64 different lighting conditions. In our database, 64 frontal faces of different illuminated images are used instead of pose and expression given that the main focus is to handle only illuminated images. On the other hand, CMU-PIE database is comprised of 68 different subjects having different pose, illumination and expressions. Each subject contains 43 illuminated images and 21 flashes with ambient light on or off. In our dataset only 43 frontal face images of varying lighting conditions per person are used for evaluation.
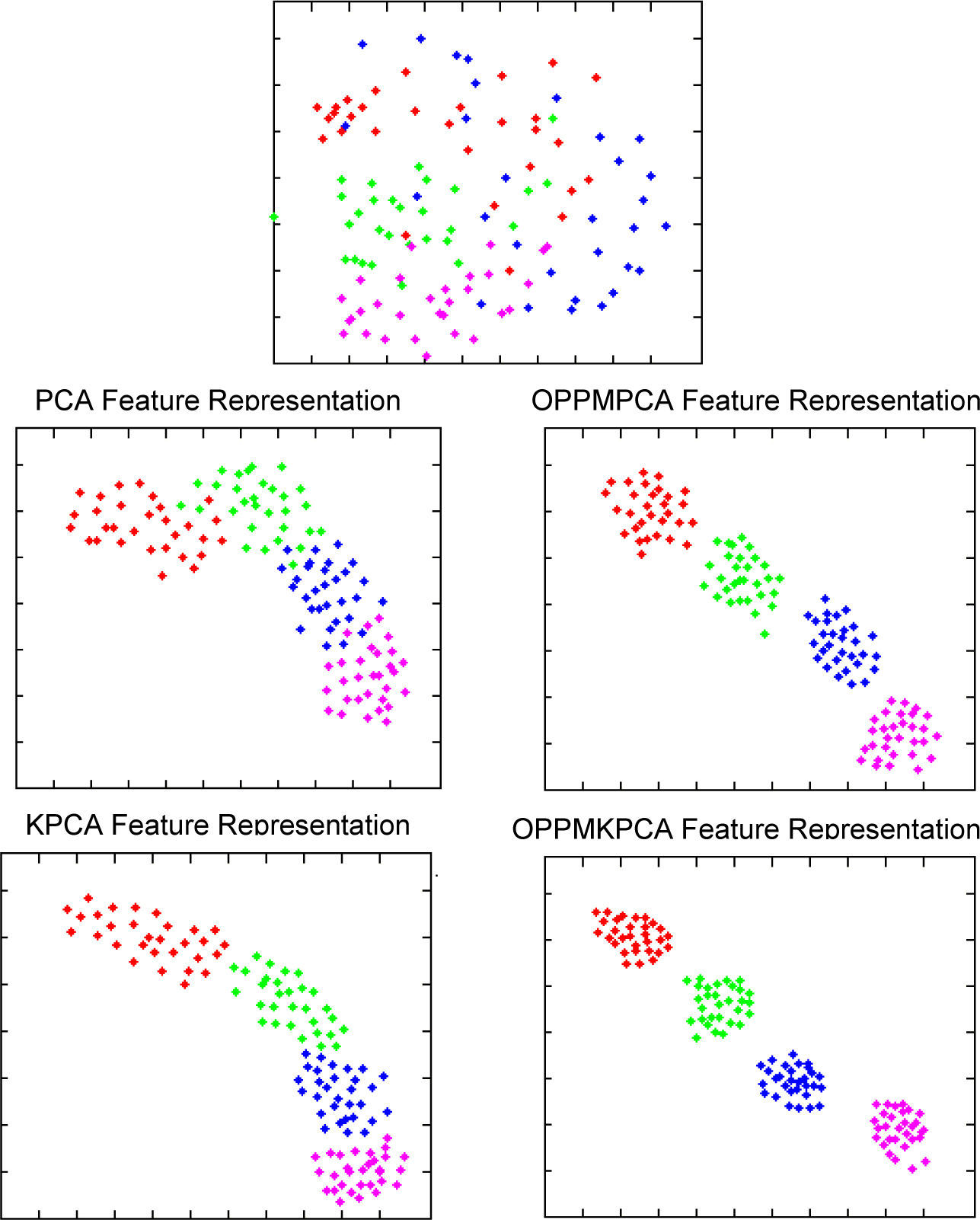
3.1Feature RepresentationThe main goal of representing features is to graphically represent the scatter of data using LDA and KLDA subspace methods as described in the algorithm proposed in this paper. In testing process, facial features of 4 subjects with 30 different samples per person are projected onto the subspace. Figure 5 reveals the most significant feature bases obtained from two subspace methods.
3.2Euclidian Distance AnalysisIn this experiment the difference is calculated between the output face obtained from OPPM and original image in order to analyze similarity between the two images respectively. The Euclidean distance is shown in Eq. 7.
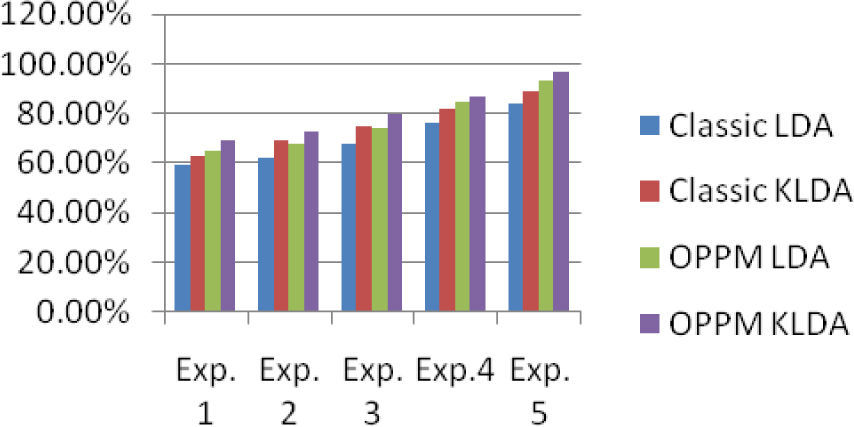
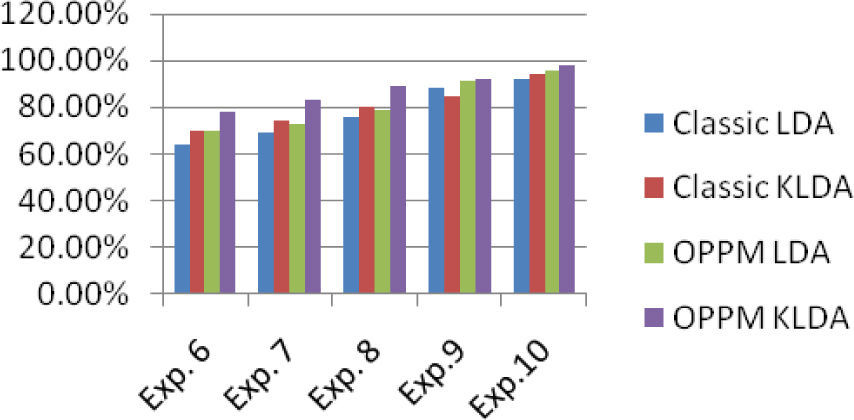
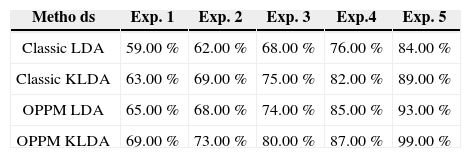
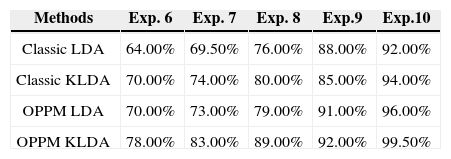
where fo and fs are the original and output images respectively. Moreover, same equation is used to calculate the histogram normalization of fo and fh. However, the difference between original and output images and sample histogram normalization of illumination is very vast. More specifically, the Euclidean distance between fo and fs is very small as compared to the distance between simple histogram normalization. The main reason behind this is that in OPPM algorithm the non-illuminated pixels are morphed with the reference side of illuminated pixels. The histogram normalization changes the color contrast of face due to which the actual pixel values are changed that causes the difference between images.3.3Experiments ResultsThe effectiveness of the proposed technique is evaluated with aforementioned databases. For each subject of Yale-B database, randomly select the illuminated and non-illuminated faces. For different experiment sets test, we choose different number of images e.g., from Yale – B a 5 to 10 images dataset per individual out of 64 images per person is selected. Same process is used for CMU-PIE different images dataset and for other five different datasets random images per person are chosen. In this experiment we analyze that as the number of training sets are increased, the false acceptance rates are decreased. Let Ω denotes the random trained subset that shows the number of training sets. The more the value of Ω, the more will be the recognition rate. Table 1 and Table 2 show the recognition rates with different number of training sets from 6 to 10 frontal images per person. Same type of experiment is performed with Yale-B and CMU-PIE databases. The graphical representation of both experiments is depicted in Figure 6 and Figure 7. The comparison is performed with classic LDA and KLDA by just applying histogram normalization.
Performance Comparison On Yale-B Frontal Images.
| Metho ds | Exp. 1 | Exp. 2 | Exp. 3 | Exp.4 | Exp. 5 |
|---|---|---|---|---|---|
| Classic LDA | 59.00 % | 62.00 % | 68.00 % | 76.00 % | 84.00 % |
| Classic KLDA | 63.00 % | 69.00 % | 75.00 % | 82.00 % | 89.00 % |
| OPPM LDA | 65.00 % | 68.00 % | 74.00 % | 85.00 % | 93.00 % |
| OPPM KLDA | 69.00 % | 73.00 % | 80.00 % | 87.00 % | 99.00 % |
The recognition rates on both databases show that the kernel version of LDA produces round about 7% to 8% more results than the plain LDA.
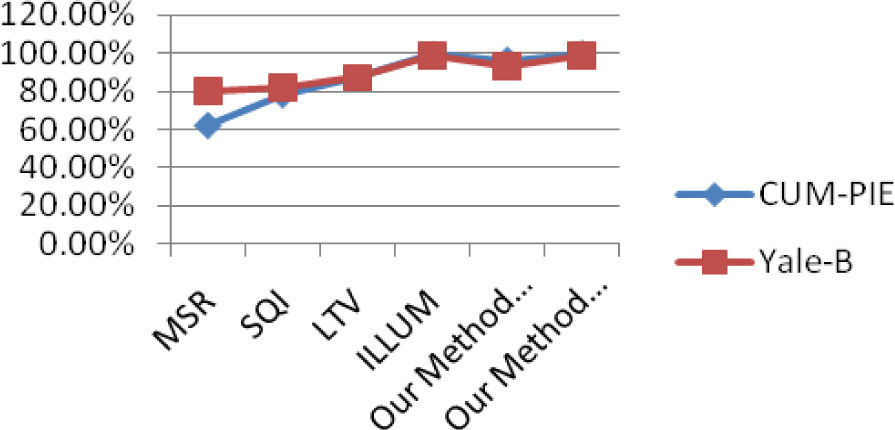
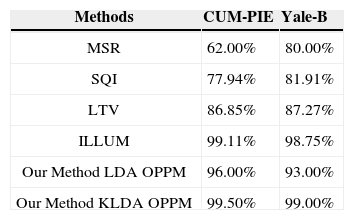
4ComparisonA comparison of proposed method is made with other illumination invariant face recognition methods presented by different authors. Comparison is performed on two databases namely CMU-PIE and Yale-B on the basis of average recognition rates given by different authors. Comparison cannot be made directly because every author has presented different architecture of illumination based face recognition. For training a database to recognize faces authors use different number of faces per individual. Table 3 shows the performance comparison of proposed method with other methods that use minimum to maximum faces per individual. In this paper, average recognition rates defined by different authors are compared and analyzed. The comparison is performed on multi-scale retinex (MSR) [22], self-quotient image (SQI) [24; 25], logarithm total variation (LTV) 27] and ILLUM [33] as shown in Table 3 and graphical representation of Figure 8.
The basic subspaces methods for face recognition are PCA and LDA. Both work on global facial features and depend on pixels values. In face recognition the illumination problem becomes more complex while trying to solve it by using these subspace methods. To overcome such dilemma, an OPPM framework is proposed by transforming pixels from non-illumination side to illuminated side. The proposed illumination normalization technique uses histogram normalization method that increases the contrast of image by changing the original pixels values. As far as within and between class scatter matrix of LDA is concerned, the property of LDA is violated by changing the pixels value of face images which states that it maximizes the margin in between class scatter matrix while minimizing the margin within class scatter matrix. The main purpose of proposed algorithm in this paper is that it handles the limitation that arises after preprocessing step of illumination normalization. Consequently, the recognition rate increases which minimizes the within class scatter and achieves almost 35% to 50% recognition rate.