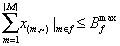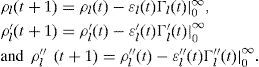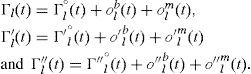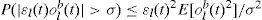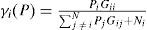The Convergence Scheme on Network Utility Maximization in Wireless Multicast Networks

Abstract

With the ever-increasing wireless data application recently, considerable efforts have been focused on the design of distributed explicit rate scheme based on Network Utility Maximization (NUM) or wireless multi-hop mesh networks. This paper describes a novel wireless multi-hop multicast flow control scheme for wireless mesh networks via 802.11, which is based on the distributed self-turning Optimal Proportional plus Second-order Differential (OPSD) controller. The control scheme, which is located at the sources in the wireless multicast networks, can ensure short convergence time by regulating the transmission rate. We further analyze the theoretical aspects of the proposed algorithm. Simulation results demonstrate the efficiency of the proposed scheme in terms of fast response time, low packet loss and error ration.

1

Introduction

Wireless multicast mesh networks are a promising structure, which can support high quality television broadcasts, ADSL-based broadband Internet connections and so on. However, regular wireless access points (APs) cannot satisfy transmission quality requirements of multimedia applications. Wireless video transmission via multi-hop links is fragile against background data traffic, e.g., web browsing, and the transmission may vary according to the number of the user and the limitation of links. Since 802.11-based multi-hop wireless networks implement Distributed Coordination Function (DCF) for medium access, an end-to-end route may contain several relay nodes contending for the channel resulting degradation of video quality due to increased end-to-end delay and packet probability. All of these problems have prevented the implementation of indoor cabling by 802.11 links until now.

Our proposal approach aims to improve the multimedia experience at home by providing high quality video streaming via multicast wireless mesh technology by fast convergence rate. The self-tuning multicast rate control helps to establish and maintain high quality links between multi-hops wireless nodes. We overcome the delay and optimal problems by combing wireless mesh networks with dynamic adaptable scheme. We can explain this problem in detail.

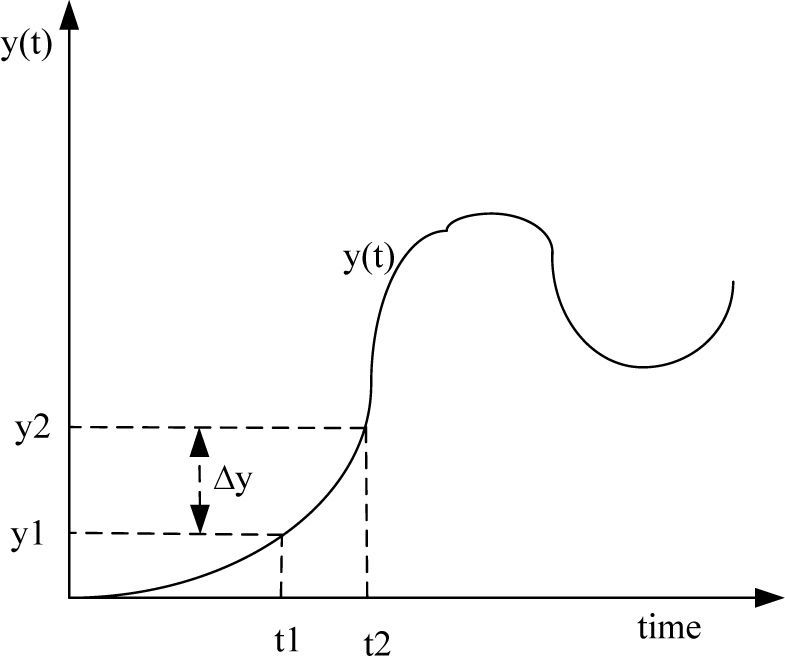
To explain the delay of rate in multi-hop network, we use Figure 1 to show the problem. In the illustration of Figure 1, we define y1 be the desired input rate at time t1. So, after some time, maybe at time t2, the input rate gradually becomes y1. However, at time t2, the desired input rate should be y2. We could find that there is an offset rate between time t2 and time t1 which degrades the network performance greatly. This problem is severe in wireless multi-hop networks due to long round–trip. Failure to take this component into consideration may result in oscillation of buffer occupancy and degrade the network performance.

Figure 1.

Illustration of algorithm motivation.

2

Related works

In prior work, 802.11 based wireless mesh networks (WMNs) have been mainly investigated for extending wireless transmission throughput [1]. Although WMNs improve the quality of the one point to many points transmission in the networks, contending is also increased in the wireless channel due to 802.11’s inherent access mechanism. To overcome increased number of packet losses and delay jitter, both of which are especially harmful for video, the authors of [2] presented enhanced distributed channel access 802.11 (EDCA) to provide quality of service (QoS) via different priority traffic classes with different contention window size and arbitration inter-frame space (AIFs) values. In [3], many schemes are presented to improve the video quality over wireless transmission by designing smart prioritization together with mesh networking. However, beside of signal collapse, the multi-hop wireless links can cause congestion or even congestion collapse if adequate flow control is not provided. Flow control thus plays an important role in the traffic management of multicast multi-hop communications. Without an adequate flow control scheme being implemented, the bottleneck link might cause its buffer to overflow, or cause excessive queuing delay or even deadlock [4]. Then, intensive research has been done on wireless mesh rate control [5], [6],[7]. To overcome multi-hop delay constraints, Hou [8] investigated maximizing throughputs for QoS requirements for distributed wireless mesh networks. Huang et al. [9] addressed the problem of optimal transmission rate using random delay threshold policies. To resolve the deployment issues of multicast multi-hop distributed wireless network, lots of papers have done deep research [10], [11], [12].

3

The OPSD (Optimal Proportional plus Second-order Differential) control scheme

3.1

The System Model and Notations

In a wireless multicast network, many multicast sessions are implemented along a multicast tree. The multicast source is the root of the tree. From the source, the multicast traffic flows propagate toward many multicast destinations. In general, a multicast tree is constructed at the beginning of network and it may be changed dynamically according to network topology change, members departing or relay node’s failure.

Every wireless router, which located at the branch point in the multicast tree, implements algorithm control function. The branch point is important for multimedia transmission for one time sending data requirement but spacious coverage ability. Due to the popular multimedia transcoding techniques, such as MPEG-4 video standard, many downward nodes can accept video files freely by using fine-grained multimedia techniques [13].

A rate controller is located at the rout of every router node. The outgoing links of a router is towards its downstream routers. The basic idea of flow control is as follows: Initially, the source sends data including a forward control packet (FCP) to the destinations along the route. At each router node, it computes an expected incoming data rate according to its local buffer occupancy, and construes a backward control packet (BCP) by filling this expected rate in the BCP.

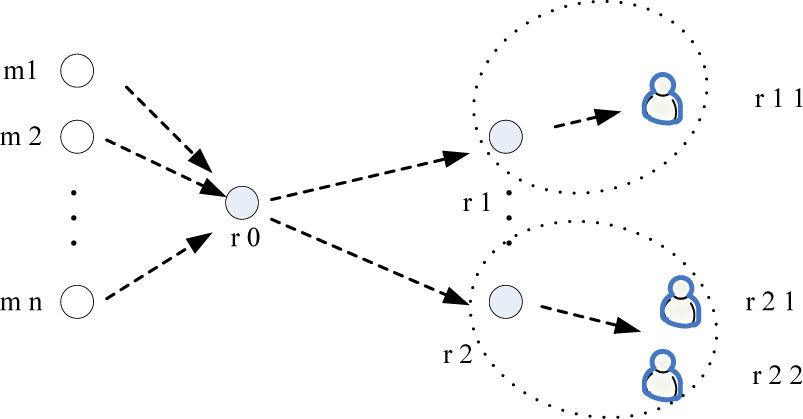
To explain our distributed control scheme in detail, as shown in Figure 2, we assume there are mmulticast sources (m₁,m₂,…,m_|M|) in the network. A multicast session may have many end users. For example, (m,n) means the n th user belonging to a multicast session m.

Figure 2.

A multicast model in which every wireless router with downstream routers or end users.

In our algorithms, the aim is to amplify the utility of wireless bandwidth to meet user’s demands to the greatest degree. So, we define some notations as below.

Define x_(m,n) as the received rate at the n’ s end user. And define x_(m,~) means the supreme received rate among multicast session m.

The dynamic multicast optimal problem on NUM can be formulated as:

P1:

So, the Primal problem of multicast network utility maximization (NUM) can be solved by the Lagrangian function as below.

The Primal problem can be changed into the Dual problem D1

D1:

According to the Dual problem, the multicast source node m updates in according to the rules below:

In Eq.8, Г_m(t) is an estimated system value including noises, which is calculated by:

where Γm°(t) is the practical value from a sub-gradient method in Eq. (10).

In Eq.10, the temporal variables ρ(t), ρ′(t), ρ(t)″ can be calculated in each wireless node at the branch of virtual multicast tree as :

Moreover, the Γl(t),Γl'(t),Γl"(t) can be obtained by

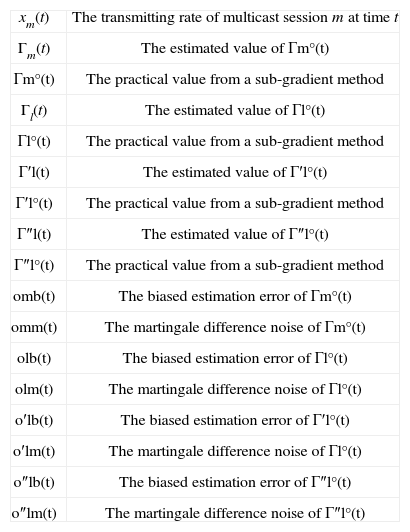
For clear understanding, we introduce the notations as below.

Table 1.

Notations in the algorithms.

xm(t)	The transmitting rate of multicast session m at time t
Гm(t)	The estimated value of Γm°(t)
Γm°(t)	The practical value from a sub-gradient method
Гl(t)	The estimated value of Γl°(t)
Γl°(t)	The practical value from a sub-gradient method
Γ′l(t)	The estimated value of Γ′l°(t)
Γ′l°(t)	The practical value from a sub-gradient method
Γ″l(t)	The estimated value of Γ″l°(t)
Γ″l°(t)	The practical value from a sub-gradient method
omb(t)	The biased estimation error of Γm°(t)
omm(t)	The martingale difference noise of Γm°(t)
olb(t)	The biased estimation error of Γl°(t)
olm(t)	The martingale difference noise of Γl°(t)
o′lb(t)	The biased estimation error of Γ′l°(t)
o′lm(t)	The martingale difference noise of Γl°(t)
o″lb(t)	The biased estimation error of Γ″l°(t)
o″lm(t)	The martingale difference noise of Γ″l°(t)

3.2

System optimal analysis

Theorem 1: The algorithms of Eqs.1, 2, 3, 4, 5 and 6 converge in distribution to global optimum with probability 1 under the conditions of A1 – A4.

A1) The noise terms Γl(t),Γ′l(t),Γ″l(t),Γm(t) are independent on iterations.

A2)ε(t)>0,ε(t)→0,∑n=0∞ε2(t)<∞(∀εl(t),ε′l,ε″l,εm(t)).

A3) The biased errors olb(t),o′lb(t),o″lb(t),omb(t) have nonnegative constant bound.

A4) The martingale difference noises have bound:

Proof: The convergence proof is a special case of work [14]. We give a sketch of proof as follows.

Let(x*,ρ*,ρ′*,ρ″*) be the point where x* is the unique optimum solution to the primal problem.

Define the Lyapunov function V(x, ρ,ρ′,ρ″) as below:

V(x,ρ,ρ′,ρ″)

=(x − x*)^{2 +} min(ρ − ρ*)^{2 +} min(ρ′ − ρ′*)²

+ min(ρ″ − ρ″*)²

And define the set

A_Ω ≅{{x,ρ,ρ′,ρ″}:V(x,ρ,ρ′,ρ″) ≤ Ω}

There can be many (x(t),ρ(t),ρ′(t),ρ″(t)) within any definite Ω > 0.

Consider Г_l(t) for instance. Since Г_l(t) has the boundary, combining A1, it yields ε_l(t)Г_l(t) →0.

Considering A2, we get εl(t)olb→0. For any small positive σ, use Chebyshev’s Inequality, one has

Using Borel-Cantelli Lemma and A4, we conclude that εl(t)olb(t)>σ is finite with probability 1 [15].

Then, using the Martingale Inequality [16] and A3, we can proof that Ω can be selected unlimited small, so { x(t),λ(t),μ_q(t),μ_△(t),t → ∞ } converges with probability 1 to the optimal point.

Theorem 1 proves the existence of stability and convergence of distributed algorithms of NUM under feedback noises and control delay in wireless mesh networks.

4

Performance

To evaluate the performance of the proposed multicast rate control method, we pay more attention to the related important parameters: sending rates of source nodes, convergence time and network utilization in our distributed algorithms.

We assume Signal to Interference Ratio (SIR) for the i^th logical link is defined as

where G_ij is the path loss from the transmitter on logical link j to the receiver on logical link i, taking into account propagation loss and normalization factors, and G_ii is the path gain for the intended transmission on logical link i, taking into account propagation loss and other factors such as spreading gain and the effect of beam forming. For a large class of modulation, the attainable data rate can be written as Eq.12. Since systems are interference limited where N_i is much smaller than the total interference, γ_i is approximated as γi=PiGii∑j≠iNPjGij. Assume the wireless mesh network uses U (x_(m,n)) = logx_(m,n) to achieve fairness among flows. Table 2 presents the parameters of the simulations.

Table 2.

Parameters of the simulations.

εl	εl=0.45ε′l
ε′l	1/n (n is the iteration)
ε″l	1/2n (^n is the iteration)
εm	1/n (^n is the iteration)
K	1
Wq	10MHz
Ni	3mW
Pi	100Mw
Pj	100Mw
Delay	20ms ~ 50ms
Topology region	500×500 m^2
Node number	20

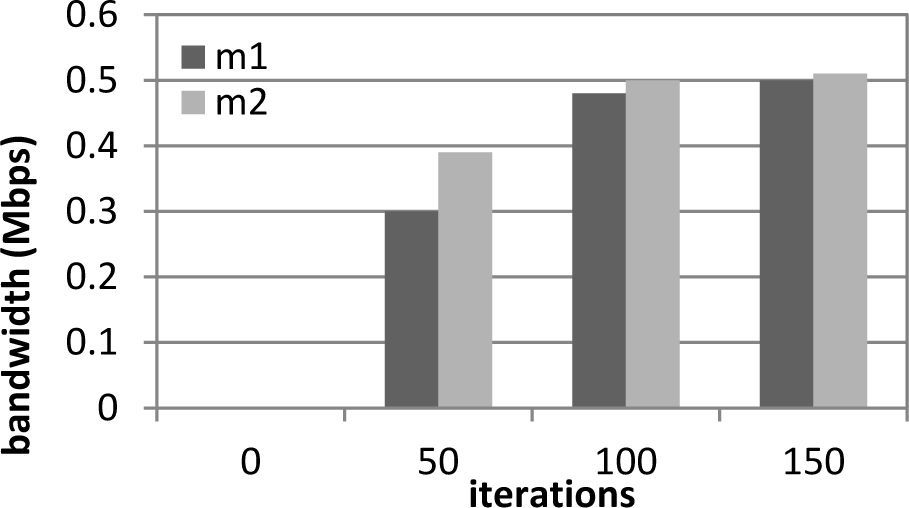
There are 20 nodes in a large area in which two multicast sessions are deployed. The results are shown in Fig. 3 ~ 6.

Figure 3.

Bandwidths of m1 and m2 at R0 (Iterations between 0 to 150).

Figure 4.

Bandwidths of m1 and m2 at R0 (Iterations between 150 to 300).

Figure 5.

Utility of m1 and m2 (Iterations between 0 to 150).

Figure 6.

Utility of m1 and m2 (Iterations between 150 to 300).

Figure 3 gives the bandwidth change of m1 and m2 at R0 when the iterations from 0 to 150. Figure 4 gives the bandwidth change of m1 and m2 at the same location when the iterations from 150 to 300. We find the bandwidth curves of m1 and m2 reach the steady state after 100 iterations time.

To test our distributed algorithms, we delete one end user from multicast session m1 at 150 iterations. We can find that the bandwidth of m1 decreases from 0.5Mbps to 0.2Mbps. However, in the same time, the bandwidth of m1 increases slightly.

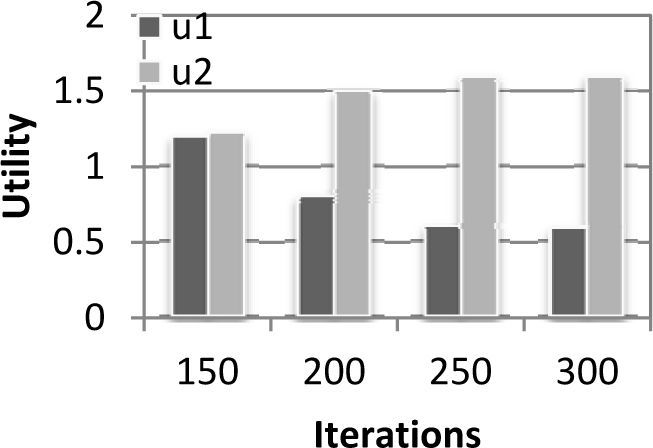
Figure 5 gives the utility change of m1 and m2 when the iterations from 0 to 150. Figure 6 gives the utility change at the same location when the iterations from 150 to 300.

We can see the utility of m1 and m1 are stable after 120 iterations. However, according to user departing, the utility of m1 decreases from 1.2 to 0.8Mbps. However, in the same time, the utility of m2 increases slightly.

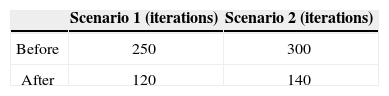
To test the convergence time of the optimal distributed multicast algorithms, two scenarios are presented. In the first scenario, there are 4 end users who receive 2 multicast sessions respectively. In the second scenario, there are 6 end users who received 2 multicast sessions respectively. That is to say, two users are added to be the multicast session receivers. Table 3 compared the difference of convergence time after applying the OPSD with the time with before using it. From table 3, we can find the convergence time is shorter after implementing the OPSD algorithms. Thus, our distributed multicast rate control method ensures good system performance.

Table 3.

Convergence time after adopting OPSD algorithms.

	Scenario 1 (iterations)	Scenario 2 (iterations)
Before	250	300
After	120	140

5

Conclusion

In this paper, we try to resolve the problem of slow transient response due to the long feedback time in wireless multicast networks. Delayed congestion feedback can cause excessive queue buildup and packet loss at bottleneck links especially in multicast. We proposed a novel Optimal Proportional plus Second-order Differential (OPSD) control which has capability to diminish oscillations in distributed wireless mesh networks via 802.11. The merit of our distributed algorithms is that they can achieve the optimums quickly. As evident from the analyses and simulation results, the proposed control scheme can improve the network performance.

Our further research along this line of study would investigate how to choose control parameters according to delay time in distributed wireless multicast mesh networks.

Acknowledgements

This work was supported by the National Science Foundation of China under Grant (No. 61202470, No.61072051), the Initial Scientific Research Fund (No.1200050487), Wuhan Science and Technology Project (No.2013010501010148).