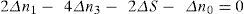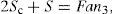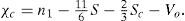The Euler-Poincaré Formula Through Contact Surfaces of Voxelized Objects

Abstract

Two new versions of the Euler-Poincaré formula are proposed considering two new defined cuboids: the tetra-voxel and the octo-voxel, without losing information on the number of vertices and edges. The well-known relationship between contact and enclosing surface concepts, as well as the relationships between vertices, edges and enclosing surfaces, allowed us to compute an innovative algorithm for obtaining alternative versions of the Euler-Poincaré formula. This is a very important topological descriptor of 3D binary images. We considered not only topological but geometric aspects. Our method was compared to other proposals, obtaining that our proposed contact surface-based method offers more advantages.

Resumen

Se proponen dos nuevas versiones de la fórmula Euler-Poncaré. Para ello se consideran dos definiciones de cuboides: los tetra-voxeles y los octo-voxeles, de forma que no haya pérdida de información en el número de vértices y aristas. La conocida relación entre superficie envolvente y superficie de contacto, así como sus relaciones con los vértices y aristas, nos permitió implementar un nuevo algoritmo para obtener versiones alternativas de la fórmula Euler-Poincaré, la cual es un descriptor topológico muy importante para imágenes binarias 3D. No solamente consideramos los aspectos geométricos sino también topológicos. El método propuesto fue comparado con otros, y obtuvimos que el nuestro, basado en la superficie de contacto, ofrece mayores ventajas.

1

Introduction

Many works about calculating Euler-Poincaré formula (also known as Euler characteristic or Euler number) have appeared in previous studies [1] - [12]. In these papers, an effort to compute Euler characteristic is made to find the number of holes (genus) in 2D objects.

The problem of computing Euler-Poincaré formula for 3D (three-dimensional) objects is a challenge because a volumetric representation is suitable to be used, since cavities and tunnels are part of many objects in the real world. Some papers have showed up to solve the problem of obtaining the Euler-Poincaré formula for 3D objects [15] - [21].

A way to compute new versions of the Euler number is in terms of the complexes. In fact, some of them maintain vertices and edges in their proposals. See for example [11] and [25]. In these papers, algorithms travel through an object and compute Euler number given a list of vertices, and moving through an object vertex by vertex, and then calculate number of edges. One of the contributions of this paper is to find a new version without computing vertices and edges.

Euler-Poincaré formula is an important topological invariant that 3D objects have, and can be adapted as a shape descriptor [22]., It can also be used to estimate the connectivity of a structure [13]. The Euler number has been widely applied to solve specific problems. For example, Vogel and Roth [17] calculated Euler characteristic to determine soil pore structure. Pierret et al., [14], used it to reconstruct and quantify macropores. Uchiyama et al., [16] considered each voxel face connected; next, they calculated Euler-Poincaré formula directly by clustering and labeling entire bones. Lehmann et al., [18] analyzed the effect of geometry on water flow and fluid distribution. In part of their work they employed the Euler characteristic to predict fluid phase distribution in porous media. Velichko et al., [20] utilized the Euler characteristic to differentiate graphite morphologies. This allows the understanding growth mechanisms and cast iron properties.

By using the contact perimeter and contact area, respectively, Bribiesca [29] proposed recently, a method to compute Euler characteristic, or genus, on 2D and 3D of face thin connected objects. He proved his method by considering, in the 2D case, different pixels representations, such as square, triangular and hexagonal resolution cells; in the 3D case, the voxels with different polyhedral representations, like unit cubes and octahedrons. In our paper, we also use the idea of computing the contact area and introduce two types of cuboids: the octo-voxel and the tetra-voxel applied in two proposed alternative versions of the Euler-Poincaré formula.

The rest of the paper is organized as follows: In section 2, we give some concepts utilized throughout the paper. In section, 3 we propose a method for obtaining the new Euler number expressions. In section 4, we describe the way to obtain the required numbers of octo-voxels, tetra-voxels, enclosing surfaces and edges. In section 5, we apply the method to a sample of 3D voxelized objects. In section 6, results and discussions are presented. Finally, in section 7, we give our conclusions.

2

Some important concepts

In this section we provide some important concepts and definitions used throughout this paper.

Definition 1. A voxel v is a resolution cell of a three-dimensional grid, that has three Cartesian coordinates x(i,j,k)={(r,s,t)∈R³:{|r-i| ≤ 1/2, |s-j| ≤ 1/2, |t-k| ≤ 1/2} and an intensity value, v_ijk={0,1}. If the intensity of the voxel is 1, we can say 1-voxel, whereas if the intensity is 0 we can say 0-voxel.

Definition 2. ΔS_c is the unit area shared by faces of two adjacent voxels when they touch.

Definition 3. ΔS is the unit outer area of the faces shared between a 1-voxel and 0-voxel.

Definition 4. Contact surface area S_c is the summation of all contacts given by two faces when two voxels touch.

Definition 5. Enclosing surface area S is the summation of all ΔS_i faces adjacent to 0-voxels faces.

Definition 6. When a 0-voxel is Turned on it becomes a 1-voxel.

Definition 7. Simplex refers to one of the composed parts of a polyhedron, such as one of its vertices, edges, faces, or volume.

2.1

The well-known Euler number expression

The Euler-Poincaré formula relates to the numbers of vertices, edges, faces, pieces of 3D regions, pieces of 4D (four- dimensional) regions, etc, of graphs, polygons, polyhedra, and even higher-dimensional polytopes. This formula can be presented in many different ways. For a single 3D polyhedral body without any holes or cavities, Euler [23] originally stated it as:

Poincaré [24] extended the formulation to a D-dimensional space:

where n_i denotes an element of dimensionality i, or simplexes; e.g., n₀ represents the number of vertices, n₁ the edges, n₂ the faces and n₃ represents the volume elements. An alternative way that permits us to find topological invariance is to define the Euler-Poincaré formula, χ, as

Unlike Equation (2), in which the solution is given by its right side, Betti numbers [25,26] are the solution for Equation (3). Of course, since the original expression of the Euler characteristic was given for polytopes, in Equation (3), we can also work with irregular or non polyhedral objects, such as depicted in Figure 1. In this figure, the object has a D=3 dimension, and χ =1. Clearly if the object consists of O simply connected components, n₀ - n_{1 +} n₂ - n₃ counted over the entire object would be just O. Next, suppose that a tunnel is introduced into the image, for example, by drawing an edge through the 0‘s area between two existing vertices (see Figure 2 left) on a border. This change gives an addition to χ of 0-1+0-0, so that Δχ =-1. Therefore Δχ =-1 will hold for any distinct tunnel added to the image, whereas if a cavity is introduced by drawing a surface between existing vertices and edges, Δχ =+1, and Euler-Poincaré formula is increased by +1 (see Figure 2 right). Then, if the complete 3D-image consists of O objects, T tunnels (also known as genus) and C cavities, we will have [25],

Figure 1.

Two triangulations for a 3D solid object: a cuboid.

Figure 2.

Adding a tunnel (left) or a surface (right) to a 3D object.

Now, since triangulation principle (see triangulation method [1,25]) is valid for 3D binary objects, n₀ will be the number of crossing points of the voxels, n₁ the edges, n₂ the internal and external faces of the voxels, and n₃ the number of voxels.

2.2

Well defined cavities

In this paper we consider face-connected adjacent voxels. If a 0-voxel is not face connected, we proceed to turn on another voxel to obtain face connectivity (Definition 6), taking care not to change the topology of the object, nor its shape. In [25] to avoid modifying the topology of the objects, a detailed analysis on deleting and turning on voxels is made. Face connectivity permits to avoid cases like that depicted in Figure 4, in which a cavity is connected to another 0-voxel through a vertex (or an edge).

An object can be seen as composed of a region and its border. Of course, this concept should be defined as follows: given a shape, its border points satisfy the condition that a neighborhood of radii ε, centered on one of its border points, contains points of both the inner and outer region. In our paper, the objects are not continuous but discretized for the minimal discrete elements, the voxels. If we change the above mentioned for a continuous case, the discretized objects have borders, such that their voxels satisfy the assumption that a neighborhood of radii \delta and centered in one such voxel contains both inner and outer region voxels.

As it is well known, the different neighbors x(i,j,k) of a voxel centered in position v(p,q,r), are defined by the neighborhoods of Equation (5).

The current voxel v in its N⁽⁶⁾ neighborhood can share only one or more faces with its neighbors, whereas, if in N⁽¹²⁾ neighborhood it can share only edges.

In N⁽¹⁸⁾ neighborhood v can share its faces and edges. Finally, in N⁽²⁶⁾ the voxel can share faces, edges and vertices. (see Figure 3) for an illustration.

Figure 3.

The four different neighborhoods around a central voxel: a)N⁽⁶⁾, the voxel has six neighbors adjacent to its faces, b) N⁽¹²⁾, the voxel has 12 neighbors adyacent to its 12 edges c) N⁽¹⁸⁾, the voxel has 18 neighbors adjacent to its 12 edges and its 6 faces, and d) N⁽²⁶⁾, the voxel has 26 neighbors adjacent to its edges, faces, and also to its eight vertices.

When the input data correspond to regions (particularly cavities or tunnels) originally separated by a vertex (see Figure 4) or an edge, we shall proceed to strengthen the barrier between the two regions, simply turning on a voxel. This is, if a 0-voxel is in the N⁽²⁶⁾ neighborhood of another 0-voxel, a well defined barrier between them has to appear. In such cases the cavities (tunnels) will be separated by the minimum image element, the voxel.

Figure 4.

Cavities are given by 0-voxels, and can be joined by a vertex. In this case, turning on one of the 0-voxels joined by a vertex reinforces the barrier between the two cavities.

A 1-voxel v is said to be emerging after a 0-voxel is turned on, and causes no decrease and no increase in the number of connected components, holes and cavities in a given 3D object. Notice that we use an emerging voxel without modify the number of cavities and tunnels in the local region where v appears. So, we take into account only cavities (tunnels) with face connected voxels. When a 0-voxel has one of the mentioned 26 neighbors, we proceed to turn it on.

3

The proposed χ

In this section we present two concepts that will help simplify the known Euler-Poincaré formula, the octo-voxel and the tetra-voxel.

3.1

Relationship between vertices, edges, enclosing surfaces and voxels.

The following definition and an important relationship between contact surface and enclosing surface of a voxelized object allows us to obtain our proposed contact surface-based Euler number χ.

Definition 8. An octo-voxel is a 2×2×2 volume of eight adjacent voxels.

Lemma 1. Given a voxelized object, let n₀ be the number of vertices, n₁ the number of edges, n₃ the number of voxels, and S the enclosing surface. Then V_o = 2n₁-4n₃-2S-n₀ is increased by 1 if and only if an octo-voxel is completed. So, V_o denotes the number of octo-voxels.

Proof:

The proof is by construction. Consider a unit cube as a voxel. In this case n₀=8, n₁=12, n₃=1 and S=6, so V_o =0. Given a unit cube (see Figure 5, n₃=1) if we add to one of its faces more edges and external faces in such way that another adjacent unit cube is considered (Figure 5, n₃=2), we clearly see that, n₀ and S are increased by 4, whereas n₃ by 1 and n₁ increases by 8, which implies ΔV_o = 0. The same happens when adding other four vertices and faces to other of its faces. To complete the parallelepiped of four unit cubes (Figure 5, n₃ = 4), two more vertices and two more external faces are needed. As it can be seen, in these cases ΔV_o = 0 again.

Figure 5.

Constructing the tetra-voxel: from n₃=1 to n₃=4, and the octo-voxel: from n₃=1 to n₃=8.

Now, let us complete a cube of eight hexahedra from the last parallelepiped. If another unit cube is placed on one of the faces, four vertices and four faces are needed. By adding another two hexahedra, two vertices and two faces are necessary. In all these cases ΔV_o = 0. As can be observed, while the octo-voxel is not completed, a change in S has the same amount as a change in n₀.

The problem of knowing ΔV_o = 0 corresponds to solve the next equation for the changes Δn₁, ΔS, Δn₀ while looking for different configurations, before completing an octo-voxel,

Before completing an octo-voxel, we can increase the number of voxels by 1. So,

under the following restrictions: ΔS ≤ 5, Δn₀ ≤ 4, Δn₁ ≤ 8 and ΔS = Δn₀.

The solutions for Equation (7) are: [Δn₁,ΔS,Δn₀] = [8,4,4] for the steps 2,3 and 5 and [5,2,2], while for steps 4, 6 and 7, are respectively, as shown in Figure 5.

On the other hand, for those cases in which ΔV_o is incremented by 1, we have,

Clearly, the solution is [Δn₁,ΔS,Δn₀] = [3,0,1], which is the configuration when an octo-voxel has been completed. This means that, to complete the cube, by adding the eighth unit cube, only one vertex and one unit cube (Δn₀ = 1 and Δn₃ = 1, respectively) are needed, whereas three more edges (Δn₁ = 3) and no new external faces (ΔS=0) are necessary. So, ΔV_{o =} 1. This result means that 2n₁ - 4n₃- 2S -n₀ will be increased by 1, if and only if, an octo-voxel is completed. □

Recently, Bribiesca [29] proposed a relationship between a contact surface of a voxelized object and its enclosing surface.

where S_c is the contact surface area, S is the area of the enclosing surface, and a is the voxel face area (in this case a is equal to one) and F is the number of polyhedron faces. This equation will be highly important to obtain our proposed χ_c and to provide the proof of the next theorem.

Theorem 1. Let F be the number of polyhedron faces. The contact surface-based Euler number can be written in terms of V_o, contact S_c and enclosing S surface, as follows:

Proof: According to Proposition 1, we have,

n₀ = 2n₁ - 4n₃ - 2S - V_o

substituting this Equation in Equation (4) we get,

χ = 2n₁ - 4n₃ - 2S - V_o - n₁ + n₂ - n₃.

or,

χ = n₁ - 5n₃ - 2S + n₂ - V_o

But, n₂ is the total number of object faces: n₂ = S + S_c and, from Equation (9), n₃ = (S + 2S_c)/F. So, we have,

or,

Simplifying, we obtain,

In the particular case the polyhedron is a unit cube, Equation (10) can be rewritten in the next corollary.

Corollary 1. Euler number for objects composed of 6-connected unit cube can be expressed by

Proof: Let us consider F=6 in Eq.(10) and demonstration is immediate. The reader can verify it easily.

After the demonstration of Theorem 1, follows the Corollary 1, and a new interesting equation in terms of contact and enclosing surface of a 3D binary object has been achieved.

Even more, considering again Equation (11), χ_c can be rewritten in terms of the number of voxels, n₃ as in Equation (12) of Corollary 2.

Corollary 2. Euler number for objects composed of 6-connected unit cube can be expressed in terms of the edges, enclosing surface, voxels and octo-voxels as:

Proof: From Equation (9) substitute S_c in Equation (11). □

This last equation now appears in terms of number of edges n₁, enclosing surface S and, number of voxels and octo-voxels (n₃ and V_o, respectively). Of course, in an implementated program, counting the voxels, at the same time, allows us to know the number of octo-voxels.

3.2

Relationship between edges and enclosing surface

In this subsection we introduce the tetra-voxel and find a relationship between edges and enclosing surface, which allows us to obtain an important and simplified Euler-Poincaré Formula.

Definition 9. A tetra-voxel is an array of four composed voxels, that forms a cuboid of any of these combinations: 1×2×2, or 2×1×2, or 2×2×1.

Relationship between number of edges and enclosing surface is given by tetra-voxel definition as in the next theorem.

Theorem 2. Let V_t be the number of tetra-voxels. This can be expressed in terms of edges and enclosing surface as in the following equation,

where n₁ is the whole number of edges, and S the enclosing surface of the object.

Proof: The proof of this theorem, is analogous to Lemma 1. To support the demonstration refer to Figure 5 from n₃ = 1 until n₃ = 4. □

Corollary 3. Euler-Poincaré formula can be written in terms of enclosing surface, voxels, tetra-voxels and octo-voxels as:

Proof. From Equation (13), substitute n₁ in Equation (12). □

Definition 10. Let the super-voxel V_s be expressed as V_s = 2n₃ - V_t+V_o, which is the operation between the different cuboids defined: voxels, tetra-voxels and octo-voxels, respectively.

Then, the Euler number proposed can be rewritten as in the following corollary:

Corollary 4. Let S be the enclosing surface of a 3D voxelized object and V_s its super-voxel. The Euler number can be expressed simply in terms of its enclosing surface and its super-voxel as:

Proof. By substituting Definition 10 in Equation (14).

As it can be seen, now Euler-Poincaré formula has been simplified in terms of enclosing surface and the defined cuboids. This relates the shape of the object and its interior! So, we think this equation is an important contribution to the state-of-the-art.

4

Voxel neighborhood analysis context

Equation (12) can be performed by counting the voxels, octo-voxels, surfaces and edges, whereas to perform Equation (14), what mainly needs to be determined is V_s and S. We conceive a 3D object as an arrangement of ones (the 1-voxels) and zeros (the 0-voxels) ordered in slices, columns and rows (see Figure 6).

Figure 6.

Defined coordinates (i,j,k) to order the covering of voxels.

Let v_ijk be the voxel with coordinates x(i,j,k) (i.e. rows, columns and slices, respectively). To count the 1-voxels, we go to the arrangement in a scanline order. To compute correctly the enclosing surface, the first and final slices, are full of zeros, as well as the first and last columns and first and last rows.

The total number of 1-voxels are as follows,

While checking each voxel v_ijk, we have to verify its 2 × 2 × 2 neighborhood to count the number of octo-voxels V_o. If such a neighborhood is full of 1-voxels, an octo-voxel has to contribute to the summation. So, the total number of octo-voxels is,

Also, while checking the voxel v_ijk, we have to verify its 1 × 2 × 2, or 2 × 1 × 2, or 2 × 2 × 1 neighborhood to count the number of tetra-voxels V_t. If such a neighborhood is full of 1-voxels, a tetra-voxel has to contribute to the summation. So, the total number of tetra-voxels is,

where [p,q,r]={[0,0,0]} ∪ {p=0 ⇒ q,r ∈ {0,1}; q=0 ⇒ p,r ∈ {0,1};r=0 ⇒ p,q∈{0,1}}.

On the other hand, to count the number of outer faces, we have to verify if one or more faces of the voxel x(i,j,k) is exposed to the background, i.e. if one or more of the neighbor voxels: x(i,j-1,k), x(i,j,k-1), x(i-1,j,k), x(i,j+1,k), x(i+1,j,k), x(i,j,k+1) represent 0-voxels. For each of these 0-voxels, the number of outer faces, S, is increased by one: #S = 1. So,

Given n disjoint 1-voxels in an image, clearly the total number of edges is n₁(v₁,v₂,...v_n)=12n. However, if the voxels share their edges as happens in a 3D grid, counting the edges means taking into account the neighborhood in which the voxels are adjacent. If two voxels, v_p,v_q, are adjacent in the N⁽⁶⁾ neighborhood, then n₁(v_p,v_q)=12*2-4 because both share four edges in the grid.

To count the edges, we check the arrangement of zeros and ones in the scan line order. From the origin of coordinates (row=0, column=0, slice=0) we start to cover all the 1-voxels. The first visited voxel has twelve edges; however, the next number #e of edges could vary depending whether the next voxel is either zero or one. Assuming we are covering the array of voxels and that we reached voxel v_p as shown in Figure 7, as in the order mentioned above. If (h) represents the neighborhood, how many edges #n₁^(h) should be added to the v_p neighbors count?

Figure 7.

Current voxel and its ten neighbors checked.

The answer is: the voxel edges in N⁽⁶⁾, say # n₁⁽⁶⁾, minus the voxel edges in only N⁽¹²⁾, say # n₁⁽¹²⁾.

This is given in the next equation:

To compute each of the terms of the last equation, we should take into account the next analysis. The voxel v_p has the following neighbors in the N⁽⁶⁾: x₆(i-1,j,k); x₇(i,j-1,k); x₈(i,j,k-1). Notice that, until now, we have not checked the three other vicinity voxels. If one of the voxels associated to these coordinates is a 1-voxel, then #n₁⁽⁶⁾ = 12-4=8. If there are two, #n₁⁽⁶⁾ =12-4-3=5; if there are three: #n₁⁽⁶⁾ =12-4-3-2=3. Now, depending on the number of 1-voxels in this neighborhood, we have to add 12, 8, 5, or 3 to the edges.

Theorem 3. Let m be the number of 1-voxels adjacent to the v_p voxel, and considering N⁽⁶⁾ neighborhood, we should add the following edges to the total v_p voxel number:

where m ∈ [0,3]. The proof can easily be made by substituting the integers of the just mentioned interval. Equation (21), is an ad hoc expression constructed to obtain the values for n₁⁽⁶⁾, i.e., when substituting the integers of m in Equation (21), we obtain 12,8,5, or 3, respectively. □

We additionally have to consider the 1-voxels in the N⁽¹²⁾ neighborhood, in which edges could be shared:

Thus, the edge-component for the N⁽¹²⁾ is determined as sum of the fulfilled conditions: #n₁⁽¹²⁾={0,1,2,3,4,5} are the edges shared if none, one or more of these conditions are fulfilled. So, the total numbers to be added to the counted edges are:

5

Application of the new Euler number expressions

The proposed χ_c formulas mainly given in Equations. (12) and (15) and the method given in the last section to implement them, has been carried out. Some objects with tunnels and/or cavities have been used to prove our proposed χ_c formula. We tested

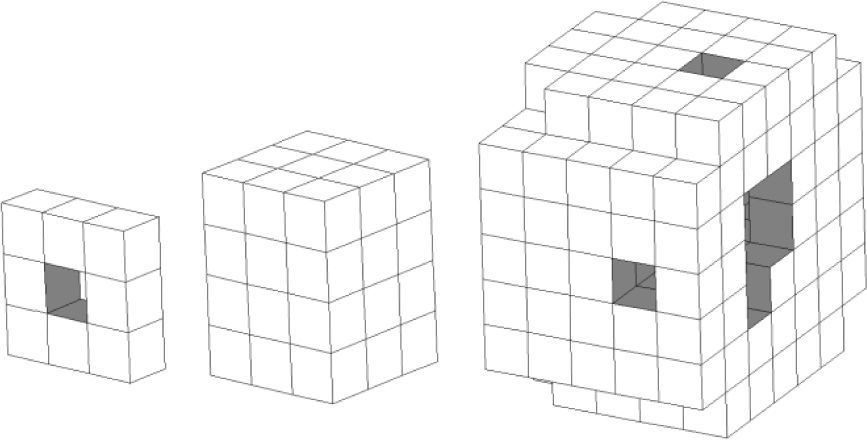
Equations (12) and (15) with 15 different object shapes having different cavities and tunnels. To demonstrate our proposed formula, we applied it to the simple objects of Figure 8. The first object, Object0, is composed of 8 voxels and one tunnel. Of course, no octo-voxels are present. The second object, Object1, is a cuboid composed of 36 voxels. No tunnels, cavities and octo-voxels are present. The third object of Figure 8. Object2, is composed of 37 voxels, and three tunnels.

Figure 8.

Objects to apply the method; a) Object0, with a tunnel going through, b) Object1, with no cavities and no tunnels, c) Object2, with three tunnels.

Figure 9, presents two different points of view of Object2 for a better assessment of its tunnels. In contrast, Figure 10 shows an object with two tunnels and two cavities, called Sphere5. Notice that the tunnels and cavities are exposed. In Figure 11, a cheese-like object is shown. This object is composed of a higher number of voxels, 728,082, and has one cavity and four tunnels. In Figure 12. a vase sample and its voxelized version are shown, whereas in Figure 13 there is a cavity. In Figure 14 a bookcase in wichtwo tunnels and three cavities are shown.

Figure 9.

Two different points of view of the Object2 showing its tunnels shape.

Figure 10.

Sphere object with two tunnels and two cavities.

Figure 11.

Cheese voxelized object, composed of 782 082 voxels. The object has four tunnels and one cavity.

Figure 12.

A Vase; a) original b)voxel representation. The object has two tunnels and one cavity.

Figure 13.

A middle part of the closed vase; a) original b) voxel representation.

Figure 14.

The bookcase showing its three cavities and two tunnels.

Finally, Figure 15, represents objects of the same Euler characteristic. They correspond to a Torus, a Cup and a Dragon.

Figure 15.

cup, dragon and a torus objects having only one tunnel (handle). They have the same Euler characteristic.

6

Results and Discussion

Table 1, has a summary of the main results. We tested χ_c with a different number of cavities and tunnels for sphere objects, as it can be appreciated in Table 1. In Table 1, Torush has two tunnels and no cavities, so its Euler number is -1. On the other hand, Object0, Torus and Dragon have no cavities and one tunnel, whereas vase has one cavity and two tunnels, and the Euler number is 0 in these four cases. Object1, sphere0 and sphere5 have the same number of tunnels and cavities, so its Euler number is 1. Sphere2 has two cavities and one tunnel, whereas bookcase has three cavities and two tunnels, so their Euler number is 2.

Table 1.

Results of the proposed Euler number to a sample objects.

Object	C	T	n1	S	Vo	Vt	n3	χc
Object0	0	1	64	32	0	0	8	0
Object1	0	0	184	66	12	52	36	1
Object2	0	3	225	102	0	21	37	-2
Sphere0	0	0	32,911	3,360	8,222	26,191	9,824	1
Sphere1	3	0	32,645	3,834	7,698	24,977	9,596	4
Sphere2	2	0	32,553	3,960	7,558	24,633	9,526	3
Sphere3	2	0	32,542	4,022	7,494	24,498	9,506	3
Sphere4	2	1	32,539	4,026	7,492	24,487	9,503	2
Sphere5	2	2	32,472	4,158	7,358	24,156	9,438	1
Torus	0	1	36,167	6,538	6,756	23,091	9,802	0
Torush	0	2	35,980	6,708	6,547	22,564	9,686	-1
Dragon	0	1	141,656	18,844	31,846	103,968	40,772	0
Bookcase	3	2	17,803	5,484	1,389	6,835	4,093	2
Vase	1	2	65,374	20,440	4,786	24,494	14,964	0
Cheese	1	4	2,265,744	81,148	687,860	2,103,448	728,082	-2

Sphere2 and sphere3 have two cavities and no tunnels, and their Euler number is 3. Sphere1 has three cavities and no tunnel, and its Euler number is 4. Finally, object2 has no cavities and three tunnels, whereas cheese has one cavity and four tunnels, so their Euler number is -2.

Figures 9 to 15 show the objects used for the experiments.

As has it been explained, two new expressions of Euler Poincaré Formula have been obtained considering a relationship between contact surfaces in voxelized objects. In fact, the concept of octo-voxels allows us to know the number of vertices, n₀, that initially appears in the original Euler number expression, without computing it directly. Moreover, the concept of tetra-voxels allows us to know the number of edges, n₁, also, without, computing it directly. On the other hand, n₂, the number of faces (contact and external), has been also simplified by computing only the outer surfaces of the 3D voxelized objects. We can get this by inspecting only if there is a pair of 1- and 0-voxel as neighbors in the 3D grid. To count the cuboids, we simply visit the voxels and inspect the vicinity.

We have proposed look for an Euler-Poincaré formula by analyzing the relationship between simplexes (vertices, edges, faces and volume elements). The proposed formulas are rich in shape parameters, like the relationship between contact and enclosing surfaces. V_t is related tovertices and enclosing surface. V_o is related to vertices, edges, voxels and enclosing surface.

As we note, Equation (12) is an expression that contains explicitly edges, enclosing surface and cuboids, whereas Equation (15) contains only enclosing surface and cuboids.

To go further in the computation of new topological characteristics, like connected components, number of tunnels and cavities, we think these equations can help other researchers to find shape descriptors, that relate not only enclosing surfaces, contact surfaces and number of voxels (as has been done in [29]), but also vertices and edges, in order to have a better understanding in the object shapes.

6.1

Comparison to other methods

In our proposed method, to compute Euler-Poincaré formula is considered to check each voxel only once, and a series of conditions are implemented to obtain the different parameters when inspecting the 26-neighborhood.

For alternative ways to compute the Euler number, some other interesting methods have been reported.

We compared our method with other four recent works: (1) Toriwaki and Yonekura [25] proposed a new Euler number in terms of connectivity. (2) Lin et. al [27] proposed a new Euler number by a local analysis topology, and expressed a new formula without knowing the number of simplex nor the shape parameters of the geometry object. In these two works, despite a detailed analysis was performed, no tested objects were presented. (3) Bribiesca [21] first skeletonized the object and computed a new Euler number expression. His proposed Euler number is in terms of enclosing and contact surfaces, but without knowing the number of simplexes. (4) Saha and Chaudhuri [28], firstly skeletonized the object, and then computed a new Euler number, not knowing number of simplexes nor more parameter shapes. In these two papers, the methods were applied to very simple objects after squeletonization, which involves more computation time.

6.2

Computational advantage of our method

On the one hand, mathematically speaking, V_s of Equation (15) represents all the operations that have to be made with cuboids, i.e. with voxels, tetra-voxels and octo-voxels. On the other hand, computationally speaking, V_s can be computed in only one visit of the whole binary file. As Figure. 6 suggests, the object can be stored in a binary file of zeros and ones. Each 1-voxel (represented by 1 in a binary file) encountered contributed to the summation given by Equation (16). Right, before visiting another voxel, the vicinity of the current voxel has to be inspected, to know if it belongs to a tetra- or an octo-voxel. For contributing to the summations of Equations (17) and (18) depends if the neighbor voxels are turned on (1-voxels) in the four or eight array neighborhood. On the other hand, the surface can be computed also in the same visit, simply by checking if each 1 of the data file is a neighbor of a 0 (i.e. if a 1-voxel is a neighbor of a 0-voxel). On the other hand, computing the standard Euler formula given in Equation (3), is more complex and hard to work with binary files. Besides of the analysis made above, a rigorous geometric analysis has to be made to compute adequately the original Euler number, because simplexes have to be managed for each 1 in the binary file, i.e. eight vertices, 12 edges and six faces, of a unit cube, have to be handled in memory storage for each 1 of the file. Clearly, this requires more source code in programming and more complexity in time processing.

So, Equations (14) or (15) are easier to compute than the standard formula.

From our proposed formulas, we can indirectly determine the number of vertices, edges and contact faces, i.e., we can know them from the other relations obtained through the paper. Our method is rich in parameter shapes, because we know the number of vertices, edges, and also, the relationship between enclosing and contact surface, which allows us to know how compact an object is. The discrete compactness is a shape descriptor given in literature [29], that has been used to analyze and recognize object shapes [30] - [32]. As we mentioned it above, these equations can help other researchers to find shape descriptors. Table 2, summarizes this analysis and discussion.

Table 2.

Comparison of our method with recent methods.

Criterion	Saha (1996)	Toriwaki (2002)	Lin (2008)	Bribiesca (2010)	Our Method
No Skeletonization	No	Yes	Yes	No	Yes
Maintaines number of simplexes	No	No	No	No	Yes
Contains shape parameters	No	No	No	Yes	Yes
Tested in samples	Yes	No	No	Yes	Yes

7

Conclusions

In this paper, we have presented a new method to compute the Euler-Poincaré Formula for 3D objects. Our method consists of considering a voxelized object with tunnels and/or cavities, thanks to the relationship between contact voxel faces with enclosing surface. The introduction of the octo-voxels and tetra-voxels, allows us to propose two new versions of the Euler-Poincaré formula. Specifically, a very simple and elegant equation has been obtained. It relates the enclosing surface with the interior of an object. Implementing such an equation is very simple: when checking each voxel, we know whether the voxel is part of an octo-voxel or tetra-voxel and if it is part of the enclosing surface or not.

As a future work, the relationships found between simplexes could be used to relate geometrical and topological aspects that allow other researchers finding shape descriptors.

Acknowledgements

This paper commemorates our appreciated colleague, Jens-Peer Kuska, who passed away in July, 2009.