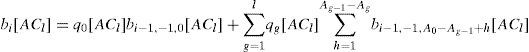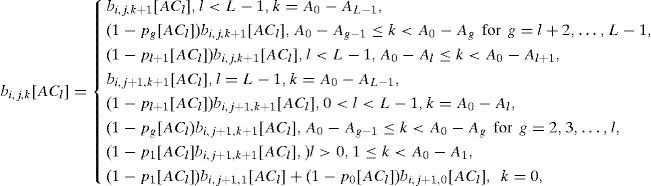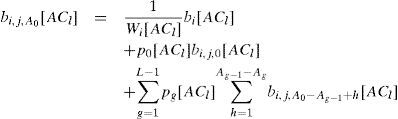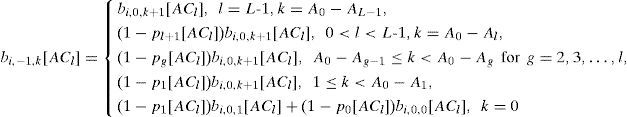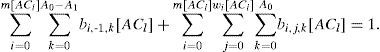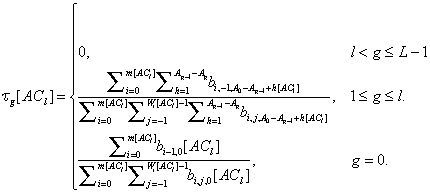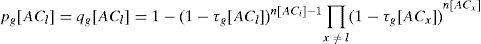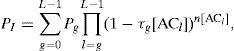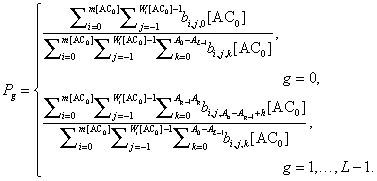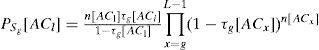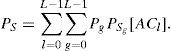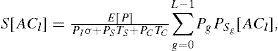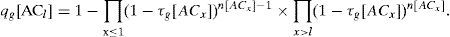Throughput Analysis Model for IEEE 802.11e EDCA with Multiple Access Categories

Abstract

IEEE 802.11e standard has been specified to support differentiated quality of service (QoS), one of the critical issues on the conventional IEEE 802.11 wireless local area networks (WLANs). Enhanced Distributed Channel Access (EDCA) is the fundamental and mandatory contention-based channel access method of IEEE 802.11e, and delivers traffic based on differentiated Access Categories (ACs). A general three dimensional Markov chain model of IEEE 802.11e EDCA for performance analysis is proposed in this paper. The analytical model considers multiple stations with an arbitrary number of different ACs. It also differentiates the contention window (CW) sizes and the arbitration interframe spaces (AIFSs), and considers virtual collision mechanism. Based on the model, the saturation throughput of EDCA is derived, and the accuracy of the proposed model is validated via simulations.

1

Introduction

IEEE 802.11 wireless local area networks (WLANs) [1] have been widely used for high speed wireless Internet access. However, there are many quality-of-service (QoS) limitations in the original IEEE 802.11 WLAN standard [1] because it was basically developed to serve best effort services. Its fundamental access mechanism for the medium access control (MAC) layer, Distributed Coordination Function (DCF) [1], cannot satisfy the increasing demand for real-time application support. Thus, a new standard amendment, IEEE 802.11e [2], has been specified to support differentiated QoS requirements over IEEE 802.11 WLANs. It provides differentiated service classes in the MAC layer so that it can deliver real-time multimedia traffic in addition to traditional data packets [2].

In IEEE 802.11e, a new MAC access mechansm named Hybrid Coordination Function (HCF) is defined [2]. The HCF consists of two channel access methods for the support of differentiated QoS. One of them is a contention-based channel access method named Enhanced Distributed Channel Access (EDCA), and the other one is HCF Controlled Channel Access (HCCA). EDCA is the fundamental and mandatory method of IEEE 802.11e and delivers traffic based on differentiated Access Categories (ACs), while HCCA is optional and requires centralized polling and scheduling algorithms to allocate the resources. This paper covers the mandatory EDCA access method only.

Some analytical models for IEEE 802.11e EDCA method have been proposed in the literature [3, 4, 6-16]. The performance of the EDCA method has been explored by means of the analytical models, with the goal being to either predict analytically performance metrics or to understand the behavior of the EDCA method.

Xiao [3, 4] enlarges Bianch’s Markovian model [5] to a model with differentiated contention window (CW) sizes, and analyzes the effects of the differentiated CW sizes on the throughput. However, the arbitration interframe space (AIFS) differentiation and the virtual collision mechanism specified in the IEEE 802.11e standard [2] are not included. Xiao assumes equal AIFS to all ACs and considers incorrectly that the collision probability controls the backoff activity, which is actually controlled by the channel busy probability. Zhang et al.[6] also assume that the collision probability is the same as the channel busy probability.

Robinson and Randhawa [7] and Hui and Devetsikiotis [8] propose a performance model to analyze the saturation throughput of EDCA by differentiating both the CW sizes and the AIFSs. However, the virtual collision mechanism is not included in [7], and the retry limit feature is neglected in [8]. Furthermore, it is assumed that each station has only one queue for one AC, and the possibility of backoff suspension is not clearly analyzed in their models [7, 8].

Kong et al.[9] analyze the throughput performnance of differentiated service traffic. They consider that during the AIFS period, if the channel is sensed busy by an AC, its remaining AIFS period is frozen and defrozen again when the channel is sensed idle again. However, the remaining AIFS period cannot be frozen and has to restart from the beginning. Furthermore, the contension zone specific transmission probability caused by using different AIFSs is not considered in [9].

Tantra et al.[10] present a three-dimensional Markov chain model, where each station has four queues for four different ACs. The model considers both the effect of using differentiated AIFSs and the effect of backoff suspension. However, they assume three higher priority ACs have the same AIFS value. Furthermore, they do not consider the possibility of backoff suspension for the higher priority ACs.

Xiong and Mao [11] consider only two ACs for analytical simplicity, and limit their study to one AC per station. In [11], two Markov chain models are created for two ACs separately, and the transmission probability of a station in a generic time slot is assumed to be constant. The probability that a higher priority AC station sees an idle time slot depends which contention zone the time slot belongs to. Although they obtain two different contension zone specific probabilities, the Markov chain for the higher priority AC uses only the average probibility. The model proposed in this paper remove the above problem.

Lee et al.[12] consider the contention zone specific probabilities that a station sees an idle time slot, which is ignored for higher priority AC in [11]. However, three higher priority ACs have the same AIFS value in [12]. In this paper, the model in [12] is extended to the model, where each station carries traffic from an arbitrary number of different ACs.

Taher et al.[13] develop a discrete-time Markov chain model that takes into account most features, including the transmission opportunity limit (TXOP Limit), of the 802.11e EDCA method under both the non-saturation and the saturation traffic condition. Tursunova and Kim [14] propose a mathematical model for IEEE 802.11e EDCA under non-saturation condition. However, the collision probability and the channel busy probability are assumed to be constant in [13, 14]. Furthermore, virtual collision mechanism is not considered in [14], and it is assumed that each station is using only one AC.

In this paper, we propose a more general three dimensional Markov chain model of IEEE 802.11e EDCA. The proposed analytic model considers multiple stations, each of which has an arbitrary number of different ACs. The model differentiates the CW sizes and the AIFS values of different ACs, and considers virtual collision mechanism. We assume that traffic load is saturated and only one frame is transmitted in each TXOP. Based on the proposed model, we evaluate the throughput performance of the EDCA with an arbitrary number of different ACs. The results of our analytical model are then verified using simulations.font.

2

Enhanced distributed channel access

The IEEE 802.11 DCF has no functionality to support QoS requirements. To overcome this drawback and enhance the conventional DCF, IEEE 802.11e EDCA has been specified. EDCA provides differentiated and distributed channel access for packets with different priorities in a station. EDCA handles application needs by mapping their traffic into four different ACs: AC_BK for background traffic, AC_BE for best effort traffic, AC_VI for video traffic, and AC_VO for voice. Individual AC is differentiated by a set of its own EDCA parameters, namely CW_min, CW_max, and AIFS [15], where CW_min and CW_max are initial and maximum CW sizes of binary exponential backoff, respectively, and AIFS is the time interval a packet of a given AC has to wait after the channel becomes idle before it can start the backoff process or transmit [16]. EDCA assigns smaller values of CW_min, CW_max, and AIFS to ACs with higher priorities.

After i, i ≤ m, collisions, the backoff counter is selected uniformly from range [0,min(2ⁱCW_min, CW_max) −1],where m is the maximum number of allowable retransmissions. When the total number of retransmissions equals m, no further retransmissions are attempted, and the packet is discarded [16]. In EDCA mechanism, each station implements a queue for each AC. Packets belonging to different ACs within a single station may collide with each other when their backoff counters decrements to zero simultaneously. This phenomenon is called a virtual collision in IEEE 802.11e EDCA and is prevented by letting the highest priority involved in the collision win the contention [16].

3

Analysis without virtual collision

We model the backoff operation of each station with a Markov chain. Our approach is similar to that of [7]. In this section, we assume that each station implements only one of the multiple ACs in EDCA. Thus, we do not consider virtual collision, which will be handled in Section 4.

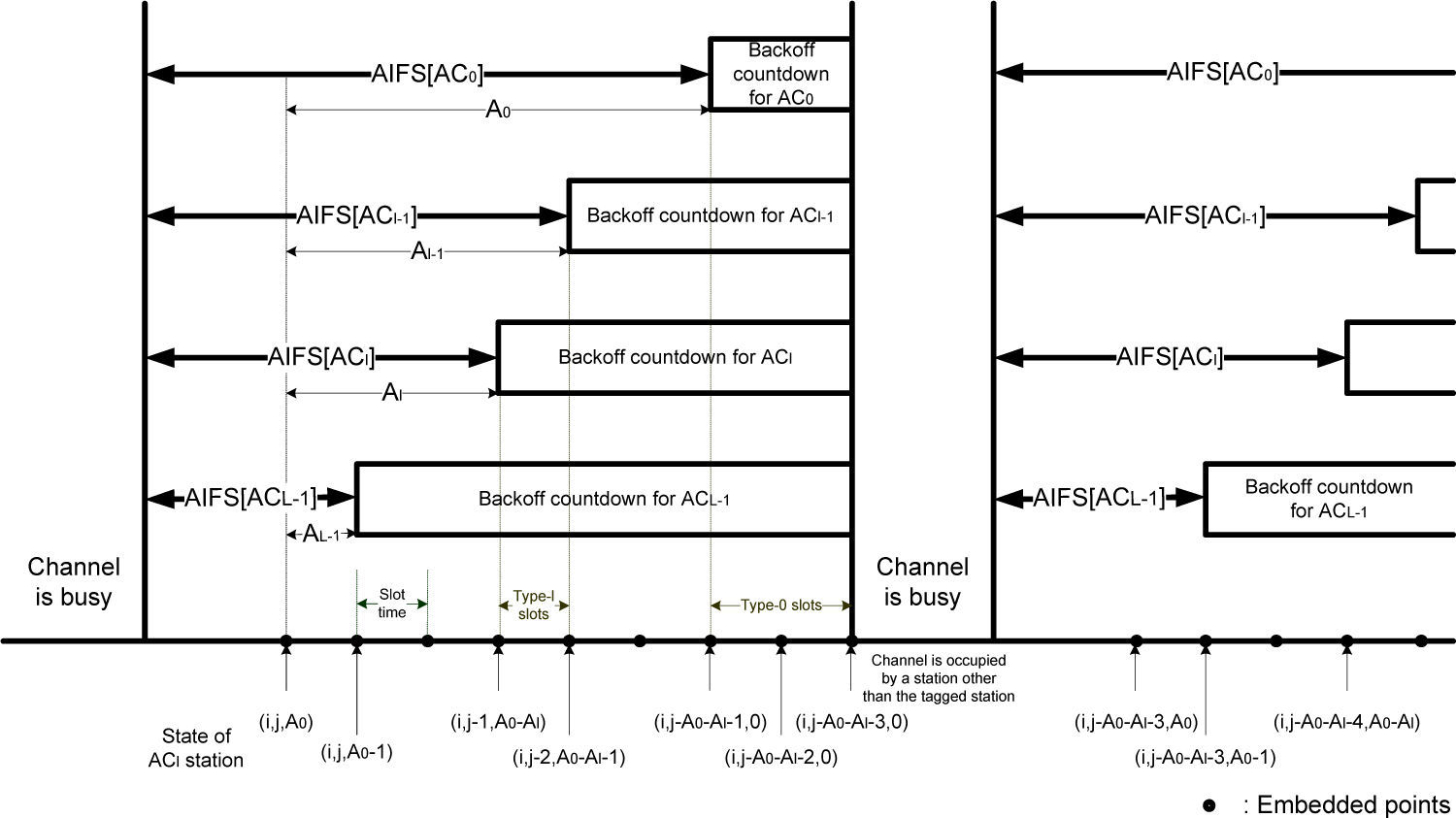
This paper supports up to L ACs from the lowest priority service class AC₀ to the highest one AC_L-1. We use different Markov chains for different ACs. Thus, L different Markov chains are required. For l = 0,1,…, L – 1, the state of a given tagged station implementing AC_l is considered at the following embedded point; the boundary of each slot time at which the backoff counter for AC_L-1 is active (see Figure 1).

Figure 1.

Embedded points.

Note that, in EDCA, the backoff counter is frozen when a transmission is detected in the channel, and reactivated at the beginning of the last slot of the corresponding AIFS. Let s(t) be the stochastic process representing the number of retransmissions of the tagged station at the embedded point t. The value of s(t) ranges from 0 (the first backoff stage) to m[AC_l] (the retransmission limit) for AC_l. Let b(t) be the stochastic process representing the value of the backoff counter for the tagged station at time t. After each packet transmission, the value of the backoff counter for the tagged station implementing AC_l is assumed to be considered from the beginning of the last slot of the AIFS for AC_L-1 instead of AC_l, and remain frozen until the last slot of the AIFS for the tagged station, which is just for computational convenience and has no effect on the performance of EDCA. When s(t) = i, the value of b(t) ranges from −1 to W_i[AC_l] −1, where W_i[AC_l] is given by min(2ⁱCW_min[AC_l], CW_max[AC_l]). Note that, in EDCA, when the backoff counter of a station expires, the station has to wait for an extra idle backoff slot in order to transmit its packet. The value b(t) = −1 represents the end of the extra idle slot. The stochastic process r(t) represents the remaining AIFS period for AC₀ at time t. The value of r(t) ranges from 0 to A₀ ≡ AIFS[AC₀] – AIFS[AC_L–1] + 1.

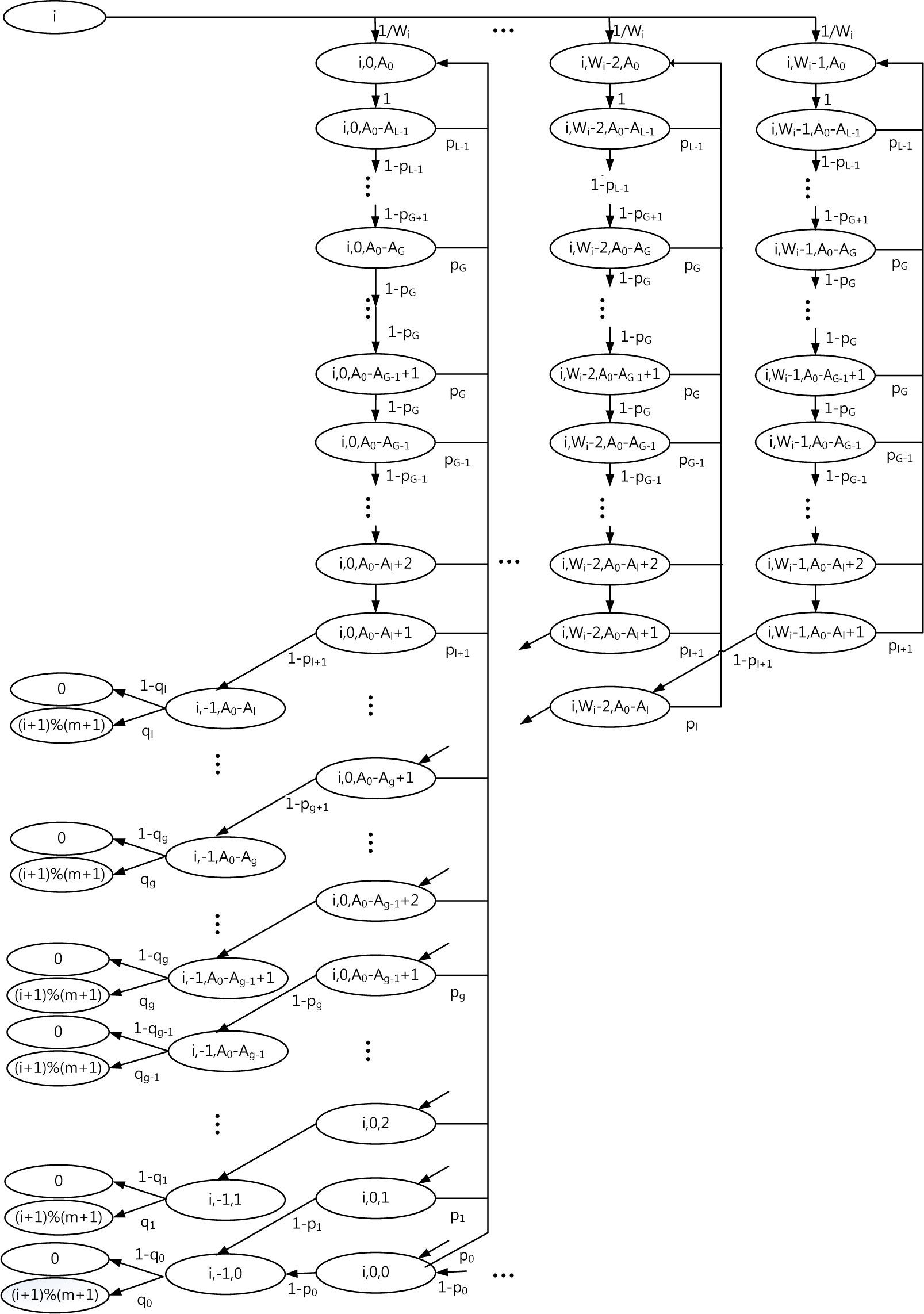
The process {(s(t), b(t), r(t))} is a Markov chain under the assumption that p_g[AC_l] (the probability that, from the AC_l station’s point of view, at least one of the other stations transmit a packet during a type-g slot) and q_g[AC_l] (the probability that a packet from the tagged AC_l station encounters a collision when it is transmitted during a type- g slot) are independent of the number of retransmissions, where type- l slots are the slots between the end of AIFS[AC_l] and AIFS[AC_l−1], and type- 0 slots are the slots after the end of AIFS[AC₀]. Figure 2 shows the transition diagram of {(s(t), b(t), r(t))} for the tagged station implementing AC_l, where a%b denotes the remainder of the division of a by b and W_i, m, p_g, and q_g are used instead of W_i[AC_l], m[AC_l], p_g[AC_l] and q_g[AC_l], respectively. In Figure 2, the states t’s, i = 0,1,…, m[AC_l], are introduced, which will be eliminated when the stationary probabilities are normalized.

Figure 2.

State transition diagram.

Let b[AC_l] andb_i,j,k[AC_l] be the stationary distribution. We have

where A_g ≡ AIFS[AC_g] − AIFS[AC_L-1]+1 for and g = 0,1,…, L-1 (See Figure 1). We also have the followings:

and

where bi,wi[ACl],k[ACl]=0 for all k and b_i,j,k [AC_l] = 0 for 0 ≤ k ≤ A_{0 −} A_{l −} W_i[AC_l] + j + 1;

for i =0,1, …,m[AC_l]. Each of the state stationary probabilities can be expressed in terms of b₀[AC_l] and obtained by imposing the normalization condition

For l = 0,1, …, L-1, the probabilities τ_g[AC_l] that a station of AC_l transmits in a type- g slot is given by

The probabilities p_g[AC_l] and q_g[AC_l] are given by

for g, l = 0,1…, L-1, where n[AC_l] is the number of stations implementing AC_l. The probability P_I that a slot is idle is

where the probability P_g that an arbitrary slot is a type- g slot is given by

The probability PSg[ACl] that a slot contains a successful transmission of AC_l under the condition that the slot is a type- g slot is given by

for g, l = 0,1…, L-1. The probability P_C that a slot time contains a collision is

where

The saturation throughput of AC_l is given by

where E[P] is the average length of packet payload, σ is the length of a slot time, T_S is the average length of a successful transmission, and T_C is the average length of a collision. The values of T_S and T_C are given in [7].

4

Analysis with virtual collision

We consider the case that each station runs an arbitrary number of different queues with different ACs. [7]. Owing to virtual collision, when two or more queues of a station have backoff counters of zero, the highest priority queue is favored and is given the chance to access the medium. The lower priority ones still see the collision, and they will increase their backoff stages and choose other backoff counters [7].

For the virtual collision case, we use the same approach as in Section 3 with the following differences [7]. Firstly, since each station now has multiple queues, a Markov chain is used to model each queue instead of each station. Secondly, the virtual collision changes the collision probabilities seen by individual queues because the highest priority queue will not see the collision with the lower priority queues of the same station [7]. The collision probability q_g[AC_l] is now given by

Then, if we want to see the throughput of AC_l in a station, the station can be viewed as one with a single AC_l and the above collision probability q_g[AC_l]. Accordingly, all analytic results in Section 3 can be used even when we consider the virtual collision.

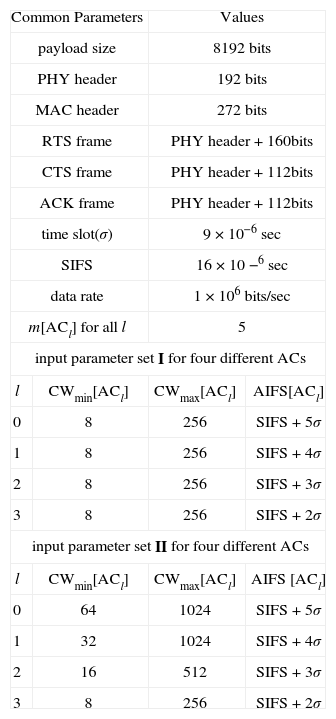
5

Numerical results

In order to evaluate the throughput performance of ACs in IEEE 802.11e EDCA, we use the values of system parameters shown in Table 1 for both analytical and simulation results.

Table 1.

Examples of the System Parameters.

Common Parameters		Values
payload size		8192 bits
PHY header		192 bits
MAC header		272 bits
RTS frame		PHY header + 160bits
CTS frame		PHY header + 112bits
ACK frame		PHY header + 112bits
time slot(σ)		9 × 10^−6 sec
SIFS		16 × 10 −^6 sec
data rate		1 × 10^6 bits/sec
m[ACl] for all l		5
input parameter set I for four different ACs
l	CWmin[ACl]	CWmax[ACl]	AIFS[ACl]
0	8	256	SIFS + 5σ
1	8	256	SIFS + 4σ
2	8	256	SIFS + 3σ
3	8	256	SIFS + 2σ
input parameter set II for four different ACs
l	CWmin[ACl]	CWmax[ACl]	AIFS [ACl]
0	64	1024	SIFS + 5σ
1	32	1024	SIFS + 4σ
2	16	512	SIFS + 3σ
3	8	256	SIFS + 2σ

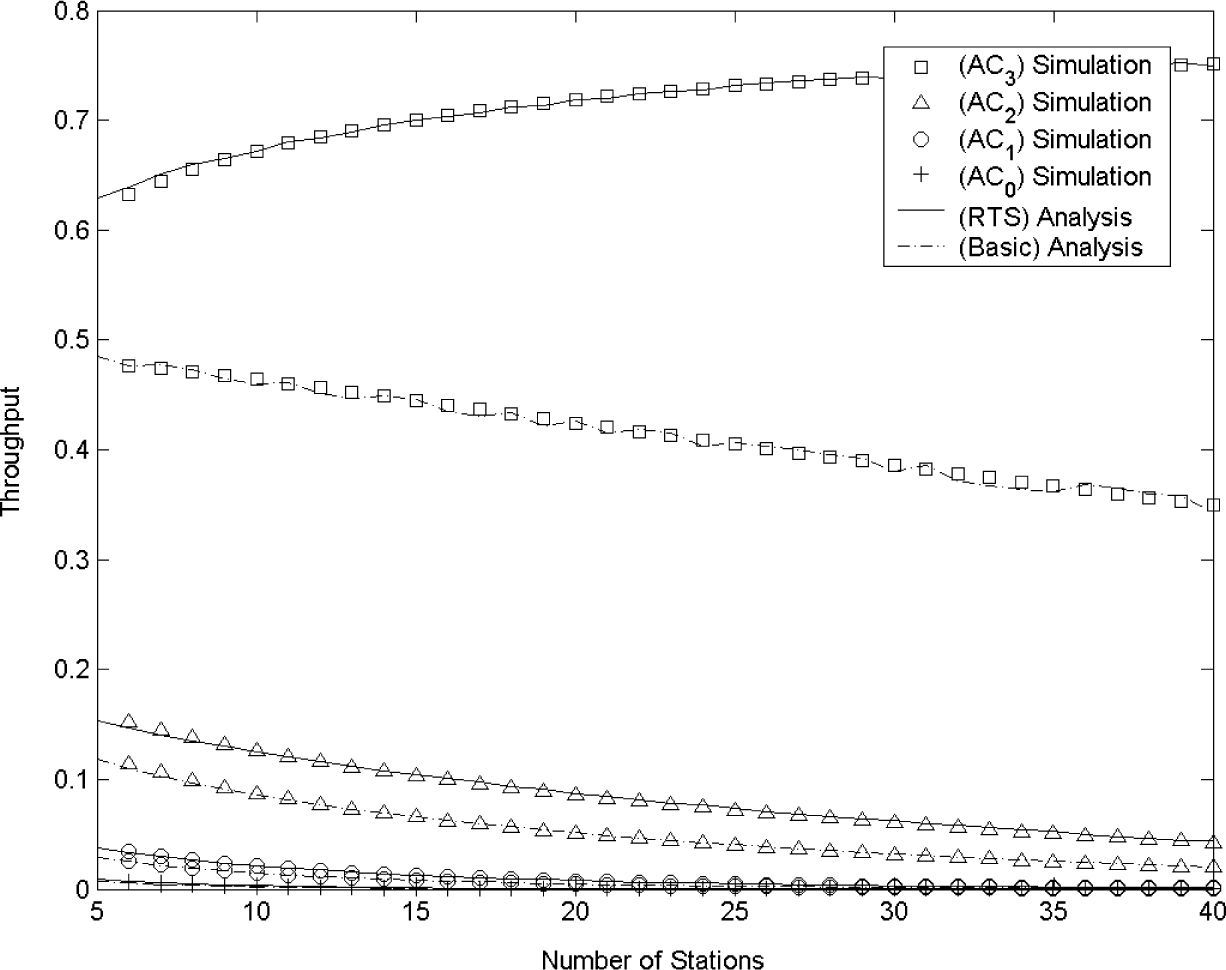
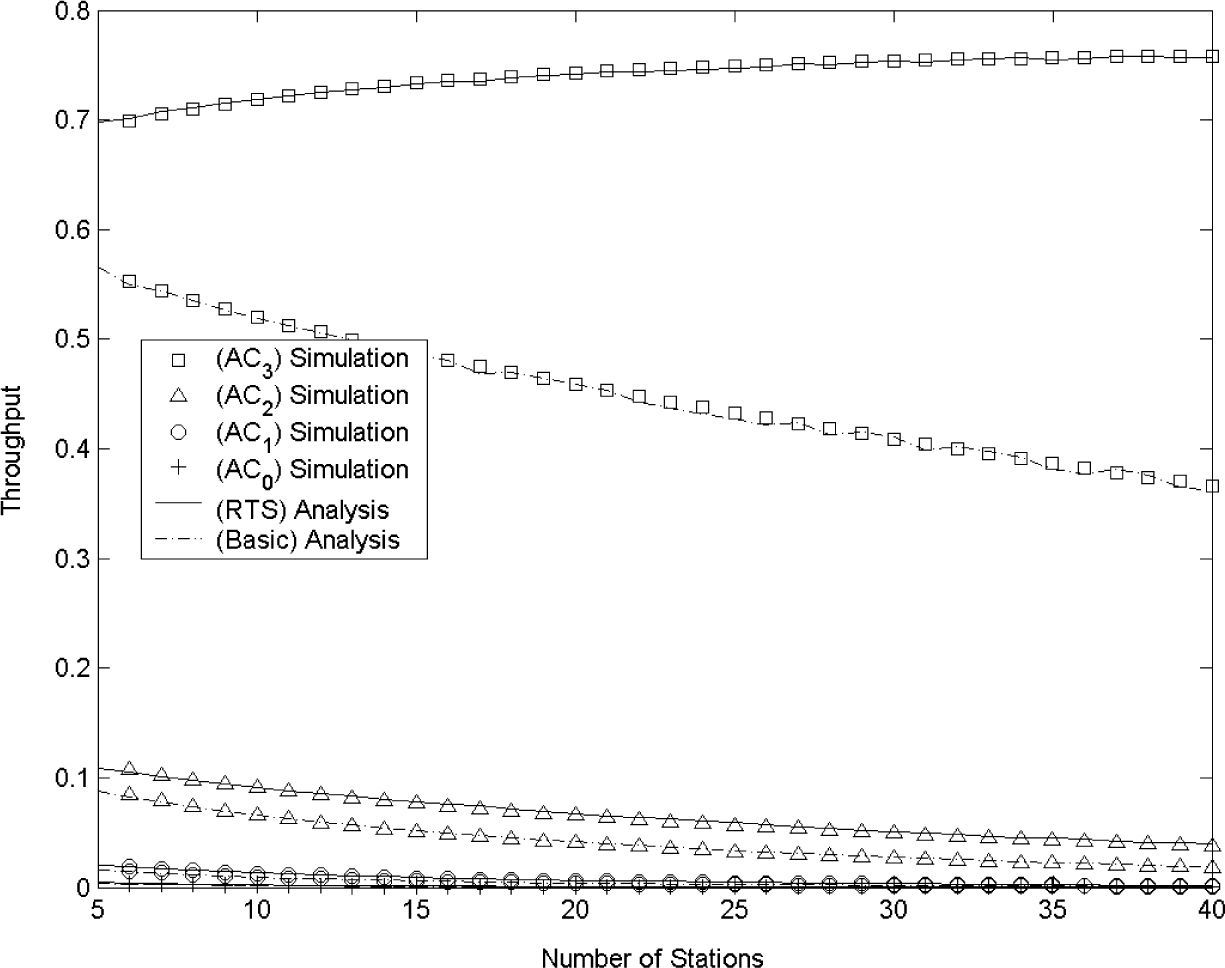
Figures 3 and 4 show the saturation throughput of four ACs in EDCA for basic access and RTS/CTS exchange methods. From the figures we see the differentiation in saturation throughput of four ACs due to the CW size, the AIFS value, and the virtual collision in IEEE 802.11e EDCA. In order to validate our model, we have conducted simulations, and simulation results are also plotted in Figs. 3 and 4. The figures indicate that the analytic results of our proposed model are closely matched with the simulation results for both basic access and RTS/CTS exchange methods. This means that our new proposed model for the analysis of EDCA can show faithfully the performance of the EDCA mechanism.

Figure 3.

Saturation throughput: input parameter set I.

Figure 4.

Saturation throughput: input parameter set II.

From Figures 3 and 4 we can also investigate the followings. In Figure 3, we investigate the impact of the AIFS parameter and the virtual collision on the performance differentiation among stations of various ACs. Figure 3 shows the saturation throughput as a function of the number of stations with different AIFS parameters and the same CW size as in the input parameter set I. Since it is reported that the virtual collision has little effect on the performance [10], Figure 3 reveals that AIFS has a pronounced effect on service differentiation. Figure 4 shows the saturation throughput as a function of the number of stations for the input parameter set II with the same AIFS parameter set as in Figure 3. In this case the performance differentiation is introduced due to different values of CW_min[AC_l] and CW_max[AC_l] for the various AC queues as well as the different values of AIFS.

The numerical results indicate that EDCA can provide rate differentiation among stations of various ACs. The higher the priority of AC is, the higher the throughput for the AC due to smaller CW sizes and smaller AIFS values. In addition, as expected, the performance of EDCA with RTS/CTS enabled shows better throughput over all ACs than that of EDCA for basic access method, because the RTS/CTS exchange method reduces a waste of resource due to collisions.

6

Conclusions

In this paper, a more general three dimensional Markov chain model to analyze IEEE 802.11e EDCA protocol under saturated traffic load was proposed. The proposed analytic model considered multiple stations with an arbitrary number of different ACs. It also differentiated the CW sizes and the AIFS values of different ACs and considers virtual collisions. Based on the proposed model, we analyzed the saturation throughput of different ACs in EDCA. The results of our analytical model were then verified using simulations. The analytical results are very accurate, compared with the simulation result for various EDCA parameters.

Acknowledgements

This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2013R1A1A4A01013094).