Background subtraction models based on mixture of Gaussians have been extensively used for detecting objects in motion in a wide variety of computer vision applications. However, background subtraction modeling is still an open problem particularly in video scenes with drastic illumination changes and dynamic backgrounds (complex backgrounds). The purpose of the present work is focused on increasing the robustness of background subtraction models to complex environments. For this, we proposed the following enhancements: a) redefine the model distribution parameters involved in the detection of moving objects (distribution weight, mean and variance), b) improve pixel classification (background/foreground) and variable update mechanism by a new time-space dependent learning-rate parameter, and c) replace the pixel-based modeling currently used in the literature by a new space-time region-based model that eliminates the noise effect caused by drastic changes in illumination. Our proposed scheme can be implemented on any state of the art background subtraction scheme based on mixture of Gaussians to improve its resilient to complex backgrounds. Experimental results show excellent noise removal and object motion detection properties under complex environments.
Los modelos de substracción de fondo basados en mezcla de Gaussianas han sido ampliamente usados para la detección de objetos en movimiento en diversas aplicaciones de visión computacional. Sin embargo, la substracción de fondo sigue siendo un problema abierto, particularmente en escenas de video donde existen cambios drásticos de iluminación y fondo dinámico. El presente trabajo tiene por objetivo incrementar la robustez de los modelos de substracción de fondo en ambientes complejos, para esto se propone: a) redefinir los parámetros de la distribución de mezclas que afectan la detección de objetos en movimiento (peso, media y varianza de la distribución); b) mejorar la clasificación de pixels (fondo/objeto) y el mecanismo de actualización de las variables mediante la aplicación de un nuevo parámetro de velocidad de aprendizaje que depende de la historia temporal y espacial de los objetos en movimiento c) reemplazar el modelo de substracción de fondo a nivel de pixel usado actualmente por un modelo que cubre una región espacio-temporal para la eliminación de ruido causado por cambios drásticos de iluminación. Las propuestas pueden ser implementadas en cualquier esquema de sustracción de fondo basado en mezcla de Gaussianas para mejorar su respuesta en situaciones de fondos complejos. Resultados experimentales del modelo muestran su excelente capacidad para la eliminación de ruido y detección de objetos en movimiento en ambientes de fondo complejo.
Background subtraction models have been widely used for detecting or localizing moving objects in video scenes. It represents a fundamental step in several computer vision applications, such as video surveillance, vehicular traffic analysis, object tracking, and recently human activity recognition (running, dancing, jumping, etc.) [1-6]. However, background subtraction is not an easy task, schemes must be able to adapt to complex environments such as illumination changes, different weather conditions in the scene (snow, rain, wind, etc.), and subtle changes in the backgrounds such as waves on the water, water fountains, moving tree branches, etc. (Fig.1). False positives can be induced by drastic illumination changes, while false negatives may be due to similarities between objects and background [1].
Several schemes have been developed to deal with the above problems, which can be categorized in three groups [7]: a) temporal difference, in these techniques the difference between two or three consecutive video frames is significantly bigger in regions with motion, thus motion can be segmented with respect to static regions; b) optical flow, the goal of optical flow estimation is to compute an approximation to the motion field from time-varying image intensity relative to the observer in the scene (usually a camera). Objects with different motion pattern than the background are tagged as objects in motion (for example, background camera motion can be distinguished from the objects in motion); c) background subtraction, it builds a pixel-based model of the background in an image sequence so that, regions significantly different from the model are classified as foreground objects.
Among these categories, background subtraction models have proven to be more robust under different background environments (depending of course on the way the background is modeled). Generally speaking, background subtraction models in the literature include the following three modules: background model, variables-update mechanism, and training for the initialization of the model. The simplest background model considers a unimodal distribution for modeling the pixel intensity and/or color, as in Pfinder application [8] for object tracking. Pfinder uses a multiclass statistical model requiring a static scene for the initialization process in order to yield good results (no reports are available for outdoor environments). Horprasert et al., 1999 [9], introduced new parameters for the modeling of an image pixel (a big step forward in background subtraction): mean, standard deviation of the color space (RGB), luminance variation and chrominance variation. Monnet et al., 2003 [10], proposed a real-time scheme for modeling dynamic scenes such as ocean waves and trees shaken by the wind; however, the scheme requires a long initialization period without objects in motion in order to model the background. Additionally, there are difficulties in detecting objects moving in the same direction as the waves. Mittal and Paragios, 2004 [11], developed a background subtraction model based on adaptive kernels. The scheme works on complex backgrounds, but the computational cost is high. Li et al., 2004 [12], proposed a Bayesian architecture that incorporates spatial and temporal spectral properties in order to characterize each background pixel. Their method can deal with both static and dynamic backgrounds. In Ridder et al., 1995 [13], each pixel is modeled with the Kalman filter, showing robustness to illumination changes. In the work of Piccardi & Jan, 2004 [14] and Han et al., 2007 [15], the mean-shift method is applied to model the background.
Currently, the Gaussian mixture model is one of the most popular schemes for background subtraction, because of its ability to handle slow illumination changes, slow and periodic object motion, camera noise, etc. The article of Stauffer and Grimson, 1999 [16], is one of the most representative works in this area. They modeled each pixel with a mixture of Gaussians and applied the Expectation-Maximization method for updating the model parameters. The system can deal with illumination changes (up to a certain degree), detect slow object motion, and objects in motion can be removed from the scene. Following this idea, Shen, et al., 2012 [17], applied the mixture Gaussian model on sensor networks with restricted energy supply and limited CPU processing capabilities. Their contribution is the application of compressive sensing to reduce the dimensionality of the problem (number of pixels to process) for both, energy consumption and realtime scene processing.
Our goal in this work is to increase the robustness of background subtraction schemes based on the Gaussian mixture model. In particular, we propose the following enhancements for scenes in complex environments (dynamic backgrounds): a) Noise elimination during pixel classification as background or foreground; b) reduction of drastic variations in illumination; and c) elimination of high frequency motion that affects the identification of moving objects. Our proposal can be implemented in any state of the art scheme in the literature based on mixture of Gaussians in order to deal with dynamic backgrounds.
The paper is organized as follows. Section 2 introduces the background subtraction algorithm based on Gaussian mixture models. Section 3 describes the proposed changes to the background subtraction algorithm in order to deal with complex backgrounds. Finally, conclusions are presented in section 4.
2Mixture of Gaussians Method for Background SubtractionBackground subtraction or background modeling in computer vision refers to estimating an image background from a sequence of images or video using a statistical model. The main assumption is that the observer (camera) is static, and only objects move around in the scene. One of the easiest ways for background modeling is to take an image of the scene without objects in motion; this represents the background model. Any object not represented in the background image can be identified by using the absolute difference between consecutive frames, that is every pixel in the image I(i,j)t (image at time t) is compared against the estimated background image Bˆ:
This solution is sufficient under controlled environments. In arbitrary conditions such as outdoor scenes, illumination is a time-dependent variable for which adaptive models of the background are required. In the following section we introduce the concept of adaptive background models using mixture of Gaussians and current updates.
2.1Mixture of Gaussians (MoG)Gaussian mixture model was introduced by Stauffer and Grimson in 1999 [16]. The idea of scheme is to provide a pixel-based multimodal representation of the background for the elimination of repetitive motion such as water-light reflection, moving tree branches, etc. They considered a pixel X(x0, y0) in the video sequence as a random process represented as a time series. At any time t, what is known about the pixel X(x0, y0) is its history:
where Ii is the sequence of images up to time t. Fig.2 shows the pixels in a scene with strong illumination variation (pixels in red) and pixels with real object motion (pixels in blue). The actual problem is to filter out the noise (red pixels) while preserving those pixels representing real objects in motion (blue pixels). For this, the history {X1,..., Xt}
is modeled by a mixture of K Gaussian distributions; so the probability of observing the current pixel Xt is
where K is the number of distributions, wit is an estimate of the weight (what portion of the data is accounted for by this Gaussian) of the ith Gaussian in the mixture at time t, μit is the mean value of the ith Gaussian in the mixture at time t, ∑it is the covariance matrix of the ith Gaussian in the mixture at time t, Θt represents the vector of parameters in the model Θ=(w1t,...,wKt,μ1t,...,μKt,∑it) at time t, and, η() is the Gaussian probability density function
K is determined by the available memory and computational power, which can be considered fixed [16, 17], variable [20], or adaptive [19] (more complicated regions require more Gaussian components than stable ones). Also for computational reasons the covariance matrix is assumed to be of form [15]
In order to compute the vector of parameters that best represents the data history {X1,..., Xt}, the maximum likelihood estimation function is applied
and maximizing
2.2Background SubtractionOnce the mixture of Gaussians is defined for background subtraction, the next steps is to determine which of the K distribution the actual pixel Xt belongs to and update the vector parameter of the model. For this, Stauffer y Grimson, 1999 [16], estimated the concordancep(k|Xt,Θold) of the pixel Xt with every single distribution k∈K of the mixture. The concordance is positive if Xt < 2.5σ from µ, which can also be expressed in terms of the Mahalanobis distance
with positive concordance if dk < 2.5 (that is, 98.76% of a 1-D Gaussian distribution). For higher dimensions, the X2 (Chi-square) distribution with n degrees of freedom and confidence interval Y is used instead; positive concordance is represented by dk2
If several distributions have the same minimum distance, the one that maximizes wk/||∑k||F (where F is the Frobenius norm) is selected. This is in favor of the distribution that accounts for the most pixels (big w and small variance). If none of the distributions matches the new pixel, the least probable distribution is replaced by a new distribution with mean µ = Xt high σ2 and small weight wk/||∑k||F. This is the way new objects are incorporated to the background. Finally, the K distributions are sorted with respect to wk/||∑k||F, and only the combination of the first B distributions that overcome the threshold Th are selected as the background model.
The last step is to compute the binary image (background-foreground) out of the background model. The B distributions are compared with the distribution of the new pixel (let´s call it) kˆ then if kˆ∈B, the new pixel is part of the background otherwise is part of a moving object. The weight of new pixel distribution is updated as follows:
where α = 1⁄(N + 1), qk,t = 1 for the distribution with the minimum distance or qk,t = 0 for the rest (Eq. 5). Similarly, µk and σk for the new pixel distribution are also updated
where
2.3Learning Rate (a)One of the main problems with adaptive mixture Gaussian models is to balance the speed at which objects are taken into the background once they stop moving; this is known as learning rate. In the literature, the learning rate is controlled by a fixed global value α∈[0,1]; unfortunately, the adaptability or convergence of the distributions to new situations maybe different for different applications or even the same scene. Objects can remarkably be absorbed either too slow or too fast, affecting the segmentation of background and foreground (see example of Fig.3). If a is chosen too big (close to 1), the convergence speed improves but the model becomes very sensitive to environmental noise. Under these situations, the model is indifferent to past events (see Eq. 6).
2.4External Factors Affecting Moving Object DetectionAs mentioned in section 1, subtle changes in the background such as water waves, water fountains, rain, moving tree branches, etc., inhibit the correct classification of background and objects in motion in a scene. To tackle these problems (up to a certain extent), Teixeira et al., 2007 [21], assumed that illumination variations in a scene are caused by a multiplicative factor k affecting the real color of the pixel. Under this case, the resultant color vector is co-linear to the reference vector (Fig.4). The co-linearity test consists in evaluating the angle between the current pixel vc and the reference pixel vr (previous pixel value),
If cosθ is greater than a threshold ThI ≈ 1, the vector is considered co-linear, which confirms that the pixel change was produced by an illumination change. Fig.2 (second row) shows some examples for which Teixeira’s algorithm [21] (known as
cascade algorithm), identifies some pixels as colinear (pixels marked in red) and some other as objects in motion (pixels marked in blue). Co-linear pixels maintain their previous classification (background in this case), keeping only the pixels representing motion as shown in Fig.2 third row.
3Proposed Changes for Robust Background SubtractionIn this section, we describe our contribution for improving background subtraction and object-motion detection (section 2) in complex environments (outdoor scenes in Fig.1). We have selected the cascade algorithm [21] as a test bed and reference point to measure the performance quality of our proposal. Cascade algorithm is known as one of best schemes for background subtraction, but any scheme in the literature based on MoG can also be used for this purpose.
In particular, our proposal considers the modification of the following parameters for robust background subtraction model: variance of the model (σ2), learning rate (α), new distance metric for estimating the density function of the current pixel, and the use of spatio-temporal region for the MoG instead of the commonly used pixel-based representation.
3.1Variance (σ2) and Learning Rate (α)The definition of variance (σ2) and weight (w) (see Eq. 1 and Eq. 6), are of great importance for the segmentation of the scene background and foreground. Background pixels have small σ2 and big w because they represent more stable conditions, that is new pixels are found in concordance with the current background distribution. One of the problems in previous methods is that the variance is not bounded to a minimum. In an image sequence in which most of the pixels are considered as background, the variance may take very small values (< 1×10E −16) introducing noise in the segmented scene (very narrow Gaussian distribution for which some pixels may incorrectly be classified as objects, such as the red pixels in Fig.2 second row). To avoid this situation, we propose the use of each color component (or channel) for the pixel classification and define a minimum variance value each component may take:Algoritmo 1: New σ2 definition
forall k ∈ {1 to K}
for All z ∈ {1 to NChannels}
Si σz,k < SigmaMinimumz
σz,k = SigmaMinimumz
end
end
end
where K is the number of distributions in the MoG, NChannels is the number of channels in the chosen color space (3 channels for the YUV color space). In our experiments, the best values for SigmaMinimumz = [2.0, 2.3, 2.3]. With this new definition, drastic illumination changes (Y component) can be filtered out by testing separately the stability of the UV components (as shown at the end of this section and section 3.3).
The learning rate α (speed at which parameters are updated in Eqs. 6-8) is considered as a fixed global parameter in most schemes, which is not always useful in scenes with different object-motion speed. We propose a decreasing quasi-global space-time variable α to control not only the speed at which objects are absorbed by the background, but also to filter out illumination changes of the background. Initially, our α takes in a big value and gradually decreases to a minimum threshold αmin. Once the system is statistically stable (background has been completely modeled) a smaller value of α can now be used only in statistical stable regions of the scene (it is not a global parameter anymore). After some experiments with α, the definition with the best results is
The space dependency of α(t) is somewhat hidden, it is not related to specific coordinates. What we mean is that, α(t) changes according to the statistics of each region in particular (which in turns depends on the moving objects in the scene). For example, a scene without moving objects will have only one time-varying learning rate defined by Eq. 10; a more complex scene will have as many learning rates as objects in the scene with different statistical behavior. To incorporate the advantages of a small α, we verify if the current pixel iteration t and the previous t-n iterations (for n=3) were identified as foreground (moving object), in this case we fix α = 0.005 (therefore α depends on the particular statistics on each region).
The advantages of Eq.10 are:
- •
The initial frames have big learning rate value (for t=0, α=½), useful in sequences with many objects in motions, which need to be quickly absorbed by the background.
- •
.It can deal with drastic changes in illumination (recall that small learning rate means more weight to past history as shown in Eqs. 6-8).
- •
The problem of fast object assimilation by the background is eliminated once the system stabilizes.
The results of the new parameter definition for the variance and learning rate are shown in Figs.5-7 with α = 0.005, α-dual (our definition in Eq. 10), and α-dual with variance threshold following Algorithm-1 respectively for three different video shots. The three columns in each figure represent the original video sequence, the difference between two frames, and detected motion by the MoG. It can be seen that our proposal removes additional noise coming from illumination changes (Fig.7).
Background model with dual α, and variance with threshold (Algorithm 1).
They should have descriptive captions. They should be mentioned in the main text.
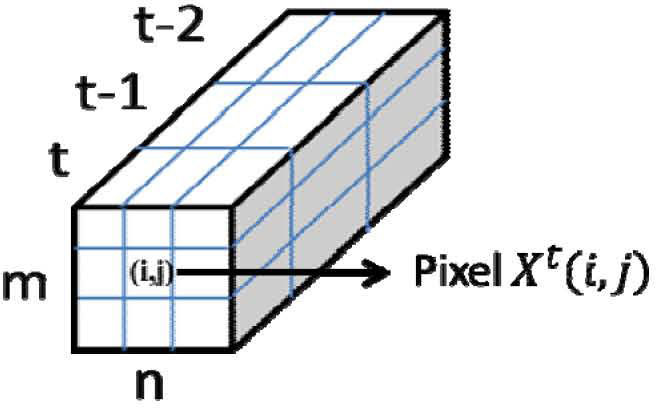
3.2Píxel Based vs Region Based Background ModelingIn previous schemes, each pixel in the scene is modeled with a MoG. In order to filter out high frequency motion present in the background, we propose a region-based background modeling represented by a space-time cube with dimension mnt, where mn represent the spatial-dimension and t the time-dimension (Fig.8). In the model, each region mnt is represented by the arithmetic mean with m= n= t= 5.
On scenes with dynamic background such as the Waterfountain and WaterSurface our region-based model shows excellent results as shown in Fig.9. The second row represents the pixel-based model and the third row our region-based model using the arithmetic mean. Depending on the frequency of each particular scene background, mnt dimension can be adjusted accordingly.
3.3Background-Foreground ClassificationA s mentioned in section 2.2, the Mahalanobis distance (Eq. 4) is the main metrics for deciding which mixture of Gaussian better represents the current pixel [16, 18, 21]. This distance makes use of a global threshold for both illumination and color components. In our proposal we differentiate the confidence interval for each color component YUV; color components (UV) are set to higher confidence interval than the illumination component (Y). In case of drastic changes in illumination, our decision is based only on the color components; if they do not change, we conclude the region classification has not changed at all (filtering out illumination changes). In our case, we use the following distance metric to find the concordance of the region with a specific distribution
where the index k represents the distribution of the mixture to be used in the evaluation, and j represents the color components YUV. The confidence interval for the experiments are YUV= {99.9%, 99.5%, 99.5%} equivalent to Th = {10.83, 7.88, 7.88}. The results between Dk,j*2 (Eq.11) and Dk,j2 (Eq. 4) are shown in Fig.10. Our proposed distance for each color component (last row in Fig.10) is more robust to illumination changes than the one considering the same threshold values for all components.
3.4Final Scheme ImplementationWe implemented the entire set of proposals described in sections 3.1-3.3 into the Cascade algorithm [21], and evaluate its performance against the original or unmodified algorithm using two different video sequences WaterSurface, and PETS2001_3_1 as shown in Fig.11. As can be seen, our proposed method adapts very rapidly to drastic changes in illumination and dynamic backgrounds without missing real objects in motion (greater than the filter size described in section 3.2). It is important to point out that our proposal completely eliminates high frequency background noise due to the presence of water-wave motion.
Object detection using the cascade algorithm [21] and our final proposal.
In general terms, our results are excellent and in agreement with our theoretical assumptions and developments for the following reasons: a) the inclusion of independent threshold for each color component (YUV) eliminates drastic illumination changes. It was confirmed that cloud and sun motions affect primarily the Y component and not UV components; b) the introduction of a minimum variance for each color component (Algorithm 1) reduces the number of false positives in the presence of noise (MoG are not too narrow anymore as previous works); c) the application of a space-time filter eliminates up to a certain extent high-frequency noise immerse in complex environments or backgrounds such as water waves, rain, tree-branches shaken by wind, etc. Finally, the most important characteristic in our model is that all these variables are tunable for a specific background modeling application.
4ConclusionsWe have shown that background subtraction schemes base on mixture of Gaussians exhibit some deficiencies when applied to complex environments, that is scenes with dynamic background or drastic illumination changes in the background (as for example water waves, water fountains, tree branches motion, rain, etc.). In this work we proposed some simple but effective techniques that notably improve current results reported in the literature. In particular our proposal includes: a) new time-space adaptive learning rate parameter; b) new variance definition with minimum threshold; c) different confidence intervals and distance metrics for each color representation YUV; d) pixel-based modeling is replaced by time-space dependent region-based model representation (cube). Our scheme shows excellent results compared to Teixeira, et al., 2997 [21], which is considered one of the best schemes in the literature.
















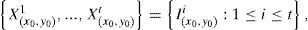

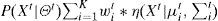

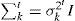
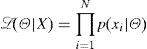
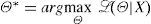
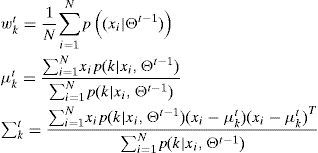
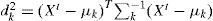
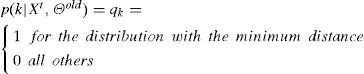
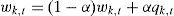
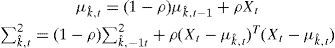
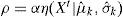

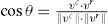







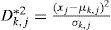

![Object detection using the cascade algorithm [21] and our final proposal. Object detection using the cascade algorithm [21] and our final proposal.](https://static.elsevier.es/multimedia/16656423/0000001200000003/v2_201505081651/S1665642314716323/v2_201505081651/en/main.assets/thumbnail/gr11.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)