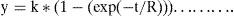Discriminación temporal condicionada: una evaluación de efectos de secuencia

Resumen

En una tarea de discriminación temporal condicionada con humanos se evaluó el aprendizaje promovido por diferentes secuencias de pares tiempo-ubicación. En concreto, 6 grupos se expusieron a diferentes secuencias de pares, las cuales fueron seleccionadas para incluir diferentes niveles de información. De la más básica a la más inclusiva, el orden de las secuencias fue el siguiente: Aleatoria, Permutaciones, Desordenada, Rampa, Decreciente y Creciente. Los resultados indicaron cierto nivel de discriminación. Además, se observó que a mayor cantidad de fuentes de información la cantidad de aciertos fue mayor y las trayectorias de aciertos entre bloques fueron más pronunciadas o su asíntota fue más alta. Las diferencias más consistentes se observaron al comparar en conjunto las primeras tres secuencias respecto a las últimas tres. Los resultados son discutidos a través de dos aproximaciones empleadas en el área de aprendizaje.

Abstract

Through a conditional temporal discrimination task with humans was assessed the learning promoted by different pair sequences. In detail, six groups were exposed to different paired sequences, which were selected to include different levels of information. From the most basic to the most inclusive, the order of the sequences was as follows: Random, Permutations, Disordered, Ramp, Decreasing and Incremental. The results showed that the relationship between information sources amount and hits was direct, and the trajectories between blocks was traced in such groups, or, alternatively, their asymptote was higher. However, the most consistent and significant differences were observed when comparing the first three sequences together over the last three. The results are discussed through two approaches used in the learning area.

Introducción

Un método que frecuentemente se aplica en el estudio de la estimación temporal es el de bisección. Este método usa el tiempo de presentación de un estímulo como señal condicional de la respuesta correcta. Por ejemplo, una duración corta (2 s) que se presenta sobre la tecla central blanca de una caja de prueba para palomas indica que una respuesta a la tecla lateral verde será reforzada; una duración larga (16 s) presentada en la tecla blanca indica que una respuesta en la tecla lateral roja será reforzada. Este procedimiento genera rápidamente una discriminación de duraciones. Dado que la respuesta correcta depende de la duración presentada (corta o larga), a este procedimiento se le denomina discriminación temporal condicionada (Arantes y Machado, 2011; Ludvig, Balci y Longpre, 2008; Platt y Davis, 1983; Stubbs, 1968).

El procedimiento de discriminación temporal condicional es muy útil puesto que permite que, una vez establecida la discriminación, en una segunda fase se presenten otras duraciones no reforzadas, entre los valores corto y largo, obteniendo así una especie de gradiente de generalización. La importancia de ese gradiente radica en que se puede determinar el punto de indiferencia que indica la discriminación entre la duración corta y la duración larga.

En una extensión del procedimiento de discriminación temporal condicionada, Church y Lacourse (1998, 2001) emplearon un procedimiento de aprendizaje temporal serial. Los autores consideran que, en general, los animales ajustan su conducta con base en la experiencia previa. En este contexto, consideran que todos los programas temporales se pueden concebir como tareas de rastreo temporal. En ellos, una duración presentada en un momento particular es una señal de la duración siguiente. Para evaluar las condiciones en que una duración adquiere las propiedades de señal, los autores utilizaron una tarea de discriminación temporal en la que se manipuló la capacidad predictiva de una duración. Con ese fin se utilizó una colección de 12 intervalos (desde 2.57 hasta 209.09 s). Esta variedad de duraciones permitió evaluar diferentes secuencias (i.e., Aleatoria, Permutaciones, Desordenada, Rampa, Decreciente y Creciente) que diferían en términos de la capacidad predictiva de una duración de la siguiente o siguientes duraciones. Cabe resaltar que para ese estudio no se establecieron asociaciones entre duraciones y diferentes alternativas ambientales de respuesta; en su lugar se requirió a los sujetos establecer asociaciones entre las duraciones adyacentes y se utilizó la pausa posreforzamiento como un indicador de la expectativa del organismo sobre el siguiente intervalo.

En general, los resultados de ese trabajo mostraron que: en secuencias con estructuras simples (Creciente, Decreciente y Rampa), la pausa posreforzamiento estuvo controlada por los intervalos posteriores, más que por los promedios globales, o los promedios de los intervalos recientes. Ese resultado no fue observado para las secuencias restantes (Desordenada, Permutación y Aleatoria) con estructuras complejas (Church y Lacourse, 1998). Lo anterior implica que únicamente las estructuras simples promovieron cierto grado de discriminación entre duraciones y eso facilitó que elementos posteriores de la secuencia pudieran ser anticipados.

El presente trabajo combina los dos procedimientos arriba revisados de tal forma que la respuesta correcta es condicional a la duración, como en el caso de la discriminación temporal condicionada. Sin embargo, en esta tarea, con un mayor número de duraciones, a partir de un procedimiento de discriminación temporal condicionada tradicional, y usando las secuencias empleadas por Church y Lacourse (1998), se investiga si las duraciones adquieren capacidad como estímulos discriminativos de eventos no temporales asociados a la entrega de reforzamiento. Dado que las mismas duraciones se utilizan para todos los grupos, la dificultad para responder la tarea utilizando únicamente el tiempo como clave temporal fue equivalente.

Un segundo propósito del presente estudio tiene que ver con la naturaleza del aprendizaje generado por las diferentes condiciones programadas. En particular, se relaciona con la cuestión de la gradualidad del aprendizaje. En concreto, la secuenciación de los valores permite evaluar si la ponderación de las duraciones recientes es pequeña, en cuyo caso se espera aprendizaje gradual; en cambio, si la ponderación de los eventos recientes es grande se espera un ajuste rápido (Church y Lacourse, 1998; Rescorla y Wagner, 1972).

A fin de evaluar la curva de aprendizaje, utilizamos el razonamiento de Mazur y Hastie (1978) aplicado a diferentes tareas. Entre otras, los autores analizan el aprendizaje en tareas de pares asociados (Brown, 1968; Gagné, 1950; McGuire, 1961; Melton, 1970; Millar, 1975; Newman, 1966; Plotkin, 1943; Rogers, Hertzog y Fisk, 2000; Wickens, 1982). Las tareas de pares asociados comparten algunas propiedades con las tareas de discriminación condicionada ya que también establecen asociaciones entre pares de eventos (Sidman y Tailby, 1982; Torres y López-Rodríguez, 2004).

En lo particular, se equiparan con el estudio de secuencias de pares asociados. Ese tema generó una cantidad importante de trabajos principalmente en los años 60 (Battig, Brown y Nelson, 1963; Brown y Battig, 1962; Martin y Saltz, 1963; McGuire, 1961; Newman y Saltz, 1962; Stein, 1969) pero en la actualidad no se tienen antecedentes directos. Sin embargo, recientemente se ha incrementado la cantidad de trabajos en el área de aprendizaje de secuencias; un tema con el que se comparte interés, al menos parcialmente (Fountain, 2008; Muller y Fountain, 2010, 2016; Rowan, Fountain, Kundey y Miner, 2001).

Retomando el trabajo citado de Mazur y Hastie (1978), las curvas de aprendizaje en el estudio de pares asociados no solo representan la descripción empírica del curso del aprendizaje, sino que están fuertemente vinculadas con los procesos que subyacen a la adquisición. Por esa razón, en este trabajo seguimos la estrategia propuesta por dichos autores.

Resumiendo, los objetivos de este trabajo fueron los siguientes: 1) extender el estudio de aprendizaje serial temporal hacia participantes humanos, ya que en lo general los procedimientos de estimación temporal utilizados con animales suelen ser adaptados para evaluar comportamiento humano (Vázquez-Lira y Orduña, 2011); 2) realizar una descripción cuantitativa del aprendizaje en la tarea, y 3) evaluar los parámetros de ajuste considerando la naturaleza del aprendizaje promovido por cada tipo de secuencia.

Dado lo anterior se identifica que el presente trabajo tiene implicaciones a dos niveles: 1) metodológico, al proponer una tarea utilizada con animales para estudiar aprendizaje serial con humanos (una adaptación), y 2) teórico, al intentar describir el aprendizaje observado en la tarea para realizar inferencias sobre su desarrollo.

Método

Participantes

Sesenta adolescentes de 12 y 13 años (edad = 12.9, DE = 0.45), de los cuales 26 eran mujeres y 34 eran hombres. Los participantes cursaban el 1.^er año de secundaria al momento de la aplicación de la tarea. Todos participaron de forma voluntaria (se solicitó el respectivo consentimiento informado firmado por los participantes y sus padres) y provinieron de una escuela pública del Distrito Federal. Se garantizó que los participantes no tuvieran experiencia previa en estimación temporal. El criterio de inclusión fue que finalizaran el entrenamiento (descrito más adelante) en menos de 3 min. Posteriormente, los participantes fueron asignados, de forma aleatoria, a uno de los 6 grupos, n = 10.

Materiales y aparatos

Los participantes fueron evaluados individualmente en un cuarto aislado. Se utilizaron 5 computadoras Toshiba^® modelo satellite de 14” con procesador Core i5 para presentar la tarea, la cual se programó utilizando la plataforma Psychopy (Peirce, 2007) versión 1.80.03 programada en Python. Se usaron 5 audífonos Sony^® modelo MDR-EX15LP para aislar a los participantes del ruido de ambiente. Además, se utilizaron 5 ratones Verbatim^® 98106 para registrar las respuestas.

Procedimiento

Todos los participantes recibieron dos diferentes condiciones experimentales: una de preexposición y otra de exposición a las secuencias. La preexposición fue la misma para todos los participantes, y la tarea consistió en seleccionar la ubicación de un portero en 5 zonas diferentes de una portería (arriba-izquierda, arriba-derecha, centro, abajo-izquierda, abajo-derecha) utilizando como clave el tiempo en que se presentó un estímulo compuesto por una imagen (un tirador) y un sonido (de un «beep») con el propósito de detener un tiro penal. El estímulo compuesto varió su duración dentro del rango de 0.28 hasta 0.8 s (valores extremos) y tres valores intermedios distribuidos en una escala aproximadamente logarítmica (0.37, 0.48 y 0.63 s). La asociación entre la duración del estímulo compuesto y la ubicación correcta recibió retroalimentación en cada ensayo: en caso de acertar, el portero detenía el balón y en caso contrario se registraba un gol (fig. 1). En esta fase, cada duración se presentó hasta que el participante logró realizar tres respuestas correctas consecutivas. Es decir, en caso de error la misma duración se repitió tres ocasiones más. Por lo tanto, el mínimo de respuestas fue de 15. Al término de la preexposición se presentó una pantalla informando que iniciaba una fase diferente, con la siguiente indicación: «Ahora podemos comenzar el juego».

Figura 1.

Muestra el esquema de presentación de estímulos durante la tarea. A la izquierda se presenta el estímulo utilizado como clave temporal (un «tirador») así como los valores de duración utilizados. A la derecha se muestran las zonas permitidas para el registro de la tarea. Los números fueron agregados exclusivamente para este diagrama, con el objetivo de ilustrar la relación existente entre duraciones y ubicaciones espaciales.

En la última fase los participantes fueron asignados aleatoriamente a una de las 6 diferentes secuencias. Las secuencias fueron obtenidas a partir de una lista de 10 elementos, compuesta por dos elementos de cada duración. Para la secuencia Creciente (Inc) las duraciones se presentaron de menor a mayor en dos ocasiones por bloque (0.28, 0.37, 0.48, 0.63, 0.8, y se repitió). En la secuencia Decreciente (Dec) las duraciones se presentaron de mayor a menor en dos ocasiones por bloque (0.8, 0.63, 0.48, 0.37, 0.28 y se repitió). En la secuencia Rampa (Ram) se presentó una secuencia ascendente seguida por una descendente (0.28, 0.37, 0.48, 0.63, 0.8, 0.8, 0.63, 0.48, 0.37, 0.28). En la secuencia Desordenada ([Des] constante) una misma secuencia sin ningún orden particular fue repetida durante los 12 bloques (0.63, 0.37, 0.28, 0.37, 0.48, 0.28, 0.63, 0.8, 0.48, 0.8). Para la secuencia Permutaciones ([Per] variable) diferentes combinaciones de la lista de 10 elementos se presentaron en los bloques (muestreo sin reemplazo). Por último, para la secuencia Aleatoria (Ale) las duraciones fueron seleccionadas de la lista original de 10 elementos, permitiendo su repetición en la selección (muestreo con reemplazo).

Esta última fase fue semejante a la preexposición, salvo por las siguientes variaciones: 1) se dividió a los ensayos en 12 bloques de 10 ensayos cada uno; dentro de cada bloque, se controló la cantidad de exposiciones por duración para que en la mayoría de los grupos, excepto para el grupo aleatorio, cada duración se presentara en dos ocasiones, garantizando que el número de exposiciones fuese igual para todas las duraciones (24 ensayos); 2) además de la retroalimentación brindada por la ubicación final del tiro penal, por cada acierto el participante recibió un punto en un contador acompañado por un sonido (aplausos); de lo contrario, el participante no recibió puntos y se presentó un sonido diferente (abucheos); 3) al término de cada bloque se presentó una pantalla azul por 3 s y se inició otro inmediatamente.

Registro conductual

Se registró la latencia de respuesta, el tiempo desde que termina la presentación del tirador hasta que el participante selecciona una de las ubicaciones. De acuerdo con Garaizar y Vadillo (2014), versiones de Psychopy superiores a 1.80 registran de forma precisa y confiable intervalos superiores a 16.5 ms. Adicionalmente, se registró la selección final del participante, considerada como la ubicación en la cual el participante colocó al guardameta. Si la ubicación seleccionada coincidió con la ubicación del disparo entonces se registró un acierto; de lo contrario se registró un error.

Reducción y análisis de datos

Se analizó lo siguiente: 1) la cantidad de respuestas al centro para cada duración; 2) la proporción de aciertos por bloque; 3) los parámetros que brindaron el mejor ajuste a los aciertos por bloque de cada grupo, con base en una función exponencial; 4) la cantidad de bloques requeridos para alcanzar la asíntota, y 5) la proporción de respuestas correctas totales.

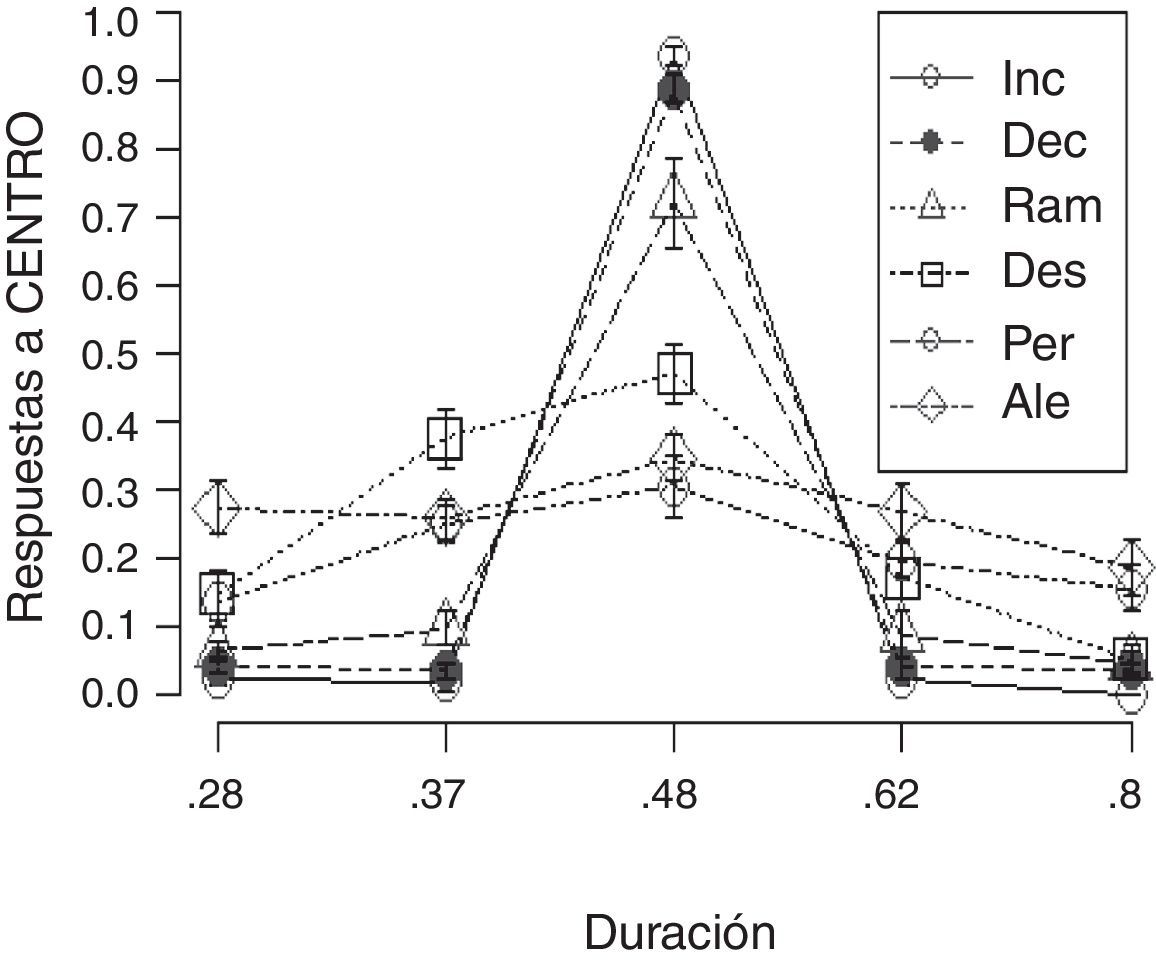
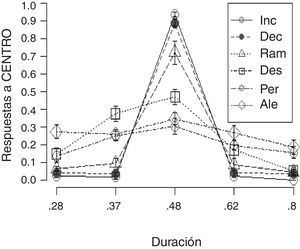
Resultados

Para evaluar la discriminación entre duraciones se evaluó la cantidad de respuestas al centro (asociada con la duración intermedia) para cada una de las duraciones. De ese modo, se obtuvo una distribución similar a un gradiente de discriminación temporal para cada grupo, permitiendo comparar la precisión de la discriminación y la simetría de la misma (fig. 2). Con el objetivo de comparar entre secuencias, se obtuvo su índice de discriminación y se realizó un ANOVA entre secuencias. Debido a que el supuesto de homogeneidad de varianzas fue violado [F (5, 54) = 4.198, p < 0.01], los datos fueron reescalados en un rango de 0-1 y posteriormente trasformados (logit). Al comparar entre grupos se apreciaron diferencias estadísticamente significativas [F (5, 54) = 23.67, p < 0.001]. Al realizar comparaciones planeadas ortogonales se identificaron las siguientes diferencias significativas: 1) los tres grupos que presentaron secuencias con cambios graduales (Inc, Dec y Ram) mostraron ser diferentes en conjunto respecto a los otros tres grupos (Des, Per y Ale) [t(54) = 9.72, p < 0.001]; 2) el grupo Ram fue diferente respecto a los otros dos grupos en los que se repitió la misma secuencia dentro de un bloque en conjunto (Inc y Dec) [t(54) = 4.00, p < 0.001]; y 3) hubo diferencias entre el grupo Inc y Dec [t(54) = 2.58, p < 0.05]. Las otras dos comparaciones restantes, Ale vs. (Des y Per) y Des (constante) vs. Per (variable), no resultaron significativas.

Figura 2.

Se muestra la proporción de respuestas a la ubicación central (relacionada con la duración media) por grupo para cada una de las duraciones utilizadas. Las barras de error muestran el error estándar.

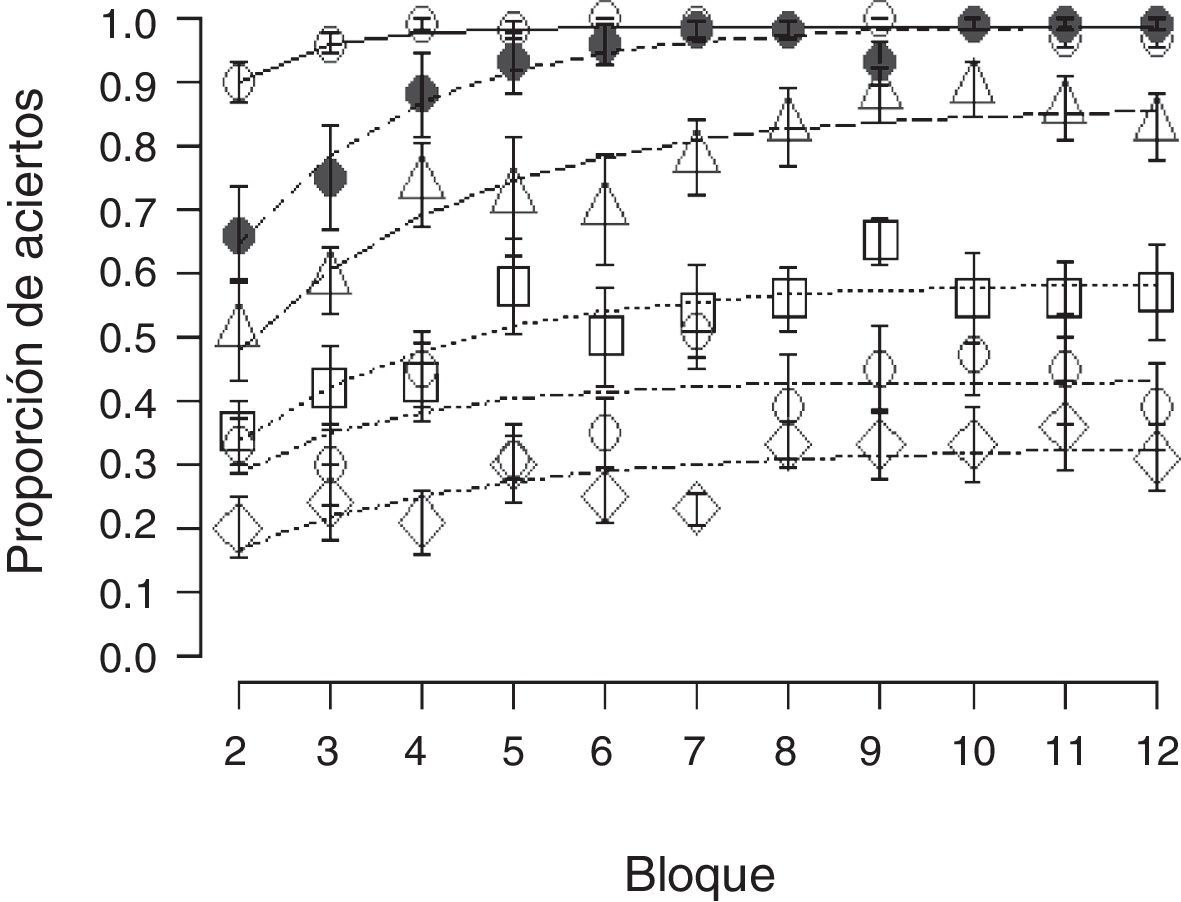
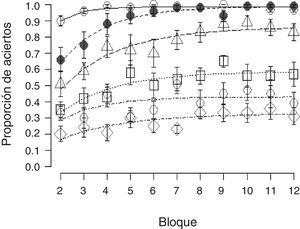
Por otra parte, en la figura 3 se muestra la proporción de aciertos por secuencia en los últimos 11 bloques. Para comparar estadísticamente los resultados se realizó un ANOVA mixto con «secuencia» como factor entre grupos y «bloque» como factor de medidas repetidas. El test de Mauchly indicó que el supuesto de esfericidad fue violado; por tal motivo, los grados de libertad se ajustaron utilizando la corrección de Greenhouse-Geisser (¿ = 0.66). En la comparación de secuencia se apreciaron diferencias significativas [F (5, 54) = 67.8, p < 0.001]. Por otra parte, al evaluar el efecto de medidas repetidas se encontraron diferencias significativas de bloque [F (6.682, 360.813) = 15.325, p < 0.001]. Sin embargo, dado que el término de interacción también resultó significativo, en este caso los efectos principales fueron condicionales entre sí [F (33.40, 360.813) = 1.566, p < 0.05]. Por tanto, se analizó el efecto de interacción con base en un análisis de tendencias polinomial; las tendencias que resultaron significativas fueron la lineal [F (5, 54) = 4.38, p < 0.01], la cuadrática [F (5, 54) = 6.67, p < 0.001] y la cúbica [F (5, 54) = 5.41, p < 0.001]. Por tal motivo, y por parsimonia con el área de aprendizaje, se ajustó la función exponencial de dos parámetros a los datos (Mazur y Hastie, 1978):

Figura 3.

Se presenta la proporción de aciertos promedio por grupo para los últimos 11 bloques. Los grupos se representan con las siguientes marcas: Aleatorio con rombos vacíos; Permutación con elipses vacíos; Desordenado con cuadros vacíos; Rampa con cuadros vacíos; Decreciente con círculos llenos, y Creciente con círculos vacíos. Las barras de error muestran el error estándar. Las líneas muestran el mejor ajuste de una función exponencial a los datos.

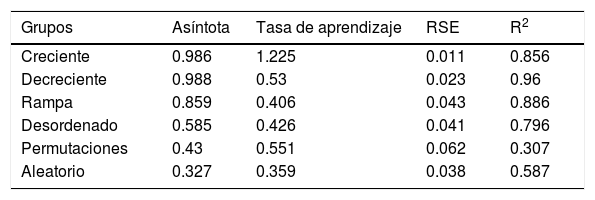
Donde y es la proporción de aciertos estimada por bloque t. El parámetro k representa el nivel asintótico por cada serie de datos. Por último, el parámetro R es un estimado de la tasa de cambio. Con base en un algoritmo no lineal, nls del programa R (Baty et al., 2015), se obtuvo la combinación de parámetros que redujo al mínimo el error residual. En la tabla 1 se muestran los parámetros que brindaron el mejor ajuste a los datos promedio de cada grupo.

Tabla 1.

Parámetros de ajuste de la función exponencial de 2 parámetros para los datos promedio de cada grupo (últimos 11 bloques)

Grupos	Asíntota	Tasa de aprendizaje	RSE	R^2
Creciente	0.986	1.225	0.011	0.856
Decreciente	0.988	0.53	0.023	0.96
Rampa	0.859	0.406	0.043	0.886
Desordenado	0.585	0.426	0.041	0.796
Permutaciones	0.43	0.551	0.062	0.307
Aleatorio	0.327	0.359	0.038	0.587

R²: proporción reducida de error; RSE: error estándar residual.

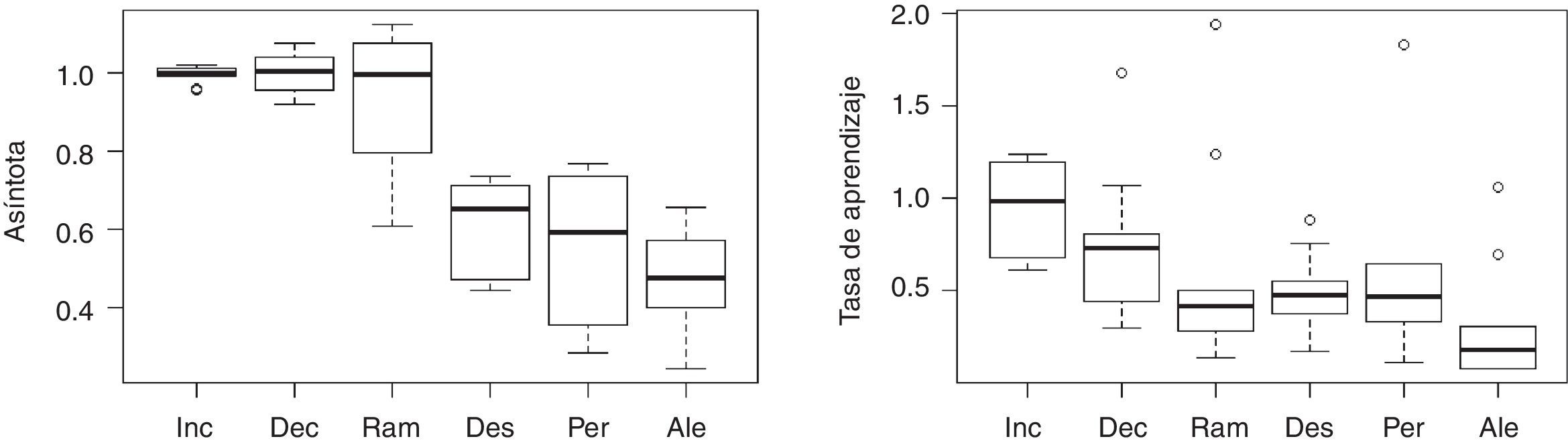
El ajuste de la función exponencial a los datos de cada participante permitió la comparación de parámetros entre grupos. Al contrastar el parámetro asíntota entre secuencias, no se superó el análisis de homogeneidad de varianzas [F (5, 54) = 3.9676, p < 0.01]. Sin embargo, en un análisis en la inspección visual de los diagramas de caja (ver el panel izquierdo de la figura 4), se corroboró que las únicas diferencias notables se aprecian al comparar Inc, Dec y Ram vs. Des, Per y Ale.

Figura 4.

En el panel izquierdo se muestra la distribución del parámetro relacionado con la asíntota de cada grupo. En el panel de la derecha se presenta la distribución del parámetro relacionado con la tasa de aprendizaje de cada grupo.

Al comparar el parámetro relacionado con la tasa de cambio entre grupos se realizó un ANOVA. En dicha comparación se identificaron diferencias significativas de secuencia [F (5, 54) = 2.757, p < 0.05] (ver diagramas de caja en el panel derecho de la figura 4). Se procedió a realizar un análisis ortogonal y se ratificó que únicamente las tres secuencias con cambios graduales mostraron ser diferentes en conjunto respecto a las otras tres secuencias en conjunto [t(54) = 2.494, p < 0.01].

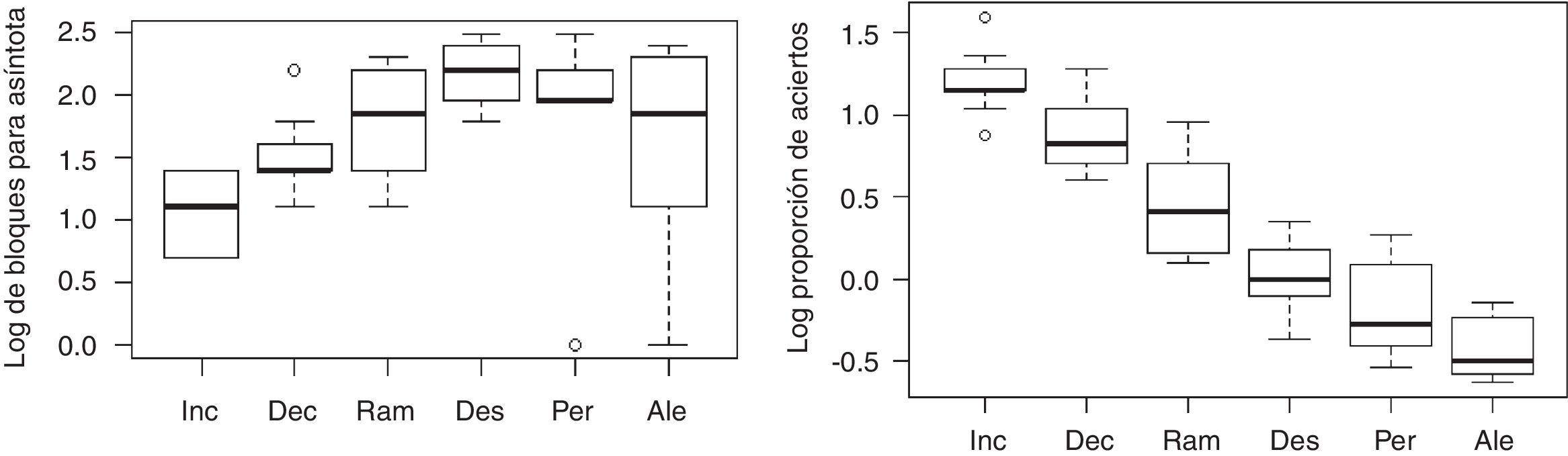
Otro indicador que permite comparar la velocidad de aprendizaje es la cantidad de bloques hasta conseguir el máximo de aciertos alcanzados por un participante. Al comparar entre secuencias se identificó que los datos no superaron la prueba de homogeneidad de varianzas [F (5, 54) = 4.69, p < 0.01], y los datos fueron transformados a logaritmos (panel izquierdo de la figura 5). Al realizar un ANOVA entre secuencias se identificaron diferencias significativas [F (5, 54) = 4.38, p < 0.01]. Dado lo anterior, se procedió a la comparación ortogonal, la cual arrojó los siguientes resultados: 1) las tres secuencias graduales (Inc, Dec y Ram) mostraron ser diferentes en conjunto respecto a las otras tres secuencias (Des, Per y Ale) [t(54) = 2.66, p < 0.01]; 2) la secuencia Ram fue diferente respecto a las otras dos secuencias en las que se repitió la misma secuencia dentro de un bloque en conjunto (Inc y Dec) [t(54) = 2.49, p < 0.01]; 3) las diferencias entre las secuencias Inc y Dec fueron marginales [t(54) = 1.77, p = 0.08]; 4) en este caso, la secuencia Ale no mostró ser significativamente diferente a las otras dos secuencias en las que se controló la cantidad de presentaciones de cada duración (Des y Per) [t(54) = 1.31, p = 0.19]; 5) las diferencias entre los grupos Des (constante) y Per (variable) fueron marginales [t(54) = 1.31, p = 0.059].

Figura 5.

En el panel de la izquierda se presenta la cantidad de bloques necesarios para alcanzar la asíntota por cada secuencia (abscisa). Los datos fueron transformados a logaritmos. En el panel de la derecha se presenta la comparación de la proporción de aciertos por secuencia (abscisa). Los datos fueron transformados a logit.

Por otra parte, en la comparación de la proporción de aciertos totales entre secuencias se identificó que los datos no superaron la prueba de homogeneidad de varianzas [F (5, 54) = 4.823, p < 0.01] y los datos fueron transformados a logit (panel derecho de la figura 5). Al realizar un ANOVA entre secuencias se identificaron diferencias significativas [F (5, 54) = 70.62, p < 0.001]. Al realizar comparaciones ortogonales planeadas se encontró que: 1) las secuencias Inc, Dec y Ram mostraron ser diferentes en conjunto respecto a las secuencias Des, Per y Ale [t(54) = 16.94, p < 0.001]; 2) la secuencia Ram fue diferente respecto a las dos secuencias en las que se repitió en dos ocasiones la misma secuencia dentro de un bloque en conjunto (Inc y Dec) [t(54) = 6.357, p < 0.001]; 3) también se apreciaron diferencias entre las secuencias Inc y Dec [t(54) = 2.937, p < 0.01]; 4) y por último se identificaron diferencias entre la secuencia Ale y las secuencias en las que la cantidad de presentaciones fue equivalente para todas la duraciones en conjunto (Des y Per) [t(54) = 3.627, p < 0.01]; 5) sin embargo, las diferencias entre la secuencia Des (constante) y Per (variable) fueron marginales [t(54) = 1.913, p = 0.063].

Discusión

El presente trabajo tuvo los siguientes objetivos: evaluar el aprendizaje promovido por claves temporales asociadas a diferentes ubicaciones en un procedimiento con humanos, realizar una descripción formal del aprendizaje en la tarea y contrastar el aprendizaje promovido por cada tipo de secuencia. Respecto al primero de los objetivos, con base en las medidas de discriminación y la proporción de aciertos, en todas las secuencias se apreció que los datos estuvieron por encima del nivel de azar. Por lo tanto, esos resultados corroboran que es posible generar discriminación condicionada (Torres y López-Rodríguez, 2004) usando claves temporales (Arantes y Machado, 2011; Ludvig et al., 2008; Platt y Davis, 1983; Stubbs, 1968) en una tarea con humanos (Alfaro y López-Rodríguez, 2016). En lo particular este trabajo mostró que se pueden discriminar valores inferiores a un segundo, con diferencias logarítmicas entre valores temporales utilizados.

En este trabajo, a diferencia de lo que se hace en el método de bisección, se utilizó la duración intermedia como base para obtener una función de discriminación temporal. Aunque esa decisión implica omitir información sobre el punto de transición, el análisis realizado aporta información sobre la precisión en la discriminación y la simetría de la misma. Con base en ese indicador se apreció que las tres secuencias con mayor cantidad de fuentes de información (Inc, Dec y Ram) fueron las que propiciaron mayor discriminación. De forma consistente a lo observado en estudios previos, los valores lejanos entre sí propiciaron menor cantidad de errores, es decir, se facilitó su discriminación (Alfaro y López-Rodríguez, 2016; Allan, 1979; Getty, 1975). En este trabajo también se ratificó que, con excepción de la secuencia Des, la cantidad de respuestas al centro exhibió un patrón de respuestas relativamente simétrico, probablemente atribuible al uso de valores distribuidos de forma logarítmica.

Por otra parte, al analizar el proceso de aprendizaje a través del ajuste de una función exponencial a los aciertos por bloque, se identificó cierta interacción entre parámetros. La comparación de parámetros de ajuste confirmó que las diferencias más notables fueron apreciadas al comparar las secuencias Inc, Dec y Ram vs. Des, Per y Ale. Lo anterior sugiere que cuando se logra identificar un patrón o estructura general a aprender, se ve favorecida su adquisición, ya sea con asíntotas más altas o una tasa de aprendizaje mayor, respecto a otro tipo de secuencias.

La tendencia de cambios decrecientes, observada en la proporción de aciertos entre bloques, puede describirse a través de diferentes funciones, a saber: exponencial, hiperbólica (Heathcote, Brown y Mewhort, 2000; Newell y Rosenbloom, 1981). Sin embargo, algunos trabajos enfatizan las implicaciones teóricas de preferir utilizar alguna de las funciones mencionadas (López-Rodríguez, Menez-Díaz y Gallardo-Pineda, 2014; Mazur y Hastie, 1978). Mazur y Hastie (1978) y relacionan el tipo de función empleada con diferentes supuestos sobre el proceso de aprendizaje. Concretamente, para la función exponencial se asume que los aciertos incrementan su probabilidad porque se lleva a cabo un proceso de reemplazo de respuestas; esta interpretación implica implícitamente una habilidad limitada para recordar información. Por otra parte, para la función hiperbólica se asume que los aciertos incrementan su probabilidad porque se lleva a cabo un proceso de acumulación de respuestas, implicando implícitamente una habilidad para recordar más información.

Elegir una función para interpretar los datos observados puede resultar un tanto arbitrario. Sin embargo, es posible que la respuesta y/o medida considerada, el tipo de procedimiento y en especial la retroalimentación brindada durante la tarea influyan para elegir cuál interpretación es más plausible. En este caso: la respuesta requerida fue la anticipación de un evento en función de una clave temporal, la medida utilizada fue la proporción de aciertos por bloque y el procedimiento involucró únicamente ensayos de prueba, brindando retroalimentación inmediata a la ejecución. Dado lo anterior, es posible que, si la respuesta del participante fuese correcta, incrementara en probabilidad. En cambio, cuando fuese incorrecta, se debilitaría y entonces aumentaría la posibilidad de que los errores se reemplazaran por respuestas correctas. Con base en lo anterior, es más plausible considerar que el proceso de actualización de probabilidades sea de reemplazo, tal como lo mencionan Church y Lacourse (1998, 2001), ya que en estas situaciones la respuesta puede ser guiada por una ventana restringida de eventos.

En concordancia con lo anterior, la cantidad de bloques para alcanzar la asíntota sugiere una interpretación con base en el modelo de Rescorla y Wagner (1972). En dicha interpretación se considera que a menor cantidad de bloques para alcanzar la asíntota (mayor tasa de cambio), más peso se brinda a eventos recientes. Considerando eso, se aprecia que para las secuencias regulares los bloques hasta alcanzar la asíntota fueron pocos (sobre todo en Inc y Dec). Lo anterior muestra que el peso de eventos recientes para guiar la respuesta fue más alto, quizá indicando que la mejor pista para guiar la siguiente respuesta es la retroalimentación y/o clave del ensayo previo. Sin embargo, dado que lo anterior no se cumplió en todo momento para la secuencia Ram, es posible que una cantidad ligeramente mayor de ensayos fuera necesaria para controlar la respuesta. Por otra parte, para las secuencias Des y Per se apreció una diferencia marginal, que implica que para Per se requieren menos bloques para alcanzar la asíntota. Lo anterior posiblemente indica que en el caso de la secuencia Per, la respuesta, además de estar guiada por la información de la clave temporal vigente, también es influida por las claves presentadas en el mismo bloque, ya que las claves presentadas previamente al interior de un bloque disminuyen su probabilidad de presentación, mientras que para Des se involucran más eventos ya que es más importante recordar el orden de las claves temporales presentadas en los bloques previos. Por último, la variabilidad apreciada en la secuencia Ale podría reflejar las diferencias individuales para guiar la respuesta. Es decir, es posible que tenga lugar una comparación entre la clave presentada y una historia que es variable y dependiente del participante.

La cantidad de aciertos totales indicó que a mayor cantidad de fuentes de información se obtuvieron más aciertos. En este estudio las diferencias entre los grupos Des y Per fueron solo marginales, lo cual es coincidente con los estudios que no reportan diferencias entre secuencias constantes y variables (Martin y Saltz, 1963).

Este resultado, en conjunto con las diferencias observadas en las comparaciones restantes, sugiere que no basta con la repetición de una secuencia para facilitar su aprendizaje, sino que la organización de la secuencia podría jugar un papel importante para facilitar su aprendizaje. Por tanto, este hallazgo enfatiza que es probable que alguna fuente de información adicional a la repetición de una secuencia pueda ser responsable de las diferencias entre secuencias constantes y variables reportadas en algunos estudios previos.

Otro resultado sobresaliente al comparar entre secuencias fueron las diferencias observadas entre las secuencias Inc y Dec, ya que la única diferencia entre esas secuencias fue el orden de los cambios entre duraciones. Para dar cuenta de dicha diferencia es posible considerar dos hipótesis tentativas: 1) familiaridad, es decir, por cuestiones de historia de aprendizaje previo (como aprender a contar) resultó más sencillo identificar secuencias que van de menor a mayor; 2) facilidad para percibir diferencias temporales, de acuerdo con la evidencia obtenida en estudios de estimación temporal; además, pese a utilizar una escala logarítmica, discriminar entre valores más grandes resulta ligeramente más difícil que discriminar entre valores pequeños (Wearden, 1996; Wearden y Ferrara, 1995). De acuerdo con el segundo argumento, dado que el grupo Inc inició con una discriminación con duraciones cortas, eso pudo facilitar la discriminación y la identificación de la secuencia. En el caso de la secuencia Dec, ocurrió lo opuesto, retrasando la discriminación entre claves temporales, así como la identificación de la estructura de la secuencia.

En general, las curvas de aprendizaje se pueden interpretar desde dos posturas diferentes, a saber: la concepción de multiproceso (Muller y Fountain, 2010, 2016) y el modelo de Rescorla y Wagner (1972). En la concepción multiproceso se asume que cuando se presenta más de una configuración de claves para predecir un evento posterior, las claves que los componen no compiten entre sí, sino que cada una aporta cierto grado de información respecto al total del compuesto. Con base en lo anterior, en las secuencias Inc, Dec y Ram se espera que al retirar las claves de orden, la proporción de aciertos disminuya moderadamente. Lo anterior denotaría que las claves adicionales al orden, entre ellas las asociaciones entre las duraciones y las alternativas de respuestas, habrían sido fortalecidas simultáneamente con las claves retiradas.

Por otra parte, el modelo propuesto por Rescorla y Wagner (1972) supone que cuando dos o más claves están relacionadas de forma conjunta con la predicción de un evento posterior, cada una de las asociaciones posibles compiten entre ellas por la fuerza asociativa del evento posterior. De tal manera que alguna de ellas ganaría la mayor parte de la fuerza asociativa y las otras quedarían relativamente débiles. Con base en lo anterior, y en conjunto con los datos de este trabajo, es plausible asumir que retirar las claves de orden en los grupos Inc, Dec y Ram evidenciaría un efecto de ensombrecimiento (Mackintosh, 1976) de las duraciones.

Por último, es importante resaltar que la renovación del interés por estudiar el aprendizaje de secuencias ha generado avances importantes en la comprensión de los factores involucrados en diferentes tareas. Sin embargo, llama la atención la ausencia de trabajos recientes sobre secuencias de pares asociados, ya que los resultados del presente trabajo y la discusión ofrecida muestran que, a partir de una variante del procedimiento utilizado aquí, es factible contrastar dos interpretaciones importantes para el área de aprendizaje de secuencias.

Agradecimientos

Se agradece a la DGAPA la beca que recibió el primer autor durante los dos años de estancia posdoctoral. Así mismo se agradece a PAPIIT DGAPA el apoyo recibido en el proyecto PAPIIT IN 306315.