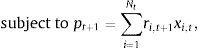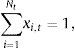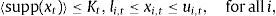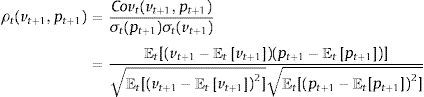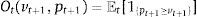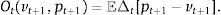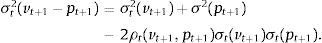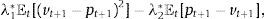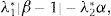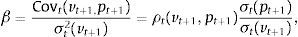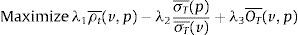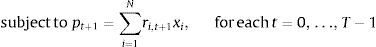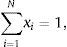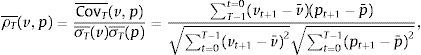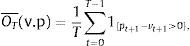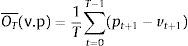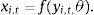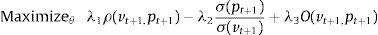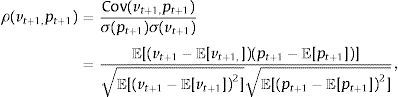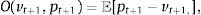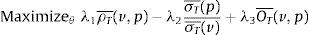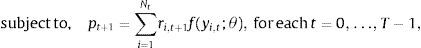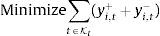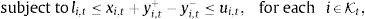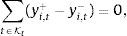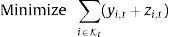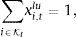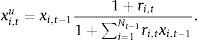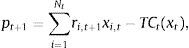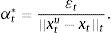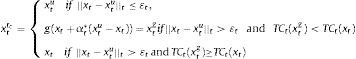Index tracking and enhanced indexation using a parametric approach

Abstract

Based on the work of Brandt et al. (2009), we formulate an index tracking and enhanced indexation model using a parametric approach. The portfolio weights are modeled as functions of assets characteristics and similarity measures of the assets with the index to track. This approach permits handling non-linear and nonconvex objectives functions that are difficult to incorporate in existing index tracking and enhanced indexation models. Additionally, this approach gives the investor more information about the portfolio holdings since the optimization is performed over portfolio strategies. Finally, an empirical implementation and an analysis of selected characteristics are presented for the S&P500 index.

Resumen

Basándonos en el trabajo de Brandt et al. (2009), formulamos un modelo de seguimiento de índices e indexación mejorada utilizando un enfoque paramétrico. Los pesos de cartera se modelan como funciones de características de activos y medidas de similitud de los activos con el índice objeto de seguimiento. Este enfoque permite tratar funciones de objetivos no lineales y no convexos, difíciles de incorporar en modelos de indexación mejorada y seguimiento de índices existentes. Además, proporciona al inversor más información sobre los valores en cartera porque la optimización se lleva a cabo en torno a estrategias de portafolio. Por último, se presenta una implementación empírica y un análisis de características seleccionadas del índice S&P500.

1

Introduction

Index tracking is a type of passive management strategy which consists of designing a portfolio (tracking portfolio or index fund) to replicate the behavior of a broad market index. The popularity of index funds, as mentioned in Cornuejols and Tütüncü (2007), relies on both theoretical (market efficiency) and empirical (performance and costs) reasons. If the market is efficient, it is not possible to obtain superior risk-adjusted returns by active management portfolio strategies. Because the market portfolio captures the efficiency of the market through diversification, it is a theoretically reasonable strategy to invest in an index fund. Moreover, many empirical studies show that, on average, active portfolio managers do not outperform the major indices. Also, active management generally incurs costly research activities and compensation to the fund managers. These costs can be avoided by an index tracking strategy.

Index tracking also has two sub-strategies: full replication and partial replication. In a full replication strategy, all the names in the index are bought (and held) in the exact proportions as they appear in the index. On the other hand, the partial replication strategy holds fewer assets than the total number of assets in the index; however, the assets to include and their weights need to be determined. For example, Cornuejols and Tütüncü (2007) and Canakgoz and Beasley (2008), for example, mention that the main disadvantages of the full replication strategy are the high transaction costs to rebalance all the positions in the index, the difficulty to hold very small proportions of some stocks, and the illiquidity of certain stocks (especially in small-cap indices). For Rudd (1980), the main advantage of partial replication is the decrease in administrative overhead and administration costs (custodial and accounting).

Enhanced indexation or enhanced index tracking, in the words of Canakgoz and Beasley (2008) “aims to reproduce the performance of a stock market index, but to generate excess return (return over and above the return achieved by the index)”. Usually, the objective in the enhanced indexation problem is to maximize alpha while the beta of the portfolio remains close to one, or to maximize excess return (over the index) by keeping the tracking error bounded to some quantity. The main distinction with the tracking problem is that enhanced indexation can be seen as an active strategy to beat a benchmark under the same risk.

Different from the index tracking approach, enhanced indexation (using fewer assets than the index) lacks the theoretical foundation of the market efficiency, since holding fewer assets cannot ensure full diversification of the portfolio. Additionally, many of the approaches use only information contained in the return (price) series. Without additional information or differences in expected returns forecasts, it is hard to identify the “mispriced” securities to include in the portfolio. With lower diversification than the index, it is logical to expect the generation of positive excess returns over the index as a trade-off with the portfolio's beta, the overall risk, or the correlation coefficient with the index. Therefore, it is crucial to analyze carefully the in-sample and out-of-sample performance of the enhanced tracking portfolios to analyze the corresponding risk-return trade-off and the consistency of the tracking strategy.

In this paper, we propose a parametric approach for index tracking and enhanced indexation based on the work of Brandt, Santa-Clara, and Valkanov (2009). We formulate a multi-objective non-linear optimization problem with a small number of decision variables. Our objective function decomposes (approximately) the variance of the tracking error or the portfolio beta into the correlation coefficient of the portfolio and the index and the ratio of their standard deviations. Notice that when the correlation coefficient is close to one and the standard deviations are close to each other, the variance of the tracking error goes to zero and the beta of the portfolio goes to one. Consequently, this specification of the tracking component is more flexible than the ones existing in the literature. For the enhanced component, although other objectives can be proposed, we usually maximize the average excess returns over the index.

As in the portfolio optimization approach of Brandt et al. (2009), we use information inside and outside the return series to build our portfolios. However, due to the time horizon (daily or weekly) of typical index tracking problems, we exclude some of the factors used in Brandt et al. (2009) which explain the cross-section of assets returns. For example, we omit the book-to-market ratio because daily book values are not observable. We consider it of interest to include information on the similarity of the stock's returns with the index returns, under the premise that it is reasonable that stocks behaving similarly to the index have potential to form a part of the tracking portfolio. Also, we include some measures of “momentum” of the stocks to beat the index assuming that the “momentum” will continue in the near future.

In the parametric approach, the portfolio weights are functions of selected characteristics of the stocks. We want to determine how to assign importance to these characteristics depending on the particular trade-off defined in the objective function. By assigning importance levels, it is straightforward to find portfolio strategies and not just portfolio weights. We can then analyze how these strategies change according to the importance given to the tracking or enhanced components of the objective. These features give the investor more information about the portfolio holdings than typical approaches in the literature. Also, the parametric approach is flexible enough to handle cardinality constraints, transactions cost (in various ways), and lower and upper bounds on the portfolio weights.

We implement the parametric approach to build a tracking or enhanced tracking portfolio¹ for the S&P500 index, using as characteristics market capitalization, alpha and beta of the individual stocks. The empirical results show that holding stocks with high market capitalization results in tracking portfolios with high correlation coefficient with the index. Stocks with beta close to one are useful to keep the ratio of standard deviations close to one, while including stocks with high alpha is used to increase the excess returns over the index. The in-sample performance was similar to other models in the literature, and the out-of-sample performance was very robust, especially for the tracking component of the objective. Additionally, the level of turnover was acceptable, and, from examining the maximum and minimum portfolio weights, the tracking portfolios were well-diversified.

The organization of the paper is as follows, Section 2 presents a brief literature review. In Section 3, we describe the typical enhanced tracking model. In Section 4, we develop in detail the parametric approach. In Section 5, we add some refinements to the “plain” parametric model including transaction costs and lower/upper bounds on the portfolio weights. Section 6 describes some characteristics that can be used in the parametric approach. In Section 7, we present the empirical application for the S&P500 index. We conclude in Section 8.

2

Literature review

Since the late 1970s the problem of index tracking has drawn attention from the financial and operations research literature. Now we have many different approaches, in particular to design index tracking funds using partial replication. Next, we mention some of the most common approaches for index tracking. The following is by no means a complete literature survey of index tracking. For further information, the reader can look at the references mentioned in each of the cited documents.

Commonly, the index tracking problem with partial replication is formulated as a mixed-integer programming model, which is challenging to solve to optimality using “traditional” integer programming and optimization techniques. This structure leaves room for the use of a variety of heuristics, metaheuristics and other solution approaches. It is typical in this approach to minimize some function that measures the distance between the index returns (or normalized prices) and those of the tracking portfolio in a specific calibration period. Another common objective in these formulations is to try to construct a tracking portfolio with beta (relative to the benchmark) close to one. Those models contain the assumption that the returns (or prices) will have the same statistical behavior in the next period(s). Complete formulations in this framework include transactions costs, rebalancing policies and other features and constraints. In this line, we refer to Beasley, Meade, and Chang (2003), Gaivoronski, Krylov, and van der Wijst (2005), Canakgoz and Beasley (2008), and the references therein.

Markowitz-type formulations are commonly used in index tracking where the tracking error variance (variance of the portfolio that is long in the tracking portfolio and short in the index) is minimized under other appropriate constraints. For this formulation, it is necessary to estimate the covariance matrix of all assets in the index, for which available data may not be sufficient. Instead, the returns-based style analysis of Sharpe (1988, 1992), based on the minimization of the tracking error relative to a weighted combination of indices, can be used. For example, related to this kind of formulation, Derigs and Nickel (2003) estimated the covariance matrix and the expected returns using a linear factor model based on macro-economic variables. They solve the tracking problem using a simulated annealing based on metaheuristic. While such factor models are tractable, the general problem with tracking error variance minimization is the difficulty in estimating a covariance matrix for the returns of all assets in the index.

Another type of model considers the inclusion of other variables (most commonly economic ones) in addition to the returns (or price series). For example, in Oh, Kim, and Min (2005), the stocks forming the index fund are computed in two steps. In the first step, stocks are ranked by a priority function that includes “fundamental” variables (standard error of the asset's beta, average trading amount and average market capitalization). Initial weights of the index tracking portfolio are then selected using a heuristic procedure. In the second step, a genetic algorithm is used to optimize the relative weights of the selected stocks, with the constraint that the portfolio beta should be close to one.

Corielli and Marcellino (2006) introduced the idea of reproducing a linear factor model structure for index tracking. They assume that stock prices evolve according to a linear factor model, and form an objective to build a tracking portfolio with the same factor structure as the index. However, to implement the procedure, the factor loading matrix needs to be estimated in order to find the optimal portfolio weights. Additionally, the cardinality of the tracking portfolio is satisfied by a heuristic procedure which works by ordering the factors according to their correlation with the index, and then includes those stocks that replicate the factors with a decided accuracy.

Clustering techniques are also used to construct tracking portfolios. For example, Focardi and Fabozzi (2004) describe an index-tracking methodology based on time-series clustering. They argue that because the estimation of all the covariances between assets of a broad market index (needed for a next period optimization) is computationally burdensome and produces noisy results, a hierarchical clustering of the asset's time series is a more robust way to reveal the correlation structure. In their application, they used the Euclidean distance between stock prices as the basis of their clustering. In a similar direction, Cornuejols and Tütüncü (2007) present an index-tracking problem based on clustering stocks with similar correlation coefficients of returns. To find the stocks in the tracking portfolio, they solved a large scale integer programming model, for which, Lagrangian relaxation and subgradient methods can produce good upper bounds. After selecting the stocks, the weights are determined proportionally to their market capitalization.

Other interesting techniques for index tracking are the cointegration approach of Alexander (1999) and Alexander and Dimitriu (2005) and the stochastic programming approach of Stoyan and Kwon (2007). As an additional example in continuous time, Yao, Zhang, and Zhou (2006) formulate the index tracking problem as a stochastic optimal control problem and solved it using semidefinite programming.

In the case of enhanced indexation, since the cardinality constraint (to hold fewer assets than the index) is usually imposed, almost all of the approaches and techniques for partial replication can be used after some modifications. The reader interested in the enhanced indexation literature can consult Section 2.2 of Canakgoz and Beasley (2008).

3

The enhanced indexation problem

Suppose from time t to t + 1 the index has a return w ν_{t + 1}, and at time t, N_t stocks² form the index. Each stock i has a return r_{i,t + 1} from date t to t + 1 and an associated vector of firm characteristics y_i,t observed at date t. These characteristics can be related to the explanation of returns, e.g., the market capitalization of the stock, the book-to-market ratio, lagged returns, etc., and to similarity measures with the index, e.g., correlation, mean-absolute deviation with respect to the index, maximum deviation with respect to the index, etc.

Originally, the investor, who tries to track an index or to form an enhanced index tracking portfolio³ at time t, wants to solve the following problem (P) by selecting the appropriate portfolio weights x_i,t for i = 1,…, N_t:

where p_{t + 1} is the return of the tracking portfolio and ρt(vt+1,pt+1) is the correlation coefficient (conditional to the information up to time t) of the returns of the index and the tracking portfolio, more specifically:

Additionally, O_t is a measure of out-performance of the tracking portfolio with respect to the index. Some common choices of O_t are given by

or

In the objective function, we have that λ₁ ≥ 0 measures the weight given to the correlation coefficient between the tracking portfolio and the index. In the same way, λ₂ ≥ 0 is the weight given to the “risk” component, i.e., the part of the objective function used to avoid constructing tracking portfolios with higher standard deviation than the index. Since the tracking portfolio is less diversified than the index, the standard deviation of the tracking portfolio tends to be higher than the one of the index. This objective then tends to match both standard deviations, i.e., to make the ratio close to one. For the enhanced component (with λ₃ ≥ 0), expression (2) represents the probability (also conditional to the information up to time t) that the tracking portfolio has a greater return than the index. In a similar way, (3) represents the excess return of the tracking portfolio with respect to the index.

Summarizing the objective of problem (P), we are maximizing a multi-objective function using linear scalarization, in which the tracking component is given by the correlation coefficient minus the ratio of the standard deviations of the returns of the tracking portfolio and the index, while the enhanced component is measured by either the excess return of the tracking portfolio with respect to the index or the probability of beating the returns of the index. Additionally, by setting the parameters λ₁,λ₂ and λ₃, we determine the implicit trade-offs between the different components of the objective. For example, λ₁ > 0, λ₂ > 0 and small values of λ₃ correspond mostly to a tracking-only strategy. Next, we will discuss how our objective is related to common objectives in the literature, as well as, the advantages of using both the correlation coefficient and the ratio of standard deviations to measure the tracking performance.

The objective function of the returns-based style analysis (RBSA) of Sharpe (1988, 1992) is to minimize the conditional variance of the tracking error given by σt2(vt+1−pt+1). We can expand the tracking error to have

If (σt(pt+1)/σt(pt+1))≈1 and ρt(vt+1,pt+1)≈1, then the variance of the tracking error will be close to zero. Therefore, the enhanced component of our objective function correctly measures the ability of the enhanced index fund manager to contribute to the portfolio performance (in a sense that the performance is separated from the tracking error). Additionally, the separation of the conditional correlation coefficient and the conditional standard deviations ratio gives more freedom to the design of the tracking portfolio.

In the enhanced index tracking literature, two common minimization objectives⁴ (with λ1*,λ1*≥0) are given by:

where in (5), we have that β and α come from the following linear regression model: pt+1=α+βvt+1+εt+1.

Notice that in (4), which is a similar objective to the one used in Beasley et al. (2003), one can show that minimizing Et[(vt+1−pt+1)2] is equivalent to minimizing σt2(vt+1−pt+1)+(Et[vt+1]−Et[pt+1])2. Therefore, we are indirectly trying to match the first moments of v_{t + 1} and p_{t + 1}. This fact will directly affect the weight given to the enhanced component.

Objective (5), which is used in Canakgoz and Beasley (2008), clearly separates the tracking component from the enhanced component; but, even in the case of β = 1, we could have that σ(pt+1)>σ(vt+1). We could find α-positive strategies (with β close to 1) but most likely with higher overall risk. Since,

If we have that (σt(pt+1)/σt(pt+1))≈1 and ρt(vt+1,pt+1)≈1, then β will be close to one. Therefore, our objective function (in the tracking component) indirectly minimizes the variance of the portfolio and tries to achieve values of β close to one.

In the constraints of (P), we have that supp (xt)={i:xi,t>0},<.> represents the cardinality of a set, and K_t is a positive integer (smaller than N_t) representing the maximum number of stocks with positive weight in the tracking portfolio at time t. The last constraint of the formulation imposes some lower or upper bound constraints on the tracking portfolio.

Under the assumptions that the index return for each t is an i.i.d. random variable, the vector of returns of the stocks for each t is a multivariate i.i.d. random vector (the index returns and the stock returns are not independent). Considering Nt=N,Kt=K and ui,t=ui, we can reformulate problem (P) using its sample counterpart that avoids the time dependence of the portfolio weights, i.e., ensures xi,t=xi for all t. We can then find the optimal portfolio weights x by solving the following problem (PI) with a calibration period [1,T]

li≤xi≤ui, for all i

where

or

where v¯=∑t=0T−1vt+1/T and p¯=∑t=0T−1pt+1/T. Problem (PI) can be viewed as a non-linear and non-concave mixed integer programming model which is very difficult to solve even for small values of N and K. For a similar version of the problem, but, with a quadratic objective, the reader can consult Bienstock (1996).

4

Parametric approach for enhanced indexation

Instead of solving (PI) using mixed integer programming techniques, we use the parametric approach in Brandt et al. (2009) to formulate an alternative (but not equivalent) problem where the portfolio weights are specified as a function of the stocks characteristics by

The function f should take into account the last three constraints of the original formulation (P) to produce feasible portfolio allocations for the enhanced index model. If we consider l_i,t = 0 and u_i,t = 1 for all i, a possible function f (with no closed form) can be obtained using the following steps:

• Step 1 Let xi,t*=x¯i,t+(1/A)θTyˆi,t, where x¯i,t is some initial portfolio (for example, if x¯i,t=(1/Nt) our “initial” portfolio is the equally-weighted portfolio), yˆi,t are the characteristics of stock i, standardized cross-sectionally to have zero mean and a standard deviation of one across all stocks at date t and 1/A is a normalization factor used to avoid aggressive allocations and achieve more robustness in the results. Following Brandt et al. (2009), we set A = K_t.

• Step 2 Let xi,t**=max[0,xi,t*]/∑j=1j=1max[0,xj,t*], notice that ∑t=1Ntxi,t**=1 and xi,t**≥0 for all i=1,...,Nt.

• Step 3 Consider the assets with the largest K_t weights of xt**, and set the weight of the other assets to zero. Break ties arbitrarily. Let these re-defined weights be xit+.

• Step 4 Finally, let xi,t=(xi,t+/∑j=1Ntxj,t+). Notice that x_t satisfies 〈supp(xt)〉≤Kt,∑i=1Ntxi,t=1, and 0≤xi,t≤1, for all i=1,…,Nt.

An important aspect of the parameterization is that the coefficients θ are invariant across assets and time. Constant coefficients across time mean that the coefficients that maximize the objective are the same for all dates; therefore, they also maximize the investor's objective unconditionally. This fact implies that we can formulate the following unconditional optimization problem (PP) with respect to θ:

where

or

and f(yi,t;θ) generates weights x_i,t that satisfy the cardinality constraint, upper and lower bounds, and sum to one. It is then possible to estimate the coefficients θ by maximizing the corresponding sample analog (SPP):

where the definitions of the terms are the same as in (PI). The only variables to be computed are the coefficients θ that are imbedded in f(yi,t;   θ). The portfolio weights x_i,t have been parameterized by a function of the stocks’ characteristics. Now, we only need to find the vector θ that usually contains only a few elements. Therefore, the dimensionality of the problem has been dramatically reduced, but the new difficulty with this parameterization is that it generates a non-concave, non-differentiable and non-linear unconstrained problem which has to be solved using appropriate optimization techniques. Again, notice that problems (PI) and (SPP) are not equivalent, i.e., the optimal x_i,t can be different in the two models.

The elements of the vector θ can be directly compared (due to the normalization of the characteristics). This comparison gives intuition about the class of stocks that are going to be included in the tracking portfolio. Notice that, by finding θ, we are basically finding a trading strategy. Additionally, K_t is not fixed to a constant K during the calibration period, so, we can control the cardinality of the tracking portfolio in general ways. However, in our numerical examples we fix K_t = K for all t. In the next section, we present a series of refinements of the basic model to allow the inclusion of portfolio weight constraints and transaction costs.

5

Refinements and extensions

5.1

Upper and lower bounds on portfolio weights

The portfolio x_t, resulting from the simple policy in the last section, is not likely to satisfy the lower and upper bounds I_t and u_t. However, we can address this deficiency by solving a LP problem to find new optimal weights xtlu. If we denote as Kt the set of assets selected in the “initial” tracking portfolio x_t, we have the following LP model called (UB1):

yi,t+, yi,t−≥0, for each i∈Kt

From the LP above, the optimal portfolio weights will be given by xtlu=xi,t+yi,t+−yi,t− for all i∈Kt, where we assume the feasibility of (UB1). An alternative LP is given in Cornuejols and Tütüncü (2007), which we call (UB2):

subject to li,t≤xi,tlu≤ui,t, for each i∈Kt,

xi,tlu−xi,t≤yi,t, for each i∈Kt

xi,t−xi,tlu≤zi,t, for each i∈Kt

yi,t,zi,t,xi,tlu≥0, for each i∈Kt.

As in the case of (UB1), this also assumes the feasibility of (UB2). Consequently, we can construct a portfolio weight function xi,t=f(yi,t,θ) (that satisfies the lower and upper limits constraints) by following the steps in Section 4 and adding one more step (Step 5), which consists of solving either (UB1) or (UB2) (if possible).

5.2

Transaction costs and turnover

Transaction costs and turnover are two very important variables in any portfolio optimization problem since they tell us how costly it is to implement the optimal strategy and how much the portfolio changes over time. Even though there are multiple approaches for rebalancing a tracking portfolio, we only describe two general cases which can be handled by the parametric approach.

Recall that at time t our optimal tracking portfolio (from the optimization problem) is x_t. The current tracking portfolio is no longer x_t−1 (tracking portfolio chosen at time t − 1) due to the realized return in the period t − 1 to t. We call the current tracking portfolio (unbalanced) as xtu. For every asset i, we have

Now, we can define the turnover of the tracking portfolio at time t as Tt=∑i|xi,t−xi,tu|. The net return of the tracking portfolio under proportional transaction costs will be given by

where TCt(xt)=∑iδi,t|xi,t−xi,tu| and δi,t is the proportional transaction cost assigned at time t to stock i. Hence, we can proceed with the optimization problem described in Section 4.

However, it may not be optimal to rebalance the tracking portfolio completely from xtu to x_t. Now, we apply a boundary-type policy for transaction costs inspired by the work of Leland (2000) and also considered in Brandt et al. (2009). First, define xtα=xt+αt(xtu−xt) with αt≥0 (notice that 〈supp(xtα)〉 is not necessarily less than or equal than K_t) and introduce a threshold ¿_t > 0 that “limits” the amount of rebalancing under a certain norm ||·||_t. The parameter α_t is such that αt||xtu−xt||t≤εt, and we let αt* be

The transaction cost policy is not to rebalance if x_t and xtu are close enough under the norm ||·||_t and the parameter ¿_t (so that both the norm and the threshold define the no-trade region) and, depending of the magnitude of the transaction costs, to rebalance to some “intermediate” allocation between x_t and xtu (given by the value of at*) or to rebalance to the “optimal” allocation x_t. If we denote xttC as the tracking portfolio chosen for time t in the presence of the transaction costs policy, we have

where the function g is such that it produces feasible allocations for the enhanced index tracking problem and ||·||_t is usually the Euclidean distance but scaled by the cardinality of the portfolio K_t, i.e., ||xt−xtu||t=∑t=1Nt(xi,t−xi,tu)2/Kt. Finally, notice that it is also possible to establish set frequency of rebalancing, i.e., daily, weekly, etc.

6

Selection of appropriate characteristics

In this section, we consider stock characteristics that can be used to construct the weights of the tracking portfolio, i.e., the vector y_i in the portfolio weights function f. In Brandt et al. (2009), the characteristics were selected based on their capacity to explain the cross-section of expected returns. Consequently, market capitalization, book to market ratio and lagged return were included in their corresponding empirical application.

Those characteristics will be identified with y^mkt, y^btm and y^ret, and their coefficients in θ will be denoted by θ_mkt,θ_btm and θ_ret. However, for tracking purposes it would be beneficial to include some characteristics that can reflect the ability of a stock to track or beat the index. Based on the tracking objective functions of Gaivoronski et al. (2005), and Oh et al. (2005), and the enhanced tracking objectives of Canakgoz and Beasley (2008), the following characteristics can be included:

• •

  Correlation of the stock return with the index return: Given a time-window twcorr, this characteristic is given by yi,tcorr=ρ(v,ri) where v={vt−twcorr,…,vt}, and ri={ri,t−twcorr,…,ri,t}, and its coefficient is identified with θ_corr in the vector θ

• •

  Maximum deviation of the stock return with respect to the index return: Given a time-window twmm, this characteristic is given by yi,tmm=maxk∈[t−twmm,t]|vk−ri,k|, and its coefficient is identified with θ_mm in the vector θ.

• •

  Mean absolute deviation of the stock return with respect of the index return: Given a time-window twmad, this characteristic is given by yi,tmad=∑k=t−twmadt|vk−ri,k|/(tw+1), and its coefficient is identified with θ_mad in the vector θ.

• •

  Beta deviation: Given a time-window twβ, this characteristic is given by yi,tβ=βi,t−1, where βi,t, is the OLS slope of the regression ri=αi,t+βi,tv+εt where v={vt−twβ,…,vt} and ri=ri,t−twβ,…,ri,t, and its coefficient is identified with θβ in the vector θ.

• •

  Alpha: Given a time-window twα (usually equal to twβ), this characteristic is given by yi,tα=αi,t, where αi,t is the OLS intercept of the regression ri=αi,t+βi,tv+εt where v={vt−twα,…,vt} and ri={ri,t−twα,…,ri,t}, and its coefficient is identified with θα in the vector θ.

7

Numerical example - enhanced tracking of the S&P500

In this section, we present an empirical application of the parametric index tracking and enhanced indexation model. We consider the S&P500 as the index with the objective as defined in Section 3. We report the optimization results, more specifically, the in-sample and out-of-sample performance of the tracking portfolios. First, we present some relevant information about the data used in this particular application.

7.1

Data

To implement the model, the returns of the index, the returns of the stocks and the time series of characteristics are needed. The time frequency chosen was daily and the calibration period was 124 days to be consistent with common applications in the literature that use 75–250 days for calibration. For example, Gaivoronski et al. (2005) used different lengths of the calibration period: 75, 150 and 250 trading days. Our calibration period corresponds to the period 2011/10/03 to 2012/03/30. The out-of-sample performance is evaluated using the next 42 days (two months of trading) and corresponds to the period 2012/04/02–2012/05/31. The daily index returns and stock returns were obtained using the CRSP database⁵ and information of index constituents at the end of each month was obtained through the Compustat database. The final number of stocks was 475 with the following criteria to include a stock in the sample:

• •

  presence in the S&P500 at the end of each month of the calibration period;

• •

  presence of a complete history of returns during the calibration period;

• •

  maintenance of symbol during the calibration period (i.e., no change of stock name).

For characteristics, we used market capitalization, alpha and beta deviation. For market capitalization, for each date t we multiply the price of the stock times the number of shares outstanding. For other characteristics, i.e., alpha and beta deviation, we used twα=twβ=42 trading days to compute the appropriate value of the definitions in Section 6. Finally, based on some empirical studies of DeMiguel, Garlappi, and Uppal (2009), x¯i,t was considered to be the equally weighted portfolio in Step 1 of Section 4.

7.2

Working with three characteristics: market capitalization, beta deviation and alpha

As noted earlier, we work with three characteristics: market capitalization, beta deviation and alpha. Their weights are given by θ_mkt,θ_β and θ_α, respectively. Market capitalization was selected due to its capacity to explain returns as well as the fact that the S&P500 is a market-capitalization index. Alpha and beta deviation contain important information about a particular stock relative to the index. In particular, α is used to assess the ability of a stock to outperform the index and can also be considered as a measure of momentum. Beta is used to assess the risk of the stock compared to the index. Additionally, both are computed from the same OLS regression, and have been used recently in the enhanced indexation problem (for example, in Canakgoz and Beasley (2008)). Note that y^β in Section 6 was defined as |β−1|. Consequently, low values of this characteristic indicate that the particular beta is close to 1, and after the cross-section normalization it will take negative values.

In this part of the paper, we consider various cases of the objective function in (PP). In the first case, we maximize the correlation coefficient of the returns of the index and the tracking portfolio, i.e., λ₁ = 1, λ₂ = 0, and λ₃ = 0. The second case includes in the objective the ratio of the standard deviations, i.e., λ₁ = 1, λ₂ = 1, and λ₃ = 0. While we do not include the enhanced component in these two initial cases, we observe different behavior of the objective due to different effects of the characteristics. These cases are important since they correspond to versions of a classical index tracking problem that considers the correlation coefficient and the variance of the tracking portfolio. In particular, we wish to track the S&P500 using 75 stocks (i.e., 15% of its components). To construct the function f, we follow the steps given in Section 4 using as initial tracking portfolio the equally weighted portfolio. Also, we do not include transaction costs, or lower and upper bounds on the portfolio weights. The objective is computed using the calibration period of 124 days corresponding to the trading days between 2011/10/03 and 2012/03/30 (as mentioned in the Data section). Since we are using a calibration period, it is clear that we are using problem (SPP), which is the sample analog of problem (PP).

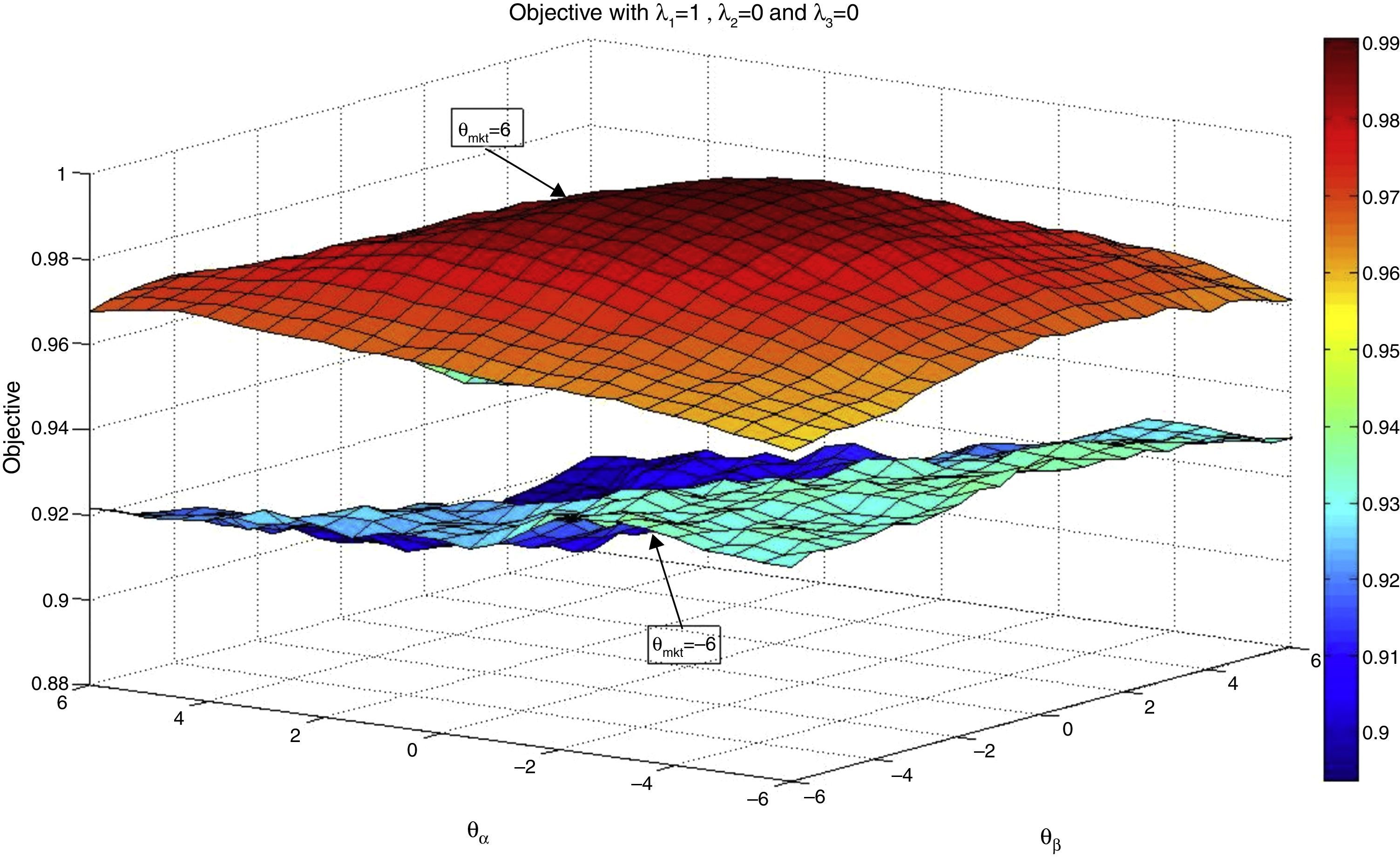
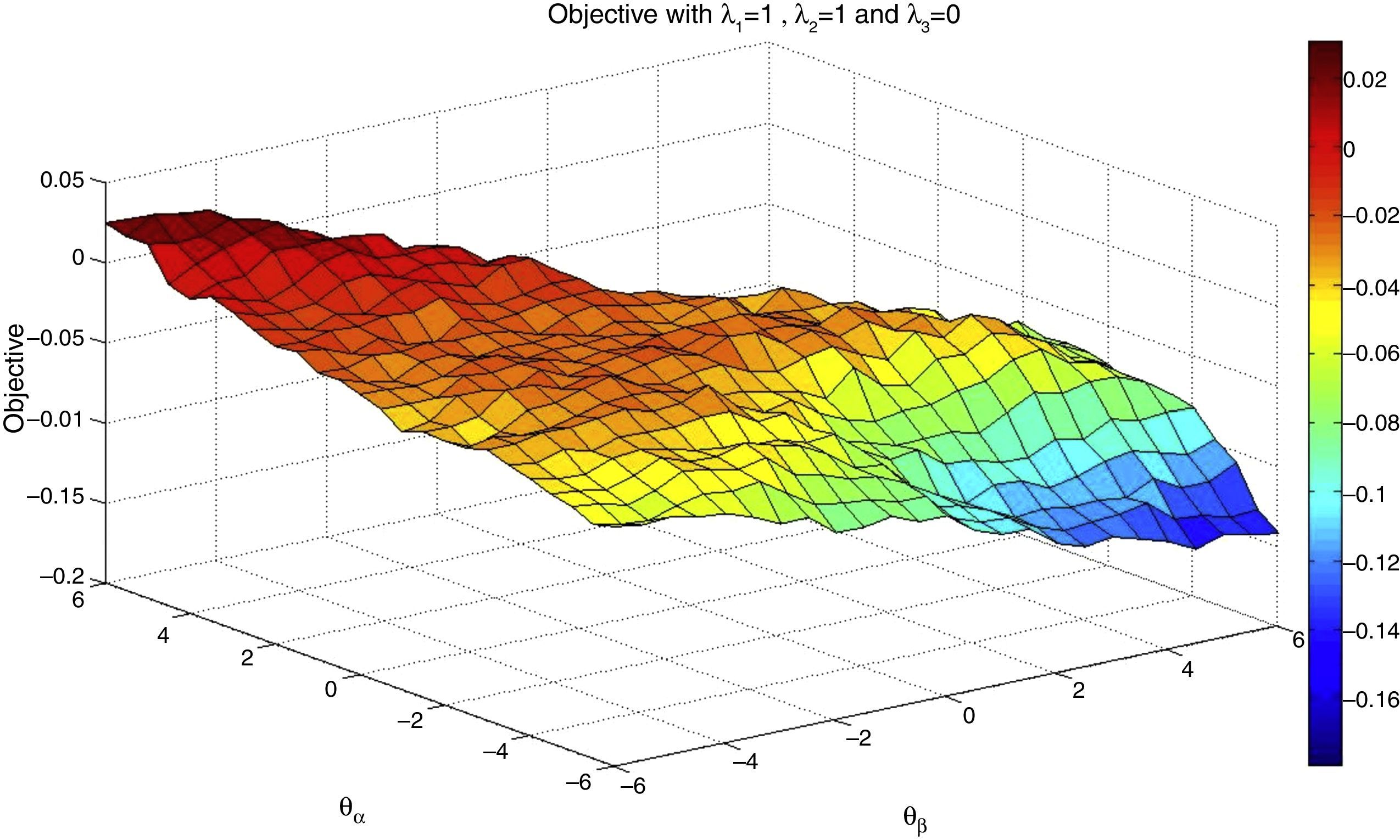
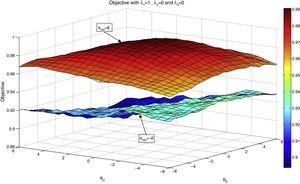
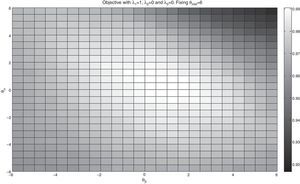
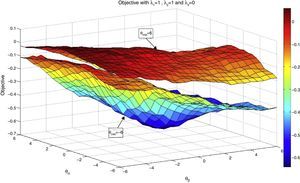
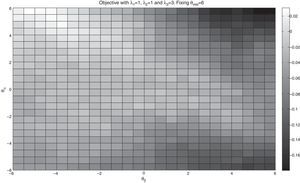
Figs. 1 and 2 correspond to the case of λ₁ = 1, λ₂ = 0, and λ₃ = 0 with K = 75. In Fig. 1, we show two surfaces, the upper one corresponds to fixing θ_mkt = 6 and moving θ_α and θ_β between −6 and 6 in 0.5 steps, and the lower surface corresponds to θ_mkt = −6 using the same range for the other two coefficients. Notice that higher values of θ_mkt include stocks with greater presence in the index in the tracking portfolio. As expected, this fact increases the correlation coefficient of the tracking portfolio and the index. With θ_mkt = 6 we obtain correlation coefficients higher than 0.99; while using θ_mkt = −6, we obtain maximum values that are approximately 0.89.

Fig. 1.

Surface of objective of (PP) with λ₁ = 1,λ₂ = 0 and λ₃ = 0 with K = 75. The upper surface corresponds to θ_mkt = 6 and the lower corresponds to θ_mkt = −6.

Own elaboration.

Fig. 2.

Color map of the objective of (PP) with λ₁ = 1, λ₂ = 0 and λ₃ = 0 with K = 75 and fixing θ_mkt = 6.

Own elaboration.

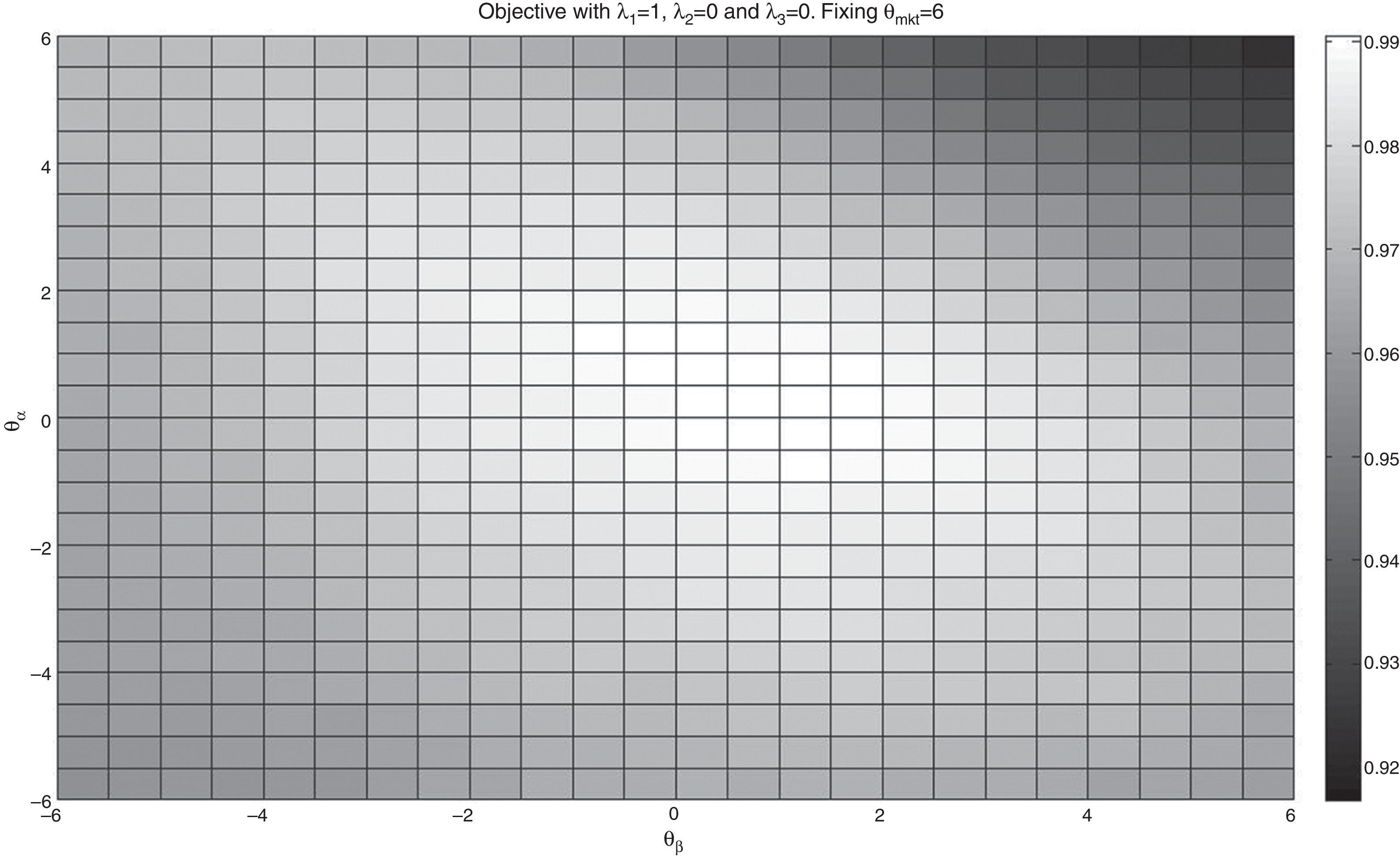
In Fig. 2, we show a color map of the surface corresponding to θ_mkt = 6. From this figure, we can observe the influence of θ_β and θ_α in the maximization of the correlation coefficient. Notice that the values of θ_α that maximize the objective is centered on zero; therefore, alpha appears to have little relevance for maximizing the correlation coefficient. The case of θ_β is relatively similar by presenting values centered at zero for the maximum values of the objective.

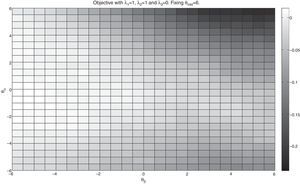
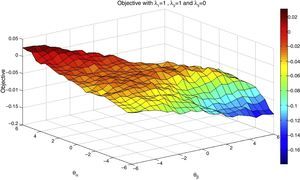
Next, we include in the objective the ratio of the standard deviations; recall that by giving weight to this part of the objective (λ₂ > 0) we aim to reduce the variance of the tracking portfolio with respect to the index. For motivational purposes, we now use λ₁ = 1, λ₂ = 0, and λ₃ = 0 and K = 75. The new objective is a more complete tracking objective since we both maximize the correlation coefficient and keep the ratio of the variances close to 1. Under the same conditions as in the previous case, we similarly display Figs. 3 and 4.

Fig. 3.

Surface of objective of (PP) with λ₁ = 1, λ₂ = 0 and λ₃ = 0 with K = 75. The upper surface corresponds to θ_mkt = 6 and the lower corresponds to θ_mkt = −6.

Own elaboration.

Fig. 4.

Color map of the objective of (PP) with λ₁ = 1, λ₂ = 1 and λ₃ = 0 with K = 75 and fixing θ_mkt = 6.

Own elaboration.

In Fig. 3, we again observe that for tracking purposes, giving more weight to stocks with high market capitalization results in better tracking performance (both correlation and standard deviations ratio). Additionally, as we can observe in Fig. 4, higher values of the objective function correspond to small values of θ_β, i.e., stocks with beta close to 1 are more likely to be considered. Therefore, by including stocks with a beta close to 1, we can expect somehow to match the variances of the index and the tracking portfolio. The effect of θ_α for tracking purposes is not very significant since the higher values of the objective occur around θ_α = 0. Finally, as we can observe from all the previous results, depending of the nature of the objective, the weights given to the characteristics are different and are in line with empirical facts in the financial data.

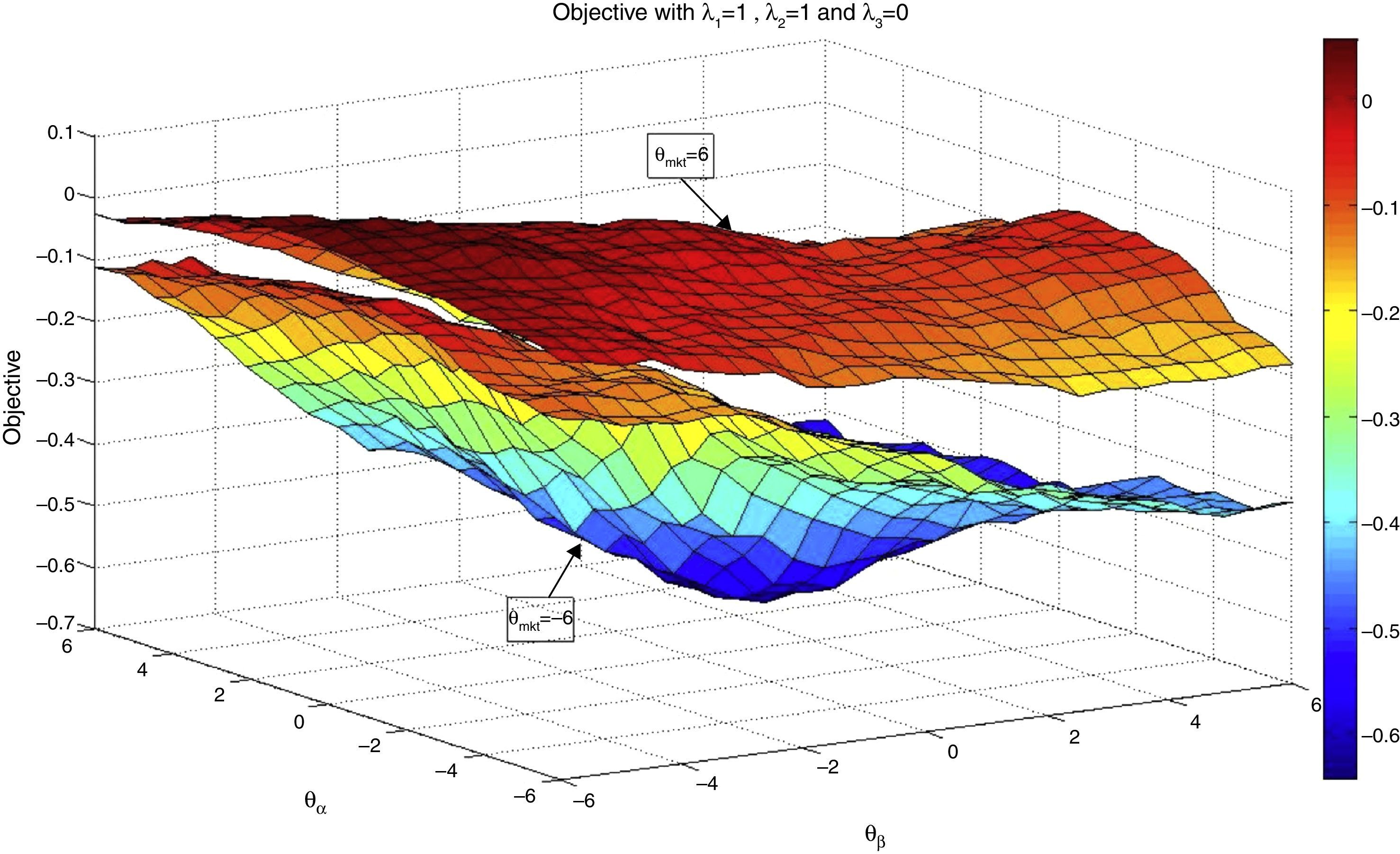
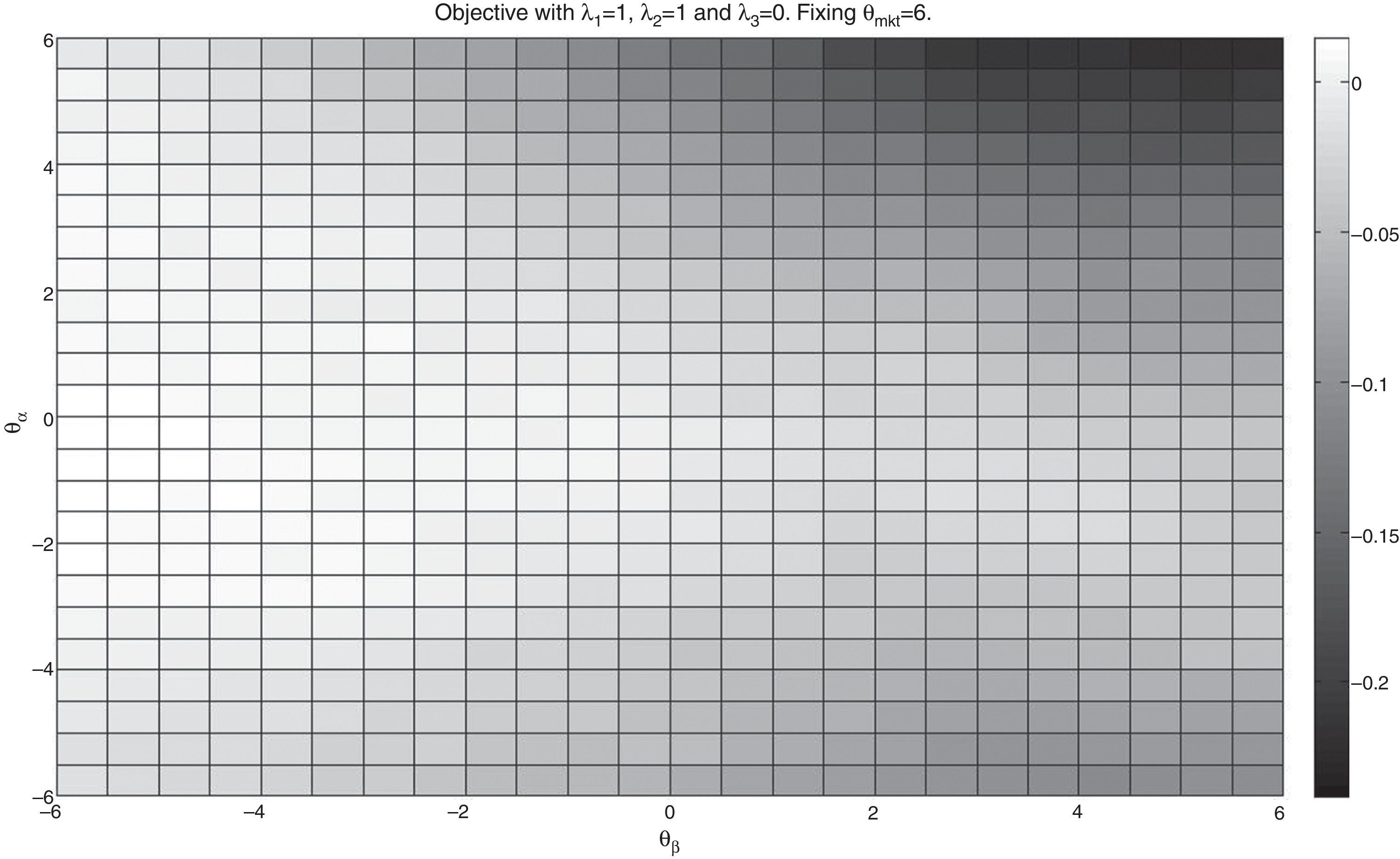
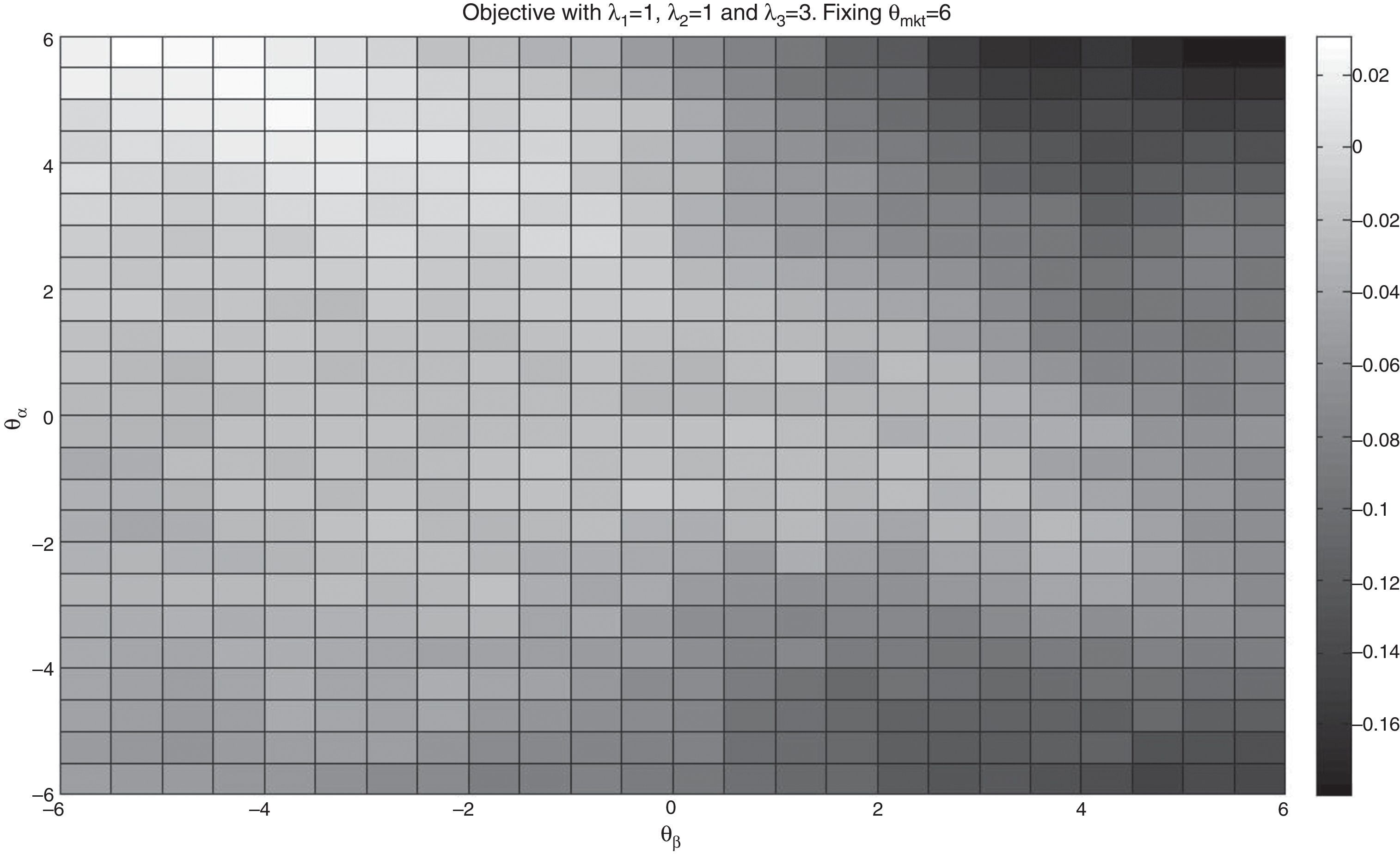
We also include a case with the enhanced component in the objective function. The outperformance measure selected was the average daily excess returns of the portfolio over the index (in percentage). In Figs. 5 and 6 (color map), we show the results for the case λ₁ = 1, λ₂ = 1, and λ₃ = 3 (always keeping K = 75) and fixing θ_mkt = 6. We can observe that the higher values of the objective occur in the left upper corner of the plot i.e., low θ_β and high θ_α. This indicates that including high alpha stocks increases the possibility of higher returns of the tracking portfolio while high values of θ_mkt and low values of θ_β collaborate with the strict tracking component (correlation and variance).

Fig. 5.

Surface of objective of (PP) with λ₁ = 1, λ₂ = 1 and λ₃ = 3 with K = 75 and fixing θ_mkt = 6. The function O in the objective is given by the excess return of the tracking portfolio with respect to the index.

Own elaboration.

Fig. 6.

Color map of the objective of (PP) with λ₁ = 1, λ₂ = 1 and λ₃ = 3 with K = 75 and fixing θ_mkt = 6. The function O in the objective is given by the excess return of the tracking portfolio with respect to the index.

Own elaboration.

7.3

Optimizing with three characteristics

In this part, we continue with the objective given in (PP) with coefficients given by θ = (θ_mkt, θ_α, θ_β). Again, we do not include transaction costs or lower and upper bounds on the portfolio weights. We study the effects of changing K, λ₁ and λ₃ in the objective function. We impose a constraint of the standard deviation ratio in the optimization problem to avoid exploring the effect of λ₂. In-sample and out-of-sample results are presented.

More important than finding the optimal value of the problem (PP), we focus on the effects and behavior of the selected characteristics in the enhanced indexation problem. Again, since we are optimizing over a fixed period of history, we are basically solving problem (SPP) which is the sample counterpart of problem (PP). Because of that, we sketch our “optimization” procedure as follows:

• Step 1 Construct a grid of values of the coefficients.

• Step 2 Evaluate the (particular) objective function for each of the vectors of the grid.

• Step 3 Impose a constraint on the standard deviations ratio to filter the combination of coefficients to be considered.

• Step 4 Sort the (filtered) vector of coefficients by their objective value. Group the sorted data into n subgroups.

• Step 5 For the subgroup with the greatest values of the objective, report the average value of the coefficients. Those values are considered estimates of the “optimal” values.

• Step 6 Evaluate the average coefficients found in Step 5 in the corresponding objective function. Report the objective function value as well as other relevant variables.

The results correspond to θ = (θ_mkt, θ_α, θ_β) with −6 ≤ θ_mkt, θ_α, θ_β in 0.5 intervals. This produces 15 625 vectors of characteristics to evaluate for each selected K. Also, we impose the constraint that the ratio of standard deviations should be less than or equal to 1.05. After filtering the characteristics that satisfy the aforementioned constraint in Step 3, we took n = 150 to be the number of subgroups in Step 4. To define θ_α and θ_β, we used a time window of 42 trading days. The measure of out-performance O_t is the excess return of the tracking portfolio over the index. The cardinality values considered were K = 25, 30, 40 and 50. These are usual values for K; for example, Canakgoz and Beasley (2008) in their empirical application used 40 stocks of a universe of 457 to track the S&P500. While no transactions costs are considered in this section, they are considered in the next section.

We also used a non-linear optimization package, KNITRO 6.0, to solve the optimization problem to verify the accuracy of the answers given by our procedure. The results were similar on average; however, the optimal solution found with the solver was sensitive to the starting point, which suggests performing a preliminary exploration analysis to select appropriate starting points. Also, note that the lack of structure in the optimization problem makes it difficult to claim optimality.

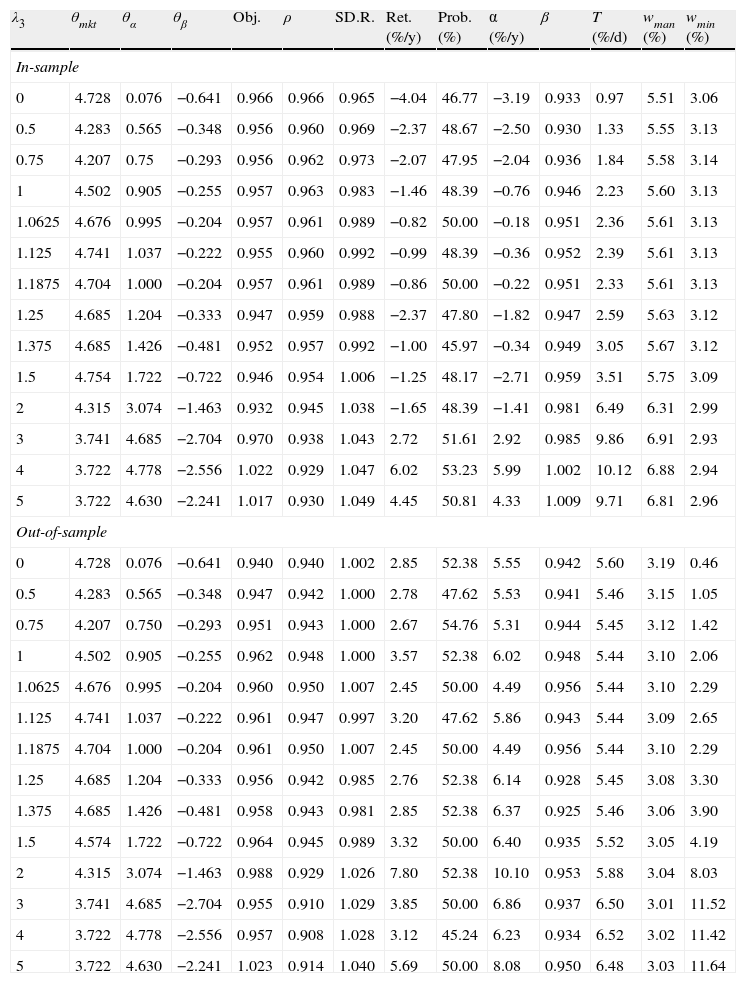
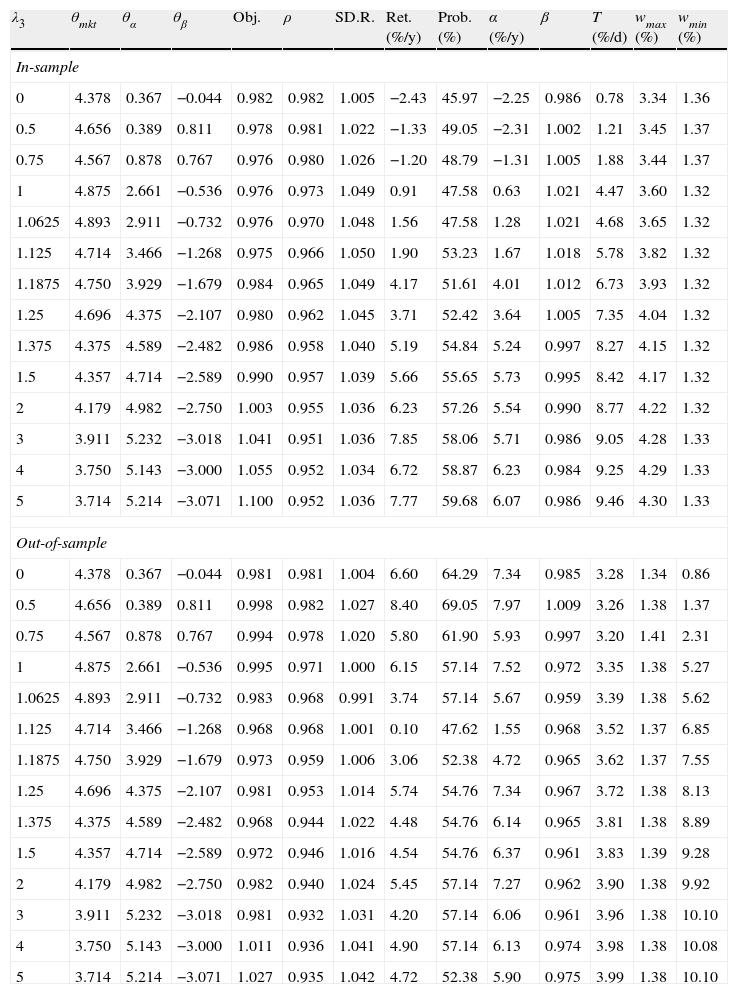
Tables 1–4 present detailed information about the in-sample and out-of-sample performance of the “optimal” tracking portfolios of this section. Each table corresponds to a particular choice of K(K = 25, K = 30, K = 40, K = 50) and shows the following information: λ₃ (with λ₁ always fixed at 1), the “optimal” coefficients (using the optimization procedure explained before), the objective function values (recall that the correlation coefficient and the standard deviation ratio are dimensionless but the average daily return was taken in percentage), the correlation coefficient (ρ) of the index and the “optimal” tracking portfolio returns during the calibration/testing period, the standard deviation ratio (SD.R.) of the returns of the tracking portfolio and the index during the calibration/testing period, the average yearly annualized excess return of the tracking portfolio over the index during the calibration/testing period (Ret.%/y), the average probability of beating the index over the calibration/testing period (Prob %), alpha in percentage per year (α%/y) and beta (β) of the regression of the portfolio returns against the index returns during the calibration/testing period, the average daily turnover as defined in Section 5.2 (T%/d), and the average maximum (w_max) and minimum (w_min) average weight of the tracking portfolios (given in percentage). Notice that some of variables are computed as averages during the calibration/testing period since every day the tracking portfolios change due to different values of the (normalized) characteristics.

Table 1.

Results in-sample and out-of-sample for λ₁ = 1 and K = 25.

λ3	θmkt	θα	θβ	Obj.	ρ	SD.R.	Ret. (%/y)	Prob. (%)	α (%/y)	β	T (%/d)	wman (%)	wmin (%)
In-sample
0	4.728	0.076	−0.641	0.966	0.966	0.965	−4.04	46.77	−3.19	0.933	0.97	5.51	3.06
0.5	4.283	0.565	−0.348	0.956	0.960	0.969	−2.37	48.67	−2.50	0.930	1.33	5.55	3.13
0.75	4.207	0.75	−0.293	0.956	0.962	0.973	−2.07	47.95	−2.04	0.936	1.84	5.58	3.14
1	4.502	0.905	−0.255	0.957	0.963	0.983	−1.46	48.39	−0.76	0.946	2.23	5.60	3.13
1.0625	4.676	0.995	−0.204	0.957	0.961	0.989	−0.82	50.00	−0.18	0.951	2.36	5.61	3.13
1.125	4.741	1.037	−0.222	0.955	0.960	0.992	−0.99	48.39	−0.36	0.952	2.39	5.61	3.13
1.1875	4.704	1.000	−0.204	0.957	0.961	0.989	−0.86	50.00	−0.22	0.951	2.33	5.61	3.13
1.25	4.685	1.204	−0.333	0.947	0.959	0.988	−2.37	47.80	−1.82	0.947	2.59	5.63	3.12
1.375	4.685	1.426	−0.481	0.952	0.957	0.992	−1.00	45.97	−0.34	0.949	3.05	5.67	3.12
1.5	4.754	1.722	−0.722	0.946	0.954	1.006	−1.25	48.17	−2.71	0.959	3.51	5.75	3.09
2	4.315	3.074	−1.463	0.932	0.945	1.038	−1.65	48.39	−1.41	0.981	6.49	6.31	2.99
3	3.741	4.685	−2.704	0.970	0.938	1.043	2.72	51.61	2.92	0.985	9.86	6.91	2.93
4	3.722	4.778	−2.556	1.022	0.929	1.047	6.02	53.23	5.99	1.002	10.12	6.88	2.94
5	3.722	4.630	−2.241	1.017	0.930	1.049	4.45	50.81	4.33	1.009	9.71	6.81	2.96
Out-of-sample
0	4.728	0.076	−0.641	0.940	0.940	1.002	2.85	52.38	5.55	0.942	5.60	3.19	0.46
0.5	4.283	0.565	−0.348	0.947	0.942	1.000	2.78	47.62	5.53	0.941	5.46	3.15	1.05
0.75	4.207	0.750	−0.293	0.951	0.943	1.000	2.67	54.76	5.31	0.944	5.45	3.12	1.42
1	4.502	0.905	−0.255	0.962	0.948	1.000	3.57	52.38	6.02	0.948	5.44	3.10	2.06
1.0625	4.676	0.995	−0.204	0.960	0.950	1.007	2.45	50.00	4.49	0.956	5.44	3.10	2.29
1.125	4.741	1.037	−0.222	0.961	0.947	0.997	3.20	47.62	5.86	0.943	5.44	3.09	2.65
1.1875	4.704	1.000	−0.204	0.961	0.950	1.007	2.45	50.00	4.49	0.956	5.44	3.10	2.29
1.25	4.685	1.204	−0.333	0.956	0.942	0.985	2.76	52.38	6.14	0.928	5.45	3.08	3.30
1.375	4.685	1.426	−0.481	0.958	0.943	0.981	2.85	52.38	6.37	0.925	5.46	3.06	3.90
1.5	4.574	1.722	−0.722	0.964	0.945	0.989	3.32	50.00	6.40	0.935	5.52	3.05	4.19
2	4.315	3.074	−1.463	0.988	0.929	1.026	7.80	52.38	10.10	0.953	5.88	3.04	8.03
3	3.741	4.685	−2.704	0.955	0.910	1.029	3.85	50.00	6.86	0.937	6.50	3.01	11.52
4	3.722	4.778	−2.556	0.957	0.908	1.028	3.12	45.24	6.23	0.934	6.52	3.02	11.42
5	3.722	4.630	−2.241	1.023	0.914	1.040	5.69	50.00	8.08	0.950	6.48	3.03	11.64

Own elaboration.

Table 2.

Results in-sample and out-of-sample for λ₁ = 1 and K = 30.

λ3	θmkt	θα	θβ	Obj.	ρ	SD.R.	Ret. (%/y)	Prob. (%)	α (%/y)	β	T (%/d)	wmax (%)	wmin (%)
In-sample
0	4.707	0.598	−0.891	0.967	0.967	0.987	−4.96	42.74	−4.39	0.954	1.44	4.85	2.47
0.5	4.337	0.402	0.087	0.963	0.968	1.007	−2.46	47.77	−2.87	0.976	1.05	4.85	2.51
0.75	4.337	0.707	−0.141	0.961	0.968	1.006	−2.17	48.01	−3.42	0.974	1.58	4.85	2.50
1	4.679	1.411	−0.857	0.957	0.964	1.011	−1.65	48.89	−3.78	0.974	2.67	4.95	2.46
1.0625	4.482	1.804	−1.321	0.957	0.963	1.003	−1.40	47.16	−2.80	0.966	3.70	5.18	2.44
1.125	4.589	2.500	−1.821	0.958	0.964	0.991	−1.35	48.00	−1.55	0.956	5.28	5.46	2.41
1.1875	4.571	2.750	−2.071	0.957	0.959	0.992	−0.50	48.56	−1.62	0.952	5.96	5.59	2.40
1.25	4.429	3.321	−2.375	0.956	0.955	1.006	0.06	47.58	0.57	0.961	6.99	5.78	2.38
1.375	4.196	3.643	−2.500	0.957	0.949	1.010	1.35	49.19	1.89	0.959	7.79	5.89	2.38
1.5	4.018	4.357	−3.107	0.951	0.942	1.004	1.46	50.81	2.17	0.946	8.51	6.09	2.37
2	4.035	4.543	−3.057	0.958	0.943	1.016	1.86	52.42	2.41	0.958	8.76	6.08	2.38
3	3.935	5.189	−3.078	0.993	0.935	1.049	4.98	52.42	5.23	0.981	9.65	6.10	2.39
4	3.814	5.421	−3.156	1.034	0.930	1.049	6.77	51.81	5.66	0.978	10.13	6.12	2.39
5	3.752	5.874	−3.204	1.049	0.926	1.050	6.36	53.23	6.50	0.990	10.64	6.12	2.40
Out-of-sample
0	4.707	0.598	−0.891	0.957	0.957	1.001	1.19	52.38	3.14	0.958	4.84	2.49	1.15
0.5	4.337	0.402	0.087	0.975	0.959	1.009	8.11	66.67	9.69	0.968	4.72	2.51	1.05
0.75	4.337	0.707	−0.141	0.979	0.958	1.004	7.61	61.90	9.47	0.962	4.72	2.51	2.19
1	4.679	1.411	−0.857	0.969	0.952	1.000	4.48	50.00	6.76	0.952	4.79	2.47	3.87
1.0625	4.482	1.804	−1.321	0.968	0.954	0.991	3.40	52.38	6.00	0.945	4.94	2.47	4.69
1.125	4.589	2.500	−1.821	0.956	0.944	0.981	2.75	54.76	6.20	0.927	5.09	2.50	5.90
1.1875	4.571	2.750	−2.071	0.952	0.944	0.982	1.81	54.76	5.22	0.927	5.16	2.50	6.29
1.25	4.429	3.321	−2.375	0.954	0.943	0.971	2.23	47.62	6.18	0.916	5.28	2.50	7.85
1.375	4.196	3.643	−2.500	0.961	0.942	1.005	3.52	47.62	6.06	0.946	5.37	2.50	9.19
1.5	4.018	4.357	−3.107	0.944	0.933	1.005	1.90	45.24	4.79	0.938	5.56	2.49	10.38
2	4.035	4.543	−3.057	0.945	0.927	1.010	2.28	42.86	5.27	0.936	5.58	2.49	10.48
3	3.935	5.189	−3.078	0.940	0.924	1.009	1.36	47.62	4.49	0.932	5.71	2.48	11.62
4	3.814	5.421	−3.156	0.983	0.914	1.016	4.39	52.38	7.76	0.929	5.77	2.48	11.51
5	3.752	5.874	−3.204	1.001	0.894	1.062	5.53	50.00	7.94	0.950	5.83	2.47	12.43

Own elaboration.

Table 3.

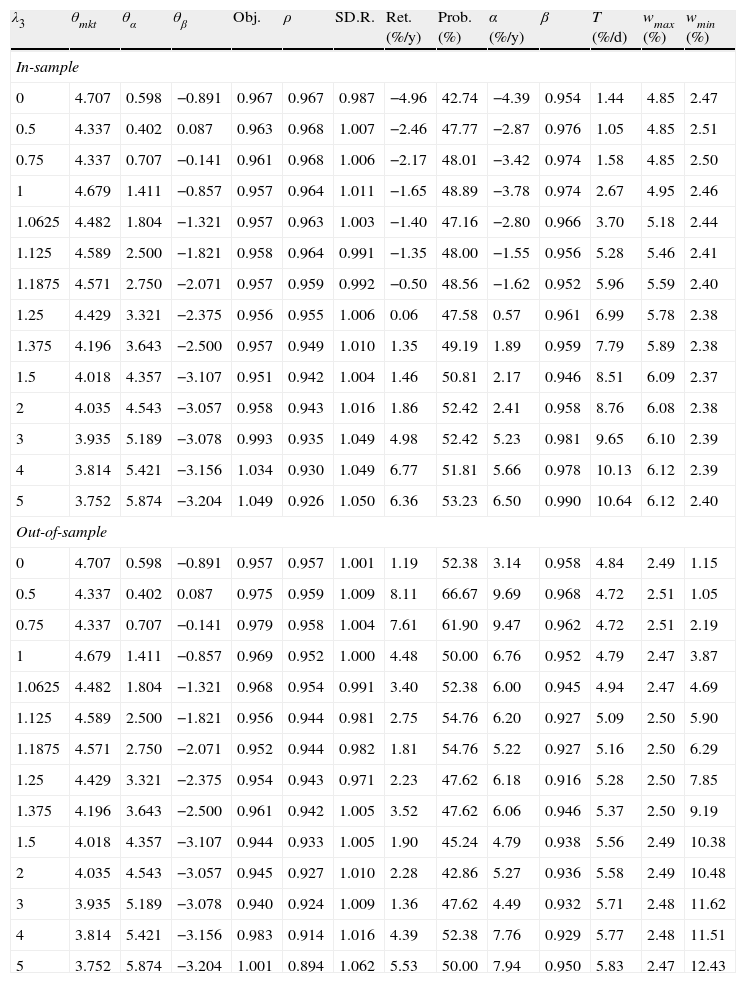
Results in-sample and out-of-sample for λ₁ = 1 and K = 40.

λ3	θmkt	θα	θβ	Obj.	ρ	SD.R.	Ret. (%/y)	Prob. (%)	α (%/y)	β	T (%/d)	wmax (%)	wmin (%)
In-sample
0	4.389	0.433	−0.233	0.975	0.975	1.013	−1.85	45.16	−1.69	0.988	1.13	3.91	1.79
0.5	4.500	0.344	0.167	0.973	0.975	1.016	−0.85	47.98	−1.91	0.991	0.89	3.94	1.80
0.75	4.789	0.278	0.756	0.972	0.973	1.011	−0.47	50.00	−0.26	0.984	1.06	4.03	1.82
1	4.125	3.071	−1.554	0.965	0.961	1.048	1.14	48.00	0.53	1.006	6.19	4.55	1.73
1.0625	3.893	3.643	−2.018	0.964	0.955	1.039	2.28	46.77	2.38	0.992	7.57	4.76	1.73
1.125	3.857	4.018	−2.286	0.974	0.954	1.040	4.46	51.61	4.57	0.992	8.22	4.84	1.73
1.1875	3.804	4.393	−2.571	0.971	0.949	1.043	4.78	52.42	4.92	0.990	8.72	4.92	1.73
1.25	3.821	4.982	−3.000	0.982	0.947	1.039	7.41	55.65	7.63	0.984	9.48	4.98	1.72
1.375	4.286	5.179	−3.179	0.975	0.949	1.034	4.85	52.42	5.10	0.982	9.16	4.96	1.72
1.5	4.188	5.143	−3.179	0.981	0.948	1.038	5.68	50.81	5.90	0.984	9.34	4.97	1.72
2	4.100	5.245	−3.234	1.001	0.949	1.034	6.71	54.03	6.98	0.981	9.34	4.99	1.72
3	4.045	5.335	−3.278	1.031	0.948	1.035	7.23	54.84	7.50	0.981	9.49	5.00	1.72
4	3.970	5.578	−3.301	1.045	0.945	1.041	6.50	55.65	7.91	0.984	9.89	5.00	1.72
5	3.902	5.856	−3.310	1.093	0.943	1.047	7.87	55.65	8.05	0.987	10.08	5.00	1.73
Out-of-sample
0	4.389	0.433	−0.233	0.974	0.974	1.007	3.57	66.67	4.45	0.981	3.84	1.82	0.80
0.5	4.500	0.344	0.167	0.989	0.978	1.025	5.44	61.90	5.31	1.003	3.82	1.79	0.71
0.75	4.789	0.278	0.756	0.996	0.977	1.024	6.37	66.67	6.34	1.001	3.83	1.81	0.94
1	4.125	3.071	−1.554	0.971	0.962	1.003	2.33	54.76	3.95	0.965	4.20	1.79	7.18
1.0625	3.893	3.643	−2.018	0.968	0.956	1.006	2.88	50.00	4.68	0.961	4.37	1.79	8.46
1.125	3.857	4.018	−2.286	0.960	0.950	0.991	2.43	50.00	5.16	0.942	4.46	1.79	9.10
1.1875	3.804	4.393	−2.571	0.961	0.941	1.000	4.30	57.14	7.12	0.941	4.54	1.79	9.69
1.25	3.821	4.982	−3.000	0.942	0.930	1.020	2.48	54.76	4.92	0.948	4.62	1.80	10.43
1.375	4.286	5.179	−3.179	0.940	0.930	1.017	1.77	54.76	4.25	0.947	4.57	1.80	9.95
1.5	4.188	5.143	−3.179	0.941	0.932	1.020	1.54	54.76	3.85	0.950	4.58	1.80	9.99
2	4.100	5.245	−3.234	0.946	0.931	1.019	1.87	54.76	4.24	0.949	4.61	1.80	10.48
3	4.045	5.335	−3.278	0.972	0.927	1.027	3.90	52.38	6.18	0.952	4.63	1.80	11.61
4	3.970	5.578	−3.301	0.988	0.922	1.047	4.30	50.00	5.98	0.964	4.67	1.80	11.82
5	3.902	5.856	−3.310	1.031	0.919	1.056	5.82	54.76	7.23	0.970	4.70	1.80	10.95

Own elaboration.

Table 4.

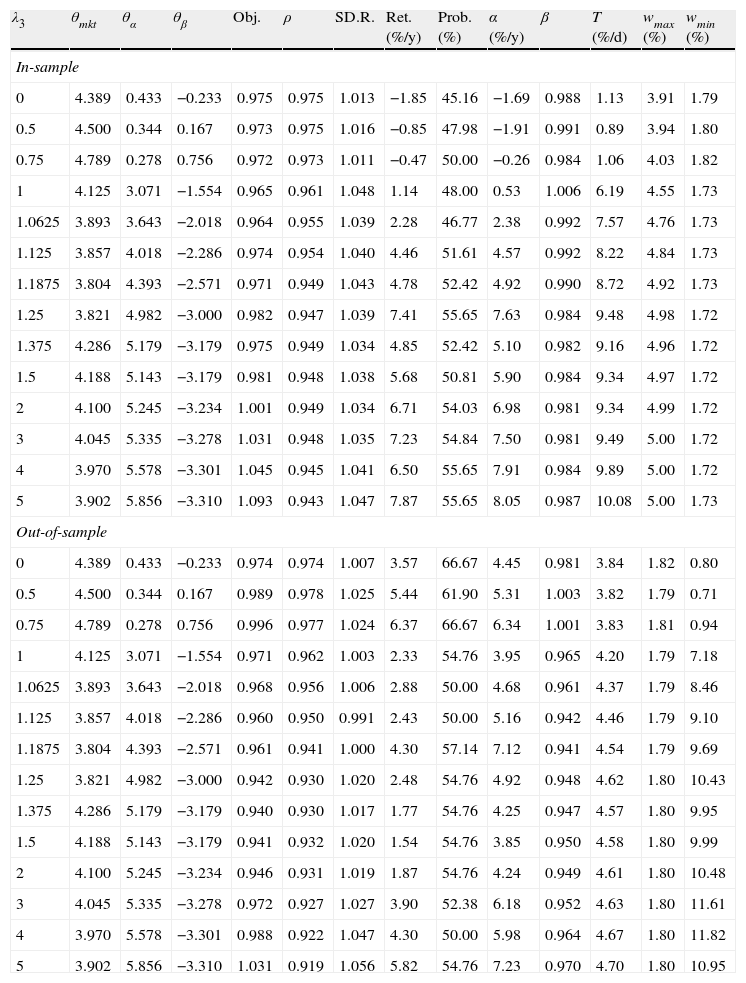
Results in-sample and out-of-sample for λ₁ = 1 and K = 50.

λ3	θmkt	θα	θβ	Obj.	ρ	SD.R.	Ret. (%/y)	Prob. (%)	α (%/y)	β	T (%/d)	wmax (%)	wmin (%)
In-sample
0	4.378	0.367	−0.044	0.982	0.982	1.005	−2.43	45.97	−2.25	0.986	0.78	3.34	1.36
0.5	4.656	0.389	0.811	0.978	0.981	1.022	−1.33	49.05	−2.31	1.002	1.21	3.45	1.37
0.75	4.567	0.878	0.767	0.976	0.980	1.026	−1.20	48.79	−1.31	1.005	1.88	3.44	1.37
1	4.875	2.661	−0.536	0.976	0.973	1.049	0.91	47.58	0.63	1.021	4.47	3.60	1.32
1.0625	4.893	2.911	−0.732	0.976	0.970	1.048	1.56	47.58	1.28	1.021	4.68	3.65	1.32
1.125	4.714	3.466	−1.268	0.975	0.966	1.050	1.90	53.23	1.67	1.018	5.78	3.82	1.32
1.1875	4.750	3.929	−1.679	0.984	0.965	1.049	4.17	51.61	4.01	1.012	6.73	3.93	1.32
1.25	4.696	4.375	−2.107	0.980	0.962	1.045	3.71	52.42	3.64	1.005	7.35	4.04	1.32
1.375	4.375	4.589	−2.482	0.986	0.958	1.040	5.19	54.84	5.24	0.997	8.27	4.15	1.32
1.5	4.357	4.714	−2.589	0.990	0.957	1.039	5.66	55.65	5.73	0.995	8.42	4.17	1.32
2	4.179	4.982	−2.750	1.003	0.955	1.036	6.23	57.26	5.54	0.990	8.77	4.22	1.32
3	3.911	5.232	−3.018	1.041	0.951	1.036	7.85	58.06	5.71	0.986	9.05	4.28	1.33
4	3.750	5.143	−3.000	1.055	0.952	1.034	6.72	58.87	6.23	0.984	9.25	4.29	1.33
5	3.714	5.214	−3.071	1.100	0.952	1.036	7.77	59.68	6.07	0.986	9.46	4.30	1.33
Out-of-sample
0	4.378	0.367	−0.044	0.981	0.981	1.004	6.60	64.29	7.34	0.985	3.28	1.34	0.86
0.5	4.656	0.389	0.811	0.998	0.982	1.027	8.40	69.05	7.97	1.009	3.26	1.38	1.37
0.75	4.567	0.878	0.767	0.994	0.978	1.020	5.80	61.90	5.93	0.997	3.20	1.41	2.31
1	4.875	2.661	−0.536	0.995	0.971	1.000	6.15	57.14	7.52	0.972	3.35	1.38	5.27
1.0625	4.893	2.911	−0.732	0.983	0.968	0.991	3.74	57.14	5.67	0.959	3.39	1.38	5.62
1.125	4.714	3.466	−1.268	0.968	0.968	1.001	0.10	47.62	1.55	0.968	3.52	1.37	6.85
1.1875	4.750	3.929	−1.679	0.973	0.959	1.006	3.06	52.38	4.72	0.965	3.62	1.37	7.55
1.25	4.696	4.375	−2.107	0.981	0.953	1.014	5.74	54.76	7.34	0.967	3.72	1.38	8.13
1.375	4.375	4.589	−2.482	0.968	0.944	1.022	4.48	54.76	6.14	0.965	3.81	1.38	8.89
1.5	4.357	4.714	−2.589	0.972	0.946	1.016	4.54	54.76	6.37	0.961	3.83	1.39	9.28
2	4.179	4.982	−2.750	0.982	0.940	1.024	5.45	57.14	7.27	0.962	3.90	1.38	9.92
3	3.911	5.232	−3.018	0.981	0.932	1.031	4.20	57.14	6.06	0.961	3.96	1.38	10.10
4	3.750	5.143	−3.000	1.011	0.936	1.041	4.90	57.14	6.13	0.974	3.98	1.38	10.08
5	3.714	5.214	−3.071	1.027	0.935	1.042	4.72	52.38	5.90	0.975	3.99	1.38	10.10

Own elaboration.

7.3.1

In-sample performance for θ = (θ_mkt, θ_α, θ_β)

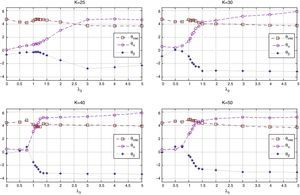
First, we study the behavior of the “optimal” coefficients as a function of the cardinality parameter K and the coefficient λ₃. Additionally, we assess the effect of λ₃ and K on the correlation coefficient, the portfolio return, the probability of out-performance, turnover and the average maximum and minimum weight given to an asset in the tracking portfolio.

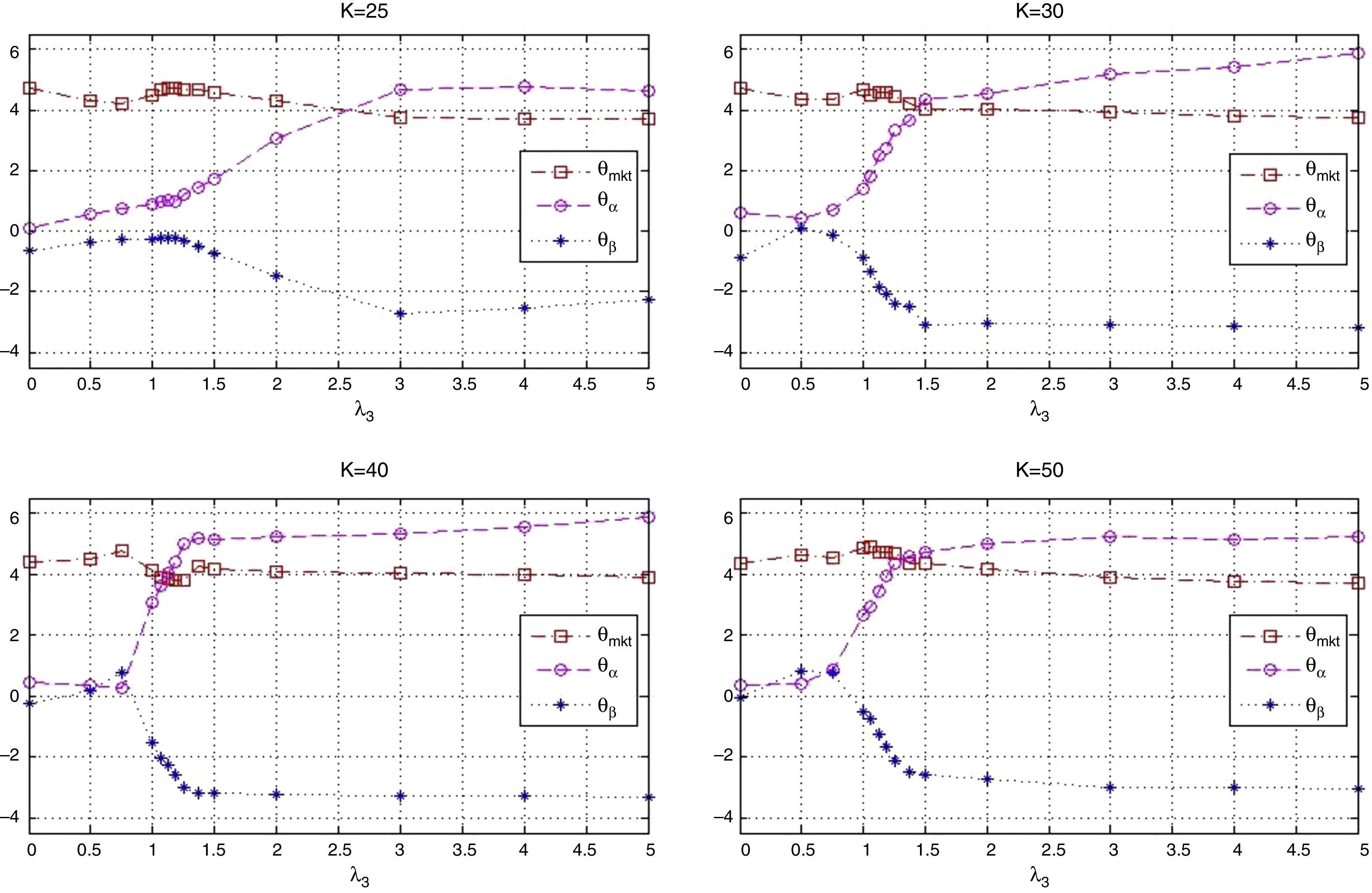
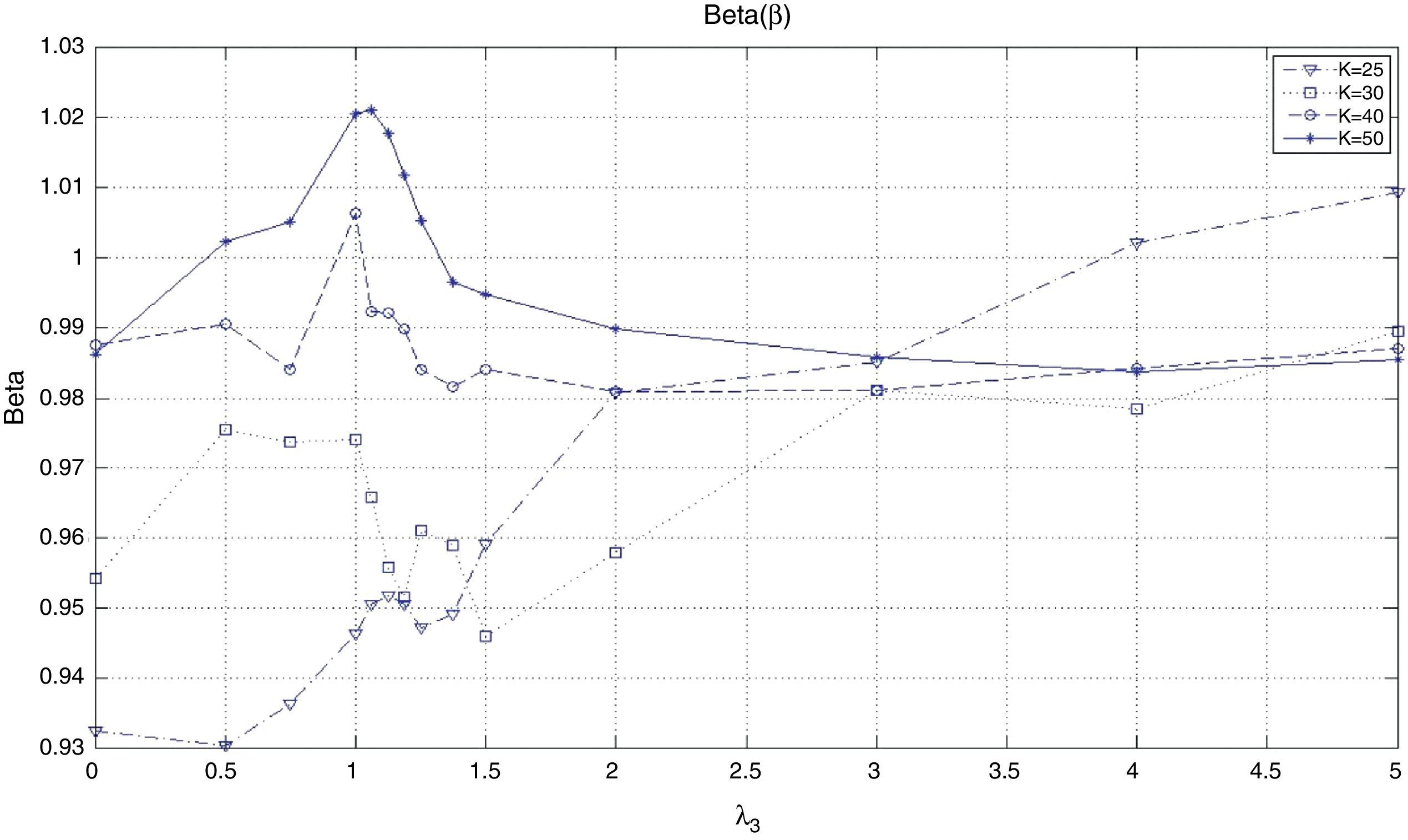
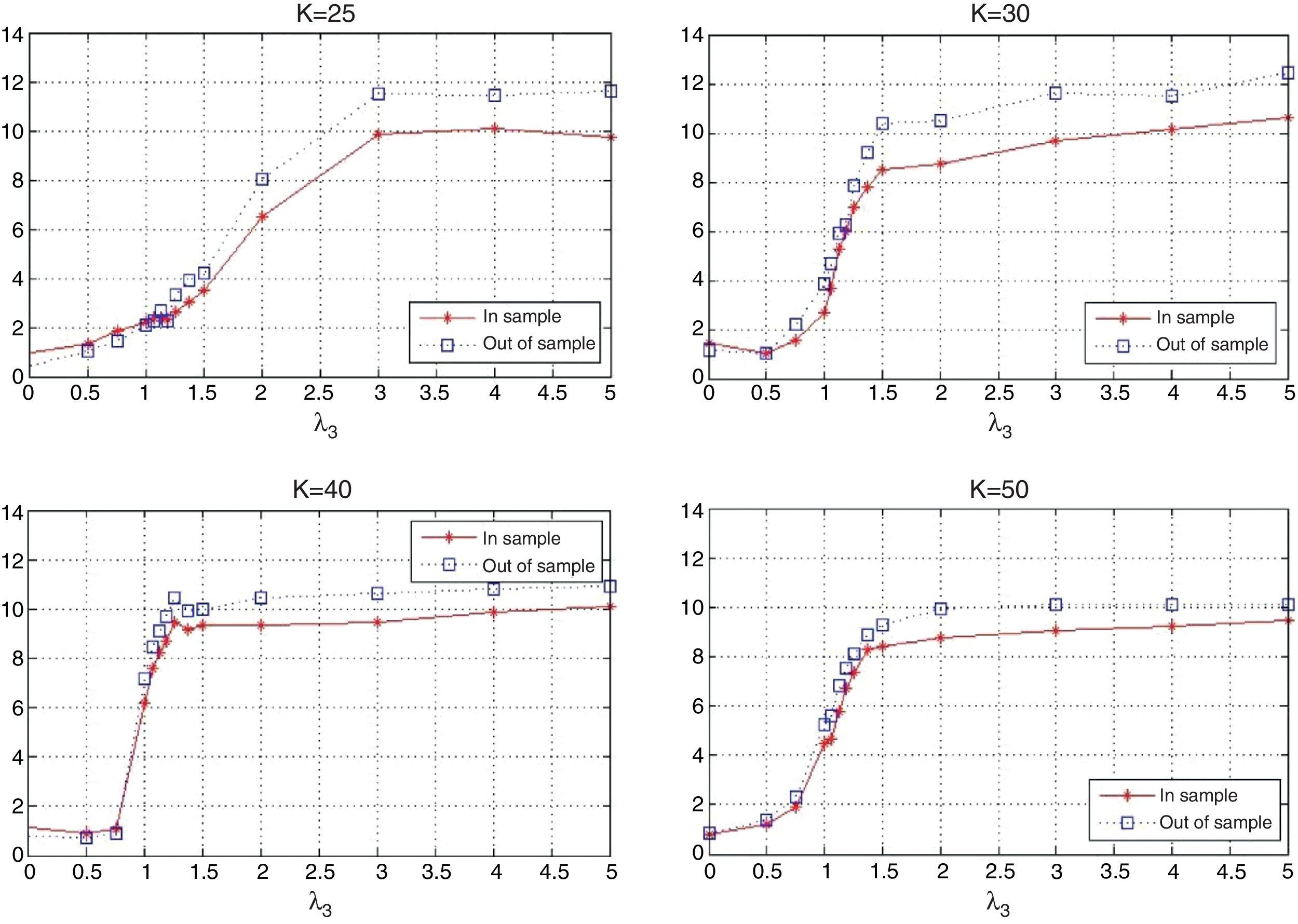
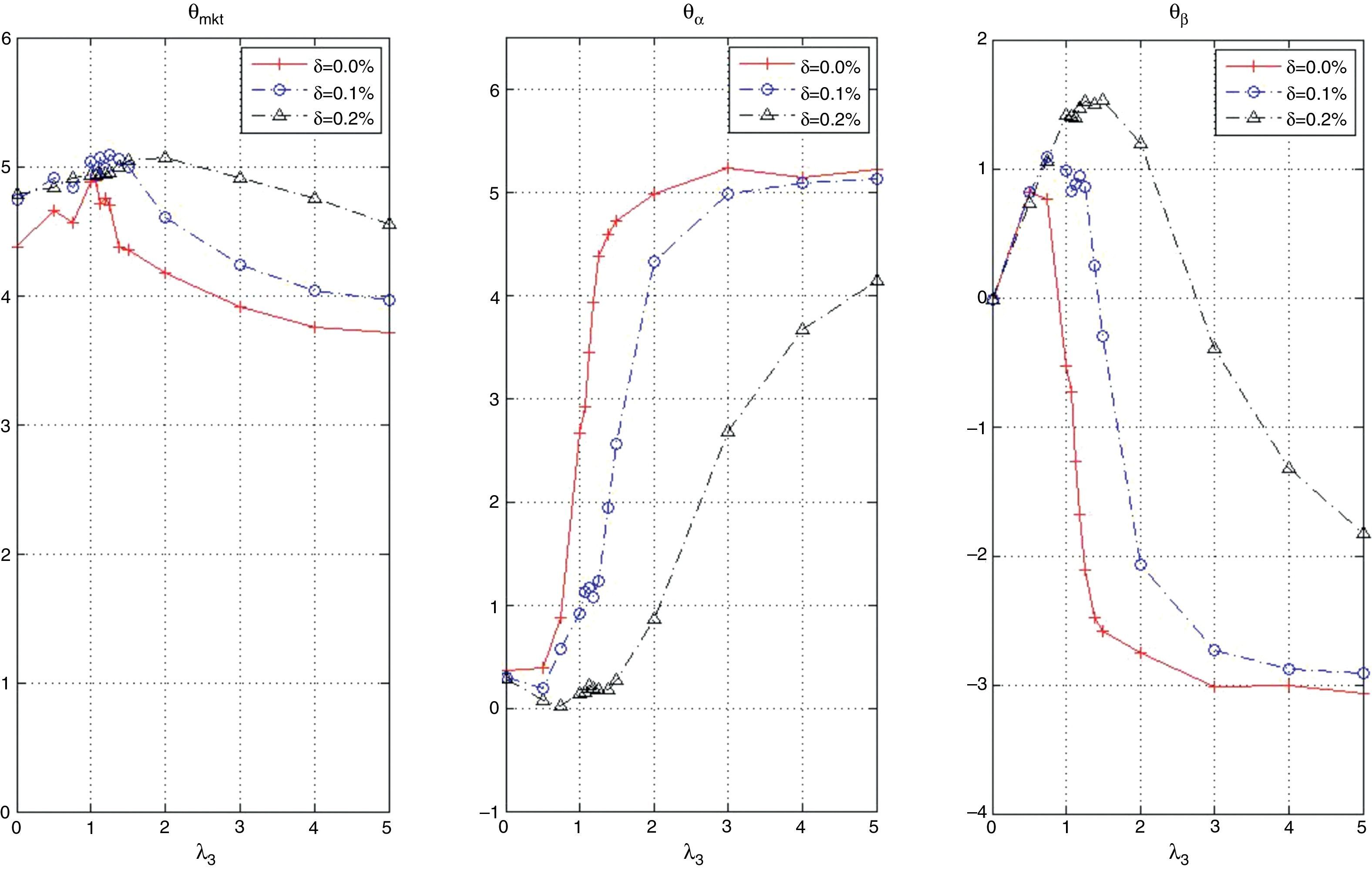
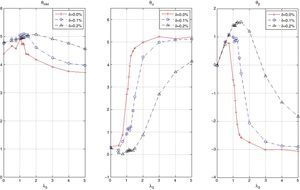
Fig. 7 shows the optimal value of the vector of coefficients. We observe that all plots show similar behavior. The “optimal” policies then appear independent of the cardinality of the tracking portfolio. For low values of λ₃, the more important characteristic is θ_mkt which takes positive values (around 4); on the other hand, θ_α and θ_β do not appear to be very significant. For tracking purposes, this suggests giving more weight to stocks with high market capitalization (relative to other stocks in the index). As we increase λ₃, and give more importance to the excess return of the tracking portfolio, we tend to increase the participation of stocks with high alpha and low beta deviation. By increasing θ_α, we put preference to stocks with a recent history of relatively high alpha; but, to maintain the variance ratio constant, it is necessary to include stocks with low beta deviation (|β−1|), i.e., stocks with beta close to one. Also, notice that, after certain values of λ₃, the behavior of the optimal characteristics is practically constant (λ₃ ≈ 3 for K ≈ 25, λ₃ ≈ 1.5 for K = 30, 40 and 50). In conclusion, the tracking performance is mostly given by stocks with high market capitalization, while the enhancement performance is given by stocks with high alpha; however, it is necessary to include stocks with low beta deviation to control the standard deviation ratio and to maintain relatively high correlation with the index.

Fig. 7.

Optimal coefficients (θ_mkt, θ_α, θ_β) as a function of λ₃ with λ₁ = 1, using the excess return as performance measure, and under the constraint that the standard deviations ratio should be ≤1.05.

Own elaboration.

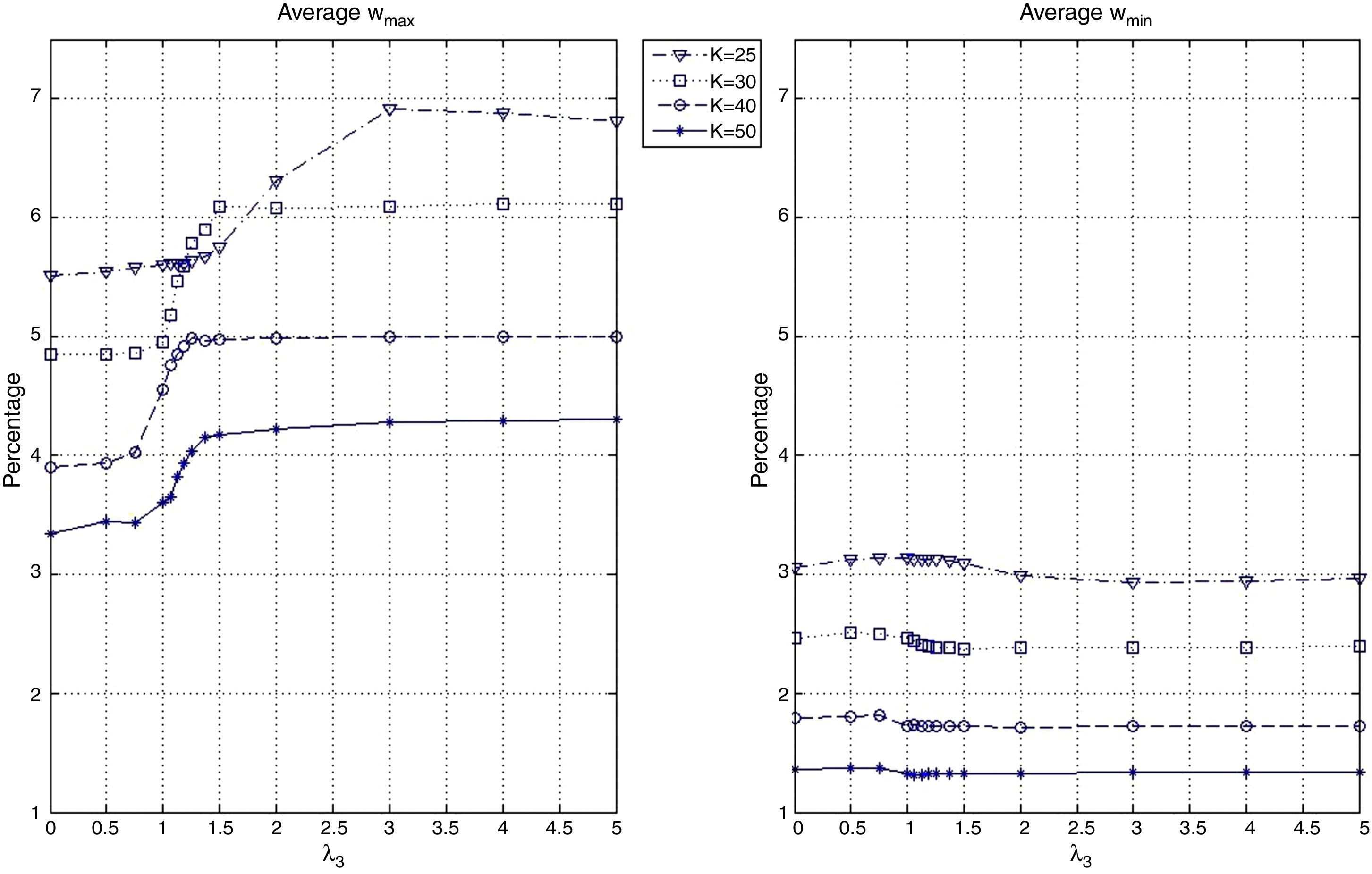
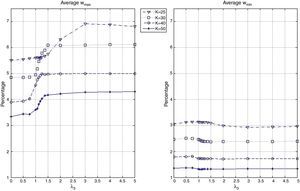
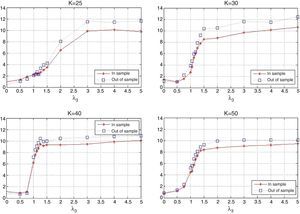
The behavior of the portfolio weights is shown in Fig. 8. We report the average maximum and minimum weights in the “optimal” tracking portfolios as a function of λ₃. In general, we can observe that the tracking portfolios tend to be well-diversified, avoiding excessive concentration in certain assets. They also avoid very small positions in the assets, especially for low values of K. For example, when K = 25, the average maximum weight is close to 7% while the average minimum weight is around 3%. For K = 50, the average maximum weight is close to 4% while the minimum weight is around 1.3%. Finally, as expected, the maximum and minimum weights are decreasing functions of K.

Fig. 8.

Average maximum (w_max) and minimum (w_min) weight in the tracking portfolio for different values of K and λ₃ using (y^mkt, y^α, y^β) as characteristics.

Own elaboration.

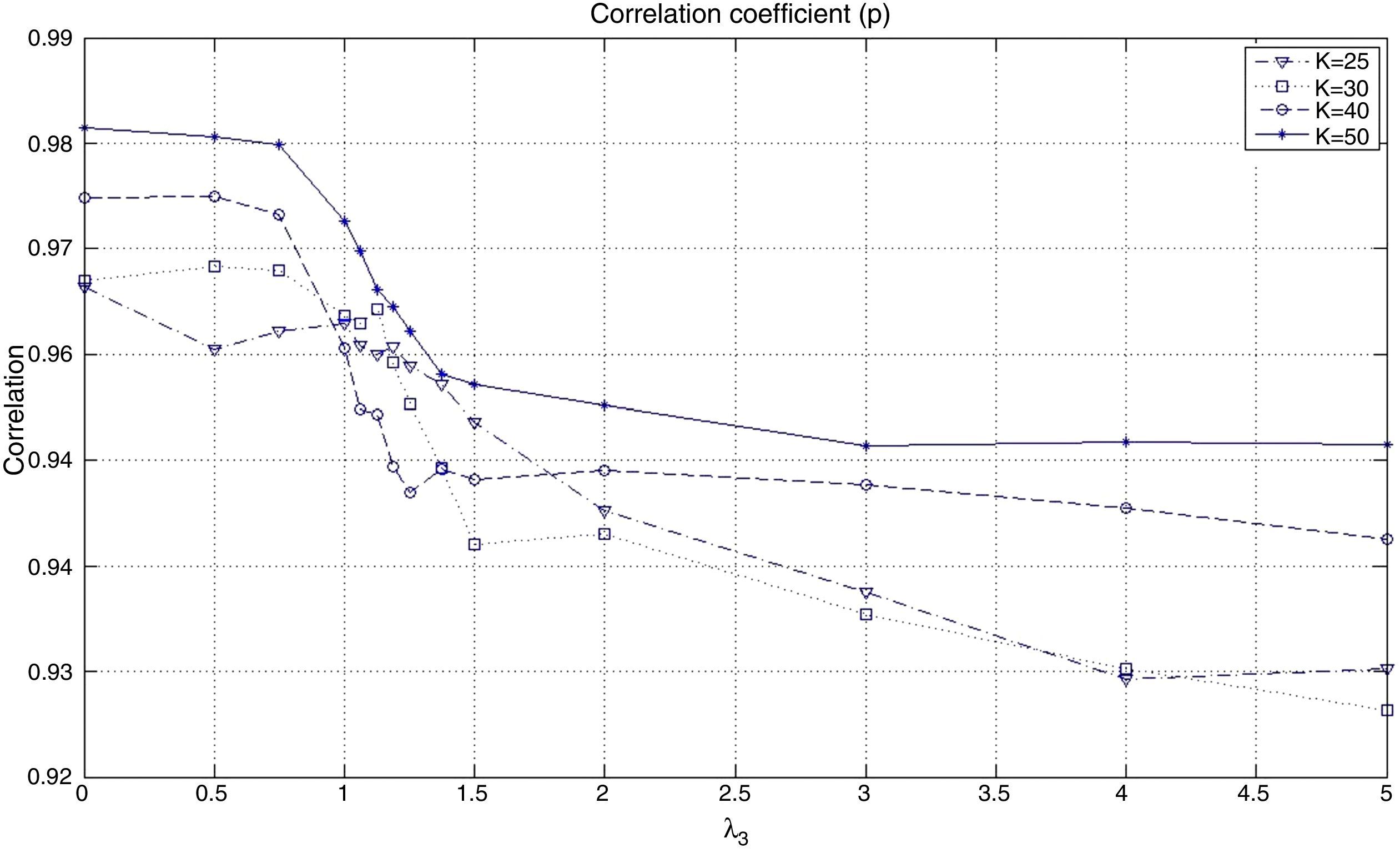
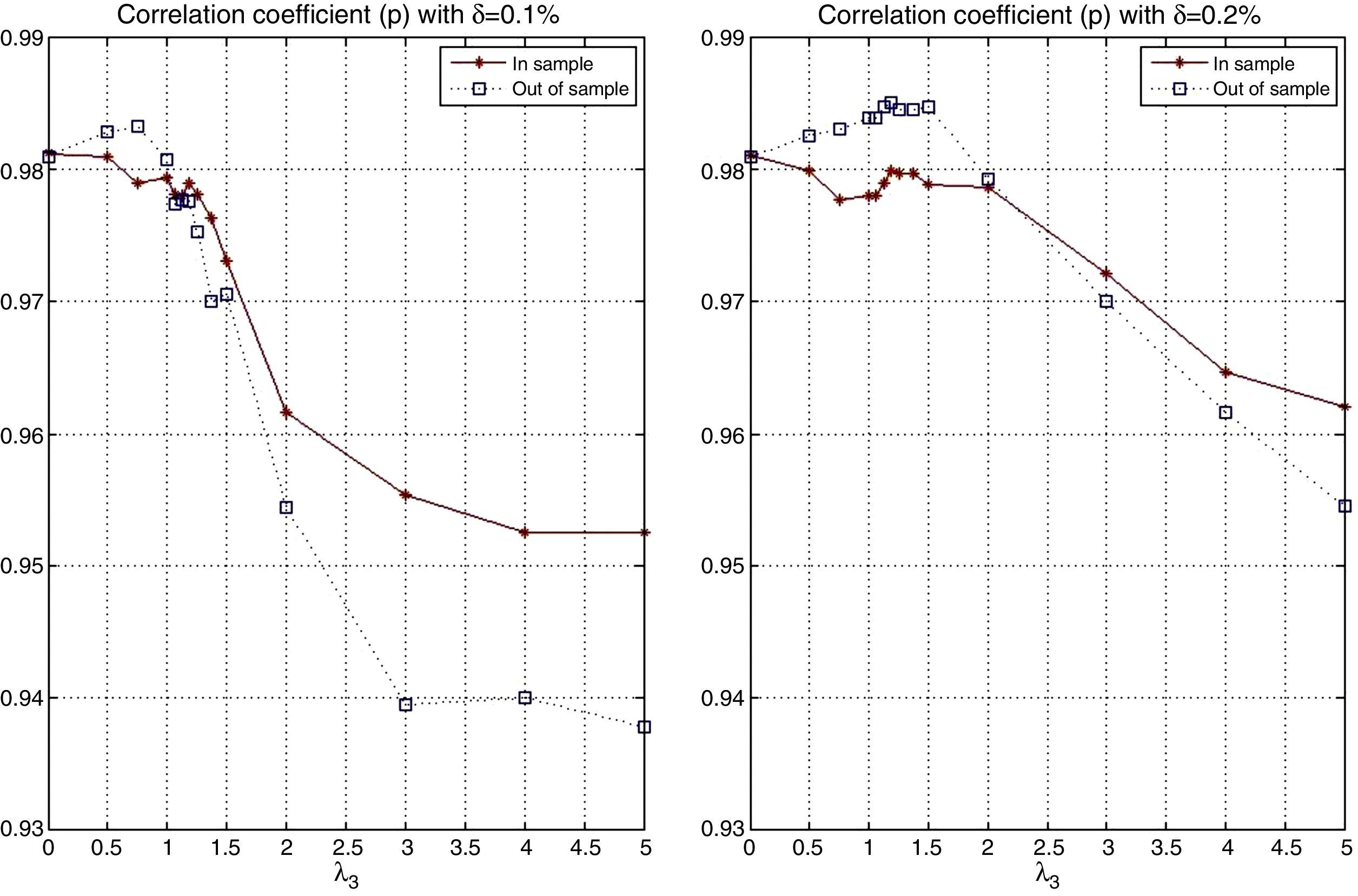
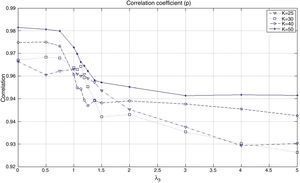
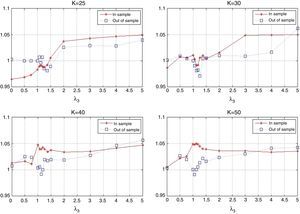
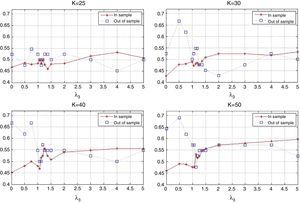
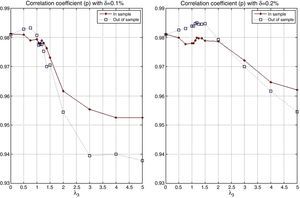
Fig. 9 shows the behavior of the correlation coefficient (ρ) of the tracking portfolio and the index for different values of λ₃ and K Notice that in general (for a fixed K), ρ is a decreasing function of λ₃, i.e., under “constant” variance the enhancement component tends to reduce the correlation to search for more profitable stocks. When λ₃ = 0 with K = 50, we have ρ ≈ 0.98 and with K = 25 we have that ρ ≈ 0.97. However, for λ₃ = 5 and K = 50 we have ρ ≈ 0.95, and ρ ≈ 0.93 when K = 25. Additionally, as expected, the correlation coefficient is generally higher for higher values of K (especially for low values of λ₃). This observation indicates that diversification improves the performance relative to ρ.

Fig. 9.

Correlation coefficient of the tracking portfolio for different values of K and λ₃ using (y^mkt, y^α, y^β) as characteristics.

Own elaboration.

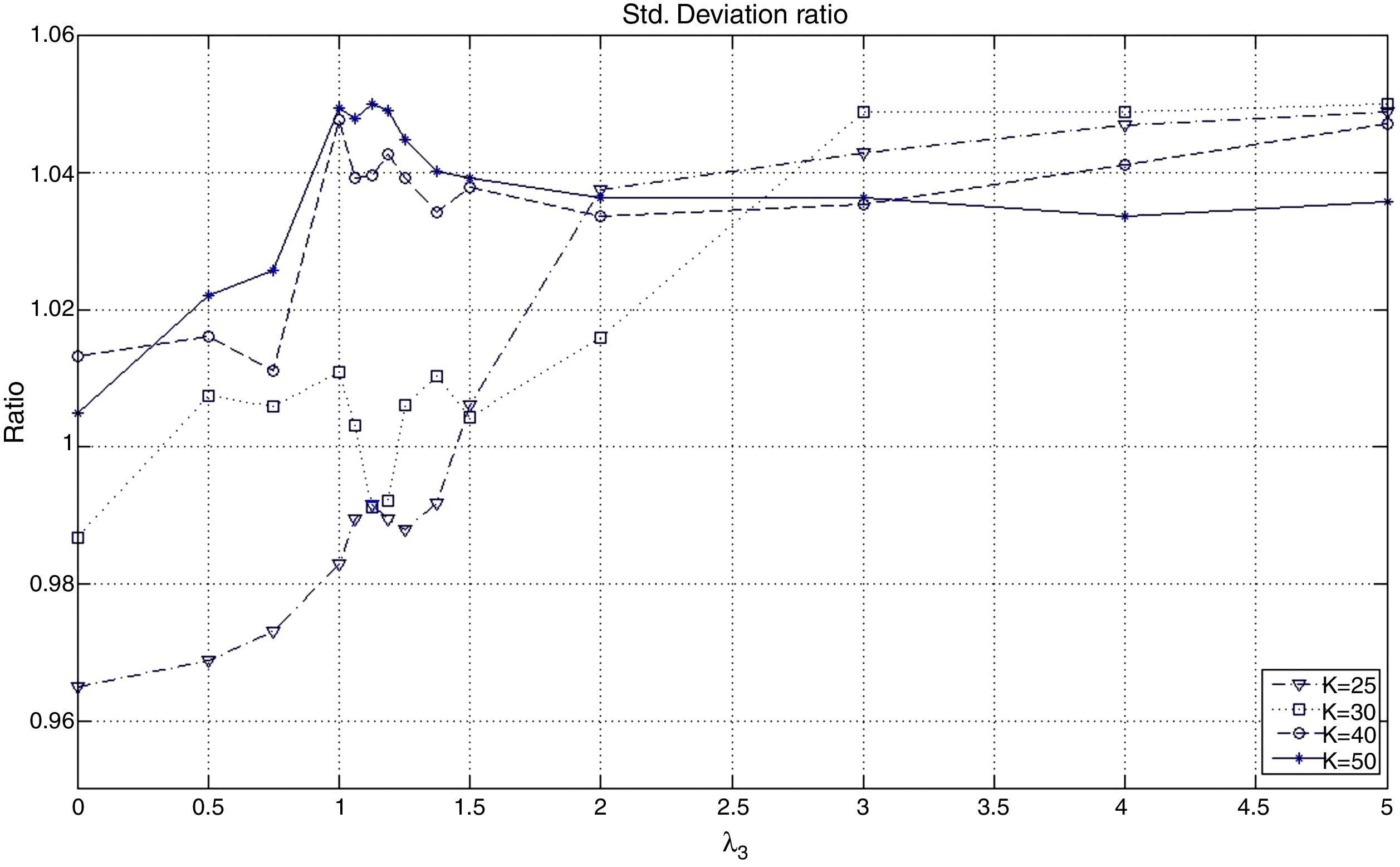
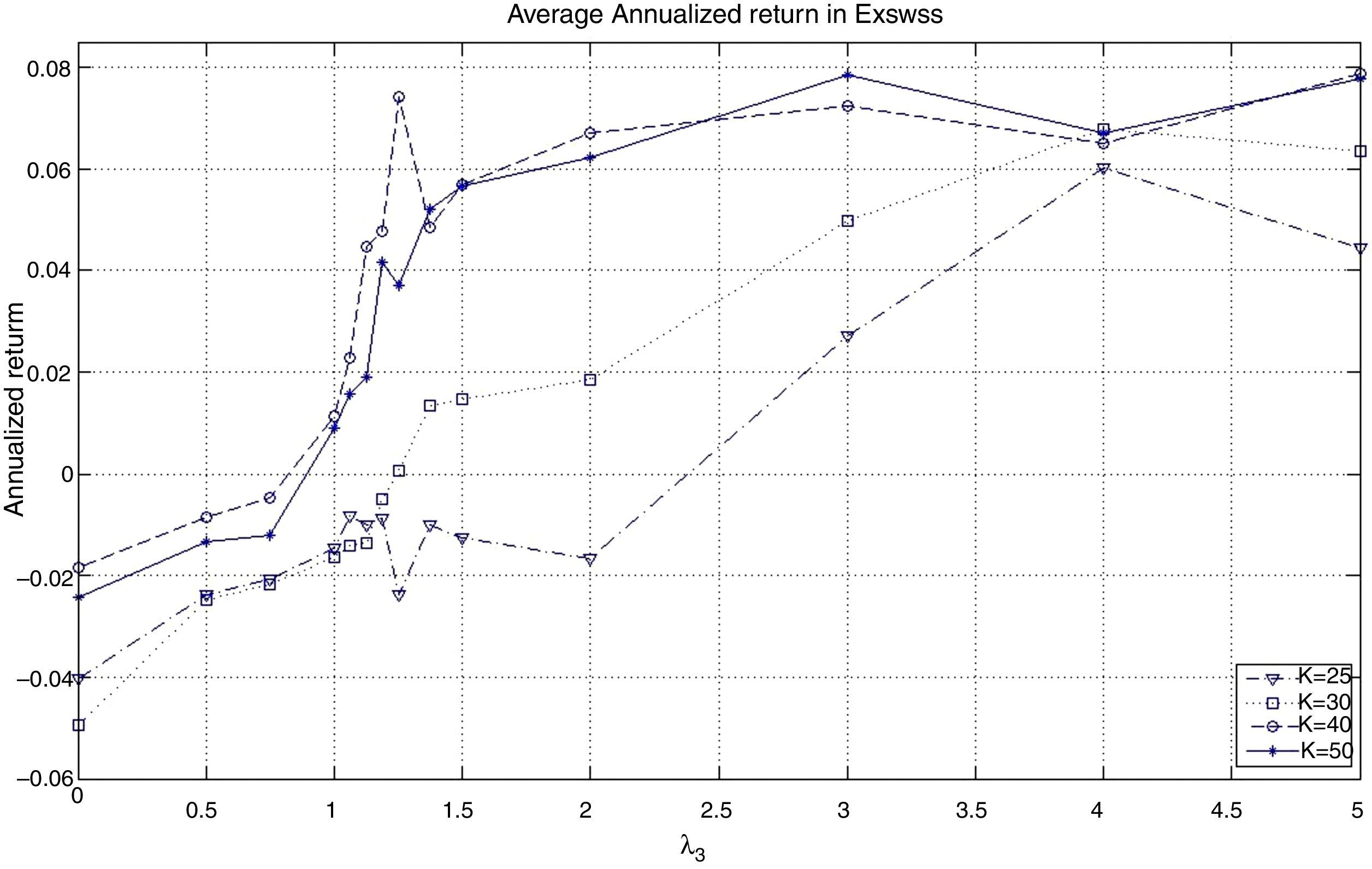
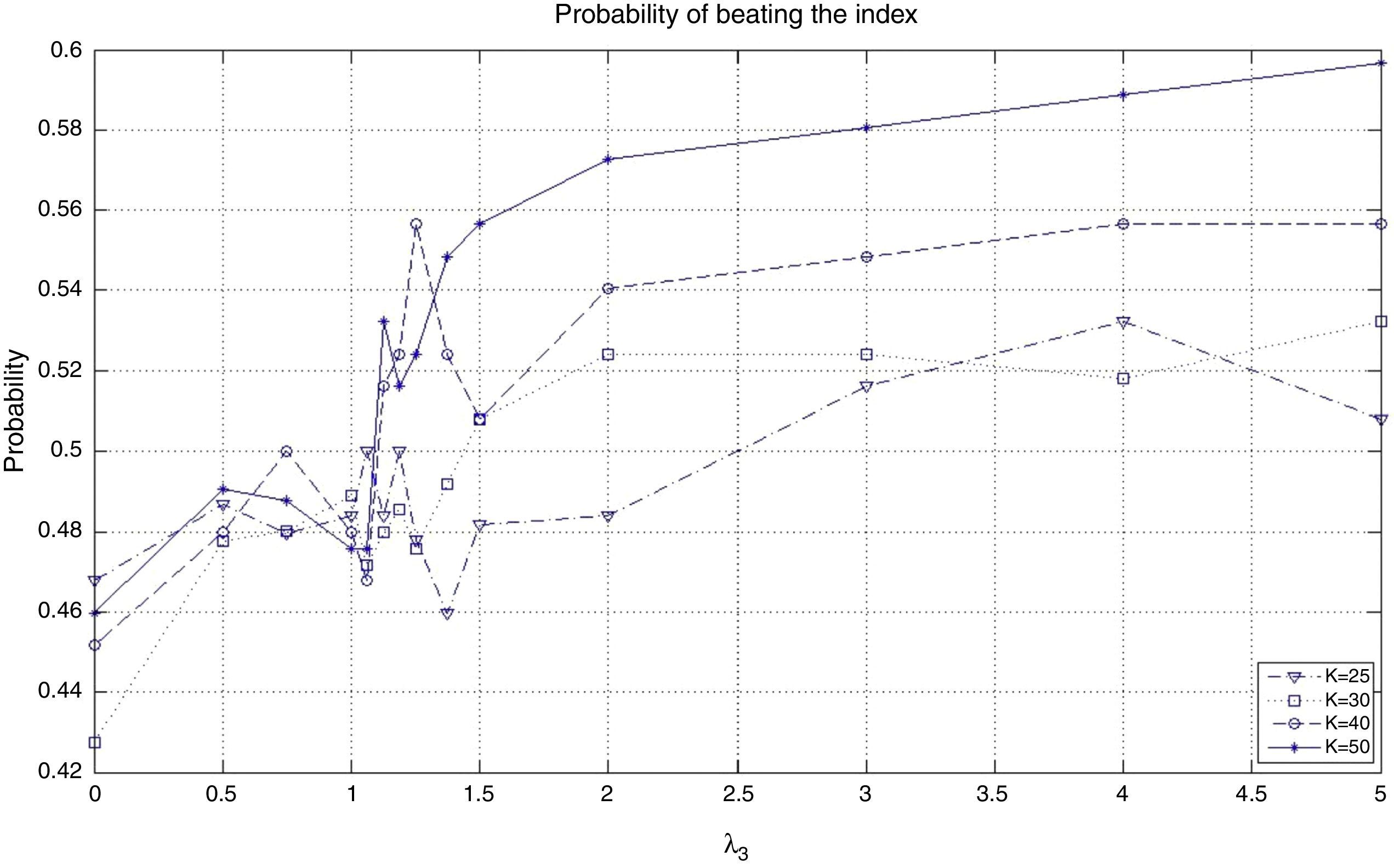
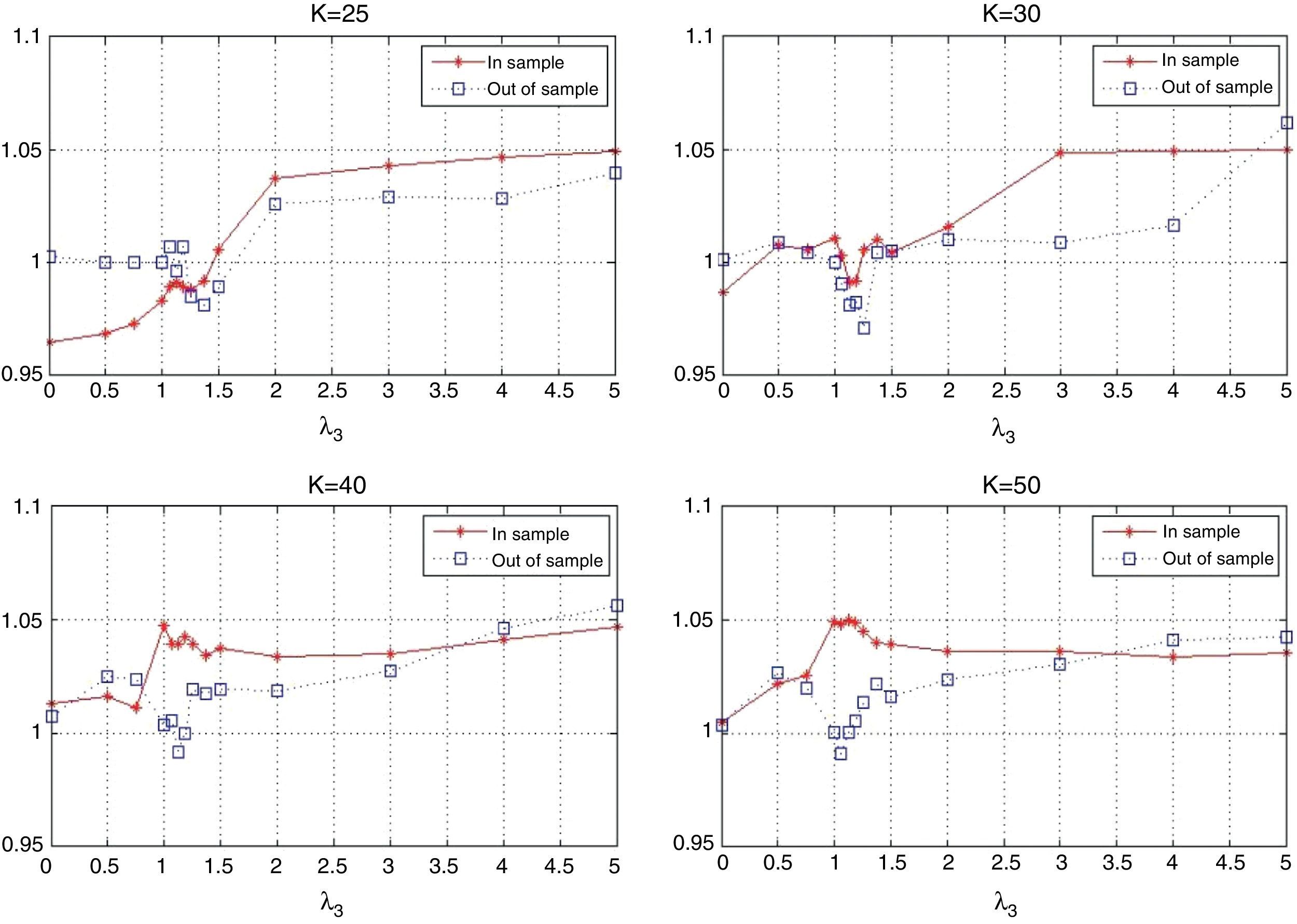
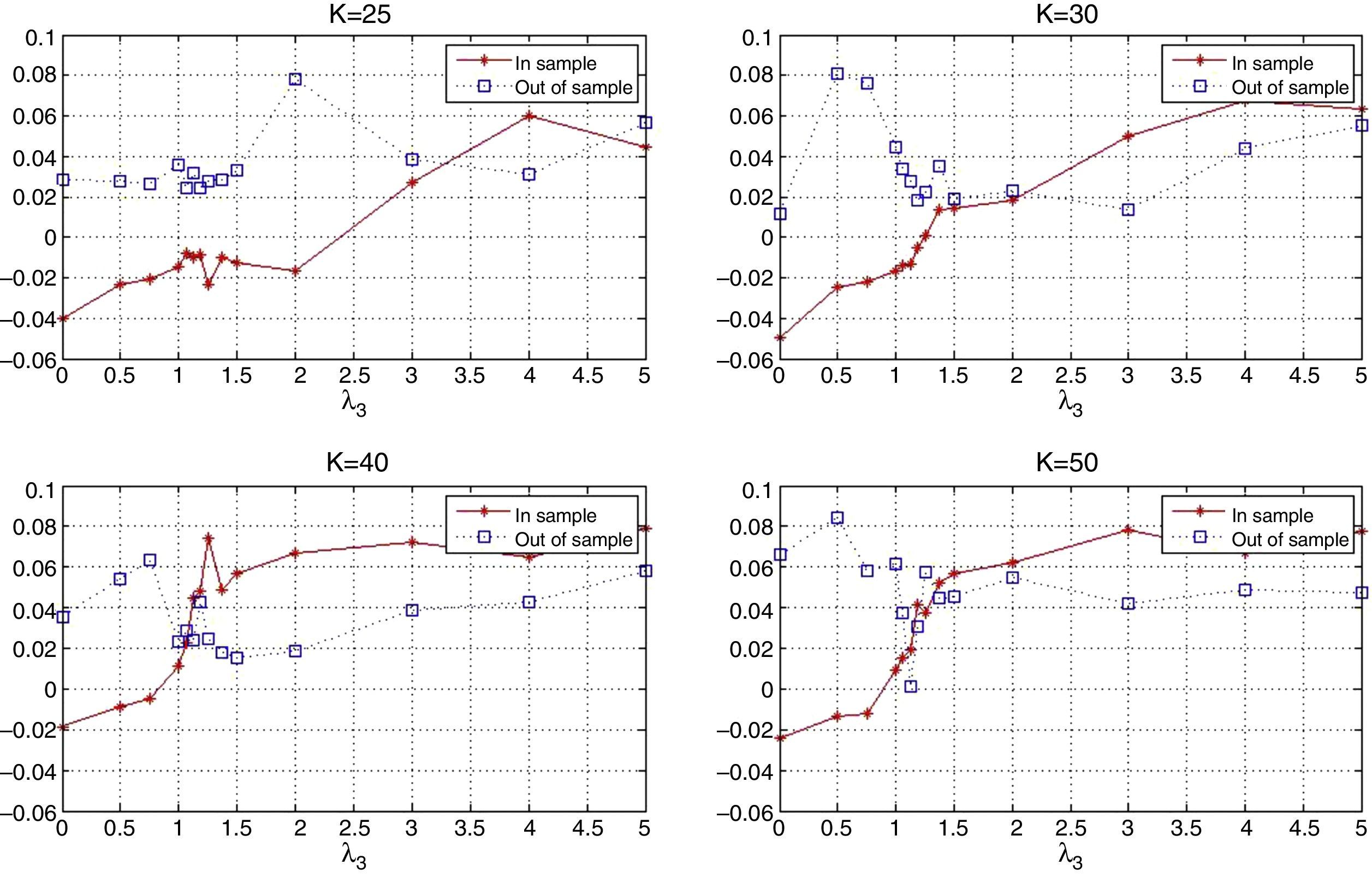
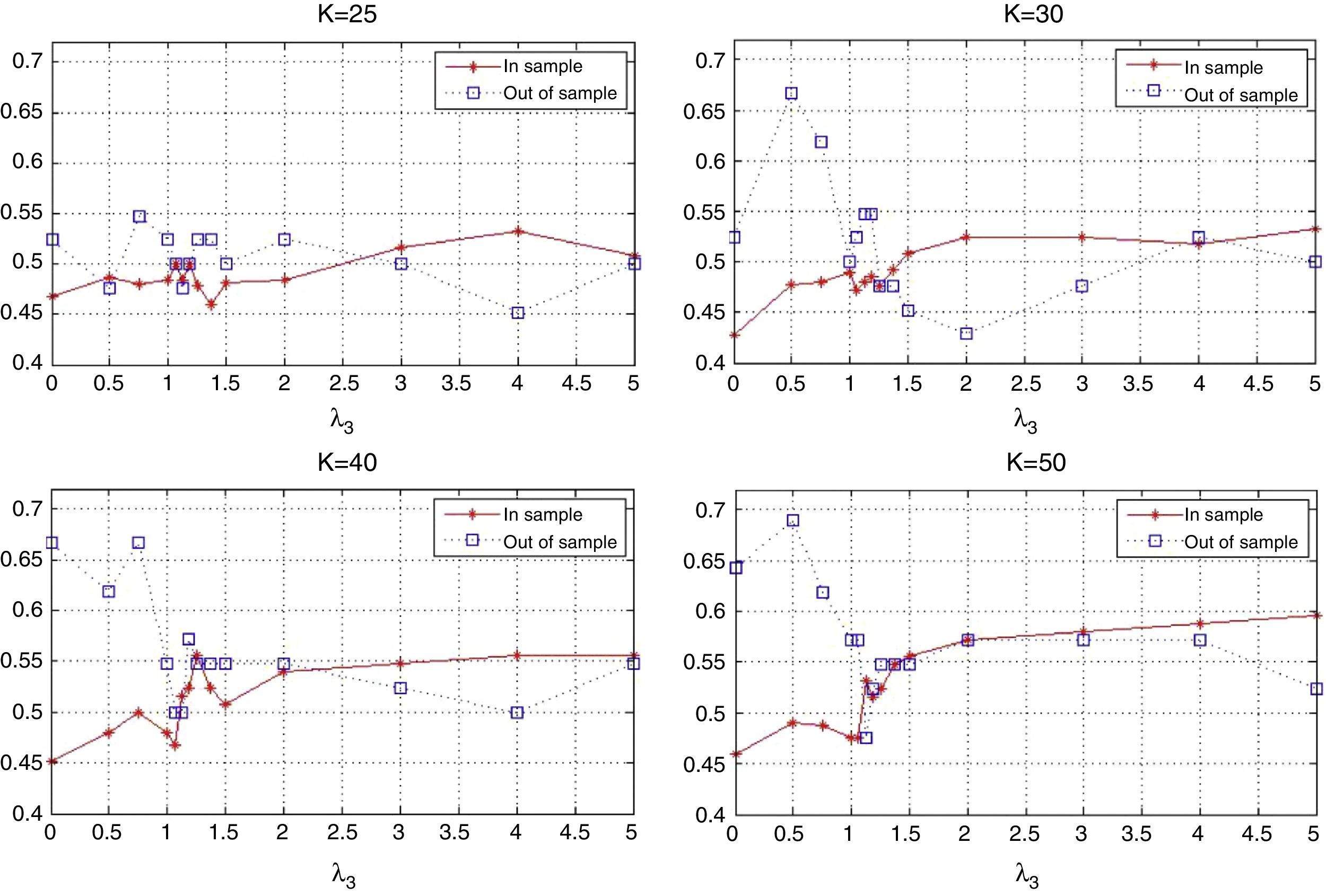
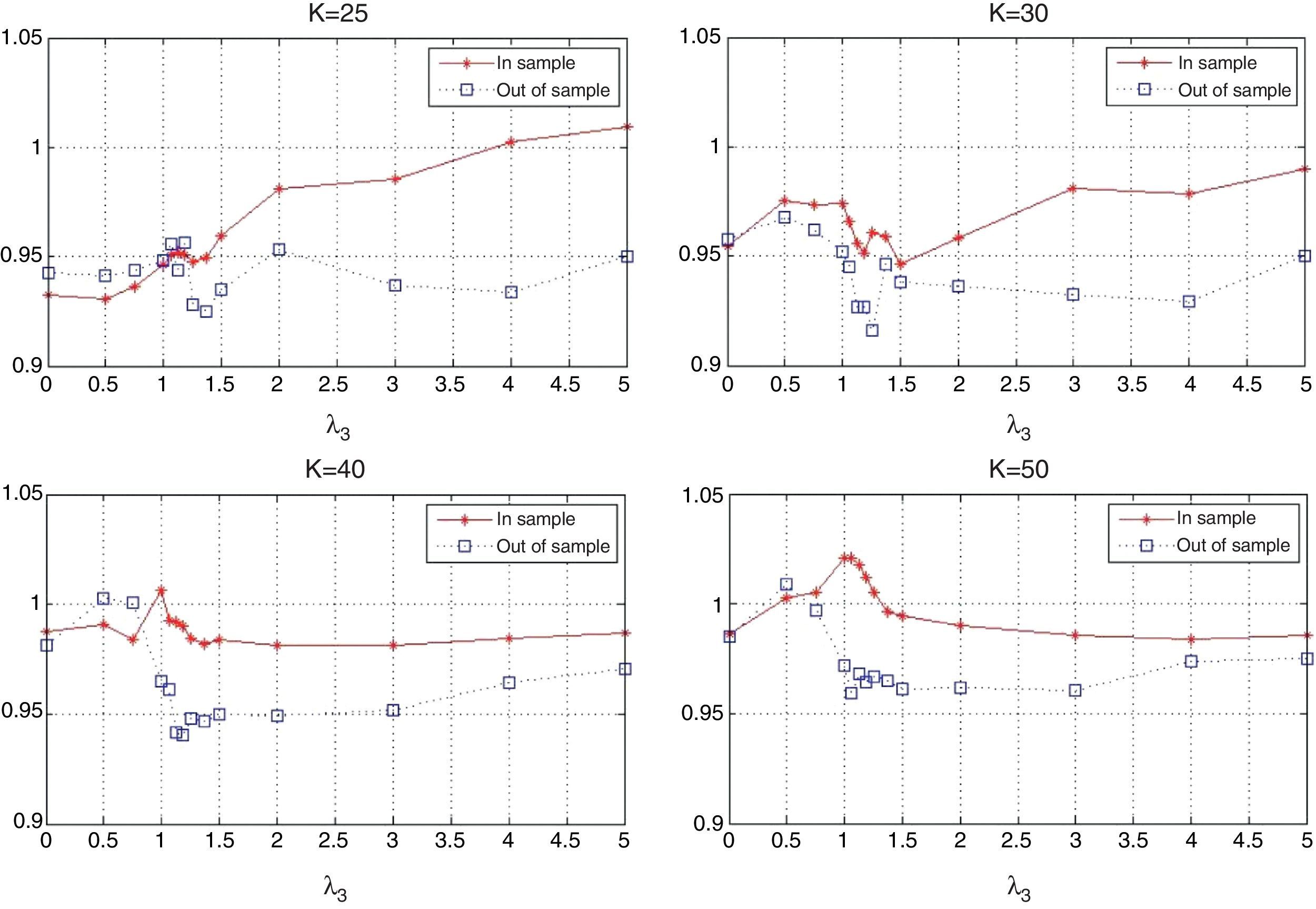
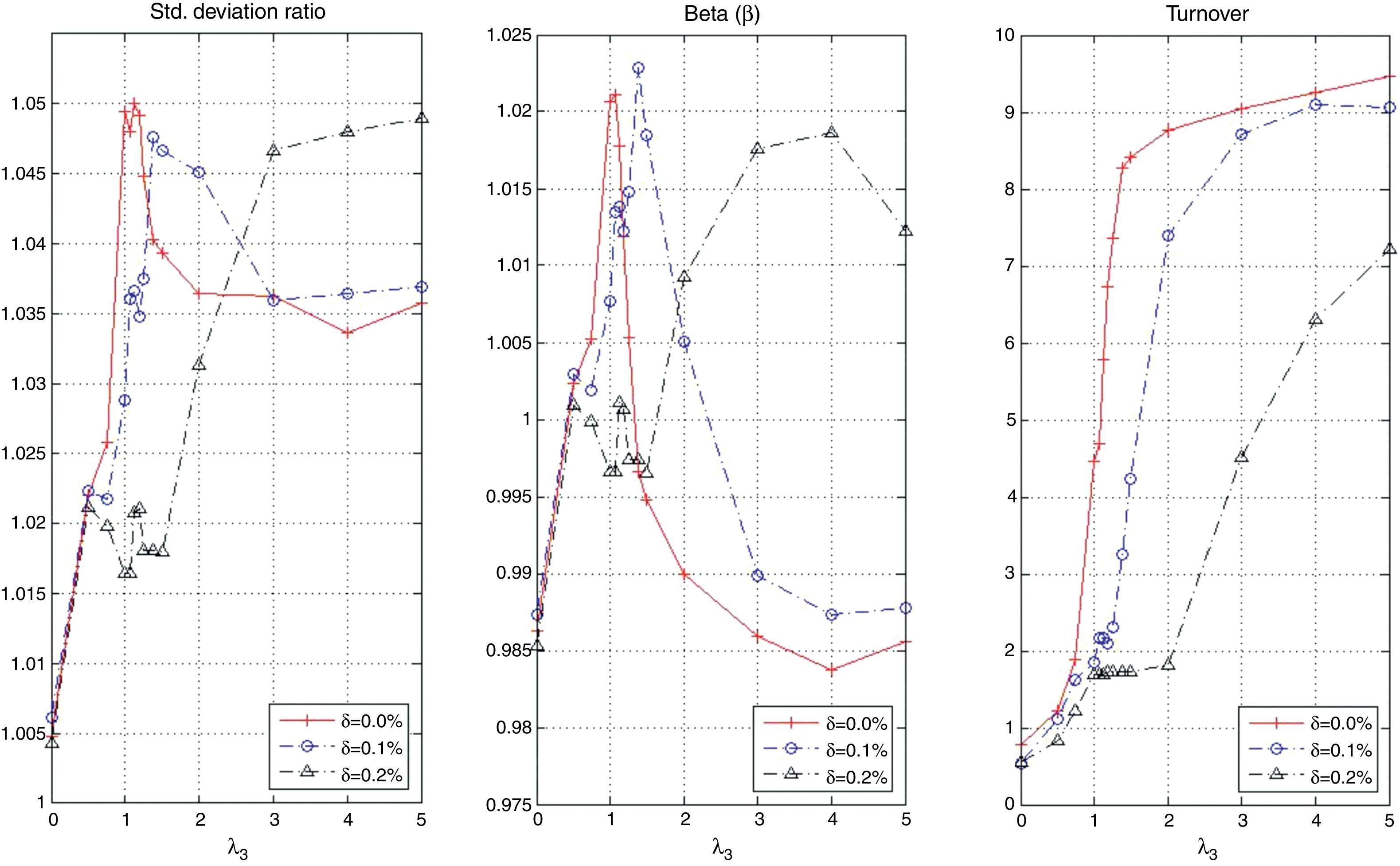
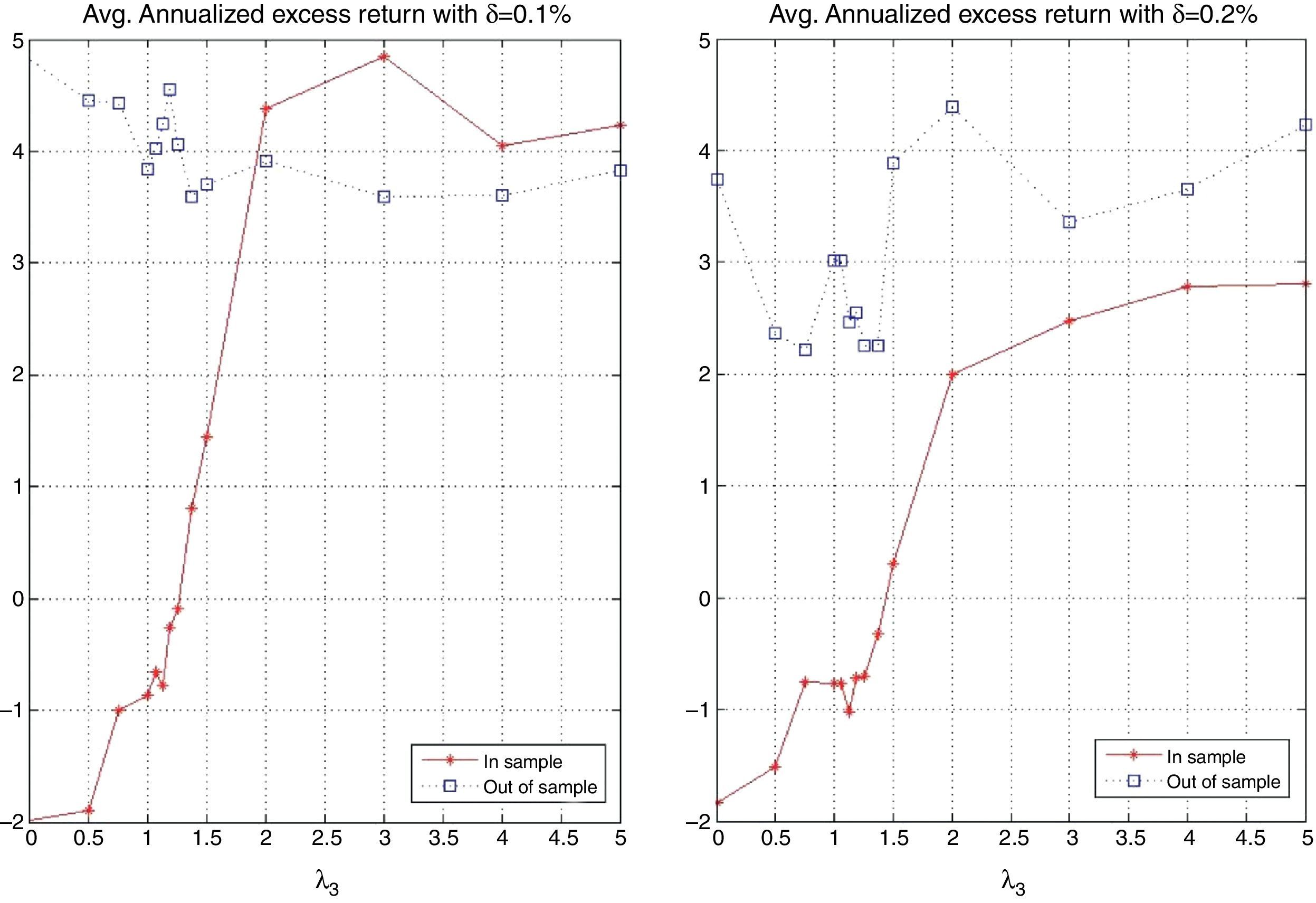
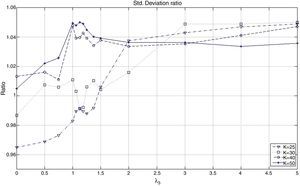
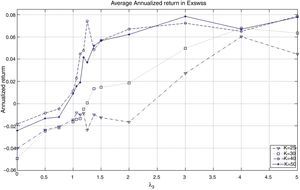
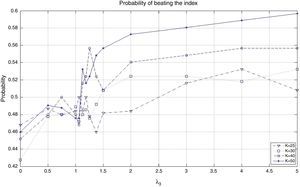
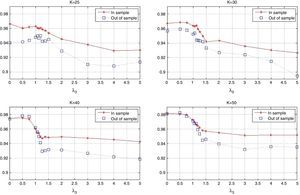
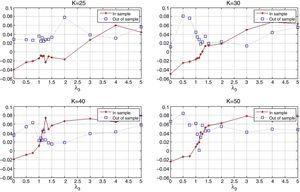
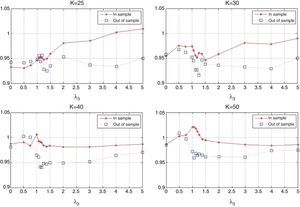
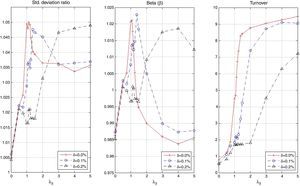
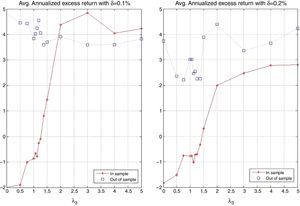
The behavior of the standard deviation ratio is shown in Fig. 10. By construction, the ratio should be less than 1.05 (recall that the reported values are reported for the vector of average coefficients). Notice that for low values of λ₃, the variance ratio tends to be smaller due to the presence of high market capitalization stocks that generally are less volatile than the index. But, as λ₃ increases, so do positions in riskier stocks, increasing the ratio. Figs. 11 and 12 show, respectively, the behavior of the expected annualized return of the tracking portfolio (in excess of the index), and the probability that the tracking portfolio beats the index. Both variables present the similar logical pattern, i.e., as λ₃ increases, the corresponding variable tends to increase; but, for high values of λ₃, both variables tend to stabilize. Hence, in general, the higher the K, the higher the return and the probability of out-performance. This means that more α-aggresive and diversified portfolios show higher probability of beating the index under a similar variance.

Fig. 10.

Ratio of standard deviations of the tracking portfolio with respect to the index for different values of K and λ₃ using (y^mkt, y^α, y^β) as characteristics.

Own elaboration.

Fig. 11.

Average annualized return in excess of the tracking portfolio with respect to the index for different values of K and λ₃ using (y^mkt, y^α, y^β) as characteristics.

Own elaboration.

Fig. 12.

Probability to beat the index of the tracking portfolio for different values of K and λ₃ using (y^mkt, y^α, y^β) as characteristics.

Own elaboration.

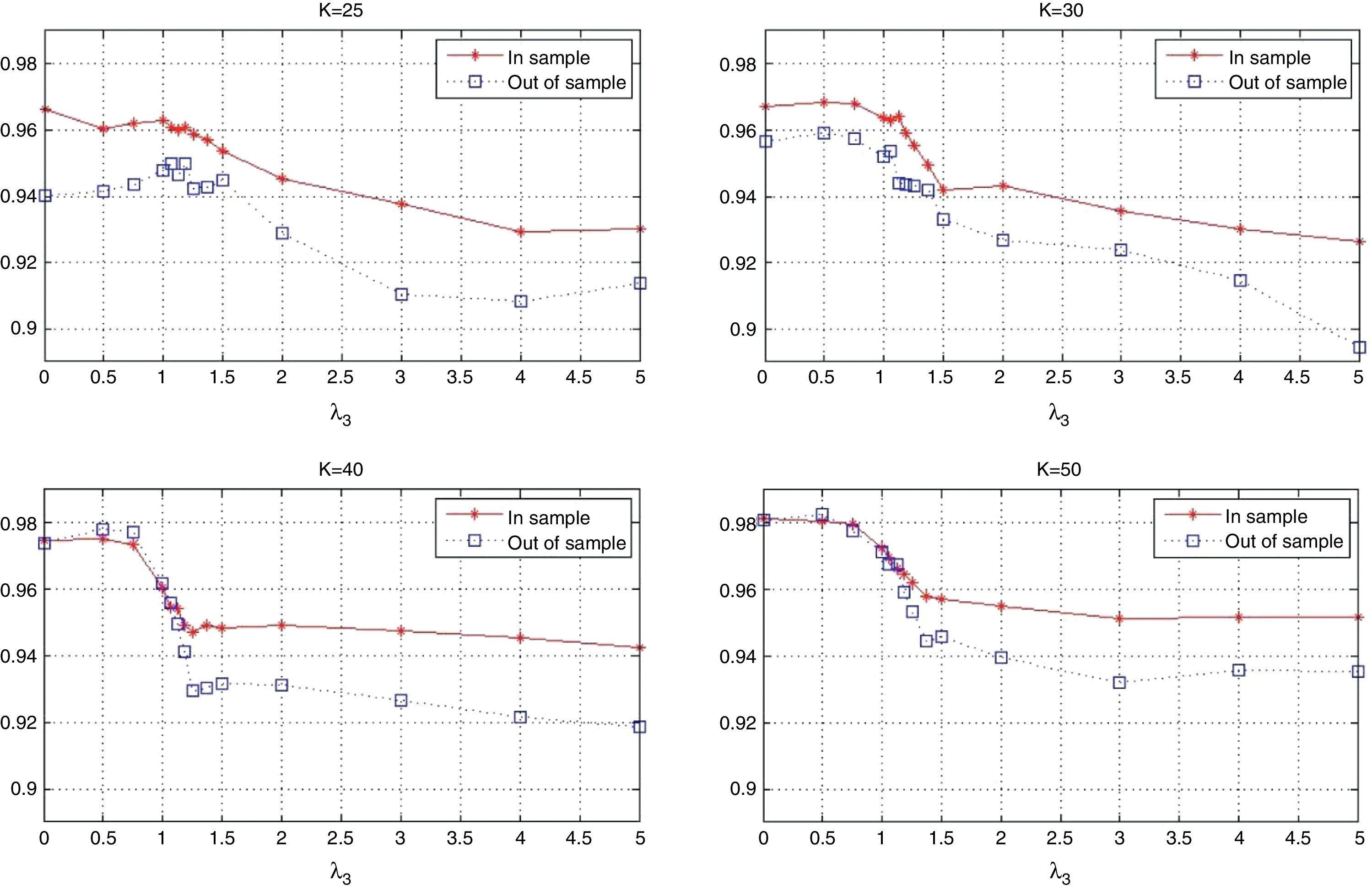
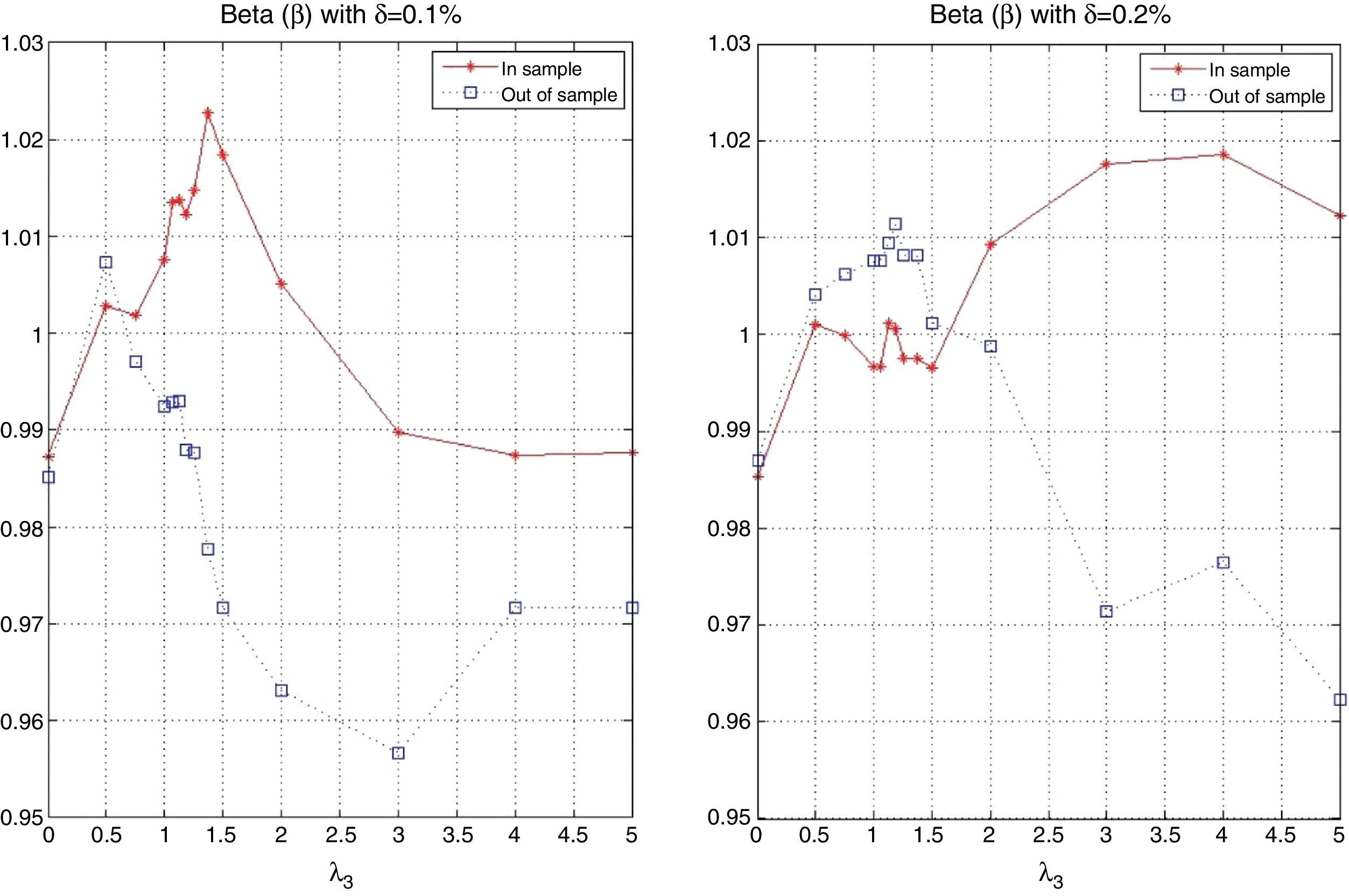
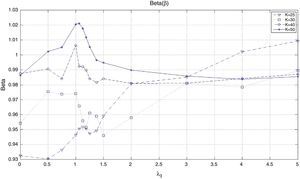
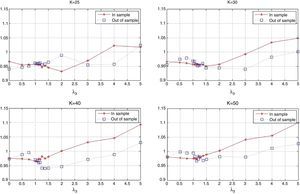
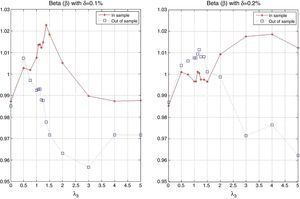
Fig. 13 displays the in-sample beta (β) for the different tracking portfolios. For K = 25, K = 30 and low and moderate values of λ₃, the tracking portfolios tend to produce values of β lower than one. This can be explained by the presence of stocks with high market capitalization which usually have smaller betas than one. However, for λ₃ approximately greater than 2.5, beta remains almost constant fluctuating between 0.98 and 0.99. In the case of K = 40 and K = 50, because of the greater level of diversification, beta fluctuates between 0.98 and 1.02 for all values of λ₃, i.e., basically the loss in ρ is compensated by an increment in the ratio of standard deviations.

Fig. 13.

Beta (β) of the tracking portfolio for different values of K and λ₃ using (y^mkt, y^α, y^β) as characteristics.

Own elaboration.

Notice that an investor can construct a tracking portfolio that matches the returns of the index (excess return close to zero) by choosing the appropriate trade-off parameter λ₃. For example, in the case of K = 50, the corresponding λ₃, that generates a tracking portfolio with approximately zero excess return over the index is between 0.75 (annualized excess returns of −1.20%) and 1 (annualized excess returns of 0.91%). To find a λ₃, that generates closer returns, the investor can perform a line search. Additionally, note that tracking policies for low values of λ₃ depend heavily on the inclusion of stocks with relative high market capitalization. Consequently, this generates portfolio strategies that are heavily concentrated in one class of assets and might produce excessive dependence on the performance of that group. This observation recommends choosing tracking policies which offer greater levels of diversification even though they may lose some tracking performance.

7.3.2

Out-of-sample performance for θ = (θ_mkt, θ_α, θ_β)

The out-of-sample period consists of the 42 trading days (2 months) immediately following the calibration period. The main issue of the out-of-sample performance is to check whether the optimal in-sample portfolio policy (vector of coefficients) is robust, i.e., whether the main properties of the in-sample period are preserved. To perform a “hard” out-of-sample test, we maintain the value of the vector of coefficients fixed at their optimal in-sample value during the testing period, i.e., we do not update the value of the vector as new information arrives. We present the comparison between the in-sample and out-of-sample performance for all the variables considered in the previous section and additionally includes the tracking portfolio turnover.

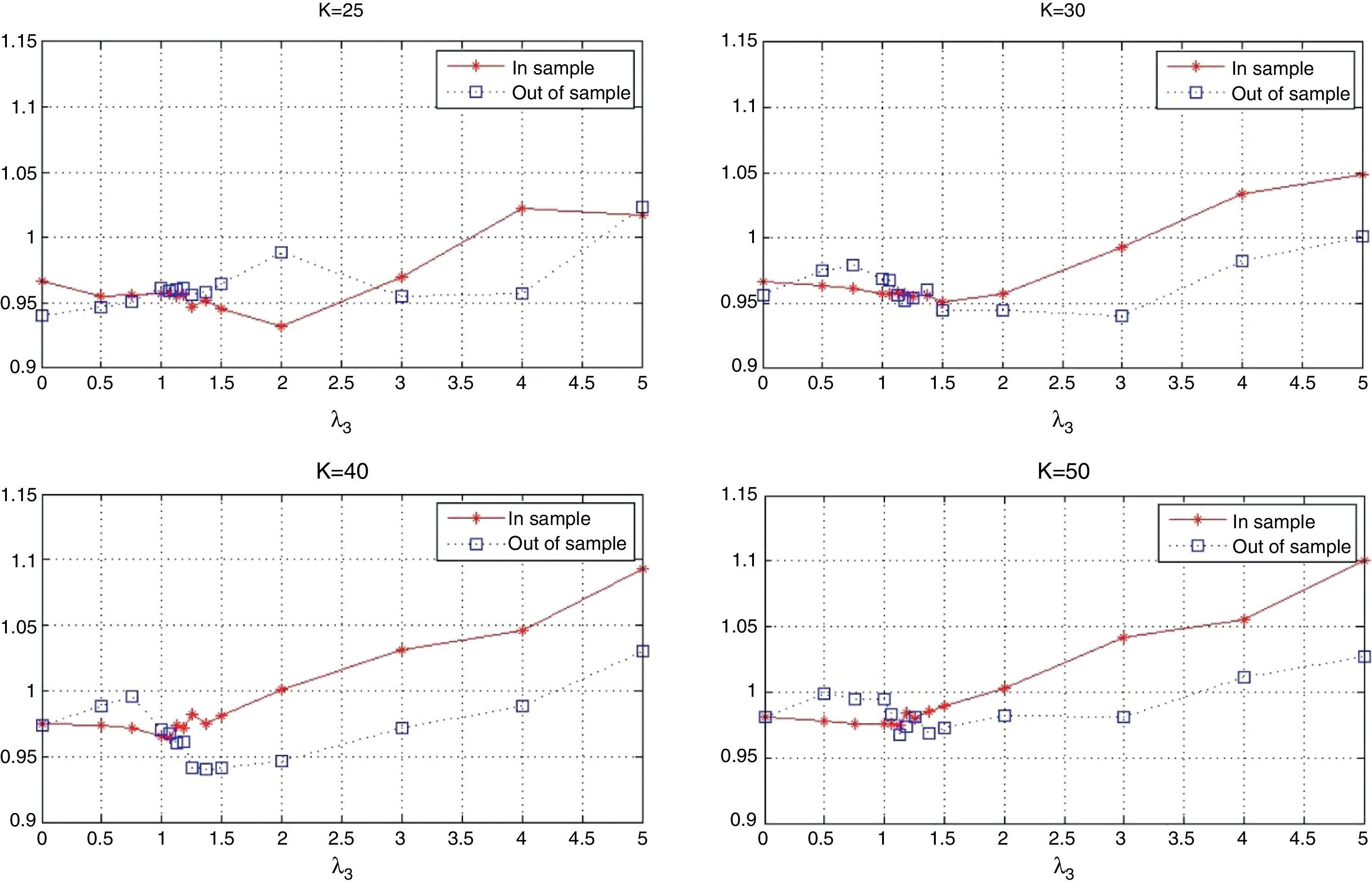
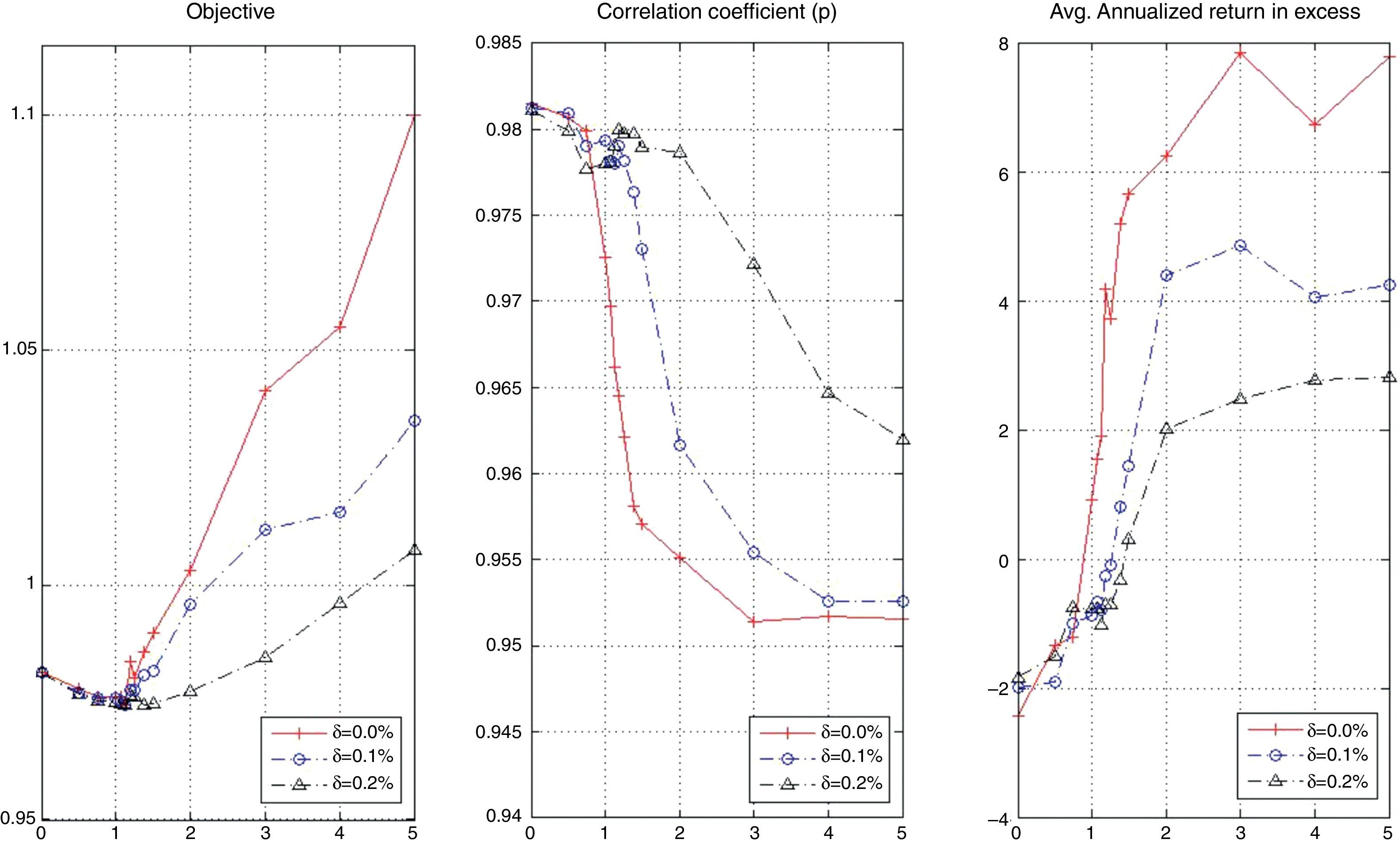
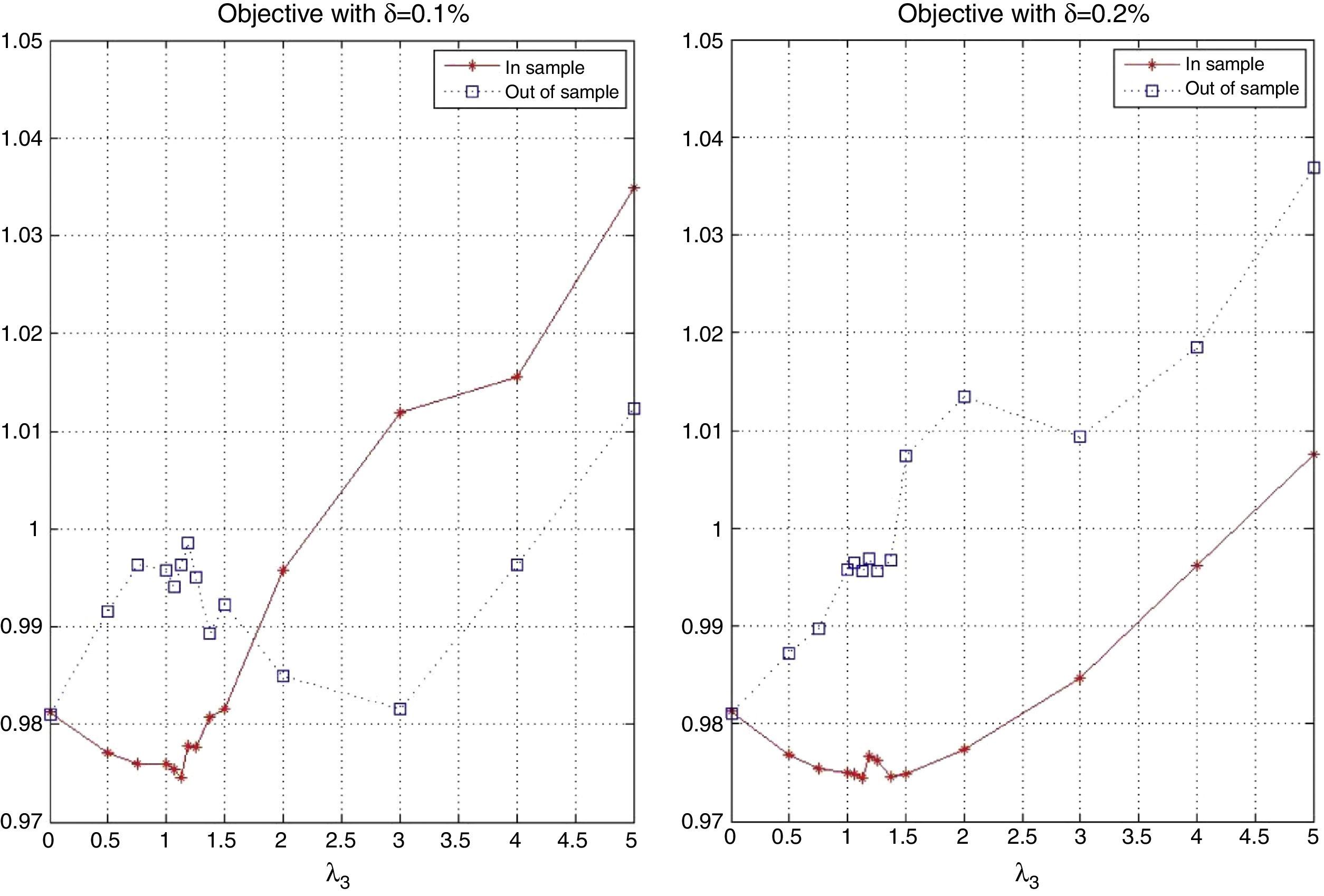
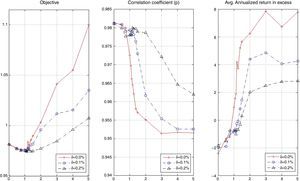
First, we compare the in-sample and out-of-sample objectives. The information is summarized in Fig. 14, which includes four plots, each corresponding to a particular value of K (25, 30, 40 or 50). In general, the in-sample and out-of-sample objectives are relatively close. Recall that the objective is the sum of the sample correlation coefficient of returns and λ₃ times the average daily excess return of the tracking portfolio over the index (in percentage). Notice that for values of λ₃ approximately less than 1.5, we observe that both performances are similar. This suggests that the tracking performance is more robust than the enhancement performance, i.e., high market capitalization and moderate values of alpha and beta deviation generate robust portfolio policies. On the other hand, for higher values of λ₃, the in-sample performance is generally better out-of-sample. These facts confirm the intuition that finding a profitable portfolio policy is harder than finding a good tracking-only portfolio policy.

Fig. 14.

In-sample and out-of-sample objective (as a function of λ₃) for different values of K and y = (y^mkt, y^α, y^β).

Own elaboration.

Figs. 15 and 16 contain the in-sample and out-of-sample behavior of the correlation coefficient (ρ) and the standard deviation ratio. In the case of ρ, we can observe that out-of-sample performance improves as K increases, especially for low values of λ₃. Also, as λ₃ increases, the in-sample and out-of-sample results present some significant but reasonable differences. Aggressive portfolio policies tend to lose out-of-sample performance in ρ. With respect to the standard deviation ratios, we observe that, in the out-of-sample period, the constraint on the standard deviations ratio (less than or equal to 1.05) is maintained with the exception of two cases corresponding to very aggressive allocations.

Fig. 15.

In-sample and out-of-sample correlation coefficient (as a function of λ₃) for different values of K and y = (y^mkt, y^α, y^β).

Own elaboration.

Fig. 16.

In-sample and out-of-sample standard deviation ratio (as a function of λ₃) for different values of K and y = (y^mkt, y^α, y^β).

Own elaboration.

Figs. 17 and 18 exhibit the in-sample and out-of-sample performance of the annualized average return and the probability to beat the index. In general, both plots show the same pattern. We can clearly observe that the robustness in these variables is relatively low compared with the robustness of the tracking variables (correlation and standard deviation ratio). However, an important aspect is that the in-sample trend is captured in the out-of-sample period for high values of λ₃ (more than 2). Fig. 19 is related to the beta of the tracking portfolios. We generally observe similar in-sample and out-of-sample performance of β for low values of λ₃. For other values of λ₃, we observe a reduction of β to a level of approximately 0.95. This reduction is expected since the values of ρ have been reduced while maintaining a very stable ratio of standard deviations.

Fig. 17.

In-sample and out-of-sample average annualized return for different (as a function of λ₃) values of K and y = (y^mkt, y^α, y^β).

Own elaboration.

Fig. 18.

In-sample and out-of-sample probability of beating the index (as a function of λ₃) for different values of K and y = (y^mkt, y^α, y^β).

Own elaboration.

Fig. 19.

In-sample and out-of-sample beta (as a function of λ₃) for different values of K and y = (y^mkt, y^α, y^β).

Own elaboration.

In general, in the out-of-sample period, stocks with high market capitalization had good performance. This fact generated a positive effect for policies that relied mostly on large values of y^mkt and low vales of the other characteristics; in general, this occurs for low values of λ₃. This excessive dependence can be avoided with the selection of λ₃ to produce more diversified portfolios in terms of characteristics. Moreover, notice that the higher market capitalization performance mostly affected the excess returns, the probability of beating the index, and alpha, i.e., the out-performance variables. The correlation coefficient, ratio of standard deviation, and beta were robust out of sample.

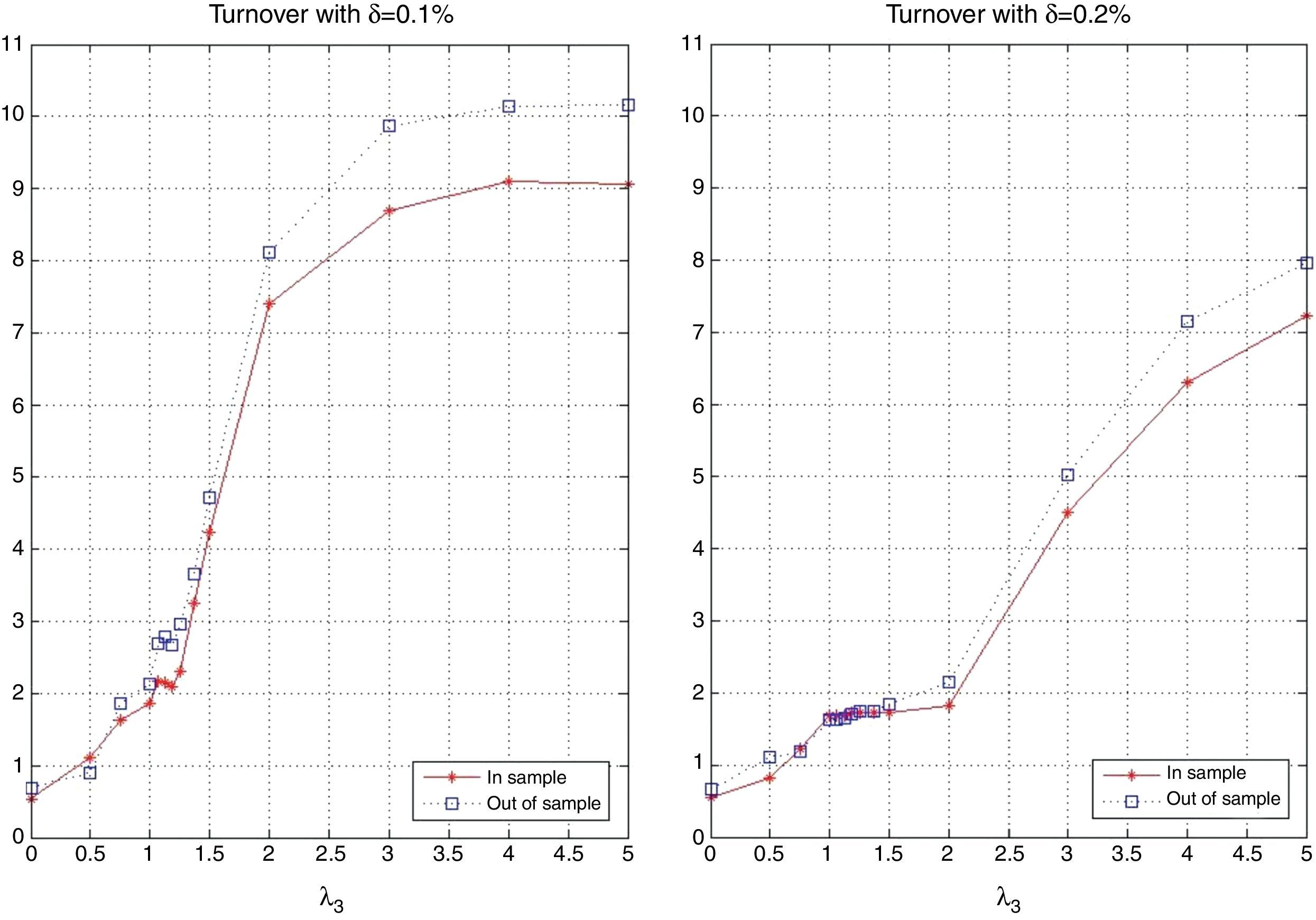
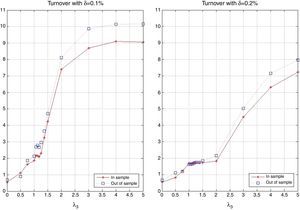
Recall that in this application, we are implicitly considering daily rebalancing to the “new” optimal portfolio weights. The in-sample and out-of-sample average turnover is shown in Fig. 20. We can observe that both turnovers are similar; but, the turnover of the in-sample period tends to be smaller than that of the out-of-sample period, especially for high values of λ₃. The turnover increases with λ₃ since more aggressive portfolio policies generally involve high turnover. For small values of λ₃, our tracking portfolio is mostly composed with large-cap stocks. Since market capitalization is a stable characteristic, its behavior in the cross-section is generally maintained through time. Therefore, the turnover of such portfolio policies tends to be low. Contrarily, alpha and beta deviation are less stable in time and consequently in the cross-section, producing high levels of turnover. In general, low levels of turnover correspond to including stocks with stable characteristics over time.

Fig. 20.

In-sample and out-of-sample average turnover (as a function of λ₃) for different values of K and y = (y^mkt, y^α, y^β).

Own elaboration.

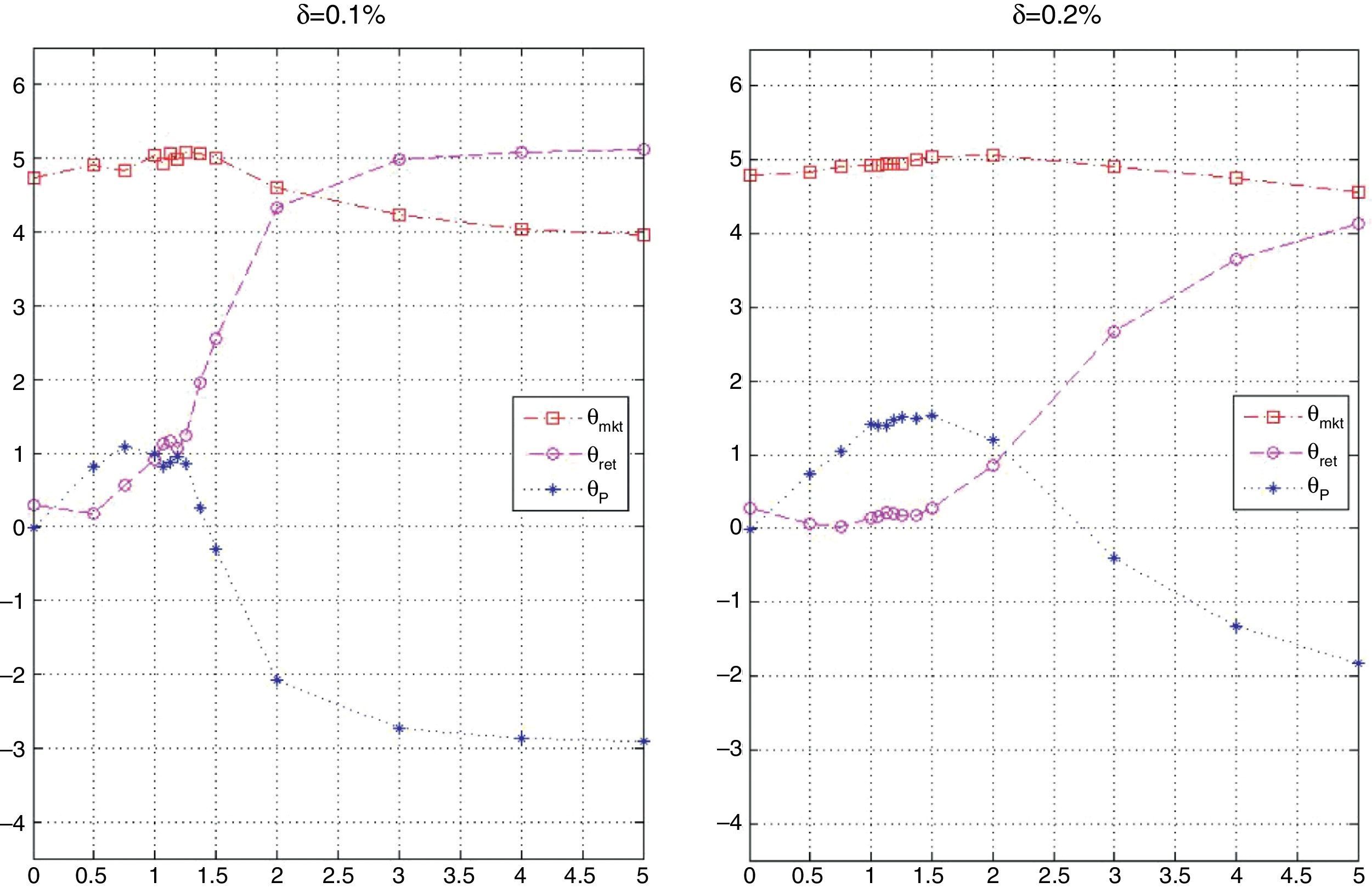
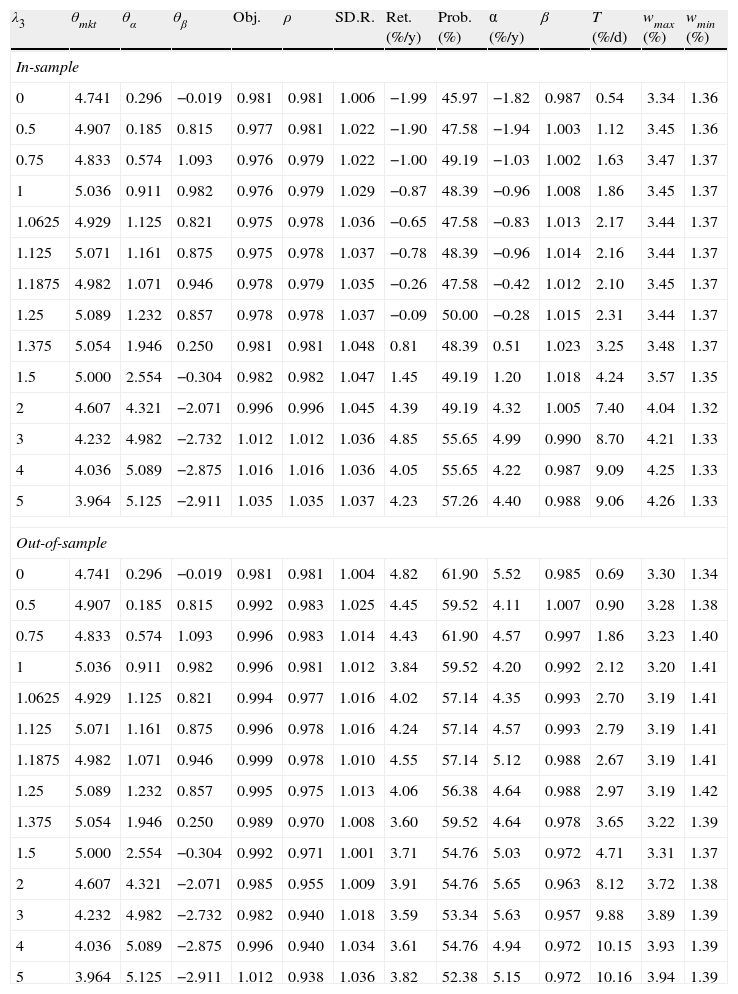
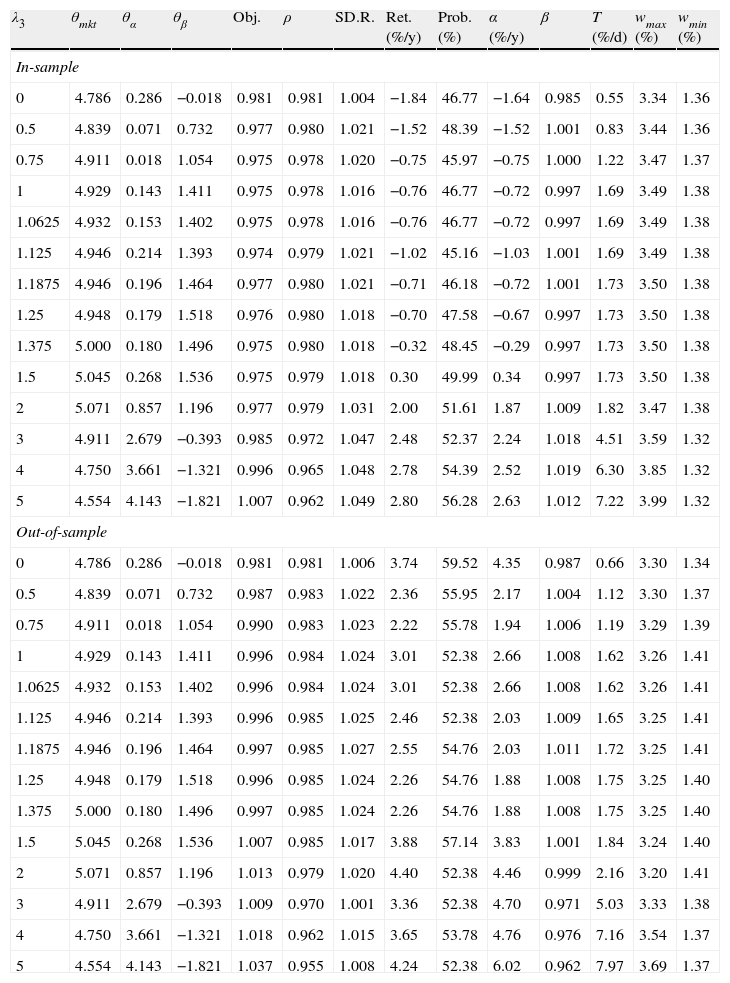
7.4

Transaction costs

In this section, we implement the parametric approach including transaction costs. We only consider the full rebalancing strategy described in Section 5.2. We assume equal transaction costs for all assets and dates, i.e., δ_i,t = δ for all i and t. Considering the parameters for transaction costs in Brandt et al. (2009), Canakgoz and Beasley (2008) and Gaivoronski et al. (2005), we consider two cases: δ = 0.1% and δ = 0.2% (notice that the case without the inclusion of transaction costs corresponds to having δ = 0.0%). First, we study the in-sample behavior of the optimal characteristics and the other variables as a function of δ then, we analyze and compare the in-sample and out-of-sample performance of the tracking portfolios. Since the results obtained are similar for the values of K considered in the previous section, we restrict the results by considering only the case of K = 50. The numerical results are contained in Tables 5 and 6.

Table 5.

Results in-sample and out-of-sample for λ1=1   with   δ=0.1%   and   K=50.

λ3	θmkt	θα	θβ	Obj.	ρ	SD.R.	Ret. (%/y)	Prob. (%)	α (%/y)	β	T (%/d)	wmax (%)	wmin (%)
In-sample
0	4.741	0.296	−0.019	0.981	0.981	1.006	−1.99	45.97	−1.82	0.987	0.54	3.34	1.36
0.5	4.907	0.185	0.815	0.977	0.981	1.022	−1.90	47.58	−1.94	1.003	1.12	3.45	1.36
0.75	4.833	0.574	1.093	0.976	0.979	1.022	−1.00	49.19	−1.03	1.002	1.63	3.47	1.37
1	5.036	0.911	0.982	0.976	0.979	1.029	−0.87	48.39	−0.96	1.008	1.86	3.45	1.37
1.0625	4.929	1.125	0.821	0.975	0.978	1.036	−0.65	47.58	−0.83	1.013	2.17	3.44	1.37
1.125	5.071	1.161	0.875	0.975	0.978	1.037	−0.78	48.39	−0.96	1.014	2.16	3.44	1.37
1.1875	4.982	1.071	0.946	0.978	0.979	1.035	−0.26	47.58	−0.42	1.012	2.10	3.45	1.37
1.25	5.089	1.232	0.857	0.978	0.978	1.037	−0.09	50.00	−0.28	1.015	2.31	3.44	1.37
1.375	5.054	1.946	0.250	0.981	0.981	1.048	0.81	48.39	0.51	1.023	3.25	3.48	1.37
1.5	5.000	2.554	−0.304	0.982	0.982	1.047	1.45	49.19	1.20	1.018	4.24	3.57	1.35
2	4.607	4.321	−2.071	0.996	0.996	1.045	4.39	49.19	4.32	1.005	7.40	4.04	1.32
3	4.232	4.982	−2.732	1.012	1.012	1.036	4.85	55.65	4.99	0.990	8.70	4.21	1.33
4	4.036	5.089	−2.875	1.016	1.016	1.036	4.05	55.65	4.22	0.987	9.09	4.25	1.33
5	3.964	5.125	−2.911	1.035	1.035	1.037	4.23	57.26	4.40	0.988	9.06	4.26	1.33
Out-of-sample
0	4.741	0.296	−0.019	0.981	0.981	1.004	4.82	61.90	5.52	0.985	0.69	3.30	1.34
0.5	4.907	0.185	0.815	0.992	0.983	1.025	4.45	59.52	4.11	1.007	0.90	3.28	1.38
0.75	4.833	0.574	1.093	0.996	0.983	1.014	4.43	61.90	4.57	0.997	1.86	3.23	1.40
1	5.036	0.911	0.982	0.996	0.981	1.012	3.84	59.52	4.20	0.992	2.12	3.20	1.41
1.0625	4.929	1.125	0.821	0.994	0.977	1.016	4.02	57.14	4.35	0.993	2.70	3.19	1.41
1.125	5.071	1.161	0.875	0.996	0.978	1.016	4.24	57.14	4.57	0.993	2.79	3.19	1.41
1.1875	4.982	1.071	0.946	0.999	0.978	1.010	4.55	57.14	5.12	0.988	2.67	3.19	1.41
1.25	5.089	1.232	0.857	0.995	0.975	1.013	4.06	56.38	4.64	0.988	2.97	3.19	1.42
1.375	5.054	1.946	0.250	0.989	0.970	1.008	3.60	59.52	4.64	0.978	3.65	3.22	1.39
1.5	5.000	2.554	−0.304	0.992	0.971	1.001	3.71	54.76	5.03	0.972	4.71	3.31	1.37
2	4.607	4.321	−2.071	0.985	0.955	1.009	3.91	54.76	5.65	0.963	8.12	3.72	1.38
3	4.232	4.982	−2.732	0.982	0.940	1.018	3.59	53.34	5.63	0.957	9.88	3.89	1.39
4	4.036	5.089	−2.875	0.996	0.940	1.034	3.61	54.76	4.94	0.972	10.15	3.93	1.39
5	3.964	5.125	−2.911	1.012	0.938	1.036	3.82	52.38	5.15	0.972	10.16	3.94	1.39

Own elaboration.

Table 6.

Results in-sample and out-of-sample for λ1=1   with   δ=0.2%   and   K=50.

λ3	θmkt	θα	θβ	Obj.	ρ	SD.R.	Ret. (%/y)	Prob. (%)	α (%/y)	β	T (%/d)	wmax (%)	wmin (%)
In-sample
0	4.786	0.286	−0.018	0.981	0.981	1.004	−1.84	46.77	−1.64	0.985	0.55	3.34	1.36
0.5	4.839	0.071	0.732	0.977	0.980	1.021	−1.52	48.39	−1.52	1.001	0.83	3.44	1.36
0.75	4.911	0.018	1.054	0.975	0.978	1.020	−0.75	45.97	−0.75	1.000	1.22	3.47	1.37
1	4.929	0.143	1.411	0.975	0.978	1.016	−0.76	46.77	−0.72	0.997	1.69	3.49	1.38
1.0625	4.932	0.153	1.402	0.975	0.978	1.016	−0.76	46.77	−0.72	0.997	1.69	3.49	1.38
1.125	4.946	0.214	1.393	0.974	0.979	1.021	−1.02	45.16	−1.03	1.001	1.69	3.49	1.38
1.1875	4.946	0.196	1.464	0.977	0.980	1.021	−0.71	46.18	−0.72	1.001	1.73	3.50	1.38
1.25	4.948	0.179	1.518	0.976	0.980	1.018	−0.70	47.58	−0.67	0.997	1.73	3.50	1.38
1.375	5.000	0.180	1.496	0.975	0.980	1.018	−0.32	48.45	−0.29	0.997	1.73	3.50	1.38
1.5	5.045	0.268	1.536	0.975	0.979	1.018	0.30	49.99	0.34	0.997	1.73	3.50	1.38
2	5.071	0.857	1.196	0.977	0.979	1.031	2.00	51.61	1.87	1.009	1.82	3.47	1.38
3	4.911	2.679	−0.393	0.985	0.972	1.047	2.48	52.37	2.24	1.018	4.51	3.59	1.32
4	4.750	3.661	−1.321	0.996	0.965	1.048	2.78	54.39	2.52	1.019	6.30	3.85	1.32
5	4.554	4.143	−1.821	1.007	0.962	1.049	2.80	56.28	2.63	1.012	7.22	3.99	1.32
Out-of-sample
0	4.786	0.286	−0.018	0.981	0.981	1.006	3.74	59.52	4.35	0.987	0.66	3.30	1.34
0.5	4.839	0.071	0.732	0.987	0.983	1.022	2.36	55.95	2.17	1.004	1.12	3.30	1.37
0.75	4.911	0.018	1.054	0.990	0.983	1.023	2.22	55.78	1.94	1.006	1.19	3.29	1.39
1	4.929	0.143	1.411	0.996	0.984	1.024	3.01	52.38	2.66	1.008	1.62	3.26	1.41
1.0625	4.932	0.153	1.402	0.996	0.984	1.024	3.01	52.38	2.66	1.008	1.62	3.26	1.41
1.125	4.946	0.214	1.393	0.996	0.985	1.025	2.46	52.38	2.03	1.009	1.65	3.25	1.41
1.1875	4.946	0.196	1.464	0.997	0.985	1.027	2.55	54.76	2.03	1.011	1.72	3.25	1.41
1.25	4.948	0.179	1.518	0.996	0.985	1.024	2.26	54.76	1.88	1.008	1.75	3.25	1.40
1.375	5.000	0.180	1.496	0.997	0.985	1.024	2.26	54.76	1.88	1.008	1.75	3.25	1.40
1.5	5.045	0.268	1.536	1.007	0.985	1.017	3.88	57.14	3.83	1.001	1.84	3.24	1.40
2	5.071	0.857	1.196	1.013	0.979	1.020	4.40	52.38	4.46	0.999	2.16	3.20	1.41
3	4.911	2.679	−0.393	1.009	0.970	1.001	3.36	52.38	4.70	0.971	5.03	3.33	1.38
4	4.750	3.661	−1.321	1.018	0.962	1.015	3.65	53.78	4.76	0.976	7.16	3.54	1.37
5	4.554	4.143	−1.821	1.037	0.955	1.008	4.24	52.38	6.02	0.962	7.97	3.69	1.37

Own elaboration.

7.4.1

In-sample performance with transaction costs

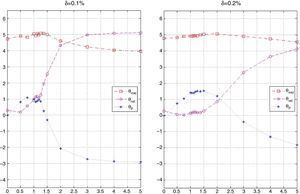
Fig. 21 is analogous to Fig. 7 but for different values of δ (in particular δ = 0.1% and δ = 0.2%). We observe a similar pattern in all the plots, with the difference that the λ₃ for which θ_α and θ_β start to become more significant (values generally greater than 1) is an increasing function of δ Therefore, the presence of transaction costs makes the strategy of holding high market capitalization stocks more dominant since that policy generates low turnover. To clarify this point further, Fig. 22 shows the optimal values of θ_mkt, θ_α and θ_β obtained with different values of δ as a function of λ₃. We can observe from the left plot that, in general, as δ increases, θ_mkt also increases. From the central plot, we can observe a similar behavior for θ_α (increasing as λ₃ increases) but the aggressiveness of the positions in θ_α decreases in δ. In the case of θ_β, we again observe similar patterns, with the difference that for moderate values of λ₃ the strategies become more dependent on stocks with positive θ_β(selecting stocks with beta moderately different than 1) to achieve a certain level of return due to the lower turnover generated by θ_β(compared with θ_α). For high values of λ₃ and as δ increases, the strategy become less dependent on including stocks with beta close to 1 (small θ_β) since the position in θ_α is not as aggressive as in the case of zero transaction costs.

Fig. 21.

Optimal coefficients (θ_mkt, θ_α, θ_β) as a function of λ₃ with λ₁ = 1 and K = 50 for δ = 0.1% (left) and δ = 0.2% (right).

Own elaboration.

Fig. 22.

Optimal coefficients (θ_mkt, θ_α, θ_β) as a function of λ₃ and δ with λ₁ = 1 and K = 50.

Own elaboration.

Fig. 23 shows the in-sample behavior of the objective, ρ, and the average annualized return as a function of λ₃ and δ. The main observation to notice is that for δ = 0.2% the maximization of the objective is achieved mostly by the maximization of ρ, which is considerably larger (for λ₃ greater than 1) than in the cases of δ = 0.0% and δ = 0.1%. Fig. 24 presents the same information but for the ratio of standard deviations, beta, and average turnover. We observe that the ratio is consistently greater than one but the beta of the portfolio moves approximately between 0.985 and 1.02. Notice that for low values of λ₃, the portfolio beta for δ = 0.2% fluctuates around one due to the stability of the ratio of standard deviations. In general, the riskiness of the portfolios is compensated by the decrease in ρ to obtain portfolios with beta close to one. We can observe that because of transactions costs, the portfolios incur less turnovers. The average turnover for δ = 0.2% (especially for medium to large values of λ₃) is significantly lower than that of δ = 0.0% and δ = 0.1%.

Fig. 23.

In-sample objective, correlation coefficient and average annualized return as a function of λ₃ and δ with λ₁ = 1 and K = 50.

Own elaboration.

Fig. 24.

In-sample ratio of standard deviations, beta and average turnover as a function of λ₃ and δ with λ₁ = 1 and K = 50.

Own elaboration.

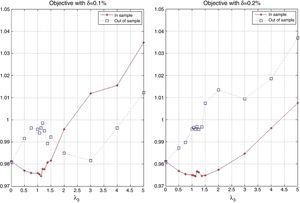
Finally, notice that the portfolios with close to zero excess return over the index were obtained for λ₃ between 1.25 and 1.375 for δ = 0.1% and between 1.375 and 1.5 for δ = 0.2%. For the case of zero transaction costs, the range of λ₃ was between 0.75 and 1. More transaction costs then imply giving more weight to out-performance in the objective to find a tracking portfolio with excess return close to zero.

7.4.2

Out-of-sample performance with transaction costs

In-sample and out-of-sample profiles for δ = 0.1% and δ = 0.2% corresponding to the optimal objective function value are relatively different as shown in Fig. 25. This difference can be explained by the performance of the correlation coefficient and the excess return over the index that can be seen in Figs. 26 and 27, respectively. Remember that in the case of no transaction costs the tracking component was more robust than the enhanced component. In the presence of transaction costs, we observe the same behavior; therefore, the good out-of-sample performance for δ = 0.2% is justified mostly by its reliance on the correlation coefficient (having greater values of ρ compared with the other cases). In the case of the excess returns, good performance for low values of λ₃ can be explained by the excellent returns obtained by the stocks with higher market capitalization during the testing period, which cannot be generalized for other periods.

Fig. 25.

In-sample and out-of-sample objective (as a function of λ₃) for δ = 0.1% (left), δ = 0.2% (right), λ₁ = 1 and K = 50.

Own elaboration.

Fig. 26.

In-sample and out-of-sample correlation coefficient (as a function of λ₃) for δ = 0.1% (left), δ = 0.2% (right), λ₁ = 1 and K = 50.

Own elaboration.

Fig. 27.

In-sample and out-of-sample average annualized excess return (as a function of λ₃) for δ = 0.1% (left), δ = 0.2% (right), λ₁ = 1and K = 50.

Own elaboration.

From Tables 5 and 6, we can observe that out-of-sample values for the ratio of standard deviations are well below the 1.05 limit. Consequently, the variance of the tracking portfolios (relative to the one of the index) is preserved during the testing period even in the case of aggressive allocations in θ_α. Moreover, Fig. 28 shows the in-sample and out-of-sample betas that are maintained in the range 0.96–1.02. Notice that the tendency out-of-sample is to produce values of beta slightly smaller than one due to the presence of stocks with higher y^mkt. The turnover of the portfolios almost presents no difference in-sample and out-of-sample, which is important since it is closely related to the stability of the characteristics over time. The aforementioned fact is shown in Fig. 29. Finally, the average maximum and minimum portfolio weights remain stable, avoiding increasing aggressive allocations with the increment of λ₃.

Fig. 28.

In-sample and out-of-sample beta (as a function of λ₃) for δ = 01% (left), δ = 0.2% (right), λ₁ = 1 and K = 50.

Own elaboration.

Fig. 29.

In-sample and out-of-sample average turnover (as a function of λ₃) for δ = 0.1% (left), δ = 0.2% (right), λ₁ = 1 and K = 50.

Own elaboration.

8

Conclusions and final remarks

We have developed a parametric approach for index tracking and enhanced indexation that has advantages over existing models. First, the parametric model optimizes over stock's characteristics (that can be seen as strategies) and not over portfolio weights. The portfolio weights are the result of the chosen strategy, giving a qualitative idea of the portfolio composition. Second, this approach reduces the dimensionality of the optimization problem compared with mixed-integer programming methods. Nonetheless, a low-dimensional, unconstrained non-linear optimization problem needs to be solved. Third, the proposed objective function summarizes typical objective functions in the index tracking and enhanced indexation literature.

By maximizing an objective including the correlation coefficient (between the portfolio and the index) minus the ratio of standard deviations (portfolio with respect to the index) plus an out-performance measure (typically the excess return of the portfolio over the index), we can control the importance given to the tracking objective (correlation plus standard deviation) and the enhanced objective. By design, the tracking portfolios under the parametric approach try to achieve a beta of one with respect to the index and to minimize the variance of the tracking error simultaneously. Other models consider only one of these variables, leaving the other free. Also, our objective correctly separates the tracking objective from the enhanced component, giving more freedom to the modeler to decide on particular weights given to each part of the objective.

The selection of appropriate stock characteristics in the parametric model is a delicate issue. We have proposed the use of similarity measures of the stocks with the index as characteristics, plus others that explain the cross section of asset returns. Although we did not evaluate all possible characteristics to use, market capitalization, alpha and beta produced in-sample and out-of-sample results that are in line with economic intuition. Holding stocks with high market capitalization resulted in constructing portfolios with high correlation coefficient with an index that is cap-weighted as is the S&P500. Alpha, on the other hand, was used to obtain higher levels of excess returns over the index, while stocks with beta close to one were useful to keep the ratio of standard deviations close to one.

The out-of-sample performance showed that the correlation coefficient and the ratio of standard deviations have a robust behavior, i.e., the in-sample and out-of-sample performances were very close to each other. However, the out-performance part was less robust. This fact is expected since many empirical studies have shown that forecasting the correlation and standard deviations is more accurate than forecasting expected returns. However, we were able to capture some out-of-sample momentum with the inclusion of alpha as a characteristic. Additionally, our results showed that the only way to extract more excess returns while keeping the standard deviations close to each other is by a reduction in the correlation coefficient with the index. Also, more aggressive strategies (in the sense of trying to achieve greater excess returns over the index) involve higher levels of turnover since the cross sectional behavior of the characteristics that collaborate with the out-performance component are more volatile than those involved in tracking-only purposes.

The main problem of our approach (with the set of characteristics and the particular example we have chosen) is that the tracking-only strategies rely very strongly on positions in stocks with high market capitalization (relative to the others in the index). Therefore, the portfolio is exposed to the performance of this particular group of stocks. In some cases, that strategy can be profitable (as in our case) and in other cases not. It is then recommended to choose strategies that mix different types of assets to avoid excessive exposure to a particular sector or group of stocks. This can be controlled by the trade-off parameters in the objective function or by including more characteristics.

Finally, we mention additional research that can be done with respect to the parametric model for index tracking and enhanced indexation. For example, the implementation of the more sophisticated transaction costs policies described in the paper, the analysis of performance of the parametric model under other choices of characteristics, trading frequencies, time horizons and indices (e.g., it could be of interest to see if market capitalization continues to be important to track other types of indices that are not market-cap weighted), the use of multiple disjoint in-sample (calibration) and out-of-sample periods, and the elaboration of an empirical comparison of the parametric approach with other widely recognized models in the literature.

Acknowledgment

We thank Jeremy Staum for his valuable comments and suggestions.